Abstract
The Rashba effect has recently attracted great attention owing to emerging physical properties associated with it. The interplay between the Rashba effect and the Zeeman effect, being produced by the exchange field, is expected to broaden the range of these properties and even result in novel phenomena. Here we predict an insulator-to-conductor transition driven by the Rashba–Zeeman effect. We first illustrate this effect using a general Hamiltonian model and show that the insulator-to-conductor transition can be triggered under certain Rashba and exchange-field strengths. Then, we exemplify this phenomenon by considering an Ag2Te/Cr2O3 heterostructure, where the electronic structure of the Ag2Te monolayer is affected across the interface by the proximity effect of the Cr2O3 antiferromagnetic layer with well-defined surface magnetization. Based on first-principles calculations, we predict that such a system can be driven into either insulating or conducting phase, depending on the surface magnetization orientation of the Cr2O3 layer. Our results enrich the Rashba–Zeeman physics and provide useful guidelines for the realization of the insulator-to-conductor transition, which may be interesting for experimental verification.
Similar content being viewed by others
Introduction
The Rashba effect is a momentum-dependent spin splitting of the energy bands driven by spin-orbit coupling (SOC)1. This phenomenon has recently stimulated vigorous research, owing to its potential application in spintronics2. The Rashba effect occurs in material systems with broken space-inversion symmetry such as surfaces3, interfaces4, and certain bulk materials5,6,7. The SOC effect allows an electrical control of the spin degree of freedom that is interesting for device applications. For example, using the Rashba effect has been proposed for design of a spin field-effect transistor8. Electrically switchable SOC parameter has been explored to design valley-spin valves9 and valley-spin logic gates10. Furthermore, various physical phenomena such as current-induced spin polarization11, the spin Hall effect12, and the spin galvanic effect13,14 have been inspired or reinvigorated.
The Rashba-affected material systems may also exhibit a Zeeman effect. The Zeeman effect is characterized by the momentum-independent spin splitting of the energy bands and is associated with the interaction of spin with an external magnetic field or an exchange field. The Zeeman energy is typically ~0.1 meV/T and therefore is relatively small for applied external fields of a few Tesla or less. In contrast, the internal exchange fields arising from intrinsic magnetization15, doped magnetic transition metals16 or ferromagnetic (FM)17, antiferromagnetic (AFM)18, and multiferroic19 insulator substrates owing to magnetic proximity effects20 can be sizable (~102–103 T) and hence produce a non-negligible Zeeman splitting of the energy bands.
The interplay between the Rashba and Zeeman effects (abbreviated below as the Rashba–Zeeman effect) is expected to produce novel features not found in pure Rashba- or Zeeman-affected systems. For example, broken time-reversal symmetry owing to the exchange field gives rise to the anomalous Hall effect21. In addition, magnetically doped Rashba systems demonstrate entanglement of the spin-orbit and magnetic orders. For example, the recent experimental work on Mn-doped GeTe has demonstrated that the Rashba spin helicity can be altered by magnetization switching22, and conversely, the magnetization can be reversed by polarization switching23 or by the current-induced spin-orbit torque24. Moreover, the Rashba–Zeeman effect can also affect the quantum transport properties. For example, it has been demonstrated that in quantum-point-contact InSb nanowires with sizable Rashba SOC, the measured conductance plateau could be tuned from e2/h to 2e2/h by the magnetic field orientation25.
In this work, we predict another striking phenomenon—an insulator-to-conductor transition induced by the Rashba–Zeeman effect in a two-dimensional (2D) system. The band structure of the 2D material can be controlled by the exchange field orientation, and under certain Rashba and exchange field strengths exhibits an insulator-to-conductor transition. We explore this phenomenon for a realistic system—a monolayer of Ag2Te deposited on an AFM Cr2O3 (0001) substrate. Owing to broken inversion symmetry, an Ag2Te monolayer exhibits a sizable Rashba band splitting, while the Cr2O3 substrate has a robust surface magnetization coupled to the AFM order parameter and provides an exchange field affecting the electronic structure of the Ag2Te through the proximity effect. Based on density-functional theory (DFT) calculations, we demonstrate that such a system can be driven into either insulating or conducting phase, depending on the boundary magnetization orientation of the Cr2O3 layer.
Results and discussion
Hamiltonian model and phase diagram
We first illustrate the insulator-to-conductor transition using a general Hamiltonian model. We consider a 2D direct band-gap semiconductor with the Rashba effect dominating at the band edges, affected by the exchange field arising from a magnetic insulator substrate (Fig. 1a). A single-band k·p Hamiltonian of this system can be written as follows:
Here, indices c and v indicate the bottom of the conduction band and the top of the valence band, respectively. The first term represents the kinetic energy with mc,v being the electron effective mass, Ec,v is the band edge energy, the third term is the Rashba SOC with αc,v being the Rashba parameters. The last term is the Zeeman term, where σ is the Pauli spin matrix, Δ is the exchange field, and the unit vector \({\hat{\mathbf m}}\) denotes the field orientation.
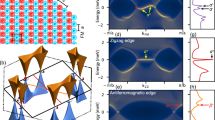
a Schematic illustration of the Rashba 2D system on top of a magnetic insulator. Red arrows denote the exchange field whose orientation is determined by the unit vector \({\hat{\mathbf m}} = \left( {sin\theta cos\varphi ,sin\theta sin\varphi ,cos\theta } \right)\) in spherical coordinates. b 3D plot of the calculated band structure with \({\hat{\mathbf m}}\) being parallel to z axis \({\hat{\mathbf m}}||{\hat{\mathbf z}}\) or y axis \({\hat{\mathbf m}}||{\hat{\mathbf y}}\) for mc = –mv = 0.5 m0, αc = αv = 1.0 eV Å, E0 = 0.1 eV, Δ = 0.03 eV. c, d Phase diagram in the (E0, Δ) plane for αc = αv = 1.0 eV Å. c and in the (E0, α) plane for α = αc = αv and Δ = 0.01 eV d. The phase boundaries are determined by Egz = 0 or Egy = 0. The red star in c indicates a set of parameters corresponding to the band structure in b.
This model realistically describes certain types of 2D materials deposited on a magnetic insulator substrate. Specifically, there exist a handful of 2D direct band-gap semiconductors, such as Ag2Te26, BiSb27, and LiAlTe228 monolayers whose electronic structure around the conduction band minimum and the valence band maximum can be well described by the single-band Rashba model. When these monolayers are deposited on a proper magnetic insulator substrate, their electronic structure is expected to be well captured by Eq. (1) provided that the effect of the substrate is dominated by the exchange field. The latter requirement entails a weak electronic hybridization between the 2D material and the substrate, which is expected to be valid for a sufficiently wide band-gap insulator.
Figure 1b shows the calculated electronic structure based on Hamiltonian (1) for typical parameters corresponding to the model. It is seen that the energy spectrum represents four bands (two conduction bands and two valence bands) whose appearance depends on the exchange field orientation. For the exchange field parallel to the z axis (\({\hat{\mathbf m}}||{\hat{\mathbf z}}\)), the band gap is opened, whereas for the exchange field parallel to the y axis (\({\hat{\mathbf m}}||{\hat{\mathbf y}}\)), the band gap is closed. Thus, by controlling the magnetization direction of the substrate it is possible to achieve a phase transition in the 2D system from the insulating state to the conducting state.
To elucidate this phase transition in more detail, we derive an analytic expression for the band gap. For \({\hat{\mathbf m}}||{\hat{\mathbf z}}\), the band gap Egz is given by (see Supplementary Note 1)
where E0 = Ec − Ev is the band gap in the absence of the Rashba–Zeeman effect. For \({\hat{\mathbf m}}||{\hat{\mathbf y}}\) (or \({\hat{\mathbf m}}||{\hat{\mathbf x}}\)), the band gap Egy (or Egx) reads
Note that in Eqs. (2) and (3), the negative sign of the band gap implies band inversion and thus no band gap.
Using Eqs. (2) and (3), we obtain the band gaps Egz and Egy depending on parameters of the model. Figure 1c, d shows the resulting phase diagrams in the (E0, Δ) and (E0, α) planes, respectively. It is seen that there are three distinctly different phases I, II, and III classified according to the sign of the band gaps Egz and Egy. The two-phase boundaries (shown by black lines in Fig. 1c, d) are determined by Egz = 0 or Egy = 0. For phases I and III, both band gaps are positive (phase I) or negative (phase III), indicating the trivial phase transition from insulator-to-insulator (phase I) or from conductor to conductor (phase III). For phase II, we observe a nontrivial insulator-to-conductor transition or via versa as a result of changing the exchange field orientation from the z axis to the y(x) axis. The illustration of this transition is revealed in the band structure of Fig. 1b, which corresponds to a set of parameters indicated by the red star in Fig. 1c.
It is evident that there is a certain range of parameters for which the insulator-to-conductor transition occurs. A smaller E0 always yields the conductor phase, whereas larger E0 requires the strong exchange field to induce the insulator-to-conductor transition. A larger Rashba parameter favors the transition for the system with larger E0. Supplementary Figure 2 shows that the insulator-to-conductor transition is not only limited by equal Rashba parameters αc and αv and effective masses mc and mv but can also occur for non-equal parameters (see Supplementary Note 2).
Electrical conductivity and anomalous Hall conductivity
The predicted insulator-to-conductor transition can be probed by measuring electrical conductivity. We calculate the conductivity σxx of the 2D system within the approximation of a constant relaxation time τ, as discussed in Supplemental Note 3. Figure 2a shows σxx as a function of Fermi energy EF. In the absence of the exchange field, Δ = 0, σxx for conduction bands can be expressed analytically as follows (see Supplementary Note 3)
where \(E_R = m_c\alpha _c^2{\mathrm{/}}\left( {2\hbar ^2} \right)\) is the Rashba energy and \(\sigma _0 = e^2\tau E_R{\mathrm{/}}\left( {\pi \hbar ^2} \right)\) is the conductivity unit. This limiting case is shown in Fig. 2a by the dashed line. We see distinct energy dependent behaviors below and above the conduction band minimum. When Δ ≠ 0, σxx depends on the exchange field orientation \({\hat{\mathbf m}}\). It is seen that around EF = 0, the conductivity is zero for \({\hat{\mathbf m}}||{\hat{\mathbf z}}\) (red line in Fig. 2a), whereas the conductivity is nonzero for \({\hat{\mathbf m}}||{\hat{\mathbf y}}\) in the whole energy range (blue line in Fig. 2a). For higher Fermi energy, σxx scales linearly with EF, as expected from Eq. (4).
a Longitudinal conductivity σxx (in unit of \(\sigma _0 = e^2\tau E_R/\left( {\pi \hbar ^2} \right)\) as a function of Fermi energy EF for \({\hat{\boldsymbol m}}||{\hat{\boldsymbol z}}\)\(, {\hat{\boldsymbol m}}||{\hat{\boldsymbol y}}\) and zero exchange field Δ = 0. b σxx as a function of θ for EF = 0 and φ = 90°. c Anomalous Hall conductivity σxy as a function of EF for φ = 90° and different θ. d σxy as a function of θ for EF = 0 (magnified five times, blue line) and EF = 0.05 eV (red line) for φ = 90°. b, d the rose and aqua colored regions represent the insulating (I) and conducting (C) phases, respectively. The other parameters are fixed as mc = −mv = 0.5 m0, αc = αv = 1.0 eV Å, E0 = 0.1 eV, Δ = 0.03 eV.
Figure 2b shows σxx as a function of azimuthal angle θ for φ = 90° and EF = 0. The critical points for the insulator-conductor transition are around θ = 0.13π and θ = 0.87π. In the conducting phase (aqua color), σxx versus θ can be well described by \(\sigma _{xx}(\theta ) = \sigma _{xx}(0) + \left[ {\sigma _{xx}\left( {\pi /2} \right) - \sigma _{xx}(0)} \right]sin^2\theta\) (blue solid line), which is the conventional behavior known for anisotropic magnetoresistance29. Overall, changing the magnetization orientation of the substrate reveals perfect anisotropy in the conductivity of the 2D system.
Probing the anomalous Hall conductivity σxy provides another way to explore the phase transition. We calculate σxy assuming that there is only an intrinsic contribution to the anomalous Hall conductivity30. This contribution is determined by the Berry curvature as discussed in the Supplemental Note 4. Figure 2c shows the calculated σxy of the 2D system as a function of EF for different angles θ (determined in Fig. 1a). It is seen that σxy is zero in the energy gap region when \({\hat{\mathbf m}}||{\hat{\mathbf z}}\) (θ = 0° or θ = 180°). For θ = 45° or θ = 135°, the gap is closed and σxy is nonzero in the whole energy range.
Figure 2d shows σxy as a function of θ changing continuously from 0° to 180°. For EF = 0 (blue circles and line in Fig. 2a), we observe the same critical points for the insulator-conductor transition at around θ = 0.13π and θ = 0.87π. This transition disappears for EF = 0.05 eV (red circles and line in Fig. 2d) consistent with Fig. 2c. For any Fermi energy, there is a sign change in σxy at θ = 90°. This sign change is are explained by the properties of the Berry curvature Ωz, as demonstrated in Supplementary Fig. 4.
The above approach can be expanded to other types of SOC, such as the Dresselhaus SOC31 or the Rashba-Dresselhaus SOC32,33. The analysis of the 2D systems, which exhibit these types of SOC shows that a similar insulator-to-conductor transition can be observed in both models (see Supplementary Note 5 for details).
DFT results for Ag2Te/Cr2O3
Next, we discuss a possible realization of the insulator-to-conductor transition in a realistic system, namely a monolayer of Ag2Te deposited on a magnetic Cr2O3 (0001) substrate. A buckled Ag2Te monolayer possesses a 2D hexagonal lattice of the P6mm symmetry and has a sizable band gap of 150 meV26. Owing to broken inversion symmetry, an Ag2Te monolayer exhibits Rashba band splitting with a large Rashba parameter of 3.84 eV Å34 (see Supplementary Note 6 for details). In a non-centrosymmetric corundum structure, Cr2O3 is a magnetoelectric AFM insulator which belongs to the magnetic space group is R\(\bar 3^\prime\)c′. It exhibits the surface magnetization, which is an intrinsic property of all magnetoelectric antiferromagnets35,36. This magnetization is electrically switchable with an AFM order parameter of Cr2O3, as has been demonstrated in experiment37. The exchange coupling between Cr2O3 and Ag2Te across the interface in the Ag2Te/Cr2O3 structure is mediated by the surface magnetization through the proximity effect. The recent work has shown that a topological phase of graphene can be tuned by magnetization orientation in a graphene/Cr2O3 system38.
Figure 3a shows the atomic structure (produced using the VESTA software39) of the Ag2Te/Cr2O3(0001) system consisting of monolayer Ag2Te and Cr2O3 substrate composed of 6 and 12 atomic layers of O and Cr, respectively. The magnetic moments of Cr atoms in Cr2O3 are aligned parallel in the (0001) plane and antiparallel along the (0001) direction. The Cr2O3 surface is terminated by a single layer of Cr, which has the lowest surface energy40. As seen from Fig. 3b, the interface atomic configuration has one Te atom and one Ag atom located at the hollow (H) sites and another Ag atom located at the top (T) site of the Cr2O3 (0001) surface. This atomic configuration is among three possible highly symmetric atomic structures which have the lowest energy (see Supplementary Note 7).
a Atomic structure of monolayer Ag2Te on top of Cr2O3(0001) surface. Gray arrows denote the magnetic moments of Cr atoms. b Top view of the Ag2Te/Cr2O3 structure. H1/H2 and T represent hollow and top sites, respectively. The black lines denote the unit cell, where the primitive vectors are given by \({\boldsymbol{a}}_1 = a{\hat{\boldsymbol x}}\), \({\boldsymbol{a}}_2 = - a{\mathrm{/}}2{\hat{\boldsymbol x}} + \sqrt 3 a{\mathrm{/}}2{\hat{\boldsymbol y}}\). and a is the lattice constant. d The Brillouin zone with high-symmetry k points indicated, where the primitive vectors are given by \({\boldsymbol{b}}_1 = 2\pi {\mathrm{/}}a{\hat{\boldsymbol x + }}2\pi {\mathrm{/(}}\sqrt 3 a{\mathrm{)}}{\hat{\boldsymbol y}},{\boldsymbol{ b}}_2 = 4\pi {\mathrm{/(}}\sqrt 3 a{\mathrm{)}}{\hat{\boldsymbol y}}\).
Figure 4a shows the calculated band structure of Ag2Te/Cr2O3 for magnetization parallel to the z axis. It is noteworthy that the bands near the Fermi energy arise predominantly from the Ag2Te layer, suggesting weak electronic hybridization between Ag2Te and Cr2O3. Orbital-projected band structure indicates that the bands near the Fermi energy are mainly composed of the Ag-s, d and Te-p orbitals (see Supplementary Note 8), consistent with the previous results26,34. A band gap of ~16 meV is observed, and the Zeeman-type spin splitting at the Γ point is 2Δ = 131 meV for the bottom of conduction bands. The Rashba-type SOC of the conduction bands is evident from the in-plane spin texture shown in Fig. 4b, c.
a Layer projected band structure of Ag2Te/Cr2O3(0001) for magnetization parallel to z axis. The red and blue circles denote the projection onto the Cr2O3 and Ag2Te layers, respectively. Inset: spin projected band structure with color quantifying the expectation value of sz component. Spin textures around the Γ point at the bottom two conduction bands denoted by b CB1 and c CB2. The in-plane spin components sx and sy are shown by arrows while the out-of-plane spin component sz is indicated by color.
Next, we investigate the effect of magnetization orientation on the electronic band structure. Figure 5 shows the calculated results. It is seen that for the in-plane magnetization, i.e., when \({\hat{\mathbf m}}||{\hat{\mathbf x}}\) (Fig. 5a) or \({\hat{\mathbf m}}||{\hat{\mathbf y}}\) (Fig. 5b), the band structure reveals a conducting phase characterized by electron and hole pockets crossing the Fermi energy. In contrast, for the out-of-plane magnetization (\({\hat{\mathbf m}}||{\hat{\mathbf z}}\)), a band gap of 16 meV opens and the system is driven into an insulator phase (Fig. 5c). Thus, the Ag2Te/Cr2O3 system can be either a conductor or an insulator depending on the surface magnetization direction of Cr2O3 substrate.
Band structure around the Γ point for magnetization parallel to a, d x axis \(({\hat{\mathbf m}}||{\hat{\mathbf x}}),\) b, e. y axis \(({\hat{\mathbf m}}||{\hat{\mathbf y}})\), c, f. z axis \(({\hat{\mathbf m}}||{\hat{\mathbf z}})\). a–c Band dispersion along certain k paths. d–f 3D plot of the band structures around the Γ point. d, e Fermi contours with the red (blue) line representing the hole (electron) pocket. c Fitting to the conduction band around the Γ point is shown by the red line.
We note that in the above calculations, the polarization of Ag2Te was pointing downward. For polarization pointing upward, the buckling height between Ag and Te layers is suppressed and the bond length between Te and Cr increases, suggesting that the Rashba effect and Zeeman field are both suppressed. The insulator-to-conductor transition does not occur. Also, it is noteworthy that the insulator-to-conductor transition is Cr2O3 thickness independent, as expected from the exchange field arising from the magnetic proximity effect at the interface.
Figure 5d–f show 3D plots of the band structure for different magnetization orientations. The Fermi contours, which are shown in insets of Fig. 5d, e, suggest that the hole pocket is nearly a circle centered around the Γ point (red lines), whereas the electron pocket (blue lines) appears in the ky < 0 (kx > 0) quadrant for \({\hat{\mathbf m}}||{\hat{\mathbf x}}\) (\({\hat{\mathbf m}}||{\hat{\mathbf y}}\)). This behavior can be well explained by the Rashba–Zeeman model proposed earlier. According to Eq. (1), around the conduction band minimum, the dispersion along the ky direction for \({\hat{\mathbf m}}||{\hat{\mathbf x}}\) can be expressed as \(E_c^ - = \hbar ^2k_y^2{\mathrm{/}}2m_c + E_c - \sqrt {\left( {\alpha _ck_y + {\Delta} } \right)^2}\). Here Δ is negative owing to a higher band energy for spin up than for spin down (inset in Fig. 4a). Thus, we have \(E_c^ - \left( {k_y\, <\, 0} \right) < E_c^ - \left( {k_y\, > \,0} \right)\), indicating that the band energy at ky < 0 is lower than that at ky > 0, which yields the band branch at ky < 0 crossing the Fermi energy. The appearance of the electron pocket at kx > 0 for \({\hat{\mathbf m}}||{\hat{\mathbf y}}\) can be explained in the same way. We note that the shapes of the electron pockets are different for \({\hat{\mathbf m}}||{\hat{\mathbf x}}\) and \({\hat{\mathbf m}}||{\hat{\mathbf y}}\) owing to a higher k-order contribution.
Our k·p model can be used to describe the DFT calculated band structure of Ag2Te/Cr2O3. Using Supplementary Eq. (1), we fit the conduction band around the Γ point (red line in Fig. 5c). The fitting yields the following Hamiltonian parameters: mc = 0.5 m0, αc = 1.89 eV Å, Ec = 0.03 eV. According to Supplementary Eqs. (5) and (12), the insulator-to-conductor transition can occur under the condition \(E_c \,<\, {\Delta} + m_c\alpha _c^2{\mathrm{/}}2\hbar ^2\). This condition is indeed satisfied, which is seen by plugging the fitted parameters into the above inequality.
Experimentally, the predicted insulator-to-conductor transition can be observed in the Ag2Te/Cr2O3 (0001) heterostructure where a 180° AFM domain wall is formed in Cr2O3 between two domains with a uniform perpendicular-to-plane Néel vector pointing in opposite directions. In this case, in the domain wall region, the continuous rotation of the surface magnetization in Cr2O3 results in the formation of a conducting phase of Ag2Te, whereas within the domains, Ag2Te remains insulating (semiconducting). Thus, the enhancement of the electrical conductivity is expected in the domain wall region.
It is noteworthy that the predicted insulator-to-conductor transition in Ag2Te/Cr2O3 may only be observed in the low temperature regime owing to the small band gap of ~16 meV (see Supplementary Note 9). Even though, as seen from Supplementary Fig. 10b, a sizable difference in conductivity between \({\hat{\mathbf m}}||{\hat{\mathbf z}}\) and \({\hat{\mathbf m}}||{\hat{\mathbf y}}\) does exist even at room temperature.
In addition to the Ag2Te/Cr2O3 system, there are other potential candidates with different 2D materials and magnetic substrates to explore the insulator-to-conductor transition. For example, the above mentioned BiSb27 and LiAlTe228 monolayers have a smaller band gap and giant Rashba parameters. The magnetic insulator materials can be extended to FM EuO41 and CrI342,43, and ferrimagnetic YIG44. In comparison with AFM Cr2O3, these magnetic insulators have an advantage of controlling their magnetization by an external magnetic field.
Noteworthy is the fact that the predicted insulator-to-conductor transition is different from the conventional metal–insulator transitions driven by structural distortions, magnetic ordering, and electron correlations via Peierls, Mott, and Slater mechanisms45. Within the proposed mechanism, neither the structural distortions nor magnetostructural transitions or electron correlations are essential. The proposed mechanism is also different from the recently predicted insulator-to-conductor transition in van der Waals spin valves46. For the latter, gap closing or opening at the Dirac point is due to a change of the on-site potentials via the Zeeman effect and SOC is absent.
In summary, we have predicted the insulator-to-conductor transition that can be triggered by the exchange field via the Rashba–Zeeman, Dresselhaus-Zeeman or Rashba-Dresselhaus-Zeeman effect in 2D/FM or 2D/AFM systems and demonstrated its possible realization for a realistic Ag2Te/Cr2O3 heterostructure using first-principles calculations. We hope that our work will enrich the Rashba–Zeeman physics and stimulate experimental studies of the predicted phenomenon.
Methods
DFT calculations
Our atomic and electronic structure calculations were performed using the projector-augmented wave method47,48 implemented in the Vienna ab initio simulation package49. An energy cutoff of 400 eV for the plane wave expansion, generalized gradient approximation50 for the exchange and correlation functional with Hubbard-U correction Ueff = 2 eV on Cr-d orbital51 were adopted throughout. A 4 × 4 × 1 k-point grid for Brillouin zone integration was used for structural relaxation and a 10 × 10 × 1 grid was used for self-consistent electronic structure calculations. The optimized in-plane lattice constant of 4.86 Å for Ag2Te was found close to the optimized in-plane lattice constant of 4.97 Å (experimental value 4.95 Å52) for bulk Cr2O3, so that the lattice mismatch was ~2%. We fixed the in-plane lattice constant to be 4.95 Å in all our calculations. The atomic coordinates were fully relaxed in the absence of SOC with the force tolerance of 0.01 V/Å. The DFT-D3 method with Becke–Jonson damping was used to include the van der Waals corrections53. A vacuum region of >20 Å along the z direction was imposed in the supercell calculations.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The related codes are available from the corresponding authors upon reasonable request.
References
Rashba, E. Properties of semiconductors with an extremum loop. 1. Cyclotron and combinational resonance in a magnetic field perpendicular to the plane of the loop. Sov. Phys. Solid State 2, 1109–1122 (1960).
Manchon, A., Koo, H. C., Nitta, J., Frolov, S. M. & Duine, R. A. New perspectives for Rashba spin-orbit coupling. Nat. Mater. 14, 871–882 (2015).
LaShell, S., McDougall, B. A. & Jensen, E. Spin splitting of an Au(111) surface state band observed with angle resolved photoelectron spectroscopy. Phys. Rev. Lett. 77, 3419 (1996).
Caviglia, A. D. et al. Tunable Rashba spin-orbit interaction at oxide interfaces. Phys. Rev. Lett. 104, 126803 (2010).
Ishizaka, K. et al. Giant Rashba-type spin splitting in bulk BiTeI. Nat. Mater. 10, 521–526 (2011).
Di Sante, D., Barone, P., Bertacco, R. & Picozzi, S. Electric control of the giant Rashba effect in bulk GeTe. Adv. Mater. 25, 509–513 (2013).
Tao, L. L. & Wang, J. Strain-tunable ferroelectricity and its control of Rashba effect in KTaO3. J. Appl. Phys. 120, 234101 (2016).
Datta, S. & Das, B. Electronic analog of the electro-optic modulator. Appl. Phys. Lett. 56, 665 (1990).
Tao, L. L. & Tsymbal, E. Y. Two-dimensional spin-valley locking spin valve. Phys. Rev. B 100, 161110(R) (2019).
Tao, L. L., Naeemi, A. & Tsymbal, E. Y. Valley-spin logic gates. Phys. Rev. Appl. 13, 054043 (2020).
Edelstein, V. M. Spin polarization of conduction electrons induced by electric current in two-dimensional asymmetric electron systems. Sol. State Commun. 73, 233 (1990).
Sinova, J. et al. Universal intrinsic spin Hall effect. Phys. Rev. Lett. 92, 126603 (2004).
Ivchenko, E. L. & Pikus, G. E. New photogalvanic effect in gyrotropic crystals. JETP Lett. 27, 604 (1978).
Ganichev, S. D. Spin-galvanic effect and spin orientation by current in non-magnetic semiconductors. Int. J. Mod. Phys. B 22, 113–114 (2008).
Jiang, P., Li, L., Liao, Z., Zhao, Y. X. & Zhong, Z. Spin direction controlled electronic band structure in two dimensional ferromagnetic CrI3. Nano Lett. 18, 3844–3849 (2018).
Cheng, Y., Zhang, Q. & Schwingenschlögl, U. Valley polarization in magnetically doped single-layer transition-metal dichalcogenides. Phys. Rev. B 89, 155429 (2014).
Yang, H. X. et al. Proximity effects induced in graphene by magnetic insulators: first-principles calculations on spin filtering and exchange-splitting gaps. Phys. Rev. Lett. 110, 046603 (2013).
Xu, L. et al. Large valley splitting in monolayer WS2 by proximity coupling to an insulating antiferromagnetic substrate. Phys. Rev. B 97, 041405 (2018).
Ibrahim, F. et al. Unveiling multiferroic proximity effect in graphene. 2D Mater. 7, 015020 (2020).
Žutić, I., Matos-Abiague, A., Scharf, B., Dery, H. & Belashchenko, K. Proximitized materials. Mater. Today 22, 85–107 (2019).
Culcer, D., MacDonald, A. & Niu, Q. Anomalous Hall effect in paramagnetic two-dimensional systems. Phys. Rev. B 68, 045327 (2003).
Krempasky, J. et al. Entanglement and manipulation of the magnetic and spin–orbit order in multiferroic Rashba semiconductors. Nat. Commun. 7, 13071 (2016).
Krempaský, J. et al. Operando imaging of all-electric spin texture manipulation in ferroelectric and multiferroic Rashba semiconductors. Phys. Rev. X 8, 021067 (2018).
Yoshimi, R. et al. Current-driven magnetization switching in ferromagnetic bulk Rashba semiconductor (Ge, Mn)Te. Sci. Adv. 4, 9989 (2018).
Kammhuber, J. et al. Conductance through a helical state in an Indium antimonide nanowire. Nat. Commun. 8, 478 (2017).
Ma, Y., Kou, L., Dai, Y. & Heine, T. Two-dimensional topological insulators in group-11 chalcogenide compounds: M2Te (M = Cu, Ag). Phys. Rev. B 93, 235451 (2016).
Singh, S. & Romero, A. H. Giant tunable Rashba spin splitting in a two-dimensional BiSb monolayer and in BiSb/AlN heterostructures. Phys. Rev. B 95, 165444 (2017).
Liu, Z., Sun, Y., Singh, D. J. & Zhang, L. Switchable out-of-plane polarization in 2D LiAlTe2. Adv. Electron. Mater. 5, 1900089 (2019).
McGuire, T. & Potter, R. Anisotropic magnetoresistance in ferromagnetic 3d alloys. IEEE Trans. Magn. 11, 1018–1038 (1975).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539 (2010).
Tao, L. L., Paudel, T. R., Kovalev, A. A. & Tsymbal, E. Y. Reversible spin texture in ferroelectric HfO2. Phys. Rev. B 95, 245141 (2017).
Stroppa, A. et al. Tunable ferroelectric polarization and its interplay with spin–orbit coupling in tin iodide perovskites. Nat. Commun. 5, 5900 (2014).
Tao, L. L. & Tsymbal, E. Y. Persistent spin texture enforced by symmetry. Nat. Commun. 9, 2763 (2018).
Noor-A-Alam, M., Lee, M., Lee, H. J., Choi, K. & Lee, J. H. Switchable Rashba effect by dipole moment switching in an Ag2Te monolayer. J. Phys. Condens. Matter 30, 385502 (2018).
Andreev, A. F. Macroscopic magnetic fields of antiferromagnets. JETP Lett. 63, 758–762 (1996).
Belashchenko, K. D. Equilibrium magnetization at the boundary of a magnetoelectric antiferromagnet. Phys. Rev. Lett. 105, 147204 (2010).
He, X. et al. Robust isothermal electric control of exchange bias at room temperature. Nat. Mater. 9, 579–585 (2010).
Takenaka, H., Sandhoefner, S., Kovalev, A. A. & Tsymbal, E. Y. Magnetoelectric control of topological phases in graphene. Phys. Rev. B 100, 125156 (2019).
Momma, K. & Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276 (2011).
Wysocki, A. L., Shi, S. & Belashchenko, K. D. Microscopic origin of the structural phase transitions at the Cr2O3 (0001) surface. Phys. Rev. B 86, 165443 (2012).
Lukashev, P. V. et al. Spin filtering with EuO: insight from the complex band structure. Phys. Rev. B 85, 224414 (2012).
Huang, B. et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 546, 270–273 (2017).
Paudel, T. R. & Tsymbal, E. Y. Spin filtering in CrI3 tunnel junctions. ACS Appl. Mater. Int. 11, 15781–15787 (2019).
Cherepanov, V., Kolokolov, I. & Lvov, V. The saga of YIG: Spectra, thermodynamics, interaction and relaxation of magnons in a complex magnons. Phys. Rep. 229, 81–144 (1993).
Imada, M., Fujimori, A. & Tokura, Y. Metal-insulator transitions. Rev. Mod. Phys. 70, 1039 (1998).
Cardoso, C., Soriano, D., García-Martínez, N. A. & Fernández-Rossier, J. Van der Waals spin valves. Phys. Rev. Lett. 121, 067701 (2018).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Íñiguez, J. First-principles approach to lattice-mediated magneto-electric effects. Phys. Rev. Lett. 101, 117201 (2008).
Finger, L. W. & Hazen, R. M. Crystal structure and isothermal compression of Fe2O3, Cr2O3, and V2O3 to 50 kbars. J. Appl. Phys. 51, 5362 (1980).
Grimme, S., Ehrlich, S. & Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comp. Chem. 32, 1456 (2011).
Acknowledgements
This research was supported by the National Science Foundation through the E2CDA program (grant ECCS-1740136) and the Semiconductor Research Corporation (SRC) through the nCORE program. Computations were performed at the University of Nebraska Holland Computing Center.
Author information
Authors and Affiliations
Contributions
L.L.T. and E.Y.T. conceived the project. L.L.T. carried out numerical calculations. Both authors discussed the results and wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tao, L., Tsymbal, E.Y. Insulator-to-conductor transition driven by the Rashba–Zeeman effect. npj Comput Mater 6, 172 (2020). https://doi.org/10.1038/s41524-020-00441-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-020-00441-0