Sample spinning to mitigate polarization artifact and interstitial-vacancy imbalance in ion-beam irradiation

Abstract

Accelerator-based ion-beam irradiation has been widely used to mimic the effects of neutron radiation damage in nuclear reactors. However, ion radiation is most often monodisperse in the incoming ions’ momentum direction, leading to excessive polarization in defect distribution, while the scattering under neutron irradiation is often more isotropic and has less radiation-induced polarization. Mitigation of the excess-polarization as well as the damage non-uniformity artifact might be crucial for making the simulation of neutron radiation by ion-beam radiation more realistic. In this work, a general radiation polarization theory in treating radiation as external polar stimuli is established to understand the natural material responses in different contexts, and the possibility to correct the defect polarization artifact in ion-beam irradiation. Inspired by Magic Angle Spinning in Nuclear Magnetic Resonance, we present a precise sample spinning strategy to reduce the point-defect imbalance effect in ion-beam irradiation. It can be seen that with optimized surface inclination angle and the axis of sample rotation, the vacancy-interstitial population imbalance, as well as the damage profile non-uniformity in a designated region in the target are both reduced. It is estimated that sample spinning frequency on the order of kHz should be sufficient to scramble the ion momentum monodispersity for commonly taken ion fluxes and dose rates, which is experimentally feasible.

Introduction

The degradation of structural materials under neutron irradiation in nuclear reactors has critically limited the safety and economy of nuclear fission and fusion energy¹. The design-life for a nuclear reactor is usually >40 years, thus it is desired that any structural components such as the reactor vessel should be mechanically robust under such long-term radiation exposure². In doing so, the shutdown and maintenance of reactors can be avoided as much as possible. However, verification of whether a material could survive under such extreme environments is difficult, not only because of the long exposure time required but also the limited facilities for performing neutron irradiation experiments. Such an experimental challenge has significantly increased the difficulty of reactor licensing as well as impeded the development of more radiation-tolerant structural materials that could enable better nuclear power plants.

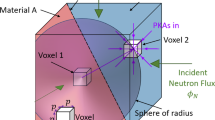
A well-used proxy for neutron radiation is ion-beam irradiation to mimic the effect of neutron irradiation, because heavy ions creates lattice displacements more quickly (~1–100 displacements per atom (DPA) per day) than neutrons (usually ~1 DPA per year in thermal-neutron test reactor). Also, ion-beam irradiation is safer as it rarely activates the material, more controllable, and more economic since accelerators are more affordable than neutron sources of comparable damage intensity^1,3,4. Despite these advantages, accelerator-based ion-beam irradiation differs from reactor conditions in the following aspects^1,3,5,6. First, ion-beam radiation can only penetrate a shallow depth that usually ranges from a few nanometers to tens of microns (depending on the ion energies), thus only a smaller region is irradiated. Testing the mechanical properties of such materials is challenging. Second, ion-beam irradiation might introduce high concentration of impurity atoms into the system. Third, the momentum of neutrons in a reactor is more isotropic (Fig. 1a), whereas that of energetic ions from an accelerator-generated beam is usually highly monodisperse (Fig. 1b), leading to a spatial defect imbalance which is one kind of neutron-atypical effects. The displaced atoms (mainly existing as interstitials) by ion-beam irradiation would leave their vacancy counterparts behind owing to the forward scattering. Addressing all three issues stated above is of critical significance for making accelerator-based test truly representative of reactor conditions.

Fig. 1: Illustration of the momentum distribution for the first-generation energetic ions (Z₁s).

a Momentum distribution is nearly-isotropic in reactor-based damage. b Momentum monodispersity in accelerator-based damage. c A proposed sample spinning strategy to mitigate the momentum monodispersity of ion-beam irradiation.

The first problem can be resolved by performing small-scale mechanical testing⁷. The second one can be ameliorated by adopting self-ion irradiations that do not significantly alter the composition of the target^6,8,9,10, and concurrent multiple-ion-beams injection¹¹ to account for the ions generated by transmutations under neutron irradiation. However, there is a lack of reports about how to solve the third problem practically. The momentum monodispersity (Fig. 1b) in accelerator-based ion-beam irradiation can cause systematic deviation in the defect densities from that of reactor-based neutron radiation (Fig. 1a). In standard fission reactor, neutrons tend to come in from many directions. The first-generation energetic ions, Z₁s, (red sphere in Fig. 1a, which could be charged fission fragments in the case of fission, or elastically scattered native atoms) are created when a neutron scatters off a nucleus or induces fission. The momentum of the first-generation energetic ions has a more isotropic distribution. We use the word “more” isotropic here, knowing that neutron velocities in real reactors also have an angular distribution, depending on where the material is (e.g., near a neutron reflector), but it is definitely far from a delta-function. In contrast, in most accelerator-based ion radiation, the first-generation energetic ion, (red sphere in Fig. 1b), which could be a self-ion, tends to have a fixed energy and momentum every time it hits the material (a delta-functional momentum distribution). Even with multiple beams and/or ion energy combinations^12,13, the distribution of momentum direction in the 4π solid angle is still often a delta-function.

If we draw an analogy between atomic and electronic populations, and consider vacancies as charge “holes”, while interstitials as “electrons”, then Fig. 1b would be similar to how a plasmonic material responds to an externally applied electric field. Generally speaking, a vector response will be elicited with a vector stimuli (electric field or ion radiation) on any material, cf. the linear-response theory of Onsager¹⁴. However, when assessing radiation damage, we frequently consider it to be a scalar quantity (e.g., DPA) that depends on a scalar ion flux or fluence. This might be justified for the idealized case like isotropic neutron flux in 4π solid angle, which tends to cancel out the direct polar response (the local material also needs to satisfy some symmetry condition to not elicit an indirect polar response like radiation-induced segregation near a grain boundary (GB), which will be discussed later), but such assumption clearly does not hold in traditional accelerator-based ion-beam irradiation, which tends to give the most polar response in defect densities (denoted as excess-polarization artifact (EPA) as illustrated in Fig. 1b). The reality of anisotropic neutron flux (e.g., near a neutron reflector) falls somewhere in between. Thus, a general theoretical discussion about the vector or polar natures of radiation damage and radiation stimuli is necessary to understand the natural situation in anisotropic neutron flux, or can be used to correct the EPA in ion-beam tests where the degree of polarization is more extreme.

In this work, we first build a general radiation polarization theory (RPT) to illustrate the vector formulation of material responses to radiation stimuli at both microscopic and macroscopic scales. Inspired by magic angle spinning in nuclear magnetic resonance (MAS-NMR), a sample spinning strategy (SSS) as illustrated in Fig. 1c and Fig. 2a is proposed to mitigate the defect polarization in target material caused by accelerator-based ion momentum monodispersity. We further show that with well-designed surface inclination angle and the axis of sample rotation, a fast-enough rotation of the sample (~kHz) would randomize the ion momentum monodispersity and mitigate the defect imbalance effect in a macroscopic region of target material.

Fig. 2: Illustration of defect imbalance and material’s response to it.

a Illustration of the cancellation of the positive-p(x) region with negative-p(x) region by spinning the sample. The black contours illustrate the region of significant defect concentration generation from SRIM/IM3D MC calculations. b The depth profiles of vacancies, interstitials and I-V net excesses for self-ion irradiation in iron with ion energy of 5 MeV and normal incidence, computed by IM3D. c Illustration of the material’s response with the influence of material anisotropy. The initial mass flow ∆P induced by Z₁ hit at t = t_P may not be same as the final mass flow ∆P_∞ at $t = t_{\mathrm{P}} + \tau$ owing to the sink biases (S1 may attract interstitials, whereas S2 may attract vacancies).

Results

Radiation polarization theory

A pervasive conceptual oversimplification is that radiation damage is a scalar effect, that is, it only depends on a scalar flux or fluence, and ignores the vector characteristics of neutron-scattered ions, fission products radiation, and ion-beam ions. If we consider radiation as an external stimulus in the context of Onsager’s linear-response theory¹⁴, then the general response should call for a vector/tensor formulation, that is no different from how people treat material response in strain, electric or light field. In this subsection, we aim to provide an argument for a vector formulation of material response to radiation, i.e., a “polar” theory from a fundamental defect kinetics perspective. We will first illustrate the microscopic material response to the primary radiation damages (PRDs) by a first-generation energetic ion Z₁. Then, a coarse-graining method is adopted to correlate the macroscopically averaged response of materials with that of microscopic defect polarization by considering the effect of material anisotropy or microstructural sink bias.

When a first-generation energetic ion Z₁ interacts with target, the atomic displacements are likely created right after the hit, and roughly lasting in a timescale of t_P (~femtosecond to 10 picoseconds) until all atoms come to rest^15,16. The spatial distributions of PRDs such as vacancies $c_{\mathrm{V}}^{\mathrm{p}}({\mathbf{x}})$ and interstitials $c_{\mathrm{I}}^{\mathrm{p}}({\mathbf{x}})$ evolve and there is a lot of defect recombination during such period. Here, the $c_{\mathrm{V}}^{\mathrm{p}}({\mathbf{x}})$ and $c_{\mathrm{I}}^{\mathrm{p}}({\mathbf{x}})$, where x is the location (x, y, z) and the superscript “P” stands for “primary radiation damage”, take the unit of # m⁻³ (# is the number of defects), whose interpretation is the ensemble-averaged defect concentration over many ion trajectories per single hit of an energetic Z₁ at the material at x = 0, and far away from other hits. The primary radiation defects $c_{\mathrm{I}}^{\mathrm{p}}({\mathbf{x}})$/$c_{\mathrm{V}}^{\mathrm{p}}({\mathbf{x}})$ in a timescale of t_P can be predicted by Monte Carlo (MC) code SRIM (Stopping and range of ions in matter)^17,18 or IM3D (Irradiation of materials in 3D)¹⁵, which generally specify the starting conditions for modeling future annealing and damage evolutions^1,15,16,19. For simplicity, we have agglomerated di-vacancies and vacancy clusters into $c_{\mathrm{V}}({\mathbf{x}})$, and di-interstitials and interstitial clusters into $c_{\mathrm{I}}({\mathbf{x}})$, with a generalized interpretation of $c_{\mathrm{V}}({\mathbf{x}})$ as characterizing mass-deficient defects, and $c_{\mathrm{I}}({\mathbf{x}})$ as characterizing mass-excess defects in reference to the undamaged crystal, similar to the nomenclature of electron and hole carrier distributions in semiconductors.

Then, the expected interstitial-vacancy (I-V) net excess concentration by the PRDs can be defined as

$$p\left( {\mathbf{x}} \right) \equiv c_{\mathrm{I}}^{\mathrm{P}}\left( {\mathbf{x}} \right) - c_{\mathrm{V}}^{\mathrm{P}}\left( {\mathbf{x}} \right)$$

(1)

Such point-defect imbalance in ion-beam irradiation arises from two aspects, the ion forward scattering effects and the injected interstitials along the ion-projected range^5,6, indicating that the I-V imbalance in target materials is introduced right after the energetic ion hitting. For standard accelerator-based ion-beam irradiation with the beam pointing along the z direction, we could have a large swath (millimeters in x and y, which is the broad ion-beam spot size (σ_i), and microns in z, which is the ion-projected range) of DPA-exposed contiguous region with $\left\langle {p({\mathbf{x}})} \right\rangle\, < \,0$ or $\left\langle {p({\mathbf{x}})} \right\rangle \, > \, 0$, as the “−” and “+” regions shown in Fig. 2a. For example, the depth profiles of PRDs including vacancies and interstitials, estimated from the benchmark calculation of self-ion irradiation in iron with ion energy of 5 MeV and normal incidence, are shown in Fig. 2b. It shows that the contiguous “+” region locates deeper than the “−” region from the depth profile of I-V net excesses (black solid line). More details are provided in Supplementary Note 2.

The center of mass of deficiency and center of mass of excess after a PRD event by the first-generation energetic ion Z₁ can be defined as:

$${\mathbf{x}}_ - \equiv \frac{\displaystyle{{\int} {\;p({\mathbf{x}}){\mathbf{x}} \;{d^3{\mathbf{x}}} } }}{{\displaystyle{\int} {\;p({\mathbf{x}}) \;{d^3{\mathbf{x}}} } }},\;p\left( {\mathbf{x}} \right) \, < \,0$$

(2)

$${\mathbf{x}}_ + \equiv \frac{{\displaystyle{\int} {\;p({\mathbf{x}}){\mathbf{x}} \;{d^3{\mathbf{x}}} } }}{{\displaystyle{\int} {\;p({\mathbf{x}}) \;{d^3{\mathbf{x}}} } }},\;p({\mathbf{x}})\, > \,0$$

(3)

Generally speaking, there will be a finite offset or polarization in defect densities.

$${\mathbf{P}} \equiv {\mathbf{x}}_ + - {\mathbf{x}}_ -$$

(4)

In the framework of radiation polarization, we can think of the momentum distribution p(Z₁) by the hit of the first-generation energetic ion Z₁ as the external stimulus, and ∆P as the material response (mass flow). For single crystal with T_d point-group symmetry or higher, it can be shown that the ∆P generated per Z₁ event should be parallel to p(Z₁) in the linear-response regime. Although reactor-based neutron exposure will also generate such polarization per Z₁ leaf, recall that p(Z₁) is nearly isotopically distributed in 4π solid angle, so the time-average of the polarization vectors owing to PRDs in interior locations of a T_d-and-higher symmetry single crystal, with no microstructural sink biases, should be zero:

$$\left\langle {{\Delta}{\mathbf{P}}} \right\rangle = 0$$

(5)

even though there will be polarization fluctuations generated inside the crystal. In other words, with momentum isotropy, the vacancy (V) clouds and the interstitial (I) clouds generated by multiple energetic ions/fission fragments overlap randomly, giving no spatial preference for any particular kind of cloud (I or V) in the bulk, at least from the PRDs (defect sink biases may cause polarization, which will be discussed later).

But this will not be true for a setup of accelerator-based ion-beam irradiation. Owing to the ion momentum monodispersity (the momentum distribution is a delta-function $\delta( {{\mathbf{p}}( {Z_1}) - {\mathbf{p}}_0})$ as shown in Fig. 1b), a persistent polarization in defect densities will be driven directly by the PRDs. Because $c_{\mathrm{V}}({\mathbf{x}})$ and $c_{\mathrm{I}}({\mathbf{x}})$ are so fundamental to microstructural evolution, a persistent polarization in their distribution by PRDs across a distance of microns (for MeV level ion-beam irradiation) can cause serious artifacts, or neutron-atypical effects, from a fundamental perspective of defect kinetics⁵.

The ensuing microscopic mass flows after a PRD event can also be affected by the detailed arrangements of sink microstructures (sink biases) in materials. After one hit, suppose no more new hits arrive thereafter, the point-defect imbalance pattern p(x) from PRD will gradually evolve, by diffusive annealing to sinks (GBs, dislocations, second phase particles, voids etc.). The sinks themselves may induce local polarizations owing to the sink biases, as possible sink biases shown in Fig. 2c, certain types of sinks (S1, may be dislocation) like to attract interstitials, and certain types of sinks (S2, may be GB) like to attract vacancies. Such inherent sink biases may change or even reverse the initial mass polarization ∆P from Z₁ hit, to ∆P_∞ locally over a characteristic timescale τ. Such regional ∆P_∞ preferences can vary spatially, depending on the detailed arrangement of sink microstructures in materials. For example, it is easy to imagine a low-symmetry crystal (e.g., triclinic) would give a polar response in strain, electric or magnetic polarization, even when exposed to isotropic radiation.

The above-mentioned ∆P (at t = t_P) and ∆P_∞ (at t >> t_P) are the microscopic mass flows inside the materials induced by a single Z₁ hit. Correspondingly, the macroscopic polarization in materials P^macro is related to the spatial coarse-graining of those microscopic mass flows. Two possibilities exist after spatial coarse-graining owing to the difference in material microstructures: (a) there is no discernable preferences in the polarization in any macroscopic direction after any spatial coarse-graining. For example, the three-dimensional (3D) random polycrystals, which are defined as parapolar materials; (b) there is still a discernable preference in the polarization in some macroscopic directions after any spatial coarse-graining owing to the material anisotropy. For example, the layered material such as Cu-Nb bilayer thin films, in which there is clear asymmetry in z even after macroscopic spatial coarse-graining in x, y. Although such strongly textured material geometry may not be as prevalent in nuclear structural materials, for completeness we define them as ferropolar materials.

As radiation exposure is a form of external stimulation, the macroscopic polarization, P^macro, (or the material response) of the material could be parameterized as:

$${\mathbf{P}}^{{\mathrm{macro}}} = \alpha K\left\langle {{\Delta}{\mathbf{P}}} \right\rangle + \beta K{\mathbf{P}}^{{\mathrm{ferro}}}$$

(6)

where K is the radiation dose rate in the unit of DPA per second, P^ferro is a non-zero vector for the ferropolar systems, and α, β are proportionality constants that may be temperature dependent. The first term originates from the PRDs at $t = t_{\mathrm{P}}$ by Z₁ hit, and the second term denotes the relaxational contribution from t_P to $t_{\mathrm{P}} + \tau$ process as described in Fig. 2c, both terms are proportional to the dose rate K. A non-zero macroscopic polarization P^macro means there exists radiation-driven net mass-flow macroscopically inside the material, related to the voiding tendency in target materials (see Supplementary Note 3). The following discussion is related to the possible macroscopic polarization under the radiation stimuli with the influence of material anisotropy.

For a parapolar material medium (β = 0 in Eq. 6) under neutron radiation condition, the time-average of the polarization vectors is zero from the PRDs ($\left\langle {{\Delta}{\mathbf{P}}} \right\rangle = 0$ as illustrated by Eq. 5), so one gets P^macro(x^macro) = 0 uniformly, with the same voiding tendency for all x^macro macroscopically. But with accelerator-based ion surrogate radiation and momentum monodispersity, we will have ${\mathbf{P}}^{{\mathrm{macro}}} = \alpha K\left\langle {{\Delta}{\mathbf{P}}} \right\rangle\, \ne \,0$. This can cause a physical artifact of increasing voiding tendencies in the near-surface region where P^macro points away from (this macroscopically defined region is losing atoms overall, as “−” region shown in Fig. 2a, c), and suppressing voiding tendency in further-away region that P^macro points to (this macroscopically defined region gains atoms overall, as “+” region shown in Fig. 2a, c), for example, which are different from that in neutron radiation with the same dose rate. This would then be considered as a neutron-atypical artifact (see Fig. 1b).

Although for the ferropolar material medium (β ≠ 0 in Eq. 6), even the momentum-isotropic neutron exposure would cause macroscopic polarization, ${\mathbf{P}}^{{\mathrm{macro}}} = \beta K{\mathbf{P}}^{{\mathrm{ferro}}}\, \ne \,0$ because of built-in preference. In this context, the macroscopic polarization is a natural effect and not an artifact. A common example is the radiation-induced segregation, e.g., Cr-depletion in near-GB region in stainless steels induced by isotropic neutron exposure can cause preferential and directional stress corrosion cracking along the Cr-depleted boundary²⁰. With the same reasoning, consider a Cu-Nb bilayer film (macroscopic in x, y) with large-area phase boundaries extended in-plane. Even when exposed to isotropic neutrons, a void sheet may preferentially extend along the Cu-Nb phase boundary macroscopically owing to the preferences to gain interstitials in the Nb layer but trap vacancies inside the phase boundary²¹. Such directional preference of mass flow and neutron damage owing to ${\mathbf{P}}^{{\mathrm{macro}}} = \beta K{\mathbf{P}}^{{\mathrm{ferro}}}$ would still be natural, and is not an artifact.

As discussed above, the corollary of RPT is that any deviation from the ideal-neutronic ${\mathbf{P}}^{{\mathrm{macro}}} = \beta K{\mathbf{P}}^{{\mathrm{ferro}}}$ response at the same dose rate K would be considered as excess polarization. So in the framework of RPT (Eq. 6), there is still need to achieve $\left\langle {{\Delta}{\mathbf{P}}} \right\rangle = 0$ in macroscopic regions (or at least in regions surrounding the region of interest) for ion-beam irradiation. Another way to think about it is that the artificial mass-flow contribution caused by momentum-monodisperse primary radiation can be considered somewhat equivalent to changing the sink bias of a free surface or a phase boundary that extends macroscopically in x, y. Because of this, a scheme to fast-rotate sample is proposed to mitigate possible artifacts (see Fig. 1c and Fig. 2a) in ion-beam irradiation, akin to MAS-NMR²². We will show next that if the surface inclination angle and the axis of sample rotation are designed judiciously in the framework of SSS, then we can cause certain designated macroscopic region R with significantly reduced defect imbalance between $\left\langle {c_{\mathrm{I}}^{\mathrm{P}}\left( {\mathbf{x}} \right)} \right\rangle$ and $\left\langle {c_{\mathrm{V}}^{\mathrm{P}}\left( {\mathbf{x}} \right)} \right\rangle$ (i.e., ∇·P^macro ≈ 0), as Fig. 2a illustrates, even with accelerator-based ion-beam surrogate radiation.

Sample spinning strategy

The SSS framework is designed with a general procedure illustrated in Fig. 3a, to achieve the effective mixing of the ion momentum and reduction of defect imbalance during ion irradiation with monochromatic kinetic energy. The degrees of freedom (DOFs) in SSS are schematically illustrated in the Cartesian coordinate system in Fig. 3b. When the ion-beam b of monochromatic kinetic energy E comes in at an angle θ with respect to the flat surface normal n, we have

$${\mathbf{b}} \cdot \left( { - {\mathbf{n}}} \right) \equiv \left| {\mathrm{b}} \right|{\mathrm{cos}}\theta ,\;\left| {\mathbf{n}} \right| = 1$$

(7)

Thus, the ion momentum is denoted by a vector (E, θ) or (E, cosθ), where θ is the ion momentum direction. The sample is being rotated, so the normal direction is rotating with it,

$${\mathbf{n}}\left( t \right) = {\mathbf{R}}({\mathbf{a}},\;\phi ){\mathbf{n}}_0$$

(8)

where ${\mathbf{n}}_0$ is the initial sample normal direction, ${\mathbf{R}}({\mathbf{a}},\;\phi )$ is rotational matrix along axis a, and $\phi = \omega t$ is the right-handed rotational angle:

$${\mathbf{R}}({\mathbf{a}},\;\phi )^{ - 1} = ({\mathbf{R}}\left( {{\mathbf{a}},\;\phi } \right))^T = {\mathbf{R}}({\mathbf{a}},\; - \phi )$$

(9)

The beam spot that is being irradiated can be the origin of rotation, so it is always on the beam path. Therefore, all the system cares directional cosine of ion beam with respect to the sample during the rotation:

$${\mathrm{cos}}\theta \left( t \right) \equiv - {\mathbf{b}} \cdot {\mathbf{n}}\left( t \right) = - {\mathbf{b}} \cdot {\mathbf{R}}\left( {{\mathbf{a}},\;\phi = \omega t} \right){\mathbf{n}}_0$$

(10)

The directional cosine of beam is also defined as the momentum channel mixing in SSS (Fig. 3aII), which can be written in an alternatively way:

$$f\left( \phi \right) \equiv {\mathrm{cos}}\theta \left( t \right) = ({\mathbf{R}}({\mathbf{a}},\;\phi = - \omega t)( - {\mathbf{b}})) \cdot {\mathbf{n}}_0$$

(11)

As shown in Fig. 3b, if we fix the initial sample normal ${\mathbf{n}}_0$, the surface inclination angle θ₀ would be counted as 1 DOF. Then, choosing the rotation axis a in relation to ${\mathbf{n}}_0$ and b involves another 2 DOFs (a is expressed in θ₁, θ₂). Therefore, the ion momentum mixing (or f factor) in SSS, described by the surface inclination angle and axis of sample rotation $\left( {\theta _0,\;\theta _1,\;\theta _2} \right)$ in the setup, can be worked out to be:

$$\begin{array}{*{20}{l}}f\left( \phi \right) \equiv {\mathrm{cos}}\theta \left( t \right)= {\mathrm{sin}}\theta _0{\mathrm{sin}}\theta _1\left[ {{\mathrm{cos}}\theta _1{\mathrm{sin}}\theta _2\left( {1 - {\mathrm{cos}}\phi } \right) - {\mathrm{cos}}\theta _2{\mathrm{sin}}\phi } \right]\\ +\, {\mathrm{cos}}\theta _0[1 - {\mathrm{sin}}^2\theta _1\left( {1 - {\mathrm{cos}}\phi } \right)]\end{array}$$

(12)

A graphical illustration of the f factor in SSS in 3D is shown in Fig. 3c. When the sample is being rotated with speed $\phi = \omega t$ (from 0 to 2π), the smearing from quite a bit of ion with different momentum monodispersity can be achieved. For any depth-dependent quantity $a\left( {z;\;E,\;{\mathrm{cos}}\theta } \right)$, where $z \equiv {\mathbf{b}} \cdot {\mathbf{x}}$ is the depth into sample, $\left( {E,\;f \equiv {\mathrm{cos}}\theta } \right)$ is the ion momentum vector, can be obtained from the integration of its 3D spatial distribution $a\left( {{\mathbf{x}};\;E,\;f} \right)$ and pre-calculated by SRIM/IM3D¹⁵. For instance, the depth profiles of I-V net excesses can be expressed as:

$$p\left( z \right) \equiv {{\iint \nolimits_{\!\!\!\!\!-\infty}^{\infty}} {\;p\left( {\mathbf{x}} \right)}\;dxdy }$$

(13)

while the depth profiles of vacancies $c_{\mathrm{V}}\left( z \right)$ and interstitials $c_{\mathrm{I}}\left( z \right)$ can also be obtained from their spatial distributions $c_{\mathrm{V}}\left( {\mathbf{x}} \right)$ and $c_{\mathrm{I}}\left( {\mathbf{x}} \right)$ respectively. The above-mentioned depth profiles of PRDs based on SRIM/IM3D simulate the broad-beam irradiation in single- or multi-layered target materials, which take the unit of # nm⁻¹ ion⁻¹. The depth profile of damages in SSS can be simply defined as just the vacancy profile, $d(z) \equiv c_{\mathrm{V}}\left( z \right)$, or any other definitions, like DPA that can also be mathematically calculated from the vacancy concentration¹⁸.

Fig. 3: Illustration of SSS framework.

a Workflows of SSS. b Schematic setup of SSS in Cartesian coordinate system, the ion momentum status (E, θ) in SSS during the sample rotation is determined by surface inclination angle θ₀, and the rotation axis (θ₁, θ₂). The illustration of ion momentum mixing f in 3D c and linear d forms for specific parameters $\left( {\theta _0 = 0.4,\;\theta _1 = 0.8,\;\theta _2 = 3.4} \right)$, for which not all the ions participate in the averaging. e Another f profile in one-linear form with specific parameters $\left( {\theta _0 = 0.2,\;\theta _1 = 0.8,\theta _2 = 2.2} \right)$, for which all the ions participate in the averaging.

With fast-rotate of the sample, each ion channel owns an equal probability participating in the following average (Fig. 3aIII),

$$\bar A\left( z \right) \equiv \frac{{\displaystyle{\int \nolimits_0^{2\pi}} H\left( {f\left( \phi \right)} \right)f\left( \phi \right)a(z;\;E,\;f) \;d\phi}}{{\displaystyle{\int \nolimits_0^{2\pi}} H\left( {f\left( \phi \right)} \right)f\left( \phi \right) d\phi}}$$

(14)

where $H\left( \cdot \right)$ is the Heaviside step function, only the positive f factor participating in the averaging. Just like the “Sun” or the diurnal cycle, if f is negative, the “Sun” has set, the beam is shining on the thick back, which would have no influence on the spot of interest, and does not participate in the averaging, as illustrated by the dash lines in Fig. 3c. Similar to the “Winter” effect, when the directional cosine is low the shadow is long, and the flux is low (note that the perpendicular energy is low as well, but that is a separate effect), so we need to multiply by weight $H\left( {f\left( \phi \right)} \right)f\left( \phi \right)$ in the averaging, as all statistical averaging is based on the ion flux count (number of incident ions hitting unit area of observation). As the f profiles shown in the simple one-liner forms in Fig. 3d, e, there are two typical situations. In one case shown in Fig. 3e, the “Sun” never sets, all the ions participate in the averaging; while in another case shown in Fig. 3c, d, there is a long “night”, which can also introduce enough channels to scramble the ion momentum monodispersity but obviously less efficient in terms of beam time and cost.

Through SSS, the average damages $\bar D$ and I-V excesses $\bar P$ for specific $\left( {\theta _0,\;\theta _1,\;\theta _2} \right)$ can be obtained. Suppose the target of SSS is to mitigate the mean-squared averaged I–V excesses in the designated macroscopic region R, also denoted as the COST function:

$$COST \equiv {\mathrm{cost}}\left( {\theta _0,\;\theta _1,\;\theta _2} \right) = {\int_{z_1}^{z_2}} {\bar P^2(z;\;E,\;f)\;dz}$$

(15)

where $\left[ {z_1,\;z_2} \right]$ is the desired depth window of R (millimeters in x and y, which is the beam spot size). Then, the carpet bombing approach is utilized to find the global optimum of the above COST, in which we make dense grids in the $\left( {\theta _0,\;\theta _1,\;\theta _2} \right)$ space, evaluate the COST for every grid point, and find the global optimum/minimum (see Fig. 3a). In addition, the average damages in the same region is also expected to be flatter with SSS, and a lower boundary condition is set to avoid the depth window $[z_1,\;z_2]$ beyond the resultant ion-projected range in SSS,

$$\bar D\left( z \right)\; > \;D_{{\mathrm{desired}}}$$

(16)

where the finite positive value of $D_{{\mathrm{desired}}}$ is expected for SSS system.

To implement SSS, an open-source MATLAB program POLARASE was developed accordingly²³. The self-ion irradiation in iron, which is widely used to study the radiation damage in iron or steels, is selected as a model system to quantify the efficiency of SSS. With such ion-target system, we will give a detailed discussion on the inputs, outputs, as well as the efficiency and generalization of SSS.

Machine learning models of PRDs in ion momentum space

The case study is performed by using the self-ion irradiation in iron with monochromatic kinetic energy 5 MeV. From the above detail mathematics, it can be seen that the depth distributions of PRDs $a\left( {z;\;E,\;f \equiv {\mathrm{cos}}\;\theta } \right)$, including damages and I-V net excesses, pre-calculated by IM3D, are used as inputs in SSS framework (Fig. 3a). Confidently identifying the fine details of the defect imbalance upon the high precision of the corresponding distribution of interstitials and vacancies. However, it is known that the damages and I-V net excesses predicted by MC sampling are noisy, especially for the I-V excesses (more details are shown in Supplementary Note 5). This is due to the statistical fluctuations from the MC simulation with binary collision approximation in SRIM/IM3D code^15,17. Taking the benchmark calculation of self-ion irradiation in iron with a monochromatic kinetic energy of 5 MeV and normal incidence (θ = 0) as example (Supplementary Fig. 3), the I-V excess concentration is about four orders of magnitude smaller than that of damage distribution^6,10 and definitely noisy. Therefore, it is necessary to reduce the noise or find a surrogate model that best fits the given information.

For this purpose, we utilize the machine learning (ML) method with Back Propagation neural network (BP NN)^24,25 to predict surrogate models of I-V net excesses and damages in ion depth-momentum space, as shown in Fig. 4a. For the data generation, the depth profiles of $a\left( {z;\;E,\;f \equiv \cos\theta } \right)$ with different ion momenta $\left( {E = 5\;{\mathrm{MeV}},\;\theta = 0..\pi /2} \right)$, related to $f = 0..1$, are pre-calculated by IM3D. There are total 90 depth profiles for ion obliquely irradiations with oblique angles range from 0 to π/2 with an interval of π/180 are sampled and collected as the data sets. The NN fitting are adopted to train the cumulative density distribution function $\left( {{\mathrm{CDF}},\;\tilde a\left( {z;\;E,\;\theta } \right)} \right)$ of the IM3D-computed density concentration:

$$\tilde a\left( {z;\;E,\;\theta } \right) = {\int_0^z} {a(z;\;E,\;\theta )dz}$$

(17)

then the surrogate probability density distributions can be obtained by taking the derivative of the NN-fitted CDF with respect to the ion depth z,

$$a_{{\mathrm{fitted}}}(z;\;E,\;\theta ) = \frac{{\partial \tilde a_{{\mathrm{fitted}}}(z;\;E,\;\theta )}}{{\partial z}}$$

(18)

more details are provided in the “Methods” section^26,27.

Fig. 4: ML-based surrogate models of I-V excesses and damages as inputs of SSS.

a The ML workflows with NN fitting, in which the depth profiles of any PRD quantity $a\left( {z;\;E,\;\theta } \right)$ for self-ion irradiation in iron with ion energy of 5 MeV and incident angle $\left( {\theta = 0.. \frac{\pi }{2}} \right)$ are predicted by IM3D to generate data sets; the ML-based surrogate models of PRDs in depth-momentum space are obtained by NN-fitting method with PRDs as output and depth-angle as inputs. b Comparison of I-V net excesses between NN-predicted and IM3D-calculated results, identified as smooth surface and scattered dots, respectively. c The shading plot of NN-predicted I-V excesses in ion depth-momentum space, the centers of mass of deficiency $\left( {{\mathbf{x}}_ - } \right)$ and excess $\left( {{\mathbf{x}}_ + } \right)$ are identified by the red and blue dots, respectively. d Angle dependence of the estimated defect polarization. e Comparison of damages between NN-predicted and IM3D-calculated results, identified as smooth surface and scattered dots, respectively. f The shading plot of NN-predicted damages in depth-momentum space, the peaks of damage are identified by the blue dots.

The density concentration of I-V net excesses $p\left( {z;\;E = 5\;{\mathrm{MeV}},\;\theta = 0..\pi /2} \right)$ in depth-momentum space predicted by IM3D are noise as the scattered dots in Fig. 4b shown. It becomes much smoother in their cumulant manner $\left( {\tilde p\left( {z;\;E,\;\theta } \right)} \right.$ as the scattered dots shown in Supplementary Fig. 4a. Then, the CDF profiles of I-V net excesses in depth-momentum space are fitted by NN method. The parity plot for IM3D-computed I-V excesses vs NN-predicted values are shown in Supplementary Fig. 4a'. The surrogate model shows an extremely high-prediction accuracy with the mean-squared error (MSE) ~2 × 10⁻⁵ for the fitted cumulant I-V excesses per ion, as well as the variance between the NN-predicted and IM3D-calculated results are R = 0.9997 (see Fig. 4b and Supplementary Fig. 4a’). Such regression model can well predict the I-V imbalance in the considered ion momentum space. Then, the fitted I-V excesses are plotted as the smooth curved surface shown in Fig. 4b.

To illustrate the polarization of defect densities (see Eqs. 2–4), the centers of the mass of deficiency and excess are roughly estimated by:

$${\mathbf{x}}_ - \sim z_{ {\mathrm{min}}\;p\left( {z;\;E,\;\theta } \right)},\;{\mathbf{x}}_ + \sim z_{ {\mathrm{max}}\;p\left( {z;\;E,\;\theta } \right)}$$

(19)

that are the depths at where the I-V excesses reach their minima and maxima for ion with specific momentum (E, θ), as identified by the red and blue dots in the shading plot of I-V excess concentration, respectively (Fig. 4c). There is apparent polarization in defect densities for the ion-beam irradiation due to the momentum monodispersity. For the ion with the same monochromatic energy that is obliquely injecting, the defect polarization is slightly enlarged (shadow is long) with the ion obliquely angle increasing (or the directional cosine decreasing), as the Fig. 4d shown.

The NN incremental curve fitting method used above is also general for other depth-dependent quantities. As shown in Fig. 4e, the damage (or vacancy) concentration is also fitted by following the same procedures. The IM3D-computed damages are less noise when compared with that of I-V excesses (see the scatted dots in Fig. 4e), which can be well predicted by the regression model with R ~ 1 for cumulant damages per ion (see Supplementary Fig. 4b, b’). The damage peaks, as identified by the blue dots in the shading plot in Fig. 4f, shift to the sample surface with ion inclination angle increasing (or the directional cosine decreasing).

The artifact associated with near-surface defect-depleted zone is generally observed in ion-irradiated materials since the surface serves as strong sink for defects including vacancy- and interstitial-type clusters. It can also be seen that, with the directional cosine of ion decreasing, the energy component along z direction shrinks significantly, and vacancies amass at near-surface region owing to the surface sink as well as the surface sputtering effect. Thus, the near-surface depleted zone should be excluded from the ion-neutron correlation analysis, such width is estimated less than 0.1 μm for the self-ion irradiation in steels with energy of 5 MeV at relatively low temperature²⁸.

Mitigation of the defect imbalance by SSS

As shown in Fig. 5a, b, we try to mitigate the I-V imbalance in a large depth swath with depth of 0.1–1.3 μm from surface with the average damage concentration larger than 8 nm⁻¹ ion⁻¹ within the same region, which is roughly the average damage concentration within the ion hit contours for the ion with normal incidence. According to the framework of SSS, the carpet bombing approach is adopted to search the global optimum of the figure of merit, for which fine grids of 90 × 90 × 360 with an interval of π/180 in $\left( {\theta _0 = 0..\frac{\pi }{2},\;\theta _1 = 0..\frac{\pi }{2},\;\theta _2 = 0..2\pi } \right)$ space are meshed to ensure the convergence in grid size. It is calculated that the global minimization of mean-squared averaged net excesses in such a region can be reached when the sample being tilted by $\theta _0 = 0.12$, and being fast rotated around axis identified as $\left( {\theta _1 = 0.77,\;\theta _2 = 0.28} \right)$.

Fig. 5: Minimization of defect imbalance in target material through SSS.

The distribution of average I-V excesses a and average damages b with optimized ion momentum mixing, compared with that of ion momentum channels with oblique incidence, as well as the normal incidence. Ion momentum mixing ploted in 3D c and one-linear d forms for the optimized parameters of $\left( {\theta _0 = 0.12,\;\theta _1 = 0.77,\;\theta _2 = 0.28} \right)$. Self-ion irradiation in iron with ion energy of 5 MeV and a desired depth window of 0.1–1.3 μm are selected in this case study. Only parts of the ion momentum channels are plotted for clarity in Fig. 5a-c.

With the optimized surface inclination angle and axis of sample rotation, the average I-V imbalance (calculated according to Eq. 14 with dϕ = π/180), as the bold black lines shown in Fig. 5a, is significantly minimized in the certain designated macroscopic region R (1.2 μm in z, millimeters in x and y) with a quasi-flat average damage/dose distribution (bold blue lines in Fig. 5b) in the same region based on SSS. The ion momentum mixing expressed by the f profile in 3D and one-linear forms in this case study are plotted in Fig. 5c, d, showing that all the ions participate in the average for this design.

Here, the root-mean-square errors (RMSE) of the I-V excess p(z) and damage d(z) concentration are tallied to clarify the efficiency of SSS on minimization of I-V imbalance and damage non-uniformity:

$${\mathrm{RMSE}} = \sqrt {\frac{1}{N} {\sum \limits_{i = 1}^N} \left| {A_{\mathrm{i}} - Y} \right|^2}$$

(20)

where Y is the desirable reference value for quantity A, for which zero and the mean value of damage in the area of interest are used for the I-V excesses and damages, respectively. As listed in Table 1, the RMSE of the average quantities in the certain designated macroscopic region R based on SSS are significantly reduced compared to that of monochromatic ion-beam with normal incidence. The degree of I-V imbalance drops by more than a factor of three, from 6.08 × 10⁻⁴ to 1.86 × 10⁻⁴ nm⁻¹ ion⁻¹, and the degree of damage non-uniformity drops by more than a factor of six, from 4.85 to 0.76 nm⁻¹ ion⁻¹ in the region of interest, just by rotating the sample judiciously, irradiated by a mono-energetic ion beam.

Table 1 RMSE of SSS optimized for low-p and uniform-d outcome versus the unoptimized protocol of normal incidence.

Another example for self-ion irradiation in iron with monochromatic kinetic energy 3.5 MeV are shown in Supplementary Note 6. It can be seen from Supplementary Fig. 5 that both of the defect imbalance and damage non-uniformity artifacts in a macroscopic region (0.9 μm in depth) is significantly reduced with the optimized sample tilt parameters of $\left( {\theta _0 = 0.52,\;\theta _1 = 0.79,\;\theta _2 = 0.21} \right)$. The f profile indicates that there is less efficient in term of beam time and cost since a small part of ions does not participate in the total average according to Eq. 14.

Sample rotation frequency

Here, we would like to give an order-of-magnitude scaling analysis of how fast the rotation should be, in order to have successive interstitial/vacancy clouds overlapping and possibly canceling the defect imbalance, as illustrated in Fig. 2a. Modern MAS-NMR uses sample spinning as fast as 100 kHz (10^–5 s period), which is mechanically feasible²². But clearly there should also be a lower rotation speed limit for good mixing. To do this, we estimate the DPA in the affected region by Z₁ hit (see Supplementary Notes 3-4) and compare with that in accelerator-based ion-beam irradiation experiments to examine the precise meaning of “good mixing”.

A most basic view of radiation damage is that everything originates from the sudden defect showers of PRDs, the $c_{\mathrm{I}}^{\mathrm{P}}\left( {\mathbf{x}} \right)$ and $c_{\mathrm{V}}^{\mathrm{P}}\left( {\mathbf{x}} \right)$, which are so drastically distinct from the thermal equilibrium defect concentrations $c_{\mathrm{I}}^{{\mathrm{eq}}}$ and $c_{\mathrm{V}}^{{\mathrm{eq}}}$ that are spatially uniform. The extent of the defect showers, delineated by the solid lines in Fig. 2a, can be defined as a set $\left\{ {{\mathbf{x}}:\;c_{\mathrm{I}}^{\mathrm{P}}\left( {\mathbf{x}} \right)\, > \,0.1c_{\mathrm{I}}^{{\mathrm{eq}}}} \right\} \cup \left\{ {{\mathbf{x}}:\;c_{\mathrm{V}}^{\mathrm{P}}\left( {\mathbf{x}} \right)\, > \,0.1c_{\mathrm{V}}^{{\mathrm{eq}}}} \right\}$, with quite arbitrarily value of 10% background to define the extent of this region of interest (the equilibrium vacancy concentration in pure iron at room temperature is ~10¹¹ m⁻³). The size scale of such “notable isosurface” of physically significant excess vacancy or excess interstitial site fraction is assumed to be a cylinder with h in height, and 2r in diameter (Fig. 2a). For a basic estimation, let us take 5 MeV Fe²⁺ self-ion irradiation into steel for example²⁹. We can choose h to be the SRIM-predicted ion-projected range together with longitudinal straggling ~1.62 μm, and r to be the lateral straggling ~0.25 μm, so the affected area A ≈ πr² ~ 2 × 10⁻¹³ m² and the affected volume is V = hA ~ 31.8 × 10⁻²⁰ m³, which contains N ~ 2.7 × 10¹⁰ atomic sites for bcc lattices. Inside such notable isosurface region, there will be N_d ~ 6917.5 point defects created according to the Norgett-Robinson-Torrens formula (see Supplementary Note 4)³⁰. Therefore, the average DPA in the affected region per single hit is estimated to be N_d/N ~ 0.25 × 10⁻⁶ DPA per hit. With the same accelerator-based ion-beam irradiation, a macroscopic ion fluence of ϕ = 4.6 × 10¹⁷ Fe ions cm⁻² corresponds to an accumulation of 4.6 × 10²¹ ions m⁻² × A ≈ 9 × 10⁸ repeated hits on this region (for simplicity, we can pretend the incoming ions repeatedly hits at the same region). This would give a total damage of 0.25 × 10⁻⁶ DPA per hit × 9 × 10⁸ hits ~225 DPA, agreeing substantially with the average dose in the ion-projected range as calculated in the previous experiment studies²⁹.

Modern accelerator-based heavy-ion irradiation with exposure rate K = 10⁻⁵−10⁻³ DPA per second are technically feasible for iron-based target materials^5,6,29,31,32. It is easy to see that the requisite SSS sample rotation frequency should be proportional to the same-area hit rate, ${\mathrm{Freq}}\sim K/(N_{\mathrm{d}}/N)$, if the next hit on the same region should come from a substantially different angle from the previous hit on this same region. That is, if a marked microscopic region of interest (h × A cylinder) sustains 1000 hits per second on average, then if the sample rotation speed is ~ 5000 rotations per second, then two consecutive hits on the same region would likely come from very different angles, leading to substantial I-V excess density cancelation effect, and the artificial excess polarizations do not get the chance to accumulate. Thus, the corresponding rotating speeds are estimated in a range of ~40–4000 rotations per second on the defect region. This means that, with the above K-dependent rotation frequency, we would have a very good chance at completely scrambling the ion momentum monodispersity from one hit to the next immediate hit. As seen at the local coordinate frame of the affected region, it just like in solar radiation, one could be made to believe the Sun (ion beam) rotates around us (sample), substantially similar to what this notable isosurface region of interest would have experienced in neutron radiation from one hit to the next hit. Even if we double, triple the designated affected region to also monitor hits on the next-nearest neighbor regions on the imagined superlattice, we see that a rotation frequency in an order of range from 0.1 to 10 kHz (corresponding to dose rate of 10⁻⁵–10⁻³ DPA per second) would be more than sufficient to randomize the hit-direction correlation between one hit on the present defect isosurface, and the next immediate hit on it or any adjacent defect isosurfaces, thus achieving the goal of breaking momentum monodispersity.

Discussion

The momentum monodispersity of accelerator-based ion-beam irradiation would cause a permanent polarization effect and significant deviation in defect populations from that of reactor conditions, denoted as excess polarity. This polar effect is verifiable and even useful, for example, recently, Su et al.³³ have taken advantage of such momentum directionality to control the configurational outcome of primary knock-on atom with a focused electron beam in a transmission electron microscope. Here, unified frameworks of RPT and SSS are proposed to mitigate the EPA in ion-beam irradiation versus reactor conditions by randomizing the ion momentum vectors that impact a given region. The idea is that for a given hit region with defect density already significantly affected by polarization, the next hit at approximately the same spot should come with a significantly decorrelated (scrambled) momentum direction. An open-source code POLARASE was developed to implement SSS. POLARASE uses PRDs of ion-target system with specific ion energy calculated by IM3D as inputs, and the general control variables include the sample rotate frequency, ion energy E, and ion momentum status corresponding to the sample inclination angle and rotation axis (θ₀, θ₁, θ₂).

A rapidly rotating mechanical apparatus has been successfully used to spread out the ion-beam energy³⁴. Also, the ultra-fast sample spinning up to 100 kHz is mechanical feasible by using modern MAS-NMR²². The dose rate-dependent lower rotation speed limits in SSS for the good ion momentum mixing have been estimated for commonly used self-ion irradiation in iron. Similar to the primary knock-on space formalism built by Su et al.³³, the ion momentum in SSS framework could be controlled by the surface inclination angle and the axis of sample rotation, then the ion momenta with respect to the sample would be efficiently randomized from one microscopic hit to the next microscopic hit on the same region by a “fast-enough” sample rotation.

One of the critical inputs for SSS is the precise model of the IM3D-predicted I-V excesses in depth-momentum space, which are noisy and nonlinear in a high-dimensional space. The conventional curve fitting methods, depending on specific mathematical forms among variables, have limitations in precisely representing such nonlinear high-dimensional dependencies. Here, we resort to modern ML methods based on Back Propagation neural network to predict the I-V net excesses in a cumulant representation. Such numerical methods have been successfully used to reduce the error of dataset representation^26,27. Our NN surrogate model is shown to be efficient and accurate in predicting I-V net excesses with a limited amount of IM3D-calculated data. Such a method is also generally applicable to other PRD quantities.

Two cases of self-ion irradiation in iron with specific energies were used to show the efficiency of SSS. But we would like to say that SSS is also general for other ion energies or heavy-ion-metal (or alloy) systems. When using SSS, one should also note that (a) the averaging in SSS only make sense in the broad-beam limit, where the beam spot size is much bigger than the area of interest ($\sigma _{\mathrm{i}} \gg \sigma _{\mathrm{s}}$, where σ_s is millimeters and may be the sample size). It does not work for nano-beam or nano-target (surface not flat) experiments^35,36. (b) When one chooses the maximum depth range of the designated optimized region, the regions corresponding to the free surface and implanted ion peak zone should be avoided, as the local defect distributions could be dramatically varying in these areas. Thus, deeper depth region R with nearly no defect imbalance is achievable with higher ion-beam energy.

It is worth mentioning that it is the final state of the materials, not the path taken, that should be of concern in the determination of equivalence between neutron and ion radiation for the post-irradiation test¹. Based on the SSS, in the designated optimized region with almost no neutron-atypical defect imbalance, nor strong gradient in DPA distribution, artifacts in materials such as swelling suppression and strong chemical element segregation along the ion-projected range would be expected to be minimized^5,37.

Philosophically, there are some interesting points in the present design of the ion momentum mixing by rotating the target sample. The ion momentum mixing in SSS can be rewritten into

$$f \equiv {\mathrm{cos}}\theta \left( t \right) = A{\mathrm{cos}}\left( {\phi + B} \right) + C$$

(21)

So there are three continuous DOFs, A, B, C, which is exactly equivalent to program the “Sun” or the diurnal cycle. It is as if one can tune (a) the latitude one sits on Earth, (b) the season, and (c) the earth-rotation axis in relation to the Earth-sun plane (something one cannot actually tune as human beings). As the 3D rotation illustrations shown in Figs. 3 b, c and 5 c, the blue line is the current Earth-sun distance vector, the green line is the latitude, and the red line is the Earth’s self-rotation axis. Programming these three DOFs generally allows satisfactory erasure of EPA in ion-beam radiation, with a fast-enough rotation that scrambles the incoming ion angle from one hit to the next hit in the vicinity of the same PRD region.

In conclusion, we established a general RPT and a precise SSS technique to mitigate the EPA and point-defect imbalance in accelerator-based ion-beam irradiation. It shows that sample spinning frequency on the order of hundreds to thousands Hz that depends on the ion fluxes, from a basic estimation by the self-ion irradiation in iron, would be more than sufficient to scramble the ion momentum monodispersity. With the optimized surface inclination angle and the axis of sample rotation through SSS, a certain designated macroscopic region with significantly reduced I-V imbalance and quasi-flat damage distribution in material can be obtained. Such an experimentally feasible design (fast-rotate sample) to minimize the defect imbalance as well as the damage non-uniformity artifacts in ion-beam irradiation is a significant step toward developing procedures in effectively using accelerator-based ion-beam irradiation as a surrogate of reactor-condition irradiation.

Methods

IM3D setup for the self-ion irradiation in iron

The self-ion irradiations in iron are simulated by using the IM3D code¹⁵. Based on fast indexing of scattering integrals and the stopping power database of SRIM¹⁷, IM3D can simulate ion irradiation in arbitrary target shapes, and ion beam in arbitrary directions. More importantly, with excellent parallel scaling performance, the efficiency of IM3D is >10⁴ times faster than SRIM. For current self-ion irradiations in iron, the displacement threshold energy $E_{\mathrm{d}} = 40\;{\mathrm{eV}}$ is used in the calculation³. For each calculation, the profiles of PRDs are ensemble-averaged over total 10⁶ ion trajectories per single hit, to get better ensemble-averaged defect productions. The detailed simulation parameters for ion beam and targets are listed in Supplementary Table 2. The target is divided into n³ bins with the edge length ${\Delta}l = 30$ nm. To obtain the I-V imbalance, the full cascades method is used to trace the entire cascade trajectories of both ions and displaced target atoms in detail, although it would overestimate the damage concentration than that from the Quick Kinchin-Pease method^15,17,18.

Machine learning

We utilize the ML method with BP NN³⁸ implemented in Matlab to predict the surrogate models of I-V net excesses and damages as functions of depth and ion momentum, since the conventional curve fitting methods, depending on specific or given mathematical relationship among variables, have limitations in precisely assessing a complex multi-dimensional mathematical relation. Taking the NN surrogate model of I-V excesses for example, the NN training procedures and parameters are set as follows. As illustrated in Fig. 4a, when a BP NN is created, for points in $(\theta ,\;z,\;p)$ 3D space, the $\left( {\theta ,\;z} \right)$ are treated as input vectors, whereas the corresponding p vectors are treated as the target vectors. The input vectors and target vectors are randomly divided with 70% used for training, 15% for validation, and 15% for testing. A four-layer feed-forward BP network with a “tansig” transfer function in the hidden layer and “purelin” transfer function in the output layer is constructed³⁹. The three hidden neurons are set to 20, 10, 5, respectively. The Bayesian Regularization training algorithm is used^40,41, the performance of the training is estimated by MSE between the target and the output vectors. The dropout technique is used to prevent overfitting.