Abstract
Ionic liquids play an important role in many technological applications and a detailed understanding of their frontier molecular orbitals is required to optimize interfacial barriers, reactivity and stability with respect to electron injection and removal. In this work, we calculate quasiparticle energy levels of ionic liquids using first-principles many-body perturbation theory within the GW approximation and compare our results to various mean-field approaches, including semilocal and hybrid density-functional theory and Hartree–Fock. We find that the mean-field results depend qualitatively and quantitatively on the treatment of exchange–correlation effects, while GW calculations produce results that are in excellent agreement with experimental photoelectron spectra of gas phase ion pairs and ionic liquids. These results establish the GW approach as a valuable tool for understanding the electronic structures of ionic liquids.
Similar content being viewed by others
Introduction
Ionic liquids (ILs) are salts formed of molecular cations and anions that exist in the liquid state at or near room temperature. They find widespread use as solvents1,2, dispersants3,4,5, and electrolytes6,7,8, and exhibit several unusual properties, including high electrochemical stability windows9,10 and very low equilibrium vapor pressures11,12. From a fundamental point of view, it is important to understand the character of the frontier molecular orbitals and determine their quasiparticle energy levels in ILs, as these determine technologically important properties, such as band alignment at interfaces, reactivity, and stability with respect to electron injection or removal. In recent years, a number of experimental and theoretical investigations of the electronic structure of ILs have been reported. For example, photoelectron spectroscopy has been used to study the valence band electronic structure of liquid ILs and IL vapors consisting of neutral cation–anion pairs13,14,15,16,17,18,19.
To gain a detailed understanding of the properties of ILs, many groups have carried out calculations based on density-functional theory (DFT)20,21,22,23,24. To model photoemission experiments, several studies compared the Kohn–Sham (KS) eigenvalues obtained from DFT calculations to the measured photoelectron spectra16,17,19,25. This practice is based on the observation that in many materials KS eigenvalues can be useful approximations to quasiparticle energies that are measured in photoemission spectroscopy. However, it is well known that the quantitative agreement between KS eigenvalues and quasiparticle energies often depends sensitively on the choice of exchange–correlation functional. In recent years, several DFT-based approaches, including Koopmans’ corrected functionals, ranged-separated hybrid functionals, or dielectric dependent functionals, have been developed that can produce good agreement between KS eigenvalues and quasiparticle energies26,27,28,29,30,31. Despite this, many DFT studies of the electronic structure of ILs employ simpler exchange–correlation functionals, such as semilocal or traditional hybrid functionals.
Moreover, it is well known that KS eigenenergies cannot be rigorously interpreted as quasiparticle energies (with the exception of the energy of the highest occupied molecular orbital (HOMO)32), which are measured in photoemission spectroscopy. True quasiparticle energies of all occupied and empty states can be obtained from Green’s function techniques, such as the GW approach. In the GW approach, the one-electron Green’s function G is obtained by solving the Dyson equation with a self-energy, which is given by the product of the Green’s function and the screened interaction W. In principle, the GW self-energy should be evaluated using the fully interacting Green’s function and screened interaction. In practice, however, a mean-field Green’s function G0 and a mean-field screened interaction W0 obtained from a DFT or Hartree–Fock (HF) calculation are often used. (We use the term “mean-field theory” to refer to HF theory and DFT approaches with approximate exchange–correlation functionals.) This approximation, termed G0W0, has been demonstrated to produce highly accurate quasiparticle energies for a wide range of materials. For example, previous work has shown that G0W0 calculations can predict band gaps in solids and first ionization energies of small molecules with high accuracy33,34,35,36,37,38,39. Similarly, G0W0 yields accurate results for the position of the d-bands in noble metals relative to the Fermi level40,41,42, whereas standard DFT functionals do not. A downside of the G0W0 method is that the results can depend on the mean-field starting point. To overcome this problem, partially and fully self-consistent GW schemes have been introduced43,44,45.
In this work, the GW method is used to study the electronic structures of ILs. As a case study, the electronic structure of the 1-ethyl-3-methylimidazolium tetrafluoroborate ([EMIM][BF4]) ion pair is analyzed in detail with a focus on the nature of the frontier molecular orbitals in this system. Calculated quasiparticle energies from G0W0 calculations are also compared against recent photoemission measurements of several different ILs. In particular, gas phase spectra of IL vapors are compared against simulated spectra of free ion pairs, and liquid phase spectra of ILs are compared against theoretical calculations of periodic crystalline ILs. In all cases, excellent agreement between measured photoemission spectra and GW calculations is found, while DFT results depend sensitively on the treatment of exchange–correlation effects.
Results
[EMIM][BF4] ion pair
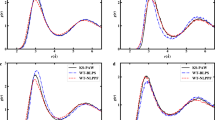
We first consider the electronic structure of the [EMIM][BF4] ion pair (Fig. 1). Figure 2 shows the calculated densities of states (DOS) of the [EMIM][BF4] ion pair from different levels of theory. The leftmost column contains results from three different mean-field methods: HF, DFT with the PBE0 functional46, and DFT with the Perdew–Burke–Ernzerhof (PBE) functional47. The Mulliken decomposition48 of the total DOS into cation and anion contributions is also shown. The three curves exhibit significant quantitative and qualitative differences. For example, while PBE predicts that the HOMO orbital is centered on the anion, PBE0 and HF place the HOMO orbital on the cation and the associated HOMO energies differ by several electron volts among the different approaches. To illustrate this point further, isosurface plots of the HOMO-1, HOMO, and LUMO orbitals are shown in Fig. 3. The three leftmost columns show that PBE, PBE0, and HF predict three different sets of frontier orbitals in this system. In particular, all three frontier orbitals are localized on the [EMIM] ion in HF, while the HOMO-1 in PBE0 and PBE is on the [BF4] ion. In PBE, the HOMO is also localized on [BF4]. These results demonstrate the difficulty of answering questions about the nature and energies of the frontier orbitals in ILs based on energy eigenvalues and orbitals from mean-field approaches.
The differences between PBE (PBE0) and evSCGW@PBE (evSCGW@PBE0) arise because the energy ordering of the orbitals changes when their eigenvalues are recalculated using the GW method. The one-electron wavefunctions themselves are not updated. When Hartree–Fock theory is used as the starting point for evSCGW calculations, the energy ordering of the frontier orbitals of the [EMIM][BF4] ion pair does not change.
Calculated DOS from G0W0 and eigenvalue self-consistent GW (evSCGW) calculations are shown in the middle and rightmost columns of Fig. 2. Already at the G0W0 level, the dependence on the mean-field starting point is significantly reduced and all G0W0 results predict that the HOMO orbital lies on the [EMIM] cation. The starting point dependence is even weaker in the evSCGW results. The frontier orbitals from the GW calculations are shown in the rightmost three columns of Fig. 3 and are in qualitative agreement with each other. In particular, all frontier orbitals are localized on the [EMIM] ion. Note that the mean-field wavefunctions are not updated in either G0W0 or evSCGW, explaining the different shapes of the lowest unoccupied molecular orbital (LUMO) state of evSCGW@HF compared to evSCGW@PBE and evSCGW@PBE0. Instead, changes in the frontier orbitals arise due to changes in the energy ordering of the one-electron eigenstates when the eigenvalues are recalculated using the GW method. In [EMIM][BF4], G0W0 and evSCGW change the ordering of the frontier orbitals when using a PBE or PBE0 starting point, but not when using an HF starting point.
It is also instructive to consider the absolute energy levels of the frontier orbitals. The calculated energies of the HOMO and the LUMO of the [EMIM][BF4] ion pair from different levels of theory are given in Table 1. The HOMO energies from different mean-field approaches differ by almost 4 eV with HF giving the lowest value (−10.60 eV) and PBE giving the highest (−6.80 eV). This spread is significantly reduced by the one-shot G0W0 correction with G0W0@HF still giving the lowest value (−11.03 eV) and G0W0@PBE giving the highest (−10.44 eV). Eigenvalue self-consistency does not change the G0W0@HF result but shifts the G0W0@PBE result down by 0.6 eV. The mean-field and GW results can also be compared to Δ-self-consistent-field (ΔSCF) calculations. The ΔSCF method has been previously used to predict electrochemical stability windows in ILs24,49. We find that the ΔSCF method predicts the HOMO level to lie between −9.1 and −10.2 eV when PBE, PBE0, or HF theory are used. Given that G0W0, evSCGW, and ΔSCF still yield a range of values that span ~2 eV, the question of “what is the correct energy of the HOMO level in the [EMIM][BF4] ion pair” naturally arises. In order to obtain a theoretical reference, we have performed coupled cluster (CC) calculations at the CCSD(T) level (coupled cluster with full treatment of singles and doubles and perturbative treatment of triples) to obtain the total energies of the neutral ion pair and the ion pair cation50. The resulting HOMO quasiparticle energy (referred to as ΔCCSD(T) in the table) is found to be 10.49 eV. This value is in excellent agreement with the G0W0@PBE0 result indicating that PBE0 is a reliable mean-field starting point for GW calculations of ILs. The G0W0@PBE0 HOMO is also within 0.11 eV from the experimental value (see discussion of the experimental spectrum of the vapor above liquid [EMIM][BF4] later in the manuscript).
Considering next the LUMO level, we find that HF predicts a positive LUMO energy and therefore an unbound state, while the LUMO is bound in PBE and PBE0. G0W0, evSCGW, and ΔSCF calculations confirm that the LUMO level indeed lies above the vacuum level and is unbound.
Ion pairs: theory vs. experiment
We next compare GW results for different ion pairs to experimental photoelectron spectra of IL vapors. The simulated spectra are constructed from G0W0 calculations with a PBE0 starting point based on the “Gelius approximation,” i.e., the spectrum is a sum of atomic orbital projected DOS (pDOS) curves, each weighted by the per-electron photoionization cross-section of that subshell at the relevant photon energy51. Uniform Gaussian broadening has been applied to each theoretical spectrum.
Experimental and theoretical gas phase spectra of the 1-ethyl-3-methylimidazolium trifluoromethanesulfonate and 1-ethyl-2,3-dimethylimidazolium bis(trifluoromethylsulfonyl)imide ion pairs are shown in Fig. 4. In both cases, excellent agreement between theory and experiment is observed. We emphasize that no shifts or calibrations of any kind have been applied to the theoretical spectra, i.e., both the absolute and the relative binding energies of valence electrons in these ion pairs are predicted with excellent accuracy by the G0W0@PBE0 approach.
Interestingly, the agreement between the experimental photoelectron spectrum of vaporized [EMIM][BF4] and the G0W0@PBE0 result for the free ion pair is somewhat worse than for the ion pairs discussed above, see Fig. 5. In particular, peaks A, B, and D’ are missing from the simulated spectrum, and the intensity ratios of peaks D, E, and F are different from the experimental ones. In previous studies, it has been observed that the two ions of the [EMIM][BF4] ion pair can react to form an adduct upon heating52,53. Figure 6 shows the structure of the adduct. To assess whether adduct formation is responsible for the differences between the simulated and the measured spectra, we performed GW calculations on the adduct. We then added the adduct spectrum to the ion pair spectrum assuming that the vapor is a 1.5:1 mixture of ion pairs and adducts. Figure 5 shows that the resulting spectrum is in much better agreement with the measurement. In particular, peaks B and D’ are present and the intensity ratios of peaks D, E, and F are correct, but peak A is still missing. Including eigenvalue self-consistency or using a different mean-field starting point was also not found to reproduce peak A; see Supplementary Information. We therefore hypothesize that this missing peak originates from a different decomposition product or an ion pair dimer.
ILs in the condensed phase
Finally, we also carry out GW calculations of ILs in the condensed phase and compare them to experimental photoelectron spectra. In principle, the simulated spectrum of the IL should be obtained by averaging results of different liquid configurations. However, performing many GW calculations of large unit cells is computationally extremely challenging. Instead, we instead carry out GW calculations on ILs in a solid, crystalline phase. This approximation is justified as the internal structures of the ions and their average coordination environments are similar in the solid and liquid phases. Figure 7 shows the unit cells of the three crystalline ILs 1-butyl-3-methylimidazolium hexafluorophosphate ([BMIM][PF6]), [EMIM][BF4], and 1-butyl-3-methylimidazolium chloride ([BMIM]Cl) and also compares the simulated G0W0@PBE0 spectra to experimental photoelectron spectra taken in the liquid phase. In photoemission measurements of liquids and solids, the experimental binding energies are given relative to the Fermi level, but since the position of the Fermi level relative to the band edges is not known a priori, the calculated spectra have been shifted by a constant amount to best match the experiment. Excellent agreement between theory and experiment is found for [BMIM][PF6] and [EMIM][BF4]. In the case of [EMIM][BF4], peaks I and II are correctly reproduced, which is an improvement over previous DFT results15. In the spectrum of [BMIM]Cl, the separation between the two most intense peaks (peaks I and IV) is overestimated by approximately 1.3 eV, but otherwise the measured spectrum is reproduced with good accuracy. The results shown in Figs. 4 and 7 demonstrate that the GW method is very well suited for predicting quasiparticle energy levels in ILs and free ion pairs.
Discussion
An alternative method for modeling photoelectron spectra of ILs based on DFT was proposed in ref. 54. In this study, it was shown that experimental spectra of liquid ILs can be reconstructed from DFT partial DOS curves of free ion pairs by shifting the cation and anion partial DOS curves relative to each other by an amount that is determined on a case-by-case basis. The size of these shifts was originally interpreted as the difference between the average electrostatic potentials experienced by the cation and the anion. Our GW results, however, suggest that this interpretation needs to be revised. In particular, Fig. 2 shows that the GW self-energy corrections give rise to a significant relative shift of the anion and cation partial DOS curves. This shift does not arise from electrostatic effects but instead from a more accurate treatment of exchange and correlation effects. Therefore, the shifts applied in ref. 54 do not arise solely from electrostatic effects and should be interpreted as empirical corrections that contain contributions from both self-energy effects and changes in average electrostatic potential.
Detailed knowledge of the character of the frontier molecular orbitals and their quasiparticle energies is of crucial importance for understanding the electronic structures of ILs. In this study, we have shown that interpreting DFT KS eigenvalues as true quasiparticle energies can lead to qualitatively and quantitatively inaccurate results. This problem can be overcome by the GW method which produces results that are in excellent agreement with state-of-the-art photoemission data. These results suggest that the GW method is a useful tool for studying the electronic structure of ILs and can be used to gain insights into electronic properties that are relevant to IL devices, such as band alignment at interfaces and stability with respect to electron injection and removal.
Methods
Electronic structure calculations
All HF, DFT, and GW calculations reported in this work were performed using the FHI-aims electronic structure program55,56,57 that uses atom-centered local basis functions defined on a numerical grid. The geometries of the free ion pairs were relaxed using DFT with the PBE0 exchange–correlation functional until the forces on the atoms were <0.005 eV/Å. van der Waals (vdW) interactions were accounted for using the Tkatchenko–Scheffler method58. For each ion pair, a number of different configurations were manually constructed, and in the end the relaxed geometry with the lowest energy was used for the DOS calculations. The default “tight” numerical basis sets were used during the geometry optimizations. For the bulk crystals, the calculations were performed at experimental geometries from X-ray crystallography59,60. The implementation of the GW method in FHI-aims is described in ref. 61. The self-energy was calculated on the imaginary frequency axis with 100 frequency points, and the Pade approximation with 16 fitting parameters was used for the analytical continuation of the self-energy onto the real axis. For the G0W0 and evSCGW calculations, the NAO-VCC-nZ basis sets were used (NAO-VCC-4Z for the ion pairs and NAO-VCC-3Z for the bulk solids)62. All of the occupied and empty electronic states spanned by the basis sets were included in the GW calculations. A graph showing basis set convergence is included in the Supplementary Information. The bulk calculations were performed at the Gamma point only. The GW calculations were performed on the UK’s national supercomputer Archer. The calculations of the free ion pairs were run on 8 nodes (192 processors in total) and a typical G0W0 calculation took approximately 4 h. The calculations of the bulk solids (approximately 100 atoms per unit cell) were run on 64 nodes (1536 processors in total) and a typical G0W0 calculation took approximately 13 h. CC calculations for determining the vertical first ionization energy of the [EMIM][BF4] ion pair were performed using NWChem63. The geometry relaxed at the PBE0 + vdW level of theory was used. The total energies of the neutral ion pair and the ion pair cation were calculated at the CCSD(T) level of theory, using cc-pVTZ (correlation-consistent, valence triple zeta with polarization functions) basis sets64.
Data availability
The structures of all of the ion pairs and solids considered in this work are given in the Supplementary Information.
References
Rogers, R. D. Ionic liquids-solvents of the future? Science 302, 792–793 (2003).
Welton, T. Room-temperature ionic liquids. Solvents for synthesis and catalysis. Chem. Rev. 99, 2071–2084 (1999).
Boukherissa, M. et al. Ionic liquids as dispersants of petroleum asphaltenes. Energy Fuels 23, 2557–2564 (2009).
Wu, B. et al. Functionalization of carbon nanotubes by an ionic-liquid polymer: dispersion of Pt and PtRu nanoparticles on carbon nanotubes and their electrocatalytic oxidation of methanol. Angew. Chem. Int. Ed. 48, 4751–4754 (2009).
Zhou, X. et al. Dispersion of graphene sheets in ionic liquid [bmim][PF6] stabilized by an ionic liquid polymer. Chem. Commun. 46, 386–388 (2010).
Balducci, A. et al. High temperature carbon-carbon supercapacitor using ionic liquid as electrolyte. J. Power Sources 165, 922–927 (2007).
Buzzeo, M. C., Evans, R. G. & Compton, R. G. Non-haloaluminate room-temperature ionic liquids in electrochemistry - a review. ChemPhysChem 5, 1106–1120 (2004).
Galiñski, M., Lewandowski, A. & Stepniak, I. Ionic liquids as electrolytes. Electrochim. Acta 51, 5567–5580 (2006).
Van Aken, K. L., Beidaghi, M. & Gogotsi, Y. Formulation of ionic-liquid electrolyte to expand the voltage window of supercapacitors. Angew. Chem. Int. Ed. 54, 4806–4809 (2015).
Hayyan, M., Mjalli, F. S., Hashim, M. A., AlNashef, I. M. & Mei, T. X. Investigating the electrochemical windows of ionic liquids. J. Ind. Eng. Chem. 19, 106–112 (2013).
Ludwig, R. & Kragl, U. Do we understand the volatility of ionic liquids? Angew. Chem. Int. Ed. 46, 6582–6584 (2007).
Esperança, J. M. S. S. et al. Volatility of aprotic ionic liquids - a review. J. Chem. Eng. Data 55, 3–12 (2010).
Fogarty, R. M. et al. Electron spectroscopy of ionic liquids: experimental identification of atomic orbital contributions to valence electronic structure. Phys. Chem. Chem. Phys. 21, 18893–18910 (2019).
Kuusik, I. et al. Valence band photoelectron spectra of [EMIM][BF4] ionic liquid vapor: evidences of electronic relaxation. J. Mol. Liq. 223, 939–942 (2016).
Kuusik, I. et al. Valence electronic structure of [EMIM][BF4] ionic liquid: photoemission and DFT+D study. RSC Adv. 8, 30298–30304 (2018).
Kuusik, I. et al. Valence electronic structure of [EMIM][B(CN)4]: ion-pair vs. bulk description. RSC Adv. 9, 33140–33146 (2019).
Kuusik, I. et al. The electronic structure of ionic liquids based on the TFSI anion: a gas phase UPS and DFT study. J. Mol. Liq. 294, 111580 (2019).
Lovelock, K. R. J., Villar-Garcia, I. J., Maier, F., Steinrück, H.-P. & Licence, P. Photoelectron spectroscopy of ionic liquid-based interfaces. Chem. Rev. 110, 5158–5190 (2010).
Ulbrich, A., Reinmller, M., Beenken, W. J. & Krischok, S. Photoelectron spectroscopy on ionic liquid surfaces - theory and experiment. J. Mol. Liq. 192, 77–86 (2014).
Kirchner, B. In Ionic Liquids Vol. 290 (ed. Kirchner, B.) 213–262 (Springer, 2008).
Zahn, S. & Kirchner, B. Validation of dispersion-corrected density functional theory approaches for ionic liquid systems. J. Phys. Chem. A 112, 8430–8435 (2008).
Angenendt, K. & Johansson, P. Ionic liquid structures from large density functional theory calculations using mindless configurations. J. Phys. Chem. C. 114, 20577–20582 (2010).
Ishizuka, R. & Matubayasi, N. Effective charges of ionic liquid determined self-consistently through combination of molecular dynamics simulation and density-functional theory. J. Comput. Chem. 38, 2559–2569 (2017).
Ong, S. P., Andreussi, O., Wu, Y., Marzari, N. & Ceder, G. Electrochemical windows of room-temperature ionic liquids from molecular dynamics and density functional theory calculations. Chem. Mater. 23, 2979–2986 (2011).
Reinmöller, M. et al. Theoretical reconstruction and elementwise analysis of photoelectron spectra for imidazolium-based ionic liquids. Phys. Chem. Chem. Phys. 13, 19526 (2011).
Kronik, L. & Kmmel, S. (eds) First Principles Approaches to Spectroscopic Properties of Complex Materials (Springer, 2014).
Borghi, G., Ferretti, A., Nguyen, N. L., Dabo, I. & Marzari, N. Koopmans-compliant functionals and their performance against reference molecular data. Phys. Rev. B 90, 075135 (2014).
Skone, J. H., Govoni, M. & Galli, G. Nonempirical range-separated hybrid functionals for solids and molecules. Phys. Rev. B 93, 235106 (2016).
Kronik, L., Stein, T., Refaely-Abramson, S. & Baer, R. Excitation gaps of finite-sized systems from optimally tuned range-separated hybrid functionals. J. Chem. Theory Comput. 8, 1515–1531 (2012).
Shimazaki, T. & Asai, Y. First principles band structure calculations based on self-consistent screened Hartree-Fock exchange potential. J. Chem. Phys. 130, 164702 (2009).
Brawand, N. P., Vrs, M., Govoni, M. & Galli, G. Generalization of dielectric-dependent hybrid functionals to finite systems. Phys. Rev. X 6, 041002 (2016).
Janak, J. F. Proof that ∂E/∂ni = ϵ in density-functional theory. Phys. Rev. B 18, 7165–7168 (1978).
Hybertsen, M. S. & Louie, S. G. First-principles theory of quasiparticles: calculation of band gaps in semiconductors and insulators. Phys. Rev. Lett. 55, 1418–1421 (1985).
Hybertsen, M. S. & Louie, S. G. Electron correlation in semiconductors and insulators: band gaps and quasiparticle energies. Phys. Rev. B 34, 5390–5413 (1986).
Louie, S. G. In Topics in Computational Materials Science (ed. Fong, C. Y.) Ch. 4 (World Scientific, 1998).
Bruneval, F. & Marques, M. A. L. Benchmarking the starting points of the approximation for molecules. J. Chem. Theory Comput. 9, 324–329 (2013).
Caruso, F., Dauth, M., van Setten, M. J. & Rinke, P. Benchmark of approaches for the GW 100 test set. J. Chem. Theory Comput. 12, 5076–5087 (2016).
Sharifzadeh, S., Tamblyn, I., Doak, P., Darancet, P. T. & Neaton, J. B. Quantitative molecular orbital energies within a G0W0 approximation. Eur. Phys. J. B 85, 323 (2012).
Onida, G., Reining, L. & Rubio, A. Electronic excitations: density-functional versus many-body Green’s-function approaches. Rev. Mod. Phys. 74, 601–659 (2002).
Bernardi, M., Mustafa, J., Neaton, J. B. & Louie, S. G. Theory and computation of hot carriers generated by surface plasmon polaritons in noble metals. Nat. Commun. 6, 7044 (2015).
Marini, A., Onida, G. & DelSole, R. Quasiparticle electronic structure of copper in the GW approximation. Phys. Rev. Lett. 88, 016403 (2001).
Yi, Z., Ma, Y., Rohlfing, M., Silkin, V. M. & Chulkov, E. V. Quasiparticle band structures and lifetimes in noble metals using Gaussian orbital basis sets. Phys. Rev. B 81, 125125 (2010).
van Schilfgaarde, M., Kotani, T. & Faleev, S. Quasiparticle self-consistent G W theory. Phys. Rev. Lett. 96, 226402 (2006).
Caruso, F., Rinke, P., Ren, X., Scheffler, M. & Rubio, A. Unified description of ground and excited states of finite systems: the self-consistent G W approach. Phys. Rev. B 86, 081102 (2012).
Vlek, V., Baer, R., Rabani, E. & Neuhauser, D. Simple eigenvalue-self-consistent Δ-GW0. J. Chem. Phys. 149, 174107 (2018).
Adamo, C. & Barone, V. Toward reliable density functional methods without adjustable parameters: the PBE0 model. J. Chem. Phys. 110, 6158–6170 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Mulliken, R. S. Electronic population analysis on LCAO-MO molecular wave functions. II. Overlap populations, bond orders, and covalent bond energies. J. Chem. Phys. 23, 1841–1846 (1955).
Karu, K., Ruzanov, A., Ers, H., Ivanitev, V., Lage-Estebanez, I. & García de la Vega, J. Predictions of physicochemical properties of ionic liquids with DFT. Computation 4, 25 (2016).
Raghavachari, K., Trucks, G. W., Pople, J. A. & Head-Gordon, M. A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 157, 479–483 (1989).
Gelius, U. & Siegbahn, K. ESCA studies of molecular core and valence levels in the gas phase. Faraday Discuss. Chem. Soc. 54, 257 (1972).
Clarke, C. J. et al. Thermal stability of dialkylimidazolium tetrafluoroborate and hexafluorophosphate ionic liquids: situ bulk heating to complement in situ mass spectrometry. Phys. Chem. Chem. Phys. 20, 16786–16800 (2018).
Taylor, A. W., Lovelock, K. R. J., Jones, R. G. & Licence, P. Borane-substituted imidazol-2-ylidenes: syntheses in vacuo. Dalton Trans. 40, 1463 (2011).
Yoshimura, D. et al. Electronic structure of ionic liquids at the surface studied by UV photoemission. J. Electron Spectros. Relat. Phenom. 144, 319–322 (2005).
Blum, V. et al. Ab initio molecular simulations with numeric atom-centered orbitals. Comput. Phys. Commun. 180, 2175–2196 (2009).
Havu, V., Blum, V., Havu, P. & Scheffler, M. Efficient integration for all-electron electronic structure calculation using numeric basis functions. J. Comput. Phys. 228, 8367–8379 (2009).
Levchenko, S. V. et al. Hybrid functionals for large periodic systems in an all-electron, numeric atom-centered basis framework. Comput. Phys. Commun. 192, 60–69 (2015).
Tkatchenko, A. & Scheffler, M. Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data. Phys. Rev. Lett. 102, 073005 (2009).
Choudhury, A. R., Winterton, N., Steiner, A., Cooper, A. I. & Johnson, K. A. In situ crystallization of low-melting ionic liquids. J. Am. Chem. Soc. 127, 16792–16793 (2005).
Holbrey, J. D. et al. Crystal polymorphism in 1-butyl-3-methylimidazolium halides: supporting ionic liquid formation by inhibition of crystallization. Chem. Commun. 1636–1637 (2003).
Ren, X. et al. Resolution-of-identity approach to Hartree-Fock, hybrid density functionals, RPA, MP2 and with numeric atom-centered orbital basis functions. New J. Phys. 14, 053020 (2012).
Zhang, I. Y., Ren, X., Rinke, P., Blum, V. & Scheffler, M. Numeric atom-centered-orbital basis sets with valence-correlation consistency from H to Ar. New J. Phys. 15, 123033 (2013).
Valiev, M. et al. NWChem: a comprehensive and scalable open-source solution for large scale molecular simulations. Comput. Phys. Commun. 181, 1477–1489 (2010).
Dunning, T. H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 90, 1007–1023 (1989).
Acknowledgements
J.M.K. and J.L. acknowledge support from EPRSC under Grant No. EP/R002010/1 and from a Royal Society University Research Fellowship (URF\R\191004). Via J.L.’s membership of the UK’s HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work used the ARCHER UK National Supercomputing Service. I.K. and V.K. acknowledge Estonian Centre of Excellence in Research project “Advanced materials and high-technology devices for sustainable energetics, sensorics and nanoelectronics” TK141 (2014-2020.4.01.15-0011). K.R.J.L. acknowledges support from a Royal Society University Research Fellowship (URF\R\150353).
Author information
Authors and Affiliations
Contributions
J.M.K. performed the calculations. J.M.K. and I.K. analyzed the results and performed the comparisons with experimental data. K.R.J.L. suggested the decomposition pathway for [EMIM][BF4] and helped with the analysis of the results. The manuscript was written by J.M.K. and J.L. with the help from other authors. I.K. and V.K. proposed and initiated the project. J.L. supervised the investigation.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kahk, J.M., Kuusik, I., Kisand, V. et al. Frontier orbitals and quasiparticle energy levels in ionic liquids. npj Comput Mater 6, 148 (2020). https://doi.org/10.1038/s41524-020-00413-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-020-00413-4