Introduction

In recent years, since the emergence of novel two-dimensional (2D) graphene-related materials1,2,3,4 with hexagonal lattice symmetry, a new degree of freedom of electrons, i.e., valley5,6, has attracted intensive attention. In analogy to charge and spin, the valley degree of freedom constitutes the binary logic states in solids, leading to possible applications for information processing. The field of valleytronics has flourished with the study of H-phase group-VI transition metal dichalcogenides (TMDs)7,8,9,10, due to their inequivalent K+ and K− valleys11. Till now, various functional devices have been achieved in valleytronics, such as valley separator, valley filter, valley valve, electron beam splitter and logic gate12,13,14,15,16. Yet, the energy degeneracy of the two prominent valleys does not meet the requirement of nonvolatility in next-generation information technology. Efforts in valley degeneracy lifting have been made in TMDs using external fields17,18,19,20,21,22,23,24,25,26,27,28,29,30. Recently, the concept of ferrovalley materials, as a new member of the ferroic family, was proposed. The existence of spontaneous valley polarization, resulting from either ferromagnetism in hexagonal 2D materials31 or ferroelectricity with orthorhombic lattice32 renders nonvolatile valleytronics applications realizable.

The development of valleytronics is indeed very similar to that of spintronics. As is well known, in the field of spintronics, half-metals33, where one spin channel is metallic while the other is semiconducting or insulating, can provide completely spin-polarized currents by filtering the current into a single spin channel without any external operations. Therefore, such states are of great importance in both theoretical study and practical applications of spintronics. For valleytronics, the analogous field of spintronics, the following questions are naturally raised: whether there is a half-valley-metal state, in which electrons are of metallic characters at one valley, whereas at the opposite valley they keep semiconducting? If the answer is yes, is there any novel property associated with this half-valley metal?

Furthermore, the quantum valley Hall effect, rooted in the spatial noncentrosymmetry, has been extensively studied in various valley systems34,35,36,37. Through additionally introducing the time-reversal symmetry broken, the valley-polarized quantum anomalous Hall effect has been proposed in model calculations38 and then demonstrated in first-principle calculations39, which combines valleytronics and topology, two hot topics in condensed-matter physics, together. However, valley Hall current is absent in the proposed systems, making the detection of the Hall effect difficult. Another question then arises, is it possible to find a natural system with both the quantum anomalous Hall effect and the valley index, or in another term, quantum anomalous valley Hall effect (QAVHE)?

In this article, starting from the two-band k·p model, we successfully gain the desired half-valley-metal state. Then we achieve this new state in ferrovalley H-FeCl2 monolayer, which possesses strong spin–orbit coupling (SOC) effect and large exchange interaction of transition-metal-d electrons, by tuning the on-site Coulomb interaction. The electrons around the Fermi level of the system are 100% valley and 100% spin polarized with Dirac cone-like linear dispersion. More interestingly, the QAVHE is revealed in H-FeCl2 monolayer with appropriate on-site Coulomb interaction, while the valley-related special optical properties are still remained.

Results and discussion

Two-band k·p model

Similar to H-VSe2 with hexagonal structure31, a two-band k·p model including magnetic interaction is employed here to describe the electronic properties near the K± in the 2D Brillouin zone (BZ) of monolayers of magnetic H-phase TMDs. The conduction state \(\psi _1^\tau = \left| {d_{z^2}} \right\rangle\) and the valence state \(\psi _2^\tau = \left( {\left| {d_{x^2 - y^2}} \right\rangle + i\tau \left| {d_{xy}} \right\rangle } \right){\mathrm{/}}\sqrt 2\) are chosen as the basis functions with index τ = +1 (−1) denotes the point K+ (K−). Then, the total effective Hamiltonian of the system is given as:

$$H({\boldsymbol{k}}) = \left[ {\begin{array}{*{20}{c}} {\frac{{\Delta} }{2}{\,\mathrm{ + }}\,\varepsilon + \sigma \tau \lambda _c - sm_c} & {t(\tau q_x - iq_y)} \\ {t(\tau q_x + iq_y)} & { - \frac{{\Delta} }{2} + \varepsilon + \sigma \tau \lambda _v - sm_v} \end{array}} \right],$$
(1)

here Δ is the band gap of the TMD monolayer without magnetism and the SOC effect at the valleys K±, ε is a correction energy bound up with the Fermi level, t is the effective nearest-neighbor hopping integral, and q = k − K± is the relative momentum vector with respect to the valleys K±. λc(v) and mc(v) respectively demonstrate the spin splitting derived from the SOC effect and the effective exchange splitting at the bottom of conduction band (CB) (the top of valence band, VB). Spin is indexed by σ with +1 (–1) for spin-up (down) state.

When we focus on the spin-down channel, the spin index in the SOC and exchange interaction terms is –1. By diagonalizing the above Hamiltonian, we obtain the energy spectra:

$$E(\psi ^\tau ){\,\mathrm{ = }}\,\frac{1}{2}\left[ {2\varepsilon - \tau (\lambda _{\mathrm{c}} + \lambda _v){\mathrm{ + }}(m_c + m_v) \pm \sqrt {({\Delta}^ \prime )^2 + 4t^2(q_x^2{\mathrm\,{ + }}\,q_y^2)} } \right].$$
(2)

Here we introduce the gap parameter \({\Delta} ^\prime = {\Delta} - \tau (\lambda _v - \lambda _c){\mathrm{ + }}m_c - m_v\), which corresponds to the energy difference between \(\psi _1^\tau\) and \(\psi _2^\tau\) states at the two valleys (qx = qy = 0). For a single valley, through tuning the SOC (τλv(c)) and the exchange effect (mc(v)), Δ′ could be positive, zero, and even negative. Note here a negative Δ′ indicates an interesting state with inverted band ordering, i.e. E (\(\psi _1^\tau\)) < E (\(\psi _2^\tau\)). Whereas for Δ′ = 0, the metallic state without energy gap could be expected. In addition, it is interesting to point out that the valley splitting, i.e., energy difference between the band gap at K+ (\(E_{\rm{g}}^{{\rm{K}}_{+}}\) = Δ + λv − λc + mc − mv) and K− (\(E_{\rm{g}}^{{\rm{K}}_{-}}\) = Δ − λv + λc + mc − mv), possesses the magnitude of 2\(|\lambda _{\mathrm{v}} - \lambda _c|\), merely depending on the SOC effect. As an element-sensitive effect, the SOC term is generally hard to be affected. The valley splitting is thus treated as a constant in the following discussions.

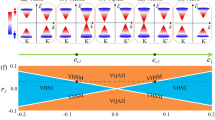
Starting from the schematic band structures of traditional ferrovalley materials, as shown in Fig. 1a, we find that the band gap of the two valleys can be regulated by the exchange interaction (\(|m_c - m_v|\)) synchronously. When we decrease the band gap at K+ valley, the one at K−will be reduced as well (shown in Fig. 1b). Such kind of simultaneous band gap changing provides the possibilities to obtain the desirable critical state, as shown in Fig. 1c, of which at one valley the gap is closed while at the other one the gap is still open. Interestingly, for K− valley with Δ′ = 0, it owns a linear dispersion\(E(\psi ^\tau ) = \frac{1}{2}[2\varepsilon - \tau (\lambda _{\mathrm{c}} + \lambda _v){\mathrm{ + }}(m_c + m_v) \pm {\mathrm{2}}tq]\), similar to that of the Dirac cone. Yet, it corresponds to a single spin channel.

Fig. 1: The schematic band structures near valleys K+ and K–.
figure 1

For ferrovalley states with a larger and b smaller gap, c half-valley-metal states with one of the valley has zero gap. \(E_{\rm{g}}^{{\rm{K}}_{+}}\) (\(E_{\rm{g}}^{{\rm{K}}_{-}}\)) represents the allowed interband transitions excited by circularly polarized light at K+ (K−) valley with only spin-down channel.

Full size image

Here, we name the state like Fig. 1c as half-valley metal, where one valley presents metal properties and the other is still in semiconductor status. Note that due to the unbroken symmetry, the optical selection rule35 is still held, i.e., the circularly polarized light is still locked with valley chirality. To be specific, for K+ valley with gap, only left-circularly polarized light can be absorbed. An interesting phenomenon thus emerges: when we use the left-circularly polarized light to make detection, we find the system has finite band gap. Whereas for the right-circularly polarized one, the systems will reflect the light just like metal does. We would like to mention that besides the one based on the optical selection rule, other peculiar properties, such as 100% spin-polarized conduction electron, are expected for such half-valley-metal state, since it is born of the half-metallic one. In addition, since the SOC effect is already considered in the above analysis, the 100% spin polarization is robust. This is in strong contrast to the traditional half metal33, in which the SOC effect will generally mix the spin-up and spin-down states, making the system not exactly 100% spin polarized. Whereas for the normal Dirac half metal40, characterized by a band structure with a gap in one channel but a Dirac cone in the other, the SOC effect always opens a band gap and eventually makes the system going to be semiconductor. Therefore, the half-valley-metal may be a true Dirac half metal with 100% spin polarization.

In order to explore the Hall effect, we then calculate the Berry curvature of the system. Here, we consider the spin-resolved Berry curvature from the Kubo formula41:

$${\Omega} _n^{ \uparrow ( \downarrow )}\left( {\mathbf{k}} \right) = - \mathop {\sum}\limits_{n\prime \ne n} {\frac{{2\rm{Im} \left\langle {\left. {\varphi _{n,{\mathbf{k}}}^{ \uparrow ( \downarrow )}} \right|v_x\left| {\varphi _{n\prime ,{\mathbf{k}}}^{ \uparrow ( \downarrow )}} \right.} \right\rangle \left\langle {\left. {\varphi _{n\prime ,{\mathbf{k}}}^{ \uparrow ( \downarrow )}} \right|v_y\left| {\varphi _{n,{\mathbf{k}}}^{ \uparrow ( \downarrow )}} \right.} \right\rangle }}{{(E_{n\prime }^{ \uparrow ( \downarrow )} - E_n^{ \uparrow ( \downarrow )})^2}}} ,$$
(3)

The summation is over all the occupied states. Here, En represents the eigenvalue of the Bloch function \(\varphi _{n,{\mathbf{k}}}^{ \uparrow ( \downarrow )}\), while both vx and vy are the velocity operators in the x and y directions, defined as \(v_x = \frac{{\partial H}}{{\partial k_x}}\) and \(v_y = \frac{{\partial H}}{{\partial k_y}}\). In terms of the k·p model Hamiltonian parameterization Berry curvature can be simplified as:

$${\Omega} _z({\mathbf{k}}) = \frac{{2t^2\tau {\Delta} ^\prime }}{{[4t^2(q_x^2 + q_y^2) + ({\Delta} ^\prime )^2]^{\frac{3}{2}}}},$$
(4)

Integrating the Berry curvature over the first BZ in the 2D system gives the total Chern number\(C = \frac{1}{{2\pi }}\mathop {\sum}\nolimits_n {\mathop {\int}\nolimits_{BZ} {d^2} } {\mathbf{k}}{\Omega} _z({\mathbf{k}})\)42.

From Eq. (4) we can easily know that the Berry curvature is significant only around the valley and its sign is determined by the sign of the product of τ and Δ′. Note that in ordinary valley systems, Δ′ is generally positive, though the magnitude may be different as in the case of ferrovalley state, at K+ and K− valleys. This indicates that the Berry curvatures have opposite signs at the two valleys, as they possess different τ. Consequently, the Chern number is generally zero due to the opposite contribution to the integration of Ωz from the two valleys. This immediately brings a conjecture. As we mentioned earlier, Δ′ could even be negative with appropriate mc and mv. If we further increase \(|m_c - m_v|\), the system will stride over the half-valley-metal state, and Δ′ at K− will change from zero to negative value while at K+ it is still with positive sign. At this moment, the product τΔ′ has the same positive sign at K+ and K− valleys. By integrating the Berry curvature in the first BZ, we should get a nonzero Chern number, suggesting now the system is in the topological state. And, as a result, we expect the QAVHE will occur in this system.

First-principle calculations

In order to verify the results anticipated by the k·p model, we then carry out ab initio calculations. We choose H-FeCl2 as our sample system, as Fe ions generally demonstrate larger exchange splitting. Figure 2a, b shows its geometric structures. In such a monolayer, an intermediate layer of hexagonally arranged Fe atoms is sandwiched between two layers of Cl atoms. Each Fe atom is surrounded by six Cl atoms.

Fig. 2: Basic physical properties of H-FeCl2 monolayer.
figure 2

a Top and b side view of H-FeCl2 monolayer. c Phonon spectrum of H-FeCl2 monolayers. d Orbital projected band structures of H-FeCl2 monolayer with Ueff = 0 eV. The radius of dots is proportional to its population in corresponding states: blue symbols represent spin-down components of both Fe-dxy and Fe-\(d_{x^2 - y^2}\) orbitals on cation-Fe, red ones for spin-down components of Fe-\(d_{z^2}\) orbitals, green ones for both Fe-dxz and Fe-dyz characters, and pink symbols represent spin-up Fe-d states. σ+ and σ− represent the left-handed and right-handed radiation, respectively. Inset in (b) is the sketch of the first Brillouin zone with the high symmetry points.

Full size image

The optimized lattice constant is 3.364 Å, and the angle of Cl–Fe–Cl is 76.6°. The magnetic moment of Fe is calculated to be 4.00 μB, in consistent with previous theoretical results of H-FeCl243 and T-FeCl244. In its bulk phase, FeCl2 is reported to be an antiferromagnetic insulator with space group P3\(\bar m\)1, consisting of a sequence of –Cl–Fe–Cl–Cl–Fe–Cl– layers where the Cl–Cl layers are bound by weak Van der Waals forces45. At present, there is no related experimental report about the monolayer FeCl2. To determine the dynamical stability of H-FeCl2 monolayer, its phonon spectrum along the high symmetry lines within the first BZ is shown in Fig. 2c. The absence of imaginary frequencies demonstrates the stability of FeCl2 monolayer in H-phase, which is in agreement with other theoretical work43.

The valley-shaped dispersion near K+ and K− points is clearly seen in the band structures of the FeCl2 monolayer (Fig. 2d). The spin-down Fe-3\(d_{z^2}\) orbitals occupy the bottom of CB, while spin-down Fe-3dxy and Fe-3\(d_{x^2 - y^2}\) characters hold the top of VB at the two k points. Spin-down components of Fe-dxz and Fe-dyz locate at higher energy range. For the spin-up Fe-d states, they are in the energy range below −1 eV, far away from the Fermi level. Furthermore, we analyze the symmetries of K+ and K− points. The irreducible representations (IRs) at K+ are 2E1/2 and 2E5/2 for the top VB and bottom CB, respectively. At K−, however, they are 2E1/2 (top VB) and 2E3/2 (bottom CB). The different symmetry for bottom CB makes the K+ and K− points unequal. When the left-handed incident light (2E′ symmetry) with frequency ~ (Eg/ħ) comes, according to the great orthogonality theorem that the electric-dipole transition is allowed only if the reduced direct product representation between the initial state IRs and the incident light IRs contains the representation of the final state, we can obtain that: 2E1/2 ⊗ 2E′ = 2E5/2.Therefore it can only be absorbed at K+ point. Similarly, the optical absorption at the K− point can be excited merely by the right-handed circularly polarized light (1E′ symmetry) due to the relation 2E1/2 ⊗ 1E′ = 2E3/2. Such dependence of optical selection rules on k points signifies that K+ and K− points in H-FeCl2 monolayer can be regarded as two prominent valleys.

Interestingly, thanks to the coexistence of ferromagnetism and the SOC effect, two valleys here are intrinsically nonequivalent. The valley splitting, defined as ΔE = \(\left| {E_{\rm{g}}^{{\rm{K}}_{+}} - E_{\rm{g}}^{{\rm{K}}_{-}}} \right|\), where \(E_{\rm{g}}^{{\rm{K}}_{\pm}}\) is the band gap at K± valley, becomes 106 meV, which is a little bit larger than that in VSe2 (90 meV)31. Such valley splitting is also exactly represented in the 106 meV red shift of the optical band gap of right-handed radiation, compared with that of the left-handed one, as is shown in Fig. 3a. The chirality-dependent optical band gap proves H-FeCl2 monolayer as an intrinsic ferrovalley material.

Fig. 3: The imaginary parts of complex dielectric function ε2 for monolayer H-FeCl2.
figure 3

a Ueff = 0 eV (with primary valley polarization) and b Ueff = 1.80 eV. Red (blue) symbols with lines represent right-handed (left-handed) polarized light. The insert in (b) corresponds to the system with negative magnetic moment.

Full size image

Previous analysis starting from the minimal k·p model proposes the feasibility of achieving the half-valley-metal states and the QAVHE. For the H-FeCl2 monolayer, the effective U parameter (Ueff) is adopted to describe the strong-correlated effect of electrons in 3d shell of Fe atoms. Figure 4a, as a reference, presents the original state of H-FeCl2 without U. When an Ueff is applied, VB occupied by Fe-dxy and Fe-\(d_{x^2 - y^2}\) moves up, Fe-\(d_{z^2}\) dominated CB correspondingly goes down. Once Ueff reaches up to 1.67 eV, as shown in Fig. 4b the band gap gets closed initiatively at K− valley, meanwhile a narrow band gap is kept at K+ valley, signifying the half-valley-metal status. Note that the band structure at the K− valley now demonstrates the Dirac cone shaped linear dispersion, perfectly reproduced the characteristic anticipated by our k·p model. It provides mass-free electron mobility, in favor of charge and spin transport. After the critical state we further increase Ueff. The Fe-\(d_{x^2 - y^2}\) and Fe-dxy occupied bands continue to move up, while bands of the Fe-\(d_{z^2}\) components go down, at both of the two valleys. For the case in Fig. 4c with Ueff = 1.80 eV, the CB and VB are still in the process of getting closed at K+ valley. Yet at the K− valley, the CB and VB are apart from each other. Here the components of bottom CB and top VB at K− are completely exchanged compared with that of the original H-FeCl2 monolayer state. Now, the IRs at K− change to 2E3/2 and 2E1/2 for the top VB and bottom CB, respectively. The transition relationship 2E3/2 ⊗ 2E′ = 2E1/2 corresponds to the left-handed light absorption at K− valley. The same transition results at K+ and K− valleys indicate that only left-handed light can be absorbed in this state. When the effective U is up to 1.90 eV, we can gain the other half-valley-metal state (Fig. 4d), where the K− valley holds the optical visible band gap and the K+ valley is metallic, opposite to the case shown in Fig. 4b. Further increasing Ueff makes the components of CB and VB at K+ valley reversed as well. Fe-dxy and Fe-\(d_{x^2 - y^2}\) occupied VB start to move up while Fe-\(d_{z^2}\) occupied CB goes down which means the system starts to turn back to the ferrovalley state. We choose Ueff = 3 eV as an example (Fig. 4e), the components Fe-dxy and Fe-\(d_{x^2 - y^2}\) occupy CB, while Fe-\(d_{z^2}\) starts take over VB. Though the K+ valley absorbs right-handed polarized light while K− takes left-handed polarized light, the narrow optical band gap absorption still corresponds to right-handed polarized light, indicating the redistribution of the two valleys compared with that of without Ueff.

Fig. 4: Band structures of H-FeCl2 monolayer.
figure 4

a Ferrovalley state with Ueff = 0 eV, b half-valley-metal state with Ueff = 1.67 eV, c topologically nontrivial state with Ueff = 1.80 eV, d half-valley-metal state with Ueff = 1.90 eV, e Ferrovalley state with Ueff = 3 eV, f the same as c but with opposite magnetic moment. Blue symbols represent spin-down components of Fe-dxy and Fe-\(d_{x^2 - y^2}\) orbitals. Red ones are spin-down states for Fe-\(d_{z^2}\) characters. Light blue (light red) is for spin-up components of Fe-dxy and Fe-\(d_{x^2 - y^2}\) orbitals. The IRs of states have been labeled using the Mulliken notations.

Full size image

Between the two half-valley-metal states, both two valleys correspond to the left-handed polarized light absorption. We calculate the circular polarized light absorption with applied 1.80 eV U values in Fig. 3b. It is clear to see that the absorption peak completely comes from the left-handed light, which is of great benefit to design the optical filter. The inset map corresponds to the inverted magnetic moment system, of which band structure clearly displayed in Fig. 4f. As expected, the system will absorb right-handed light when the magnetization and then valley polarization reverses, which is confirmed by our calculation. This unique property suggests that, when the normal light incidents into the material, only the specific circularly polarized light can be absorbed and its fluorescence spectrum is also chirality dependent.

The Berry curvature and Chern number of the monolayer FeCl2 is calculated with varied U value from 0 to 2.5 eV and the topological phase diagram is shown at Fig. 5c. Taking Ueff = 1.80 eV as an example, we obtain the Berry curvatures for the whole VBs of the first BZ in Fig. 5a. The calculated Berry curvatures are almost zero except those points around the K+ and K− valleys, as expected. In addition, they are of the same sign near two valleys, just the values are different. Integration over the Berry curvatures gives a nonzero Chern number (=1). This confirms our previous conjecture and indicates the existence of topological edge states within the insulating bulk gap.

Fig. 5: Topological properties of monolayer FeCl2.
figure 5

a Berry curvature in the momentum space in arbitrary units with Ueff = 1.80 eV. b Crystal and band structures of FeCl2 ribbons with a zigzag edge (shown in red boxes). The ribbon width is 55.4 Å in unit cell. The conducting edge state is shown as red line. Light red region denotes bulk bands. c Phase diagram of monolayer FeCl2 with varied Ueff. The half-valley metallic state (shown as HVM in the figure as the down arrow indicated) is between the ferrovalley state and the topological nontrivial state, which can demonstrate quantum anomalous valley Hall effect (QAVHE).

Full size image

We then calculated the edge states of a semi-infinite system of FeCl2 with a zigzag edge when Ueff = 1.80 eV. As shown in Fig. 5b, there does exist the edge state connecting the conduction and valence bands, which is consistent with the Chern number calculation. Conclusively, among the two half-valley-metal states the nontrivial topological state is relative robust. The QAVHE state is kept while effective U values varying from 1.67 to 1.90 eV. In our case, the system with the QAVHE retains the valley degree of freedom, therefore brings quantum anomalous Hall effect into valleytronics.

In summary, combining first-principle calculations with two-band k·p model, we demonstrate the possibility of realizing the new ferrovalley member, half-valley-metal, which allow the electrons conduct at one valley, whereas display the semiconducting states at the other valley. This is indeed a critical state of the valley system, where the conduction electrons are fully spin and valley polarized. It demonstrates dramatic chirality-dependent optical properties. Interestingly, the system can evolve from topologically trivial to nontrivial state with nonzero Chern number. In this topological valley state, the QAVHE with valley degree of freedom is confirmed, which ensures the non-dissipative high-performance electrons transportation in valleytronics. We hope these new concepts will enrich our understanding about valleytronics, which may accelerate its applications in the field of information processing and optoelectronics.

Methods

Computational details

All calculations are performed in the framework of density functional theory using the Vienna Ab Initio Simulation Package46. Interactions between valence electrons and ionic cores are described with the projector augmented wave method47. The generalized gradient approximation with Perdew–Burke–Ernzerh parametrization was applied48. A plane wave basis set with a cutoff energy of 600 eV is used to expand the wave functions. The 2D BZ integration is sampled by an 18 × 18 × 1 k-grid mesh for calculations of electronic properties. A vacuum layer with a thickness of 20 Å is set in the calculation for monolayer FeCl2 to ensure decoupling between periodic FeCl2 layers. For structural relaxation, all the atoms are allowed to relax until the atomic force on each atom is smaller than 0.001 eV Å−1. Both the lattice constant and the atomic positions are fully optimized. The SOC effect49 is explicitly included in the calculations. To assess the dynamical stability of the H-FeCl2 monolayer under different strains, we calculate their phonon dispersion by using the Quantum-ESPRESSO50 code. For the optical property calculation, we adopt our own code OPTICPACK, which has been successfully used in various systems51,52. To describe the strong-correlated effect of Fe-3d electrons, the Dudarev’s approach of the LSDA + U scheme is adopted53, in which only the effective U (Ueff) based on the difference between the on-site Coulomb interaction parameter (U) and exchange parameters (J) is meaningful. We further calculated the Chern number and edge states with the software package Wannier tools54 using the renormalized effective tight binding Hamiltonian.