Abstract
Spatially resolved time and voltage-dependent polarization dynamics in PbTiO3 thin films is explored using dynamic piezoresponse force microscopy (D-PFM) in conjunction with interferometric displacement sensing. This approach gives rise to 4D data sets containing information on bias-dependent relaxation dynamics at each spatial location without long-range electrostatic artifacts. To interpret these data sets in the absence of defined physical models, we employ a non-negative tensor factorization method which clearly presents the data as a product of simple behaviors allowing for direct physics interpretation. Correspondingly, we perform phase-field modeling finding the existence of ‘hard’ and ‘soft’ domain wall edges. This approach can be extended to other multidimensional spectroscopies for which even exploratory data analysis leads to unsatisfactory results due to many components in the decomposition.
Similar content being viewed by others
Introduction
Polarization dynamics in ferroelectric materials directly underpin multiple applications ranging from non-volatile memories1, tunneling barriers2,3,4, and field-effect transistors5,6. These complex dynamics provide insight into the fundamental mechanisms by which electromechanical coupling occurs, often explaining the origin of giant functional responses7,8,9,10,11,12,13,14,15,16. Such dynamics include domain wall motion, polarization rotation, and nanodomain characteristics, all of which have been described using macroscopic phenomenological models, as well as statistical models16,17,18,19,20. However, the central microscopic mechanisms responsible for the aforementioned kinetics remain largely unexplored and misunderstood.
The advent of Piezoresponse Force Microscopy (PFM)17,18,19,20,21 in the mid-90s enabled visualization of ferroelectric domains in open-surface films and ferroelectric capacitors, often with sub-10 nm resolution22,23,24,25,26,27. These imaging studies have been further extended to map domain evolution under applied fields28,29,30,31 and as a function of time32,33 and temperature34, providing information on domain wall motion and nucleation mechanisms and frozen disorder26,35,36,37,38,39,40,41,42. In parallel, several spectroscopic imaging techniques in PFM have been developed43,44. In Piezoresponse Force Spectroscopy (PFS), a PFM signal is measured as a function of the magnitude of a dc voltage pulse applied to the probe, providing information on the bias dependence of the PFM signal45. The latter, in turn, is related to the size of the domain formed below the probe and thus provides information on thermodynamics and kinetics of domain switching46,47,48. Nonetheless, several key challenges remain in the interpretation of microscopic mechanisms responsible for ferroelectric behavior.
The proliferation of multidimensional PFM methods brought forth the challenge of efficient and high-veracity data analysis, i.e., reduction of a 3, 4, or 5D data set into 2D maps representing material properties in the most efficient manner. Such analysis is relatively straightforward if the functional model representing materials response to external stimuli is known, allowing for direct least-square functional fits to extract material parameters. Yet this is rarely the case for locally measured responses, necessitating development of strategies based on information theory methods. This complexity and difficulty in interpretation stems from the fact that existing analysis methods address the dimensions of the measurement parameter space individually, as opposed to treating them as linked. Most of the existing methods such as principal component analysis49,50, non-negative matrix factorization51,52, and independent component analysis53 are limited to factorizing matrices, whereas for multidimensional data with multiple spectroscopic axes (for instance, time and voltage), the intrinsic form of the data is a tensor. Subsequently, information can be lost during the flattening of the tensor into a matrix that can be factorized using these tools.
A related challenge in multidimensional PFM is signal interpretation54,55. It is well known the measured PFM signal is often beset by non-piezoelectric contributions, e.g., long-range electrostatics, as well as artifacts that arise from e.g., contact resonance changes56,57. While a number of measurement techniques have been developed to quantify the electrostatic contribution, and mechanisms such as full-band excitation or dual AC resonance tracking can circumvent the resonance shift issue, achieving quantitative measurements in PFM is still a difficult undertaking58,59,60.
Here, we use recently developed dynamic piezoresponse force microscopy (D-PFM)61, which provides information on the time and voltage dependence of the piezoresponse in each spatial location, to understand the polarization dynamics in a ferroelectric system. As a model material system, we choose tetragonal PbTiO3 (PTO) as it exhibits a dense a-c domain structure ideal for studying ferroelectric relaxation dynamics (Fig. 1a–c). To isolate the true electromechanical dynamics of the system, D-PFM measurements were employed via interferometric displacement sensing (IDS)58,62 in a coupled atomic force microscope. Unlike traditional PFM which is an angular measurement of the cantilever motion, interferometric displacement sensing uses a laser focused directly above the tip, which is routed back to an interferometer enabling accurate measurements of tip displacement, as shown in Fig. 2a. Note, IDS eliminates the long-range electrostatics that originate from the interaction between the cantilever shank and sample, which is a key source of spurious background signal and artifacts, and quantifies the tip displacement. D-PFM in conjunction with interferometric displacement sensing provides a new paradigm for measuring local ferroelectric properties and their dynamics under a field.
a Standard optical beam deflection (OBD) piezoresponse force microscopy and interferometric displacement sensing (IDS) configuration where OBD is reflected at an angle off the cantilever and IDS is reflected directly above the tip, b applied voltage wave form (red) and entire grid spatially averaged relaxation response (blue) from dynamic piezoresponse force microscopy.
Results and Discussion
Understanding polarization dynamics in a ferroelectric system
The representative surface topography is illustrated in Fig. 1a, showing a surface roughness of 4.1 nm (RMS) and topographical features as large as 20 nm in height. The corresponding band-excitation PFM amplitude and phase images are shown in Fig. 1b, c, respectively, exhibiting a well-defined two-level domain structure. For the (001) tetragonal ferroelectric, the domains can be readily classified as a- (in-plane) and c- (out of plane) domains, identified as the low and high amplitude regions in Fig. 1b, respectively.
To understand polarization dynamics in this system, D-PFM measurements with IDS are performed across a spatial grid. Specifically, the PFM response (see Fig. 2b, blue) at a single position is measured as a function of time after a voltage pulse following a triangular envelope (see Fig. 2b, red), and the measurement is repeated across a grid of points, building up a spatial map of the relaxation dynamics. The size of the generated data set is a 60 × 60 spatial grid with 128 relaxation time steps measured at 6 ms intervals, and 16 distinct voltage pulses. The response averaged over the whole image is illustrated in Fig. 2b, showing clear relaxation processes. Note that the direction and magnitude of relaxation strongly depends on the set voltage amplitude. Importantly, measured with IDS, it is evident that relaxations exist, and given that switching occurs, that domain wall motion is also activated under the applied fields used. We note that long-range electrostatics can also be a dominant cause of relaxation in such spectroscopies measured using traditional optical beam deflection, so the measurement of local relaxations is an improvement on the existing technique60.
To understand the polarization dynamics of such a dense domain structure, we choose to perform D-PFM on a smaller area to provide better resolution of a/c domain features (Fig. 3a). Given this is a large multidimensional dataset, for a first visualization we performed k-means clustering on the entire multidimensional dataset (including time) to segment the image into k = 5 clusters; k-means is an unsupervised machine learning algorithm that automatically assigns each pixel to belong to a member of the kth class (or cluster) such that the within-cluster sum of squares is minimized. The k-means map is shown in Fig. 3d, and the associated cluster means (the respective cluster’s average piezoresponse versus time) are plotted in Fig. 3b, c, e, f, h. It is evident there are changes in the hysteresis loop depending on the location, i.e., a-domain or c-domain, and it is noteworthy that the relaxation process varies across the a-c domain as shown by the line profile of the loops along the circled region in Fig. 3d, and plotted in Fig. 3g. Here, the relaxation appears to be asymmetric with respect to the a/c domain boundary. However, it is difficult to extract meaningful quantitative information from such a representation due to high noise and variability. We note also that Fig. 3 shows two distinct types of c-domains: one type embedded within the c/a domain structure, and another (on the right side of image 3(a)) which appears separated and much larger. The reason for low response in the c-domain embedded in the c/a structure 4 is likely due to the geometry: with a large volume fraction of a-domains in the probed volume of the tip, the c-domain fraction is likely much smaller, leading to suppressed response.
a Interferometric displacement sensing piezoresponse map at voltage pulse 15 V and time 0.0 s, (b, c, e, f, h) Averaged time-dependent hysteresis loops taken from locations determined by k-means clustering in Fig. 3d; the loop labels are colored corresponding to the cluster membership, d k-means clustering on entire multidimensional dataset, g piezoresponse amplitude vs time for line profile which spans a/c-domain boundary to edge of adjacent a-domain (left to right, respectively) in Fig. 3d. Time color bar corresponds to time dependence of piezoresponse displayed in Fig. 3b, c, e, f, h.
To gain quantitative insight into the spatial and voltage variability of the relaxation phenomena, we employed non-negative tensor factorization (NTF), which is commonly used in a variety of statistics to reduce n-dimensional tensorial data to a more compact representation whilst still reproducing (to some tolerance) the original values63. Here, we restricted the study the piezoresponse amplitude, which is always positive, and thus satisfies the non-negativity constraint of NTF. The details of the algorithm are available in ref. 63, but briefly, we note that we may write the piezoresponse amplitude as a tensor X of order 3 (the respective orders being space, voltage and time), \({\mathbf{X}} \in {\Bbb R}^{M1 \times M2 \times M3}\). In our case, M1 = 3600 for the vectorized spatial positions, M2 = 128 for the time dimension, and M3 = 16 for the number of voltage steps. Then, NTF aims to determine a decomposition of X such that:
where \(a_k \in {\Bbb R}^{M1},b_k \in {\Bbb R}^{M2},c_k \in {\Bbb R}^{M3},\) K is the rank, and \(\circ\) represents an outer product of vectors. An alternative way to write this problem is that we attempt to find the matrices A,B,C where \({\mathbf{A}} = \left[ {a_1, \ldots ,a_k} \right],{\mathbf{B}} = \left[ {b_1, \ldots ,b_k} \right],{\mathbf{C}} = \left[ {c_1, \ldots ,c_k} \right]\) and then find the matrices subject to the constraint that all elements of these matrices remains non-negative, i.e.,:
where \({\mathbf{A}},{\mathbf{B}},{\mathbf{C}} = \mathop {\sum }\limits_{k = 1}^K a_k \circ b_k \circ c_k,\)and F is the Frobenius norm. In general, we wish to choose a low number for K, but still large enough that good approximation for X can still be found. Note, this is the same for traditional multivariate analysis, i.e., non-negative matrix factorization (NMF)51,52. However, unlike in traditional NMF, the NTF algorithm used here results in 3 vectors for each specific k value, i.e., one for the spatial position (interpreted as loadings), one for the voltage vector and one for the time vector. Lastly, it should be noted that unlike NMF, which does not have uniqueness for the approximation, optimum solutions for NTF can be unique under some soft conditions64.
Figure 4 shows the NTF analysis of the D-PFM data corresponding to the full voltage-time sweep. The larger maps are A matrices, which have been reshaped into 2D matrices and can be considered as loading or abundance maps commonly seen in NMF or principal component analysis (PCA). The smaller insets consist of matrices B and C and are recognized as the voltage and time dependences. It is important to note that the NTF analysis with rank 4 results in a reconstruction error of ~10%. Remarkably, the complex time and voltage-dependent dynamics can be represented as a sum of 4 time-dependent components with voltage-dependent coefficients. This is especially important because we do not know, a priori, how the voltage pulse will affect the system’s relaxations.
Examination of the components reveals component 1 (Fig. 4a) is more prevalent at negative voltages while component 2 (Fig. 4b) is favored at positive voltages with contrasting relaxation behavior, both of which spatially correspond to c-domains as seen in the abundance maps. Figure 4c shows component 3, which is spatially correlated to a-c domain boundaries with a preference towards one a-c domain orientation, in corroboration with clustering seen in Fig. 3d. The strong asymmetry can be attributed to the tilt of the ferroelastic a-c domain walls, with the volume fraction of the c-domain in the probed volume changing asymmetrically as the tip is moved away/towards an a-c domain boundary65. Indeed, we observed such an asymmetry in a previous report, where the nonlinearity in the measured piezoresponse as a function of applied AC field was modeled in a similar system, and the asymmetric response across the ferroelastic interface was reproduced66. Here, we note that this asymmetry is reproduced from the data with a purely unsupervised analysis technique. The expanded view of the bottom-left corner of the abundance map in Fig. 4c is shown in Fig. 5a, and the asymmetric contrast is clearly visible across the c/a interface in the average profile, plotted in Fig. 5b. Component 4 (Fig. 4d) seems to be isolated to transient effects associated with domain nucleation events. Additionally, all four components exhibit monotonic relaxation behavior and obey dual exponential relaxations (Fig. 4, see fit in insets). Finally, component 2 appears to show some non-physical effect which is not seen in any individual (“pure”) pixel; indeed, performing NTF on the c-domains and a-domains separately does not result in such a component. Care must be taken to not ascribe physical mechanisms when the unmixing is not ideal as is the case for this component.
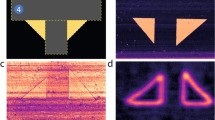
Asymmetric relaxation response from c/a domain boundaries may be ascribed to the existence of a “hard” and “soft” c/a/air junction. a Component 2 from NTF, abundance map, lower left region only. b Average profile along the x-direction of (a), clearly showing the oscillation in the abundance map due to the different relaxation behavior. c Schematic of the “hard” and “soft” junctions. The “soft” junction results in more wall motion during field application, and consequently more relaxation.
The fits for the dual exponential behavior of all four components are displayed in Table 1 showing distinguishable relaxation times for each component (single exponential fits in Table S1). Component 1, 2, and 4 have orders of magnitude difference in the two relaxation times, where the much larger relaxation time (on the order of minutes) might be attributed to slow polarization dynamics, whether it be electrochemical or purely ferroelectric in origin. Indeed, other studies on electrochemically active materials show the possibility of electrochemical dipoles causing such relaxations in local AFM measurements, and we cannot discount this here67.
On the other hand, somewhat faster dynamics can be expected for lateral domain wall motion, although this will still be a creep process68. Indeed, if one expects a creep velocity of ~100 nm/s, then the domain wall displacement in 5 ms is 5 nm, which should be sufficient to cause detectable changes in the response of a strong ferroelectric for a probing volume dictated by the tip radius (r~10 nm). Thus, we suggest that the fast process is dictated by lateral domain wall motion, whilst the slower process is likely mediated by electrochemical processes.
A possible mechanism for the observed spatial variability in relaxation behavior of component 3 (also Fig. 3g) is the existence of “soft” and “hard” edges at the ferroelastic interface (as described in our previous report66), i.e., when the tip is on the right side of the c/a boundary (Fig. 5c), the domain wall is more labile, and therefore less relaxation is observed when the bias is removed. On the other hand, when the tip is on the left side of the c/a boundary, only the “hard” edge of the ferroelastic wall is activated, resulting in a large relaxation due to the higher energy penalty. To explore the feasibility of the proposed mechanism, we performed phase-field modeling on a PbTiO3 thin film coherently grown on a KTiO3 substrate, with a1(100) and c(001) tetragonal domains and c/a domain walls in the equilibrium state (Fig. 5c). A constant local tip bias of 2.0 V was applied on the film surface near the “soft” and “hard” edges of the 90◦ domain walls with the infield domain structures illustrated in Fig. 5d, e. It is seen that under 2.0 V the switched c-domain (00–1) under the tip near the “soft” edge (Fig. 5d) grows larger and deeper in size than the one near the hard edge (Fig. 5e), indicating a clear preference for switching on the “soft” side. Furthermore, when the tip biases are removed, the domain structure begins to relax, as seen in Fig. 5f–i. Clearly the relaxation is larger for the “hard” edge (the switched domain shrinks to a much smaller size), and the original domain structure is mostly restored, as compared to the “soft” edge switching. We believe this because the switched domain is less stable on the “hard” side due to the large energy penalty, such that the relaxation is faster. Our phase-field simulation thus clearly shows the difference of domain switching and relaxation near the “soft” and “hard” edges of the 90◦ domain wall. The observations of this asymmetry, in combination with the phase-field modeling, suggest that ferroelectric domain wall motion is a strong component of the observed electromechanical relaxation behavior; however as stated earlier, we cannot discount that other mechanisms may also play a role.
Finally, to conclude our investigation of the NTF analysis on D-PFM relaxation data and the associated mechanisms, shown in Fig. 6 is a direct NMF comparison. Figure 6a–d shows the relaxation components plotted alongside the loading maps for −15V pulse (Fig. 6e–h) and +15 V pulse (Fig. 6i–l) for the 4 components. At negative biases, little difference is observed in the abundance maps indicating the relaxation behavior is a convolution of all relaxation components. In contrast, large positive biases show a preference towards component 1 and component 4, as seen in the abundance maps. It is noteworthy the positive bias/component 4 highlights the interesting relaxation dynamics seen at the a-c domain boundaries. However, it lacks correlation to the larger a-domain/c-domain, i.e., the spatial, temporal, and voltage relationship for this mechanism is not intuitively observed. Nevertheless, NMF produces 64 abundance maps (4 for each voltage) and 4 relaxation components resulting in a hard to interpret representation of the multidimensional dataset and further emphasizing the need for tensor rather than matrix factorization. Furthermore, the technique comparison clearly illustrates NTF’s ability to maintain interconnected relationships between multiple variables.
To summarize, spatially resolved time and voltage-dependent polarization dynamics in multidomain PbTiO3 films are explored using D-PFM in conjunction with interferometric displacement sensing. To extract physically relevant and simple behaviors from the 4D D-PFM data sets, we introduce the non-negative tensor factorization method. We observe distinct relaxation mechanisms and ferroelectric behavior associated with relaxation of domain walls and dipole realignments with an enhanced relaxation behavior at one side of the a-c domain wall. We then perform phase-field modeling to capture this asymmetric relaxation process finding the underlying mechanism to be the presence of “hard” and “soft” domain edges. Finally, to conclude the importance of NTF, we directly compare results derived from the traditional multivariate analysis technique, NFM, finding an underwhelming representation of the multidimensional dataset. This manuscript highlights the advancements in both PFM data acquisition and multidimensional analysis, and the applicability of NTF to broader scientific areas.
Methods
Experimental
As a model system, we have chosen a 700 nm-thick PbTiO3 thin film grown by chemical vapor deposition on (001) KTaO3 substrates with an SrRuO3 conducting buffer layer; this film displays a dense polydomain structure as previously reported69,70. The PFM was performed using a commercially available atomic force microscopy (Cypher, Oxford Instruments) fitted with an interferometric displacement sensor.
Simulation (phase-field)
In the phase-field simulation we use polarization vector Pi = (Px, Py, Pz) as the order parameter to describe the ferroelectric state in the PbTiO3 thin film. The temporal evolution of Pi is calculated by minimizing the total free energy F with respect to Pi by numerically solving the time-dependent Landau–Ginzburg–Devonshire (LGD) equations71,
where x is the spatial position, t is the time, L is the kinetic coefficient related to the domain wall mobility. The total free energy F of the PbTiO3 thin film includes the Landau, gradient, elastic, and electrostatic energies, i.e.,
where V is the total volume of the system, εij and Ei denote the components of strain and electric fields, respectively. Detailed expressions of each free energy density can be found in ref. 72. Equation (3) is numerically solved using a semi-implicit spectral method73 based on a 3D geometry sampled on a 128Δx × 128Δy × 32Δz system size, with Δx = Δy = Δz = 1.0 nm. The thickness of the film, substrate, and air are 20Δz, 10Δz, and 2Δz, respectively. The temperature is T = 25 °C, and an isotropic relative dielectric constant (κii) is chosen to be 50. The gradient energy coefficients are set to be G11/G110 = 0.6, while G110 = 1.73 × 10−10 C−2m4N. The Landau coefficients, electrostrictive coefficients, and elastic-compliance constants are collected from ref. 72.
To model a local contact of a scanning probe tip, we specify the electrical potential distribution on the bottom (ϕ1) and top surface (ϕ2) of the PbTiO3 film as,
in which ϕ0 is the tip bias, (x0, y0) is the tip position and γ is the half-width half magnitude of the tip. Here we chose γ = 5 nm.
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Code availability
The python scripts used during the current study are available from the corresponding author on reasonable request.
Change history
11 February 2021
A Correction to this paper has been published: https://doi.org/10.1038/s41524-020-00405-4
References
Waser, R. Nanoelectronics and Information Technology: Advanced Electronic Materials and Novel Devices (John Wiley & Sons, Inc., 2003).
Tsymbal, E. Y. & Kohlstedt, H. Applied physics—tunneling across a ferroelectric. Science 313, 181–183 (2006).
Maksymovych, P. et al. Polarization control of electron tunneling into ferroelectric surfaces. Science 324, 1421–1425 (2009).
Gruverman, A. et al. Tunneling electroresistance effect in ferroelectric tunnel junctions at the nanoscale. Nano Lett. 9, 3539–3543 (2009).
Miller, S. L. & McWhorter, P. J. Physics of the ferroelectric nonvolatile memory field-effect transistor. J. Appl. Phys. 72, 5999–6010 (1992).
Mathews, S., Ramesh, R., Venkatesan, T. & Benedetto, J. Ferroelectric field effect transistor based on epitaxial perovskite heterostructures. Science 276, 238–240 (1997).
Damjanovic, D. Ferroelectric, dielectric and piezoelectric properties of ferroelectric thin films and ceramics. Rep. Prog. Phys. 61, 1267–1324 (1998).
Zhang, S. T. et al. High-strain lead-free antiferroelectric electrostrictors. Adv. Mater. 21, 4716-+ (2009).
Rodel, J. et al. Perspective on the development of lead-free piezoceramics. J. Am. Ceram. Soc. 92, 1153–1177 (2009).
Gharb, N. B., Trolier-McKinstry, S. & Damjanovic, D. Piezoelectric nonlinearity in ferroelectric thin films. J. Appl. Phys. 100, 044107 (2006).
Glinchuk, M. D. & Stephanovich, V. A. Dynamic properties of relaxor ferroelectrics. J. Appl. Phys. 85, 1722–1726 (1999).
Glinchuk, M. D. & Stephanovich, V. A. Theory of the nonlinear susceptibility of relaxor ferroelectrics. J. Phys.-Condens Mat. 10, 11081–11094 (1998).
Takenaka, H., Grinberg, I., Liu, S. & Rappe, A. M. Slush-like polar structures in single-crystal relaxors. Nature 546, 391-+ (2017).
Setter, N. et al. Ferroelectric thin films: review of materials, properties, and applications. J. Appl. Phys. 100, 051606 (2006).
Vugmeister, B. E. & Rabitz, H. Kinetics of electric-field-induced ferroelectric phase transitions in relaxor ferroelectrics. Phys. Rev. B 65, 024111 (2001).
Huang, Y.-C. et al. Giant enhancement of ferroelectric retention in BiFeO3 mixed-phase boundary. Adv. Mater. 26, 6335–6340 (2014).
Hong, J. W., Park, S.-i & Khim, Z. G. Measurement of hardness, surface potential, and charge distribution with dynamic contact mode electrostatic force microscope. Rev. Sci. Instrum. 70, 1735–1739 (1999).
Güthner, P. & Dransfeld, K. Local poling of ferroelectric polymers by scanning force microscopy. Appl. Phys. Lett. 61, 1137–1139 (1992).
Franke, K., Besold, J., Haessler, W. & Seegebarth, C. Modification and detection of domains on ferroelectric PZT films by scanning force microscopy. Surf. Sci. 302, L283 (1994).
Gruverman, A., Auciello, O. & Tokumoto, H. Scanning force microscopy for the study of domain structure in ferroelectric thin films. J. Vac. Sci. Technol. B: Microelectron. Nanometer Struct. Process. Meas. Phenom. 14, 602–605 (1996).
Hidaka, T. et al. Formation and observation of 50 nm polarized domains in PbZr1−xTixO3 thin film using scanning probe microscope. Appl. Phys. Lett. 68, 2358–2359 (1996).
Franke, K. Evaluation of electrically polar substances by electric scanning force microscopy. Part II: Measurement signals due to electromechanical effects. Ferroelectr. Lett. Sect. 19, 35–43 (1995).
Gruverman, A., Auciello, O. & Tokumoto, H. Imaging and control of domain structures in ferroelectric thin films via scanning force microscopy. Annu. Rev. Mater. Sci. 28, 101–123 (1998).
Gruverman, A., Auciello, O., Ramesh, R. & Tokumoto, H. Scanning force microscopy of domain structure in ferroelectric thin films: imaging and control. Nanotechnology 8, A38–A43 (1997).
Gruverman, A. L., Hatano, J. & Tokumoto, H. Scanning force microscopy studies of domain structure in BaTiO3 single crystals. Jpn. J. Appl. Phys. Part 1 - Regul. Pap. Short. Notes Rev. Pap. 36, 2207–2211 (1997).
Balke, N., Bdikin, I., Kalinin, S. V. & Kholkin, A. L. Electromechanical imaging and spectroscopy of ferroelectric and piezoelectric materials: state of the art and prospects for the future. J. Am. Ceram. Soc. 92, 1629–1647 (2009).
Kalinin, S. V., Rar, A. & Jesse, S. A decade of piezoresponse force microscopy: progress, challenges, and opportunities. Ieee Trans. Ultrason. Ferroelectr. Freq. Control 53, 2226–2252 (2006).
Balke, N. et al. Direct observation of capacitor switching using planar electrodes. Adv. Funct. Mater. 20, 3466–3475 (2010).
Khomchenko, V. A. et al. Synthesis and multiferroic properties of Bi0.8A0.2FeO3 (A = Ca,Sr,Pb) ceramics. Appl. Phys. Lett. 90, 242901 (2007).
Woo, J., Hong, S., Min, D. K., Shin, H. & No, K. Effect of domain structure on thermal stability of nanoscale ferroelectric domains. Appl. Phys. Lett. 80, 4000–4002 (2002).
Hong, S. In Nanoscale Phenomena in Ferroelectric Thin Films (ed Seungbum Hong) 111–131 (Springer US, 2004).
Polomoff, N. A., Premnath, R. N., Bosse, J. L. & Huey, B. D. Ferroelectric domain switching dynamics with combined 20 nm and 10 ns resolution. J. Mater. Sci. 44, 5189–5196 (2009).
Nath, R., Chu, Y.-H., Polomoff, N. A., Ramesh, R. & Huey, B. D. High speed piezoresponse force microscopy: <1 frame per second nanoscale imaging. Appl. Phys. Lett. 93, 072905 (2008).
Kalinin, S. V. & Bonnell, D. A. Temperature dependence of polarization and charge dynamics on the BaTiO3(100) surface by scanning probe microscopy. Appl. Phys. Lett. 78, 1116–1118 (2001).
Tiedke, S. et al. Direct hysteresis measurements of single nanosized ferroelectric capacitors contacted with an atomic force microscope. Appl. Phys. Lett. 79, 3678–3680 (2001).
Pertsev, N. et al. Dynamics of ferroelectric nanodomains in BaTiO3 epitaxial thin films via piezoresponse force microscopy. Nanotechnology 19, 375703 (2008).
Chen, L. et al. Formation of 90 elastic domains during local 180 switching in epitaxial ferroelectric thin films. Appl. Phys. Lett. 84, 254–256 (2004).
Rodriguez, B. J. et al. Domain growth kinetics in lithium niobate single crystals studied by piezoresponse force microscopy. Appl. Phys. Lett. 86, 012906 (2005).
Paruch, P., Kolton, A. B., Hong, X., Ahn, C. H. & Giamarchi, T. Thermal quench effects on ferroelectric domain walls. Phys. Rev. B. 85, 214115 (2012).
Xiao, Z., Poddar, S., Ducharme, S. & Hong, X. Domain wall roughness and creep in nanoscale crystalline ferroelectric polymers. Appl. Phys. Lett. 103, 112903 (2013).
Blaser, C. & Paruch, P. Subcritical switching dynamics and humidity effects in nanoscale studies of domain growth in ferroelectric thin films. N. J. Phys. 17, 013002 (2015).
Zhao, T. et al. Electrical control of antiferromagnetic domains in multiferroic BiFeO3 films at room temperature. Nat. Mater. 5, 823–829 (2006).
Vasudevan, R., Jesse, S., Kim, Y., Kumar, A. & Kalinin, S. Spectroscopic imaging in piezoresponse force microscopy: new opportunities for studying polarization dynamics in ferroelectrics and multiferroics. MRS Commun. 2, 61–73 (2012).
Kalinin, S. V., Rodriguez, B. J. & Kholkin, A. L. In Encyclopedia of Nanotechnology (ed Bharat Bhushan) 2117–2125 (Springer Netherlands, 2012).
Roelofs, A. et al. Differentiating 180 degrees and 90 degrees switching of ferroelectric domains with three-dimensional piezoresponse force microscopy. Appl. Phys. Lett. 77, 3444–3446 (2000).
Molotskii, M. I. & Shvebelman, M. M. Dynamics of ferroelectric domain formation in an atomic force microscope. Philos. Mag. 85, 1637–1655 (2005).
Morozovska, A. N., Eliseev, E. A., Bravina, S. L. & Kalinin, S. V. Resolution-function theory in piezoresponse force microscopy: wall imaging, spectroscopy, and lateral resolution. Phys. Rev. B 75, 174109 (2007).
Morozovska, A. N. et al. Thermodynamics of nanodomain formation and breakdown in scanning probe microscopy: Landau-Ginzburg-Devonshire approach. Phys. Rev. B 80, 214110 (2009).
Wold, S., Esbensen, K. & Geladi, P. Principal component analysis. Chemomet. Intell. Lab. Syst. 2, 37–52 (1987).
Schölkopf, B., Smola, A. & Müller, K. Nonlinear component analysis as a Kernel eigenvalue problem. Neural Comput. 10, 1299–1319 (1998).
Paatero, P. Least squares formulation of robust non-negative factor analysis. Chemomet. Intell. Lab. Syst. 37, 23–35 (1997).
Paatero, P. & Tapper, U. Positive matrix factorization: a non-negative factor model with optimal utilization of error estimates of data values. Environmetrics 5, 111–126 (1994).
Comon, P. Independent component analysis, a new concept? Signal Process. 36, 287–314 (1994).
Vasudevan, R. K., Balke, N., Maksymovych, P., Jesse, S. & Kalinin, S. V. Ferroelectric or non-ferroelectric: why so many materials exhibit “ferroelectricity” on the nanoscale. Appl. Phys. Rev. 4, 021302 (2017).
Harnagea, C., Pignolet, A., Alexe, M. & Hesse, D. Piezoresponse scanning force microscopy: what quantitative information can we really get out of piezoresponse measurements on ferroelectric thin films. Integr. Ferroelectr. 44, 113–124 (2002).
Hong, S., Shin, H., Woo, J. & No, K. Effect of cantilever–sample interaction on piezoelectric force microscopy. Appl. Phys. Lett. 80, 1453–1455 (2002).
Harnagea, C., Pignolet, A., Alexe, M. & Hesse, D. Higher-order electromechanical response of thin films by contact resonance piezoresponse force microscopy. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 53, 2309–2322 (2006).
Collins, L., Liu, Y., Ovchinnikova, O. & Proksch, R. Quantitative electromechanical atomic force microscopy. ACS Nano 13, 8055–8066 (2019).
Balke, N. et al. Exploring local electrostatic effects with scanning probe microscopy: implications for piezoresponse force microscopy and triboelectricity. ACS Nano 8, 10229–10236 (2014).
Balke, N. et al. Differentiating ferroelectric and nonferroelectric electromechanical effects with scanning probe microscopy. ACS Nano 9, 6484–6492 (2015).
Kumar, A. et al. Dynamic piezoresponse force microscopy: spatially resolved probing of polarization dynamics in time and voltage domains. J. Appl. Phys. 112, 052021 (2012).
Kelley, K. P. et al. Thickness and strain dependence of piezoelectric coefficient in BaTiO3 thin films. Phys. Rev. Mater. 4, 024407 (2020).
Kim, J. & Park, H. In High-Performance Scientific Computing: Algorithms and Applications (eds Michael W. Berry et al.) 311–326 (Springer London, 2012).
Mørup, M. Applications of tensor (multiway array) factorizations and decompositions in data mining. Wiley Interdiscip. Rev.: Data Min. Knowl. Discov. 1, 24–40 (2011).
Ganpule, C. et al. Role of 90 domains in lead zirconate titanate thin films. Appl. Phys. Lett. 77, 292–294 (2000).
Vasudevan, R. K. et al. Nanoscale origins of nonlinear behavior in ferroic thin films. Adv. Func. Mater. 23, 81–90 (2013).
Yu, J. et al. Resolving local dynamics of dual ions at the nanoscale in electrochemically active materials. Nano Energy 66, 104160 (2019).
Tybell, T., Paruch, P., Giamarchi, T. & Triscone, J.-M. Domain wall creep in epitaxial ferroelectric Pb(Zr0.2Ti0.8)O3 thin films. Phys. Rev. Lett. 89, 097601 (2002).
Li, L. et al. Direct imaging of the relaxation of individual ferroelectric interfaces in a tensile‐strained film. Adv. Electron. Mater. 3, 1600508 (2017).
Morioka, H. et al. Suppressed polar distortion with enhanced Curie temperature in in-plane 90°-domain structure of a-axis oriented PbTiO3 Film. Appl. Phys. Lett. 106, 042905 (2015).
Chen, L.-Q. Phase-field method of phase transitions/domain structures in ferroelectric thin films: a review. J. Am. Ceram. Soc. 91, 1835–1844 (2008).
Haun, M. J., Furman, E., Jang, S. J., McKinstry, H. A. & Cross, L. E. Thermodynamic theory of PbTiO3. J. Appl. Phys. 62, 3331–3338 (1987).
Chen, L. Q. & Shen, J. Applications of semi-implicit Fourier-spectral method to phase field equations. Comput. Phys. Commun. 108, 147–158 (1998).
Acknowledgements
The experimental portion of this work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division (R.K.V., K.K.). A portion of this research was conducted at the Center for Nanophase Materials Sciences, which also provided support (S.J., S.V.K.) and is a US DOE Office of Science User Facility. The algorithm portion was sponsored (R.K.) by the Laboratory Directed Research and Development Program of Oak Ridge National Laboratory, managed by UT-Battelle, LLC, for the U.S. Department of Energy (DOE). This research used resources of the Compute and Data Environment for Science (CADES) at the Oak Ridge National Laboratory, which is supported by the Office of Science of the U.S Department of Energy under Contract No. DE-AC05-00OR22725. This work was partially supported by the JSPSKAKENHI Grant Nos. 15H04121, and 26220907 (H.F.).
Author information
Authors and Affiliations
Contributions
K.P.K. and R.K.V. performed the experimental measurements; Y.R. and Y.C. carried out phase-field modeling simulations; Y.E. and H.F grew the thin films; K.P.K, L.L., S.S., R.K., and R.K.V. applied tensor factorization algorithm to spectroscopy data; S.J. developed data acquisition system; K.P.K., R.K.V., and S.V.K. wrote initial draft and participated in data interpretation; All authors participated in discussions and contributed in finalizing the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kelley, K.P., Li, L., Ren, Y. et al. Tensor factorization for elucidating mechanisms of piezoresponse relaxation via dynamic Piezoresponse Force Spectroscopy. npj Comput Mater 6, 113 (2020). https://doi.org/10.1038/s41524-020-00384-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-020-00384-6