Abstract
Conventional metasurfaces have demonstrated efficient wavefront manipulation by using thick and high-aspect-ratio nanostructures in order to eliminate interactions between adjacent phase-shifter elements. Thinner-than-wavelength dielectric metasurfaces are highly desirable because they can facilitate fabrication and integration with both electronics and mechanically tunable platforms. Unfortunately, because their constitutive phase-shifter elements exhibit strong electromagnetic coupling between neighbors, the design requires a global optimization methodology that considers the non-local interactions. Here, we propose a global evolutionary optimization approach to inverse design non-local metasurfaces. The optimal designs are experimentally validated, demonstrating the highest efficiencies for the thinnest transmissive metalenses reported to-date for visible light. In a departure from conventional design methods based on the search of a library of pre-determined and independent meta-atoms, we take full advantage of the strong interactions among nanoresonators to improve the focusing efficiency of metalenses and demonstrate that efficiency improvements can be obtained by lowering the metasurface filling factors.
Similar content being viewed by others
Introduction
Optical metasurfaces enable wavefront manipulation by spatially arranging sub-wavelength phase-shifter elements on a flat surface1. Almost all of the existing designs rely on the search of a library of pre-determined phase-shifter elements, meta-atoms, which introduces spatially localized phase shifts to the incident wavefront2. A critical requirement for the optimal design of metasurfaces is that every meta-atom must be electromagnetically independent from its neighbors3 to assure local control of the light rather than over a macroscopic area of the metasurface. Consequently, in order to tightly localize light inside the meta-atoms, most metasurfaces for wavefront control require high-index-contrast between the phase-shifter elements and the surrounding medium4, and fabrication of high-aspect ratio structures with deep sub-micron features and gaps, making mass volume production and hybrid integration extremely challenging5,6,7.
There is an increasing demand to reduce the metasurface thickness and meta-atom complexity while retaining high optical efficiency, which could circumvent the fabrication of high-aspect-ratio structures, and therefore facilitate higher-level integration of metasurfaces with electronics, MEMS8,9, and deformable substrates10,11,12. Recent attempts to demonstrate light manipulation with thinner waveguides have resulted in incomplete phase modulation and an intrinsic reduction in performance13. A promising approach is to use ultrathin dielectric nanoresonators, which exhibit electrical and magnetic dipolar resonances whose spectral response can be geometrically tuned14,15,16 to provide both high transmission and full 2π phase control17. However, unlike tall waveguides with strong transversal confinement of light, ultrathin nanoresonators have long evanescent electromagnetic fields that reach beyond adjacent neighbors, coupling their resonances and making the conventional design of phase-gradient metasurfaces virtually impossible. Thus, for interacting meta-atoms, the optical properties of non-homogenous arrays, as required in a metalens layout, deviate significantly from the library of homogenous arrays. As a result, all of the thin resonator-based metasurfaces demonstrated to-date are either limited to slow and uniform phase changes, such as small-angle deflectors18,19,20, or limited to wavelengths longer than the visible, where materials with very high refractive index are available21.
On one hand, the limited availability of high-index materials in the visible spectrum represents a fundamental limitation to the design of high-efficiency ultrathin dielectric metasurfaces, mostly because the refractive indexes of all the low-absorption materials available for dielectric nanophotonics are not high enough to minimize interactions among resonators22. On the other hand, the conventional design approach is inherently limited in efficiency for extreme wave manipulation (e.g., large-angle deflection, near-field focusing), due to insufficient discretization of continuous phase mapping23 and local impedance mismatch between input and output wavefronts24, while strong non-local metasurfaces provide a promising solution24.
Inspired by recent developments in computational inverse design approaches to produce nanophotonics25 devices and metasurfaces26,27 with tailored responses, we have developed an inverse design strategy based on evolutionary optimization (EO) to demonstrate the thinnest (t ≈ λ/5) metalenses with the highest efficiencies in the visible spectrum. Instead of trying to avoid or minimize the interactions among meta-atoms, we build a general inverse design workflow that takes full advantage of interactions and leverages it to design high-performance metalenses. We employ a genetic algorithm (GA) to mimic natural selection in order to determine the optimal spatial arrangement of nanoresonators to achieve the desired optical performance, through an interface with finite-difference time-domain (FDTD) simulation. The optimal inverse designs are experimentally fabricated and shown to significantly improve the focusing efficiency when compared with conventional intuitive design by library search.
Results
Ultrathin metasurfaces with non-local interactions
The studied metasurfaces are based on TiO2, a dielectric material fully compatible with semiconductor fabrication processes, with a relative high refractive index and negligible dissipation in the visible spectrum28, which has been widely used in waveguide-type metasurfaces5,6, but not in resonant metalenses. Our ultrathin metasurfaces consist of polarization-independent circular shaped TiO2 resonators fabricated on a fused silica glass substrate and embedded in HSQ, a spin-on-glass material with refractive index comparable to glass and compatible with CMOS and MEMS fabrication processes29. The HSQ layer not only provides a protective coating for the nanostructures (similar to the SU-8 coating used in ref. 30), but also serves as an optical passivation layer for the resonant meta-atoms whose resonances are sensitive to the encasing environment.
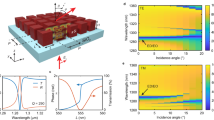
In order to demonstrate the presence of strong interactions among resonators, we study the transmission and phase shifting properties of square and hexagonal arrays of the same circular resonators under illumination along its axis of symmetry (z axis)14,15,16. We use FDTD solvers (implemented in Lumerical) to build a database of transmission and phase values, by varying the resonator’s geometrical parameters (disc radius r, edge-to-edge gap g, and thickness t). The thickness was optimized to ensure both high efficiency and robust nanofabrication. Figure 1 shows the transmission (a and d) and phase (b and e) dependence on the in-plane geometry for square (top) and hexagonal (bottom) arrays with thickness t = 115 nm. When the geometric parameters meet the Huygens condition, i.e., spectral matching of the electric dipole and magnetic dipole, the back-scattering of light by both dipoles in the incidence direction is canceled, leaving only forward propagation (white dashed circles in Fig. 1a, b, d, e)17. It is clearly shown that the geometrical location of the Huygens condition changes significantly with the arrangement of the nanoresonators. For the square array, the phase can be modulated while maintaining high transmission, following a path of constant pitch (white dashed lines, pitch p = 2r + g = 310 nm) through the Huygens condition region (white dashed circles). The phase shift dependence on disc radius along this path (Fig. 1c) is usually used as a library of meta-atoms to create conventional phase-gradient metasurfaces. However, the same library path (white dashed lines in Fig. 1d, e) provides significantly different responses for the hexagonal arrays (Fig. 1f). The electromagnetic fields distribution also changes with the local arrangement (insets of Fig. 1c, f), in spite of the fact that the radius and gaps between discs are exactly the same. This demonstrates that the ultrathin resonators are strongly coupled and influenced by their neighbors. As comparison, since waveguides are only weakly coupled31, their transmission and phase responses in the meta-atom library are almost identical for square and hexagonal arrays (Supplementary Fig. 1). Therefore, the conventional intuitive design of matching the optical phase profile with phase-shifter elements from a library of pre-determined building blocks (Fig. 2a–c) is only applicable for independent high-aspect-ratio waveguides, but will be problematic for coupled ultrathin dielectric resonators, as the local arrangement will deviate from the pre-determined homogenous configurations.
FDTD simulation results of the transmission and phase shift experienced by a uniform wavefront of light after propagation through a homogeneous and periodic nanoresonator array (circular TiO2 nanodiscs on glass substrate and embedded in HSQ medium). Square arrays: a transmission and b phase shift as a function of the disc radius and edge-to-edge gap; c transmission and phase for a resonator library with constant pitch of 310 nm and varying disc radius (following the path marked by white dashed lines in a, b). Hexagonal arrays: d transmission and e phase shift as a function of the disc radius and edge-to-edge gap; f transmission and phase for the same library with constant pitch (310 nm) and varying disc radius in hexagonal arrangement. The insets in c, f show the side views of the electric energy density in a resonator array (pitch 310 nm, radius 125 nm) for square and hexagonal arrangements, respectively.
a Ideal phase profile of a focusing lens. The inset equation corresponds to the 1D phase profile of a cylindrical lens, where x is the radial position relative to the lens center and f is the focal length. b A pre-determined meta-atom library (disc radius vs. phase shift diagram), similar to Fig. 1c. The phase profile is discretized using sub-wavelength meta-atoms with radius obtained from the pre-determined library, in order to generate a phase profile that is closest to the continuous phase profile. c A typical metalens layout designed by library search. The appropriate discs are placed in a constant-pitch lattice, in order to reproduce the ideal phase map. d Electric energy density distribution in the x–z cross-section of an ideal focusing lens. The lens is illuminated by an incident plane wave from the bottom and focuses the light to a focal spot at a distance f above the lens plane. e Evolutionary optimization workflow: genetic algorithm with an interface to FDTD simulation. f A typical aperiodic metalens layout designed by evolutionary optimization.
Inverse design based on evolutionary optimization
In this work, we demonstrate an inverse design strategy based on EO, which considers interactions among strongly coupled thin resonators through an interface to FDTD simulation (Fig. 2d–f). We employ GA to mimic natural selection in order to determine the optimal arrangement of meta-atoms to achieve the target performance32. Our objective is to identify an arrangement of nanoresonators that maximizes the device performance i.e., the focusing efficiency. Figure 2d depicts the “ideal” axial electric energy density of a focusing metalens illuminated by a plane wave from the bottom that sends 100% of the light to a diffraction-limited focal spot at the pre-determined focal length. The inverse design workflow to achieve this target performance is summarized in Fig. 2e. In this workflow, we first randomly generate a population Np (~tens to hundreds33) of metasurface structures. For each member in the population, the target properties (e.g., phase profile, transmission, and focusing intensity) are evaluated by solving Maxwell’s equations (FDTD simulations) for the entire device structure. In a departure from conventional GA approach, our evolutionary procedure also takes advantage of clustering the populations into different classes; this classification is done based on performance of individual populations and the resultant grouping improves the diversity of the pool (see ref. 34 for details on the grouping). Our evolutionary process allows winning classes (representing better set of individuals) to expand their sizes; this translates into a more expanded search of the phase space allowing us to explore solutions near possible global minimum. Each class (i.e., group of population) explores a specific section of the structural phase space and avoids bias on solutions arising from use of individual populations in a purely conventional GA search. Next, our workflow computes the weighted sum of errors in prediction over all the populations, which is defined as its objective function (OF). As mentioned earlier, the OF here is set to maximize the focusing efficiency, which is computed from the intensity curve at the focal spot, as detailed in the methods section. The member I of the population is represented as a set given by Eq. (1),
where \(x_i^\prime = x_i/l_x\) and \(r_i^\prime = r_i - r_{\min }/r_{\max } - r_{\min }\) are the normalized position and radius of meta-atom i after sorting them according to position, lx is the length of the device, rmax and rmin are the maximum and the minimum allowed values for the radius. The initial pool is randomly generated to start the search. The OF (focusing efficiency) values of the members in this initial pool are computed based on FDTD simulations. The members are then sorted by their OF values. A certain number of m best members among the total Np are chosen, which are then subjected to genetic operations. The probability of a member being selected for genetic operation is determined by its OF. The genetic operations included in our algorithm are (i) mutation, (ii) crossover, (iii) inversion, (iv) replacement by random structure. The details of the operation and their associated probabilities are provided in the methods section (see Supplementary Fig. 2 for a schematic representation). These operations result in “offspring” members containing the traits (binary segments) from their parent structures. Out of the Np members, and the offsprings, only the best Np set of metasurface structures are retained for the next generation. Such an optimization routine ensures that only good parameter sets survive after each generation. Upon repeating this workflow for sufficient generations, we sample diverse regions in the structural space before the run converges35, i.e., the OF values for a minimum members in the population are below a prescribed tolerance (see the methods section and the convergence curve in Supplementary Fig. 3). Typically, tens of such GA runs starting with different random population are necessary to scour the parameter space36; we choose ~10 best configurations from each of these GA runs, which give similar OF values. One such sample optimized metasurface configuration obtained using our inverse design workflow is depicted in Fig. 2f. Interestingly, we note that the typical EO designed layouts (e.g., Fig. 2f) consist of an aperiodic arrangement of nanoresonators with a geometry significantly different than the one expected from the Huygens conditions but resulting in a metalens with better performance.
The inverse design workflow described above was used to optimize cylindrical metalenses for different numerical apertures (NAs) in the visible range, which were then cross-validated by experimental fabrication and characterization. In Fig. 3a, we compare the focusing efficiency η vs. NA of simulated and fabricated metalenses using both EO and conventional design methods. The main result of the study is evident in this figure: the lenses designed using EO (orange line) have focusing efficiencies much larger than conventional designs (blue line) for all the NAs considered. As expected, the efficiency decreases with increasing NA, because it is more challenging to fit the rapidly changing phase profile in the periphery of a lens with large NA. For small NAs, the phase spatial change is slow and the arrangement of phase-shifter elements does not deviate too much from the homogeneous library. The EO approach does not differ too much from the conventional design, although it slightly improves the lens focusing efficiency (e.g., NA = 0.17, ηconventional ~ 70%, while ηEO ~ 77%). For larger NAs, the phase changes more rapidly and the conventional designed layouts suffer severe deviation from the homogeneous library. In this case, the non-local interactions play an important role and the EO designed lenses significantly improve the focusing efficiency compared with conventional designs (e.g., for NA = 0.51, ηconventional ~ 30%, while ηEO ~ 60%).
a Comparison of focusing efficiency vs. numerical aperture (NA) of cylindrical lenses by conventional and EO designs. For all the NAs studied, the EO designed metalenses are more efficient to focus light. b Scanning electron microscopy images of the meta-atoms arrangement for lenses with NA = 0.51 and 0.77, and the corresponding measured light intensity distribution along the axial direction (x–z plane) for both conventional and EO designs. c Comparative analysis of the metalens filling factors for various NAs. The metalenses designed using interactive meta-atoms have smaller fill factor than the ones designed using non-interacting ones. Size bar for the SEM is 2 μm, and 500 nm for the zoom-in.
In order to verify the focusing efficiency improvement of the EO designed metalenses, we fabricated lenses for green light (λ = 532 nm) with NA of 0.17, 0.51, 0.77, 0.87, and 0.92 (NA = 0.17 corresponding to a lens diameter of 12 μm and a focal length f of 35 μm, and the rest corresponding to a lens diameter of 12, 24, 36, 48 μm, respectively, with a constant f of 10 μm). We used a high-precision fabrication process, where the thickness was controlled by atomic layer deposition (ALD), and the in-plane geometry was patterned by e-beam lithography and reactive ion etching (Supplementary Fig. 4). The experimental efficiencies are shown in Fig. 3a for the EO (orange circles) and conventional (blue circles) designs, which are in good agreement with the simulation results.
The fabricated metalenses were characterized by scanning electron microscopy (SEM) before deposition of the HSQ coating. Figure 3b (see also Supplementary Fig. 5) compares the SEMs of different lens layouts, which verifies the aperiodic nature of the EO designed lenses. The measured intensity distributions along the lens axial direction are also shown in Fig. 3b, which are in agreement with theoretical simulations (Supplementary Fig. 6). In conventional designs, the ideal phase profile cannot be implemented due to the non-local interactions between resonators and as a consequence, there is light going to diverging directions and satellite peaks, causing a reduction in the amount of light reaching the focal point. In the EO designed metalenses, the interactions among resonators are considered, resulting in an aperiodic layout with higher focusing efficiency since most of the light is directed toward the focal point. Both conventional and EO designed metalenses have diffraction-limited focal spots (Supplementary Fig. 7).
The aperiodic layouts, especially for larger NAs, are composed of clustered discs with a larger range of size variation, leaving more empty spaces among adjacent clusters than conventional periodic layouts. As a result, the EO designs have filling factors consistently smaller than the filling factors of metalenses designed by conventional library search (Fig. 3c). The fact that a metasurface with a smaller filling factor yields higher efficiency is counterintuitive in conventional design methodology, where the phase-shifter elements have to be located as close as possible to each other in order to manipulate light efficiently3. This is because, instead of multiple independent phase-shifters, a group of closely spaced nanoresonators together with surrounding empty space work as a whole constitutive element, which could create complex collective optical modes to enhance or suppress scattering of light along specific directions. Similar features were recently observed in asymmetric cluster (dimer) nanoantenna arrays, which were used to improve the efficiency for large-angle deflection23,37. The proposed inverse computational approach introduces more possibilities for the design of metalenses while maintaining their thickness much smaller than the operating wavelength. The results of Fig. 3 indicate that the intrinsic electromagnetic interactions among nanoresonators can be used to globally engineer the metasurface response in order to optimize its far-field optical performance.
Discussion
Although the metalenses designed by evolutionary algorithms demonstrated significant performance improvements, there are no reasons to assume that we have reached the performance limit for these ultrathin metasurfaces, especially for high NAs. As NA increases, the interactions play a more significant role and thus, there is more room to further improve the metalenses performance. To achieve higher efficiencies, other machine learning, optimization algorithms, and emerging concepts could be implemented, such as topology optimization which exploits multiple spatially overlapping optical modes38,39, and metagratings with tailored bianisotropic inclusions which enable unitary efficiency without the need of deeply sub-wavelength elements40.
The advent of big-data analytics has brought to the forefront powerful techniques such as deep-learning and artificial intelligence (AI)-guided approaches such as Monte Carlo Tree Search (MCTS)41, which may help identify better optimal configurations than those reported in this work. Although GA and other evolutionary approaches have limitations arising from slow convergence to solution, we note that the optimization of an entire spherical lens design that has non-local interactions is non-trivial for any AI or machine-learning technique. In the case of deep-learning algorithms, one typically needs to train on a data set comprising of several 100,000 to millions of focal intensity maps of lens derived from FDTD calculations. Hence, there is a lot of computational cost that is paid upfront. On the other hand, the evolutionary design requires 1000s of iterations to converge but is highly parallelizable. The various populations of the GA could be simultaneously run on different cores in a supercomputer. Thus, the computational efficiency to train would be high even if the cost is also high. Therefore, regardless of the optimization scheme used, the key challenge lies in the fact that non-local interactions in ultrathin metasurfaces have a complex design landscape. Navigating through this landscape necessitates the simultaneous consideration of a large number of nanoscale resonators, which is non-trivial for any deep learning, MCTS or evolutionary approach.
In the future, such computational inverse design strategies can pave the way towards realizing large-scale ultrathin metasurfaces with multiple functions and/or extreme performances at much lower fabrication demands than those being designed to-date. For example, our approach could be beneficial to recent metalenses designs involving meta-atom structures which make use of local interactions to demonstrate broadband achromatic metasurfaces42,43 but are still limited to the search of a pre-determined library with high-aspect-ratio structures. Similarly, it could be useful to enhance recent inverse design computational frameworks that do not consider interactions among phase-shifter units44, in order to design metalenses for applications involving multi-wavelengths45 or multi-angle illumination.
To the best of our knowledge, this is the first study that tries to perform a global structural optimization while concurrently accounting for non-local interactions between nanoscale resonators. This design strategy handles strongly coupled meta-atoms and enables higher efficiency metalenses with lower filling factor than the conventional designs by library search. This approach allowed us to demonstrate the highest efficiency for the thinnest (t ≈ λ/5) transmissive metalens for visible light. The low-aspect-ratio nanostructures are more compatible with standard mass-produced fabrication techniques46 and good candidates for building flat optical elements that can be easily integrated onto CMOS electronics and MEMS devices.
Methods
Numerical simulation
A commercial FDTD software (Lumerical) was used for nanoresonator and device simulations. To build a database, a uniform TiO2 nanoresonator array was simulated by a single nanodisc with periodic boundary conditions in both x and y axes. The light transmission was quantified as the power transmitted through the nanoarray, normalized by the source power. The geometric parameters of both radius and gap were swept (Fig. 1; Supplementary Fig. 1). For device simulation, a cylindrical lens was constructed by a layout of nanodiscs along the x axis, with periodic boundary conditions in the y axis, and incident wave polarization in the y axis. The focal intensity profile (|E|2) was recorded and fitted to a Gaussian distribution \(I = ae^{ - \frac{{\left( {x - b} \right)^2}}{{2c^2}}}\) to calculate the focal spot power (\(\sqrt {2\pi } ac\)) and spot size (FWHM). The lens focusing efficiency was defined as the focal spot power divided by the power of a glass background with the same size as the lens.
Evolutionary algorithm
The optimization process begins by first randomly generating an initial pool of Np structures. The design constrains enforced during the search process are
where gmin is the minimum allowed value of the gap between adjacent meta-atoms. After the initial pool is generated, the OF for each member is computed using FDTD simulation. Then, m parent structures are chosen for genetic operations with probabilities based on the fitness, which is computed as
where OFI, OFmin and OFmax are the OF of the member I, the minimum and maximum value of OF in the pool corresponding to the current generation. The probability for a given structure being selected is \({{p}}_{\mathrm{I}} = \frac{{{{f}}_{\mathrm{I}}}}{{\sum {{f}}_{\mathrm{I}}}}\). Genetic operations included in our algorithm are described as follows (Supplementary Fig. 2a).
Mutation
Mutation alters/perturbs the position and the radius of one or more meta-atoms in a given parent structure. The probability for a meta-atom to be altered is randomly generated from a normal distribution.
Crossover
Crossover operations (Supplementary Fig. 2b) involve two parents, say, parent A and parent B. In a 1 pt crossover operation, an imaginary slicing line x = xs is randomly generated. All the meta-atoms with xi < xs (xi > xs) in parent A and xi > xs (xi < xs) in parent B are combined to produce offspring A (offspring B). In a 2 pt crossover operation, 2 such slicing lines are generated and the meta-atoms in between the lines are swapped between parent A and parent B to produce offsprings. Similarly, in a 3 pt slicing operation 3 slicing lines are generated and the alternating segments of parent A and B are swapped to produce the offsprings.
Inversion
During inversion, the position of the meta-atoms is inverted with respect to the center of the structure.
Replacement by random structure
The offsprings during this operation is simply a completely random design. This operation helps in retaining the diversity in the pool.
Assigned probability for the genetic operations during our search were 0.6, 0.2, 0.1, 0.1 for mutation, crossover, inversion, replacement by random structure, respectively. This is partially inspired by the success of genetic algorithm for crystal structure predictions47,48,49, where the position of the basis atoms and the lattice vectors are optimized to have minimum energy. In addition, during the genetic evolution (especially at an early stage), some offspring designs diverge the incident light, which produce offsprings that converge light after an inversion operation. Different variations of the crossover included in our algorithm are performed with equal probability. The above-mentioned genetic operations can sometimes produce offsprings with overlapping meta-atoms. In such cases, the overlapping meta-atoms are deleted and a new meta-atom is introduced if there is enough space after satisfying the design constrains mentioned above. Out of the Np structures in the pool and the m offsprings, the best Np structures are promoted to the pool of the next generation and the cycle continues until the OFs of the best Np /8 members differ no more than 2%. The value of Np and m used during the search is 40 and 16.
All the cases were converged within 250 generations, although an improved design close to (within 3% or less than) the converged best is obtained much earlier than that, typically around 60-80 generations (Supplementary Fig. 3). The conventional design by library search was included in the initial pool, which was not necessary but helped to speed up the EO process. Take the NA 0.51 lens as an example, starting with all random structures converged after 464 generations. The converged design is different but shares some similarity considering that the phase values are relative in an ideal phase profile (Supplementary Fig. 8a), and also provides comparable performance (2% less in the maximum intensity).
As the device scales up, the EO process becomes computationally expensive due to increasing volume of the parameter space (number of resonators), and system size for the FDTD simulations, which scales as O(N4), where N is the number of mesh grids. To improve the scalability, we simulate and optimize the entire metasurfaces, but address them in a sequence of increasing lens radius step by step, i.e., 6, 12, 18, 24 μm, with a constant f of 10 μm. In this way, for a given lens, the optimization of the central part is already converged, where the design is fixed, and GA is applied for the peripheral part only, which maintains a low volume of the parameter space and ensures efficient allocation of computational resources without repeating workload. When stitching a new peripheral part to the existing optimized central part, the boundary is offset inward to allow a 1 μm buffer zone (see an example in Supplementary Fig. 8b), which is sufficient to account the non-local interactions, while significantly reducing the computation expense. After optimization of the additional peripheral part, the buffer zone converges to a different design, demonstrating the effect of non-local interactions.
Nanofabrication
The metasurfaces were composed of TiO2 nanoresonator, whose thickness was precisely controlled by ALD, and the in-plane geometry was patterned by e-beam lithography, which is shown schematically in Supplementary Fig. 4. Glass substrates with 115 nm TiO2 ALD film were spin-coated with a bilayer of e-beam resist PMMA, and then 10 nm Au was sputtered as a conductive layer. The samples were patterned by a single step of e-beam lithography. After exposure, the Au conductive layer was removed by wet etching. The samples were developed in MIBK/IPA 3:1 at 4 °C with ultrasonication for 1 min. A 10 nm Cr layer was deposited by e-beam evaporation and then lift off, forming hard masks for pattern transfer. After dry etching of TiO2 and wet etching of Cr masks, metasurfaces of TiO2 nanoresonator arrays were formed on the glass substrates, and then embedded in HSQ coating.
Optical characterization
An inverted microscope (Olympus IX73) was used to image the metasurface samples in transmission. A home-built set-up was used to introduce a green laser (wavelength 532 nm, Opto Engine) from the top of the microscope. The focal plane images were taken in order to characterize the focusing efficiency and focal spot size. Similar to the simulation, the measured focal intensity profile was fitted to a Gaussian distribution to calculate the focal spot intensity and FWHM. The lens focusing efficiency was defined as the focal spot intensity divided by the glass background intensity of the same size as the lens. Image stacks were taken while moving the stage in z-direction automatically (Prior ES10ZE Focus Controller) and then processed to obtain the x–z intensity distribution.
Data availability
The data that support the findings of this study are available from the authors upon reasonable request.
Code availability
Code and workflow developed in this study are available from the authors upon reasonable request.
References
Yu, N. F. & Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 13, 139–150 (2014).
Khorasaninejad, M. & Capasso, F. Metalenses: versatile multifunctional photonic components. Science 358, 1146–1154 (2017).
Lalanne, P. & Chavel, P. Metalenses at visible wavelengths: past, present, perspectives. Laser Photonics Rev. 11, 1600295 (2017).
Chang-Hasnain, C. J. & Yang, W. J. High-contrast gratings for integrated optoelectronics. Adv. Opt. Photonics 4, 379–440 (2012).
Khorasaninejad, M. et al. Metalenses at visible wavelengths: diffraction-limited focusing and subwavelength resolution imaging. Science 352, 1190–1194 (2016).
Khorasaninejad, M. et al. Polarization-insensitive metalenses at visible wavelengths. Nano Lett. 16, 7229–7234 (2016).
Liddle, J. A. & Gallatin, G. M. Nanomanufacturing: a perspective. ACS Nano 10, 2995–3014 (2016).
Roy, T. et al. Dynamic metasurface lens based on MEMS technology. APL Photonics 3, 021302 (2018).
Arbabi, E. et al. MEMS-tunable dielectric metasurface lens. Nat. Commun. 9, 812 (2018).
She, A., Zhang, S. Y., Shian, S., Clarke, D. R. & Capasso, F. Adaptive metalenses with simultaneous electrical control of focal length, astigmatism, and shift. Sci. Adv. 4, eaap9957 (2018).
Zhu, J., Dexheimer, M. & Cheng, H. Reconfigurable systems for multifunctional electronics. npj Flex. Electron. 1, 1–13 (2017).
Kamali, S. M., Arbabi, E., Arbabi, A., Horie, Y. & Faraon, A. Highly tunable elastic dielectric metasurface lenses. Laser Photonics Rev. 10, 1002–1008 (2016).
Liu, C. H. et al. Ultrathin van der Waals metalenses. Nano Lett. 18, 6961–6966 (2018).
Kuznetsov, A. I., Miroshnichenko, A. E., Brongersma, M. L., Kivshar, Y. S. & Luk’yanchuk, B. Optically resonant dielectric nanostructures. Science 354, 2472 (2016).
Fu, Y. H., Kuznetsov, A. I., Miroshnichenko, A. E., Yu, Y. F. & Luk’yanchuk, B. Directional visible light scattering by silicon nanoparticles. Nat. Commun. 4, 1527 (2013).
Staude, I. et al. Tailoring directional scattering through magnetic and electric resonances in subwavelength silicon nanodisks. ACS Nano 7, 7824–7832 (2013).
Decker, M. et al. High-efficiency dielectric Huygens’ surfaces. Adv. Opt. Mater. 3, 813–820 (2015).
Yu, Y. F. et al. High-transmission dielectric metasurface with 2 phase control at visible wavelengths. Laser Photonics Rev. 9, 412–418 (2015).
Zhou, Z. P. et al. Efficient silicon metasurfaces for visible light. ACS Photonics 4, 544–551 (2017).
Ollanik, A. J., Smith, J. A., Belue, M. J. & Escarra, M. D. High-efficiency all-dielectric Huygens metasurfaces from the ultraviolet to the infrared. Acs Photonics 5, 1351–1358 (2018).
Zhang, L. et al. Ultra-thin high-efficiency mid-infrared transmissive Huygens meta-optics. Nat. Commun. 9, ARTN 1481 (2018).
Baranov, D. G. et al. All-dielectric nanophotonics: the quest for better materials and fabrication techniques. Optica 4, 814–825 (2017).
Paniagua-Dominguez, R. et al. A metalens with a near-unity numerical aperture. Nano Lett. 18, 2124–2132 (2018).
Mohammadi Estakhri, N. & Alù, A. Wave-front transformation with gradient metasurfaces. Phys. Rev. X 6, 041008 (2016).
Molesky, S. et al. Inverse design in nanophotonics. Nat. Photonics 12, 659–670 (2018).
Liu, Z. C., Zhu, D. Y., Rodrigues, S. P., Lee, K. T. & Cai, W. S. Generative model for the inverse design of metasurfaces. Nano Lett. 18, 6570–6576 (2018).
Malkiel, I. et al. Plasmonic nanostructure design and characterization via deep learning. Light Sci. Appl. 7, ARTN 60 (2018).
Shannon, R. D., Shannon, R. C., Medenbach, O. & Fischer, R. X. Refractive index and dispersion of fluorides and oxides. J. Phys. Chem. Ref. Data 31, 931–970 (2002).
Yang, C.-C. & Chen, W.-C. The structures and properties of hydrogen silsesquioxane (HSQ) films produced by thermal curing. J. Mater. Chem. 12, 1138–1141 (2002).
Arbabi, A. et al. Miniature optical planar camera based on a wide-angle metasurface doublet corrected for monochromatic aberrations. Nat. Commun. 7, ARTN 13682 (2016).
Arbabi, A., Horie, Y., Ball, A. J., Bagheri, M. & Faraon, A. Subwavelength-thick lenses with high numerical apertures and large efficiency based on high-contrast transmitarrays. Nat. Commun. 6, 7069 (2015).
Jenkins, W. M. Towards structural optimization via the genetic algorithm. Comput. Struct. 40, 1321–1327 (1991).
Ai, S. L. & Wang, Y. D. Application of improved genetic algorithms in structural optimization design. Commun. Comput. Inf. Sci. 236, 480–487 (2011).
Loeffler, T. D., Chan, H., Gray, S. & Sankaranarayanan, S. K. R. S. “Teamwork Makes the Dream Work”: tribal competition evolutionary search as a surrogate for free-energy-based structural predictions. J. Phys. Chem. A 123, 3903–3910 (2019).
Kinaci, A. et al. Unraveling the planar-globular transition in gold nanoclusters through evolutionary search. Sci. Rep. 6, ARTN 34974 (2016).
Patra, T. K. et al. Defect dynamics in 2-D MoS2 probed by using machine learning, atomistic simulations, and high-resolution microscopy. ACS Nano 12, 8006–8016 (2018).
Khaidarov, E. et al. Asymmetric nanoantennas for ultrahigh angle broadband visible light bending. Nano Lett. 17, 6267–6272 (2017).
Sell, D. et al. Ultra-high-efficiency anomalous refraction with dielectric metasurfaces. Acs Photonics 5, 2402–2407 (2018).
Sell, D., Yang, J. J., Doshay, S., Yang, R. & Fan, J. A. Large-angle, multifunctional metagratings based on freeform multimode geometries. Nano Lett. 17, 3752–3757 (2017).
Ra’Di, Y., Sounas, D. L. & Alù, A. Metagratings: beyond the limits of graded metasurfaces for wave front control. Phys. Rev. Lett. 119, 067404 (2017).
Browne, C. B. et al. A survey of monte carlo tree search methods. IEEE Trans. Comput. Intel. AI 4, 1–43 (2012).
Chen, W. T. et al. A broadband achromatic metalens for focusing and imaging in the visible. Nat. Nanotechnol. 13, 220–226 (2018).
Shrestha, S., Overvig, A. C., Lu, M., Stein, A. & Yu, N. Broadband achromatic dielectric metalenses. Light Sci. Appl. 7, 85 (2018).
Pestourie, R. et al. Inverse design of large-area metasurfaces. Opt. Express 26, 33732–33747 (2018).
Cai, H. et al. Ultrathin transmissive metasurfaces for multi-wavelength optics in the visible. Appl. Phys. Lett. 114, 071106 (2019).
Sreenivasan, S. V. Nanoimprint lithography steppers for volume fabrication of leading-edge semiconductor integrated circuits. Microsyst. Nanoeng. 3, 17075 (2017).
Glass, C. W., Oganov, A. R. & Hansen, N. USPEX—evolutionary crystal structure prediction. Comput. Phys. Commun. 175, 713–720 (2006).
Revard, B. C., Tipton, W. W. & Hennig, R. G. in Prediction and Calculation of Crystal Structures: Methods and Applications (eds Sule Atahan-Evrenk & Alan Aspuru-Guzik) 181–222 (Springer International Publishing, 2014).
Srinivasan, S. et al. Machine learning the metastable phase diagram of materials. Preprint at https://arxiv.org/abs/2004.08753.
Acknowledgements
This work was performed at the Center for Nanoscale Materials, a U.S. Department of Energy Office of Science User Facility, and supported by the U.S. Department of Energy, Office of Science, under Contract No. DE-AC02-06CH11357. This research used resources of the National Energy Research Scientific Computing Center, a U.S. Department of Energy Office of Science User Facility, supported by the U.S. Department of Energy, Office of Science, under Contract No. DE-AC02-05CH11231.
Author information
Authors and Affiliations
Contributions
H.C., S.K.R.S., and D.L. conceived and designed the project. H.C and S.S. contributed equally. H.C. and D.L. designed the metasurfaces, performed FDTD simulation, experimental validation, and data analysis. S.S., T.L., and S.K.R.S. developed the inverse design framework and performed the evolutionary optimization. A.M. and L.S. performed TiO2 deposition. D.G. contributed to the optical characterization. H.C., S.S., D.C., S.K.R.S., and D.L. interpreted data and wrote the manuscript. All the authors contributed to the preparation of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cai, H., Srinivasan, S., Czaplewski, D.A. et al. Inverse design of metasurfaces with non-local interactions. npj Comput Mater 6, 116 (2020). https://doi.org/10.1038/s41524-020-00369-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-020-00369-5
This article is cited by
-
Advancing wavefront shaping with resonant nonlocal metasurfaces: beyond the limitations of lookup tables
Scientific Reports (2024)
-
Low-overhead distribution strategy for simulation and optimization of large-area metasurfaces
npj Computational Materials (2022)
-
Designing the collective non-local responses of metasurfaces
Communications Physics (2021)