Abstract
Quantum computers hold promise to enable efficient simulations of the properties of molecules and materials; however, at present they only permit ab initio calculations of a few atoms, due to a limited number of qubits. In order to harness the power of near-term quantum computers for simulations of larger systems, it is desirable to develop hybrid quantum-classical methods where the quantum computation is restricted to a small portion of the system. This is of particular relevance for molecules and solids where an active region requires a higher level of theoretical accuracy than its environment. Here, we present a quantum embedding theory for the calculation of strongly-correlated electronic states of active regions, with the rest of the system described within density functional theory. We demonstrate the accuracy and effectiveness of the approach by investigating several defect quantum bits in semiconductors that are of great interest for quantum information technologies. We perform calculations on quantum computers and show that they yield results in agreement with those obtained with exact diagonalization on classical architectures, paving the way to simulations of realistic materials on near-term quantum computers.
Similar content being viewed by others
Introduction
In the last three decades, atomistic simulations based on the solution of the basic equation of quantum mechanics have played an increasingly important role in predicting the properties of functional materials, encompassing catalysts and energy storage systems for energy applications, and materials for quantum information science. Especially in the case of complex, heterogeneous materials, the great majority of first-principles simulations are conducted using density functional theory (DFT), which is in principle exact but in practice requires approximations to enable calculations. Within its various approximations, DFT has been extremely successful in predicting numerous properties of solids, liquids, and molecules, and in providing key interpretations to a variety of experimental results; however it is often inadequate to describe so-called strongly-correlated electronic states1,2. We will use here the intuitive notion of strong correlation as pertaining to electronic states that cannot be described by static mean-field theories. Several theoretical and computational methods have been developed over the years to treat systems exhibiting strongly-correlated electronic states, including dynamical mean-field theory3,4 and quantum Monte-Carlo5,6; in addition, ab initio quantum chemistry methods, traditionally developed for molecules, have been recently applied to solid state problems as well7. Unfortunately, these approaches are computationally demanding and it is still challenging to apply them to complex materials containing defects and interfaces, even using high-performance computing architectures.
Quantum computers hold promise to enable efficient quantum mechanical simulations of weakly and strongly-correlated molecules and materials alike8,9,10,11,12,13,14,15,16,17; in particular when using quantum computers, one is able to simulate systems of interacting electrons exponentially faster than using classical computers. Thanks to decades of successful experimental efforts, we are now entering the noisy intermediate-scale quantum (NISQ) era18, with quantum computers expected to have on the order of 100 quantum bits (qubits); unfortunately this limited number of qubits still prevents straightforward quantum simulations of realistic molecules and materials, whose description requires hundreds of atoms and thousands to millions of degrees of freedom to represent the electronic wavefunctions. An important requirement to tackle complex chemistry and material science problems using NISQ computers is the reduction of the number of electrons treated explicitly at the highest level of accuracy19,20. For instance, building on the idea underpinning dynamical mean field theory (DMFT)3,4, one may simplify complex molecular and material science problems by defining active regions (or building blocks) with strongly-correlated electronic states, embedded in an environment that may be described within mean-field theory21,22,23.
In this work, we present a quantum embedding theory built on DFT, which is scalable to large systems and which includes the effect of exchange-correlation interactions of the environment on active regions, thus going beyond commonly adopted approximations. In order to demonstrate the effectiveness and accuracy of the theory, we compute ground and excited state properties of several spin-defects in solids including the negatively charged nitrogen-vacancy (NV) center24,25,26,27,28,29,30, the neutral silicon-vacancy (SiV) center31,32,33,34,35,36 in diamond, and the Cr impurity (4+) in 4H-SiC37,38,39. These spin-defects are promising platforms for solid-state quantum information technologies, and they exhibit strongly-correlated electronic states that are critical for the initialization and read-out of their spin states40,41,42,43,44,45. Our quantum embedding theory yields results in good agreement with existing measurements. In addition, we present theoretical predictions for the position and ordering of the singlet states of SiV and of Cr, and we provide an interpretation of experiments that have so far remained unexplained.
Importantly, we report calculations of spin-defects using a quantum computer46,47. Based on the effective Hamiltonian derived from the quantum embedding theory, we investigated the strongly-correlated electronic states of the NV center in diamond using quantum phase estimation algorithm (PEA)8,48 and variational quantum eigensolvers (VQE)49,50,51, and we show that quantum simulations yield results in agreement with those obtained with classical full configuration interaction (FCI) calculations. Our findings pave the way to the use of near term quantum computers to investigate the properties of realistic heterogeneous materials with first-principles theories.
Results
General strategy
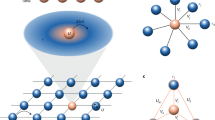
We summarize our strategy in Fig. 1. Starting from an atomistic structural model of materials (e.g., obtained from DFT calculations or molecular dynamics simulations), we identify active regions with strongly-correlated electrons, which we describe with an effective Hamiltonian that includes the effect of the environment on the active region. This effective Hamiltonian is constructed using the quantum embedding theory described below, and its eigenvalues can be obtained by either classical algorithms such as exact diagonalization (FCI) or quantum algorithms.
The full system is separated into an active space and its environment, with the electronic states in the active space described by an effective Hamiltonian solved with either classical (e.g., full configuration interaction, FCI) or quantum algorithms (e.g., phase estimation algorithm (PEA), variational quantum eigensolver (VQE)). The effective interaction between electrons in the active space includes the bare Coulomb interaction and a polarization term arising from the dielectric screening of the environment (see text), which is evaluated including exchange-correlation interactions.
Embedding theory
A number of interesting quantum embedding theories have been proposed over the past decades52. For instance, density functional embedding theory has been developed to improve the accuracy and scalability of DFT calculations53,54,55,56,57. Density matrix embedding theory (DMET)58,59,60 and various Green’s function based approaches61,62, e.g., DMFT, have been developed to describe systems with strongly-correlated electronic states. At present, ab initio calculations of materials using DMET and DMFT have been limited to relatively small unit cells (a few tens of atoms) of pristine crystals, due to their high computational cost63,64. In this work, we present a quantum embedding theory that is applicable to strongly-correlated electronic states in realistic heterogeneous materials and we apply it to systems with hundreds of atoms. The theory, inspired by the constrained random phase approximation (cRPA) approach65,66,67, does not require the explicit evaluation of virtual electronic states68,69, thus making the method scalable to materials containing thousands of electrons. Furthermore, cRPA approaches contain a specific approximation (RPA) to the screened Coulomb interaction, which neglects exchange-correlation effects and may lead to inaccuracies in the description of dielectric screening. Our embedding theory goes beyond the RPA by explicitly including exchange-correlation effects, which are evaluated with a recently developed finite-field algorithm70,71.
The embedding theory developed here aims at constructing an effective Hamiltonian operating on an active space (A), defined as a subspace of the single-particle Hilbert space:
Here, teff and Veff are one-body and two-body interaction terms that take into account the effect of all the electrons that are part of the environment (E) in a mean-field fashion, at the DFT level. An active space can be defined, for example, by solving the Kohn–Sham equations of the full system and selecting a subset of eigenstates among which electronic excitations of interest take place (e.g., defect states within the gap of a semiconductor or insulator). To derive an expression for Veff that properly accounts for all effects of the environment including exchange and correlation interactions, we define the environment density response function (reducible polarizability) \({\chi }^{{\rm{E}}}={\chi }_{0}^{E}+{\chi }_{0}^{{\rm{E}}}f{\chi }^{E}\), where \({\chi }_{0}^{{\rm{E}}}={\chi }_{0}-{\chi }_{0}^{{\rm{A}}}\) is the difference between the polarizability of the Kohn–Sham system χ0 and its projection onto the active space \({\chi }_{0}^{{\rm{A}}}\) (see Supplementary Information (SI)). χE thus represents the density response outside the active space. The term f = V + fxc is often called the Hartree-exchange-correlation kernel, where V is the Coulomb interaction and the exchange-correlation kernel fxc is defined as the derivative of the exchange-correlation potential with respect to the electron density. We define the effective interactions between electrons in A as
given by the sum of the bare Coulomb potential and a polarization term arising from the density response in the environment E. When the RPA is adopted, the exchange-correlation kernel fxc is neglected in Eq. (2) and the expression derived here reduces to that used within cRPA. We represent χE and f on a compact basis obtained from a low-rank decomposition of the dielectric matrix68,69 that allows us to avoid the evaluation and summation over virtual electronic states. Once Veff is defined, the one-body term teff can be computed by subtracting from the Kohn–Sham Hamiltonian a term that accounts for Hartree and exchange-correlation effects in the active space (see SI).
Embedding theory applied to spin-defects
The embedding theory presented above is general and can be applied to a variety of systems for which active regions, or building blocks, with strongly-correlated electronic states may be identified: for example active sites in inorganic catalysts or organic molecules or defects in solids and liquids (e.g., solvated ions in water). Here we apply the theory to spin-defects including NV and SiV in diamond and Cr in 4H-SiC. Most of these defects’ excited states are strongly-correlated (they cannot be represented by a single Slater determinant of single-particle orbitals), as shown e.g., for the NV center in diamond by Bockstedte et al.72 using cRPA calculations. We demonstrate that our embedding theory can successfully describe the many-body electronic structure of different types of defects including transition metal atoms; our results not only confirm existing experimental observations but also provide a detailed description of the electronic structure of defects not presented before, which sheds light into their optical cycles.
We first performed spin-restricted DFT calculations using hybrid functionals73 to obtain a mean-field description of the defects and of the whole host solid. The spin restriction ensures that both spin channels are treated on an equal footing and that there is no spin-contamination when building effective Hamiltonians. Based on our DFT results, we then selected active spaces that include single-particle defect wavefunctions and relevant resonant and band edge states. We verified that the size of the chosen active spaces yields converged excitation energies (see SI). We then constructed effective Hamiltonians (Eqs. (1)–(2)) by taking into account exchange-correlation effects, and we obtained many-body ground and excited states using classical (FCI) and, for selected cases, quantum algorithms (PEA, VQE). All calculations were performed at the spin triplet ground state geometries obtained by spin-unrestricted DFT calculations, thus obtaining vertical excitation energies (equal to the sums of zero phonon line (ZPL) and Stokes energies). It is straightforward to extend the current approach to compute potential energy surfaces at additional geometriesFootnote 1, so as to include relaxations and Jahn–Teller effects36,72. In Fig. 2 we present atomistic structures, single-particle defect levels, and the many-body electronic structure of three spin-defects. Several relevant vertical excitation energies are reported in Table 1, and additional ones are given in the SI. In the following discussion, lower-case symbols represent single-particle states obtained from DFT and upper-case symbols represent many-body states.
(a), (b), and (c) present results for the negatively-charged nitrogen vacancy (NV) in diamond, the neutral silicon vacancy (SiV) in diamond, and the Cr impurity (4+) in 4H-SiC, respectively. Left panels show spin densities obtained from spin unrestricted DFT calculations. Middle panels show the position of single-particle defect levels computed by spin restricted DFT calculations. States included in active spaces (see text) are indicated by blue vertical lines. Right panels show the symmetry and ordering of the low-lying many-body electronic states obtained by exact diagonalization (FCI calculations) of effective Hamiltonians constructed with exchange-correlation interactions included.
For the NV in diamond, we constructed effective Hamiltonians (Eq. (1)) by using an active space that includes a1 and e single-particle defect levels in the band gap and states near the valence band maximum (VBM). Our FCI calculations correctly yield the symmetry and ordering of the low-lying 3A2, 3E, 1E and 1A1 states. The vertical excitation energies reported in Table 1 show that including exchange-correlation effects yields results in better agreement with experiments than those obtained within the RPA. The results obtained within RPA (0.476/1.376/1.921 eV for 1E/1A1/3E states) are in good agreement with cRPA results reported in72 (0.47/1.41/2.02 eV).
In the case of the SiV in diamond, we built effective Hamiltonians using an active space with the eu and eg defect levels and states near the VBM, including resonant \({e}_{u}^{\prime}\) and \({e}_{g}^{\prime}\) states. Effective Hamiltonians including or neglecting exchange-correlation effects yield similar results, with the excitation energies obtained beyond RPA being slightly higher. We predicted the first optically-allowed excited state to be a 3Eu state with vertical excitation energy of 1.59 eV, in good agreement with the sum of 1.31 eV ZPL measured experimentally31 and 0.258 eV Stokes shift estimated using an electron-phonon model36. Our calculations predicted a 3A2u state 11 meV below the 3Eu state, in qualitative agreement with a recent experimental observation by Green et al.35, which proposed a 3A2u-3Eu manifold with 7 meV separation in energy. The small difference in energy splitting between our results and experiment is likely due to geometry relaxation effects are not yet taken into account in our study. In addition to states of u symmetry generated by eu → eg excitations, we observed a number of optically dark states of g symmetry (gray levels in Fig. 2b) originating from the excitation from the \({e}_{g}^{\prime}\) level and the VBM states to the eg level.
Despite significant efforts33,34,35,36, several important questions on the singlet states of SiV remain open. These states are crucial for a complete understanding of the optical cycle of the SiV center. Our predicted ordering of singlet states of SiV is shown in Fig. 2b. We find the vertical excitation energies of the 1A1u state to be slightly higher than that of the 3A2u-3Eu triplet manifold, suggesting that the intersystem crossing (ISC) from 3A2u or 3Eu to singlet states may be energetically unfavorable (first-order ISC to lower 1Eg and 1A1g states are forbidden). We note that the 1Eu and 1A2u states are much higher in energy than 1A1u and are not expected to play a significant role in the optical cycle. In addition the first-order ISC process from the lowest energy singlet state 1Eg to the 3A2g ground state is forbidden by symmetry. Overall our results indicate that the 3A2g state is populated through higher-order processes and therefore the spin-selectivity of the full optical cycle is expected to be low. While more detailed studies including spin-orbit coupling are required for definitive conclusions, our predictions shed light on the strongly-correlated singlet states of SiV and provide a possible explanation for the experimental difficulties in measuring optically-detected magnetic resonance of SiV.
We now turn to Cr in 4H-SiC, where we considered the hexagonal configuration. We constructed effective Hamiltonians with the half-filling e level in the band gap and states near the conduction band minimum including resonance states. Upon solving the effective Hamiltonian, we predict the lowest excited state to be a 1E state arising from e → e spin-flip transition, with excitation energy of 1.09 (0.86) eV based on embedding calculations beyond (within) the RPA. Results including exchange-correlation effects are in better agreement with the measured ZPL of 1.19 eV37, where the Stokes energy is expected to be small given the large Debye-Waller factor39. There is currently no experimental report for the triplet excitation energies of Cr in 4H-SiC, but our results are in good agreement with existing experimental measurements for Cr in GaN, a host material with a crystal field strength similar to that of 4H-SiC38. We predict the existence of a 3E + 3A1 manifold at ≃ 1.4 eV and a \({}^{3}E^{\prime} {+}^{3}{A}_{2}^{\prime}\) manifold at ≃ 1.7 eV above the ground state (Fig. 2c), resembling the 3T2 manifold (1.2 eV) and 3T1 manifold (1.6 eV) for Cr in GaN observed experimentally74. We note that in many cases it is challenging to study materials containing transition metal elements with DFT75. The agreement between FCI results and experimental measurements clearly demonstrates that the embedding theory developed here can effectively describe the strongly-correlated part of the system, while yielding at the same time a quantitatively correct description of the environment.
Quantum simulations of spin-defects
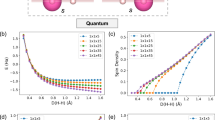
The results presented in the previous section were obtained using classical algorithms. We now turn to the use of quantum algorithms. To perform quantum simulations with PEA and VQE, we constructed a minimum model of an NV center including only a1 and e orbitals in the band gap. This model (four electrons in six spin orbitals) yields excitation energies within 0.2 eV of the converged results using a larger active space. In Fig. 3 we show the results of quantum simulations.
The energy of the 3A2 ground state manifold is set to zero for convenience. a PEA estimation of ground and excited states of the NV center. Error bars represent the uncertainties due to the finite number of ancilla qubits used in the simulations; dashed lines show classical FCI results. b VQE estimation of ground state energy, starting from \(\left|a{e}_{x}{\bar{e}}_{x}{e}_{y}\right\rangle\) state (MS = 1, see text). c VQE estimation of ground state energy, starting from \(\left|a\bar{a}{e}_{x}{\bar{e}}_{x}\right\rangle\) state (MS = 0); strongly-correlated \(\frac{1}{\sqrt{2}}\left(\left|a\bar{a}{e}_{x}{\bar{e}}_{y}\right\rangle +\left|a\bar{a}{\bar{e}}_{x}{e}_{y}\right\rangle \right)\) state (MS = 0 state in the 3A2 manifold) is obtained with VQE.
We first performed PEA simulations with a quantum simulator (without noise)46 to compute the energy of 3A2, 3E, 1E, and 1A1 states. We used molecular orbital approximations of these states derived from group theory26 as initial states for PEA, which are single Slater determinant for 3A2 (MS = 1) and 3E (MS = 1) states, and superpositions of two Slater determinants for 1E and 1A1 states. As shown in Fig. 3a, PEA results converge to classical FCI results with an increasing number of ancilla qubits.
We then performed VQE simulations with a quantum simulator and with the IBM Q 5 Yorktown quantum computer47. We estimated the energy of the 3A2 ground state manifold by performing VQE calculations for both the single-Slater-determinant MS = 1 component and the strongly-correlated MS = 0 component. Within a molecular orbital notation, MS = 1 and MS = 0 ground states can be represented as \(\left|a\bar{a}{e}_{x}{e}_{y}\right\rangle\) and \(\frac{1}{\sqrt{2}}\left(\left|a\bar{a}{e}_{x}{\bar{e}}_{y}\right\rangle +\left|a\bar{a}{\bar{e}}_{x}{e}_{y}\right\rangle \right)\), respectively, where a, ex, ey (spin-up) and \(\bar{a}\), \({\bar{e}}_{x}\), \({\bar{e}}_{y}\) (spin-down) denote a1 and e orbitals. To obtain the MS = 0 ground state, we used a closed-shell Hartree–Fock state \(\left|a\bar{a}{e}_{x}{\bar{e}}_{x}\right\rangle\) as reference; the MS = 1 ground state is itself an open-shell Hartree–Fock state, so we started with a higher energy reference state \(\left|a{e}_{x}{\bar{e}}_{x}{e}_{y}\right\rangle\) in the 3E manifold. We used unitary coupled-cluster single and double (UCCSD) ansatzes49 to represent the trial wavefunctions. Fig. 3b and c shows the estimated ground state energy as a function of the number of VQE iterations, where VQE calculations performed with the quantum simulator correctly converges to the ground state energy in both the MS = 1 and MS = 0 case. Despite the presence of noise, whose characterization and study will be critical to improve the use of quantum algorithms76, the results obtained with the quantum computer converge to the ground state energy within a 0.2 eV error. Calculations of excited states with quantum algorithms will be the focus of future works.
Discussion
With the goal of providing a strategy to solve complex materials problems on NISQ computers, we proposed a first-principles quantum embedding theory where appropriate active regions of a material and their environment are described with different levels of accuracy, and the whole system is treated quantum mechanically. In particular, we used hybrid DFT for the environment, and we built a many-body Hamiltonian for the active space with effective electron-electron interactions that include dielectric screening and exchange-correlation effects from the environment. Our method overcomes the commonly used random phase approximation, which neglects exchange-correlation effects; importantly it is applicable to heterogeneous materials and scalable to large systems, due to the algorithms used here to compute response functions70,71. We emphasize that the embedding theory presented here provides a flexible framework where multiple effects of the environment may be easily incorporated. For instance, dynamical screening effects can be included by considering a frequency-dependent screened Coulomb interaction, evaluated using the same procedure as the one outlined here for static screening; electron-phonon coupling effects can be incorporated by including phonon contributions in the screened Coulomb interactions. Furthermore, for systems where the electronic structure of the active region is expected to influence that of the host material, a self-consistent cycle in the calculation of the screened Coulomb interaction of the environment can be easily added to the approach.
We presented results for spin-defects in semiconductors obtained with both classical and quantum algorithms, and we showed excellent agreement between the two sets of techniques. Importantly, for selected cases we showed results obtained using a quantum simulator and a quantum computer, which agree within a relatively small error, in spite of the presence of noise in the quantum hardware. We made several predictions for excited states of SiV in diamond and Cr in SiC, which provide important insights into their full optical cycle. We also demonstrated that a treatment of the dielectric screening beyond the random phase approximation leads to an accurate prediction of excitation energies.
The method proposed in our work enables calculations of realistic, heterogeneous materials using the resources of NISQ computers. We demonstrated quantum simulations of strongly-correlated electronic states in considerably larger systems (with hundreds of atoms) than previous studies combining quantum simulation and quantum embedding19,20,21,22,23. We have studied solids with defects, not just pristine materials, which are of great interest for quantum technologies. The strategy adopted here is general and may be applied to a variety of problems, including the simulation of active regions in molecules and materials for the understanding and discovery of catalysts and new drugs, and of aqueous solutions containing complex dissolved species. We finally note that our approach is not restricted to strongly-correlated active regions and will be useful also in the case of weakly correlated systems, where different regions of a material may be treated with varying levels of accuracy. Hence we expect the strategy presented here to be widely applicable to carry out quantum simulations of materials on near-term quantum computers.
Methods
Density functional theory
All ground state DFT calculations are performed with the Quantum Espresso code77 using the plane-wave pseudopotential formalism. Electron-ion interactions are modeled with norm-conserving pseudopotentials from the SG15 library78. A kinetic energy cutoff of 50 Ry is used. All geometries are relaxed with spin-unrestricted DFT calculations using the Perdew-Burke-Ernzerhof (PBE) functional79 until forces acting on atoms are smaller than 0.013 eV / Å. NV and SiV in diamond are modeled with 216-atom supercells; Cr in 4H-SiC is modeled with a 128-atom supercell. The Brillouin zone is sampled with the Γ point.
Construction of effective Hamiltonians
Construction of effective Hamiltonians is performed with the WEST code69, starting from wavefunctions of spin-restricted DFT calculations. For this step, we remark that the use of hybrid functional is important for an accurate mean-field description of defect levels, even though the geometry of defects are well represented at the PBE level. We used a dielectric dependent hybrid (DDH) functional73 which self-consistently determines the fraction of exact exchange based on the dielectric constant of the host material. In particular, 17.8% and 15.2% of exact exchange were used for the calculations of defects in diamond and 4H-SiC, respectively. The DDH functional was shown to yield accurate band gaps of diamond and silicon carbide, as well as optical properties of defects41,42,80,81,82. After hybrid functional solutions of the Kohn–Sham equations are obtained, iterative diagonalizations of χ0 are performed, and density response functions and fxc of the system are represented on a basis consisting of the first 512 eigenpotentials of χ0. Finite field calculations of fxc are performed by coupling the WEST code with the Qbox83 code. FCI calculations84 on the effective Hamiltonian are carried out using the PySCF7 code.
Quantum simulations
In order to carry out quantum simulations, a minimum model of the NV center is constructed by applying the embedding theory with a1 and e orbitals beyond the RPA.
In PEA simulations, the Jordan–Wigner transformation85 is used to map the fermionic effective Hamiltonian to a qubit Hamiltonian, and Pauli operators with prefactors smaller than 10−6 a.u. are neglected to reduce the circuit depth, which results in less than 10−4 a.u. (0.003 eV) change in eigenvalues. In order to achieve optimal precision, the Hamiltonian is scaled such that 0 and 2.5 eV are mapped to phases ϕ = 0 and ϕ = 1 of the ancilla qubits, respectively. We used the first-order Trotter formula to split time evolution operators into 4 time slices.
In VQE simulations, the parity transformation9 is adopted. For the simulation of the MS = 1 state, the resulting qubit Hamiltonian acts on four qubits and there are two variational parameters in the UCCSD ansatz. For the simulation of the MS = 0 state, we fixed the occupation of the a orbital and the resulting qubit Hamiltonian acts on 2 qubits. We replicated the exponential excitation operator twice, with parameters in both replicas variationally optimized. Such a choice results in six variational parameters, providing a sufficient number of degrees of freedom for an accurate representation of the strongly-correlated MS = 0 state. Parameters in the ansatz are optimized with the COBYLA algorithm86.
Quantum simulations are performed with the QASM simulator and the IBM Q 5 Yorktown quantum computer using the IBM Qiskit package46. Each quantum circuit is executed 8192 times to obtain statistically reliable sampling of the measurement results.
Data availability
Data that support the findings of this study are available through the Qresp87 curator at https://doi.org/10.6084/m9.figshare.12501407.
Code availability
The quantum embedding theory is implemented in the open source code WEST (west-code.org/).
Notes
For example, one may follow the strategy of ref. 72 and compute excited states of defects along given normal modes, which are usually obtained from delta-SCF calculations. This type of treatment, albeit approximate, provides valuable insights into the vibrational properties of defects in excited states.
References
Cohen, A. J., Mori-Sánchez, P. & Yang, W. Insights into current limitations of density functional theory. Science 321, 792–794 (2008).
Su, N. Q., Li, C. & Yang, W. Describing strong correlation with fractional-spin correction in density functional theory. Proc. Natl Acad. Sci. USA. 115, 9678–9683 (2018).
Georges, A., Kotliar, G., Krauth, W. & Rozenberg, M. J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 68, 13–125 (1996).
Kotliar, G. et al. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 78, 865–951 (2006).
Ceperley, D. & Alder, B. Quantum monte carlo. Science 231, 555–560 (1986).
Wagner, L. K. & Ceperley, D. M. Discovering correlated fermions using quantum monte carlo. Rep. Prog. Phys. 79, 094501 (2016).
Sun, Q. et al. Py SCF: the python-based simulations of chemistry framework. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 8, e1340 (2017).
Aspuru-Guzik, A. Simulated quantum computation of molecular energies. Science 309, 1704–1707 (2005).
Bravyi, S., Gambetta, J. M., Mezzacapo, A. & Temme, K. Tapering off qubits to simulate fermionic hamiltonians. Preprint at https://arxiv.org/abs/1701.08213 (2017).
Babbush, R. et al. Low-depth quantum simulation of materials. Phys. Rev. X 8, 011044 (2018).
Kivlichan, I. D. et al. Quantum simulation of electronic structure with linear depth and connectivity. Phys. Rev. Lett. 120, 110501 (2018).
Motta, M. et al. Determining eigenstates and thermal states on a quantum computer using quantum imaginary time evolution. Nat. Phys. 16, 205–210 (2020).
Ollitrault, P. J. et al. Quantum equation of motion for computing molecular excitation energies on a noisy quantum processor. Preprint at https://arxiv.org/abs/1910.12890 (2019).
Cao, Y. et al. Quantum chemistry in the age of quantum computing. Chem. Rev. 119, 10856–10915 (2019).
Smart, S. E. & Mazziotti, D. A. Quantum-classical hybrid algorithm using an error-mitigating n-representability condition to compute the mott metal-insulator transition. Phys. Rev. A 100, 022517 (2019).
Smart, S. E., Schuster, D. I. & Mazziotti, D. A. Experimental data from a quantum computer verifies the generalized pauli exclusion principle. Commun. Phys. 2, 1–6 (2019).
Bauer, B., Bravyi, S., Motta, M. & Chan, G. K.-L. Quantum algorithms for quantum chemistry and quantum materials science. Preprint at https://arxiv.org/abs/2001.03685 (2020).
Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2, 79 (2018).
Rubin, N. C. A hybrid classical/quantum approach for large-scale studies of quantum systems with density matrix embedding theory. Preprint at https://arxiv.org/abs/1610.06910 (2016).
Yamazaki, T., Matsuura, S., Narimani, A., Saidmuradov, A. & Zaribafiyan, A. Towards the practical application of near-term quantum computers in quantum chemistry simulations: a problem decomposition approach. Preprint at https://arxiv.org/abs/1806.01305 (2018).
Bauer, B., Wecker, D., Millis, A. J., Hastings, M. B. & Troyer, M. Hybrid quantum-classical approach to correlated materials. Phys. Rev. X 6, 031045 (2016).
Kreula, J. M. et al. Few-qubit quantum-classical simulation of strongly correlated lattice fermions. EPJ Quantum Technol. 3, 1–19 (2016).
Rungger, I. et al. Dynamical mean field theory algorithm and experiment on quantum computers. Preprint at arXiv: https://arxiv.org/abs/1910.04735 (2019).
Davies, G. & Hamer, M. F. Optical studies of the 1.945 eV vibronic band in diamond. Proc. R. Soc. A348, 285–298 (1976).
Rogers, L. J., Armstrong, S., Sellars, M. J. & Manson, N. B. Infrared emission of the NV centre in diamond: Zeeman and uniaxial stress studies. N. J. Phys. 10, 103024 (2008).
Doherty, M. W., Manson, N. B., Delaney, P. & Hollenberg, L. C. L. The negatively charged nitrogen-vacancy centre in diamond: the electronic solution. N. J. Phys. 13, 025019 (2011).
Maze, J. R. et al. Properties of nitrogen-vacancy centers in diamond: the group theoretic approach. N. J. Phys. 13, 025025 (2011).
Choi, S., Jain, M. & Louie, S. G. Mechanism for optical initialization of spin in NV-center in diamond. Phys. Rev. B 86, 041202 (2012).
Doherty, M. W. et al. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 528, 1–45 (2013).
Goldman, M. L. et al. State-selective intersystem crossing in nitrogen-vacancy centers. Phys. Rev. B 91, 165201 (2015).
D’Haenens-Johansson, U. F. S. et al. Optical properties of the neutral silicon split-vacancy center in diamond. Phys. Rev. B 84, 245208 (2011).
Gali, A. & Maze, J. R. Ab initio study of the split silicon-vacancy defect in diamond: Electronic structure and related properties. Phys. Rev. B 88, 235205 (2013).
Green, B. L. et al. Neutral silicon-vacancy center in diamond: Spin polarization and lifetimes. Phys. Rev. Lett. 119, 096402 (2017).
Rose, B. C. et al. Observation of an environmentally insensitive solid-state spin defect in diamond. Science 361, 60–63 (2018).
Green, B. L. et al. Electronic structure of the neutral silicon-vacancy center in diamond. Phys. Rev. B 99, 161112 (2019).
Thiering, G. & Gali, A. The (eg ⊗ eu) ⊗ eg product jahn–teller effect in the neutral group-IV vacancy quantum bits in diamond. npj Comput. Mater. 5, 18 (2019).
Son, N. T. et al. Photoluminescence and zeeman effect in chromium-doped 4h and 6h SiC. J. Appl. Phys. 86, 4348–4353 (1999).
Koehl, W. F. et al. Resonant optical spectroscopy and coherent control of Cr4+ spin ensembles in sic and gan. Phys. Rev. B 95, 035207 (2017).
Diler, B. et al. Coherent control and high-fidelity readout of chromium ions in commercial silicon carbide. npj Quantum Inf. 6, 11 (2020).
Weber, J. R. et al. Quantum computing with defects. Proc. Natl Acad. Sci. USA. 107, 8513–8518 (2010).
Seo, H., Govoni, M. & Galli, G. Design of defect spins in piezoelectric aluminum nitride for solid-state hybrid quantum technologies. Sci. Rep. 6, 20803 (2016).
Seo, H., Ma, H., Govoni, M. & Galli, G. Designing defect-based qubit candidates in wide-gap binary semiconductors for solid-state quantum technologies. Phys. Rev. Mater. 1, 075002 (2017).
Ivády, V., Abrikosov, I. A. & Gali, A. First principles calculation of spin-related quantities for point defect qubit research. npj Comput. Mater. 4, 76 (2018).
Dreyer, C. E., Alkauskas, A., Lyons, J. L., Janotti, A. & Van de Walle, C. G. First-principles calculations of point defects for quantum technologies. Annu. Rev. Mater. Res. 48, 1–26 (2018).
Anderson, C. P. et al. Electrical and optical control of single spins integrated in scalable semiconductor devices. Science 366, 1225–1230 (2019).
Abraham, H. et al. Qiskit: an open-source framework for quantum computing. Zenodo. https://doi.org/10.5281/zenodo.2562111 (2019).
5-qubit backend: IBM Q team, \IBM Q 5 Yorktown backend speci cation V1.1.0". https://quantum-computing.ibm.com (2018).
Abrams, D. S. & Lloyd, S. Simulation of many-body fermi systems on a universal quantum computer. Phys. Rev. Lett. 79, 2586 (1997).
Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 4213 (2014).
McClean, J. R., Romero, J., Babbush, R. & Aspuru-Guzik, A. The theory of variational hybrid quantum-classical algorithms. N. J. Phys. 18, 023023 (2016).
Kandala, A. et al. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 549, 242–246 (2017).
Sun, Q. & Chan, G. K.-L. Quantum embedding theories. Acc. Chem. Res. 49, 2705–2712 (2016).
Huang, C., Pavone, M. & Carter, E. A. Quantum mechanical embedding theory based on a unique embedding potential. J. Chem. Phys. 134, 154110 (2011).
Goodpaster, J. D., Barnes, T. A., Manby, F. R. & Miller, T. F. Accurate and systematically improvable density functional theory embedding for correlated wavefunctions. J. Chem. Phys. 140, 18A507 (2014).
Jacob, C. R. & Neugebauer, J. Subsystem density-functional theory. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 4, 325–362 (2014).
Genova, A., Ceresoli, D. & Pavanello, M. Periodic subsystem density-functional theory. J. Chem. Phys. 141, 174101 (2014).
Wen, X., Graham, D. S., Chulhai, D. V. & Goodpaster, J. D. Absolutely localized projection-based embedding for excited states. J. Chem. Theory Comput. 16, 385–398 (2020).
Knizia, G. & Chan, G. K.-L. Density matrix embedding: a simple alternative to dynamical mean-field theory. Phys. Rev. Lett. 109, 186404 (2012).
Wouters, S., Jiménez-Hoyos, C. A., Sun, Q. & Chan, G. K.-L. A practical guide to density matrix embedding theory in quantum chemistry. J. Chem. Theory Comput. 12, 2706–2719 (2016).
Pham, H. Q., Hermes, M. R. & Gagliardi, L. Periodic electronic structure calculations with density matrix embedding theory. J. Chem. Theory Comput. 16, 130–140 (2020).
Lan, T. N., Kananenka, A. A. & Zgid, D. Rigorous ab initio quantum embedding for quantum chemistry using green’s function theory: screened interaction, nonlocal self-energy relaxation, orbital basis, and chemical accuracy. J. Chem. Theory Comput. 12, 4856–4870 (2016).
Dvorak, M. & Rinke, P. Dynamical configuration interaction: Quantum embedding that combines wave functions and green’s functions. Phys. Rev. B 99, 115134 (2019).
Zhu, T., Cui, Z.-H. & Chan, G. K.-L. Efficient formulation of ab initio quantum embedding in periodic systems: Dynamical mean-field theory. J. Chem. Theory Comput. 16, 141–153 (2019).
Cui, Z.-H., Zhu, T. & Chan, G. K.-L. Efficient implementation of ab initio quantum embedding in periodic systems: Density matrix embedding theory. J. Chem. Theory Comput. 16, 119–129 (2019).
Aryasetiawan, F. et al. Frequency-dependent local interactions and low-energy effective models from electronic structure calculations. Phys. Rev. B 70, 195104 (2004).
Miyake, T., Aryasetiawan, F. & Imada, M. Ab initio procedure for constructing effective models of correlated materials with entangled band structure. Phys. Rev. B 80, 155134 (2009).
Hirayama, M., Miyake, T., Imada, M. & Biermann, S. Low-energy effective hamiltonians for correlated electron systems beyond density functional theory. Phys. Rev. B 96, 075102 (2017).
Wilson, H. F., Gygi, F. & Galli, G. Efficient iterative method for calculations of dielectric matrices. Phys. Rev. B 78, 113303 (2008).
Govoni, M. & Galli, G. Large scale GW calculations. J. Chem. Theory Comput. 11, 2680–2696 (2015).
Ma, H., Govoni, M., Gygi, F. & Galli, G. A finite-field approach for GW calculations beyond the random phase approximation. J. Chem. Theory Comput. 15, 154–164 (2018).
Nguyen, N. L., Ma, H., Govoni, M., Gygi, F. & Galli, G. Finite-field approach to solving the bethe-salpeter equation. Phys. Rev. Lett. 122, 237402 (2019).
Bockstedte, M., Schütz, F., Garratt, T., Ivády, V. & Gali, A. Ab initio description of highly correlated states in defects for realizing quantum bits. npj Quantum Mater. 3, 31 (2018).
Skone, J. H., Govoni, M. & Galli, G. Self-consistent hybrid functional for condensed systems. Phys. Rev. B 89, 195112 (2014).
Heitz, R. et al. Identification of the 1.19-eV luminescence in hexagonal GaN. Phys. Rev. B 52, 16508–16515 (1995).
Anisimov, V. I., Aryasetiawan, F. & Lichtenstein, A. First-principles calculations of the electronic structure and spectra of strongly correlated systems: the lda+ u method. J. Phys. Condens. Matter 9, 767 (1997).
Kandala, A. et al. Error mitigation extends the computational reach of a noisy quantum processor. Nature 567, 491 (2019).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).
Schlipf, M. & Gygi, F. Optimization algorithm for the generation of ONCV pseudopotentials. Comput. Phys. Commun. 196, 36–44 (2015).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Pham, T. A. et al. Electronic structure of aqueous solutions: bridging the gap between theory and experiments. Sci. Adv. 3, e1603210 (2017).
Smart, T. J., Wu, F., Govoni, M. & Ping, Y. Fundamental principles for calculating charged defect ionization energies in ultrathin two-dimensional materials. Phys. Rev. Mater. 2, 124002 (2018).
Gerosa, M., Gygi, F., Govoni, M. & Galli, G. The role of defects and excess surface charges at finite temperature for optimizing oxide photoabsorbers. Nat. Mater. 17, 1122–1127 (2018).
Gygi, F. Architecture of qbox: a scalable first-principles molecular dynamics code. IBM J. Res. Dev. 52, 137–144 (2008).
Knowles, P. & Handy, N. A new determinant-based full configuration interaction method. Chem. Phys. Lett. 111, 315–321 (1984).
Jordan, P. & Wigner, E. P. About the pauli exclusion principle. Z. Phys. 47, 631–651 (1928).
Powell, M. J. A direct search optimization method that models the objective and constraint functions by linear interpolation. In Advances in optimization and numerical analysis, 51–67 (Springer, Dordrecht, 1994).
Govoni, M. et al. Qresp, a tool for curating, discovering and exploring reproducible scientific papers. Sci. Data 6, 190002 (2019).
Acknowledgements
We thank C. P. Anderson, D. D. Awschalom, T. C. Berkelbach, B. Diler, S. Dong, D. Freedman, L. Gagliardi, F. Gygi, F. J. Heremans, L. Jiang, A. M. Lewis, A. Mezzacapo, P. J. Mintun, H. Seo, S. Sullivan, S. J. Whiteley, and G. Wolfowicz for fruitful discussions and comments on the manuscript. We also thank the Qiskit Slack channel for generous help. This work was supported by MICCoM, as part of the Computational Materials Sciences Program funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences, and Engineering Division through Argonne National Laboratory, under contract number DE-AC02-06CH11357 and by AFOSR FA9550-19-1-0358. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility supported by the Office of Science of the US Department of Energy under Contract No. DE-AC02-05CH11231, resources of the Argonne Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC02-06CH11357, and resources of the University of Chicago Research Computing Center.
Author information
Authors and Affiliations
Contributions
H.M., M.G., and G.G. designed the research. H.M. implemented the quantum embedding theory and performed simulations with classical and quantum algorithms, with supervision by M.G. and G.G. All authors wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ma, H., Govoni, M. & Galli, G. Quantum simulations of materials on near-term quantum computers. npj Comput Mater 6, 85 (2020). https://doi.org/10.1038/s41524-020-00353-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-020-00353-z
This article is cited by
-
Towards near-term quantum simulation of materials
Nature Communications (2024)
-
Downfolding from ab initio to interacting model Hamiltonians: comprehensive analysis and benchmarking of the DFT+cRPA approach
npj Computational Materials (2024)
-
Readout error mitigated quantum state tomography tested on superconducting qubits
Communications Physics (2024)
-
Quantum computation of reactions on surfaces using local embedding
npj Quantum Information (2023)
-
Ab initio quantum simulation of strongly correlated materials with quantum embedding
npj Computational Materials (2023)