Abstract
Creation of a partially filled intermediate band in a photovoltaic absorber material is an appealing concept for increasing the quantum efficiency of solar cells. Recently, we showed that formation of a partially filled intermediate band through doping a host semiconductor with a transition metal dopant is hindered by the strongly correlated nature of d-electrons and the antecedent Jahn–Teller distortion, as we have previously reported. In present work, we take a step forward and study the delocalization of a filled (valence-like) intermediate band throughout the lattice: a case study of Ti- and Nb-doped In2S3. By means of hybrid density functional calculations, we present extensive analysis on structural properties and interactions leading to electronic characteristics of Ti- and Nb-doped In2S3. We find that Nb creates an occupied doublet, which can become delocalized onto the crystal at high but feasible concentrations (around 2.5 at% and above). As a consequence, doping In2S3 with adequately high concentrations of Nb allows the subgap intermediate band to conduction band absorption, which leads to higher photocurrent densities compared to pure In2S3. Ti on the other hand forms an occupied singlet intermediate band, which remains strongly localized even at high concentration of 5 at%.
Similar content being viewed by others
Introduction
The idea of multi-transition solar cells was first introduced by Wolf in 19591, 5 years after manufacturing of the first silicon p–n junction photocell. For a better utilization of the solar spectrum, he suggested to introduce deep impurity levels within the absorber band gap, e.g., by means of transition metal doping2. These levels would facilitate sequential absorption of lower-energy photons from the valence band (VB) to empty defect levels and from the filled defect levels to the conduction band (CB). However, since the intermediate impurity levels trigger the occurrence of Shockley–Read–Hall (SRH) non-radiative recombinations3,4, absorbed photons do not necessarily produce electron-hole pairs, and therefore, the idea did not evolve further until some decades later. In 1997, Luque and Martí5 demonstrated theoretically that outperforming the Shockley–Queisser (SQ) efficiency limit6 of solar cells is achievable by introducing a partially filled intermediate band (IB) instead of an isolated defect level inside the band gap. The core of their idea is that through formation of partially filled IBs, two photons with sub-band gap energies can excite electrons and generate electron-hole pairs. Furthermore, Luque et al.7 argued that the non-radiative recombination can be suppressed if wavefunctions of the impurities overlap. Such condition can be achieved at high dopant concentrations.
As a result of the two-step photon absorption associated with the presence of a partially filled IB, the efficiency of a solar cell can approach 63.1% instead of 40.7% being the SQ limit for single junction solar cells6. In order to design an intermediate-band solar cell (IBSC) with such high efficiency, one has to take into account both the magnitude of the band gap and the position of the introduced IB. For example, the maximum efficiency of 63.1% corresponds to a host semiconductor with a band gap of 1.95 eV and a partially filled IB that divides it into 1.24 eV and 0.71 eV sub-gaps5.
In recent years, several attempts have been made to find doped semiconductors, which can form an IB. Chalcopyrite compounds belonging to the Cu(In,Ga)(S,Se)2 (CIGS) family were the first thin film materials investigated as candidates for formation of IBs8,9. Besides, indium thiospinels are another class of semiconductor hosts with well-known thin-film deposition techniques, and recognized potentials for the development of an IBSC. Among these materials, β−In2S3 represents the most promising candidate for hosting intermediate bands when doped with transition metals10, since its band gap of 2.03 eV11 is very close to that of the ideal IB semiconductor. Furthermore, its advantage as possible semiconductor host for the development of an IBSC when compared to CIGS is that the thiospinels have octahedral cation sites, providing the opportunity of including transition metals in a more stable six-fold environment. β−In2S3 is an n-type semiconductor that crystallizes in a defective spinel-like structure11,12. Its optoelectronic properties have already made it an attractive material for photovoltaic applications, namely, as buffer layer in CIGS-based thin-film solar cells13,14,15.
The study of impurities in semiconductors requires the application of relatively large supercells. In this respect, (semi)local functionals with moderate computational cost became the main workhorse for investigation of doped semiconductors. Nevertheless, the theoretical interpretations of physics of such systems were affected by two well-known limitations of the (semi)local functionals: the delocalization and the band gap errors. The local density and generalized gradient approximations to density functional theory (DFT) lead to considerable errors in describing nonlocality of the screened exchange interaction and consequently the electrostatic self-interaction. The consequence of this is that an electron interacts with itself, which artificially favors its delocalization. This results in particularly sizable errors for strongly localized states, e.g., the d states of transition metals (TM)16. Furthermore, the band gap underestimation by (semi)local functionals leads to inaccurate description of electronic properties and thermodynamic charge transition levels of such systems. One can largely surmount the above-mentioned problems by using hybrid density functionals with a tuned mixing parameter or alternatively a tuned range separation parameter17,18,19. In case of GaN:Mn, for instance, standard DFT predicts partially filled three-fold degenerate states inside the band gap, whereas the range-separated hybrid functional shows splitting of t2 states into an unoccupied singlet and an occupied doublet, in excellent agreement with GW0 calculations and experiments. We reported a similar scenario for In2S3:V in our previous work20. Although the electronic and thermodynamic properties produced by hybrid functional are precise for many TM-doped systems, but it does not fulfill the generalized Koopmans theorem for every TM-doped semiconductor21,22. In such cases (e.g., Cr-doped SiC21), the exact Hartree–Fock exchange energy does not fully cancel the self-interaction error and hence the generalized koopmans’ condition (gKC)23,24 is not satisfied. In order to address this issue properly, we examine here the fulfillment of the gKC by our applied hybrid functional (HSE06). We find that for both Ti and Nb donors, the HSE06 functional shows a negligible deviation from the gKC. Hence, our obtained results are self-interaction-free.
The aim of this work is to present a careful, detailed theoretical picture of the electronic structure of Ti- and Nb-doped In2S3 and to describe under what circumstances a higher absorption of solar spectrum can be achieved in this material. This paper is arranged as follows. Results section concentrates on inclusion of Ti and Nb (which we label as ‘TM’ hereafter) on In tetrahedral and octahedral substitutional sites and provides a comparison between their formation energies. Then, the electronic structure of TM-substituted In2S3 is discussed. Thereafter, the effect of TM concentration on the formation of an impurity band and mixing enthalpies of the solutes are discussed. A complete description of the computational setup and the theory are given in methods section.
Results
Formation energy of TMs in In2S3
There are three nonequivalent crystallographic environments for In and S atoms in the β-phase of In2S3. The In substitutional sites in the crystalline matrix of In2S3 are tetrahedral 8e (In8e), octahedral 8c (In8c), and octahedral 16h (In16h) sites12, corresponding to Wyckoff notations of space-group 141. Both, In8c and In16h sites are six-fold coordinated by S and are different in their associated In–S bond lengths. In8e occupies two-thirds of the available tetrahedral cation sites, while the remaining one-third tetrahedral sites are unoccupied. Sulfur atoms are arranged on distorted cubic closed packed lattices, where the S positions are distinct due to the different occupation of the surrounding In sites. The atomic structure of the β−In2S3 unit cell is illustrated in Supplementary Fig. 1.
Figure 1 shows the calculated formation energy of TMs on 8e tetrahedral and 16h octahedral sites of In for In-rich and S-rich growth atmospheres. In this set of calculations, one TM was added to the crystalline matrix of In2S3. The formation energies are depicted from EF = 0 eV (corresponding to p-type material) to EF = 2.1 eV (corresponding to n-type material), covering the whole range of possible Fermi energies. The points, where the line slop changes represent transitions of the stable charge state of the impurity. Since the formation energies of TMs on In8c and In16h octahedral sites are close, here, we only show formation energies on In16h sites. Here, our goal is to identify the most favorable defect configuration and the charged data are shown for completeness. In order to discuss Ti and Nb as charged defects, one needs to consider the possible charge compensation mechanisms. Since the concentration of TMs are quite high, the charge compensation by means of intrinsic defects is extremely unlikely. Hence, oxidation of Ti and Nb would require presence of abundant acceptor dopants in the system. Since In2S3 is an n-type material, Ti and Nb can be essentially considered as solutes, i.e., in neutral charge state. Therefore, the only relevant finite size corrections would be due to the elastic interactions, which we safely ignored because the considered concentrations are comparable to what is experimentally achievable. Clearly, the calculated energies can not be used to predict equilibrium concentrations.
For both, In- and S-rich samples, TMs prefer to occupy In octahedral sites rather than tetrahedral sites. Due to its very low formation energy (0.06 eV at CBM), \({{\rm{Ti}}}_{{{\rm{In}}}^{16{\rm{h}}}}\) can exist in In-rich samples in very high concentrations, whereas the formation energy of \({{\rm{Ti}}}_{{{\rm{In}}}^{16{\rm{h}}}}\) in S-rich samples is one order of magnitude larger (0.59 eV at CBM). The formation energy of \({{\rm{Nb}}}_{{{\rm{In}}}^{16{\rm{h}}}}\) is 0.68 and 1.22 eV for In-rich and S-rich conditions, respectively. Intuitively, one would expect a lower formation energy of Nb/Ti under In-poor conditions. However, one has to consider that here the thermodynamic constraints are on the possible boundary phases of the solutes and the substituted elements, which leads to the coupling of their chemical potentials Eqs. (5), (6), and (7). Therefore, with the increase of the chemical potential of In under In-rich conditions, the chemical potential of the solute increases as well. The origins of the different formation energies of Ti and Nb will be discussed in subsection “Heat of solution of Ti and Nb in In2S3”.
Electronic properties of In2S3 alloyed with TMs
The calculated partial and total densities of states (DOS) of pure In2S3 is shown in Fig. 2. The calculated electronic band structure of β−In2S3 with hybrid functional is given in ref. 25. The DOS at the uppermost part of the valence band is mainly derived from the S 3p states mixing with In 4d states. Due to the small contribution of S 3s states, they are not shown here. Figure 3 shows HSE spin-polarized densities of states of Ti- and Nb-substituted In2S3, where the energy level of 0 eV corresponds to the highest occupied state. Here, four Ti or Nb ions were either accommodated in four In16h or In8c octahedral sites, corresponding to 5% concentration of these solutes. The subsequent incorporation sites are separated from each other by about 8.6 Å, which is the largest distance achievable when using the chosen supercell. It is found that the energetic position and shape of the DOS of the impurity bands are different when the solute TMs substitute In16h and In8c sites. As mentioned earlier, there are three nonequivalent crystallographic environment for S atoms in the structure of β−In2S3. Here, we refer to them as S1, S2, and S3. S1 atoms are four-fold coordinated with two In8c, one In16h, and one In8e next neighbors; S2 atoms are three-fold coordinated with two In16h and one In8c next neighbors; and S3 atoms are four-fold coordinated with three In16h and one In8e next neighbors. TMs on In16h sites are bonding with one S1, two S2, and three S3. While the ones on In8c sites are bonding with four S1 and two S2 atoms. Therefore, the lattice distortions caused by TMs on In8c or In16h sites are different.
In 2008, Palacios et al.26 studied the electronic structure of V- and Ti-doped In2S3 using DFT. For Vanadium, they found a narrow half-filled intermediate band isolated from the VB and CB of In2S3. Recently, we revisited V-doped In2S320, using hybrid functional and explained that the erroneous DFT-predicted partially filled IB was caused by neglecting the strongly correlated nature of d-electrons and the antecedent Jahn–Teller effect. In fact, trivalent V ions do not form any IB at all. And only if V ions get reduced, then, the divalent V introduce a totally-filled triplet IB within the band gap of In2S320. For Ti, they showed that when Ti replaces In octahedral site (the different In octahedral sites were not distinguished in their study), the GGA approximation predicts an overlap between the d-bands of Ti and the CB of In2S3, which yields to an IB positioned at the bottom of the conduction band. They assumed that correcting the GGA band gap would shift the position of the CBM upward and the incorporation of Ti would eventually lead to a partially filled IB inside the gap. As illustrated in our previous work20, going from semi-local PBE to HSE functional, the band gap opens from 0.84 eV to 2.03 eV, and the downward shift of the VBM is about twice larger than the upward shift the CBM, which is in contrast to the assumption of Palacios et al. We see from Fig. 3 that when Ti atoms occupy In16h sites, an occupied singlet state occurs at 0.14 eV above the VBM and an unoccupied doublet state appears in the CB. On the \({{\rm{Ti}}}_{{{\rm{In}}}^{8{\rm{c}}}}\) configuration; however, no in-gap state appears and only sulfur p states near the band edges move into the gap and reduce the band gap to 1.57 eV. In case of Nb, Fig. 3 shows that inclusion of Nb on In16h and In8c sites leads to occupied doublet in-gap states at 0.62 eV and 0.45 eV above the VBM, respectively. The electronic band structure of \({{\rm{In}}}_{28}{{\rm{S}}}_{48}\!:\!{{\rm{Ti}}}_{4}^{16{\rm{h}}}\) and \({{\rm{In}}}_{28}{{\rm{S}}}_{48}\!:\!{{\rm{Nb}}}_{4}^{16{\rm{h}}}\) are illustrated in Supplementary Fig. 2.
In the octahedral geometry of In2S3, the six neighboring ligands are oriented along the z-axis and the diagonal directions of the xy plane. Therefore, the \({d}_{{z}^{2}}\) and dxy orbitals are subject to a stronger electrostatic repulsion compared to the dxz, dyz, and \({d}_{{x}^{2}-{y}^{2}}\) orbitals. Consequently, transition metal substituents occupying these sites experience a corresponding crystal field that pushes the dxz, dyz, and \({d}_{{x}^{2}-{y}^{2}}\) orbitals (also called t orbitals) into a lower energy compared to the \({d}_{{z}^{2}}\) and dxy orbitals (also called e orbitals). In addition, due to the spin splitting, these levels further split into spin-up (t+ and e+) and spin down (t− and e−) levels. As a result of crystal field and exchange-splitting, d levels of free Ti3+ and Nb3+ have respectively [\({t}_{+}^{1}{e}_{+}^{0}{t}_{-}^{0}{e}_{-}^{0}\)] and [\({t}_{+}^{2}{e}_{+}^{0}{t}_{-}^{0}{e}_{-}^{0}\)] electronic configurations.
When entering the octahedral In site, e+ and e− levels of TM hybridize with S dandling-bond states (e(p)) and create two types of levels with e symmetry: one with a high contribution of six neighboring S atoms, referred to as dangling-bond hybrid (DBH) states and the other mostly localized on the TM atom, referred to as crystal field resonance (CFR) states27. Note that the eDBH and eCFR are bonding and antibonding levels, respectively. For the t+ and t− levels, however, there is no host level with t symmetry in the similar energy range. Therefore, the t(d) states remain largely uncoupled and the amplitude of wavefunction is mainly localized on the TM, hence a CFR state27. Consequently, the order of electronic states of Ti and Nb on octahedral In sites are as:
We note that realizing an ideal IB alloy depends on the position and occupancy of the \({t}_{{\mathrm{CFR}}}^{+}\) state. The simplified electron-filling schemes of Ti and Nb on vacant In site (\({{\rm{Vac}}}_{{\rm{In}}}^{3-}\)) are shown in Fig. 4. We see that for both Ti and Nb, the partially filled \({t}_{+}^{{\mathrm{CFR}}}\) state splits into a filled lower-energy and an empty upper-energy branch, i.e., \({t}_{+}^{{\mathrm{CFR}}}\to {a}_{+}^{1}+{e}_{+}^{0}\) for Ti and \({t}_{+}^{{\mathrm{CFR}}}\to {e}_{+}^{2}+{a}_{+}^{0}\) for Nb. The a and e notations refer to the singlet and doublet natures of these states, respectively. Note that the partially filled degenerate states are Jahn–Teller active centers, which necessiates removing the degeneracy of the intermediate state through splitting it into filled and empty states. Therefore, the onset of a partially filled IB which can trigger simultaneous VB → IB and IB → CB transitions is extremely unlikely. However, if well delocalized, the \({a}_{+}^{1}\) and \({e}_{+}^{2}\) in-gap states can increase the sub-band gap photon absorption, mostly through assisting in the IB → CB transition.
The projected e and t DOS of Ti (a), Nb (c), and V (e) on In16h site, and their schematic electron-filling diagrams (b, d, and f). Energy zero in sub-figures a, c, and e is equivalent to the highest occupied state. Sub-figures e and f are reproduced from ref. 20 with permission from the Royal Society of Chemistry.
In 2011, Ho28 used chemical vapor transport method to grow Nb-doped In2S3 films and detected below gap transitions of 1.52 and 1.42 eV. Since these transitions were not detected in undoped In2S3, he assigned them to the creation of an IB. However, it was not clear whether the observed transitions stemmed from a deep defect level or a delocalized band. Thus, the question is whether the observed intermediate levels have an unwanted localized or a beneficial delocalized character. According to our calculations, In2S3:Nb allows IB to CB transitions of 1.55 and 1.66 eV, as 5% Nb ions occupy In16h and In8c sites, respectively. We note that although the spontaneous VB to IB and IB to CB transitions (which was the primary goal of constructing IB solar cells) can not be achieved, but if the wavefunctions of doped TM become delocalized throughout the lattice, we can have IB to CB sub-band gap transitions in addition to the VB to CB transitions.
Note that as we move from left to the right along the 3d row of the periodic table, we approach the heavier 3d metals, whose atomic t and e orbitals are deeper in energy. Due to this simple rule, by increasing the atomic number along the same row, the interactions between the inserted TM and anion dangling bonds become stronger. Therefore, the t orbital of the 3d transition metals after Ti should reside below the VBM. As discussed in our previous work, the t+ state of the trivalent V splits into e+ and a+ sublevels, which reside at the top of VB and bottom of the CB, respectively. Hence, no in-gap state forms20. Going down the group 5B of periodic table from V to dubnium (Db) (or in general all d-block groups), the energy of d orbitals increases. Consequently, the t and e energies of the heavy Db should reside far above the energy levels of the light V.
Effect of concentration on the intermediate states formed by the incorporation of Ti and Nb
As mentioned before, at low concentrations, transition metal impurities are likely to introduce undesired deep defect levels inside the band gap of the host semiconductor. However, at sufficiently high concentrations, their wavefunctions become delocalized and a beneficial IB forms. In the case of In2S3, we know from the previous subsection that Ti and Nb impurities induce respectively filled singlet and doublet states inside the band gap of In2S3. However, up to this point it is not possible to predict whether such states are localized defect levels or beneficial delocalized IBs. In order to gain insights on this issue, we present in Figs. 5 and 6 the concentration-dependent spin-polarized DOS of the In2S3 doped with Ti and Nb ions that are located on the In16h sites. Furthermore, we show the partial charge density isosurfaces associated to the defect-induced states as the concentration of the doped TM increases. Since the charge density is associated to the defect wavefunction, its degree of (non)localization is associated to creation of localized or delocalized defect-induced states.
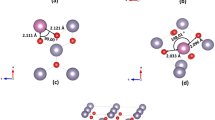
As we can see in Fig. 5a, c, e, the Ti-induced features on the electronic structures of In2S3, highlighted by the dashed box in each figure, do not show variations on their width, shape, or position as the Ti concentration increases, and only their height changes. Furthermore, their narrow shape points out that even at higher concentrations, the Ti-induced defect states would remain localized. In order to confirm this conclusion, we rely on the charge density isosurfaces of the Ti-induced defect states shown in Fig. 5b, d, f. As shown, even for a concentration of 5%, there is a rather negligible overlap between the states induced by Ti ions and host ions. This means that Ti-doped In2S3, at least for doping concentrations up to 5%, would not favor the formation of a beneficial IB.
Spin-polarized DOS computed for Ti-substituted In2S3 along with the charge density isosurfaces associated with the features induced in the band gap for a, b one, c, d two, and e, f four impurities inside the supercell. The Ti atoms are located on the available 16h In sites in the supercell and the pink box in density of states plots points out the defect states for which the correspondent charge density isosurfaces are produced using VESTA41 (displayed at 3% of their maximum value). The Ti impurities are shown in red and marked with an arrow of the same color. In and S are shown as green and blue spheres, respectively.
On the other hand, as shown in Fig. 6a, c, e, Nb-induced states in In2S3 are concentration dependent. When changing the doping concentration from 1.25 to 2.5%, the situation is analogous to the case of Ti and only the height of the defect states varies. However, when the Nb concentration reaches a value of 5%, the shape of the defect-induced states changes, too. Carrying out the same charge density analysis done for the case of Ti, we obtained the results presented in Fig. 6b, d, f. As illustrated, at the concentration of 2.5 and 5%, we see that the overlap of the defect wavefunction is achieved in all three dimensions and the introduction of a delocalized IB becomes probable. This result agrees with the wider intermediate band observed in the DOS (Fig. 6) and band structure (Supplementary Fig. 2) of the Nb-doped In2S3, which amounts to 0.39 eV, compared to 0.15 eV obtained for the Ti case. Therefore, the potentially relevant Nb-doped In2S3 with its well positioned IB can exhibit beneficial features for below gap IB → CB transitions.
Spin-polarized densities of states computed for Nb-substituted In2S3 along with the charge density isosurfaces associated with the features induced in the band gap for a, b one, c, d two, and e, f four impurities inside the supercell. The Nb atoms are located on the available 16h In sites in the cell and the pink box in density of states plots points out the defect states for which the correspondent charge density isosurfaces are produced using VESTA41 (displayed at 3% of their maximum value). The Nb impurities are shown in red and marked with an arrow of the same color. In and S are shown as green and blue spheres, respectively.
In 2017, Wägele et al.29 used X-ray diffraction, Raman spectroscopy, and scanning electron microscopy to analyze structural properties of the V-doped In2S3 for various concentrations of V. They found that even with excessive amount of V (as high as 5.8 at%) in In2S3, no additional peak appeared in the X-ray spectra and only the lattice constant decreased, which is due to difference in atomic radii of V (1.35 Å) and In (1.55 Å). V and Nb are chemically similar elements and the atomic radii of Nb (1.45 Å) is closer to that of In. In this regard, we expect that In2S3 is also stable against Nb incorporation.
The reader must be warned that the onset of a filled IB shifts the quasi-Fermi level to the top of the IB, which consequently limits the open circuit voltage (VOC) of the device. Therefore, a key area of future research would be to identify possible mechanisms of depopulating the filled IB. Photo-filling or -emptying of an IB proposed by Strandberg and Reenass30 could be helpful here as well. We note that the filled IB can be used on a device with spatially varying occupation of intermediate-band states. In such a device, the absorber has a filled IB in half of the device and an empty IB on the other half31. The theoretical efficiency of a device with spatially decoupled VB-to-IB and IB-to-CB is 52.83%, which is lower than the efficiency of an ideal partially filled IB but still significantly higher than the efficiency of the best single band gap solar cell. Based upon current state-of-the-art in the field, below gap absorption of Nb-doped In2S3 can be also further improved through an effective non-compensated pn-doping approach, which has been successfully applied in TiO232.
Heat of solution of Ti and Nb in In2S3
The heat of solution (Hs) of TMs in In2S3 were calculated according to Eq. (7) and are shown in Fig. 7. Our results indicate that there is a difference between Hs of TMs in In-rich and S-rich samples. For both Ti and Nb, substituting an In site is energetically more favorable under In-rich condition and their inclusion on S-rich samples becomes energetically more expensive. In particular, we see that the heat of solution of Ti atoms substituting the In sites are lower than Nb.
To understand the difference in solubilities of Ti and Nb in In2S3, we analyze the mechanical and chemical contributions to the calculated heat of solution33. The mechanical (or structural) effect refers to the energy stored due to the size misfit of the impurity in the host crystalline matrix. The chemical effect represents the energy stored or released due to the constitution of impurity-host bonds. Depending on the nature of the bonds, this term can be positive or negative. According to Lozovoi et al.33, we define configurations A, Av, B, and Bv as follows:
-
A: The relaxed structure of the In2S3 host;
-
Av: The same atomic structure as A, with an In atom removed from the 16h site;
-
B: The relaxed structure of \({{\rm{TMIn}}}_{31}{{\rm{S}}}_{48}\);
-
Bv: The same atomic structure as B, with the TM impurity removed from the 16h site.
Note that Av and Bv are hypothetical structures that we construct through using the relaxed A and B structures, respectively.
The change in energy due to structural effect consists of two steps; Host Removal (HR) and Structural Substitution (SS), which we define as following:
The contribution of Chemical Effect (CE) to heat of solution is defined as:
for Ti, and
for Nb.
Table 1 lists the mechanical and chemical contributions to the heat of solution of Ti and Nb in In2S3. The energy values correspond to the incorporation of 1.25% TM in In-rich samples. We see that the removal of an In atom from the host configuration (the HHR mechanism) accounts for a large increase in the energy of the system. The effect of structural substitution (HSS) is modest for Nb (0.01 eV). In case of Ti, however, there is a considerably larger lattice distortion contributed to the SS mechanism, which is due to the smaller size of Ti compared to Nb. Another distinguishing feature can be observed when the Ti (or Nb) are back into the vacant site (HCE). Since both Ti and Nb are more electropositive than In, they form stronger bonds with the six surrounding S atoms and the term HCE causes a large decrease in the energy of the system containing the alloying TM. For Ti, contribution of HCE in decreasing the heat of solution is −8.33 eV. As a consequence, the chemical decrease almost cancels the mechanical increase (sum of HHR and HSS mechanisms) in the total Hs. This results in a very low, but still positive heat of solution for Ti (0.08 eV). Note that the mechanical increase still dominates the chemical decrease, resulting in a positive heat of solution for Ti. The bonding between Nb and S is weaker compared to Ti. Therefore, the HCE is less negative for Nb and the energy consuming host removal and structural substitution can not be cancelled out by forming the weaker Nb-S bonds. Hence, the heat of solution of Nb is larger compared to Ti.
Our results indicate that the heat of solution, Hs, of Ti and Nb are positive in both In-rich and S-rich atmospheres, suggesting that their dissolution into In2S3 is an endothermic reaction. Therefore, both In-rich and S-rich samples can accommodate Ti and Nb atoms on octahedral In sites without leading to the formation of secondary phases.
Discussion
By using first principles calculations, we analyzed structural, energetic, and electronic characteristics of Ti and Nb-doped In2S3. We showed that in n-type In2S3 both Ti and Nb exist as neutral impurities (i.e., assuming the +III oxidation number) on In substitutional sites. The results show a tendency of Ti and Nb to occupy 16h octahedral In site rather than 8e tetrahedral site. In the octahedral symmetry of 16h In site, the \({d}_{{z}^{2}}\) and dxy orbitals (i.e., the e branch) of the TMs experience a stronger repulsion compared to the dxz, dyz, and \({d}_{{x}^{2}-{y}^{2}}\) orbitals (i.e., the t branch). Consequently, the \({d}_{{z}^{2}}\) and dxy orbitals are shifted to higher energies, forming doubly degenerate e(d) states inside the CB of the In2S3 for the two spin channels. The spin-up t branch (t+), however, has lower energy and can be found inside the band gap. For Ti on 16h In site, the t+ state consist of one occupied and two unoccupied levels. For Nb, however, the t+ state accommodates two electrons. Hence, consisting of two occupied and one unoccupied levels. Due to the influence of strong electron correlation effects, the filled and empty states of the TM t+ branch can not exist at the same energy level. Therefore, the threefold degeneracy of such level is removed due to an electron Jahn–Teller effect, which splits it into occupied and unoccupied sublevels. Prediction of such splittings depends on a correct description of the exchange-correlation functional, which can be tested through fulfillment of the generalized Koopmann’s theorem. Our choice of HSE functional (i.e., α = 0.25 and w = 0.13 Å−1) demonstrates an almost complete cancellation of the self-interaction error for Ti- and Nb-doped In2S3. The results clearly indicate that Ti t+ state splits into an occupied singlet at 0.14 eV above the VBM and an empty doublet inside the CB. The Nb t+ state, however, splits into an occupied doublet at 0.62 eV above the VBM and an unoccupied singlet in the CB. We have demonstrated that the occupied singlet in-gap state of Ti 16h remains highly localized even at high concentration of 5%. The occupied doublet of the Nb t+, however, shows a considerable overlap with the interacting orbitals of the neighbouring atoms at concentrations above 2.5%. This finding suggest that Nb-doped In2S3 can show below gap IB to CB transition. However, the VB to IB transition is prevented due to the absence of an empty state inside the gap. A comparison between the solubility of Ti and Nb in In2S3 shows that under similar growth conditions, Ti can exist in In2S3 at higher concentrations. Finally, we note that current study can be continued by analyzing the structural and electronic properties of other transition metals such as zirconium, hafnium, and tantalum in In2S3.
Methods
Computational details
Calculations in the framework of DFT were carried out using the Vienna ab initio Simulation Package34,35. The results were obtained using screened hybrid functional of Heyd, Scuseria, and Ernzerhof (HSE)36. The contribution of Hartree–Fock exchange, α, was set to the standard value of 0.25 and the screening range of the electron interaction was treated by adjusting the Thomas-Fermi screening parameter, w, to 0.13 Å−1, leading to a band gap of 2.03 eV13, which is in excellent agreement with experimental reports11,37. The interactions between the ionic cores and the valence electrons were described with the projector augmented-wave (PAW) approach38,39. The semi-core 3p, 4s, and 3d states of Ti and 4p, 5s, and 4d states of Nb were treated as part of the valence. The wavefunctions were expanded up to a cutoff energy of 400 eV and the Brillouin zone was sampled using a 4 × 4 × 1 k-point mesh. In all calculations the spin-polarization effects were taken into account. The convergence thresholds for electronic self-consistency and residual Hellmann–Feynman force component on each atom were set to 10−5 eV and 0.05 eV/Å, respectively. Calculations were performed for a unit cell containing 80 atoms. Both the ionic positions and the cell metric were allowed to relax.
In Table 2, we present bulk properties of the pure and TM-incorporated In2S3. A comparison between the bulk properties of the TM-incorporated on the In 8c and 16h sites and the PBE and HSE functionals is given in Supplementary Table I of the Supplementary Information file. The atomic size of In (1.55 Å) is larger than Ti (1.40 Å) and Nb (1.45 Å). Therefore, as expected, substitution of In by these transition metals reduces the size of unit cell. Furthermore, the band gap of In2S3 slightly increases upon inclusion of the TM atoms, which is expected by considering the contraction of the cells.
Fulfillment of the generalized Koopmans’ condition
As mentioned in the introduction, to assess suitability of HSE functional, one needs to test the fulfillment of the gKC. For this purpose, we quantify the non-Koopmans’ energy (\({E}_{i}^{NK}\)) using
where ϵi is the highest occupied state in the system of N electrons, and EN and EN−1 are the total energies of the N- and (N − 1)-electron systems, respectively. In case of \({E}_{i}^{NK}=0\), the gKC is fulfilled and the applied functional presents a self-interaction-free description of the orbitals. We find that using the HSE functional, the \({E}_{i}^{NK}\) is negligibly small for both Ti and Nb donors (smaller than 0.05 eV). Therefore, the applied hybrid functional correctly describes electron correlation in the system.
Calculation of formation energy and heat of solution
The defect formation energies were calculated at the theoretical equilibrium volume as
where q is the charge state, ΔE[dq] is the difference of the total energy of the cell with and without impurity, μTM and μIn are the chemical potentials of the TM and In atoms, respectively. EVBM is the energy of the valence band maximum (VBM) of the pure cell, and EF is position of the Fermi level with respect to the EVBM. Δvq is a term aligning the average electrostatic potential of the pure and defect cell containing a neutral defect.
For n dopants in the neutral charge state, the defect formation energy is equivalent to the heat of solution Hs,TM:
\({{\rm{E}}}_{{{\rm{TM}}}_{{\rm{n}}}}{{\rm{In}}}_{32-{\rm{n}}}{{\rm{S}}}_{48}\) is the total energy of the defective supercell of indium sulfide containing various TM concentrations. The term \({{\rm{E}}}_{{{\rm{In}}}_{32}}{{\rm{S}}}_{48}\) accounts for the total energy of a non-defective supercell of In2S3 with the same size as the one used for the defective systems, while n is the number of atoms added or removed from the supercell.
In Eqs. (6) and (7), the chemical potential of the incorporated TM (substituted In) is given by \({\mu }_{{\rm{TM}}}={\mu }_{{\rm{TM}}}^{{\rm{ref}}}+\Delta {\mu }_{{\rm{TM}}}\) (\({\mu }_{{\rm{In}}}={\mu }_{{\rm{In}}}^{{\rm{ref}}}+\Delta {\mu }_{{\rm{In}}}\)), where \({\mu }_{{\rm{TM}}}^{{\rm{ref}}}\) (\({\mu }_{{\rm{In}}}^{{\rm{ref}}}\)) is the total energy of the TM (In) atom in its reference phase. ΔμTM (ΔμIn) is the maximum possible change of the chemical potential of the TM (In). For staying in the stable phase field of In2S3, the following constraints must hold:
where ΔHf(In2S3) is the formation enthalpy of the β−In2S3. Here, we consider two experimental growth conditions:
-
(i)
In-rich limit: In2S3 is in equilibrium with the metallic tetragonal In-phase. This determines the upper limit of μIn, ΔμIn = 0, and the lower limit of μS, \(\Delta {\mu }_{{\rm{S}}}=\frac{1}{3}\Delta {{\rm{H}}}_{{\rm{f}}}({{\rm{In}}}_{2}{{\rm{S}}}_{3})\).
-
(ii)
S-rich limit: In2S3 is in equilibrium with the orthorhombic S-phase, whence ΔμS = 0 and \(\Delta {\mu }_{{\rm{In}}}=\frac{1}{2}\Delta {{\rm{H}}}_{{\rm{f}}}({{\rm{In}}}_{2}{{\rm{S}}}_{3})\).
Note that the chemical potentials of In and S can vary between these two limits. Furthermore, the concentrations of Ti and Nb in In2S3 are restricted by the formation of TiS2 and NbS2 as competing phases. Hence, the chemical potentials of Ti and Nb must satisfy the relations Eqs. (10) and (11), respectively,
The formation enthalpies of In2S3, TiS2, and NbS2 were calculated with the HSE functional and are listed in Table 3. The chemical potentials of Ti and Nb are referenced to the energies of their pure elemental phases, i.e., hexagonal-close-packed Ti and Nb.
Data availability
Data are available upon reasonable request from the corresponding author.
References
Wolf, M. Limitations and possibilities for improvement of photovoltaic solar energy converters: Part I: Considerations for earth’s surface operation. Proc. IRE 48, 1246–1263 (1960).
Haldane, F. D. M. & Anderson, P. W. Simple model of multiple charge states of transition-metal impurities in semiconductors. Phys. Rev. B 13, 2553–2559 (1976).
Shockley, W. & Read, W. T. Statistics of the recombinations of holes and electrons. Phys. Rev. 87, 835–842 (1952).
Hall, R. N. Electron-hole recombination in Germanium. Phys. Rev. 87, 387–387 (1952).
Luque, A. & Martí, A. Increasing the efficiency of ideal solar cells by photon induced transitions at intermediate levels. Phys. Rev. Lett. 78, 5014–5017 (1997).
Shockley, W. & Queisser, H. J. Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 32, 510–519 (1961).
Luque, A., Martí, A., Antolín, E. & Tablero, C. Intermediate bands versus levels in non-radiative recombination. Physica B Condens. Matter 382, 320–327 (2006).
Palacios, P., Sánchez, K., Conesa, J., Fernández, J. & Wahnón, P. Theoretical modelling of intermediate band solar cell materials based on metal-doped chalcopyrite compounds. Thin Solid Films 515, 6280–6284 (2007).
Martí, A., Marrón, D. F. & Luque, A. Evaluation of the efficiency potential of intermediate band solar cells based on thin-film chalcopyrite materials. J. Appl. Phys. 103, 073706 (2008).
Luque, A. & Martí, A. Understanding intermediate-band solar cells. Nat. Photonics 6, 146–152 (2012).
Rehwald, W. & Harbeke, G. On the conduction mechanism in single crystal β-indium sulfide in2 s3. J. Phys. Chem. Solids 26, 1309–1324 (1965).
Pistor, P. et al. Structure reinvestigation of α-, β - and γ-In2S3. Acta. Crystallogr. B Struct. Sci. Cryst. Eng. Mater. 72, 410–415 (2016).
Ghorbani, E. & Albe, K. A hybrid functional view of intrinsic point defects in β-In2 s3. J. Appl. Phys. 123, 103103 (2018).
Ghorbani, E. & Albe, K. Role of oxygen and chlorine impurities in β−In2S3 : a first principles study. Phys. Rev. B 98, 205201 (2018).
Ghorbani, E. & Albe, K. Influence of cu and na incorporation on the thermodynamic stability and electronic properties of β−In2S3. J. Mater. Chem. C 6, 7226–7231 (2018).
Schulthess, ThomasC., Walter, Z. S. W. H. B. G. M. S. & Temmerman, M. Electronic structure and exchange coupling of mn impurities in iii-v semiconductors. Nat. Mater 4, 838–844 (2005).
Kümmel, S. & Kronik, L. Orbital-dependent density functionals: theory and applications. Rev. Mod. Phys. 80, 3–60 (2008).
Deák, P., Aradi, B., Frauenheim, T., Janzén, E. & Gali, A. Accurate defect levels obtained from the hse06 range-separated hybrid functional. Phys. Rev. B 81, 153203 (2010).
Paier, J. et al. Screened hybrid density functionals applied to solids. J. Chem. Phys. 124, 154709 (2006).
Ghorbani, E., Erhart, P. & Albe, K. New insights on the nature of impurity levels in v-doped in2s3: why is it impossible to obtain a metallic intermediate band? J. Mater. Chem. A 7, 7745–7751 (2019).
Ivády, V., Abrikosov, I. A., Janzén, E. & Gali, A. Role of screening in the density functional applied to transition-metal defects in semiconductors. Phys. Rev. B 87, 205201 (2013).
Ivády, V. et al. Theoretical unification of hybrid-DFT and DFT + U methods for thetreatment of localized orbitals. Phys. Rev. B 90, 035146 (2014).
Lany, S. & Zunger, A. Polaronic hole localization and multiple hole binding of acceptors in oxide wide-gap semiconductors. Phys. Rev. B 80, 085202 (2009).
Lany, S. & Zunger, A. Generalized koopmans density functional calculations reveal the deep acceptor state of no in ZnO. Phys. Rev. B 81, 205209 (2010).
Ghorbani, E., Erhart, P. & Albe, K. Energy level alignment of Cu(In, Ga)(S, Se)2 absorber compounds with In2S3, NaIn5S8, and CuIn5S8 Cd-free buffer materials. Phys. Rev. Mater 3, 075401 (2019).
Palacios, P., Aguilera, I., Sánchez, K., Conesa, J. C. & Wahnón, P. Transition-metal-substituted indium thiospinels as novel intermediate-band materials: prediction and understanding of their electronic properties. Phys. Rev. Lett. 101, 046403 (2008).
Raebiger, H., Lany, S. & Zunger, A. Charge self-regulation upon changing the oxidation state of transition metals in insulators. Nature 453, 763–766 (2008).
Ho, C.-H. Enhanced photoelectric-conversion yield in niobium-incorporated In2S3 with intermediate band. J. Mater. Chem. 21, 10518–10524 (2011).
Wägele, L. A., Rata, D., Gurieva, G. & Scheer, R. Structural analysis of co-evaporated In2S3 and In2S3 :V for solar cell absorber applications. Phys. Status Solidi C 14, 1600204 (2017).
Strandberg, R. & Reenaas, T. W. Photofilling of intermediate bands. J. Appl. Phys. 105, 124512 (2009).
Lin, A. & Phillips, J. Decoupling spectral overlap of intermediate band solar cells using low-high state filling. 38th IEEE Photovoltaic Specialists Conference. 000073–000077 (2012). https://doi.org/10.1109/PVSC.2012.6317571.
Wu, F., Lan, H., Zhang, Z. & Cui, P. Quantum efficiency of intermediate-band solar cells based on non-compensated n-p codoped TiO2. J. Chem. Phys. 137, 104702 (2012).
Lozovoi, A. Y., Paxton, A. T. & Finnis, M. W. Structural and chemical embrittlement of grain boundaries by impurities: A general theory and first-principles calculations for copper. Phys. Rev. B 74, 155416 (2006).
Kresse, G. & Furthmueller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Kresse, G. & Furthmueller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15 (1996).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened coulomb potential. J. Chem. Phys. 118, 8207 (2003).
Nomura, R., Konishi, K. & Matsuda, H. Single-source organometallic chemical vapour deposition process for sulphide thin films: Introduction of a new organometallic precursor \({\mathrm{Bu}}^n{\mathrm{In}}({\mathrm{SPr}}^i)_2\) and preparation of In2S3 thin films. Thin Solid Films 198, 339–345 (1991).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Bloechl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Knacke, O., Kubaschewski, O. & Hesselmann, H. Thermochemical properties of inorganic substances (Springer-Verlag, Berlin, 1991).
Momma, K. & Izumi, F. VESTA: a three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 41, 653–658 (2008).
Acknowledgements
We would like to thank Prof. Roland Scheer for helpful discussions. This work has been financially supported by Deutsche Forschungsgemeinschaft (DFG) under project No. 414750661. The computing time was provided by Jülich Supercomputing Center (Project No. HDA30) and Lichtenberg HPC computer resources at TU Darmstadt. E.G. would like to thank the Hessian Competence Center for High Performance Computing—funded by the Hessen State Ministry of Higher Education, Research and the Arts—for helpful advice.
Author information
Authors and Affiliations
Contributions
E.G. designed research, performed all simulations, analyzed results, and wrote the manuscript. D.B.Y participated in analysis and writing the manuscript. K.A. guided the theoretical analysis and supervised the study.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ghorbani, E., Barragan-Yani, D. & Albe, K. Towards intermediate-band photovoltaic absorbers: theoretical insights on the incorporation of Ti and Nb in In2S3. npj Comput Mater 6, 93 (2020). https://doi.org/10.1038/s41524-020-00350-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-020-00350-2
This article is cited by
-
Effect of different dopants on the structural and physical properties of In2S3 thin films: a review
Journal of Materials Science (2023)