Abstract
BAs is a III–V semiconductor with ultra-high thermal conductivity, but many of its electronic properties are unknown. This work applies predictive atomistic calculations to investigate the properties of BAs heterostructures, such as strain effects on band alignments and carrier mobility, considering BAs as both a thin film and a substrate for lattice-matched materials. The results show that isotropic biaxial in-plane strain decreases the band gap independent of sign or direction. In addition, 1% biaxial tensile strain increases the in-plane electron and hole mobilities at 300 K by >60% compared to the unstrained values due to a reduction of the electron effective mass and of hole interband scattering. Moreover, BAs is shown to be nearly lattice-matched with InGaN and ZnSnN2, two important optoelectronic semiconductors with tunable band gaps by alloying and cation disorder, respectively. The results predict type-II band alignments and determine the absolute band offsets of these two materials with BAs. The combination of the ultra-high thermal conductivity and intrinsic p-type character of BAs, with its high electron and hole mobilities that can be further increased by tensile strain, as well as the lattice-match and the type-II band alignment with intrinsically n-type InGaN and ZnSnN2 demonstrate the potential of BAs heterostructures for electronic and optoelectronic devices.
Similar content being viewed by others
Introduction
Boron arsenide (BAs) is an attractive electronic material due to its ultra-high thermal conductivity (~1300 W m–1 K–1),1,2,3 native p-type dopability,4 and the availability of millimeter-size single crystals as substrates for thin-film growth.3,5,6 Following the experimental validation1,2,3 of the theoretical prediction7,8 of its ultra-high thermal conductivity, research efforts have focused on its growth and fundamental characterization.9 These results include studies of the thermal, optical, electronic, and structural properties of BAs in both bulk and 2D forms.4,9,10,11,12,13,14,15,16 However, to fully evaluate its potential in electronic and optoelectronic applications, the properties of BAs heterostructures with other semiconductor materials, either as a thin film or as a substrate, must be investigated.
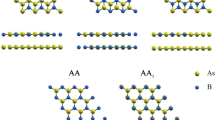
Two important degrees of freedom for thin-film engineering in device architectures are mechanical strain and band alignment. Strain arising from epitaxial mismatch strongly affects the electronic properties of materials, including the band gap,17 band alignments,18 effective masses,19 and mobility.20,21 Though the epitaxial growth of BAs thin films has not been demonstrated yet, it should be feasible under growth conditions that replicate the established chemical vapor transport growth procedure. Candidate tetrahedrally bonded substrate materials for thin-film growth on the (111) plane of BAs are ZnO (3.249 Å22), GaN (3.189 Å23), or GaAs (3.997 Å24), while for (001)-oriented BAs thin films, candidate substrates are (001) oriented rutile TiO2 (4.59 Å25) or MgF2 (4.64 Å26), which result in epitaxial strains ranging from −6% to +15% (Fig. 1a). However, the effects of mechanical strain on the electronic properties of BAs are unknown.
a Epitaxially grown BAs thin film as part of a transistor. Epitaxially straining BAs (inset) increases both the electron and the hole mobility. b Schematic of an optoelectronic device utilizing the junction between a thermally conducting BAs substrate for efficient heat extraction in conjunction with nearly lattice-matched direct-band-gap semiconductor films for efficient light emission and absorption.
On the other hand, BAs can also be utilized as a high-thermal-conductivity substrate for the epitaxial growth of other semiconductors (Fig. 1b). Specifically, the lattice constant of the (111) plane of BAs (3.380 Å1) is well matched with InGaN alloys (3.189–3.533 Å23,27,28) and disordered ZnSnN2 (~3.383 Å).29 These materials are prominent optoelectronic materials due to their direct band gap in the visible range (and the resulting strong optical absorption and emission), which can be tuned by adjusting the alloy composition (InGaN) or the degree of cation disorder (ZnSnN2),30 but they both face challenges in device applications. On the one hand, the amount of In that can be incorporated into InGaN is limited in part due to the large mismatch with the underlying substrate, typically GaN or sapphire. On the other, ZnSnN2 films are unintentionally heavily n-type in nature and require a partner p-type semiconductor in devices such as light-emitting diodes (LEDs) or solar cells. Both materials could benefit from p-type substrates with minimal lattice misfit for high-quality thin-film growth. BAs has intrinsic p-type conductivity owing to native defects such as BAs and VB as well as unintentional impurities such as C and Si,4,12 and can thus be a potential junction partner to these materials with good lattice match. However, band offsets for these hybrid structures and the assessment of their potential for device applications have not yet been determined.
In this work, we aim to understand the effect of biaxial strain on the band structure, mobility, and absolute band alignments of BAs with density functional theory (DFT) calculations and explore its possible applications in semiconductor heterostructures, either as a thin film, where biaxial strain may enhance its electronic properties, or as a substrate, where it may form advantageous heterojunctions with other materials. We show that, when epitaxially grown with 1% biaxial tensile strain, both electron and hole mobilities are increased by >60%, showing promise for fast-switching and energy-efficient transistors. These results motivate BAs as a promising thin-film semiconductor. We also propose favorable nearly lattice-matched heterojunctions of two important compounds, InGaN and ZnSnN2, with BAs, showing how BAs can be used as a high-thermal-conductivity substrate for type-II band aligned heterojunctions for photovoltaic and photodetector applications.
Results and discussion
Strain effects on the band structure and absolute band positions
We first examine the effects of strain on the band structure along the Γ–X and Γ–Z directions, which include the conduction band minimum (CBM) and valence band maximum (VBM). These results, calculated with the Heyd–Scuseria–Ernzerhof (HSE) hybrid functional and spin–orbit effects, are shown in Fig. 2a, b (Supplementary Fig. 4 shows the local-density approximation (LDA) band structure without spin–orbit effects). For the unstrained structure, the X (in-plane) and Z (out-of-plane) directions are equivalent by symmetry, and the conduction band minima along the Γ–X and Γ–Z directions are degenerate (Fig. 2a). However, biaxial strain within the (100) plane breaks the cubic symmetry and splits the degeneracy of the CBM valleys near X and Z; the lower CBM occurs along the Γ–Z (Γ–X) direction under tensile (compressive) strain (Fig. 2b). The broken symmetry under strain also affects the VBM by splitting the topmost two degenerate valence bands (Fig. 2b). These effects are important in explaining the mobility findings we discuss in the following paragraphs. Strain also shifts the absolute band positions as shown in Fig. 2c. We find that the conduction band lowers and the valence band rises in energy with increasing strain (independent of its sign) within both the (100) and (111) planes. This decreases the band gap from 1.78 eV (unstrained) to 0.89 eV (for 4% tensile strain within the (100) plane) or 1.15 eV (for 4% compressive strain within the (100) plane). We find that strain within the (100) plane decreases the band gap more than within the (111) plane. Also, while tensile strain changes the band gap more than compressive strain for the (100) plane, the opposite trend is found for the (111) plane.
a Calculated band structure of unstrained BAs along X to Γ and Γ to Z using HSE hybrid functional considering spin–orbit effects. The X and Z directions are equivalent due to the cubic symmetry. b The effect of biaxial strain within the (100) plane on the band structure of BAs. The upper panel shows the splitting of the degeneracy of the CBM valleys near X and Z under strain due to the broken symmetry. Tensile strain places electrons at the Z valley while compressive moves them to the X valleys. The bottom row shows the splitting of the degenerate topmost valence bands under strain. c Absolute band alignments of BAs relative to the vacuum level as a function of biaxial strain within the (100) (black lines) and (111) (blue lines) planes. The band gap is always reduced independent of the strain direction or sign.
Strain effects on carrier mobility
Next, we investigate the effect of tensile strain on the phonon-limited electron and hole mobility of BAs, i.e., the upper mobility limits in non-defective samples. We first evaluate the converged values by plotting the calculated mobility at 300 K versus the inverse of the number of the Brillouin-zone (BZ) sampling points and extrapolating (Supplementary Fig. 5). For unstrained BAs, we find electron and hole mobility values of 1341 and 1387 cm2 V−1 s−1 at 300 K, respectively. We find excellent agreement between our calculated electron mobilities and the results of Liu et al.13 (1400 cm2 V−1 s−1). However, there are discrepancies for the hole mobility (2110 cm2 V–1 s–1) since our mobility calculations do not include spin–orbit coupling, which results in a threefold (instead of twofold) degenerate VBM (Supplementary Fig. 4). This higher band degeneracy in the absence of spin–orbit effects results in more scattering channels and a proportionately lower mobility. In fact, our result of 1387 cm2 V−1 s−1 is almost exactly 2/3 of the value from Liu et al.13 (2110 cm2 V–1 s–1), providing evidence for the strong impact of band degeneracy on the hole mobility. We note that our calculations for the electron mobility agree well with Liu et al.13 since the CBM is not significantly affected by spin–orbit coupling. Furthermore, while the unique phonon band structure of BAs is responsible for suppressing three-particle phonon–phonon scattering and enabling its ultra-high thermal conductivity,7 we do not expect the mobilities to be similarly affected as they are controlled by a different scattering mechanism (electron–phonon coupling). A possible indirect effect, however, is that the suppression of phonon–phonon scattering may prevent the thermal relaxation of optical phonons, and the resulting higher occupation may amplify carrier scattering by optical phonons and reduce the mobility.
We next examine the mobilities of the 1% tensile-strained structure. From these calculations, we find that the in-plane and out-of-plane mobilities at 300 K for electrons are 2417 and 482 cm2 V−1 s−1, respectively, while the corresponding values for holes are 3550 and 2956 cm2 V−1 s−1. Therefore, in BAs, tensile strain increases both the electron and hole mobilities of BAs, which is consistent with Si, which has a similar band structure.20,21
By examining the band structures in Fig. 2b, we gain useful insight into the different mechanisms contributing to the increased mobility. In the case of electrons, we observe that tensile strain results in the lifting of the threefold degeneracy in the conduction band (Fig. 3a, b), with the out-of-plane minima occurring ~200 meV below the two in-plane minima for 1% strain (Fig. 2b). This energy splitting has a strong effect on the effective mass of electrons. In an unstrained crystal, where all of the conduction valleys are degenerate (Fig. 3a), the average effective mass of electrons is the directional average between the lighter transverse effective mass and the heavier longitudinal effective mass [m* = (2mt* + ml*)/3 = 0.52].11 On the other hand, in strained BAs, similar to strained silicon,21 the majority of electrons occupy the lower-energy out-of-plane valleys (Fig. 3b), so in-plane transport is governed only by the lighter transverse effective mass [m* = 0.24],11 while out-of-plane transport is governed only by the heavier longitudinal effective mass [m* = 1.09].11 This difference in effective mass therefore helps explain not only the elevated in-plane electron mobility but also the suppressed out-of-plane electron mobility. Previous work on strained silicon also found that the changes in effective mass, as opposed to reduced intervalley scattering, are the dominant mechanism affecting the electron mobility.21
Isosurfaces of the lowest conduction band at an energy 200 meV above the CBM in the first BZ for a unstrained and b 1% tensile-strained BAs. In the unstrained case all six valleys are symmetrically equivalent, while in the strained case carriers primarily populate the lower-energy out-of-plane valleys. In the case of holes, the figure shows the top valence bands for c no strain or spin–orbit coupling (threefold degenerate VBM), d no strain but with spin–orbit coupling (twofold degenerate VBM), e 1% tensile strain but no spin–orbit coupling (non-degenerate VBM), and f 1% tensile strain and spin–orbit coupling (non-degenerate VBM). The calculated hole mobilities are primarily governed by the number of channels (bands) that contribute to hole scattering.
In the case of the hole mobility, the effective masses of the topmost three valence bands at Γ are all similar to one another, so the increase of the hole mobility by strain is explained by a different mechanism: the reduction in the number of available hole-scattering channels (Fig. 3c–f). Following from our previous discussion of the unstrained case, the inclusion of tensile strain leads to the topmost valence band becoming non-degenerate, with a separation of ~115 and ~145 meV with and without spin–orbit coupling, respectively. This reduction to only one hole-scattering channel leads to an increase in the hole mobility by approximately a factor of two compared to the unstrained spin–orbit-coupling-corrected results (where there were two scattering channels). We note that our result for the strained hole mobility is not expected to be strongly affected by the inclusion of spin–orbit coupling, since the top valence band of strained BAs is non-degenerate—by a similar degree—whether spin–orbit coupling effects are included (Fig. 3f) or not (Fig. 3e). Unlike electrons, we find that strain also increases the out-of-plane hole mobility due to the same reduction in the number of hole-scattering channels. We attribute the difference between the in-plane and out-of-plane hole-mobility values to the differences of the hole effective masses under strain, as the out-of-plane effective mass (m* = 0.25) is slightly higher than the in-plane mass (m* = 0.22). The qualitative conclusions that the strain increased hole mobility is due to the reduction of interband scattering caused by degeneracy lifting via broken symmetry, while the in-plane and out-of-plane hole-effective mass differences are responsible for the slightly different values along the two orientations are consistent with a similar investigation for strained Si.21
We also examine the temperature dependence of the electron and hole mobilities in the 100–500 K range (Fig. 4a, b). For the unstrained case, we find that, below 200 K, both the electron and hole mobilities follow a power law close to T−1.5 (Fig. 4c, d), indicating a primarily acoustic deformation potential carrier-scattering mechanism. From 200 to 500 K, we find that the temperature dependence of the electron and hole mobilities of unstrained BAs follow a T−2.14 and T−2.41 power law, respectively (Fig. 4c, d), which is similar to the values found by Liu et al.13 and indicates that optical deformation potential scattering becomes the dominant carrier-scattering mechanism.31 In the presence of tensile strain, acoustic deformation potential remains the dominant carrier-scattering mechanism below 200 K. But in the 200–500 K range, the temperature dependence of the mobility changes compared to unstrained BAs—decreasing to ~T−1.8 for electrons and increasing to ~T−3.0 for holes (Fig. 4c, d)—signifying a qualitative change in the dominant electron-scattering mechanism by tensile strain. We attribute the different temperature dependence under tensile strain to the weakening (strengthening) of the optical deformation potential scattering of electrons (holes) due to the reduction of the valley (valence band) degeneracy by tensile strain.
Temperature dependence of a electron and b hole carrier mobilities of BAs under tensile strain. The solid lines with circle markers show the results for unstrained BAs from our calculations (black/red) and those of Liu et al. (blue).13 The mobilities under strain are shown for both the in-plane (dashed/squares) and out-of-plane (dotted/triangles) directions. Tensile strain increases the in-plane and reduces the out-of-plane electron mobility (due to changes to the effective mass), while it also increases both the in-plane and out-of-plane hole mobility (by breaking the topmost valence band degeneracy and reducing interband scattering). Temperature dependence of electron (c) and hole (d) mobilities shown on a log–log scale. There is a clear change in the power law governing the temperature dependence around 200 K in all cases. In the case of holes (and to a lesser extent electrons), strain increases the magnitude of the temperature dependence, indicating a change in the dominant scattering mechanism. Note that data from this work do not include spin–orbit coupling.
BAs as a lattice-matched substrate
Next, we considered heterojunctions with other semiconductors where BAs is used as a substrate and their potential device applications. According to Fig. 5a, we determine that BAs can form lattice-matched interfaces with InGaN and ZnSnN2 and can solve several challenges that arise in adapting these materials for optoelectronic devices.
a Band gap versus in-plane lattice constant for BAs, wurtzite group-III nitrides, and orthorhombic Zn-IV-nitrides. InxGa1−xN with In concentration (x) from 0.46 to 0.65 and ZnSnN2 are nearly lattice-matched to BAs with misfit strain <1%. b Band alignments of unstrained InxGa1−xN, BAs, and ZnSnN2 with respect to the vacuum level. The band positions of InxGa1−xN are plotted as a function of In content, x, while those of ZnSnN2 are plotted as a function of the long-range order parameter, S. BAs has type-II band alignments with n-type In0.5Ga0.5N and ZnSnN2, showing BAs can be a potential p-junction partner with these materials for efficient solar cell absorber. The band alignment data for InGaN is adapted from ref. 38
First, InGaN alloys have emerged as prominent optoelectronic materials due to their efficient luminescence, high absorption coefficient, and the broad tunability of their direct band gap across the entire visible spectrum by alloying (from 0.69 eV for InN32 to 3.4 eV for GaN33).23,34,35 However, the difficulty in growing high-quality InGaN films with high In concentrations limits the emission wavelengths of devices to shorter than green and is one of the major challenges for fabricating efficient InGaN-based amber and red LEDs35 for, e.g., full-color displays or efficient solar cells.36 This growth challenge arises mainly due to the lack of lattice-matched substrates. GaN-buffered sapphire (0001) is the most common substrate for InGaN growth, but the lattice mismatch between GaN and InGaN increases with increasing In composition. The calculated critical thickness for the formation of misfit dislocation decreases rapidly with increasing In composition and becomes <1 nm for In0.2Ga0.8N/GaN heterostructures,36 which is too thin for efficient light emission in LEDs and light absorption in solar cells.
Our calculations show that (111)-oriented BAs can be an alternative substrate or heterolayer for epitaxial InGaN growth. The hexagonal lattice constant of the BAs (111) plane (3.379 Å) is 5.62% larger than GaN (3.189 Å) and 4.56% smaller than InN (3.533 Å). Applying Vegard’s law, we find that BAs can serve as an excellent substrate for InxGa1−xN growth with misfit strain <1% for In compositions of ~0.47, with a band gap of 1.75 eV37 that enables red light emission. Thus, by exploiting a BAs substrate or epilayer, the light-emission wavelength range of InGaN-based devices can be expanded to cover the full visible spectrum. In addition, BAs and InxGa1−xN (0.3 < x < 1) have type-II band alignment (Fig. 5b).38 Therefore, BAs substrates or epilayers can serve as a p-type junction for InGaN-based photovoltaic devices. For an In content of 50%, the band offsets between InGaN and BAs are calculated to be 0.42 eV for the CB and 0.30 eV for the VB, which allows for the effective separation and collection of carriers.
Recently, the family of Zn-IV-N2 compounds has been proposed as a next-generation class of solar-absorber materials composed of Earth-abundant elements that can replace the costly and rare In and Ga of conventional group-III nitrides.29 Among their favorable characteristics, the tunability of their direct band gap (between 1.12 and 2.09 eV) at a fixed composition by adjusting the degree of cation disorder is of particular interest.39 Thin films of Zn-IV-N2 compounds and alloys (e.g., ZnGexSn1−xN2) have been successfully synthesized using molecular beam epitaxy40 and sputtering,41,42 and the tuning of their band gap through controlled cation disorder has been demonstrated by adjusting the growth temperature or relative ratio of source elements.39 Despite their attractive properties, there are limited studies concerning device integration and characterization with these materials since intrinsically high electron concentrations from donor point defects (VN, ON, and SnZn) hampers bipolar doping of this material.43 Using alternative methods, a ZnSnN2/p-Si heterojunction was fabricated,44 while NiO, Cu2O, and CuAlO2 have also been proposed as other suitable p-type semiconductors.45 Still, the lattice mismatch for all these materials ranges from 10% to 15%, which is too large to achieve high-crystal-quality epitaxial interfaces.
We propose n-ZnSnN2/p-BAs as an optimal hybrid structure for efficient photovoltaic applications. First, the cation disordered pseudo-wurtzite structure of ZnSnN2 has very close lattice match along the (111) plane of BAs with misfit strain <1%. Also, while ZnSnN2 is intrinsically n-type, BAs is p-type due to B-related acceptor-type point defects and its doping level can also be controlled extrinsically by Si, Ge, and Be acceptors.4 Band alignment of the heterojunction in the intrinsic case is shown in Fig. 5b with band offset energies between BAs and ordered ZnSnN2 of 0.516 eV for the VB and 0.503 eV for the CB. Thus effective separation of electrons and holes into different regions of the device is predicted. Furthermore, we note that the ideal pair of band gaps for a two-gap multi-junction photovoltaic device are 1.1 and 1.8 eV. While both BAs and ZnSnN2 materials have intrinsic gaps close to 1.8 eV, a 1.1-eV gap in ZnSnN2 may be achieved by full cation disorder or a 1.1-eV gap in BAs may be achieved by epitaxial strain up to 4%, as shown in Fig. 2c.
In summary, we examine the potential of BAs for electronic and optoelectronic device applications by predicting important electronic properties of BAs for incorporation into devices as both a substrate material and an epitaxially grown thin film. As a thin film, we find that tensile epitaxial strain increases the in-plane electron and hole mobilities to 2417 and 3550 cm2 V–1 s–1, respectively. These values represent an 80% and 68% increase over the unstrained case, a significant improvement that could lead to faster switching and more energy-efficient transistors. We find that at temperatures below 200 K acoustic deformation potential dominates carrier scattering, while above 200 K optical deformation potential becomes the dominant scattering mechanism. For bulk BAs as a substrate, we find In-rich InGaN and ZnSnN2 are candidate materials that can be epitaxially grown on BAs and form p–n junctions for lasers, LEDs, photodetectors, or photovoltaic cells. These junctions can cover the full visible spectrum, while simultaneously benefiting from the high thermal conductivity of BAs substrates for efficient heat removal.
Methods
Band structure and absolute band positions
Our DFT calculations for the band structure and band alignment use the projector augmented wave method46,47 and the HSE0648 hybrid functional as implemented in the Vienna Ab initio Simulation Package.49,50,51 For the band alignment calculation, the mixing parameter of the HSE06 functional was set to 25% for BAs, 25% for InGaN, and 31% for ZnSnN2 to match the experimentally measured band gaps3,23,41 within 0.2 eV. To construct biaxially strained structures, we first relax the cubic unit cell, fix the in-plane lattice constant (\(a_\parallel\)) under −4% to 4% strain, calculate the total energy as a function of the out-of-plane lattice constant (\(a_ \bot\)) for each \(a_\parallel\), identify the \(a_ \bot\) that minimizes the total energy (Supplementary Fig. 1), and calculate the band structure of the resulting crystal structure including spin–orbit coupling effects. For band alignment calculations, we build strained and unstrained BAs slabs consisting of 12 layers (48 atoms) along the nonpolar [110] direction and calculate the plane-averaged electrostatic potential without relaxing the ions to determine the band alignment of bulk BAs without the effects of surface dipoles by structural relaxation. We then use the energy difference between the average electrostatic potential inside the slab and in the vacuum region to align the BAs bands to vacuum. For the ZnSnN2 band alignment, we first align the order structure to the vacuum level (Supplementary Fig. 2) using the same method as BAs except that the mixing parameter of HSE06 functional is chosen to be 31%, which is commonly used in previous DFT calculations on ZnSnN2 to match the experimental band gap.30,43 Then the partially disordered ZnSnN2 is aligned to the ordered structure directly using the band eigenvalues from the DFT calculations (Supplementary Fig. 3). The justification and details of this alignment procedure are provided in Supplementary Information.
Carrier mobility
To calculate the electron and hole mobilities in strained and unstrained BAs, we use the QUANTUM ESPRESSO52 and Electron–phonon Wannier (EPW)53,54 codes. We employ the LDA and the plane-wave norm-conserving pseudopotential method. We first relax the unit cell and subsequently apply a 1% biaxial tensile strain to the (001) plane and allow the out-of-plane (perpendicular) direction to relax to find the strained structure. We also use density functional perturbation theory55 within QUANTUM ESPRESSO to calculate the phonon frequencies and displacements on a coarse 6 × 6 × 6 BZ sampling grid for the strained and unstrained geometries. We then use the EPW code to interpolate the electron–phonon coupling matrix elements to fine BZ sampling meshes (up to 120 × 120 × 120) and determine the electron and hole mobilities at 300 K for the strained and unstrained structures for free-carrier concentrations of 1018 cm−3. We also calculate the temperature dependence of mobility from 100 to 500 K with 50 K steps on fine BZ sampling meshes of 72 × 72 × 72. We did not include spin–orbit coupling effects in the mobility calculations of the strained materials due to the added code complexity and computational cost. We expect that the omission of spin–orbit coupling does not affect the calculated carrier mobilities under strain as the CBM is unaffected by spin–orbit coupling, while the degeneracy splitting of the top valence band by strain (which controls the number of hole-phonon scattering channels) is also not affected by the inclusion of spin–orbit coupling effects.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Kang, J. S., Li, M., Wu, H., Nguyen, H. & Hu, Y. Experimental observation of high thermal conductivity in boron arsenide. Science 361, 575–578 (2018).
Li, S. et al. High thermal conductivity in cubic boron arsenide crystals. Science 361, 579–581 (2018).
Tian, F. et al. Unusual high thermal conductivity in boron arsenide bulk crystals. Science 361, 582–585 (2018).
Chae, S., Mengle, K., Heron, J. T. & Kioupakis, E. Point defects and dopants of boron arsenide from first-principles calculations: donor compensation and doping asymmetry. Appl. Phys. Lett. 113, 212101 (2019).
Chu, T. L. & Hyslop, A. E. Crystal growth and properties of boron monoarsenide. J. Appl. Phys. 43, 276–279 (1972).
Xing, J. et al. Multimillimeter-sized cubic boron arsenide grown by chemical vapor transport via a tellurium tetraiodide transport agent. Appl. Phys. Lett. 112, 261901 (2018).
Lindsay, L., Broido, D. A. & Reinecke, T. L. First-principles determination of ultrahigh thermal conductivity of boron arsenide: a competitor for diamond? Phys. Rev. Lett. 111, 025901 (2013).
Feng, T., Lindsay, L. & Ruan, X. Four-phonon scattering significantly reduces intrinsic thermal conductivity of solids. Phys. Rev. B 96, 161201 (2017).
Tian, F. & Ren, Z. High thermal conductivity in boron arsenide: from prediction to reality. Angew. Chem. Int. Ed. 58, 5824–5831 (2019).
Ravichandran, N. K. & Broido, D. Non-monotonic pressure dependence of the thermal conductivity of boron arsenide. Nat. Commun. 10, 1–8 (2019).
Bushick, K., Mengle, K., Sanders, N. & Kioupakis, E. Band structure and carrier effective masses of boron arsenide: effects of quasiparticle and spin-orbit coupling corrections. Appl. Phys. Lett. 114, 022101 (2019).
Lyons, J. L. et al. Impurity-derived p-type conductivity in cubic boron arsenide. Appl. Phys. Lett. 113, 251902 (2018).
Liu, T.-H. et al. Simultaneously high electron and hole mobilities in cubic boron-V compounds: BP, BAs and BSb. Phys. Rev. B 98, 081203 (2018).
Şahin, H. et al. Monolayer honeycomb structures of group-IV elements and III-V binary compounds: first-principles calculations. Phys. Rev. B 80, 155453 (2009).
Manoharan, K. & Subramanian, V. Exploring multifunctional applications of hexagonal boron arsenide sheet: a DFT study. ACS Omega 3, 9533–9543 (2018).
Ullah, S., Denis, P. A., Menezes, M. G. & Sato, F. Tunable optoelectronic properties in h-BP/h-BAs bilayers: the effect of an external electrical field. Appl. Surf. Sci. 493, 308–319 (2019).
Yan, Q., Rinke, P., Janotti, A., Scheffler, M. & Van De Walle, C. G. Effects of strain on the band structure of group-III nitrides. Phys. Rev. B 90, 125118 (2014).
Jones, C. M. & Kioupakis, E. Effect of strain on band alignment of GaAsSb/GaAs quantum wells. J. Appl. Phys. 122, 045703 (2017).
Dreyer, C. E., Janotti, A. & Van De Walle, C. G. Effects of strain on the electron effective mass in GaN and AlN. Appl. Phys. Lett. 102, 142105 (2013).
Poncé, S., Jena, D. & Giustino, F. Hole mobility of strained GaN from first principles. Phys. Rev. B 100, 085204 (2019).
Yu, D., Zhang, Y. & Liu, F. First-principles study of electronic properties of biaxially strained silicon: effects on charge carrier mobility. Phys. Rev. B 78, 245204 (2008).
Karzel, H. et al. Lattice dynamics and hyperfine interactions in ZnO and ZnSe at high external pressures. Phys. Rev. B 53, 11425–11438 (1996).
Wu, J. When group-III nitrides go infrared: new properties and perspectives. J. Appl. Phys. 106, 011101 (2009).
Straumanis, M. E. & Kim, C. D. Phase extent of gallium arsenide determined by the lattice constant and density method. Acta Crystallogr. 19, 256–259 (1965).
Rao, K. V. K., Naidu, S. V. N. & Iyengar, L. Thermal expansion of rutile and anatase. J. Am. Ceram. Soc. 53, 124–126 (1970).
Haines, J. et al. X-ray diffraction and theoretical studies of the high-pressure structures and phase transitions in magnesium fluoride. Phys. Rev. B 64, 134110 (2001).
Hori, M. et al. Optical properties of InxGa1-xN with entire alloy composition on InN buffer layer grown by RF-MBE. Phys. Status Solidi Basic Res. 234, 750–754 (2002).
Kurouchi, M. et al. Growth and properties of In-rich InGaN films grown on (0001) sapphire by RF-MBE. Phys. Status Solidi Basic Res. 241, 2843–2848 (2004).
Senabulya, N. et al. Stabilization of orthorhombic phase in single-crystal ZnSnN2 films. AIP Adv. 6, 075019 (2016).
Makin, R. A. et al. Alloy-free band gap tuning across the visible spectrum. Phys. Rev. Lett. 122, 256403 (2019).
Ferry, D. K. First-order optical and intervalley scattering in semiconductors. Phys. Rev. B 14, 1605–1609 (1976).
Wu, J. et al. Temperature dependence of the fundamental band gap of InN. J. Appl. Phys. 94, 4457 (2003).
Vurgaftman, I. & Meyer, J. R. Band parameters for nitrogen-containing semiconductors. J. Appl. Phys. 94, 3675 (2003).
Wu, J. et al. Superior radiation resistance of alloys: full-solar-spectrum photovoltaic material system. J. Appl. Phys. 94, 6477 (2003).
Kukushkin, S. A. et al. Substrates for epitaxy of gallium nitride: new materials and techniques. Rev. Adv. Mater. Sci. 17, 1–32 (2008).
Bhuiyan, A. G., Sugita, K., Hashimoto, A. & Yamamoto, A. InGaN solar cells: present state of the art and important challenges. IEEE J. Photovolt. 2, 276–293 (2012).
Moses, P. G., Miao, M., Yan, Q. & Van de Walle, C. G. Hybrid functional investigations of band gaps and band alignments for AlN, GaN, InN, and InGaN. J. Chem. Phys. 134, 084703 (2011).
Moses, P. G. & Van de Walle, C. G. Band bowing and band alignment in InGaN alloys. Appl. Phys. Lett. 96, 021908 (2010).
Veal, T. D. et al. Band gap dependence on cation disorder in ZnSnN2 solar absorber. Adv. Energy Mater. 5, 1501462 (2015).
Quayle, P. C., He, K., Shan, J. & Kash, K. Synthesis, lattice structure, and band gap of ZnSnN2. MRS Commun. 3, 135–138 (2013).
Lahourcade, L. et al. Structural and optoelectronic characterization of RF sputtered ZnSnN2. Adv. Mater. 25, 2562–2566 (2013).
Deng, F. et al. Determination of the basic optical parameters of ZnSnN2. Opt. Lett. 40, 1282 (2015).
Chen, S., Narang, P., Atwater, H. A. & Wang, L. Phase stability and defect physics of a ternary ZnSnN2 semiconductor: first principles insights. Adv. Mater. 26, 1–5 (2013).
Qin, R. et al. Semiconducting ZnSnN2 thin films for Si/ZnSnN2 p-n junctions. Appl. Phys. Lett. 108, 142104 (2016).
Fioretti, A. N. Development of Zinc Tin Nitride for Application as an Earth Abundant Photovoltaic Absorber. PhD thesis, Colorado School of Mines (2017).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207–8215 (2003).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).
Giustino, F., Cohen, M. L. & Louie, S. G. Electron-phonon interaction using Wannier functions. Phys. Rev. B 76, 165108 (2007).
Poncé, S., Margine, E. R., Verdi, C. & Giustino, F. EPW: Electron–phonon coupling, transport and superconducting properties using maximally localized Wannier functions. Comput. Phys. Commun. 209, 116–133 (2016).
Baroni, S., de Gironcoli, S., Dal Corso, A. & Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 73, 515–562 (2001).
Acknowledgements
We thank Dr. Samuel Poncé and Kelsey Mengle for their assistance with the EPW package and mobility calculations. This work was supported by the Designing Materials to Revolutionize and Engineer our Future (DMREF) Program under Award No. 1534221, funded by the National Science Foundation. K.B. also acknowledges the support of DOE grant DE-SC0020347. This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02–05CH11231.
Author information
Authors and Affiliations
Contributions
K.B. and S.C. contributed equally to this work and performed first principles calculations, analyzed data, and wrote the paper under the supervision of E.K. Z.D. assisted first principles calculation for alloys and Z.D. and J.T.H. contributed to writing of the paper. E.K. supervised the calculation, analysis, and manuscript preparation. Funding acquisition was done by E.K. All contributors proofread the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bushick, K., Chae, S., Deng, Z. et al. Boron arsenide heterostructures: lattice-matched heterointerfaces and strain effects on band alignments and mobility. npj Comput Mater 6, 3 (2020). https://doi.org/10.1038/s41524-019-0270-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-019-0270-4
This article is cited by
-
Significant tensile elasticity of nanoscale boron arsenide
Science China Materials (2023)
-
Orchestrating the impact of antisites and vacancy defects on the elastic and optoelectronic properties of boron arsenide
Journal of Molecular Modeling (2023)
-
Harnessing wrinkling morphologies of graphene on soft substrates for mechanically programmable interfacial thermal conductance
Nano Research (2023)