Abstract
Much of computational materials science has focused on fast and accurate forward predictions of materials properties, for example, given a molecular structure predict its electronic properties. This is achieved with first principles calculations and more recently through machine learning approaches, since the former is computation-intensive and not practical for high-throughput screening. Searching for the right material for any given application, though follows an inverse path—the desired properties are given and the task is to find the right materials. Here we present a deep learning inverse prediction framework, Structure Learning for Attribute-driven Materials Design Using Novel Conditional Sampling (SLAMDUNCS), for efficient and accurate prediction of molecules exhibiting target properties. We apply this framework to the computational design of organic molecules for three applications, organic semiconductors for thin-film transistors, small organic acceptors for solar cells and electrolyte additives with high redox stability. Our method is general enough to be extended to inorganic compounds and represents an important step in deep learning based completely automated materials discovery.
Similar content being viewed by others
Introduction
Imagine having to design a new material for a target application from scratch. Conventional materials design practice relies on trial-and-error approach. One typically starts with a known material by comparing its properties against the target property, and then incorporating a compositional/structural change to update the design. This process is performed iteratively, primarily driven by intuition/experience of the materials scientist. In the recent past, with the advent of efficient physics-based modelling that span a wide length scale from atomistic to continuum regime, properties are determined in-silico to minimise efforts involved in experimental realisation of candidate materials and measurement of their properties and thus helping speed-up the design iteration process.1,2,3 This approach was further augmented by optimisation schemes that attempted at designing materials with optimum properties by using physics-based simulations informed optimisation. The latter approach is exemplified by evolutionary algorithms or other gradient based optimisation techniques when appropriate.4 It takes many, often times hundreds of simulations before a reasonable material/structure can be found. Since each simulation is computationally expensive, these methods become prohibitively slow as molecular/material/device size and complexity grow. In contrast to the optimisation approach, data-driven approaches based on materials informatics have been employed in the last decade, with particular emphasis on fingerprinting and determining previously unknown underlying correlations between structures and properties to derive “surrogate models”.5,6 More recently, machine learning approaches are rapidly emerging, where shallow learning methods like artificial neural networks (ANNs) are trained to assist the materials design process. ANNs are used to replace/minimise the computationally expensive first principles calculations in the optimisation loop, greatly reducing overall design time. For example, ANNs were used for high-throughput screening of organic molecules for use in solar cells based on ANN predicted frontier orbital energy levels.7 Further, ANNs were used to predict organic reactions,8 properties of inorganic materials.9 Recently, deep variants of the ANN are also used for molecular property predictions.10 These ANNs based methods are essentially solving the forward problem in which material properties are computed for an input molecular structure. However, actual materials design is naturally an inverse problem, that is, specific technology-enabling properties requirements are known, but often we do not have the materials that have these properties. For example, in the case of multi-junction solar cells, the band-gap, exciton binding energy and carrier mobility requirements of each layer for achieving target quantum efficiency are known, and we need to design materials that meet these requirements. Thus to advance computational materials design significantly, one needs to ask the question, can we train machines to learn designing materials? Given that the atomic composition and structure determines the material property, can machines provide suggestions on materials/structures to fabricate?
In this paper, we posit that the current state of the art materials design approaches use machine learning primarily as an enabler for implementing traditional high-throughput screening, that is, essentially solving the forward problem in a computationally efficient manner. Recent advancements in machine learning algorithms has a potential to solve the inverse materials design problem in a fully automated framework. However, development of such a framework is impeded by some key challenges. First, a compact and accurate numerical representation of molecular structures is required to digitise the known chemical space. Second, a computationally efficient structure to properties mapping is required to ensure practicality of the framework. Although ANNs partially resolve this challenge, training the ANNs require a large properties database, introducing a new challenge. Finally, an appropriate search algorithm is required that is capable of scanning a chemical space of known and hitherto unknown molecules, while ensuring that the candidate structures form a valid molecule.
We have addressed all these challenges in this paper. To resolve the first challenge, we have developed a binary representation to digitise the molecular structure. We resolve the second challenge by using semi-supervised learning approach to obtain structure to properties mapping. This semi-supervised algorithm can be trained using a smaller dataset compared to the supervised training of ANNs. We address the final challenge by approaching the inverse materials design from a Bayesian perspective11,12,13 (see Fig. 1a). At the core of this Bayesian approach is a solution of the Bayes theorem. In its most widely used form, the Bayes theorem is specified as
where the prior probabilistically encompasses available knowledge of the uncertain system,14 the likelihood is defined using new measurement or evidence,15 while the posterior denotes updated probability after assimilating the new evidence. For inverse materials design, prior probabilistically quantifies validity of a given molecular structure, whereas, the likelihood15 specifies probability of a molecular structure exhibiting our desired attributes. Our choice of this Bayesian approach is motivated by two considerations. First, optimisation methods used in the state of the art inverse materials design algorithms require specification of heuristic rules to ensure generation of valid molecular structures. In the Bayesian approach, appropriate choice of the prior distribution ensures that the search space is constrained to valid molecular structures. We use unsupervised learning16,17,18 on a large dataset of known molecular structures to quantify this prior. This unsupervised learning enables us to encode the chemical rules of molecule formation as a prior probability distribution of the Bayes theorem. Thus, the proposed approach does not require specification of any heuristic rules. Second, the optimisation methods predict a single molecular structure by maximising/minimising a desired molecular attribute. As against the single point prediction of optimisation methods, the Bayesian approach predicts posterior probability distribution that encode the chemical space of molecules with desired attributes. Sampling from this distribution allows us to generate a large set of valid molecular structures for a given application. This helps us in further accelerating the inverse materials design.
Bayesian inference shown in a is the backbone of SLAMDUNCS. The framework first digitises the molecular structures using a fingerprinting approach shown in b. The rules of chemical structure encoded in the molecular fingerprints are embedded in the RBM using unsupervised learning of molecular structures database, as shown in c. The RBM quantifies prior probability on the chemical space. Semi-supervised deep learning approach shown in d is used to obtain a molecular structure-property correlation, quantifying the likelihood of a molecular structure exhibiting the target properties. The posterior distribution combines prior in c with the likelihood in d to encode a chemical space of molecules possessing target properties. Ergodic Markov chain is simulated to sample from this posterior distribution, as shown in e.
We claim several innovations of our proposed approach. Previous approaches primarily comprised intrinsic screening with hand-crafted features,19 whereas, unsupervised learning in our approach enables us to perform intrinsic as well as extrinsic screening. Moreover, previous approaches are limited to human specified design spaces with heuristic or design intent search rules,20 whereas, the proposed approach is a fully automated artificial intelligence based materials design framework with a minimal human intervention. Our use of semi-supervised deep learning allows us to implement our proposed approach with a relatively small properties database.
We will illustrate the practicability of our approach with three exemplar organic materials design problems: n- and p-type organic semiconductors for organic thin film transistors (OTFTs),21 small organic acceptor molecules for use in organic solar cells22 and high stability electrolytes for lithium-ion batteries.23 These problems are chosen to demonstrate that in the continuous evolution of the use of computers in materials science, deep learning based inverse design presented here takes us one step forward in going beyond subject matter experts’ knowledge based intuition. In the current practice, using chemical classification of substituents and developing quantitative rules, experts can predict how electron donors and acceptors in conjugated molecules alter the reduction/oxidation potentials in specific classes or narrow range of molecules. However, as the molecule becomes more complex, properties’ predictions become increasingly hard. We first show that because our forward method is able to learn “chemical rules”, in the form of how the relative arrangement of elements and bonds in a molecule together decide its properties with high accuracy, we can predict properties of complex molecules that chemical intuition alone cannot. Further, the unsupervised learning of our approach enables us to take advantage of Bayesian inference to predict previously unknown (not in the database) molecules that have target properties. For example, to design stable molecules for electrolytes, target reduction and oxidation stability as dictated by reduction and oxidation potentials is used as an input to predict new molecules. In the case of n- and p-type semiconductors and organic solar cell acceptors target values/windows for energies of the frontier orbitals are used to design new molecules. In all cases, SLAMDUNCS is able to predict valid molecules with target properties and we then validate the properties of a small set of these new molecules using first principles simulations. While we have demonstrated inverse design here for designing organic molecules, our approach is general enough to be applied to a wide class of materials systems.
Results
Numerical representation of molecular structures
Numerical representation of molecular structures using the molecular fingerprinting forms a critical step of a data-driven inverse materials design approach. Depending on the application, different molecular descriptors such as Coulomb matrices,24 bag of bonds,25 overlap matrix,26 deep tensor neural networks,27 count of functional groups present in the structure28 etc. have been used for molecular representation at various level of granularities. Aim of this paper is to develop an inverse molecular design framework, as such, our choice of fingerprinting is primarily motivated by ease and uniqueness with which molecular descriptor can be converted to the molecular structure. We use canonical SMILES29 representation, which is a widely used text based line notation for organic molecules, as a molecular descriptor, as it allows for capturing most important chemical features of organic molecules, is particularly amenable for digital representation and it can be easily and uniquely converted to the molecular structure. Note that the SMILES representation is widely used in the literature as a molecular descriptor, however, one-hot encoding is often used to digitise the SMILES representation. In our approach, we use binary representation to digitize the SMILES. We digitise the SMILES representation by first obtaining ASCII equivalent of each SMILES character, and subsequently converting the ASCII to an eight-bit binary number (see Fig. 1b). The resultant binary vector is used as a molecular fingerprint. This approach allows molecular fingerprinting with complete positional and atomic connectivity information without using any additional chemical information. This approach has the inherent advantage of compact representation over one-hot encoding. For instance, the one-to-one mapping of SMILES representation would require 67 one-hot encoding characters. In this work, since we consider molecular structures of SMILES length upto 100 characters, the length of one-hot encoding would be 6700. Such high dimensionality substantially increases the number of parameters of the underlying deep network requiring large training dataset. Our use of 8-bit binary representation for SMILES digitisation results in a binary vector of length 800, while preserving uniqueness of the representation. As the resultant deep network has smaller number of parameters, the network can be efficiently trained using smaller training dataset.
Unsupervised learning of molecular structures
We use unsupervised learning of molecular structures to quantify prior probability distribution in our Bayesian approach. Our choice of an unsupervised learning algorithm is constrained by two considerations. As we use binary vectors as molecular descriptors, we require a machine learning architecture that can efficiently encode the binary numbers. Furthermore, the architecture is required to have capability to quantify probability distributions. Although the unsupervised learning algorithms like Gaussian mixture models30 are capable of quantifying probability distributions, they are primarily designed for real numbers, and as such, fail to efficiently encode the binary vectors. Several autoencoders31 are capable of learning to construct valid molecular structures by efficiently encoding the binary vectors, however, they fail to quantify probability distributions which is key to our proposed Bayesian approach. In our proposed approach, we use restricted Boltzmann machine (RBM)32 for unsupervised learning, as it is specifically designed for efficient encoding of binary vectors and is capable of quantifying probability distributions. Note that though the RBMs were initially developed for applications like face recognition,33 recently, RBMs are successfully used of applications in chemical and physical sciences.34 However, to the best of our knowledge, RBMs are never used for quantification of prior distribution in the Bayesian inference framework.
The RBM network consists of a visible and a hidden layer, where each node of the visible layer is connected to every node of the hidden layer (see Fig. 1c). Every node of the visible and hidden layer is a binary number that takes value of 0 or 1 with a probability. This probability is learned by training the RBM.
The probability density function of RBM is defined using a Boltzmann distribution given by
where \(Z\) is a partition function and \(E\) is the energy defined as
where \({\boldsymbol{v}}\) is visible layer, \({\boldsymbol{h}}\) is hidden layer, \({\boldsymbol{W}}\) is a weight matrix, while \({\boldsymbol{b}}\) and \({\boldsymbol{c}}\) are biases in visible and hidden layer, respectively. We use maximum likelihood estimation for training the RBM on molecular structures database.35 After training, we marginalise over \({\boldsymbol{h}}\) to obtain \(p\left({\boldsymbol{v}}\right)\).
The marginal distribution \(p\left({\boldsymbol{v}}\right)\) facilitates understanding of the SMILES representation. Training the RBM entails maximum likelihood estimation of \(p\left({\boldsymbol{v}}\right)\) that encodes both localised and neighbourhood information present in the SMILES representation. For instance, if a specific character like “A” is not present in the SMILES dataset, the trained RBM assigns it a probability zero, and as such, this character is never sampled by the RBM. Similarly, a triple bond between carbon and oxygen never exists in nature, thus, combination of characters “C \(\#\) O” is not present in the SMILES dataset. Hence, the trained RBM assigns zero probability to such sequence of characters. As such the RBM essentially learns, through probability assignments, the rules of valid molecule formation that are embedded in the SMILES representation.
We have trained the RBM using molecular structures dataset consisting of 306153 randomly chosen molecules in the compound identifier range of 1–1200000 from the PubChem database.36 We evaluate training accuracy of the RBM using its reconstruction ability. For instance, given any input vector \({\boldsymbol{v}}\) and a set of RBM weights and biases, the RBM can be used to obtain a hidden layer by sampling from \(p\left({\boldsymbol{h}}| {\boldsymbol{v}}\right)\) and subsequently obtaining a reconstructed vector by sampling from \(p\left({\boldsymbol{v}}| {\boldsymbol{h}}\right)\). We define the reconstruction error as the sum of Euclidean distance between input vectors from the training dataset and the corresponding reconstructed vectors. Supplementary Fig. 1a shows the reconstruction error reduction with number of training iterations (also known as epochs). Supplementary Fig. 1b shows reconstructed SMILES with increasing number of epochs. Reconstruction ability of the RBM increases as training progresses, as can be seen from Supplementary Fig. 1b, where reconstructed visible layer output approaches towards valid SMILES. The RBM also allows us to construct new molecular structures using Gibbs sampling.37 For a given input vector \({\boldsymbol{v}}\), we implement Gibbs sampling as follows. We first use the trained RBM to calculate \(p\left({\boldsymbol{h}}| {\boldsymbol{v}}\right)\) and obtain the hidden layer output \({\boldsymbol{h}}\) by sampling from this distribution. Subsequently, we calculate \(p\left({\boldsymbol{v}}| {\boldsymbol{h}}\right)\) and sample \({\boldsymbol{v}}\) from this distribution. We repeat these steps a pre-determined number of times to generate samples from the RBM. Finally, we convert the sampled binary vectors to SMILES representation for construction of new molecular structures. Supplementary Fig. 1c shows a set of randomly created molecular structures using Gibbs sampling.
Semi-supervised learning of structure-property correlation
We need a computationally efficient approach to forward predict the properties given a molecular structure. Due to high computational cost of first principles calculations, we use machine learning for efficient forward property predictions. Previously, different supervised learning algorithms are used in the literature38 for property prediction of a given molecule. However, supervised learning requires a very large dataset for accurate training, again incurring high computational cost. In practice, we have a very large molecular structures database, however, property values are available only for a very small subset of molecules. Supervised learning algorithms fail to fully utilise information from the molecular structures database, whereas a small size of the property database often results in the poor accuracy of the machine learning predictions. We propose a semi-supervised deep learning approach39 for structure-property correlation that can provide accurate predictions even with a comparatively small property dataset. In this approach, we first use unsupervised learning to train a Deep Belief Network (DBN)40 using the molecular structure database. DBN contains more than one hidden layers, where a pair of subsequent layers is a RBM. Thus, we construct this DBN using a stack of pre-trained RBMs.41 We have used the DBN for this unsupervised learning, as it allows us to reuse already pre-trained RBM for quantifying prior probability distribution. Moreover, since the DBN is constructed using RBMs, it has a capability to efficiently encode the binary vectors that are used as molecular descriptors. However, we cannot use the RBM for unsupervised learning of properties that are real numbers. This issue is resolved by a recently developed variant of the RBM, known as Gaussian-Bernoulli RBM42 (GB-RBM). Contrary to the RBM, visible layer of the GB-RBM is defined using a vector of real numbers with probability of each node specified using independent Gaussian distributions. We use a small property database to train this GB-RBM in an unsupervised manner.
We invert the trained GB-RBM and stack together with the DBN to construct a deep network (see Fig. 1d). We use a small structure-property database to train the resultant deep network in a supervised manner. Flexibility of this semi-supervised learning approach allow us to create a variety of deep networks like Deep Boltzmann Machine43 and Deep Neural Network,44 and train the network using same training dataset.
We have trained our network using a database of molecular orbital energies and redox potentials predicted using first principles calculation performed by density functional theory (DFT). Detailed analysis of this database is presented in Supplementary Fig. 2. Supplementary Fig. 2a shows distribution of the number of compounds against the SMILES length. Total \(85.7 \%\) of the compounds in the database have SMILES length ≤ 50 while the SMILES length ≤100 covers \(99.85 \%\) of the molecules in the database. Thus for all the results presented in this paper, we have only considered molecules with SMILES length of upto 100 characters. Dependence of properties on the molecular structures enforces correlation amongst properties for a given structure, as can be observed for highest occupied orbital (HOMO) energies and oxidation potential from Supplementary Fig. 2b and between lowest unoccupied molecular orbital (LUMO) energies and reduction potential in Supplementary Fig. 2c.
SLAMDUNCS is designed to exploit the information content in the correlations amongst properties and between the molecular structure and properties for efficient training with minimal properties dataset. We evaluate this information content using the Pearsons correlation coefficient. For any two random variables \(x\) and \(y\), the Pearsons correlation coefficient is given by
where \(cov(x,y)\) is a covariance between \(x\) and \(y\), while \({\sigma }_{x}\) and \({\sigma }_{y}\) denotes standard deviation of \(x\) and \(y\), respectively.
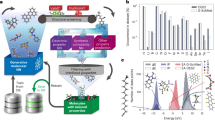
Figure 2a shows the Pearsons correlation coefficient between the molecular properties and output of every layer of the DBN, which is trained in unsupervised manner using molecular structures dataset. Even though the properties data is not used for training, every added layer of DBN increasingly extracts properties information that is embedded in the molecular structure, as is evident from the increasing correlation between properties and the DBN layer output. The highest correlation between the DBN output and properties is greater than 0.3, with the correlation reaching ±0.46 for the LUMO. This ability to extract the properties information only from the molecular structures database is a key strength of our proposed approach. Similarly, Pearsons correlation coefficient amongst properties is shown in Fig. 2b. For the DFT predicted properties in the database (left subfigure of Fig. 2b), HOMO energy show high negative correlation (−0.77) with oxidation potential, while, the LUMO energy show high negative correlation (−0.85) with the reduction potential. Moreover, HOMO energies have noticeable correlation with all the other properties. SLAMDUNCS extract this correlation by unsupervised training of GB-RBM using the properties database
Properties information embedded in molecular structures is extracted using unsupervised learning of DBN, as shown in a. The Pearson’s correlation coefficient between activation probability of each node and the properties is shown in the figure. The DBN network used in this paper is shown in the rightmost part of the figure. Highest correlation for each layer output is shown in the leftmost part of the figure. Similarly, correlation between the properties is shown in b. The quantile-quantile plot for deep learning predicted properties is shown in c. Violin plot in d shows comparison of the PDF for predicted properties and dataset. Kulback–Liebler (KL) divergence between the PDFs is also shown in the figure.
We use a structure-properties dataset for supervised training of the deep network. A total of 60000 data points are used for training while remaining data points are used for testing. We first evaluate the prediction accuracy of the trained deep network by comparing the Pearsons correlation coefficient for the predicted properties against the corresponding correlation coefficient for the properties from the dataset (left subfigure of Fig. 2b). Middle subfigure of the Fig. 2b shows Pearsons correlation coefficient obtained for predicted properties. Comparison of left and middle subfigures of Fig. 2b shows that the Pearsons correlation coefficient obtained from data and predictions are close to each other, demonstrating that the semi-supervised training approach has enabled accurate learning of the correlations amongst the properties. This learning capability is further investigated in the rightmost subfigure of the Fig. 2b, where the Pearsons correlation coefficient between the properties from the dataset and the predictions is shown. As can be observed from the figure, the correlation coefficient between properties from the dataset and the corresponding properties predicted by the deep network are close to 1.
Figure 2c shows quantile-quantile plots for the predictions using the trained network. Predictions are close to 45° line for all the properties, demonstrating high prediction accuracy of the trained network.
Error statistics for the properties prediction is summarised in Table 1. As can be observed from Table 1, coefficient of determination (\({R}^{2}\)) greater than 0.9 is achieved for all the properties. For more than \(20 \%\) of the molecules, deep learning predicts all the properties with absolute error ≤0.05 eV/V, whereas, the properties are predicted with absolute error more than 0.5 eV/V for ≤\(6.1 \%\) of the molecules. We have also compared performance of our approach against against kernel ridge and support vector regression. For comparison, we use same training and testing data for all the three aproaches. In Supplementary Table 1, we have summarised mean absolute error in prediction for these three models. As can be observed from the table, our approach performs better than both kernel ridge and support vector regression. In Pereira et al.,38 authors have compared accuracy of different sub-Angstrom level molecular descriptors and machine learning algorithms for prediction of orbital energies. We have compared our results against the best performing model reported in Pereira et al.38 This comparison is also shown in the Supplementary Table 1.
The error statistics is further explored in Supplementary Fig. 3. Supplementary Fig. 3a shows the distribution of mean absolute error as a function of smiles length, while, the cumulative distribution function (CDF) of absolute error in the property prediction is shown in the Supplementary Fig. 3b. Absolute error corresponding to CDF = 0.2 − 0.9 is also tabulated in the figure. Absolute error less than 0.065 is achieved for \(20 \%\) of the dataset, whereas for \(90 \%\) of the dataset, absolute error ≤0.427 eV/V is achieved for all the properties. We investigate failed predictions of our deep network in the Supplementary Fig. 3c, where we list five molecules with the highest error for each property. For HOMO prediction, highest error is observed for tetrapyradine. HOMO prediction error is also high for molecules consisting nitro functional group. Highest error for LUMO prediction is observed for diazene, whereas, error is also high for molecules containing azide functional group. For oxidation potential prediction, higher error is observed for molecules containing Si or F. For reduction potential prediction, highest error is observed for cumene hydroperoxide, however, a specific trend in prediction error with respect to functional groups is not observed for reduction potential prediction.
Distribution of the DFT calculated and the deep learning predicted properties is shown in Fig. 2d using violin plots. We use Kullback–Liebler (KL) divergence45 to quantify distance between these distributions. For any two probability distributions \(p\left(x\right)\) and \(q\left(x\right)\), the KL divergence between the distributions \(p\) and \(q\) is given by
The KL divergence is always non-negative, with \(KL\left[p| | q\right]=0\) only if the distributions \(p\left(x\right)\) and \(q\left(x\right)\) are same everywhere. These properties of KL divergence allows us to compare the closeness and the difference between two probability distributions. For all the properties, KL divergence is lower than 0.03, which shows that our trained network has an ability to predict the distribution of properties with high accuracy. Non-Gaussian nature of the distributions, as is evident from the violin plot, exemplifies non-linear nature of the structure-properties relationship. Low KL divergence demonstrates that this non-linearity is also accurately captured by the SLAMDUNCS.
The deep network trained in this paper essentially learns the mapping between the molecular structure and the corresponding properties. Traditionally, the deep networks are treated as deterministic models, however, the deep architectures proposed in this paper have a capability to quantify uncertainty in the model predictions. For instance when DBM is used as the deep network, we use Gibbs sampling for property prediction. The Gibbs sampling estimates complete probability distribution of the DBM output, enabling uncertainty quantification in the property predictions. When DNN is used as the deep network, we use dropout while training.46 The use of dropout in the DNN training also allows us to quantify uncertainty in the model predictions.47 For instance, the forward network can be trained with a pre-specified dropout probability. During prediction, we predict the DNN output by randomly dropping out each layer according to the dropout probability. A large number of samples are collected by repeating this procedure for pre-specified number of times. The mean, variance and other higher order moments can be calculated from these samples to efficiently quantify uncertainty in the deep learning predictions. If desired, SLAMDUNCS can admit this quantified uncertainty as a model structural uncertainty in the definition of the likelihood that ensures low posterior probability for the region with high prediction error.
We then solve the inverse materials design problem from a Bayesian inference perspective. A typical Bayesian inference solves a Bayes theorem given by
where \(p\left({\boldsymbol{v}}\right)\) is prior, \(p\left({\boldsymbol{y}}| {\boldsymbol{v}}\right)\) is likelihood and \(p\left({\boldsymbol{v}}| {\boldsymbol{y}}\right)\) is a posterior probability distribution. For inverse materials design, we specify the prior as probability that a given molecular structure is valid, whereas, the likelihood is specified as probability of molecular properties satisfying the desired attributes. We learn the prior on molecular structures database using RBM, while, we use the structures-property correlation learned using the deep network to specify the likelihood. However, the resultant posterior distribution is analytically intractable. Thus, we use a sampling based approach to approximate the posterior distribution. In particular, we use the Markov Chain Monte Carlo algorithm to sample from the posterior distribution. We initiate the Markov Chain Monte Carlo sampling from a random molecular structure, and use the Metropolis-Hastings48,49 acceptance criterion to move the chain forward. We discard pre-defined number of initial steps, known as the equilibration period, and collect the desired number of samples afterwards. The resultant Markov chain is known as the ergodic Markov chain. Structures sampled after the equilibration period provide a set of molecules with desired attributes. Key advantage of Metropolis-Hastings algorithm is its ability to sample from the posterior distribution without having to evaluate the normalising constant of the probability distribution.50 This enables conditional sampling, where we constrain the prior chemical space to molecular structures with pre-defined attributes, like minimum length of conjugated bonds or number of cyclic rings present in the molecular structures, and sample from the resultant posterior distribution.
Design of n- and p-type semiconductors for organic thin film transistors
First, we will use SLAMDUNCS to design n-type and p-type organic semiconductor molecules. In organic thin film transistor (OTFT) applications, the energy required to add an electron or remove an electron determines whether a molecule is a suitable n-type or p-type semiconductor, respectively.51 This necessitates that the energy of the lowest unoccupied molecular orbital (LUMO) is low enough for an n-type carrier so that it can accommodate an extra electron easily or that the energy of the highest occupied molecular orbital (HOMO) for p-type molecule is high enough that an electron can be removed easily. Additionally, the device performance is strongly dependent on the electronic structure of the metal-semiconductor interface. It is important to choose a metal contact with a work function that matches the highest occupied molecular orbital (HOMO) or lowest unoccupied molecular orbital (LUMO) of the organic semiconductor within a few tenths of an electronvolt, such that desirable charge injection efficiency and low operational voltage are achieved. While previous computational design studies have focused mainly on high throughput screening, here we demonstrate the applicability of SLAMDUNCS to design new molecules with target orbital energy values driven by the design intent.
In Fig. 3, we illustrate the design of n-type and p-type organic semiconductors using SLAMDUNCS. Finding high performance n-type organic semiconductors has been a challenge because, if the LUMO of the n-type molecules is not low enough, the injected electrons can be lost to species that can readily accept an electron such as the silanol groups in the semiconductor-dielectric interface or to O2/H2O molecules in ambient air.21 This leads to poor performance of the electron transport layer as carriers are annihilated. Therefore, the key to obtain stable n-type transport is to find materials with low LUMO energies. Additionally, lowering the LUMO level also helps in achieving better match with work function of the electrode which can help make an Ohmic contact. As such, we seek as low an energy value as possible for the LUMO to design an n-type OTFT device. Similarly, we desire as high an energy value as possible for the HOMO to design a p-type OTFT device. A typical OTFT device is shown is shown in Fig. 3a. The figure also shows desirable energy levels for LUMO of a n-type device (bottom left subfigure of Fig. 3a), and HOMO of a p-type device (bottom right subfigure of Fig. 3a). For n-type OTFT, we seek organic molecules with LUMO \(<-\!3.0\) eV, such that the candidate molecule can accommodate an extra electron extracted from the source. To generate a set of valid molecular structures, we simulated 1000 parallel ergodic Markov chains initialised from randomly chosen structures. Figure 3b shows orbital energies of the predicted structures. Joint probability contours are also shown in the background. As can be observed from the figure, a vast majority of candidate n-type organic semiconductors are expected to have LUMO energies in the −3.1 to −3.4 eV range with the corresponding HOMO energies in −5.5 to −7.0 eV range. A list of predicted molecular structures is provided in Supplementary Table 2. Although a large number of molecular structures are generated by simulating a number of parallel ergodic Markov chains, only 100 structures are reported in the table for brevity. Validity of the listed structures is confirmed by optimising the structures in Avogadro52 from SMILES representation. We also performed an automated search to check if the molecule is present in the PubChem database.
A typical OTFT and desirable levels of orbital energies with respect to work function of the contact are shown in a. Orbital energies of the inverse predicted molecular structures for n-type and p-type OTFTs are shown in b, c, respectively. The figure also shows joint probability contours of the orbital energies in the background. d SLAMDUNCS predicted LUMO energies are compared against the DFT calculations for 50 candidate molecular structures for n-type OTFT. Similarly, e compares SLAMDUNCS predicted and DFT calculated HOMO energies of 50 candidate p-type OTFT molecular structures.
The SLAMDUNCS predicted LUMO energies for randomly chosen 50 candidate molecular structures, that are extrinsic to the training dataset, are validated using DFT. The comparison is shown in Fig. 3d. As can be observed from the figure, SLAMDUNCS predictions matches closely with the DFT predictions. For this validation set, SLAMDUNCS predict the LUMO energies with mean absolute error of 0.1534 eV against the DFT calculations, with the maximum absolute error of 0.581 eV. It is important to note that, SLAMDUNCS automatically discovered molecules from two well-known n-type material classes: Rylene diimides and n-type polyacene materials. For example, molecules 61, 72 and 80 reported in the Supplementary Table 2 are derivatives of perylene diimide. Similarly, polyacene molecules modified by electron withdrawing groups, diethylene thiol pentacene (molecule 45 in Supplementary Table 2), dimethoxy anthracene dione (molecule 16 in Supplementary Table 2), are also predicted. Unlike conventional design approaches, our algorithm discovers these molecules automatically without the need for searching in a particular n-type material class. In addition to that, new molecules previously not reported for n-type applications, have been predicted. For example, molecules based on benzodithiophene (BDT) have been previously reported as p-type materials.53 Our inverse prediction has suggested adding electron withdrawing aldehyde group to BDT to bring the LUMO level to −3.02 eV and make it n-type. Tetrazole bonded to the nitrogen of Isoindole (molecule 37) are also another n-type molecule discovered by our algorithm. The predictions of n-type molecules in this work are based on the LUMO energy, which is only a necessary condition for easy electron injection and stable operation. However, in practice, high electron mobility constitutes the other important criterion for a molecule to be an attractive n-channel material. We have not trained SLAMDUNCS for correlation between molecular structure and mobility since mobility is determined by both molecular structure and the crystal structure of the organic molecule and thus it is computationally complex. In the Marcus theorem formalism, widely adopted for calculating charge transport in organic semiconductor crystals, the mobility is related to molecular structure through reorganisation energy and to the crystal structure through transfer integral as well as number of nearest neighbours and the hopping distance.54 We foresee that with adequate data relating molecular structure to reorganisation energy and transfer integral to train the forward model in SLAMDUNCS, inverse prediction of molecules with target mobility values is possible. Even with the capability to predict molecules with target LUMO values is very useful in considering alternatives to existing options for n-type materials.
For p-type semiconductors, we seek organic molecules with HOMO energies \(>-\!5.6\) eV that can allow efficient release of electron to the source, as shown in bottom right subfigure of the Fig. 3a. The candidate p-type organic semiconductors, as predicted by SLAMDUNCS, are expected to have HOMO energies in a narrow band of −5.6 to −5.2 eV, whereas, the LUMO energies have a comparatively wider band of \(0\ {\rm{V}}\) to \(-3\) eV (see Fig. 3c). Note that there is a small region of overlap between the candidate n-type and p-type organic semiconductors (see Fig. 3b, c). We can seek ambipolar organic semiconductors in this region, if application demands. All the predicted candidate molecular structures for p-type organic semiconductors are listed in Supplementary Table 3. We validate the SLAMDUNCS prediction for randomly selected 50 structures that are extrinsic to the training dataset. Figure 3e compare SLAMDUNCS predictions with the DFT calculations for these 50 molecular structures. As can be observed from the figure, SLAMDUNCS predicted HOMO energies match closely with the DFT calculations. For this validation set, SLAMDUNCS predicts HOMO energies with mean absolute error of 0.2021 eV against the DFT calculations, with maximum absolute error of 0.455 eV.
Examples of p-type molecules SLAMDUNCS predicted outside of the training database include amino modified acenaphthalene (molecule 26 in Supplementary Table 3) and bromine modified biphenyl dicarbonitrile (molecule 87 in Supplementary Table 3). It is interesting to point out that, SLAMDUNCS has correctly learned that even though the parent biphenyl dicarbonitrile has a HOMO level (6.49 eV) lower than the cut-off value for p-type molecules, bromine modification brings it −5.35 eV that is within the target range.
Design of non-fullerene acceptor molecules for bulk-heterojunction organic solar cells
As a second demonstration, we use SLAMDUNCS to design non-fullerene acceptors for bulk-heterojunction (BHJ) organic solar cells (OSC). The discovery of BHJ by Heeger et al.55 thrust OSCs to the forefront of photovoltaic materials research since this concept provided efficient route for exciton dissociation in many donor-acceptor systems by drastically reducing the distance travelled by exciton for separation.56 This has led to devices with high photovoltaic external quantum efficiencies and high photocurrent. However, this came at the cost of significant photovoltage losses. One strategy used to overcome this challenge is to increase the open-circuit voltage, by increasing the difference between ionisation potential of the donor and the electron affinity of the acceptor. While this leads to decrease in driving force for exciton separation at the donor:acceptor interface due to decreasing energy difference between LUMO of donor and LUMO of the acceptor, it has been demonstrated that as low as 0.1 eV LUMO offset between donor and acceptor is capable of efficient exciton separation.57 As new donor molecules are considered for BHJ, the acceptor molecules have to be energy level matched so that open circuit voltage is maximised, while still providing a driving force for the exciton separation.
Here, we demonstrate the inverse prediction capability of SLAMDUNCS to predict non-fullerene organic acceptors for use with P3HT (Poly(3-hexylthiophene-2,5-diyl)) donor, as shown in Fig. 4a. To determine the desired target attributes of the acceptor, we first calculated orbital energies of P3HT using DFT. DFT predicted LUMO energy of −2.52 eV for P3HT, thus we seek acceptors with LUMO energies in the range −2.62 to −2.72 eV that corresponds to the LUMO energies lower by 0.1–0.2 eV as compared to P3HT. We predicted a large number of candidate molecules by simulating 1000 ergodic Markov chains with equilibration period of 30000 samples. Distribution of orbital energies of the predicted molecules is shown in the Fig. 4b. This desired range of LUMO energies also bound the HOMO energies to a narrow band of −5.5 to −7.0 eV (see Fig. 4b), ensuring the hole transfer from acceptor to the donor. A list of predicted candidate organic molecules for OSC is provided in Supplementary Table 4. For brevity, we have only reported randomly selected 100 molecular structures. We performed first principle DFT calculations for the first 50 molecular structures listed in the Supplementary Table 4. In Fig. 4c, the DFT calculated LUMO energies are compared against the SLAMDUNCS predictions. The comparison shows high prediction accuracy of the SLAMDUNCS, with mean absolute error of 0.2140 eV against the DFT calculations, whereas, the maximum absolute error is 0.6877 eV. Unlike the previous example, where organic semiconductor molecules of LUMO values below a cut-off or HOMO values above a cut-off were sought, here organic acceptors were sought that have LUMO values in a very narrow range and yet SLAMDUNCS was able to predict several candidate acceptor molecules is noteworthy. For example, SLAMDUNCS has interestingly suggested an adamantane structure modified by nitrosol and Cl (molecule 27 in Supplementary Table 4) as one of the candidates. It is important to note that adamantane, which is the smallest diamondoid molecule, is not a very good electron acceptor. However, the addition of nitroso group and Cl brings the LUMO level down just enough to be in the target range.
A typical solar cell and the desired trend in orbital energies is shown in a. Orbital energies of the inverse predicted molecular structures are shown in b. The figure also shows joint probability contours of the orbital energies in the background. In c, SLAMDUNCS predicted LUMO energies are compared against the DFT calculations for 50 candidate molecular structures.
High-redox stable electrolyte design
Finally, we consider the practical problem of designing redox-stable electrolytes for lithium-ion batteries. The goal is to design new organic solvents that have both reduction and oxidation stability against the reducing potential at the anode and the oxidising potential at the cathode, respectively.23,58,59 The redox stability is determined by redox potential, which is determined by how easy it is to inject/remove an electron from the molecule and is an important parameter for the design of new electrolytes. Previously, electrolyte design relied on making minor tweaks, such as replacing an ethylene based core with a propylene based core, since electrochemical properties are not widely reported for all molecules in chemical databases. To address this issue, first principles calculation of redox potentials was used to screen molecules with the goal of populating the database with redox potentials to accelerate design of organic electrolytes with high voltage stability window for energy storage applications in consumer electronics and electric vehicles.60 Further to this, artificial neural network based forward prediction tools for predicting the oxidation and reduction potentials of organic compounds existing in the massive organic compound database, PubChem was developed by one of the co-authors.61
Here, we demonstrate the inverse prediction capability of SLAMDUNCS to predict organic structures that have reduction potential lower than the anode and an electrochemical window of 4.8 V or better. These desired attributes ensure stability of the electrolyte across full operating range of the lithium-ion cell, as shown in Fig. 5a. Thus, SLAMDUNCS is used to predict molecules with the reduction potential <−3.35 V against standard hydrogen electrode. Predicted candidate molecular structures are listed in Supplementary Table 5. Figure 5b shows the distribution of redox potentials for the predicted molecular structures. Although the marginal distributions of the redox potentials is unimodal, the joint distribution shows two distinct modes, first mode near reduction potential of −3.7 V and another mode near the reduction potential of −4.15 V. We have validated the deep learning prediction of redox potential for 50 randomly selected candidate molecules. The DFT calculation and deep learning prediction of the reduction potential is compared in Fig. 5c. For the candidate structures considered for validation, SLAMDUNCS predicts the reduction potential with maximum error of 0.5918 V and mean absolute error of 0.2004 V.
A typical lithium-ion battery and desired trend in electrolyte redox potentials is shown in a. Redox potentials of the inverse predicted molecular structures are shown in b. Joint probability contours of the redox potentials is also shown in the background. Fifty molecules are randomly selected for validation. Redox potential for the selected molecules is obtained using DFT. In c, the DFT calculated reduction potential are compared against the deep learning predictions.
Examples of new electrolyte additive molecules predicted by SLAMDUNCS include phosphoryl attached to two methyl pentane groups (molecule 55 in Supplementary Table 4) and dipropyl iodomethylcarbonate (molecule 51 in Supplementary Table 5), both of which are not in the pubchem database. Additionally, SLAMDUNCS has suggested many other molecules that are in the pubchem database but have not been considered for the electrolyte application. For example, dimethyl silyl carbonate (molecule 26 in Supplementary Table 5) and 2,4,6 triisopropyl-1,3,5-trioxane are two interesting suggestions made by the inverse prediction algorithm.
For the representative problems considered above, SLAMDUNCS predicted a large number of molecular structures extrinsic to the database that meet the primary essential criterion as required by the target application. For each application, 100 predicted molecules are listed in the Supplementary Tables 2–5 of the Supplementary Information. Table 2 lists number of molecules that are outside the training dataset or not listed in the PubChem. If the molecule is not present in the PubChem database, distance between the molecule and training dataset is reported using Levenshtein (\(\lambda\)) and Ratcliff-Obershelp (\(\rho\)) distance. Minimum distance between molecular structure and the training dataset is reported in the table. As can be observed from the table, out of the 400 predicted molecules, \(67.75 \%\) of the molecules are new.
We have validated the properties prediction by SLAMDUNCS for 50 candidate molecular structures for each application. Although highly accurate, the prediction error is found to be high for some of the candidate structures. In the Supplementary Fig. 4 of Supplementary Information, we investigate the candidate structures with highest error for each application. Top row of the figure shows initial structure for each application, while the bottom row shows the corresponding structure optimised using DFT. For p-type OTFT, initial and optimised structures are similar (see middle column of the Supplementary Fig. 4), however, the structure contains chlorine atom attached to a Benzene ring. This presence of chlorine atom results in a higher error in HOMO prediction. For n-type OTFT, initial structure obtained from the SMILES representation contains a ring of alternate carbon and oxygen atoms attached to nepthanol, however when optimised using DFT, consists of two side chains formed by breaking of the ring. Right column of the Supplementary Fig. 4 shows the candidate structure for redox-stable organic electrolyte that has highest error in reduction potential prediction. As can be observed from the figure, the candidate structure consists of two rings of four atoms. When optimized for anion using DFT (bottom structure of the right column in Supplementary Fig. 4), both the four atom rings break due to high strain. As the deep learning algorithms of SLAMDUNCS are not trained for capturing this behaviour, error in reduction potential prediction is high for this candidate structure.
Each of these applications have additional secondary criteria, such as transport properties, solvation energy, and parameters that affect processing that need to be considered while designing. The candidate structures can be down-selected considering these additional properties before experimentally realising them. Alternatively, SLAMDUNCS can be used to design molecules by simultaneously considering multiple target properties in a coherent and holistic approach.
Discussion
To summarise, we have developed a deep learning based inverse prediction framework, SLAMDUNCS, for design of materials with target properties. In particular, we apply Bayesian inference for design of organic molecules with desired properties in three representative applications: high stability electrolytes for lithium-ion batteries, n- and p-type organic semiconductors for OTFTs and small organic acceptor molecules for use in organic solar cells. We successfully generated molecules not in the database with target properties, a small subset of which were validated with first principles simulations. This is primarily enabled by our use of Bayesian framework that allowed us to obtain a set of molecular structure as against single structures predicted by the state of the art optimisation methods. Moreover, our use of RBM to encode the fundamental chemical rules allowed us to generate the molecular structures extrinsic to the database without using any heuristic or combinatorial rules, enabling fully automated design of molecules for target applications. The proposed approach is efficient and robust, we expect that it can be extended to directly design other complex materials as well, as long as a reasonably diverse dataset for learning structure-property relationship is available and that the property-relevant structural information can be digitised. This dataset can be purely experimental, purely based on physics-based calculations or a combination of the two. Currently, our forward model is trained on organic molecular database, thus, our inverse model is applicable to only problems in the organic space. Within the organic space also, it is trained to inverse predict molecules for a small set of properties such as HOMO, LUMO and Redox potentials. However, same approach can be used to train the model for other properties of the organic molecules. Additionally, the same inverse design architecture can be extended to train for predictions in the inorganic space, by properly choosing the fingerprints. Note that an alternative to the SMILES representation is required for structure encoding in the inorganic space.
While we have applied SLAMDUNCS for designing organic molecules, it can be readily adapted to design inorganic materials such as semiconductors, piezoelectric and thermoelectric materials where one would need to learn on relationship between crystal structure and properties. Our work clearly demonstrates that a fast prediction of molecules/materials with target properties is indeed possible. We strongly believe that it can be easily extended to other types of materials and a diverse set of properties, including thermal, electrical and optical performance. Moreover, SLAMDUNCS can be used for inverse prediction of molecules with multiple target properties simply by using multivariate probability distribution to quantify the likelihood function.
Methods
Reference dataset creation
The molecular properties database was generated using density functional theory (DFT) calculations on 77,547 molecules randomly selected from the PubChem database36 with compound identifier numbers between 1 and 136200. The resultant database is a well representative mixture of small and large molecules, as well as long chains, as can be seen from the distribution of number of molecules against the SMILES length (see Supplementary Fig. 2a). All the first principles calculations were performed using the Gaussian 09 software package62 with B3LYP functional and 6-311+G (d,p) basis sets with the polarised continuum model63 as a solvation environment with an effective dielectric constant of 28.86. Unconstrained optimisation was used to optimise all the geometries in this solvation environment. The oxidation and reduction reactions were respectively simulated by removing or adding an electron from the neutral molecule. The oxidation potential was obtained from the difference in the total free energies of the oxidised and neutral molecules. The reduction potential was similarly calculated from the difference in the total free energies of the reduced and neutral molecules.
Validation
A small subset of SLAMDUNCS predicted molecular structures that are not present in the reference dataset were validated using the first principles calculations. The methodology outlined for reference dataset creation was used for validating the predicted molecular structures using the first principles calculations.
Details of the deep learning Bayesian framework
The molecular structures with desired attributes are predicted using a deep learning Bayesian framework. At the core of the proposed framework is a Bayesian inference methodology that provide a completely rational data assimilation framework using the Bayes theorem. Unlike traditional data assimilation applications, SLAMDUNCS uses Bayesian inference for predicting valid molecular structures with desired attributes. In this framework, the prior is defined as a probability of validity of a molecular structure, while, the likelihood is specified in terms of the expert opinion on the desired attributes of a given application. Subsequently, we simulate an ergodic Markov chain with the posterior as a stationary distribution, this provides us a set of valid molecules with desired attributes. In the following, we provide a detailed step-by-step description of the proposed deep learning Bayesian framework.
Molecular fingerprinting
We obtain a canonical SMILES representation of known molecules from the PubChem database. In this paper, we have only considered the molecules with SMILES length less than or equal to 100 characters. For the molecules with a SMILES representation of less than 100 characters, we concatenate the SMILES string with null characters to obtain a resultant 100 character SMILES string. Each SMILES character is subsequently converted to an equivalent 8 bit binary representation, and the resultant binary vector of length 800 is used as a molecular fingerprint.
Specification of prior using restricted Boltzmann machine
Molecular fingerprinting using the binary variables allow us to represent the molecules as a Bernoulli random vector, \({\bf{v}}\). The molecular structures database, represented using Bernoulli random vectors, is treated as samples from a multivariate probability distribution \(p\left({\bf{v}}\right)\). We quantify \(p\left({\bf{v}}\right)\) using restricted Boltzmann machine (RBM). RBM is a two layer network with a probability distribution given by
where \({\bf{h}}\) denotes hidden layer. We marginalise over \({\bf{h}}\) to obtain
For all the experiments presented in this paper, the RBM is constructed using 800 visible nodes and 500 hidden nodes. This RBM is trained using a contrastive-divergence algorithm with a single Gibbs sampling step (CD1 algorithm). We have used momentum algorithm64 to implement the stochastic gradient descent for minimisation of loss in the CD1 algorithm. We use 80% of the molecular structures database and train the RBM for 5000 epochs. We start the training with learning rate \(1{e}^{-02}\) and uniformly reduce the learning rate to \(1{e}^{-05}\). Momentum is fixed at 0.5 for initial 5 epochs, which is subsequently increased to 0.9 for the remaining epochs.
Likelihood estimation using deep learning
SLAMDUNCS admit expert opinion on desired molecular attributes to define the likelihood function \(p\left({\boldsymbol{y}}| {\boldsymbol{v}}\right)\), where \({\boldsymbol{y}}\) is a vector of target properties. For a given molecular structure \({\boldsymbol{v}}\), the likelihood function quantifies probability of the molecule possessing target properties. Thus, complete specification of the likelihood function require prediction of molecular properties of the structure \({\boldsymbol{v}}\). We have used semi-supervised deep learning for molecular properties prediction. We have constructed the deep network using a stack of pre-trained RBMs.
We have first defined a DBN created by stacking three RBMs. The visible layer of the DBN consists of 800 nodes, whereas, the hidden layers are defined using 800, 500 and 200 nodes. We have used a greedy algorithm to train the DBN, where we use the molecular structures database to train the first RBM and train the subsequent RBMs using prediction of the previous RBM as the training data. All the RBMs are trained for 5000 epochs using momentum algorithm with initial momentum of 0.5 for first 5 epochs and the momentum of 0.9 for the remaining epochs. We start the training with learning rate \(1{e}^{-02}\) and uniformly reduce the learning rate to \(1{e}^{-05}\). Similarly, we have pre-trained the top GB-RBM using the properties database. We have used 20 Gibbs sampling steps and fixed learning rate of \(1{e}^{-05}\) for pre-training the GB-RBM.
We have constructed a deep network by stacking together the pre-trained DBN and GB-RBM. This deep network is trained for 1000 epochs in a supervised manner using the structure-properties database. We have used Adam optimiser65 with a fixed learning rate of 0.1 for supervised training of the deep network. To avoid overfitting, we have used dropout of 0.7 for the hidden layers.
Markov chain Monte Carlo sampling
In the final step, we combine the unsupervised learning of molecular structures with the semi-supervised deep learning of structure-property correlation using the Bayes theorem given by
The posterior distribution \(p\left({\boldsymbol{v}}| {\boldsymbol{y}}\right)\) probabilistically encompasses a chemical space of molecular structures with the desired target properties. We sample from the posterior distribution by simulating an ergodic Markov chain with \(p\left({\boldsymbol{v}}| {\boldsymbol{y}}\right)\) as a stationary distribution. We initiate the Markov chain from a random structure \({{\boldsymbol{v}}}^{0}\) and use following steps to simulate the Markov chain:
(a) Sample a candidate structure \({\boldsymbol{v}}^{*}\) from a proposal distribution \(q\left({{\boldsymbol{v}}}^{* }| {{\boldsymbol{v}}}^{i}\right)\).
(b) Compute the prior probability \(p\left({{\boldsymbol{v}}}^{* }\right)\) using Eq. 8.
(c) Use deep learning to predict the properties of the candidate structure \({{\boldsymbol{v}}}^{* }\). Obtain the likelhood \(p\left({\boldsymbol{y}}| {{\boldsymbol{v}}}^{* }\right)\) by probabilistically comparing predicted properties with the target properties \({\boldsymbol{y}}\).
(d) Compute the Metropolis-Hastings acceptance criterion
$$\alpha =\frac{p\left({\boldsymbol{y}}| {{\boldsymbol{v}}}^{* }\right)p\left({{\boldsymbol{v}}}^{* }\right)q\left({{\boldsymbol{v}}}^{i}| {{\boldsymbol{v}}}^{* }\right)}{p\left({\boldsymbol{y}}| {{\boldsymbol{v}}}^{i}\right)p\left({{\boldsymbol{v}}}^{i}\right)q\left({{\boldsymbol{v}}}^{* }| {{\boldsymbol{v}}}^{i}\right)}.$$(10)The candidate structure \({{\boldsymbol{v}}}^{* }\) is accepted with probability \(\alpha\).
To define the proposal distribution, we multiply the weights and biases of the RBM trained on the molecular structures database by a random variable \(\beta \in [0,1]\). We use this heated RBM as a proposal distribution. We use alternate Gibbs sampling to obtain a candidate molecular structure \({{\boldsymbol{v}}}^{* }\) from this proposal distribution. We start sampling after equilibration period of 30000 steps to ensure appropriate ergodicity of the Markov chain.
Data availability
The dataset used in this work is publicly available at https://github.com/piyushtagade/SLAMDUNCS.
Code availability
The codes are publicly available at https://github.com/piyushtagade/SLAMDUNCS.
References
Jain, A., Shin, Y. & Persson, K. A. Computational predictions of energy materials using density functional theory. Nat. Rev. Mater. 1, 15004 (2016).
Ceder, G. Opportunities and challenges for first-principles materials design and applications to li battery materials. MRS Bull. 35, 693–701 (2010).
Dingreville, R., Karnesky, R. A., Puel, G. & Schmitt, J.-H. Review of the synergies between computational modeling and experimental characterization of materials across length scales. J. Mater. Sci. 51, 1178–1203 (2016).
Le, T. C. & Winkler, D. A. Discovery and optimization of materials using evolutionary approaches. Chem. Rev. 116, 6107–6132 (2016).
Ramprasad, R., Batra, R., Pilania, G., Mannodi-Kanakkithodi, A. & Kim, C. Machine learning in materials informatics: recent applications and prospects. NPJ Comput. Mater. 3, 54 (2017).
Tagade, P. M. et al. Empirical relationship between chemical structure and redox properties: Mathematical expressions connecting structural features to energies of frontier orbitals and redox potentials for organic molecules. J. Phys. Chem. C 122, 11322–11333 (2018).
Pyzer-Knapp, E. O., Li, K. & Aspuru-Guzik, A. Learning from the harvard clean energy project: The use of neural networks to accelerate materials discovery. Adv. Funct. Mater. 25, 6495–6502 (2015).
Gómez-Bombarelli, R. et al. Automatic chemical design using a data-driven continuous representation of molecules. ACS Central Sci. 4, 268–276 (2018).
Ward, L., Agrawal, A., Choudhary, A. & Wolverton, C. A general-purpose machine learning framework for predicting properties of inorganic materials. NPJ Comput. Mater. 2, 16028 (2016).
Goh, G. B., Hodas, N. O. & Vishnu, A. Deep learning for computational chemistry. J. Comput. Chem. 38, 1291–1307 (2017).
Robert, C. The Bayesian choice: from decision-theoretic foundations to computational implementation (Springer Science & Business Media, 2007).
Pyzer-Knapp, E. O., Simm, G. N. & Guzik, A. A. A bayesian approach to calibrating high-throughput virtual screening results and application to organic photovoltaic materials. Mater. Horizons 3, 226–233 (2016).
Tagade, P. et al. Bayesian calibration for electrochemical thermal model of lithium-ion cells. J. Power Sources 320, 296–309 (2016).
D’Agostini, G. Bayesian reasoning in high-energy physics: principles and applications. CERN-99-03 (Cern, 1999).
Reid, N. Likelihood. J. Am. Stat. Assoc. 95, 1335–1340 (2000).
LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436 (2015).
Goodfellow, I., Bengio, Y., Courville, A. & Bengio, Y. Deep Learning, Vol 1 (MIT Press, Cambridge, 2016).
Schmidhuber, J. Deep learning in neural networks: an overview. Neural Netw. 61, 85–117 (2015).
Curtarolo, S. et al. The high-throughput highway to computational materials design. Nat. Mater. 12, 191 (2013).
Zunger, A. Inverse design in search of materials with target functionalities. Nat. Rev. Chem. 2, 0121 (2018).
Anthony, J. E., Facchetti, A., Heeney, M., Marder, S. R. & Zhan, X. n-type organic semiconductors in organic electronics. Adv. Mater. 22, 3876–3892 (2010).
Wöhrle, D. & Meissner, D. Organic solar cells. Adv. Mater. 3, 129–138 (1991).
Xu, K. Nonaqueous liquid electrolytes for lithium-based rechargeable batteries. Chem. Rev. 104, 4303–4418 (2004).
Faber, F., Lindmaa, A., von Lilienfeld, O. A. & Armiento, R. Crystal structure representations for machine learning models of formation energies. Int. J. Quantum Chem. 115, 1094–1101 (2015).
Hansen, K. et al. Machine learning predictions of molecular properties: Accurate many-body potentials and nonlocality in chemical space. J. Phys. Chem. Lett. 6, 2326–2331 (2015).
Randić, M. Generalized molecular descriptors. J. Math. Chem. 7, 155–168 (1991).
Schütt, K. T., Arbabzadah, F., Chmiela, S., Müller, K. R. & Tkatchenko, A. Quantum-chemical insights from deep tensor neural networks. Nat. Commun. 8, 13890 (2017).
Cadeddu, A., Wylie, E. K., Jurczak, J., Wampler-Doty, M. & Grzybowski, B. A. Organic chemistry as a language and the implications of chemical linguistics for structural and retrosynthetic analyses. Angew. Chem. Int. Ed. 53, 8108–8112 (2014).
Weininger, D. SMILES, a chemical language and information system. 1. introduction to methodology and encoding rules. J. Chem. Inf. Comput. Sci. 28, 31–36 (1988).
Vlassis, N. & Likas, A. A greedy em algorithm for gaussian mixture learning. Neural Process. Lett. 15, 77–87 (2002).
Elton, D. C., Boukouvalas, Z., Fuge, M. D. & Chung, P. W. Deep learning for molecular design-a review of the state of the art. Mol. Syst. Design Eng. 4, 828–849 (2019).
Hinton, G. E. A practical guide to training restricted boltzmann machines. in Neural networks: Tricks of the trade, 599–619 (Springer, 2012).
Teh, Y. W. & Hinton, G. E. Rate-coded restricted boltzmann machines for face recognition. In Advances in neural information processing systems. 908–914 (MIT Press, Cambridge, MA, 2001).
Torlai, G. & Melko, R. G. Learning thermodynamics with boltzmann machines. Phys. Rev. B 94, 165134 (2016).
Hinton, G. E. Training products of experts by minimizing contrastive divergence. Neural Comput. 14, 1771–1800 (2002).
Kim, S. et al. Pubchem substance and compound databases. Nucleic Acids Res. 44, D1202–D1213 (2015).
Gilks, W. R., Richardson, S. & Spiegelhalter, D. Markov chain Monte Carlo in practice (Chapman and Hall/CRC, 1995).
Pereira, F. et al. Machine learning methods to predict density functional theory b3lyp energies of homo and lumo orbitals. J. Chem. Inf. Model. 57, 11–21 (2016).
Bengio, Y. et al. Learning deep architectures for ai. Found. Trends Mach. Learning 2, 1–127 (2009).
Salakhutdinov, R. & Murray, I. On the quantitative analysis of deep belief networks. in Proc. 25th International Conference on Machine Learning, 872–879 (ACM, 2008).
Hinton, G. E., Osindero, S. & Teh, Y.-W. A fast learning algorithm for deep belief nets. Neural Comput. 18, 1527–1554 (2006).
Cho, K., Ilin, A. & Raiko, T. Improved learning of gaussian-bernoulli restricted boltzmann machines. in Proc. International Conference on Artificial Neural Networks, 10–17 (Springer, 2011).
Salakhutdinov, R. & Larochelle, H. Efficient learning of deep boltzmann machines. In Proc. 13th International Conference on Artificial Intelligence and Statistics, 693–700 (Proceedings of Machine Learning Research, 2010).
Silver, D. et al. Mastering the game of go with deep neural networks and tree search. Nature 529, 484 (2016).
Cover, T. M. & Thomas, J. A. Elements of information theory (John Wiley & Sons, 2012).
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I. & Salakhutdinov, R. Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learning Res. 15, 1929–1958 (2014).
Gal, Y. & Ghahramani, Z. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In Proc. International Conference on Machine Learning, 1050–1059 (Proceedings of Machine Learning Research, 2016).
Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H. & Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 21, 1087–1092 (1953).
Hastings, W. K. Monte carlo sampling methods using markov chains and their applications. Biometrika 57, 97–109 (1970).
Tierney, L. Markov chains for exploring posterior distributions. Ann. Stat. 22, 1701–1728 (1994).
Newman, C. R. et al. Introduction to organic thin film transistors and design of n-channel organic semiconductors. Chem. Mater. 16, 4436–4451 (2004).
Hanwell, M. D. et al. Avogadro: an advanced semantic chemical editor, visualization, and analysis platform. J. Cheminf. 4, 17 (2012).
Laquindanum, J. G., Katz, H. E., Lovinger, A. J. & Dodabalapur, A. Benzodithiophene rings as semiconductor building blocks. Adv. Mater. 9, 36–39 (1997).
Coropceanu, V., Li, H., Winget, P., Zhu, L. & Brédas, J.-L. Electronic-structure theory of organic semiconductors: charge-transport parameters and metal/organic interfaces. Annu. Rev. Mater. Res. 43, 63–87 (2013).
Yu, G., Gao, J., Hummelen, J. C., Wudl, F. & Heeger, A. J. Polymer photovoltaic cells: enhanced efficiencies via a network of internal donor-acceptor heterojunctions. Science 270, 1789–1791 (1995).
Huang, Y., Kramer, E. J., Heeger, A. J. & Bazan, G. C. Bulk heterojunction solar cells: morphology and performance relationships. Chem. Rev. 114, 7006–7043 (2014).
Qian, D. et al. Design rules for minimizing voltage losses in high-efficiency organic solar cells. Nat. Mater. 17, 703 (2018).
Etacheri, V., Marom, R., Elazari, R., Salitra, G. & Aurbach, D. Challenges in the development of advanced li-ion batteries: a review. Energy Environ. Sci. 4, 3243–3262 (2011).
Aurbach, D. et al. Design of electrolyte solutions for li and li-ion batteries: a review. Electrochim. Acta 50, 247–254 (2004).
Park, M. S., Kang, Y.-S., Im, D., Doo, S.-G. & Chang, H. Design of novel additives and nonaqueous solvents for lithium-ion batteries through screening of cyclic organic molecules: an ab initio study of redox potentials. Phys. Chem. Chem. Phys. 16, 22391–22398 (2014).
Park, M. S., Park, I., Kang, Y.-S., Im, D. & Doo, S.-G. A search map for organic additives and solvents applicable in high-voltage rechargeable batteries. Phys. Chem. Chem. Phys. 18, 26807–26815 (2016).
Frisch, M. J. et al. Gaussian 03, Revision D.01. Gaussian, Inc., (Wallingford, 2013)
Tomasi, J., Mennucci, B. & Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 105, 2999–3094 (2005).
Ruder, S. An overview of gradient descent optimization algorithms. arXiv preprint arXiv:1609.04747 (2016).
Kingma, D. P. & Ba, J. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 (2014).
Acknowledgements
We would like to thank Dr. Samarth Agarwal for carefully reading the paper and providing insightful suggestions.
Author information
Authors and Affiliations
Contributions
S.M.K., K.S.H., S.P., S.P.A., and P.M.T. formulated the problem. P.M.T. formulated and implemented Bayesian inference and deep learning algorithms. M.S.P. created the molecular properties database. P.M.T. carried out the calculations. S.P., S.P.A., and P.M.T analysed the results and carried out the validation. S.P.A. and P.M.T. prepared the initial draft of the paper. All authors contributed to the discussions and revisions of the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tagade, P.M., Adiga, S.P., Pandian, S. et al. Attribute driven inverse materials design using deep learning Bayesian framework. npj Comput Mater 5, 127 (2019). https://doi.org/10.1038/s41524-019-0263-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-019-0263-3
This article is cited by
-
Evaluating uncertainty-based active learning for accelerating the generalization of molecular property prediction
Journal of Cheminformatics (2023)
-
Material symmetry recognition and property prediction accomplished by crystal capsule representation
Nature Communications (2023)
-
Designing a multilayer film via machine learning of scientific literature
Scientific Reports (2022)
-
Autonomous reinforcement learning agent for chemical vapor deposition synthesis of quantum materials
npj Computational Materials (2021)
-
Machine Learning of Dislocation-Induced Stress Fields and Interaction Forces
JOM (2020)