Abstract
Graphene nanoribbons (GNRs) can be synthesized from molecular precursors with atomic precision. A prominent case is the 7-atom-wide armchair GNR made from 10,10′-dibromo-9,9′-bianthryl (DBBA) precursors on metal substrates through dehalogenation/polymerization followed by cyclodehydrogenation. We investigate the key aspects of the cyclodehydrogenation process by evaluating the energy profiles of various reaction pathways using density functional theory and the nudged elastic band method. The metal substrate plays a critical catalytic role by providing stronger adsorption for products and facilitating H desorption. For polyanthrylene on an extra layer of GNR on Au, the underlying GNR insulates it from the Au substrate and increases the reaction barriers, rendering the polyanthrylene “quasi-freestanding”. However, positive charge injection can induce localized cyclodehydrogenation. We find that this is due to the stabilization of an intermediate state through an arenium ion mechanism and favorable orbital symmetries. These results provide mechanistic insight into the effects of the metal substrate and charge injection on cyclodehydrogenation during GNR synthesis and offer guidance for the design and growth of new graphitic structures.
Similar content being viewed by others
Introduction
Graphene nanoribbons (GNRs) are a promising class of materials for future generations of nanoscale devices. Precise control of materials on an atomic level is critical to enable the fabrication of nanoscale devices and circuits. In 2010, Cai et al. reported a bottom-up fabrication of GNRs with atomic precision from 10,10′-dibromo-9,9′-bianthryl (DBBA) precursor on Au(111) and Ag(111) surfaces.1 There are two stages in the fabrication process, dehalogenation/polymerization and cyclodehydrogenation. In the first stage, the DBBA molecules are deposited onto the metal substrate and annealed at 470 K. The DBBA molecules lose bromine atoms to metal substrate, yielding surface-stabilized biradical species that serve as molecular building blocks for the targeted GNR.2 These biradical species diffuse across the surface and couple together to form polyanthrylene chains as imprinted by the specific chemical functionality pattern of the precursor molecules. In the second stage, polyanthrylene is annealed at 670 K, the surface-assisted cyclodehydrogenation process takes place and establishes extended, atomically precise GNRs. Following this pioneering work, GNRs with a variety of widths,3 edge structures,4,5 and heterojunctions6,7 have been fabricated on several different catalytic metal substrates,8,9,10 including Au,11,12,13 Ag,14,15 and Cu.2,16,17 The metal substrate is believed to play a critical role in the formation of GNRs.15,18,19 For example, efforts to grow GNRs from DBBA directly on an insulating TiO2(011)-(2 × 1) substrate only lead to polymerization but without cyclodehydrogenation.20 This is strong evidence that the metal surface is crucial for cyclodehydrogenation21 and thus for the transformation of self-assembled polyanthrylene to GNRs.
The dehalogenation and polymerization processes in the first stage are well kown.2,19,22,23 In contrast, a full mechanistic understanding of the subsequent cyclodehydrogenation process in GNR growth on Au(111) surface is lacking. Despite a plethora of experimental reports on the conversion of the polyanthrylene to GNR on various metal surfaces, such as Au(111),1 Au(110),11,13,24 Au(788),12 Ag(111),15 Cu(111),16 and Cu(110),16 theoretical investigations of GNR growth are limited and many of them21,25,26 focused on chemical environments different from those occurring in GNR fabrication. For the cyclodehydrogenation process in GNR formation on metal substrates, previous theoretical studies have focused on metal substrates and proposed two different types of domino-like reaction pathways.15,18 Bjork et al. presented a reaction pathway for the GNR growth on Au(111),18 where the cyclodehydrogenation process starts from one end of the polyanthrylene and extends through the chain in a domino-like fashion. In this pathway, a new C–C bond forms between the reaction centers after the two hydrogen atoms bonded with the reaction center atoms rotate toward the substrate. It has a barrier of 2.6 eV. This step is followed by a barrierless dehydrogenation step. Blankenburg et al. presented another reaction pathway on Ag(111),15 where the cyclodehydrogenation process also extends through the polyanthrylene in a domino-like fashion, but only on one side of the polyanthrylene chain. Unlike the former case, the C–C bond formation was shown to precede H movement. A barrier of 1.4 eV was reported per one C–C bond formation. The differences in the reaction barriers may be ascribed to the different metal substrates, reaction pathways, and van der Waals correction methods used. We note that both of these studies have been mainly focused on the synthesis of GNRs from polyanthrylene in direct contact with metal substrates.
In our previous work,27 we demonstrated that if the coverage of precursor molecules was high, a second layer of quasi-freestanding polyanthrylene could be formed on top of an underlying layer of GNR in contact with the Au(111) surface. Although a full conversion of the second-layer polyanthrylene to GNR by thermal annealing was not observed, a controllable local conversion could be realized by applying a negative sample bias pulse with a scanning tunneling microscope (STM) tip, which led to intra-ribbon heterojunctions of GNR embedded in the second layer of polyanthrylene. To gain a systematic understanding of the effects of the metal substrate, the underlying GNR layer, and charge injection from the STM tip, we investigate the key mechanistic steps in the cyclodehydrogenation process of GNR synthesis from polyanthrylene placed directly on an Au(111) substrate or as a second layer on top of an underlying GNR layer in contact with an Au(111) surface. For convenience, the underlying GNR layer on the Au surface in the latter case is denoted GNR-Au substrate. For modeling of reaction pathways in the transformation from polyanthrylene into GNR in various environments, we adopt a short bianthryl model consisting of two anthrylene units. By comparing the energy barriers between bianthryl reaction models on Au or GNR-Au substrates, we uncover the primary effect that the insulating GNR layer has on the reaction barriers. Further studies of the bianthryl model in vacuum in different charge states reveal the catalytic effect of charge injection on the cyclodehydrogenation process.
Results and discussion
Atomic structures and adsorption energies
Before investigating the mechanism of the transformation from polyanthrylene to GNR, we examine the atomic configurations of the various structures, including the first-layer polyanthrylene and GNR on Au substrate obtained at low surface coverage, and the second-layer polyanthrylene and polyanthrylene-GNR heterojunction on the GNR-Au substrate obtained at high surface coverage. We also compare the adsorption energies of polyanthrylene and GNR on Au and GNR-Au substrates. These results provide insights for the understanding of polyanthrylene to GNR transformation on different substrates.
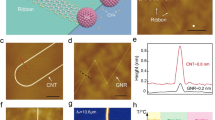
The optimized atomic structures of polyanthrylene and GNR on Au(111) at low coverage are shown in Fig. 1a, b together with simulated and experimental STM images. The simulated STM images are in good agreement with the experimental results. For polyanthrylene on Au(111), the STM image clearly shows a zigzag pattern because each tilting-up anthrylene unit appears as one bright spot. For GNR on Au(111), the STM image exhibits the typical hexagonal pattern. The good agreement between the theoretical and experimental results corroborates the formation of polyanthrylene and GNR on Au substrate at 470 and 670 K, respectively. The optimized atomic structure of polyanthrylene on top of the GNR-Au substrate is shown in Fig. 1c together with simulated and experimental STM images. The resolution of the STM image is not as sharp as of that acquired for the first-layer polymer (Fig. 1a), probably because of charge accumulation on the second-layer polyanthrylene, which is not in direct contact with the metal substrate. The lower resolution for structures on GNR-Au than on Au is consistently observed across multiple experimental measurements. Nevertheless, the zigzag signature remains the same as the first-layer polyanthrylene on Au. As revealed in our prior work,27 the second-layer polyanthrylene can be converted to GNR with atomic precision by charge injection from the STM tip at a selected location. The optimized atomic structure of thus obtained polyanthrylene-GNR heterojunction, along with its simulated and experimental STM images, is shown in Fig. 1d. The converted GNR segment has a lower height than polyanthrylene, and thus shows a darker contrast in the image. The good agreement between the calculations and experiment corroborates the formation of polyanthrylene on the GNR-Au substrate and its conversion to a polyanthrylene-GNR heterojunction after the STM charge injection.
Optimized atomic structures (top panels), simulated (middle panels), and experimental (bottom panels) STM images for a polyanthrylene on Au, b GNR on Au, c polyanthrylene on GNR-Au, and d polyanthrylene-GNR heterojunction on GNR-Au. The experimental and simulated STM images are obtained at a sample bias of −2.0 V
At low Au surface coverage, the distances between the substrate and the lowest atoms in the adsorbate, or adsorption heights, are >3 Å. Such large separations suggest that no chemical bonds are formed between the polyanthrylene or GNR and the Au surface. At high Au surface coverage, the second-layer polyanthrylene or heterojunction is also separated from the underlying GNR layer by more than 3 Å. These distances justify the adoption of vdW corrections in the calculations to obtain reliable structures and energies. Among the different methods available for vdW corrections,28,29,30 the D2 correction method29 and the non-local vdW-DF functional30 have previously been used in studies of the cyclodehydrogenation process in GNR formation on Ag(111) and Au(111) surfaces.15,18 The former is an add-on empirical correction while the latter is incorporated in a self-consistent functional. To choose between these two methods for our investigations, we compare the adsorption energies calculated by these two methods for polyanthrylene and GNR on Au and GNR-Au substrates. In the latter case, the adsorption energy of GNR instead of a polymer-GNR heterojunction on GNR-Au substrate is calculated, to provide information in the limit of a long GNR segment.
Table 1 shows the adsorption energies calculated by the D2 and vdW-DF methods for polyanthrylene and GNR directly on Au(111) and GNR-Au substrates. The quantitative values of adsorption energies are relevant to the cyclodehydrogenation process because the reaction barriers are profoundly affected by the adsorption energies of various species on different substrates. GNR has a larger adsorption energy than polyanthrylene on both substrates, regardless of the vdW correction method being used, despite having a smaller number of H atoms (due to their desorption when forming a GNR). This difference may be ascribed to the fact that the GNR is completely planar and therefore has better contact with the substrate than the polymer. With the empirical D2 correction, the adsorption energies are much stronger on the Au substrate than on the GNR-Au substrate. However, they only differ by <0.5 eV when the self-consistent vdW-DF functional is used. Furthermore, the D2 correction gives much larger adsorption energies than vdW-DF for both polyanthrylene and GNR on Au, but they become comparable when the substrate is changed to GNR-Au. These results are quite surprising and point toward a caveat in the selection of vdW correction methods for the studies of cyclodehydrogenation on top of different substrates. Due to the empirical nature of the D2 method and its prediction of the very large variations in adsorption energies on different substrates, we adopt the self-consistent vdW-DF method for the rest of the calculations.
Key factors in the transformation of polyanthrylene to GNR
Understanding of cyclodehydrogenation process at the atomic level will help provide theoretical guidance for the design and fabrication of GNRs. To that end, we study the formation pathways of cyclodehydrogenation process under different conditions: (1) on an Au substrate, (2) on a GNR-Au substrate, and (3) in vacuum with different amount of charge injections. The cyclodehydrogenation process consists of two steps: cyclization and dehydrogenation. In the cyclization step, the C6H4 groups at the edges of neighboring anthrylene units of the polyanthrylene approach each other while rotating around the central C–C bond and form new C–C bonds. Concomitantly the orbital hybridization of the reacting C atoms changes from sp2 to sp3. In the subsequent dehydrogenation step, H atoms desorb and aromatic rings form.
Substrates effect: metal substrates and insulating GNR layer
In experiments, when the coverage of the precursor molecules on Au(111) surface is >1 monolayer, a bilayer structure is formed.27 As observed in the experiment, the underlying layer of polyanthrylene can be efficiently converted to GNR by annealing. However, the second-layer polyanthrylene formed on top of the first layer of GNR does not fully convert to a GNR, even after annealing at a temperature so high as to cause its melting into one layer. It is known that a metal substrate has a significant catalytic effect on cyclodehydrogenation, yet the effect of the GNR layer separating polyanthrylene from direct contact with the metal substrate needs further investigation. Here, we calculate the energy profile for the reaction pathways on Au(111) substrate and GNR-Au substrate. We show by nudged elastic band (NEB) simulations that the first layer of GNR serves as an insulating layer and prevents the metal substrate from acting as a catalyst for the polyanthrylene to GNR transformation.
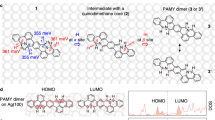
The transformation is modeled using a bianthryl oligomer as a reagent. Figure 2a shows the atomic structure of the models. In the bianthryl oligomer, the two anthryl units are connected by one C–C bond. During the transformation, the two units rotate around this bond and the four C6H4 groups pair with each other to form two new C–C bonds. Our NEB simulations unravel that the two new C–C bonds on the different sides of the bianthryl form separately: first two C6H4 groups approach each other to form one C–C bond on one side, then the other two C6H4 groups undergo the same reaction on the other side. We focus here on the first bond formation, since the second step occurs similarly. The energy profile is shown in Fig. 2b as the black curve for the cyclization (Initial to IS-I) and dehydrogenation reactions (IS-I to IS-II). The H migration steps are summarized into the dehydrogenation step from IS-I to IS-II. The details of the reaction steps are depicted in the Supplementary Fig. 1. For comparison, the energy profile for direct contact with Au(111) is shown as the red curve. The difference between the two curves is attributed to the different substrates, i.e., the polyanthrylene to GNR transformation takes place on the GNR-Au substrate versus directly on the Au surface.
a Atomic structures of bianthryl and GNR on GNR-Au. b Energy profiles of the transformation of a bianthryl molecule to a short GNR segment. The black and red curves represent systems with and without a GNR insulating layer. The first barrier is for the one-side cyclization. The second barrier is for hydrogen migration and desorption. The lower panel shows Kekulé structures of the top layer in the initial, IS-I, and IS-II states
The underlying GNR layer between the bianthryl and the Au substrate affects both cyclization and dehydrogenation significantly. In the presence of an insulating GNR layer, the cyclization barrier increases from 1.5 to 2.3 eV while the highest transition state in dehydrogenation increases from 2.3 to 3.2 eV. From the detailed reaction pathway in Supplementary Fig. 1, the highest energy barriers in dehydrogenation steps are 1.0 and 1.6 eV for the Au and GNR-Au substrates, respectively, which shows that the GNR is not a good candidate for removing hydrogen atoms. In the short bianthryl model of the polymer, the IS-I state has two unpaired electrons on the two C6H4 groups after a new C–C bond forms. The electron delocalization can be described as five π electrons on five C centers (5e/5c) in each C6H4 group. Based on the analysis shown above, the increase in barriers when changing the substrate from Au to GNR-Au for both the cyclization and dehydrogenation steps may be partially ascribed to the lower gain in the adsorption energy when converting polyanthrylene to GNR on the insulating GNR layer, compared with conversion directly on the Au surface. However, this effect turns out to be small, as can be seen from the small differences between the vdW-DF adsorption energies in Table 1. The main reason should instead be ascribed to the fact that the underlying GNR substrate does not have a strong capability to adsorb H atoms like the Au substrate. Although the underlying GNR is in contact with the Au surface, the top layer is separated from the Au surface by two vdW separations. Other possible pathways for the cyclodehydrogenation on GNR-Au exist, such as hydrogen migration and desorption as molecules to vacuum. Similar pathways on Au were studied,18 but were found to be less energetically favorable. From the energy barrier comparison between the Au and GNR-Au substrates, it can be concluded that the underlying GNR layer significantly inhibits the metal substrate-assisted cyclodehydrogenation by increasing the energy barrier. Therefore, the underlying GNR serves as an insulating layer and renders the top layer of polyanthrylene quasi-freestanding.
Charge injection effect on cyclodehydrogenation
Although the full polymer-to-GNR transformation is hardly observed for the second-layer polymer, we found in our previous work that charge injection from an STM tip can induce this transformation at arbitrary sites of the second-layer polymer on top of a GNR layer in contact with Au.25 Blankenburg et al. found earlier that charge injection from an STM tip can induce a transformation of a polymer segment in direct contact with Ag substrate.15 We also found27 that hole (positive charge) injection could induce cyclodehydrogenation reaction starting at a low STM bias, while electron (negative charge) injection does not and can instead lead to polymer decomposition at an increased STM bias. Based on the analysis of orbital symmetries for the reactant in different charge states, we were able to rationalize the distinction between hole and electron injections by tracing it back to the classical Woodward–Hoffman rules.27 To better understand the effect of hole injection on this reaction, we investigate below the energy profile and the electronic structure along the cyclodehydrogenation pathway by examining the charge states 0, + 1, and + 2. As discussed above, the insulating layer of GNR renders the top layer of polyanthrylene quasi-freestanding. Considering this effect and to avoid the interference of metal substrate in charged systems calculation, in the following we investigate the charge effect in vacuum, which also limits the computational expense. Therefore, the calculated energy profile will be only qualitatively and semi-quantitatively valid, because it omits the dielectric screening by the GNR-Au substrate. As above, the reactant is the bianthryl while the product is a short GNR segment.
Figure 3 shows the energy profiles along the reaction pathway at q = 0, + 1, and + 2, together with the Kekulé structures for the bianthryl and the three intermediate states IS-I, IS-II, and IS-III. Similarly to the reaction on a substrate, the cyclization of the initial state in vacuum gives rise to IS-I. The two H atoms could be on either the same or opposite sides of IS-I. When the H atoms are on the same side, the overall barrier is as high as 4.2 eV for the neutral case, which is consistent with the results by Bjork et al.18 Due to the very high barrier, the corresponding reaction pathway is not considered below. We thus only focus on the other alternative, in which the two H atoms remain on the opposite sides of IS-I. It is evident that the charge has a substantial effect on cyclization. As it increases from 0 to + 1 and + 2, the cyclization barrier is dramatically reduced from 2.5 to 1.6 and 1.0 eV, respectively. As explained above, the IS-I is unstable when the system is neutral because each C6H4 group involved in cyclization carries an unpaired π electron after the bond formation, which is due to hybridization change from sp2 to sp3 for only one of the six C atoms in each C6H4 group. However, when the system is positively charged, IS-I becomes a metastable state owing to the arenium ion mechanism.31 In organic chemistry, the arenium ion is a cyclohexadienyl cation that appears as a reactive intermediate in electrophilic aromatic substitution. One arenium ion per C6H4 group, or equivalently + 2 charge for the bianthryl molecule, makes the IS-I a metastable structure. Also, the Bronsted–Evans–Polanyi principle32 suggests that the energies of transition states would be lowered proportionally to the stabilization of IS-I. Obviously, the stabilization is more pronounced for q = + 2 than for + 1, due to the formation of two arenium ions versus one. Furthermore, the stabilization of IS-I with greater positive charge can be seen from the barriers for the backward reaction from IS-I to the initial state: the neutral IS-I has a vanishingly small barrier for going back, while IS-I with q = + 1 has a slightly increased but still negligible barrier for the backward reaction. Consequently, IS-I with q = 0 and + 1 has a high probability for reverting to the initial state even if it is formed. In contrast, the barrier for the backward reaction of IS-I with q = + 2 is increased to 0.4 eV, thus enhancing its survivability as a metastable state for subsequent reactions. The charge-induced reaction shows similarity with Scholl reaction, but there are also significant differences. In the charge-induced reaction, charges are supplied by the STM tip, in the form of injected or extracted electrons. We have shown that in vacuum the barriers are significantly lower when two electrons are extracted from bianthryl. In the standard Scholl reaction in a solution phase, two protons are eliminated to the solvent and are stabilized by the solvation effect. For our reaction in ultra-high vacuum on a substrate, two hydrogen atoms are eliminated forming H2 and the charges left on the organic species are compensated by the metal substrate. In the second step, IS-I is converted to IS-II through an H migration process. Since the two H atoms that must be desorbed are on opposite sides of IS-I, one of them needs to migrate to the edge and bond with the other H atom in order to desorb as an H2 molecule. We find that a sigmatropic rearrangement is a favorable path for the H migration in this step.27 For q = 0, + 1, + 2 charge injections, the reaction barriers are 1.2, 1.6, and 1.9 eV, respectively. They agree with the energy barriers reported for H migration on graphene, which are in the range of 2.0–4.0 eV.33 It appears that the positive charge injections do not lower the energy barrier for the H migration process; however, as discussed above, the barriers of the backward reaction are negligible for q = 0 and + 1 charge injections, rendering IS-I unstable with regard to the backward reaction. Therefore, it is likely that only the injection of two holes will enable IS-I to proceed toward IS-II. In the final step of dehydrogenation, two H atoms desorb from the molecule into vacuum as H2, converting IS-II to IS-III. The energy barriers for q = 0, + 1, and + 2 charge injection are 3.8, 2.9, and 2.4 eV, respectively. For this step, the lowering of the energy barrier by positive charge injection is prominent. Considering the overall energy profiles, the + 2 charge state has significantly lower energies for all intermediates and transition states; the most prominent effect is the stabilization of IS-I, due to the arenium ion mechanism.
To shed further light on the arenium ion effect, we calculate the spatial distribution of the excess charge for q = + 2 charge injection in the initial, IS-I, IS-II, and IS-III structures along the reaction pathway, which are shown in Fig. 4a–d, respectively. The spatial distribution of excess charge is the difference between the charge densities of the charged and neural systems. The isosurface value is 10% of its maximum value. For the initial, IS-II, and IS-III states, the excess charge is distributed over all edge C atoms, as a result of electrostatic Coulomb repulsion. However, in IS-I the excess charge mainly resides on the four C atoms that are close to the newly formed C–C bond. These four atoms are the recipients of excess charge in the four resonant states shown in Fig. 4e. Compared with IS-II and IS-III, IS-I is the state that is the most stabilized by the + 2 charge injection, indicating that positive charge injection provides a catalyzing effect. Stabilization of IS-I is also observed for + 1 charge injection, although its catalytic effect in the + 1 charge state may be negated by the small barrier for backward dissociation of IS-I to the initial state. Our analysis thus confirms that the experimentally observed15 controllable polymer to GNR transformation induced by STM tip is facilitated by positive excess charge and the formation of arenium ions. This mechanism may also open a new avenue for converting a completely freestanding polymer to GNR.
In summary, we have evaluated several key mechanistic effects in the growth of atomically precise graphene nanoribbons from molecular precursors. It was established that the metal substrate exerts an important catalytic effect on the cyclodehydrogenation reaction.18 From the comparison between energy barriers for reaction pathways on Au substrate and in vacuum, we can see that metal substrate significantly lowers the energy barriers of both cyclization and dehydrogenation, by providing strong adsorption and facilitating H adsorption. We also find that the metal substrate catalytic effect may be inhibited by detrimental insulation from an underlying GNR layer, which increases the energies of the intermediate states in the cyclodehydrogenation reactions as well as the transition state energies, rendering the polyanthrylene quasi-freestanding. However, our simulations show that conversion of a quasi-freestanding polyanthrylene to a second-layer GNR can be realized by positive charge injection, which leads to the formation of arenium ions that stabilize the C6H4 groups by removing the unpaired π electrons. These results provide mechanistic explanations for the experimental observations of the difficulty in thermally activated second-layer GNR growth, and shed light on the mechanism of STM-tip-induced localized second-layer GNR conversion.
Methods
Sample preparation and STM measurement
The samples were grown from DBBA molecules on Ar+-annealed Au(111) surface. The precursor molecules were deposited onto the Au substrate by sublimating at 485 K while the Au substrate was held at 470 K. Surface coverage of the Au substrate was controlled by the amount of DBBA and time of sublimation. Samples were subsequently annealed at 470 K for 30 min and 670 K for additional 30 min. Depending on the temperature, polyanthrylene and 7-atom-wide armchair graphene nanoribbon (7-aGNR) were synthesized. For simplicity, we will refer to the 7-aGNR in the following as GNR. Scanning tunneling microscopy (STM) characterization was performed at 105 K with a PtIr tip in ultra-high vacuum. The STM images were acquired at a constant current mode. The bias was applied by adjusting the voltage of the sample with respect to the tip.
Calculation methods
Ab initio density functional theory calculations were performed with the Quantum Espresso code34 using ultrasoft pseudopotentials generated by the Vanderbilt’s method35 with the Perdew–Burke–Ernzerhof exchange-correlation functional.36 The plane wave energy cutoff was 24 Ry for the Kohn–Sham wavefunctions, and 200 Ry for the charge density. To account for the van der Waals (vdW) interactions between the polyanthrylene or GNR and the Au substrate, all calculations were performed using a non-local functional with vdW corrections (vdW-DF).30,37 The atomic structures were relaxed until the forces were below the threshold of 0.025 eV/Å. The STM images were simulated for polyanthrylene and GNR on Au and GNR-Au substrates using Tersoff’s method.38 The Au(111) surface was simulated by four layers of Au atoms. The atoms in the bottom two layers were fixed while those in the top two layers were fully relaxed along with the adsorbed structures, if present. The energy barriers of the cyclodehydrogenation reactions were obtained using the climbing images39 NEB method. The forces on images were relaxed until they reached 0.1 eV/Å threshold. The reaction pathways were evaluated for bianthryl on Au and GNR-Au substrates, and bianthryl in vacuum at different charge states (q = 0, + 1, and + 2). In the systems without substrate, the supercells were constructed with ≥ 20 Å vacuum region along all directions separating the periodic images of molecules. When the substrate is included, a vacuum region ≥ 20 Å is used perpendicularly to the substrate surface, while the distance between the periodic images of adsorbates on the substrate is chosen to be ~10 Å to reflect the typical adsorbate density in the experiment, as well as to reduce the computational cost. For the periodic polymer models, three k points were used along the periodic direction, while only the Γ point was used when investigating reactions for the bianthryl models. Certain computational results, such as STM images obtained from the Quantum Espresso code, were corroborated with the RMG code.40,41
Data availability
The data that support the findings of this study are available from the corresponding author on request.
References
Cai, J. et al. Atomically precise bottom-up fabrication of graphene nanoribbons. Nature 466, 470–473 (2010).
Simonov, K. A. et al. Effect of substrate chemistry on the bottom-up fabrication of graphene nanoribbons: combined core-level spectroscopy and STM study. J.Phys. Chem. C. 118, 12532–12540 (2014).
Chen, Y.-C. et al. Tuning the band gap of graphene nanoribbons synthesized from molecular precursors. ACS Nano 7, 6123–6128 (2013).
Wang, X. et al. Room-temperature all-semiconducting sub-10-nm graphene nanoribbon field-effect transistors. Phys. Rev. Lett. 100, 206803 (2008).
Liu, J. et al. Toward cove-edged low band gap graphene nanoribbons. J. Am. Chem. Soc. 137, 6097–6103 (2015).
Cai, J. et al. Graphene nanoribbon heterojunctions. Nat. Nanotechnol. 9, 896–900 (2014).
Chen, Y.-C. et al. Molecular bandgap engineering of bottom-up synthesized graphene nanoribbon heterojunctions. Nat. Nanotechnol. 10, 156–160 (2015).
Li, Y., Zhang, W., Morgenstern, M. & Mazzarello, R. Electronic and magnetic properties of zigzag graphene nanoribbons on the (111) surface of Cu, Ag, and Au. Phys. Rev. Lett. 110, 216804 (2013).
Costa Girão, E., Liang, L., Cruz-Silva, E., Filho, A. G. S. & Meunier, V. Emergence of atypical properties in assembled graphene nanoribbons. Phys. Rev. Lett. 107, 135501 (2011).
Denk, R. et al. Exciton-dominated optical response of ultra-narrow graphene nanoribbons. Nat. Commun. 5, 1392–1403 (2014).
Massimi, L. et al. Surface-assisted reactions toward formation of graphene nanoribbons on Au(110) surface. J. Phys. Chem. C. 119, 2427–2437 (2015).
Linden, S. et al. Electronic structure of spatially aligned graphene nanoribbons on Au(788). Phys. Rev. Lett. 108, 216801 (2012).
Della Pia, A. et al. Electronic structure evolution during the growth of graphene nanoribbons on Au(110). J. Phys. Chem. C. 120, 7323–7331 (2016).
Huang, H. et al. Spatially resolved electronic structures of atomically precise armchair graphene nanoribbons. Sci. Rep. 2, 347–349 (2012).
Blankenburg, S. et al. Intraribbon heterojunction formation in ultranarrow graphene nanoribbons. ACS Nano 6, 2020–2025 (2012).
Simonov, K. A. et al. From graphene nanoribbons on Cu(111) to nanographene on Cu(110): critical role of substrate structure in the bottom-up fabrication strategy. ACS Nano 9, 8997–9011 (2015).
Han, P. et al. Self-assembly strategy for fabricating connected graphene nanoribbons. ACS Nano 9, 12035–12044 (2015).
Björk, J., Stafström, S. & Hanke, F. Zipping up: cooperativity drives the synthesis of graphene nanoribbons. J. Am. Chem. Soc. 133, 14884–14887 (2011).
Bronner, C., Björk, J. & Tegeder, P. Tracking and removing Br during the on-surface synthesis of a graphene nanoribbon. J. Phys. Chem. C. 119, 486–493 (2015).
Kolmer, M. et al. Polymerization of polyanthrylene on a titanium dioxide (011)-(2×1) surface. Angew. Chem. Int. Ed. 52, 10300–10303 (2013).
Treier, M. et al. Surface-assisted cyclodehydrogenation provides a synthetic route towards easily processable and chemically tailored nanographenes. Nat. Chem. 3, 61–67 (2011).
Grill, L. et al. Nano-architectures by covalent assembly of molecular building blocks. Nat. Nanotechnol. 2, 687–691 (2007).
Bieri, M. et al. Two-dimensional polymer formation on surfaces: insight into the roles of precursor mobility and reactivity. J. Am. Chem. Soc. 132, 16669–16676 (2010).
Massimi, L. et al. Metal-phthalocyanine ordered layers on Au(110): metal-dependent adsorption energy. J. Chem. Phys. 140, 244704 (2014).
Pogodin, S. & Agranat, I. Biphenalenylidene: the forgotten bistricyclic aromatic ene. A theoretical study. J. Am. Chem. Soc. 125, 12829–12835 (2003).
Wadumethrige, S. H. & Rathore, R. A facile synthesis of elusive alkoxy-substituted hexa-peri-hexabenzocoronene. Org. Lett. 10, 5139–5142 (2008).
Ma, C. et al. Controllable conversion of quasi-freestanding polymer chains to graphene nanoribbons. Nat. Commun. 8, 14815 (2017).
Dion, M., Rydberg, H., Schröder, E., Langreth, D. C. & Lundqvist, B. I. Van der Waals density functional for general geometries. Phys. Rev. Lett. 92, 246401 (2004).
Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 27, 1787–1799 (2006).
Thonhauser, T. et al. Van der Waals density functional: self-consistent potential and the nature of the van der Waals bond. Phys. Rev. B 76, 125112 (2007).
Wheland, G. W. A quantum mechanical investigation of the orientation of substituents in aromatic molecules. J. Am. Chem. Soc. 64, 900–908 (1942).
Evans, M. G. & Polanyi, M. Further considerations on the thermodynamics of chemical equilibria and reaction rates. Trans. Faraday Soc. 32, 1333–1360 (1936).
Han, S. S., Jung, H., Jung, D. H., Choi, S.-H. & Park, N. Stability of hydrogenation states of graphene and conditions for hydrogen spillover. Phys. Rev. B 85, 155408 (2012).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).
Laasonen, K., Car, R., Lee, C. & Vanderbilt, D. Implementation of ultrasoft pseudopotentials in ab initio molecular dynamics. Phys. Rev. B 43, 6796–6799 (1991).
Perdew, J. P., Ernzerhof, M. & Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 105, 9982–9985 (1996).
Thonhauser, T. et al. Spin signature of nonlocal correlation binding in metal-organic frameworks. Phys. Rev. Lett. 115, 136402 (2015).
Tersoff, J. & Hamann, D. R. Theory of the scanning tunneling microscope. Phys. Rev. B 31, 805–813 (1985).
Henkelman, G., Uberuaga, B. P. & J¢nsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 113, 9901–9904 (2000).
Hodak, M., Wang, S., Lu, W. & Bernholc, J. Implementation of ultrasoft pseudopotentials in large-scale grid-based electronic structure calculations. Phys. Rev. B 76, 085108 (2007).
Briggs, E. L., Sullivan, D. J. & Bernholc, J. Real-space multigrid-based approach to large-scale electronic structure calculations. Phys. Rev. B 54, 14362–14375 (1996).
Acknowledgements
A portion of this research was conducted at the Center for Nanophase Materials Sciences (CNMS), which is a DOE Office of Science User Facility. The research was funded by grants ONR N00014-16-1-3213 and N00014-16-1-3153, and DOE DE-FG02-98ER45685. The development of the RMG code was funded by NSF grant OAC-1740309. Supercomputer time was provided by NSF grant ACI-1615114 at the National Center for Supercomputing Applications (NSF OCI-0725070 and ACI-1238993). Some of the calculations were performed at the Oak Ridge Leadership Computing Facility (DOE DE-AC05-00OR22725). L.L. was supported by Eugene P. Wigner Fellowship at Oak Ridge National Laboratory.
Author information
Authors and Affiliations
Contributions
Z.X. performed the calculations. C.M. conducted the experiments. W.L., J.B., and A.-P.L. supervised the whole project. J.H. and L.L. contributed to problem formulation and data analysis. K.H. provided the molecular precursors. All authors contributed to manuscript preparation.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xiao, Z., Ma, C., Lu, W. et al. Ab initio investigation of the cyclodehydrogenation process for polyanthrylene transformation to graphene nanoribbons. npj Comput Mater 5, 91 (2019). https://doi.org/10.1038/s41524-019-0228-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-019-0228-6