Abstract
The coupling of atomic force microscopy with infrared spectroscopy (AFM-IR) offers the unique capability to characterize the local chemical and physical makeup of a broad variety of materials with nanoscale resolution. However, in order to fully utilize the measurement capability of AFM-IR, a three-dimensional dataset (2D map with a spectroscopic dimension) needs to be acquired, which is prohibitively time-consuming at the same spatial resolution of a regular AFM scan. In this paper, we provide a new approach to process spectral AFM-IR data based on a multicomponent pan-sharpening algorithm. This approach requires only a low spatial resolution spectral and a limited number of high spatial resolution single wavenumber chemical maps to generate a high spatial resolution hyperspectral image, greatly reducing data acquisition time. As a result, we are able to generate high-resolution maps of component distribution, produce chemical maps at any wavenumber available in the spectral range, and perform correlative analysis of the physical and chemical properties of the samples. We highlight our approach via imaging of plant cell walls as a model system and showcase the interplay between mechanical stiffness of the sample and its chemical composition. We believe our pan-sharpening approach can be more generally applied to different material classes to enable deeper understanding of that structure-property relationship at the nanoscale.
Similar content being viewed by others
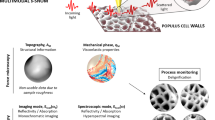
Introduction
In the last decade, improvements in instrumentation and data analytics have facilitated a paradigm-shift in correlative multimodal microscopy. For example, scanning probe microscopy in combination with other spectroscopical methods allows acquisition of localized physical properties for a wide range of materials, which can be used to characterize local chemical composition yielding unique insights into the structure–property relationship of functional materials,1,2 novel composites,3,4 and biological objects.5,6,7,8 This approach involves datasets where spatial coordinates may be augmented with one or more spectroscopic dimensions. Such datasets are then analyzed and interpreted using multivariate statistics,9,10 spectral unmixing,11 neural networks,12,13 and component analysis.14,15 As a result, it enables correlative multimodal imaging16 which can elucidate optomechanical,17 electromechanical,18,19,20 and electrochemical21 interactions in materials that would otherwise have been precluded. However, acquiring spectral datasets requires capturing a full spectrum at each spatial location. In some cases, it is possible to perform rapid imaging via full signal capture (G-mode) which is collected at the speed of scanning,22,23,24 however, this avenue is not yet available for all possible spectroscopic modes (such as chemically sensitive atomic force microscope infrared-spectroscopy (AFM-IR)). Therefore, the time required to acquire such datasets increases proportionally with the number of points, making direct acquisition of the high-resolution spectral maps difficult. Potential sample drift and degradation, as well as drastically decreased throughput of such analysis, prompt a search for alternative approaches to spectral imaging which could reliably reconstruct full-resolution dataset using reduced number of measurements.
For example, AFM-IR facilitates nanometer resolution (down to 50 nm for contact mode17 and to 10 nm for tapping mode25) morphological, chemical, and mechanical analysis. Unlike Fourier-transform infrared spectroscopy where information from all wavelengths is collected simultaneously, AFM-IR can only measure the absorption at a given wavenumber—either as a part of a spectral sweep or during the scan. Therefore, reasonable AFM-IR acquisition times (within couple of hours) can only be obtained with a sparse spectral map (with respect to spatial and spectral dimensions) and/or an absorption map at a single given wavenumber.26,27 While both these types of AFM-IR analysis approaches provide spatially resolved chemical mapping, they still do not yield a full high-resolution dataset which would be useful for correlative and discovery based analysis. One approach to the merging of spectral data contained in different channels is the use of sharpening algorithms such as data fusion.28 Such algorithms establish the relationship between known signals in the images and use it to provide context-aware interpolation for the low-resolution image. This approach can be used in the case when the functional relationship between two images (e.g., how change of one parameter is related to the change of the second one) is not precisely know a priori and needs to be established during the analysis. However, data fusion of mass spectrometry data with microscopy data that has already been demonstrated28,29,30 is prone to the generation of reconstruction artifacts. Specifically, the image formation mechanism in a secondary electron or optical image is drastically different from chemically-sensitive spectroscopical channels, so the correlation established within data fusion process implies a relationship between two channels that are not physically linked together. As a result, this assumption may generate reconstruction artifacts leading to the misrepresentation of the system, for example, sharpening algorithms combining electron microscopy (EM) and secondary ion mass-spectrometry produce results that are strongly dependent on the brightness and contrast of the EM image.31 In addition, correlations in this data fusion algorithm are built by individual spectral lines and do not account for the fact that intensities of the lines in the spectrum are heavily constrained. Meanwhile, for the case of spectral datasets, this constraint is well-understood and can be used to generate high-resolution images with higher confidence in the final result using physically meaningful constraints. For example, if the available information channels generate partially overlapping subsets of a bigger dataset (i.e., impossible or impractical to measure), this fact should be actively used throughout the reconstruction of such dataset. To achieve this, a number of pan-sharpening algorithms have been developed for the processing of satellite images to restore color images based on grayscale maps32 and restore spectral datasets from multispectral maps.33 Here, the channels used for reconstruction are intrinsically linked via known greyscale-to-color transformation. Similarly, single-wavenumber AFM-IR image and a spectral map are both subsets of the same dataset acquired using the same physical principle and are directly related to each other.
In this paper, we apply a coupled non-negative matrix factorization (CNMF) pan-sharpening (PS) algorithm for AFM-IR data to enable rapid reconstruction of high spatial resolution hyperspectral chemical imaging data. We demonstrate the restoration of the full IR spectral dataset at the resolution of a standard AFM scan with the added possibility of extracting IR spectral signatures of individual components as well as their abundances across the sample. Thus, we propose a multicomponent analysis-based approach to AFM-IR enabled by PS. We describe in detail factors influencing its results and discuss the applicability of quality metrics for the evaluation of the fusion product. Furthermore, we highlight the practical application of our method for the analysis of plant cell walls, providing a correlation between mechanical properties and chemical composition at nanoscale. We believe this PS algorithms can be readily adopted in other areas of spectral chemical imaging34 such as time-of-flight secondary ion mass spectrometry ToF-SIMS,35 and AFM mass spectrometry (AFM-MS).36
Results and discussion
Algorithm description
PS is a family of algorithms that are widely used for image processing. Fundamentally, PS relies on the fact that there is a clear and well-defined relationship between information captured by two or more channels with different spatial resolutions. For example, traditional algorithms for PS combine low resolution RGB and high-resolution grayscale maps. In this case one can routinely find the grayscale value of a pixel based on the values of individual color channels. The resulting grayscale image, however, will contain less information thus rendering the reverse calculation not possible as multiple color images can collide into the same grayscale map (meaning, multiple color images can generate the same grayscale image). However, if it is known that certain pixel i on a grayscale image has certain RGB values (ri, gi, bi) and grayscale intensity (hi), it can be assumed that a neighboring pixel j with grayscale intensity (hj) close to (hi) has RGB values (rj, gj, bj) that are also close to (ri, gi, bi). This assumed continuity of the image is generally considered feasible as RGB values of a pixel on a map correspond to a specific object, landscape feature or a type of material which is similar within some local area. For example, if two pixels belonging to a roof on a satellite image are red, it is reasonable to assume that the rest of the roof is red as well.
Same basic considerations can be applied to a more general case of spectral PS. Here, each pixel in the image is characterized by a full spectral vector (x1, x2, …, xn)i. At the same time, this full spectrum can be unambiguously condensed into RGB values (ri, gi, bi) or a grayscale intensity (hi). Here, RGB images and a sparse spectral map are used to restore the full-resolution dataset where a distinct spectrum is assigned to each pixel. The prerequisites for the PS approach are essentially the same—some degree of feature continuity as well as functional dependence between spectral and single-frequency datasets. It is worth noticing that while traditionally RGB channels are used to build single-band maps (commonly referred to as multispectral), it is possible to generalize this approach and expand it for an arbitrary set of distinct maps as long as the mathematical method of their generation from the spectral dataset is known.
In the case of AFM-IR, the 3D IR spectral dataset with low-spatial resolution is formed by acquiring point spectra on a two-dimensional grid. AFM-IR images at a fixed wavenumber (FW) play the role of multispectral maps which will be used for the full dataset estimation. It is evident that there are multiple choices for the wavenumber selection. Figure 1 displays the overall idea of PS applied for AFM-IR. In this paper, we will refer to the original full resolution dataset \({\bf{X}} = [x_1, \ldots ,x_n] \in {\Bbb R}^{m\lambda \times n}\) with a total of n points and mλ spectral bands as ground truth while the result of PS algorithm will be PS hyperspectral dataset \(\tilde{\bf Y}_{\mathrm{H}}\). H and M subscripts are designated for hyperspectral (full resolution spectral map) and multispectral data (a group of FW images). Is this paper, \({\bf{Y}}_{\mathrm{H}} \in {\Bbb R}^{m\lambda \times m}\) denotes a hyperspectral dataset with low spatial resolution and a total of m points, and \({\bf{Y}}_{\mathrm{M}} \in {\Bbb R}^{n\lambda \times n}\) is a multispectral full resolution dataset with nλ bands (each of them is a FW image). There are multiple methods of restoration the \(\tilde{\bf Y}_{\mathrm{H}}\) including, but not limited to, component substitution (CS), multiresolution analysis (MRA), Bayesian methods, neural networks (NN), and matrix factorization. Coupled non-negative matrix factorization (CNMF) was chosen due to its relatively low computational costs (lower than Bayesian and NN approaches but higher than CS and MRA) and high quality of the factorization product as indicated by relevant metrics. Another reason for such choice was the incorporated analysis of the component distribution, which allows the use of the entire spectral range for calculating the abundance maps. Since the final goal of IR chemical imaging is to pinpoint the spatial localization of individual species with distinct spectral signatures rather than the investigation of isolated IR bands, this advantage will play a significant role in correlative comparison of registered images. This approach allows for the meaningful investigation of the interplay between chemical and physical properties measured by different methods, ultimately opening a pathway for a better understanding the composition-structure–property relationship at nanoscale.
It is important to highlight that PS-based approaches actively use the knowledge of how spectral imaging and FW maps are related. This acts as additional constraints on the algorithm output. This differentiates our method from the cases where the relationship between two channels is not known a priori and is being established during the analysis.28 Thus, we incorporate our expertize in the AFM-IR technique to generate results using physically meaningful limitations. This allows to view IR spectral and spatial modes of AFM-IR operation as complimentary parts of the dataset that can be directly accessed. Specifically, a single IR wavenumber map is a slice of a 3D data cube (two physical and one spectroscopic dimension) while a low-resolution IR spectral map is a down sampled subset of the 3D data cube by its physical dimensions.
The details of CNMF are reviewed by Loncan et al. 33 In brief, the assumptions behind this method are: (a) there is a distinct number of endmembers with unique spectral characteristics, (b) the spectral image in each point is a linear combination of endmember spectra (which may or may not be presented in pure form in the dataset). Both of these are reasonable for the case of AFM-IR where a given number of materials or regions (such as chemical interface) have intrinsic IR spectra with varying intensity across the image. Thus, one can represent X as:
where \({\bf{H}} \in {\Bbb R}^{m\lambda \times \rho }\) is a matrix representing spectra of ρ endmembers, and \({\bf{U}} \in {\Bbb R}^{\rho \times n}\) is the matrix containing the abundance maps of corresponding endmembers. For a low-resolution image, it can be stated that:
where UH is the abundance map matrix of the low-resolution image and HM is the endmember matrix for the FW maps. Generally, these can be calculated from U and H if the spectral responses are known, however, directly accessing these matrices is not required. CNMF performs spectral unmixing of YH and YM and then assuming that NMF components of both decompositions are related, it combines H estimated through the first decomposition and U estimated through the second decomposition. Here we start with NMF unmixing of YH by minimizing the Frobenius norm of the difference between YH and HUH using random initial guess and multiplicate update solver. This yields the spectra of the endmembers contained in H. The second decomposition is performed to calculate U. Here, UH is spatially upsampled using bilinear interpolation and then used as an initial guess for U. To generate the initial guess for HM, we sliced H selecting only those wavenumbers that correspond to FW high resolution maps. Finally, to restore \(\tilde{\bf Y}_{\mathrm{H}}\) we multiply H and U. As a result of this operation, high-resolution abundance maps of each components are produced.
Simulated dataset
To prove the feasibility of PS via coupled NMF decomposition, we applied it to four distinct datasets. First, we created a dataset that would simulate real AFM-IR spectral data. Three types of materials with distinct IR spectra (simulated as a series of Gaussian curves, Fig. S1a) are spatially separated on a map. In addition, random noise is added (Fig. S1b). A series of FW maps similar to the one displayed in Fig. S1c and spectral low resolution map (a section is shown on Fig. S1d) were used for the fusion. The results are showcased in Fig. 2.
Pan-sharpening applied to the simulated dataset using three NMF components at a downsampling rate of 16. The FW images at spectral point 180 are shown. The FW slice of spectral dataset used for the PS a and its interpolation into the original image size b are very poor representations of the actual distribution of the band across the sample. However, the pan-sharpened image c is very close to the ground truth d. The point spectra of the pan-sharpened dataset e, f are reasonably close to the ground truth, however, some distortions are evident. Notice that with small amounts of NMF components PS also performs denoising
It is evident that the CNMF algorithm, with three spectral components, performs well at restoring the dataset. A visual examination of the maps at specific wavenumbers generated from X and \(\tilde{\bf Y}_{\mathrm{H}}\) confirms the applicability of the PS algorithm for this type of data. Additionally, as CNMF operates by extracting individual components (Fig. S2), the random noise can be removed from the data (Fig. 2e, f). When the number of components increases past three, the effect of denoising is observed to a lesser degree. In order to quantitatively evaluate the quality of CNMF-based fusion, we used a number of metrics used in the pan-sharpening community. Specifically, we used three metrics: cross-correlation (CC), spectral angle mapper (SAM), and root-mean square error (RMSE). Geometric distortion of PS result at a given wavenumber can be calculated using cross-correlation between two images. The resulting number is a measure of how similar the ground truth and the PS result are at that wavenumber. To get the global quality metric, values of CC for different wavenumbers are averaged. To estimate the spectral distortion, a spectral shape preservation is calculated in each point. This is achieved by dividing an inner product of two spectra in a given pixel (one from the ground truth and one from the PS product) by l2 norms of those spectra. This value (spectral angle mapper) indicates the level of spectral distortion in a pixel. These pixelwise SAMs are averaged to generate an overall quality measure for a PS product. Finally, RMSE is used a third metric which is sensitive to all distortions in the data reconstruction. Overall, this set of measures allows to estimate both geometrical and spectral quality of the PS algorithm as CC describes the geometric distortion, SAM represents spectral distortion, and RMSE is a general measure of PS operation. The ideal values for CC is 1, while for SAM and RMSE the ideal value is 0 which would be attained if the PS achieved a perfect dataset restoration.
We have investigated the influence of the number of NMF components as well as the downsampling rate (defined here as downsampling by the same value for both axes, e.g., a 256 × 256 map turned into 16 × 16 would have a downsampling rate of 16) and the number of FW maps used for the restoration on all three metrics (Fig. S3). It is evident that when the number of NMF component falls below the number of distinctive spectral signatures (in this case 3), the quality of restoration is poor for all of the metrics used. At the same time, even when downsampling reaches 16 (meaning that the spectral map used for the reconstruction was only 16 × 16 pixels), the metrics are barely affected. Finally, increase of the number of FW maps used did improve the results of fusion. In the simulated dataset there are 7 characteristic IR absorption peaks. While the selection of the maps does matter, it is clear that a more diverse FW input leads to a higher quality PS result. When the number of FW maps falls below 5, the results are no longer accurate. This study highlights main rules for the CNMS-based PS: (1) number of NMF components should be at least equal to the number of distinctively dissimilar spectral signatures, (2) FW maps should be acquired for more than half of the relevant peaks, and (3) the downsampling rate can be increased significantly to speed up the measurement.
One may notice that even under the best conditions for the PS algorithm, the quality metrics are far from ideal reaching only CC = 0.6 and SAM = 0.4. This is an unexpected effect of the random noise found in the dataset. When investigated closely (Fig. S4), it is clear that CNMF performs well for both noisy and clean datasets; however, the presence of random variations strongly affects metrics. CC and SAM are influenced the most while RMSE, as a metric, is more robust to noise. This is an important finding as it highlights the limited applicability of the traditional metrics used to evaluate the products of PS fusion for the case of a random noise in the dataset. Indeed, when the noise is removed, all three measures show much better results (Fig. S5).
As first part of the CNMF algorithm is the endmember extraction, it is important to ensure that the sampling for the IR spectral mapping is representative. If there is a small object with unique spectra which did not make it to the IR spectral map, indeed, the PS product will not be representative. However, if the endmembers captured during the low spatial resolution scan are sufficient (meaning, any point spectrum in the dataset can be represented as a linear combination of these endmembers), then the feature of interest will be observed. For example, Fig. 2a displays a slice of a very coarse spectral map. On this map the pattern is heavily distorted. However, as we use high-spatial channel to get the geometric information, we can effectively restore even smallest features.
Experimental AFM-IR dataset
To confirm the assessment of CNMF-PS algorithm for AFM-IR, we acquired a high-resolution spectral map so the ground truth X is known. At this stage we have used a test sample provided by Bruker Nano which is a microtomed slide of poly(methyl methacrylate) (PMMA) and polystyrene embedded in epoxy matrix. The polystyrene and epoxy used for the preparation of a test sample have almost indistinguishable spectra because of the IR laser range, so NMF analysis uses only two components here (PMMA and epoxy/polystyrene). Figure 3 displays the NMF abundance maps after the low-resolution spectral image was decomposed (a). After interpolation, abundance maps obtain high spatial resolution (b), however, these maps do not contain new context-aware information. After a second round of NMF which uses FW images, the abundance maps converge to a detailed image (c, d). As a result, the restored maps restore \(\tilde{\bf Y}_{\mathrm{H}}\) with high visual quality as evident from Fig. 3 (c–f) and Figure S6. Standard metrics of the PS fusion product evaluation also suggest that the algorithm is effective (Fig. S7). For the analysis of the experimental data, we have also added an additional step of spectra normalization that adjusts mean and standard deviation of FW images and the spectral map to match.
Pan-sharpening applied to AFM-IR dataset with a known ground truth: spectral 12 × 16 image and 3 FW maps (1604, 1730, and 1800 cm−1) were used to reconstruct the spectral 46 × 64 image with 2 NMF components. Low resolution map a cannot be efficiently interpolated as shown in b, however, a product of pan-sharpening is very close to the ground truth both in terms of information about chemical distributions shown in c, d and point spectra shown in e, f
To further illustrate the applicability of CNMF-PS, we have performed a reconstruction of a full resolution dataset using FW maps at 1041, 1153, 1605, and 1733 cm−1 and a 16 × 16 spectral map. The resulting restored dataset contains maps of IR absorption at every wavenumber available with 256 × 256 resolution. Figure 4 display the comparison of the IR maps in the X and \(\tilde{\bf Y}_{\mathrm{H}}\). Maps used in the process of the fusion (1041 and 1733 cm−1) as well as IR maps measured as control ones (such as 1363 cm−1) highlight the efficiency of the approach used here to acquire multidimension datasets (see Fig. S8 for NMF abundance maps).
Pan-sharpening applied to AFM-IR dataset: spectral 16 × 16 image and 4 FW maps (1041, 1153, 1605, and 1733 cm−1) were used to reconstruct the spectral 256 × 256 image with 2 NMF components. It is clear that PS restores dataset well after the histogram adjustment. Initial low resolution of spectral maps a cannot be efficiently interpolated b, however, pan-sharpened image allows to gather detailed information about chemical distributions c and point spectra d, e
In order to capture the high-resolution spectral map of a similar quality it would take 16 × 16 = 256 times longer, which is substantial considering that acquiring a single spectrum takes about 30 s. Reconstructing from smaller maps allows reducing acquisition time and mitigating potential sample degradation and drift.
Correlative analysis of chemical and mechanical properties using CNMF-PS
To further demonstrate practical applications of CNMF-PS algorithm, we have used it for the analysis of plant cell walls. The primary plant cell wall is a composite material composed of reinforcing cellulose microfibrils embedded in a mixture of other cell wall polymers, such as pectins, xyloglucans, and other non-cellulosic polysaccharides.37,38 There is spatial and physiochemical heterogeneity in the composition and organization of polymers in the plant cell wall that is impossible to replicate in a synthetic composite material.39,40 This heterogeneity in the cell wall correlates with different mechanical properties across the cell, and this has bearing on whole-plant growth, cell morphogenesis, and development of tissues.41,42 The intrinsic complexity of the cell wall confers a plant cell the ability to provide mechanical support and strength, yet also allow for growth and flexibility in challenging environmental conditions. Advancing our understanding of the composition and organization of polymers in the plant cell wall has practical applications in biofuel energy initiatives. For instance, it may enable alterations of the cell wall chemical composition to modify wood properties and improve processes designed for biomass delignification.43 Improved understanding of structure–property relationships that define the plant cell wall requires obtaining nanometer resolution of topological, chemical, and mechanical properties. In this work, we have prepared Arabidopsis thaliana plant stem for analysis with AFM-IR to obtain a correlated chemical and mechanical signature of the cell wall. This will provide insight as to how the chemical complexity and spatial variation within the cell wall contributes to its mechanical properties, such as adhesion, plasticity, and elasticity.
CNMF-based PS was applied for an AFM-IR dataset acquired from plant cell wall placed on a Si substrate. A sparse spectral map with 256 points (16 × 16 grid) was fused with 8 FW maps acquired at 1071, 1131, 1319, 1403, 1533, 1591, 1653, 1740 cm−1. It was found that there are two distinct spectral signatures which were identified during NMF decomposition of the spectral dataset (Fig. 5a). Strong peaks were observed in the endmember spectra of component 1 at 1591–1653 cm−1 likely corresponding to an Amide I band and component 2 at 1131 cm−1 likely corresponding to ether bond stretching. Based on these strong peak observations, component 1 was assigned as plant protein and component 2 as cell wall polysaccharides. Alonso-Simón et al. compiled a summary of wavenumbers obtained by Fourier transform infrared (FTIR) spectroscopy of cell walls and report that FTIR adsorption bands at 1120, 1140, and 1160 cm−1 correspond to xyloglucan, pectin, and cellulose, respectively.44 The abundance maps corresponding to these NMF spectral components are presented in Fig. 5b, c, which allows us to determine the distribution of the materials in the sample with respect to all peaks rather than by only one or two characteristic frequencies. Such an approach is more quantitative as it allows for efficient unmixing of overlapping IR signatures. In addition, it scales well with increasing number of the components. This is a very useful property of the CNMF-PS which makes the comparative analysis of complementary data well-grounded.
Pan-sharpening for data fusion: the restored IR dataset from a biological object was separated into two components a and correlated with the contact resonance b. The abundance maps of the components c, d shows the primary localization of corresponding chemicals. Cross-correlation clearly indicates that component 1 is soft as increasing of this component loading leads to decrease in sample stiffness shown in e, g while component 2 has the opposite effect shown in f, h. Spearman coefficient between IR component loadings and resonance shift were −0.28 and 0.28, correspondingly. Length of the scale bar on all plots is 1 μm
We collected a map of mechanical contact resonance over the sample. While the resonant frequency is heavily determined by the cantilever itself, the local properties of the surface which the tip is in contact with can shift the frequency up (for stiffer samples) or down (for less rigid ones). This is reflected on Fig. 5b: the mechanical properties are not uniform across the sample. Visual comparison between Fig. 5c, d and Fig. 5b suggests that higher polysaccharide content in a given pixel increases contact resonance frequency while protein plays the opposite role, which is in good agreement from the known properties. While cell wall polysaccharides can have Young’s moduli in the range of 2–140 GPa,45,46 proteins show stiffness in the ranges 0.03–0.3 MPa.47 We have calculated a Spearman correlation which describes the correlated monotonicity of two datasets and does not imply the normal distribution of the values being compared. If a relationship between two datasets can be perfectly described as a monotonic function, Spearman’s rank is equal to +1 or −1 depending on whether or not this monotonic function increases or decreases. This measure is convenient for the case of correlating dissimilar datasets as it does not require this relationship to be linear or even known in a closed form. As long as the relationship between physical and chemical parameters is monotonic, Spearman’s rank would be suitable for highlighting it. Indeed, Spearman’s rank for Fig. 5c and b (protein content and mechanical contact resonance) is −0.302 and for Fig. 5d and b (cell wall content and mechanical contact resonance) is +0.283 with p values being 0.0. To characterize the local similarity and highlight the regions with strongest correlation, we calculated cross-correlation within corresponding 4 × 4 kernels situated on respective images (Fig. 5e, f). Plotting these values against the IR component intensity confirms the visual assessment and the results of Spearman’s rank calculation.
The presence of a certain type of material with a distinct IR signature affects the local stiffness. Hence, in the areas where the abundance of a given component is high, we might expect strong correlation (or anticorrelation) with the resonance shift. In the areas where this component is absent the value of cross-correlation is expected to be close to zero as observed variations of the local stiffness are unrelated to the presence of a specific material. Indeed, below noise floor the IR signals and peak shift are not correlated (below white dashed line), however, if IR signal is strong enough (to the right of the white dashed line), the correlation becomes apparent. See more details in Supplementary Fig. S9. Overall, the increasing presence of component 1 leads to gradually decreasing contact resonance while component 2, on the contrary, positively contributes to the local stiffness. CNMF-PS procedure not only allows the restoration of large multidimensional datasets but also paves the way for discovery based correlative analysis where the relationship between chemical and functional responses is not known a-prior (such as comparison of local mechanical properties with the distribution of specific components).
In this paper we have demonstrated the applicability of PS algorithm to restore full spectral and full spatial resolution AFM-IR dataset. This method drastically decreases time required to acquire spectral images while simultaneously providing multicomponent analysis capability. We discuss the influence of the parameter affecting the result such as downsampling rate, number of components used for decomposition as well as number of fixed wavenumber maps involved in dataset restoration. Finally, we showcase the application of PS CNMF algorithm for the correlative analysis of plant cell walls in identifying the relationship between local mechanical properties and chemical composition. Such approaches can be readily adopted for other spectral imaging techniques utilized in chemical imaging of complex materials.
Methods
AMF-IR
All experimental AFM-IR datasets were acquired using Anasys NanoIR2-s instrument with spectral ranges 917–1173, 1311–1409, and 1505–1867 cm−1 Commercially available NanoIR probes for contact mode with force constants 0.07 N/m were used.
Plant sample preparation
Arabidopsis thaliana Columbia-0 plants were grown on soil in a growth chamber at 24 °C at a 16h/8 h light/dark photoperiod (long-day) condition. The top-most internode of four-week-old plant stems were hand sectioned using a razor blade, without being embedded. The resulting section was spread and compressed onto a SiO2/Si+ wafer substrate to obtain a sample for analysis.
Data analysis
Data processing was done using Python 3.6 using scikit-learn 0.19.2 library. All calculations were performed on a desktop computer with Intel Xeon CPU E-5–1650 v3 3.50 GHz processor and 40 GB of RAM were used to perform the computations.
Data availability
Scanning probe microscopy data used for the analysis is available from the authors upon request.
Code availability
Python scripts used for the analysis are available from the authors upon request.
References
Cui, Z. et al. Radiation-induced reduction–polymerization route for the synthesis of PEDOT conducting polymers. Radiat. Phys. Chem. 119, 157–166 (2016).
Floresyona, D. et al. Highly active poly(3-hexylthiophene) nanostructures for photocatalysis under solar light. Appl. Catal. B 209, 23–32 (2017).
Mikhalchan, A. et al. Revealing chemical heterogeneity of CNT fiber nanocomposites via nanoscale chemical imaging. Chem. Mater. 30, 1856–1864 (2018).
Brown, P. S. & Bhushan, B. Durable, superoleophobic polymer-nanoparticle composite surfaces with re-entrant geometry via solvent-induced phase transformation. Sci. Rep. 6, 21048 (2016).
Clede, S. et al. Detection of an estrogen derivative in two breast cancer cell lines using a single core multimodal probe for imaging (SCoMPI) imaged by a panel of luminescent and vibrational techniques. Analyst 138, 5627–5638 (2013).
Kochan, K., Peng, H., Wood, B. R. & Haritos, V. S. Single cell assessment of yeast metabolic engineering for enhanced lipid production using Raman and AFM-IR imaging. Biotechnol. Biofuels 11, 106 (2018).
Pancani, E. et al. High-resolution label-free detection of biocompatible polymeric nanoparticles in cells. Part. Part. Syst. Charact. 35, 1700457 (2018).
Gourion-Arsiquaud, S., Marcott, C., Hu, Q. C. & Boskey, A. L. Studying variations in bone composition at nano-scale resolution: a preliminary report. Calcif. Tissue Int. 95, 413–418 (2014).
Belianinov, A. et al. Big data and deep data in scanning and electron microscopies: deriving functionality from multidimensional data sets. Adv. Struct. Chem. Imaging 1, 6 (2015).
Somnath, S. et al. Ultrafast current imaging by Bayesian inversion. Nat. Commun. 9, 513 (2018).
Kannan, R. et al. Deep data analysis via physically constrained linear unmixing: universal framework, domain examples, and a community-wide platform. Adv. Struct. Chem. Imaging 4, 6 (2018).
Nikiforov, M. P. et al. Functional recognition imaging using artificial neural networks: applications to rapid cellular identification via broadband electromechanical response. Nanotechnology 20, 405708 (2009).
Kumar, A. et al. Spatially resolved mapping of disorder type and distribution in random systems using artificial neural network recognition. Phys. Rev. B 84, 024203 (2011).
Belianinov, A., Kalinin, S. V. & Jesse, S. Complete information acquisition in dynamic force microscopy. Nat. Commun. 6, 6550 (2015).
Jesse, S. & Kalinin, S. V. Principal component and spatial correlation analysis of spectroscopic-imaging data in scanning probe microscopy. Nanotechnology 20, 085714 (2009).
Ovchinnikova, O. S. et al. Co-registered topographical, band excitation nanomechanical, and mass spectral imaging using a combined atomic force microscopy/mass spectrometry platform. ACS Nano 9, 4260–9 (2015).
Dazzi, A. et al. AFM-IR: combining atomic force microscopy and infrared spectroscopy for nanoscale chemical characterization. Appl. Spectrosc. 66, 1365–84 (2012).
Gruverman, A., Auciello, O. & Tokumoto, H. Imaging and control of domain structures in ferroelectric thin films via scanning force microscopy. Annu. Rev. Mater. Sci. 28, 101–123 (1998).
Kalinin, S. V. & Bonnell, D. A. Imaging mechanism of piezoresponse force microscopy of ferroelectric surfaces. Phys. Rev. B 65, 11 (2002).
Thompson, G. L. et al. Electromechanical and elastic probing of bacteria in a cell culture medium. Nanotechnology 23, 245705 (2012).
Li, J. Y. et al. Strain-based scanning probe microscopies for functional materials, biological structures, and electrochemical systems. J. Materiomics 1, 3–21 (2015).
Collins, L. et al. Breaking the time barrier in Kelvin probe force microscopy: fast free force reconstruction using the G-mode platform. ACS Nano 11, 8717–8729 (2017).
Collins, L. et al. Multifrequency spectrum analysis using fully digital G Mode-Kelvin probe force microscopy. Nanotechnology 27, 105706 (2016).
Somnath, S., Belianinov, A., Kalinin, S. V. & Jesse, S. Full information acquisition in piezoresponse force microscopy. Appl. Phys. Lett. 107, 263102 (2015).
Anasys Instruments Corporation. Tapping AFM-IR: Highest performance nanoIR chemical imaging to 10nm resolution. Application note, https://www.anasysinstruments.com/wp-content/uploads/Tapping-AFM-IR.pdf (2016).
Dazzi, A. & Prater, C. B. AFM-IR: technology and applications in nanoscale infrared spectroscopy and Chemical imaging. Chem. Rev. 117, 5146–5173 (2016).
Morsch, S., Liu, Y., Lyon, S. B. & Gibbon, S. R. Insights into epoxy network nanostructural heterogeneity using AFM-IR. ACS Appl. Mater. Interfaces 8, 959–66 (2016).
Van de Plas, R., Yang, J., Spraggins, J. & Caprioli, R. M. Image fusion of mass spectrometry and microscopy: a multimodality paradigm for molecular tissue mapping. Nat. Methods 12, 366–72 (2015).
Tarolli, J. G., Bloom, A. & Winograd, N. Multimodal image fusion with SIMS: preprocessing with image registration. Biointerphases 11, 02A311 (2016).
Sobol, O. et al. First use of data fusion and multivariate analysis of ToF-SIMS and SEM image data for studying deuterium-assisted degradation processes in duplex steels. Surf. Interface Anal. 48, 474–478 (2016).
Vollnhals, F. et al. Correlative microscopy combining secondary ion mass spectrometry and electron microscopy: comparison of intensity-hue-saturation and Laplacian pyramid methods for image fusion. Anal. Chem. 89, 10702–10710 (2017).
Vivone, G. et al. A critical comparison among pansharpening algorithms. IEEE Trans. Geosci. Remote Sens. 53, 2565–2586 (2015).
Loncan, L. et al. Hyperspectral pansharpening: a review. IEEE Geosci. Remote Sens. Mag. 3, 27–46 (2015).
Belianinov, A. et al. Correlated materials characterization via multimodal chemical and functional imaging. ACS Nano 12, 11798–11818 (2018).
Ievlev, A. V. et al. Automated interpretation and extraction of topographic Information from time of flight secondary ion mass spectrometry data. Sci. Rep. 7, 17099 (2017).
Somnath, S. et al. Improved spatial resolution for spot sampling in thermal desorption atomic force microscopy—mass spectrometry via rapid heating functions. Nanoscale 9, 5708–5717 (2017).
Cosgrove, D. J. Growth of the plant cell wall. Nat. Rev. Mol. Cell Biol. 6, 850–61 (2005).
Somerville, C. et al. Toward a systems approach to understanding plant cell walls. Science 306, 2206–11 (2004).
Burton, R. A., Gidley, M. J. & Fincher, G. B. Heterogeneity in the chemistry, structure and function of plant cell walls. Nat. Chem. Biol. 6, 724–32 (2010).
Jochi, Y. et al. Spontaneous synthesis of a homogeneous thermoresponsive polymer network composed of polymers with a narrow molecular weight distribution. NPG Asia Mater. 10, 840–848 (2018).
Cosgrove, D. J. Nanoscale structure, mechanics and growth of epidermal cell walls. Curr. Opin. Plant Biol. 46, 77–86 (2018).
Gindl, W. et al. Mechanical properties of spruce wood cell walls by nanoindentation. Appl. Phys. A 79, 2069–2073 (2004).
Tetard, L. et al. Development of new methods in scanning probe microscopy for lignocellulosic biomass characterization. Ind. Biotechnol. 8, 245–249 (2012).
Alonso-Simon, A. et al. The use of FTIR spectroscopy to monitor modifications in plant cell wall architecture caused by cellulose biosynthesis inhibitors. Plant Signal Behav. 6, 1104–10 (2011).
Chanliaud, E., Burrows, K. M., Jeronimidis, G. & Gidley, M. J. Mechanical properties of primary plant cell wall analogues. Planta 215, 989–96 (2002).
Gibson, L. J. The hierarchical structure and mechanics of plant materials. J. R. Soc. Interface 9, 2749–66 (2012).
Mauri, A. N. & Añón, M. C. Mechanical and physical properties of soy protein films with pH-modified microstructures. Food Sci. Technol. Int. 14, 119–125 (2008).
Acknowledgements
AFM-IR measurements were conducted at the Center for Nanophase Materials Sciences, which is a US DOE Office of Science User Facility supported under Contract DE-AC05-00OR22725, (N.B., A.V.I., A.B., S.V.K., O.S.O). Algorithm development was part of the AI Initiative, sponsored by the Laboratory Directed Research and Development Program of Oak Ridge National Laboratory (S.J., R.K.V), managed by UT-Battelle, LLC, for the U.S. Department of Energy (DOE). The plant sciences portion of this work was supported by the Center for Engineering MechanoBiology (CEMB), an NSF Science and Technology Center, under grant agreement CMMI: 15–48571 (N.B. and M.F.).
Author information
Authors and Affiliations
Contributions
N.B. carried out acquisition of AFM-IR datasets and developed Python code. M.F. and N.B. provided samples and participated in discussion and interpretation of results. O.S.O. and S.V.K. had proposed usage of pan-sharpening for the multimodal imaging and supervised the project. S.J., A.V.I., A.B. and R.K.V. contributed to the discussion regarding the pan-sharpening algorithm.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Borodinov, N., Bilkey, N., Foston, M. et al. Application of pan-sharpening algorithm for correlative multimodal imaging using AFM-IR. npj Comput Mater 5, 49 (2019). https://doi.org/10.1038/s41524-019-0186-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-019-0186-z







