Abstract
Recent experimental works suggested that the confinement into a cylindrical nanopore induced the microphase separation of a binary liquid, despite the miscible character of its bulk counterpart. A core–shell organization was evidenced such that one of the liquids was strongly anchored to the solid surface whereas the other was confined at the center of the pore. At the same time, a study based on atomistic simulations suggested a strong heterogeneity and the absence of a separation. In this work, by refining the solid–liquid interactions to qualitatively reproduce the experimental adsorption isotherms of both single liquids, the microphase separation and the core–shell structure are captured. By tuning the surface chemistry of the nanopore to mimic hydrophilic and hydrophobic confinement, we show that it is possible to control the structural characteristics of the core–shell structure.The molecular origin of the microphase separation is then ascribed to the strong hydrogen bonds and a commensurate arrangement between the confining material and both liquids.
Similar content being viewed by others
Introduction
For three decades confinement effects at the nanoscale on the physics of fluids have been been intensively studied.1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 Many new properties have been then discovered such as the giant diffusion of liquids,16,17,18 the apparition of new phases and new transitions,19,20,21,22 giant dielectric properties,11,12,23,24,25 the increase of optical properties,26 and the possible mixing of non-miscible mixtures.27 These observations indicated that the classical understanding of the physics of liquids should be revisited in confined geometry. Whereas these effects have been largely investigated in the case of confined single components1,2,3,4,5,6,7,8,9,10,11,12,13,14 and immiscible binary mixtures,28,29,30 less works have been devoted to the confinement of miscible liquid mixtures.15,31,32,33 Recently, Muthulakshmi et al.34 reported an experimental evidence of a partial phase separation of an ethanol–water mixture confined in mesoporous silica using positron annihilation lifetime spectroscopy. They showed that a small fraction of the ethanol molecules seemed to be anchored at the silica surface.34 A similar result was also established by Guo et al.14 who have studied confinement of the ethanol–water mixture between two planar silica walls. A partial and local separation between water and ethanol close to the silica surface was thus evidenced.14 At the same time, Schmitz et al.35 have exhibited that the glycol–water mixture could undergo an interfacial separation. This phenomenon was also numerically observed by You et al.36 who exhibited a local demixing of binary hard-core Yukawa mixtures in a slitlike pore. More recently, Krycka et al.32 displayed a separation between two confined apolar liquids. At same time, Harrach et al.33 have studied the phase behavior of a mixture of isobutyric acid (iBA) and water confined in mesoporous SBA-15 silica material and have shown that the iBA-rich phase is close to the pore wall and the water-rich phase is in the center of the pores. Whereas these works only suggest a partial separation of two hydrogen bonds forming liquids or two apolar liquids near the solid surface, Morineau and co-workers15 have recently provided a direct experimental structural evidence of the microphase separation of macroscopically miscible liquids consisting of hydrogen bonds forming liquid and an apolar one. Indeed, the structure of a mixture comprising toluene (TOL) and tert-butanol (TBA) molecules confined in a cylindrical silica nanopore (MCM-41) of radius 24 Å was explored by neutron scattering and compared with the miscible bulk one.15 Using a core–shell (CS) model, the authors established, for the first time, a molecular-scale phase-separated tubular structure with the TBA molecules forming a layer at the pore surface (shell), surrounding a TOL-rich phase at the center of the pore (core). This observation was later extended down to low temperature in the glassy states and to the larger pores sizes of SBA-15.37,38 A consistent picture, showing the highly selective segregation of polar molecules at the pore surface, was deduced from binary gas adsorption experiments.31
Although these experiments revealed the presence of a microphase separation, the local organization and microscopic processes controlling the CS structure has to be clarified. In a recent numerical work, Essafri et al.39 showed that the nano-confinement of TBA/TOL mixture in a silica nanopore only induced strong heterogeneity. This result highlights then a scenario based on the local segregation rather than a core–shell organization of the confined TBA/TOL mixture. As suggested by the authors, the difference between experiment and simulation would be probably due to the hydrophilic character of the membrane that differs between both experimental and numerical studies. Therefore, the core–shell microphase separation of confined mixtures, which was experimentally evidenced by different studies, emerged as an open and challenging question for numerical methods. The current study paves the way to a thorough understanding of the phenomenon from carefully designed simulations.15,31,37,38
Using atomistic simulations, we aim to capture the CS structure and to clarify the microscopic driving force ruling it. To do so, the solid–liquid interactions were refined to qualitatively reproduce the experimental adsorption isotherm of pure TBA and TOL components confined through the silica nanopore.31 An illustration of three TBA, TOL, and silica framework is provided in Fig. 1a. This refinement allowed us to yield new insights into the molecular understanding of microphase separation. Moreover, by tuning the surface chemistry of the nanopore to mimic hydrophilic and hydrophobic porous materials, we investigated the role of the surface chemistry on the demixing.
a Illustration of tert-butanol (TBA) and toluene (TOL) molecules and silica nanoporous material with a diameter of 24 Å where yellow, red, white, and cyan colors correspond to the silicon, oxygen, hydrogen, and carbon atoms, respectively. b Density profiles of the center of mass of pure TBA and TOL confined into the nanoporous silica material obtained at 308 K and 1 bar
Results
Force field refinement
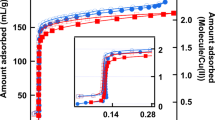
To be in line with experiment, the confining medium corresponds to a cylindrical silica nanopore of radius of 24 Å. The models and the computational procedure are given in the Methods section. Adsorption isotherms were modeled using Monte Carlo simulation in the grand canonical statistical ensemble (GCMC). Liquid–liquid and liquid–solid interactions (Utot) were taken into account by considering the electrostatic (Uelec) and the van der Waals interactions from the Lennard-Jones (LJ) model (ULJ) such that \(U_{{\mathrm{tot}}} = U_{{\mathrm{elec}}} + U_{{\mathrm{LJ}}} = \mathop {\sum}\nolimits_i^{N - 1} \mathop {\sum}\nolimits_{j \ne i + 1}^N q_iq_j/4\pi \varepsilon _0r_{ij} + 4\varepsilon _{ij}\left[ {\left( {\sigma _{ij}/r_{ij}} \right)^{12} - \left( {\sigma _{ij}/r_{ij}} \right)^6} \right],\) where qi is the partial charge of i atom, N the number of particles, rij the distance between i and j atoms, εij the depth of the potential well between i and j, and σij refers to the Van der Waals radius. To reproduce the adsorption isotherms of the pure components the solid–liquid interactions were refined. The OPLS (Optimized Potentials for Liquid Simulations) force field was used to model the TOL and TBA molecules. Indeed, it was shown that the thermodynamic properties of TBA/TOL mixtures were closely reproduced from the OPLS model.39 Whereas the intramolecular contributions (bonds, bending, and dihedral angles) were conserved as original, the partial charges were calculated using ab-initio calculations. Silica material was modeled by considering the ClayFF force field.40 All details are provided in the Methods section. To refine the LJ parameters ruling the solid–liquid interactions, we began to predict the adsorption isotherm by considering the initial force fields. Concerning the TBA adsorption through nanoporous silica, Fig. 2 shows a qualitative agreement between simulation and experiment that highlights the quality of ClayFF and OPLS force fields and their combining using the Lorentz-Berthelot mixing rules (\(\varepsilon _{ij} = \sqrt {\varepsilon _{ii}\varepsilon _{jj}}\) and σij = (σii + σjj)/2). As shown in Fig. 2 the predicted adsorption isotherm of toluene strongly differs with experiment. To improve the silica–TOL interactions we adapted the procedure discussed in ref. 41 initially developed to derive the coarse-grained parameters from atomistic simulations. The LJ parameters have been optimized by minimizing the value of the function \(F = \frac{1}{n}\mathop {\sum}\limits_{i = 1}^n {\frac{{f_i^{sim} - f_i^{exp}}}{{s_i^2}}}\) according to a procedure detailed in ref. 41. In this relation, si is the estimated statistical uncertainty, \(f_i^{sim}\) and \(f_i^{exp}\) are the values of the ith properties on n. In this work n = 2 and corresponds to the enthalpy of adsorption and adsorbed amount at low partial pressure. The minimum condition of F is that every partial derivative must be zero.41 Optimized LJ parameters are provided in Table 1. Figure 2 shows that the predicted adsorption isotherms are in fair agreement with those obtained from experiments.31 Interestingly, Fig. 2 exhibits that the capillary condensation pressure is qualitatively reproduced for both TOL and TBA components. These results allowed us to be confident in these refined interactions.
Molecular dynamics
From GCMC simulation the numbers of TOL and TBA molecules were calculated for 7 compositions (xTBA = 0, 0.24, 0.49, 0.51, 0.71, 0.83, and 1.0). Molecular dynamics (MD) simulations were subsequently carried out. As shown in Fig. 1b, for both pure components, a layering structure was observed due to the confinement effect at the nanometric scale.5 Whereas three layers are observed for both cases, the interfacial TBA layer seems closer to the silica surface, suggesting that the attractive interactions between the silica nanopore and TBA molecules are stronger. As shown in Fig. 3, the hydroxide groups (OH) of the TBA molecules point towards the silica surface. The driving force of this interfacial anchoring is probably the result of the strong hydrogen bonding (HB) network between porous silica and TBA molecules. This point will be discussed later. Interestingly, as shown in Fig. 3, this HB anchoring leads to a peculiar organization such that hydrophobic and hydrophilic (HB) domains are disposed in alternating succession. These results should probably impact the molecular structure of confined mixture. The density profile of the SiOH groups is also reported in Fig. 3. As shown in Fig. 3, the SiOH profile begins from 11.5 Å and presents a peak around 14 Å, highlighting the roughness of the surface. Calculation of the accessible volume by probing the porous volume by an atom of Argon allowed us to approximatively evaluate the pore radius at 12 Å.
From xTBA = 0.24 to 0.83, Fig. 4 (from Fig. 4a–d) shows that TBA molecules were adsorbed close to the interface constituting a first layer, whereas the toluene molecules are located right after. For xTBA = 0.83, the second and third layers correspond to a homogeneous mixture phase reminiscent of the bulk medium. Very interestingly, Fig. 4 highlights the progressive development of two phases as the TBA concentration decreases. Indeed, for xTBA = 0.71, the TBA molecules are almost only located close to the silica surface in the first adsorbed layer without TOL molecules. For xTBA = 0.49 that corresponds to the concentration where the core–shell organization was observed experimentally, the microphase separation is nearly complete. Interestingly, the distance between peaks of TOL and TBA seems to decrease as a function of the decrease in molar fraction in TBA. Indeed, whereas in Fig. 4a, b the distance between the interfacial TOL and TBA density (dTBA−TOL) is ~4 Å, the distance is greatly reduced to just ~1 Å for xTBA = 0.49 and xTBA = 0.24. The difference in the dTBA−TOL as a function of the TBA molar fraction is due to the progressive increase in TOL. Indeed, for the TBA fraction lower than 0.5 corresponding to an unsaturated solid interface in TBA molecules, the SiOH surface can then adsorb the TOL molecules. The progressive adsorption in TOL molecules at the silica surface is then at the origin of the decrease of dTBA−TOL with the increase in TOL fraction and then is at the origin of the interpenetration of TOL molecules. That can be observed from the atomic density in Fig. 5 where this progressive interpenetration as a function of xMeOH is well evidenced. Indeed, from Fig. 5a (xTBA = 0.24) to Fig. 5d (xTBA = 0.83), the decrease in dTBA−TOL and the increase in the interpenetration region (dashed circles in Fig. 5) are well established.
Profiles of radial density of the center of mass of tert-butanol (TBA) and toluene (TOL) molecules for xTBA = 0.83 (a), 0.71 (b), 0.49 (c), and 0.24 (d). The insets illustrate the core–shell organization, the TBA (red color) close to the surface and the TBA/TOL (TOL is blue colored) mixture at the center of pore; from 0.83 to 0.24 the width of the interfacial layer decreases, whereas the concentration in TBA decreases at the center of pore
We report in Fig. 6a, b the two-dimensional densities according to x and y directions for xTBA = 0.71, for TBA and TOL. As shown in Fig. 6, the demixing follows the cylindrical symmetry and a core–shell organization is highlighted with the TBA close to the interface (shell) and TOL at the center of the nanopore (core) that is in good agreement with the experiment.15 To ensure the microphase separation from a thermodynamics point of view we computed the local surface tension (γ(r))42 along the radial distance. Local surface tension expresses the surface tension through the radial r-dependent local components of the pressure tensor. Local surface tension is a local interfacial property related to the difference between the normal (Pn) and tangential (Pt) pressure components such that γ(r) = Pn(r) − Pt(r) with \(\gamma = {\int} \gamma (r)dr = {\int} {P_n} (r) - P_t(r)dr\). The mechanical equilibrium involves that the normal pressure has to be constant even through the interface, whereas the tangential component is similar than the normal one in bulk phase and presents a negative peak at the interface highlighting a region under tension. Therefore, the difference Pn(r) − Pt(r) is null in bulk phase and presents a positive peak at the interface. Even if its definition is arbitrary (how the energy between a pairwise interaction is distributed between both particles), its calculation allows us to highlight the presence of an interface. Calculation of γ(r) is detailed in the Methods section. As shown in Fig. 6c, the local surface tension presents two peaks. Actually, a peak in surface tension exhibits an interface under tension and corresponds to an interface between two phases. From 0 to 8 Å no tension is observed and the local surface tension is close to 0 mN m−1 as expected for a homogeneous liquid phase. Figure 6c emphasizes then that two interfaces identified by the first peak in γ(r) located at 10.5 Å corresponds to the tension radius of surface of tension connected to the TBA–TOL liquid–liquid interface, and the another at 11.5 Å related to the liquid–solid interface.
Figure 7a reports the profiles of the surface tension and the density of TBA, TOL, and the atoms of silica material. As shown in Fig. 7a, both peaks of tension are located close to the liquid–liquid and liquid–solid Gibbs dividing surfaces. The Gibbs model for the boundary between two phases consists of considering the finite interfacial region as a dividing surface which acts as a third phase of zero volume in which some magnitudes of physical properties such as density change abruptly. Local surface tension and density profile calculations then unambiguously highlight the phase separation of two confined TBA and TOL liquids at the nanoscale. The formation of a first TBA layer anchored at the silica surface is induced by the strong hydrogen bonds between the silanol groups SiOH of the silica material and the OH groups of the TBA molecules. Indeed, hydrogen bond numbers were computed by considering a geometrical criterium based on the quantum consideration43 where two molecules are chosen as being hydrogen bonded only if their inter-oxygen distance is less than 3.5 Å, and simultaneously the oxygen–hydrogen is less than 2.5 Å. The profile of the hydrogen bond number (nHB) per molecule was then reported in Fig. 7b for xTBA = 0.24. As shown in Fig. 7b, a peak of nHB was observed close to the silica surface beyond the bulk value. As observed in Fig. 7b, this peak is the result of two contributions, the HBs between silica wall and the OH groups of TBA and HB between TBA molecules. This highlights a strong hydrogen bonding network between TBA and silica material that is at the origin of the core–shell organization. To ensure this hypothesis, MD simulations through a weakly hydrophilic silica nanopore (WH) was carried out. Figure 8a shows that the weak ability of WH to establish interfacial hydrogen bonds between the silanol groups and the TBA molecules explains the absence of microphase separation. This bears out the fact that the interfacial anchoring from HB is the driving force to observe a microphase segregation. Interestingly, Fig. 8b exhibits that the carbon atoms of TBA and TOL are preferentially adsorbed in comparison with the hydroxide groups of TBA that underlines a hydrophobic anchoring related to the interactions between silicon and carbon atoms. It seems then that the strong interfacial hydrogen bonding network between TBA molecules and the silica material rules the preferential adsorption of TBA at the interface. To strengthen this result, MD simulation of confined TBA/TOL mixture into a pure hydrophilic nanopore for a TBA concentration of xTBA = 0.24 was carried out. The ideal hydrophilic nanopore corresponds to a water nanotube (WNT) and details on pore building and force field are provided in the Methods section. As shown in Fig. 7c, TBA molecules are preferentially adsorbed at the silica surface given the strong hydrogen bonds between TBA and water molecules leading to a core–shell structure with a homogeneous TBA/TOL mixture at the center of pore. These results indicate that the highly hydrophilic surface induces a microphase separation of TBA/TOL mixture and could also suggest that a hydrophobic surface is not able to discriminate TBA and TOL molecules because TOL is fully hydrophobic. However, Fig. 7d shows that a carbon nanotube (CNT) is also capable of separating TBA and TOL by forming a core–shell structure such that TOL and TBA molecules are respectively preferentially located at the CNT surface and at the center of pore. As shown in Fig. 9, this separation is the result of a commensurate organization due to stacking interactions between benzenic cycles of CNT and TOL molecules. To go a little further, the curvature effect was also investigated. Indeed, as often shown, the curvature induced by the cylindrical geometry can drastically impact the physical properties in relation to the slitlike confinement.17,18 We then carried out MD simulation of a TBA/TOL mixture with a TBA concentration of xTBA = 0.5 confined through two silica slitlike pores such that the confinement in term of confined volume was conserved (two silica walls separated by a distance of 24 Å as illustrated in Fig. 10a). As observed in Fig. 10b, segregation between both liquids is observed highlighting that the separation is rather ruled by the interactions between the silica surface and TBA than the pore geometry. Eventually, pore size effect was also investigated and MD simulations of confined TBA/TOL mixture with a TBA concentration of xTBA = 0.5 confined in a silica nanopore of radius of 6 Å and 18 Å were carried out. As shown in Fig. 11, the microphase separation and the core–shell organization are still observed that corroborates that the driving force is connected to the interfacial anchoring by hydrogen bonds allowing that preferential adsorption of TBA molecules. Additionally, Morineau and colleagues38 have recently shown, from Neutron scattering, that the core–shell organization was also observed with a pore radius of 43 Å. Therefore, the solid–liquid interactions and more especially the solid–liquid hydrogen bonds seem to overcome the bulk ones whatever the pore diameter leading to the microphase separation and the core–shell structure. Eventually, by comparing the structures obtained from the silica nanotube and from the CNT material (smoothness nanopore), we show that the core–shell organization is independent of the surface roughness. Although the core–shell structure is indirectly correlated to the capillary condensation, the main mechanism is related to the wetting on the silica surface and then to the interfacial interactions between TBA/TOL and the SiOH. Therefore, the microphase separation at the nanoscale cannot be related to any putative de-wetting phenomenon, nor it could be understood by considering solely the capillary condensation of the gas. Indeed, a vision of the intermolecular interactions and then the strength of wetting is needed to capture the origin of the microphase, what was performed in this work.
a Local surface tension (γ(r)) as a function of the radial distance (left axis) and radial densities of center of mass of tert-butanol (TBA) and toluene (TOL) molecules and radial density of atoms belonging to the silica material (right axis). b Profiles of the hydrogen bonds number per TBA molecules along the radial direction of the silica cylindrical nanopore. c Profile of the radial density of TBA and TOL liquids confined into a water nanotube (WNT) with a pore radius of 12 Å. d Profile of the radial density of TBA and TOL liquids confined into a carbon nanotube (CNT) with a pore radius of 12 Å
a Profile of the radial density of center of mass of tert-butanol (TBA) and toluene (TOL) molecules confined into the weakly hydrophilic silica nanopore. b Profile of the radial density of tertiary carbon (Ct), hydrogen atom of hydroxide group (HO) of TBA, and carbon of benzenic cycle (C) and methyl group (CH3) of TOL
a illustration of the confined TOL (cyan color) and TBA (red color) for xTBA = 0.5, between two silica walls separated by a distance of 24 Å. Red and yellow colors correpond to the oxygen and silicon atoms. b Profile of the axial density of centers of mass of TBA and TOL molecules confined between two silica slabs separated by a distance of 24 Å
Discussion
In this work, the TBA/TOL mixture that is homogeneous in the bulk liquid phase was confined at the nanoscale into cylindrical pores. We showed that the nano-confinement can induce, under a few conditions, microphase separation of binary mixture with a core–shell organization in line with Neutron scattering experiments. Phase separation was evidenced by highlighting both liquid–liquid and liquid–solid interfaces by means of the profiles of the density of center of mass and the local surface tension. By computing the radial profile of the hydrogen bonds number and by tuning the hydrophilicity of the surface of the silica nanopore, we established that the phase separation was ruled at the molecular scale by the strong hydrogen bonds between TBA molecules and the silica material that favors the HB anchoring. Confinement through a carbon nanotube showed an inverse core–shell structure with TOL anchored at the solid surface highlighting an hydrophobic anchoring due to a commensurate organization implying the benzenic cycles stacking. These results shed light on the possibility to control the nanostructure of multicomponent fluids under confinement at the nanoscale by tuning the surface chemistry of nanopore. The nanoconfined phase separation seems to be independent to the pore size and is essentially connected to the strength of pore–fluid interactions. As shown in Fig. 8a, the microphase separation has not been established from a weakly hydrophilic pore, whereas the core–shell structure was also recovered from a hydrophobic matrix (CNT), highlighting that the phase separation is unambiguously connected to the liquid–solid interactions. Determination of a theoretical model predicting the phase separation as a function of the strength of the solid–liquid interactions could be possible by tuning progressively (thermodynamic integration) the pore–liquid interactions (Lennard-Jones parameters and partial charges). However, it will be difficult to connect this model with the realistic materials where the interactions are too complexes. We think that the so-developed strategy consisting of the refining of the pore–wall interactions by a comparison with experiment is probably the most relevant approach. Qualitatively, the microphase separation can be then predicted if one considers a mixture of an amphiphilic component and a hydrophobic one confined in pure hydrophilic and hydrophobic pores. Although the development of a theoretical model to predict the phase separation in a nanoconfined pore seems to be difficult to connect with realistic materials, it is possible to predict the optimal conditions to observe the core–shell organization that means the maximal number of TBA molecules anchored at the surface. Indeed, the pore volume can be calculated as \({V}_{{\mathrm{pore}}} = \pi R_{{\mathrm{pore}}}^2L_z\) where Rpore is the pore radius of the nanopore while Lz is the height of the nanotube, the volume of the core region is \({V}_{{\mathrm{core}}} = \pi R_{{\mathrm{core}}}^2L_z\) such that Rcore is the radius of the core region. The volume of the interfacial zone, i.e., the shell can be then evaluated as \({V}_{{\mathrm{shell}}} = \pi L_z(R_{{\mathrm{pore}}}^2 - R_{{\mathrm{core}}}^2)\) such that Rcore = Rpore − eshell with eshell corresponding to the thickness of the interfacial shell. eshell is computed from the density profile. From the density profile calculations, we found that eshell = 4 Å. If we consider the bulk density as the interfacial density, the number of TBA molecules interfacially anchored can be calculated as NTBA,s = Vshell.ρTBA,bulk. With Rpore = 12 Å and eshell = 4 Å, an interfacial saturation of NTBA,s = 57 was predicted. Therefore, for the TBA molar fraction corresponding to a number of TBA molecules less than NTBA,s, the TBA will be fully anchored and a full core–shell organization will be observed (i.e., xTBA = 0.71, 0.49, and 0.24). Beyond NTBA,s, TBA molecules will also be located in the center of pore and in the intermediary layer. From GCMC simulations, we found that the solid interface is saturated for NTBA,s = 56 molecules that bears out our previous structural model. In Fig. 4a, the molar fraction xTBA = 0.83 corresponds to 79 TBA and 16 toluene molecules. Therefore, other TBA molecules (79–57) are distributed at the center of pore and in the intermediate layer. As shown in Fig. 1b, the first layer is located between 0 and 3 Å, the second between 3 and 7.5 Å, while the last is located between 7.5 and 12 Å. As the layer size corresponds to the molecule size and that TOL molecule is higher than TBA one, 3.5 Å vs 3.0 Å, it appears that TOL molecules have no place at the center of pore contrary to the intermediate layer where the layer size is 4.5 Å.
Eventually, the microphase separation raises exciting questions about its impact on the MD and the liquid flow in nanochannel, as suggested by the recent report on multiple glassy dynamics.37 Further insight into this aspect could be attained from ongoing experimental spectroscopy and molecular simulation studies.
Methods
Models
Silica cylindrical nanopore with a hydrophilic surface was managed by applying the procedure proposed by Bródka and Zerda.44 We generated a cylindrical cavity along the z axis of the cubic silica cell of 35.7 Å by removing the atoms within a cylinder of diameter (D) 24 Å. From their coordination numbers, we distinguished bridging oxygen (Ob) bonded to two silicon atoms from non bridging oxygens (Onb) bonded to only one silicon and bonded to one hydrogen atom (Hnb). An iterative procedure of atom (O and Si) removal was applied until only tetra-coordinated silicon atoms, bonded to a maximum of two Onbs, were present in the structure. Finally, non-bridging oxygens were saturated with hydrogen atoms to form surface hydroxyl groups. This procedure leads to a realistic description of the irregular inner surface of the porous silicate and of the interfacial interactions between the fluid and the matrix (see Fig. 2). The inner surface coverage of silanol groups was about 7.5 nm−2, which corresponds to highly hydrated protonated silica pore.44,45 Although the silica matrix was subsequently kept rigid, rotation around the Si-O bond of the hydroxyl groups was allowed from the SHAKE constraints algorithm,10,41,46 where the distance between the oxygen and hydrogen atoms are kept fixed at 1.09 Å.
Intermolecular interactions are the sum of both electrostatic and dispersive–repulsive Lennard-Jones contributions. Silica framework was modeled using the ClayFF force field developed by Cygan et al.40 Indeed, it has been shown that the potential developed by Bródka and Zerda44 was too weak and underestimated the adsorbed amount at low pressure.39,47 TBA and TOL were modeled by means of the non-polarizable flexible OPLS all atoms (AA) force field.48 Indeed, the OPLS-AA models of TBA and TOL were found to well reproduce density and structure in liquid bulk phase.48 Whereas the original Lennard-Jones parameters were initially conserved, the partial charges were calculated from ab-initio calculations. Calculation of the partial charges was carried out on the basis of 6-311G(d,p) Gaussian-type basis set. In the first time, geometry was optimized, whereas in the second stage the partial charges were calculated from the CHELPG (CHarges from ELectrostatic Potentials using a Grid-based) method.49 These calculations were performed using the Gaussian code.50
Force field parameters of silica nanopore, TOL, and TBA molecules are provided in the FIELD.txt file, the input file of DL_POLY software.51 Crossed van der Waals interactions between TOL and TBA were calculated using the Lorentz-Berthelot mixing rules. The LJ parameters between the silica nanopore and TOL were optimized to qualitatively reproduce the experimental isotherm by following the procedure developed in ref. 41. The so-optimized interactions between TOL molecules and silica material are provided in Table 1. Force field parameters of silica material, TOL, and TBA and crossed interactions can be found in the FIELD.txt file. Armchair CNT of radius 12 Å with a pore length of 100 Å was modeled by considering the uncharged force field developed by Werder et al.52 WNT was built by carving a cylindrical nanopore of radius 12 Å into an equilibrated cubic water box with a length box of 59 Å. Water molecules were modeled by considering the TIP4P/2005 model53 and were considered as frozen. Weakly hydrophilic silica membrane was also modeled by combining the Universal force field (UFF)54 for describing oxygen and hydrogen atoms, while silicon atoms were described using the DREIDING force field.55 All details are provided in ref. 39. Crossed Lennard-Jones parameters were calculated by considered the Lorentz-Berthelot mixing rules.
MD simulation
MD simulations were performed using a time step of 0.002 ps to sample 10 ns (acquisition phase). The equilibration time corresponds to 10 ns. All MD simulations have been carried out with the DL_POLY package51 using the combination of the velocity-Verlet algorithm and the Nose-Hoover thermostat.56 Numbers of confined molecules of pure TBA and TOL and binary TBA/TOL were calculated using GCMC simulation at the saturation pressure vapor and 308 K. Compositions in TBA and TOL are provided in Table 2.
Monte Carlo simulation
Monte Carlo simulations were performed in the grand canonical statistical ensemble. Periodic boundary conditions were applied in the three directions. Silica nanopore was considered as rigid and only the hydrogen of silanol can rotate from an angular move implying SiOH groups.44 Each cycle consisted of N randomly selected moves with fixed probabilities: translation of the center of mass of a randomly chosen, rotation of a randomly selected around its center of mass, change of the internal conformation using the configurational bias regrowth move57 and insertion/deletion trial move. The frequencies of each type of move are 0.20 for translation, 0.20 for rotation, 0.20 for the change of the conformation, and 0.4 for insertion/deletion. GCMC simulations consisted of 700,0000 cycles.
Surface tension calculation
Surface tension was computed using the non-exponential test-area method TA258 based upon a thermodynamic route.59 This method expresses the surface tension as a change in the free energy (F) for an infinitesimal change in the surface area performed in the constant-NVT ensemble. This infinitesimal change in the area is performed throughout a perturbation process for which the perturbed system (state A + ΔA and noted 1) is obtained from an infinitesimal change ΔA of the area A of the reference system (noted 0). The box dimensions \(( {L_x^{(1)},L_y^{(1)},L_z^{(1)}} )\) in the perturbed systems are changed using the following transformations \(L_x^1 = L_x^{(0)}\sqrt {1 \pm \xi } ,L_y^{(1)} = L_y^{(0)}\sqrt {1 \pm \xi } ,L_z^{(1)} = L_z^{(0)}/(1 \pm \xi )\) where ξ → 0. The area of a cylindrical interface is A = 2πReLz and ΔA = A [(1 ± ξ)−1/2− 1], where Re is the radius equimolar dividing surface. These transformations conserve the volume of the box in the perturbed state. This means that it is possible to express the surface tension as a difference between the perturbed and reference states. U(0)(rN) and U(1)(r′N) are the configurational energies of the systems with an area A and a configurational space rN, and an area A + ΔA and a configurational space r′N, respectively.
where <···> 0 indicates that the average is carried out over the reference state. A local version of Eq. (1) can be obtained by assuming a decorrelation of the cylindrical slabs.60
where k is the index of the cylindrical slab, Rk the radius of the cylindrical shell, \(u_{R_k}\) is the energy of the kth element, H(Rik) is the Heaviside function with H(Rik) = 1 for Ri = Rk and 0 otherwise and rij is the distance between i and j molecules.
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
References
Granick, S. Motions and relaxations of confined liquids. Science 253, 1374 (1991).
Klein, J. & Kumacheva, E. Confinement-induced phase transitions in simple liquids. Science 269, 816 (1995).
Bruni, F., Ricci, M. A. & Soper, A. K. Water confined in vycor glass. I. A neutron diffraction study. J. Chem. Phys. 109, 1478 (1998).
Soper, A. K., Bruni, F. & Ricci, M. A. Water confined in vycor glass. ii. excluded volume effects on the radial distribution functions. J. Chem. Phys. 109, 1486 (1998).
Morineau, D. & Alba-Simionesco, C. Liquids in confined geometry: how to connect changes in the structure factor to modifications of local order. J. Chem. Phys. 118, 9389 (2003).
Alcoutlabi, M. & McKenna, G. B. Effects of confinement on material behaviour at the nanometre size scale. J. Phys. Condens. Matter 17, R461 (2005).
Coasne, B., Jain, S. K. & Gubbins, K. Freezing of fluids confined in a disordered nanoporous structure. Phys. Rev. Lett. 97, 105702 (2006).
Alba-Simionesco, C. et al. Effect of confinement on freezing and melting. J. Phys. Condens. Matter 18, R15 (2006).
Ghoufi, A. et al. Molecular simulations of confined liquids: an alternative to the grand canonical Monte Carlo simulations. J. Chem. Phys 134, 074104 (2011).
Ghoufi, A., Hureau, I., Morineau, D. & Lefort, R. Hydrogen-bond-induced supermolecular assemblies in a nanoconfined tertiary alcohol. J. Phys. Chem. C 115, 17761 (2011).
Ghoufi, A., Szymczyk, A., Renou, R. & Ding, M. Calculation of local dielectric permittivity of confined liquids from spatial dipolar correlations. Europhys. Lett. 99, 37008 (2012).
Zhu, H., Ghoufi, A., Szymczyk, A., Balannec, B. & Morineau, D. Anomalous dielectric behavior of nanoconfined electrolytic solutions. Phys. Rev. Lett. 109, 107801 (2012).
Ghoufi, A., Hureau, I., Morineau, D., Renou, R. & Szymczyk, A. Confinement of tert-butanol nanoclusters in hydrophilic and hydrophobic silica nanopores. J. Phys. Chem. C 117, 15203 (2013).
Guo, X.-Y., Watermann, T. & Sebastiani, D. Local microphase separation of a binary liquid under nanoscale confinement. J. Phys. Chem. B 118, 10207 (2014).
Abdel Hamid, A. R. et al. Microphase separation of binary liquids confined in cylindrical pores. J. Phys. Chem. C 120, 9245 (2016).
Hummer, G., Rasaiah, J. C. & Noworyta, J. P. Water conduction through the hydrophobic channel of a carbon nanotube. Nature 414, 188 (2014).
Falk, K., Joly, L., Sedlmeier, F., Netz, R. R. & Bocquet, L. Molecular origin of fast water transport in carbon nanotube membranes: superlubricity versus curvature dependent friction. Nano Lett. 10, 4067 (2010).
Ghoufi, A., Szymczyk, A. & Malfreyt, P. Ultrafast diffusion of ionic liquids confined in carbon nanotubes. Sci. Rep. 6, 28518 (2016).
Kityk, A. V. et al. Continuous paranematic-to-nematic ordering transitions of liquid crystals in tubular silica nanochannels. Phys. Rev. Lett. 18, 187801 (2008).
Gruener, S. & Huber, P. Spontaneous imbibition dynamics of an n-alkane in nanopores: evidence of meniscus freezing and monolayer sticking. Phys. Rev. Lett. 103, 174501 (2009).
Grigoriadis, C. et al. Suppression of phase transitions in a confined rodlike liquid crystal. ACS Nano 5, 9208 (2011).
Nomura, K. et al. Evidence of low-density and high-density liquid phases and isochore end point for water confined to carbon nanotube. Proc. Natl Acad. Sci. USA 114, 4066 (2017).
Ballenegger, V. & Hansen, J.-P. Dielectric permittivity profiles of confined polar fluids. J. Chem. Phys. 122, 114711 (2005).
Bonthuis, D. J., Gekle, S. & Netz, R. R. Dielectric profile of interfacial water and its effect on double-layer capacitance. Phys. Rev. Lett. 107, 166102 (2011).
Zhang, C., Gygi, F. & Galli, G. Strongly anisotropic dielectric relaxation of water at the nanoscale. J. Phys. Chem. Lett. 4, 2477 (2013).
Emile, O., Emile, J. & Ghoufi, A. Influence of the interface on the optical activity of confined glucose films. J. Colloid. Interface Sci. 477, 103 (2016).
Palomarez-Baez, J. P., Panizon, E. & Ferrando, R. Nanoscale effects on phase separation. Nano Lett. 17, 5394 (2017).
Keblinsky, P., Ma, W. J., Maritan, A., Koplik, J. & Banavar, J. R. Molecular dynamics of phase separation in narrow channels. Phys. Rev. E 47, 2265 (1993).
Gelb, L. D. & Gubbins, K. E. Liquid-liquid phase separation in cylindrical pores: Quench molecular dynamics and Monte Carlo simulation. Phys. Rev. E 56, 3185 (1997).
Gelb, L. D. & Gubbins, K. E. Studies of binary liquid mixtures in cylindrical pores: phase separation, wetting and finite-size effects from Monte Carlo simulations. Phys. A Stat. Mech. Appl. 244, 112 (1997).
Dutta, S. et al. Thermodynamics of binary gas adsorption in nanopores. Phys. Chem. Chem. Phys. 18, 24361 (2016).
Krycka, K. L., Dura, J. A., Langston, L. J. & Burba, C. M. Nanoconfinement-induced phase segregation of binary benzene cyclohexane solutions within a chemically inert matrix. J. Phys. Chem. C 122, 7676 (2018).
Harrach, M. F., Drossei, B., Winschel, W., Gutmann, T. & Buntkowsky, G. Mixtures of isobutyric acid and water confined in cylindrical silica nanopores revisited: A combined solid-state nmr and molecular dynamics simulation study. J. Phys. Chem. C 119, 28961 (2015).
Muthulakshmi, T., Dutta, D., Maheshwaru, P. & Pujari, P. K. Evidence for confinement induced phase separation in ethanol–water mixture: a positron annihilation study. J. Phys. Condens. Matter 30, 025001 (2018).
Schmitz, R., Muller, N., Ullmann, S. & Vogel, M. A molecular dynamics simulations study on ethylene glycol-water mixtures in mesoporous silica. J. Chem. Phys. 145, 104703 (2016).
You, F., Yu, Y. & Gao, G. Structures and adsorption of binary hard-core yukawa mixtures in a slitlike pore: grand canonical monte carlo simulation and density-functional study. J. Chem. Phys. 123, 114705 (2005).
Abdel Hamid, A. R. et al. Multiple glass transitions of microphase separated binary liquids confined in mcm-41. J. Phys. Chem. C 120, 11049 (2016).
Mhanna, R. et al. More room for microphase separation: an extended study on binary liquids confined in sba-15 cylindrical pores. J. Chem. Phys. 146, 024501 (2017).
Essafri, I., Courtin, J. & Ghoufi, A. Numerical evidence of heterogeneity and nanophases in a binary liquid confined at the nanoscale. Mol. Sim. 44, 728 (2018).
Cygan, R. T., Liang, J. J. & Kalinichev, A. G. Molecular models of hydroxide, oxyhydroxide, and clay phases and the development of a general force field. J. Phys. Chem. B 108, 1255 (2004).
Ghoufi, A., Morineau, D., Lefort, R. & Malfreyt, P. Toward a coarse graining/all atoms force field (cg/aa) from a multiscale optimization method: an application to the mcm-41 mesoporous silicates. J. Chem. Theory Comput. 6, 3212 (2010).
Ghoufi, A. & Malfreyt, P. Importance of the tail corrections on surface tension of curved liquid-vapor interfaces. J. Chem. Phys. 146, 084703 (2017).
Luzar, A. & Chandler, D. Effect of environment on hydrogen bond dynamics in liquid water. Phys. Rev. Lett. 76, 928 (1996).
Bródka, A. & Zerda, T. W. Properties of liquid acetone in silica pores: molecular dynamics simulation. J. Chem. Phys. 104, 6319 (1996).
Puibasset, J. & Pellenq, R. J.-M. Water adsorption in disordered mesoporous silica (vycor) at 300k and 650k: a grand canonical Monte Carlo simulation study of hysteresis. J. Chem. Phys. 122, 094705 (2005).
Ryckaert, J.-P., Ciccotti, G. & Berendsen, H. J. C. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comp. Phys. 23, 327 (1977).
Pafong, E., Geske, J. & Drossel, B. On the influence of the intermolecular potential on the wetting properties of water on silica surfaces. J. Chem. Phys. 145, 114901 (2016).
Jorgensen, W. L., Maxwell, D. S. & Rives, J. Tirado Development and testing of the opls all-atom froce field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 118, 11225 (1996).
Breneman, C. M. & Wiberg, KennethB. Determining atom-centered monopoles from molecular electrostatic potentials. the need for high sampling density in formamide conformational analysis. J. Comp. Chem. 11, 361 (1990).
Frisch, M. J. et al. Gaussian Development Version, Revision I.04+ (Gaussian Inc., Wallingford, 2014).
Forester, T. R. & Smith, W. DLPOLY, CCP5 Program Library (Daresbury Lab., Warrington, 2004).
Werder, T., Walther, J., Halicioglu, R., Halicioglu, T. & Koumoutsakos, P. On the water-carbon interaction for use in molecular dynamics simulations of graphite and carbon nanotubes. J. Phys. Chem. B 107, 1345 (2003).
Abascal, J. L. F. & Vega, C. A general purpose model for the condensed phases of water: Tip4p/2005. J. Chem. Phys. 123, 234505 (2005).
Rappé, A. K., Casewit, C. J., Colwell, K. S., Goddard, W. A. III & Skiff, W. M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 114, 7863 (1992).
Mayo, S. L., Olafson, B. D. & Goddard, W. A. III Dreiding: a generic force field fo molecular simulations. J. Phys. Chem. 94, 8897 (1990).
Mechionna, S., Ciccotti, G. & Holian, B. L. Hoover NPT dynamics for systems varying in shape and size. Mol. Phys. 78, 533 (1993).
Chen, B., Potoff, J. J. & Siepmann, J. I. Monte carlo calculations for alcohols and their mixtures with alkanes. Transferable potentials for phase equilibria. 5. United-atom description of primary, secondary, and tertiary alcohols. J. Phys.Chem. B 105, 3093 (2001).
Ghoufi, A. & Malfreyt, P. Calculation of the surface tension and pressure components from a non-exponential perturbation method of the thermodynamic route. J. Chem. Phys. 136, 024104 (2012).
Gloor, G. J., Jackson, G., Blas, F. J. & de Miguel, E. Test-area simulation method for the direct determination of the interfacial tension of systems with continuous or discontinuous potentials. J. Chem. Phys. 123, 134703 (2005).
Ibergay, C. et al. Molecular simulations of the n-alkane liquid-vapor interface: interfacial properties and their long range corrections. Phys. Rev. E 75, 051602 (2007).
Author information
Authors and Affiliations
Contributions
A.G. and D.M. elaborated the project and A.G. and I.E. performed molecular dynamics simulations. A.G., D.M., and I.E. contributed to the scientific discussions and the preparation of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Essafri, I., Morineau, D. & Ghoufi, A. Microphase separation of a miscible binary liquid mixture under confinement at the nanoscale. npj Comput Mater 5, 42 (2019). https://doi.org/10.1038/s41524-019-0179-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-019-0179-y