Abstract
Simulations based on solving the Kohn-Sham (KS) equation of density functional theory (DFT) have become a vital component of modern materials and chemical sciences research and development portfolios. Despite its versatility, routine DFT calculations are usually limited to a few hundred atoms due to the computational bottleneck posed by the KS equation. Here we introduce a machine-learning-based scheme to efficiently assimilate the function of the KS equation, and by-pass it to directly, rapidly, and accurately predict the electronic structure of a material or a molecule, given just its atomic configuration. A new rotationally invariant representation is utilized to map the atomic environment around a grid-point to the electron density and local density of states at that grid-point. This mapping is learned using a neural network trained on previously generated reference DFT results at millions of grid-points. The proposed paradigm allows for the high-fidelity emulation of KS DFT, but orders of magnitude faster than the direct solution. Moreover, the machine learning prediction scheme is strictly linear-scaling with system size.
Similar content being viewed by others
Introduction
Propelled by the algorithmic developments and successes of data-driven efforts in domains such as artificial intelligence1 and autonomous systems,2 the materials and chemical sciences communities have embraced machine learning (ML) methodologies in the recent past.3 These approaches have led to prediction frameworks that are “trained" on past data gathered either by experimental work or by physics-driven computations/simulations (in which fundamental equations are explicitly solved). Once trained, the prediction models are powerful surrogates of the experiments or computations that supplied the original data, and significantly out-strip them in speed. Thus, ideally, future predictions for new cases (i.e., new materials or molecules) can simply proceed using the surrogate models. The training and prediction processes involve a fingerprinting or featurization step in which the materials or molecules are represented numerically in terms of their key attributes (whose choice depends on the application), followed by a mapping, established via a learning algorithm, between the fingerprint and the property of interest. A variety of fingerprints have been developed over the past decade such as the many-body tensor representation,4 the SOAP descriptor,5 the Coulomb matrix representation,6 the Behler-Parrinello symmetry functions7, and others.8,9
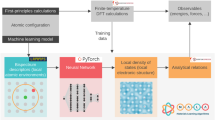
The above ideas have been employed in various ways in the last several years to create surrogate models that can emulate some aspects of density functional theory10,11 (DFT) computations.12 There is great value in this enterprise for two reasons. First, DFT, which has served as an invaluable workhorse for materials discovery,13,14,15,16,17 is still rather slow. And second, the vast streams of data that DFT computations produce are generally squandered. At its core, DFT computations involve the solution of the Kohn-Sham equation, which yields the electronic charge density, wavefunctions and the corresponding energy levels as the primary output. These entities are then used to compute the total potential energy of the system and atomic forces as the secondary output. Several other properties of interest (we will call them tertiary output) are then derived from the primary and secondary outputs, such as binding energies, elastic constants, dielectric constant, etc. Thus far, ML methodologies have been effectively used to create surrogate models to predict the secondary and tertiary outputs of DFT (Fig. 1). The ability to efficiently predict total potential energies and atomic forces (i.e., the secondary outputs of DFT) has led to ML force fields,5,7,8,18,19,20,21,22,23,24,25 which have the potential to overcome several major hurdles encountered by both the classical26 and quantum molecular dynamics (MD) simulations.27 Directly and rapidly being able to predict physical properties (the tertiary output of DFT) can enable accelerated materials discovery.14,15,28,29,30,31,32,33,34,35,36
Schematic of the hierarchical-paradigm of applying surrogate models to different outputs of first-principles calculations. The current work seeks to overcome the primary bottleneck of density functional theory (DFT), i.e. the Kohn-Sham equation, by creating machine learning models to directly predict the electronic charge density and the density of states
The present effort aims at a direct attack on the principal bottleneck of DFT computations, namely, the Kohn-Sham equation11 (the innermost arrow of Fig. 1). Our goal is the creation of strictly linear-scaling surrogate ML models to predict the primary output of DFT computations, but several orders of magnitude faster than DFT; in essence, this is an attempt to eliminate direct solution of the Kohn-Sham equation by learning and distilling down its function. Each time the Kohn-Sham equation is explicitly solved, an immense amount of data is produced; for instance, the electronic charge density or wavefunction value at every grid-point. We propose a novel fingerprinting strategy that elegantly encodes the atomic arrangement around any grid-point, which is then mapped using neural networks to the total electronic charge density and the local density of states (LDOS) at that grid-point. Summing up the LDOS over all grid-points creates the total density of states (DOS) of the entire system. Although recent endeavors have shown promise in machine-learning some aspects of electronic structure,20,37,38,39,40,41 the current work represents the first report on mapping the charge density and the entire LDOS spectrum to the local atomic environment.
As tangible demonstrations, we have developed surrogate models for predicting the electronic structure of aluminum (Al) and polyethylene (PE). Once trained, the models are shown to predict the charge density and DOS for unseen cases with remarkable verisimilitude. Our material choices (Al and PE) span metallic and covalent insulating systems containing one or more atom types. The charge density and DOS models alone open up two transformative pathways: the first is the integration of the capability to predict the electronic structure of large ensembles of atoms with classical MD simulation packages at every (few) time-steps. The second opportunity is the complete emulation of DFT, as the secondary and tertiary outputs of DFT can be determined from the surrogate model predictions of the electronic charge density and DOS, as explained toward the end of this article.
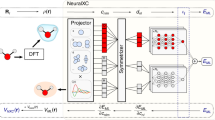
The first step of any data-driven methodology is the generation of the reference training data as depicted in Fig. 2. To this end, we performed MD simulations on the abovementioned two materials systems (Al and PE). Ten snapshots were randomly selected from the MD trajectory and DFT calculations were performed to obtain the charge density and LDOS defined at spatial grid-points. As detailed in the Methods section, these 10 snapshots exhibited a rich variety of structural environments capturing configurations significantly different from their respective equilibrium geometries. Each of the PE snapshots contained 120 atoms and 4.3 million grid-points, whereas each Al snapshot contained 144 atoms and 8.2 million grid-points. We used slab-like systems rather than bulk systems in order to align the DOS of every snapshot with the vacuum energy level (considered here as a global/absolute reference energy).
Overview of the process used to generate surrogate models for the charge density and density of states. The first step entails the generation of the the training dataset by sampling random snapshots of molecular dynamics trajectories. First-principles calculations were then performed on these systems (shown in Figure S1) to obtain the training atomic configurations, charge densities, and local density of states. The scalar (S), vector (V), and tensor (T) fingerprint invariants are mapped to the local electronic structure at every grid-point. For the charge density, this mapping is achieved using a simple fully connected neural network with one output neuron. The LDOS spectrum, on the other hand, is learned via a recurrent neural network architecture, wherein the LDOS at every energy window is represented as a single output neuron (linked via a recurrent layer to other neighboring energy windows). The trained model is then used to predict the electronic structure (i.e, DOS and charge density) of an unseen configuration
For each system, the charge density and LDOS data at the grid-points from eight snapshots were included in the training set. The data at the grid-points of the ninth snapshot were considered as a validation set to determine the number of epochs of training the neural network undergoes and finally all the data of the grid-points of the tenth randomly selected snapshot were considered as the test set.
In this work we introduce a novel rotationally invariant, grid-based representation of local atomic environment that allows the mapping of the local electronic structure at a point to its immediate atomic neighborhood. The representation technique consists of a hierarchy of features, which we refer to as scalar, vector, and tensor invariants, derived from the corresponding scalar, vector, and tensor components as described below. The scalar components capture the radial information of atoms around a grid-point while the vector and tensor components capture the angular features of the local atomic environment. We use a predefined set of Gaussian functions (k) of varying widths (σk) centered about every grid-point (g) to determine these fingerprints. The scalar fingerprint (Sk) for a particular grid-point, g, and Gaussian, k, in an N-atom, single-elemental system is defined as
where, rgi is the distance between the reference grid-point, g, and the atom, i, and fc(rgi) is a cutoff function, which decays to zero for atoms that are more than 9 Å from the grid-point. The coefficient Ck is the normalization constant for the Gaussian k and is given by \(1/(2\pi )^{3/2}\sigma _k^3\). Similarly, the components of the vector and tensor fingerprint are given by,
where, α and β represent the x, y, or z directions. The vector and tensor fingerprints can be related to the first and second partial derivatives (with respect to the x, y, and z directions) of the scalar fingerprints, respectively. Unlike the scalar fingerprint, however, the vector \(\left( {V_k^\alpha } \right)\) and tensor fingerprints \(( {T_k^{\alpha \beta }} )\) are not rotationally invariant. However, as described in the Methods section, rotationally invariant representations may be constructed from the individual components of the vector and tensor fingerprints. In the current work, the resulting five invariants (one scalar invariant, one vector invariant, and three tensor invariants), are calculated using a basis of 16 Gaussians resulting in 80 numbers, which elegantly and efficiently encode the spatial distribution of atoms around a particular grid-point. For the case of PE, a bi-elemental system, the fingerprint vector is calculated independently for the carbon and hydrogen atoms and subsequently concatenated resulting in a fingerprint vector of length 160.
These fingerprints function as the “input-layer” of a neural network, which, as universal function approximators,1 can learn the complex nonlinear mapping to the charge density and LDOS. In this work, we utilize a neural network with three hidden layers each with 300 neurons. The choice of neural network hyperparameters is justified in the Methods section. The output layer for the charge density model is a single neuron since the charge density is a scalar quantity. On the other hand, the LDOS spectrum at every grid-point is a continuous function, which can be discretized (or binned) into a specific number of energy windows. Hence, the number of neurons in the output layer of the LDOS neural network model would correspond to the total number of energy windows under consideration. More specifically, the Al and PE LDOS spectra were partitioned into 180 and 260 energy windows, respectively, each with a window (or bin) size of 0.1 eV.
The LDOS (and DOS) at a particular energy window is strongly correlated with the LDOS at neighboring energy windows. In order to capture the correlations across the entire LDOS spectrum, we utilize a bidirectional recurrent neural network layer as a precursor to the final output layer. The use of the recurrent neural network architecture to learn the LDOS spectrum is inspired by their recent successes in the prediction of correlated sequences, for instance, in speech recognition.42 The details of the architecture of the employed recurrent neural network are provided in Figure S3 of Supplementary material.
Two million grid-points from each of the training snapshots were selected at random in order to train the charge density and LDOS models. The two models were then used to predict the local electronic structure at every grid-point for the unseen test snapshot of PE and Al. Subsequently, the total DOS for the system/supercell can then be obtained by summing up the LDOS at every grid-point. Since the number of electrons for any given materials system is known a priori, one can easily obtain the Fermi level of the system through the integration of the predicted DOS (or directly from the cumulative DOS).
Results
Figure 3 summarizes the results for the prediction of charge density and DOS. The coefficient of determination (R2) of the charge density for the test cases of PE and Al were 0.999997 and 0.999955, respectively, as shown in Fig. 3a, b. The root mean square error of these predictions were approximately 4 × 10−4 e/Å3 and 6 × 10−4 e/Å3 for PE and Al, respectively. The errors metrics for the train and validation snapshots are detailed in Tables S1 and S2. The systematic improvement in accuracy on inclusion of the vector and tensor fingerprints is depicted in the inset of Fig. 3a and in more detail in Figure S4.
Parity plot for the machine learning vs density functional theory (DFT) charge density prediction for the unseen snapshot of a polyethylene (PE) and b aluminum (Al). The inset in a depicts the systematic improvement in the accuracy of the model on inclusion of the vector and tensor fingerprints. The accuracy is also shown to improve on increasing the number of Gaussians used to sample the local environment. The inset in b shows the reduction in the error of the model upon including more grid-points in the training set. The dashed blue line in the inset represents converged/lowest test-error obtained. The density of states (DOS) prediction using the recurrent neural network is shown in c, d for the unseen test snapshots of PE and Al, respectively. The vacuum level has been used as the absolute reference energy level. The Al (001) slab consisted of 8.2 million grid-points while the PE slab contained 4.4 million grid-points. The total DOS spectrum for each structure was obtained by summing up the predicted local DOS at each grid-point
Figure 3c, d shows the prediction of the DOS and corresponding Fermi levels for the unseen test structures of PE and Al. The R2 for the predicted DOS spectrum for PE and Al were 0.997 and 0.9992, respectively. The near-perfect agreement of the ML and DFT charge densities and LDOS showcase the predictive ability of the model even when using only a handful of training structures.
In order to examine the transferability of our models to extremely different atomic environments, we use our PE charge density model (referred to as Model1), trained only on pure sp3-bonded carbon configurations, to predict the charge density of PE structures with double-bond and triple-bond defects. As shown in Fig. 4a–c, Model1 successfully captures the charge density away from the defected sites but fails to do so in the immediate vicinity of the double and triple bonds. Notably, the smaller bond lengths of the sp2- and sp3-hybridized carbon leads to an overestimation of the charge density by Model1. However, as soon as we retrain Model1 on four additional MD snapshots (each) of PE with double and triple bonds we immediately observe a sharp improvement in the predictive capabilities of the new model (referred to as Model2) as depicted in Fig. 4a, b, d. A single model is capable of capturing vastly different bonding environments highlighting that although an initial model may not be general enough, the prediction capability can be systematically improved.
a, b are charge density line plots for polyethylene (PE) with double and triple bond defects, respectively. Model1, trained on eight molecular dynamics snapshots of pristine PE, is unable to accurately predict the charge density in the vicinity of the defects. Model2, trained on four additional snapshots each of PE with double and triple bonds is able to accurately capture the charge density for unseen snapshots containing such defects. c, d Parity plots of just the top-1% error points for the case of PE, PE with double-bond defect, and PE with triple-bond defect using Model1 and Model2, respectively. The lower errors of Model2 indicate that the neural network can be systematically trained/re-trained when new environments are encountered
The neural network models were trained and implemented for prediction in a graphical processing unit (GPU)-based computing system. As depicted in Fig. 5, the prediction algorithm is linearly scaling, leading to ultrafast computation times, even for millions of grid-points. DFT calculations on equivalent materials systems, performed on 48 cores of a more expensive central processing unit (CPU) node, are orders of magnitude slower and also scale quadratically. Moreover, as shown in Table S3, traditional DFT algorithms are memory intensive and cannot handle more than a few thousand atoms. There is no such limitation in the grid-based ML prediction of the electronic structure as the algorithm is highly parallelizable; for example, batches of a few thousands/millions of grid-points can be assigned to different GPUs for simultaneous prediction.
Computational time and scaling of density functional theory (DFT) vs machine learning (ML) for electronic structure predictions. DFT shows near-quadratic scaling, whereas the ML prediction algorithm shows perfect linear-scaling and is orders of magnitude faster than DFT. We note, however, that direct comparison between DFT and ML computing times is difficult as the computations were performed on different architectures. The DFT calculations were performed on an Intel Xeon Skylake node with 48 cores and 192GB of RAM. The ML predictions were performed on a single GP100 GPU with 16GB RAM. Since modern DFT codes scale (at best) quadratically, the relative cost and time benefit of the proposed ML prediction scheme is enhanced tremendously for large system sizes of tens of thousands of atoms. The details of the scaling tests are shown in Table S3
Discussion
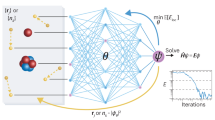
As a final comment, we mention that the predicted total DOS and charge density can be utilized to directly obtain the total energy (E) of the system.
where, ρ, Ne, EH, Exc, En–n are the charge density, number of electrons, Hartree energy, exchange-correlation energy, and nuclear–nuclear interaction energy, respectively. εi is the eigenvalue of the ith Kohn-Sham orbital. In Eq. 4, the first term \(2\mathop {\sum}\nolimits_i^{N_{\mathrm{e}}/2} \varepsilon _i\) can be written in terms of the DOS (\(2{\int}_{ - \infty }^{\varepsilon _f}\)DOS(ε)εδε) while the remaining terms are known functions of the charge density (for a given level of theory). Hence, the ML-enabled prediction of the DOS and charge density allows us to directly access the total energy, circumventing the computationally expensive Kohn-Sham equation. In Section 2 of the Supplementary material we have provided preliminary results on how the charge density predicted using ML can be used to obtain highly accurate total energies when used as a starting point for a non-self-consistent calculation. A more comprehensive investigation of obtaining the total energy from the charge density and DOS (using Eq. 4) will be addressed in a future work.
In summary, we have developed a ML capability that can learn the behavior of the Kohn-Sham equation of DFT. Once trained (on past one-time DFT results), the ML models can predict the electronic charge density and DOS given just the atomic configuration information. In contrast to recent works,40 we have demonstrated a direct grid-based learning and prediction scheme as opposed to the learning of a certain basis representation of the local electronic properties. A brief discussion of the merits and limitations of both methods is provided in Section 1 of the Supplementary material. We mention here that standard DFT calculations involve thousands or even millions of grid-points. The exceptional accuracy obtained using this grid-based approach thus comes at the cost of greater computational effort. Moreover, the learning of the grid-based LDOS is memory intensive since it requires multiple partial charge density files for every for every energy-window. Nonetheless, by taking advantage of modern GPU architectures and parallelized batch-wise training and prediction schemes, our algorithm is linear-scaling and has been shown to be several orders of magnitude faster than the parent DFT code that created the training data in the first place. Large systems, containing several tens of thousands of atoms, inaccessible to traditional DFT computations, can be routinely handled; this capability may thus be interfaced with MD software, which can then produce electronic structure results along the molecular trajectory. Other derived properties, such as energy, forces, dipole moments, etc., can be obtained from the presented models, thus leading to a practical and efficient DFT emulator, whose accuracy is purely controlled by the level of theory used to create the original data, and the size and diversity of the training dataset (which can be progressively increased and augmented, as desired). Going forward, we hope to benchmark our method using large, diverse, and well-curated datasets such as the QM9 dataset.43,44
Methods
All first-principles calculations were performed using Vienna Ab Initio Simulation Package (VASP). Slabs are used for data generation rather than bulk structures so as to obtain energy values with respect to the vacuum level. A plane wave cutoff of 500 eV and a k-point spacing of 0.2 Å−1 were utilized to obtain the training charge density and LDOS. The LDOS is defined as the density of eigenvalues in a particular energy interval at a given grid-point. The LDOS in the ith energy window \(\left( {\varepsilon _i - \frac{{\delta \varepsilon }}{2},\varepsilon _i + \frac{{\delta \varepsilon }}{2}} \right)\) can be obtained from the partial charge density as follows,
where \(\rho _{{\mathrm{partial}}}^i\) is the partial charge density arising from wavefunctions with eigenenergies in the \(\left( {\varepsilon _i + \frac{{\delta \varepsilon }}{2},\varepsilon _i - \frac{{\delta \varepsilon }}{2}} \right)\) energy window, ψn,k(r) is wavefunction at the nth band and k-point k, and \(\mathop {\sum}\nolimits_k\) denotes summation over all k-points. A 0.1 eV energy window width (δε) was used to sample the LDOS spectrum, which was further subjected to a Gaussian smearing of 0.2 eV. With respect to the VASP training data utilized in this study, the grid-based LDOS was constructed from multiple PARCHG files (one for every energy window).
PE slab data generation
Four PE polymer chains were constructed with the chain direction along the z-axis. Each polymer chain consisted of 10 carbon and 20 hydrogen atoms (120 atoms in the entire supercell). A 10 Å vacuum spacing was created in the x-direction. Classical MD (NVT) using OPLS-AA potentials was performed on the slab for 2 ns with a time-step of 1 fs at 300 K. Ten structures were chosen from the trajectory of the last 1 ns of the run.
Al slab data generation
A six-atomic layer-thick Al (001) slab was constructed with 144 atoms as depicted in Figure S1(a). A 20 Å vacuum spacing between the two surfaces was utilized. Ab initio MD at 300 K was performed on the slab for 2000 time-steps with a time-step size of 2 fs. Ten structures were then chosen at random from the generated trajectory to be included in the dataset.
Fingerprint details
The scalar fingerprint, Sk, is already rotationally invariant. The rotationally invariant form of the vector fingerprint is,
The three rotationally invariant forms of the tensor fingerprint are,
The width of the narrowest Gaussian utilized was 0.25 Å and the width of the widest Gaussian was 5 Å. Therefore, 16 Gaussians of widths ranging from 0.25 to 5 Å (sampled on a logarithmic grid) were utilized to fingerprint the grid-point. Prior to the training phase, each fingerprint column was scaled to a mean of zero and variance of one. Our initial convergence tests indicate (as depicted in the inset of Figure S4) that 16 Gaussians are more than sufficient to model both Al and PE systems. However, a more in depth system-dependent analysis of the range and number of Gaussians would likely reduce the error even further.
Neural network details
The high-level neural network API, Keras, was utilized to build the models. We used the mean-squared-error as the loss function and employed the ADAM stochastic optimization method for gradient descent. The neural network for learning/predicting the charge density consisted of three hidden layers (each with 300 neurons). The convergence of the neural network hyperparameters is indicated in Figure S5. A batch size of 5000 grid-points was used during the training phase. The neural network for the LDOS training/prediction possessed an additional fourth recurrent layer preceding the output layer. Ten recurrent neurons were linked to each of the final energy windows. In all neural networks, the RelU activation function was utilized. The charge density models took approximately an hour to train on a single GP100 GPU, whereas the recurrent neural network model for DOS took approximately 5–6 h for training.
Data availability
The data used to generate the models (and the train-validation-split details) are available online at https://khazana.gatech.edu.
References
LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436 (2015).
Geiger, A., Lenz, P. & Urtasun, R. Are we ready for autonomous driving? The KITTI vision benchmark suite. In 2012 IEEE Conference on Computer Vision and Pattern Recognition, IEEE, Piscataway, NJ, USA, 3354–3361 (2012).
Mueller, T., Kusne, A. G. & Ramprasad, R. Machine learning in materials science: recent progress and emerging applications. Rev. Comp. Ch. 29, 186–273 (2016).
Huo, H. & Rupp, M. Unified representation for machine learning of molecules and crystals. Preprint (2017) https://arxiv.org/abs/1704.06439.
Bartók, A. P., Payne, M. C., Kondor, R. & Csányi, G. Gaussian approximation potentials: the accuracy of quantum mechanics, without the electrons. Phys. Rev. Lett. 104, 136403 (2010).
Rupp, M., Tkatchenko, A., Müller, K.-R. & Von Lilienfeld, O. A. Fast and accurate modeling of molecular atomization energies with machine learning. Phys. Rev. Lett. 108, 058301 (2012).
Behler, J. & Parrinello, M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett. 98, 146401 (2007).
Botu, V. & Ramprasad, R. Learning scheme to predict atomic forces and accelerate materials simulations. Phys. Rev. B 92, 094306 (2015).
von Lilienfeld, O. A., Ramakrishnan, R., Rupp, M. & Knoll, A. Fourier series of atomic radial distribution functions: a molecular fingerprint for machine learning models of quantum chemical properties. Int. J. Quantum Chem. 115, 1084–1093 (2015).
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. 136, B864–B871 (1964).
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133 (1965).
Ramprasad, R., Batra, R., Pilania, G., Mannodi-Kanakkithodi, A. & Kim, C. Machine learning in materials informatics: recent applications and prospects. npj Comput. Mater. 3, 54 (2017).
Jain, A., Shin, Y. & Persson, K. A. Computational predictions of energy materials using density functional theory. Nat. Rev. Mater. 1, 15004 (2016).
Mannodi-Kanakkithodi, A. et al. Rational co-design of polymer dielectrics for energy storage. Adv. Mater. 28, 6277–6291 (2016).
Mannodi-Kanakkithodi, A. et al. Scoping the polymer genome: a roadmap for rational polymer dielectrics design and beyond. Mater. Today 21, 785–796 (2018).
Mounet, N. et al. Two-dimensional materials from high-throughput computational exfoliation of experimentally known compounds. Nat. Nanotechnol. 13, 246 (2018).
Tabor, D. P. et al. Accelerating the discovery of materials for clean energy in the era of smart automation. Nat. Rev. Mater. 3, 5–20 (2018).
Botu, V. & Ramprasad, R. Adaptive machine learning framework to accelerate ab initio molecular dynamics. Int. J. Quantum Chem. 115, 1074–1083 (2015).
Behler, J. Atom-centered symmetry functions for constructing high-dimensional neural network potentials. J. Chem. Phys. 134, 074106 (2011).
Schütt, K. et al. Schnet: a continuous-filter convolutional neural network for modeling quantum interactions. In Advances in Neural Information Processing Systems 30 (eds Guyon, I. et al.) 991–1001 (Curran Associates, Inc., 2017). http://papers.nips.cc/paper/6700-schnet-a-continuous-filter-convolutional-neural-network-for-modeling-quantum-interactions.pdf.
Botu, V., Batra, R., Chapman, J. & Ramprasad, R. Machine learning force fields: construction, validation, and outlook. J. Phys. Chem. C 121, 511–522 (2017).
Kolb, B., Lentz, L. C. & Kolpak, A. M. Discovering charge density functionals and structure-property relationships with prophet: a general framework for coupling machine learning and first-principles methods. Sci. Rep. 7, 1192 (2017).
Huan, T. D. et al. A universal strategy for the creation of machine learning-based atomistic force fields. npj Comput. Mater. 3, 37 (2017).
Smith, J. S., Isayev, O. & Roitberg, A. E. Ani-1: an extensible neural network potential with dft accuracy at force field computational cost. Chem. Sci. 8, 3192–3203 (2017).
Imbalzano, G. et al. Automatic selection of atomic fingerprints and reference configurations for machine-learning potentials. J. Chem. Phys. 148, 241730 (2018).
Bianchini, F., Kermode, J. R. & Vita, A. D. Modelling defects in Ni–Al with eam and dft calculations. Model. Simul. Mater. Sci. Eng. 24, 045012 (2016).
Khaliullin, R. Z., Eshet, H., Kühne, T. D., Behler, J. & Parrinello, M. Nucleation mechanism for the direct graphite-to-diamond phase transition. Nat. Mat. 10, 693 (2011).
Meredig, B. et al. Combinatorial screening for new materials in unconstrained composition space with machine learning. Phys. Rev. B 89, 094104 (2014).
Sharma, V. et al. Rational design of all organic polymer dielectrics. Nat. Commun. 5, 4845 (2014).
Kim, C., Pilania, G. & Ramprasad, R. Machine learning assisted predictions of intrinsic dielectric breakdown strength of abx3 perovskites. J. Phys. Chem. C 120, 14575–14580 (2016).
Xue, D. et al. Accelerated search for materials with targeted properties by adaptive design. Nat. Commun. 7, 1–9 (2016).
Huan, T. D. et al. A polymer dataset for accelerated property prediction and design. Sci. Data 3, 160012 (2016).
Mannodi-Kanakkithodi, A., Pilania, G., Huan, T. D., Lookman, T. & Ramprasad, R. Machine learning strategy for accelerated design of polymer dielectrics. Sci. Rep. 6, 20952 (2016).
Pilania, G. et al. Machine learning bandgaps of double perovskites. Sci. Rep. 6, 19375 (2016).
Balachandran, P. V. et al. Predictions of new ABO3 perovskite compounds by combining machine learning and density functional theory. Phys. Rev. Mater. 2, 043802 (2018).
Sanchez-Lengeling, B. & Aspuru-Guzik, A. Inverse molecular design using machine learning: generative models for matter engineering. Science 361, 360–365 (2018).
Snyder, J. C., Rupp, M., Hansen, K., Müller, K.-R. & Burke, K. Finding density functionals with machine learning. Phys. Rev. Lett. 108, 253002 (2012).
Montavon, G. et al. Machine learning of molecular electronic properties in chemical compound space. New J. Phys. 15, 1305.7074 (2013).
Schütt, K. T. et al. How to represent crystal structures for machine learning: towards fast prediction of electronic properties. Phys. Rev. B 89, 205118 (2014).
Brockherde, F. et al. Bypassing the kohn-sham equations with machine learning. Nat. Commun. 8, 872 (2017).
Schütt, K. T., Sauceda, H. E., Kindermans, P.-J., Tkatchenko, A. & Müller, K.-R. Schnet–a deep learning architecture for molecules and materials. J. Chem. Phys. 148, 241722 (2018).
Graves, A., Mohamed, A. & Hinton, G. Speech recognition with deep recurrent neural networks. In 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, IEEE, Piscataway, NJ, USA, 6645–6649 (2013).
Ruddigkeit, L., van Deursen, R., Blum, L. C. & Reymond, J.-L. Enumeration of 166 billion organic small molecules in the chemical universe database gdb-17. J. Chem. Inf. Model. 52, 2864–2875 (2012).
Ramakrishnan, R., Dral, P. O., Rupp, M. & Von Lilienfeld, O. A. Quantum chemistry structures and properties of 134 kilo molecules. Sci. Data 1, 140022 (2014).
Acknowledgements
The authors would like to thank XSEDE for the utilization of Stampede2 cluster via project ID “DMR080058N”. This work is supported by the Office of Naval Research through N0014-17-1-2656, a Multi-University Research Initiative (MURI) grant.
Author information
Authors and Affiliations
Contributions
R.R. conceptualized the paradigm of using machine learning to learn the charge density and DOS (and as a result, the energy) as a proxy to solving the Kohn-Sham equation. R.R. and A.C. conceptualized the scalar, vector, and tensor fingerprints as systematic functions of Gaussians and their corresponding partial derivatives. R.R. conceptualized the vector and tensor rotational invariants. A.C. conceptualized the grid-point-based learning of the LDOS using a combination of the aforementioned fingerprints and recurrent neural networks. A.C. developed and implemented the python-based codes and neural network models. D.K. and R.B. contributed to data preprocessing codes and data generation. L.C. contributed to DFT data generation. C.K. contributed to stream-lining of the prediction platform. All authors contributed to the development of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chandrasekaran, A., Kamal, D., Batra, R. et al. Solving the electronic structure problem with machine learning. npj Comput Mater 5, 22 (2019). https://doi.org/10.1038/s41524-019-0162-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-019-0162-7
This article is cited by
-
First-principles data for solid solution niobium-tantalum-vanadium alloys with body-centered-cubic structures
Scientific Data (2024)
-
Electronic structure prediction of multi-million atom systems through uncertainty quantification enabled transfer learning
npj Computational Materials (2024)
-
Recent advances in machine learning interatomic potentials for cross-scale computational simulation of materials
Science China Materials (2024)
-
Accurate nano-photonic device spectra calculation using data-driven methods
Applied Physics A (2024)
-
Linear Jacobi-Legendre expansion of the charge density for machine learning-accelerated electronic structure calculations
npj Computational Materials (2023)