Abstract
DNA/single-wall carbon nanotube (SWCNT) hybrids have enabled many applications because of their special ability to disperse and sort SWCNTs by their chirality and handedness. Much work has been done to discover sequences which recognize specific chiralities of SWCNT, and significant progress has been made in understanding the underlying structure and thermodynamics of these hybrids. Nevertheless, de novo prediction of recognition sequences remains essentially impossible and the success rate for their discovery by search of the vast single-stranded DNA library is very low. Here, we report an effective way of predicting recognition sequences based on machine learning analysis of existing experimental sequence data sets. Multiple input feature construction methods (position-specific, term-frequency, combined or segmented term frequency vector, and motif-based feature) were used and compared. The transformed features were used to train several classifier algorithms (logistic regression, support vector machine, and artificial neural network). Trained models were used to predict new sets of recognition sequences, and consensus among a number of models was used successfully to counteract the limited size of the data set. Predictions were tested using aqueous two-phase separation. New data thus acquired were used to retrain the models by adding an experimentally tested new set of predicted sequences to the original set. The frequency of finding correct recognition sequences by the trained model increased to >50% from the ~10% success rate in the original training data set.
Similar content being viewed by others
Introduction
In recent years, machine learning has emerged as a powerful general methodology with the ability to create well-performing predictive models from data. In particular, these techniques have become essential in bioinformatics because it is impractical to transform manually large amounts of raw sequence data into useful scientific knowledge, without requiring explicit programming instruction. Many of the important bioinformatics problems are well suited for classification algorithms, including gene annotation,1 protein function prediction,2,3 peptide binding prediction,4,5 and DNA binding prediction.6
Single-wall carbon nanotubes (SWCNTs) comprise a family of nanomaterials with remarkable electronic, optical, and mechanical properties.7 The structure of SWCNTs can be viewed as a cylinder obtained by rolling a hexagonal graphene sheet. The properties of SWCNTs are highly dependent on exactly how the graphene sheet is rolled, which is identifiable by chiral indices (n,m); all synthetic methods result in mixtures of different chiralities. Especially for electronic and optical applications, chirality control of the SWCNTs is of critical importance.8,9 A number of strategies for SWCNT separation by their chirality have been developed,10,11,12 and notable success has been achieved using special short DNA sequences called recognition sequences.13,14 These recognize specific corresponding partner SWCNTs by forming special hybrids with sufficiently different physical and chemical properties to enable their separation from mixtures.15 Furthermore, there is evidence that special recognition DNA/SWCNT hybrids are also effective as biosensors for specific molecular detection.16,17,18
Several studies have contributed to our understanding of the structural basis for sequence-specific recognition. Computational molecular modeling19,20,21,22,23 has established a number of ordered structural motifs that single-stranded DNA (ssDNA) can adopt when adsorbed onto an SWCNT. Single-molecule force spectroscopy,24,25 and solution-based studies have provided quantitative information on strength of association between ssDNA and SWCNTs.26,27 Aqueous two-phase (ATP) separations have been analyzed to quantify solubility of DNA-SWCNTs,14,28,29 and fluorescence quenching studies have been used to infer wrapping structures of recognition sequences.30
Despite all this knowledge and understanding, we have essentially no ability to predict ssDNA sequences that will form recognition pairs with SWCNTs. Discovery of new recognition sequences has relied upon systematic searches through the vast sequence space of ssDNA. For example, Tu et al.31 designed a systematic search of the DNA library by sequence pattern expansion, and achieved a success rate of ~7%. In another recent study28 some sequence patterns were found in a directed and limited search of a reduced (12-mer, T/C bases only) DNA library, achieving somewhat better performance (success rate of ~10%). We may surmise that the probability of finding a recognition sequence, conditioned upon this sequence expansion scheme, is no better than about 10%. Thus, although we have a lot of physical understanding and a reasonable amount of data, our ability to predict recognition sequences is still absent, and the search process remains time-consuming and inefficient—the number of distinct sequences in the sequence space is enormous. (For the typical sequence lengths l in the range 10–30, there are 106–1018 distinct sequences.) Clearly, a different and more systematic approach to sequence prediction is needed.
Here, we investigate a new approach to prediction of recognition sequences using machine learning (ML) techniques. The aim is to create models to classify query sequences as either recognition or non-recognition. Multiple input feature construction methods including n-gram position-specific vector (psv), n-gram term-frequency vector (tfv), combined or segmented tfv, and motif-based features6,32 were used. The models were built using a machine learning tool (WEKA).33 As an initial study for the work presented in this manuscript, we manually tried all the algorithms that the WEKA package provides for binary classification using unigram and trigram psv features. This preliminary study showed that artificial neural network and random-forest methods worked best. However, both are of similar complexity. We decided to try three different algorithms, each algorithm representing a different level of complexity. Specifically, we used three different algorithms: logistic regression (LR, simplest),34 support vector machine (SVM, moderately complex),35 and artificial neural network (ANN, most complex)35.
After training and validation using labeled data, they were used to predict new recognition sequences. The relatively small data set size, a common issue in applying machine learning techniques to problems in materials science,36 was mitigated by choosing consensus sequences from a number of models, i.e., we combined multiple models by cross-validation and selected the sequences only from the intersection of each set of classifier results. Predictions were tested experimentally using the ATP separation technique.37 We retrained the model using the updated data set. This cycle of prediction, testing, and retraining was repeated twice. Models were built on DNA sequence information only. To interpret the results in the context of previous computational19,20,21,22,23 and experimental work,14,24,25,26,27,28,29 we examined discovered motifs using saliency measures within the ANN models.
Results and discussion
Initial models—training, validation, prediction, and evaluation
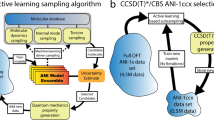
The overall scheme of our approach is shown in Fig. 1. During the first round of learning, the models were trained by using three types of algorithms (LR, SVM, and ANN) with n-gram psv and tfv (n = 1–3) using the dataset described in data collection section (listed in Table S1). The final models that gave the highest precision were chosen. This is because precision is directly related to the ability to find new recognition sequences (TP) correctly in the experiment, which is the most labor-intensive and time-consuming part of the entire process. The performance of models is shown in Tables S2 and S3. Once a model was built, we generated a query sequence set, including all possible sequences (~212). These were then classified as recognition or non-recognition sequence using each of our previously trained models. Each model typically predicted hundreds of recognition sequences, still far too many to test. Furthermore, because our training set is small relative to the size of the query sequence set (i.e. 82 vs. 4014), one needs to be wary of overfitting. To resolve these issues, we combined multiple models by cross-validation; sequences for experimental testing were selected only from the intersection of each set of classifier results.
Overall scheme to develop a model to predict and test DNA recognition sequences. First, the training data set is collected using the ATP technique. If the DNA/CNT hybrid can allow partitioning one type of SWCNT in either the top or the bottom phase, that sequence is labeled as a recognition sequence (“Y”). This is done via the NIR absorbance spectra of sorted fractions. Once the data are collected, the DNA sequences and their labels are encoded to a numeric vector, which is called input feature construction. Then, the models with three different types of classification algorithms are trained using the training set feature vectors. A generated query sequence set including all possible sequences (~212) in the 12 mer C/T library are then classified using the trained models. Limitations due to small data set size are mitigated by choosing the consensus of a number of models. The predicted recognition sequences are tested using the ATP technique again. The new data are added to the existing labeled sequence data and the models are retrained. This procedure was repeated twice
We experimentally tested the ten most frequently occurring sequences among the sequences predicted to be recognition by our classifiers (Table 1). We identified five sequences (labeled “Y”) that lead to partitioning of only one particular (n,m) SWCNT species with high yield. Figure 2 shows the absorbance spectra of the purified SWCNT species by the five sequences and the starting material. In each spectrum of the purified species, the observed sharp peaks correspond to the characteristic optical transitions of a particular (n,m) species. Considering the prediction efficiency, this is a remarkable result, with prediction efficiency of 50%, a significant improvement over the ~10% frequency of recognition sequences in the training set.28 We also found two marginal sequences that could not safely be classified as recognition sequence because they had insufficient yield or selectivity although they did show enrichment of a particular (n,m) SWCNT species in a given phase. These sequences were labeled as non-recognition sequence in order to maximize stringency of “Y” labels in the training set.
Absorbance spectra of SWCNT species purified by ATP using new sequences and the starting CoMoCAT (EG150X) mixture. The SWCNT species have been identified by their E11 and E22 peak positions (M11 for metallic species). Each spectrum is normalized at the E11 peak position (M11 for metallic species) and the baseline level of each spectrum was manually offset for visual clarity
The previously trained models were then evaluated based on their prediction errors on the newly tested sequences using Eq. (1) (depicted as a heat map in Figure S2(a)). The total prediction errors among the models using psv are not significantly different from each other, while the models using tfv showed considerable difference. Compared within the same input feature construction method, the trigram ANNs are better on both, showing a normalized prediction error of 0.38 and 0.423 for psv and tfv, respectively.
Retrained models—training, validation, and prediction
In the second round of learning, the training set was updated by including newly determined sequences by ATP separation, and the models were retrained. Ten new recognition sequences (S11–S20) were predicted and tested experimentally.
Although most retrained models showed improved validation performance (Tables S4 and S5), the actual prediction performance of 50% remained the same as that of the initial models (Table 1, Fig. 2). Note that only one sequence was determined as non-recognition sequence and the remaining four were deemed marginal (Table 1). This indicates that the retrained models performed somewhat better than initial models but not well enough to drastically increase the prediction efficiency. Four of ten predicted sequences interestingly have an ability to purify (8,5) species. Evidently, our retrained models are likely to predict recognition sequences for the (8,5) species.
Design of improved models
In the first round, to find optimal models, we used cross-validation. Although cross-validation is designed to minimize overfitting, there is still some concern because the validation set is not independent of the training set. In the second phase, we estimate the model performance based on the prediction errors calculated using a newly tested sequence set that is independent of training sets.
Figure S2(b) shows the prediction errors of the retrained models. In general, the models with tfv gave smaller error than models with psv. For the models with psv, bigram ANN, and trigram ANN and LR perform much better (with the error of 0.394, 0.405, and 0.42, respectively) than others. Among the models with tfv, trigram LR and ANN showed smaller error of 0.317 and 0.324.
Although the prior models already showed very good performance, we explored improved training methods to further enhance the prediction accuracy in the next round of experiments. First, we selected and focused on tfv, for its ability to handle sequences of different lengths. Next, we dropped the use of SVM since validation results revealed that SVM models are generally poor (Tables S2–S5 and Figure S2). We also found that the models with small n-gram of psv and tfv showed poor performance (Tables S2–S5), so higher n-gram (n = 3–5) tfv were examined in second retrained models. For ANN models, in most cases we found best performance with a single layer. Additionally, given the size of our training set, we restricted Nl to be single and Nh to be no larger than twice the size of the feature vector to avoid overfitting.
The overall optimization was previously performed on the precision because it is more important to classify actual non-recognition sequence incorrectly (i.e., low FP) than to classify actual recognition sequence incorrectly (i.e., high FN) when we test the predicted sequences in the lab. However, a better indicator of model quality should account for both FP and FN, so F1 and S scores were subsequently used for optimization. Furthermore, additional feature construction methods were examined as described in Feature construction section.
Motifs were searched for by the motif-mining tool, MERCI,32 with the minimal occurrence frequency for positive sequences fP and the maximal occurrence frequency for negative sequences fN. To avoid overfitting, the length of motifs is limited to be 5−7 bases for recognition motifs and five bases for nonrecognition motifs. In order to calculate the conditional probabilities, all possible motifs were found by setting fP to be 1 (i.e., a motif occurs at least once in the positive set) and fN to be the maximum number, 83 for second updated training set (i.e., a motif occurs anywhere in the negative set). Motifs (Figure S1) were ranked according to their conditional probabilities of recognition (denoted as “Y”) or non-recognition (denoted as “N”) sequences given motif, \(P\left( {Y\;or\;N|{\mathrm {motif}}} \right)\), and top ten motifs were chosen for both sets (Table S7).
Finally, we retrained the models using LR and ANN with simple tfv, combined or segmented tfv, and motif-based features using the updated training set (Table S8 and Figure S3).
Top five models that gave the highest F1 scores are listed in Table 2. In general, ANN showed better performance than LR, and trigram tfv and motif-based features showed high performance. ANN with simple trigram tfv (tfv3) shows the best performance, while the combined bigram and trigram tfv (tfv2–3) and bi-segmented trigram tfv (tfv2,3) show third best performances. It is interesting that combined or segmented trigram tfv do not perform better than simple tfv, even though they already contain simple tfv inside. This implies that irrelevant features can cause poor performance, which leads to the need for a saliency analysis.
Saliency analysis and overall observations
The saliency measures can be used to identify important input features. Figure S6 shows that the saliency of segmented tfv4,3 ANN models is high in the features of the first and last segment (i.e., at the ends of the sequences). Previous studies on the displacement of ssDNA by surfactants26,27 suggest that the difference between recognition and non-recognition sequences is due to structural differences at sequence ends. Saliency results support that experimental finding.
Saliency also can be used to study model performance by examining the number of irrelevant features, defined by when the standard deviation is larger than the mean value. We rank models by the ratio of the irrelevant to total features. The top four models with lowest irrelevant feature ratio are tfv3, motif-based feature with Lrec ≤ 7, the combined tfv2–3, and tfv1–2–3. These four are also the top four ANN models based on the validation results.
Figure S8 shows the n-gram frequency of the final training set. Recognition sequences evidently contain higher frequency of “CCC”, especially in the newly discovered sequences (red box). This is consistent with a previous experimental finding.28
Conclusion
The DNA/SWCNT hybrid system comprises a vast set of sequence/(n,m) combinations. A small fraction of these form recognition pairs that allow separation of individual (n,m) SWCNT from a mixture. Our considerable knowledge about their structure and thermodynamics has not previously translated into an ability to predict recognition sequences. Here, we systematically applied machine learning techniques to predict recognition sequences. For simplicity and illustrative purposes, we restricted ourselves to 12-mer sequences with a 2-letter alphabet (C & T). ML models were trained on available data, and retrained twice based on new experimental data. We showed a remarkable increase in the frequency of recognition sequences from 10% in the original training set to >50% in the model-predicted sequence sets.
To design an improved model, detailed analyses were carried out. Performance was measured in terms of evaluation parameters (F1 score) by cross-validation and prediction errors on the newly tested sets. Often model performance depends strongly on choice of sequence representation by input features. We chose a number of feature representation methods including tfv, psv, and mixed models. These methods have competing advantages when it comes to capturing information embedded in a set of sequences. When predicting new sequences to be tested experimentally, we chose on the basis of consensus of a number of methods, on the notion that the intersection of predictions made by different models would mitigate the limitations of our data set size and feature encoding schemes.
Among individual models, prediction performance of the tfv models was generally better than psv; trigram tfv models showed smaller prediction error. Based on these analyses, we directed attention to ANN and LR using tfv. We also explored new input feature construction methods such as combined or segmented tfv, and motif-based features. We obtained highly encouraging models that showed an improved F1 score of ~27% when compared to the best previous model. In general, the ANN algorithm in combination with trigram tfv showed the best performance.
As aids to model interpretation, we investigated the discovered motif and feature saliency. We found that the top ranked motifs found with no motif-length limitation contained at least eight bases. This result may suggest that at least eight bases are needed to tightly wrap around SWCNT to exhibit a specific binding characteristic. According to the saliency analysis, the sequence at the ends contributes more to the classification, consistent with experiment.26,27
One may question the representation of recognition DNA sequence prediction as a binary classification problem, since each pairs with a different SWCNT. Success despite this assumption indicates that recognition sequences may share common features although individual recognition sequences recognize a particular (n, m) species. Although our model is promising, we believe that there is considerable room for improvement. For example, recognition sequences differ in terms of selectivity, represented by purification yield. Some special sequences are known to be capable of separating enantiomers28. Yet, in the current model, these are all assigned the same label/score.
These considerations suggest future research in two major directions: one is to develop resolution-based multi-level classification. For example, multi-level classification would allow us to capture improvement in the model between the first and second rounds of experiment by allowing cases labeled as N* to be accounted for as their own level of classification. The other is the study of methods for the interpretability of ML models such as saliency analysis. More broadly, bio/nano hybrid materials made of inorganic nanostructures and sequence-defined polymers such as DNA and peptides represent an emerging class of materials that have many promising applications. Design of this new class of material inevitably has to solve the challenging problem of efficient exploration of a vast sequence space. The learnings we obtained in this work should provide some insight to the more general sequence selection problem.
Methods
Data collection
The available data on ssDNA sequences that form recognition pairs with specific SWCNTs have been obtained under varying conditions (e.g., solution conditions), sequence lengths (~8–30), and classification methods (ion-exchange chromatography, ATP, etc.). Here, we chose a recently reported set of sequences28 that were all handled under identical conditions. To reduce complexity, in this set the DNA base type was restricted to the 2-letter (Thymine;T/Cytosine;C) alphabet and DNA length was fixed to be 12 bases. This set initially contained nine recognition sequences (labeled as “Y”) and 73 nonrecognition sequences (labeled as “N”).
To test our predicted sequences experimentally, we utilized the ATP separation technique. Preparation of DNA/SWCNT hybrids and ATP separation followed the protocols described in ref. 37. Briefly, CoMoCAT SWCNTs (1 mg, SG65i grade and EG150X grade; Southwest Nanotechnologies) were suspended in 1 mL of deionized water with 0.1 M NaCl (Sigma-Aldrich) and 2 mg ssDNA (Integrated DNA Technologies). The DNA/SWCNT mixture was dispersed using tip sonication with a power output of 8 W for 1.5 h in an ice bath. The dispersion was then centrifuged at 16,000 × g for 1.5 h and the supernatant was collected. Typically, an ATP system comprising 7.76% PEG (MW 6 kDa, Alfa Aesar) and 15% polyacrylamide (PAM, 10 kDa, Sigma-Aldrich), denoted as PEG/PAM, was used for SWCNT separation, but 16% poly(vinylpyrrolidone) (PVP, MW 10 kDa, Sigma-Aldrich) and 11% Dextran 70 (DX, MW ∼70 kDa, TCI) ATP system, denoted as PVP/DX, was used for some of the DNA/SWCNT hybrids. Both DX and PVP were used as DNA/SWCNT partition modulators. UV−vis−NIR absorbance measurements were performed on a Varian Cary 5000 spectrophotometer over the wavelength range of 200−1400 nm.
Feature construction
We wish to build models that predict the class to which a sequence belongs (i.e., recognition or non-recognition). Choice of sequence representation by features is important for classifier algorithms to function well. We investigated several input feature construction (or sequence encoding) methods: position-specific vector (psv), term frequency vector (tfv), combined tfv, segmented tfv, and motif-based feature vector (mfv), described schematically in Fig. 3.
Overview of input feature construction methods explored. Feature types can be broadly categorized into two types: n-gram-based and pattern-based. The n-gram feature vectors represent DNA sequences as a collection of n-gram entities in a position-specific manner (psv), in terms of appearance frequency (tfv), or some combination of these two. In the pattern-based feature vector, following discovery of motifs in the training set, the DNA sequences are represented by the occurrence or absence of a given motif in that sequence
A common input feature construction technique in bioinformatics is fixed-length overlapping n-gram analysis, which breaks sequences into subsequences using various types of vocabulary, in the case of DNA the nucleotides or the codon types.38 Using the method, sequences can be represented by overlapping n-gram patterns.
The position-specific vector (psv) encoding method uses an indicator vector to represent each n-gram word at each position. Thus, a given sequence S can be represented by \({psv_n}(S) = \left\{ {w_{{i}{1}},w_{{i}{2}}, \ldots,w_{{i}{l}}} \right\}\), where \({w_{{i}{j}}} \in\) n-gram vocabulary; l is the number of positions that is given by (L − n + 1); L is sequence length. For example, for the sequence A = TTCTCC, with n = 2, \({w_{{i}{j}}} {\in} \left\{ {{\mathrm {{T}{T}}},{\mathrm {{T}{C}}},{\mathrm {{C}{T}}},{\mathrm {{C}{C}}}} \right\}\) and \(\it{psv_2}(A) = \left\{ {{\mathrm {{T}{T}}},{\mathrm {{T}{C}}},{\mathrm {{C}{T}}},{\mathrm {{T}{C}}},{\mathrm {{C}{C}}}} \right\}\). To enter into the ML models, the psv is converted into binary features using the one-attribute-per-value approach (i.e., {TT, TC, CT, CC} ~ {(1,0,0,0), (0,1,0,0),…, (0,0,0,1)}) by a built-in function in WEKA.33 The psv represents the entire base position information but is not suitable for long sequences as the size of the feature vector becomes large. In addition, sequences with different lengths cannot be compared easily, because they result in feature vectors of different sizes.
The term frequency vector (tfv) defines the feature vector using the frequency of the n-gram in the sequence. For sequence A, \(\it {tfv_2}(A) = \left\{ {\mathrm{1/5,2/5,1/5,1/5}} \right\}\). The tfv method loses global positional sequence information—several different sequences correspond to the same tfv—unless the word length approaches that of the sequence itself. The psv method, on the other hand, contains the complete sequence information in that there is a 1–1 mapping between psv and the original sequence, but by treating each base as a feature it does not capture more complex features very efficiently. The tfv method is computationally inexpensive, and can accommodate different sequence lengths.39 However, it has a limitation that many sequences give the same tfv, e.g, \({\it tfv_1}(T_{12}) = {tfv_1}(T_{13}) = \left\{ {1,0} \right\}\), especially for small n.
Previous work28 suggests that both frequency and position information could be important for sequence prediction, and so we considered a new encoding scheme that combines features of psv and tfv. The basic idea of the method is to divide a sequence into m (m ∈ [1,L]) smaller segments of roughly equal length ls (ls = L/m). We construct a tfv for each segment, and then tfv for the entire sequence S in the following way to include position information of each segment: \({{\mathrm {tfv}}_{m,n}}(S) = \{ {{\mathrm {tfv}}_n}({\mathrm {seg}}_1),{{\mathrm {tfv}}_n}({\mathrm {seg}}_2), \ldots ,{{\mathrm {tfv}}_n}({\mathrm {seg}}_m)\}\). Contribution to the tfv from terms that straddle segment boundaries are made according to a weighted average of their occupancy in either segment. For example, for sequence A, where m = 2 and n = 2, segment 1 = TTC, segment 2 = TCC, and overlapped segment = CT, so \({\it tfv_{2,2}}(A) = \left[ {\left\{ {1/2.5,1/2.5,0.5/2.5,0} \right\},\left\{ {0,1/2.5,0.5/2.5,1/2.5} \right\}} \right]\).
With a similar purpose in mind, but in a simpler way, a combined tfv method was also investigated. Using n-grams with different n, different properties can be captured. For example, unigram is based only on the base frequency, while trigram captures some of the location information as well as their frequency. Thus, by combining different n-gram features, one can capture more information. The combined tfv can be formed as following: \({\it tfv_{1 - 2 - \cdots - k}}(\it{S}) = \{ {{tfv}_1}(S),{{tfv}_2}(S), \ldots ,{tfv_k}(S)\}\).
We next considered features based on motifs. The basic hypothesis of this method is that there are recurring patterns or motifs in the DNA sequence which recognize a special type of SWCNT. We employed a motif-discovery tool called MERCI32 to search for motif patterns. In order to systematically select discriminative motif features, we ranked the motifs based on their conditional probabilities that a sequence is labeled “Y”, given motif: \(P\left( {Y|{\mathrm {motif}}} \right)\). The top ten recognition and non-recognition motifs were chosen for use as features. Maximum motif lengths were limited to 5–7 bases for recognition motifs and five bases for nonrecognition motifs. The extracted motifs were coded as a 20-dimensional binary feature vector, mfv. Entry m is set to “1” if motif m occurs in a given sequence and “0” otherwise.
Note that the range of all feature vectors were rescaled to the range in [−1, 1] to weigh all features equally.
Learning, validation, and evaluation
We began by evaluating a number of common learning algorithms for binary classification: logistic regression (LR) with ridge estimator,40 support vector machine (SVM) using sequential minimal optimization (SMO),41 and feedforward artificial neural network (ANN). To build and validate the classification models, we employed the open-source machine learning tool WEKA33.
To optimize the artificial neural network models, we trained them with different numbers of hidden layers (Nl) and hidden nodes (Nh). Additionally, we optimized the cost factor γ, the ratio of false positive to false negative “cost” to vary from “1”. By maximizing γ, we reduce the chance of failure in follow-up experiments.
We also tried automated ML packages to explore all models and adjust the hyperparameters automatically using the Auto-WEKA42 and “h2o”43 AutoML packages. Both packages return choices for algorithms and hyperparameters—examples are provided in SI. However, because of lack of transparency, we decided to focus on the three chosen algorithms along with “manual” optimization of hyperparameters.
The performance of each of the classifiers was evaluated using a standard tenfold cross-validation. Because the sample set is relatively small, and examples with the “Y” label smaller still, we chose not to use strategies that include training, test, and validation subsets. Instead of so splitting the training set, we tested our models by using them to predict new sets of sequences that were tested experimentally. Evaluation results can be examined by the confusion matrix, which reports the number of true positive (TP), false positive (FP), false negative (FN), and true negative (TN) predictions. To measure prediction quality, we computed the conventional evaluation parameters such as precision \(\left( {{\mathrm{Prc}} = \frac{{{\mathrm {TP}}}}{{{\mathrm {TP}}\,+\,{\mathrm {FP}}}}} \right)\), recall \(\left( {\mathrm{R} = \frac{{{\mathrm {TP}}}}{{{\mathrm {TP}} \,+\, {\mathrm {FN}}}}} \right)\), or F1 score \(\left( {F^1 \mathrm { score}= \frac{{2{\mathrm {Prc}} \,\cdot\, {\mathrm {R}}}}{{{\mathrm {Prc}} \,+\, {\mathrm {R}}}}} \right)\).
In addition, the performance was evaluated using the area under the receiver operating characteristic (ROC) curve, known as AUC.
To validate the models with newly identified sequences, normalized prediction error E is calculated by
Here, tc is the prediction probability for each instance calculated by the classifier and t is the experimentally determined truth value, “1” for recognition sequences, “–1” for nonrecognition sequences, and “0” for marginal sequences, and n is the number of instances.
Data availability
Significant additional data generated during the current study are included in the supplementary information files. All data sets are available from the corresponding author on reasonable request. Sample data sets and scripts are available at the following repository (https://bitbucket.org/jagotagrouplehigh/dna_swcnt_ml/).
References
Gupta, R. et al. Annotation of gene promoters by integrative data-mining of ChIP-seq Pol-II enrichment data. BMC Bioinforma. 11(Suppl 1), S65 (2010).
Zhao, X.-M., Wang, Y., Chen, L. & Aihara, K. Gene function prediction using labeled and unlabeled data. BMC Bioinforma. 9, 57 (2008).
Clare, A. & King, R. D. Predicting gene function in Saccharomyces cerevisiae. Bioinformatics 19, ii42–ii49 (2003).
Nielsen, M. et al. Reliable prediction of T-cell epitopes using neural networks with novel sequence representations. Protein Sci. 12, 1007–1017 (2003).
Stiffler, M. A. et al. PDZ domain binding selectivity is optimized across the Mouse Proteome. Science 317, 364–369 (2007).
Copp, S. M., Bogdanov, P., Debord, M., Singh, A. & Gwinn, E. Base motif recognition and design of DNA templates for fluorescent silver clusters by machine learning. Adv. Mater. 26, 5839–5845 (2014).
Baughman, R. H., Zakhidov, A. A. & de Heer, W. A. Carbon nanotubes—the route toward applications. Science 297, 787–792 (2002).
Eatemadi, A. et al. Carbon nanotubes: properties, synthesis, purification, and medical applications. Nanoscale Res. Lett. 9, 393 (2014).
Yang, N., Chen, X., Ren, T., Zhang, P. & Yang, D. Carbon nanotube based biosensors. Sens. Actuators B Chem. 207, 690–715 (2015).
Nish, A., Hwang, J.-Y., Doig, J. & Nicholas, R. J. Highly selective dispersion of single-walled carbon nanotubes using aromatic polymers. Nat. Nanotechnol. 2, 640–646 (2007).
Liu, H., Nishide, D., Tanaka, T. & Kataura, H. Large-scale single-chirality separation of single-wall carbon nanotubes by simple gel chromatography. Nat. Commun. 2, 309 (2011).
Arnold, M. S., Green, A. A., Hulvat, J. F., Stupp, S. I. & Hersam, M. C. Sorting carbon nanotubes by electronic structure using density differentiation. Nat. Nanotechnol. 1, 60–65 (2006).
Tu, X., Manohar, S., Jagota, A. & Zheng, M. DNA sequence motifs for structure-specific recognition and separation of carbon nanotubes. Nature 460, 250–253 (2009).
Ao, G., Khripin, C. Y. & Zheng, M. DNA-controlled partition of carbon nanotubes in polymer aqueous two-phase systems. J. Am. Chem. Soc. 136, 10383–10392 (2014).
Zheng, M. Sorting carbon nanotubes. Top. Curr. Chem. 375, 13 (2017).
Zhang, J. et al. Single molecule detection of nitric oxide enabled by d(AT)15 DNA adsorbed to near infrared fluorescent single-walled carbon nanotubes. J. Am. Chem. Soc. 133, 567–581 (2011).
Shi, J. et al. Microbiosensors based on DNA modified single-walled carbon nanotube and Pt black nanocomposites. Analyst 136, 4916 (2011).
Landry, M. P. et al. Single-molecule detection of protein efflux from microorganisms using fluorescent single-walled carbon nanotube sensor arrays. Nat. Nanotechnol. 12, 368–377 (2017).
Johnson, R. R., Charlie Johnson, A. T. & Klein, M. L. Probing the structure of DNA−carbon nanotube hybrids with molecular dynamics. Nano Lett. 8, 69–75 (2008).
Johnson, R. R., Kohlmeyer, A., Johnson, A. T. C. & Klein, M. L. Free energy landscape of a DNA−carbon nanotube hybrid using replica exchange molecular dynamics. Nano Lett. 9, 537–541 (2009).
Roxbury, D., Manohar, S. & Jagota, A. Molecular simulation of DNA β-sheet and β-barrel structures on graphite and carbon nanotubes. J. Phys. Chem. C 114, 13267–13276 (2010).
Roxbury, D., Jagota, A. & Mittal, J. Structural characteristics of oligomeric DNA strands adsorbed onto single-walled carbon nanotubes. J. Phys. Chem. B 117, 132–140 (2013).
Shankar, A., Zheng, M. & Jagota, A. Energetic basis of single-wall carbon nanotube enantiomer recognition by single-stranded DNA. J. Phys. Chem. C 121, 17479–17487 (2017).
Manohar, S. et al. Peeling single-stranded DNA from graphite surface to determine oligonucleotide binding energy by force spectroscopy. Nano Lett. 8, 4365–4372 (2008).
Iliafar, S., Mittal, J., Vezenov, D. & Jagota, A. Interaction of single-stranded DNA with curved carbon nanotube is much stronger than with flat graphite. J. Am. Chem. Soc. 136, 12947–12957 (2014).
Roxbury, D., Tu, X., Zheng, M. & Jagota, A. Recognition ability of DNA for carbon nanotubes correlates with their binding affinity. Langmuir 27, 8282–8293 (2011).
Shankar, A., Mittal, J. & Jagota, A. Binding between DNA and carbon nanotubes strongly depends upon sequence and chirality. Langmuir 30, 3176–3183 (2014).
Ao, G., Streit, J. K., Fagan, J. A. & Zheng, M. Differentiating left- and right-handed carbon nanotubes by DNA. J. Am. Chem. Soc. 138, 16677–16685 (2016).
Yang, Y., Shankar, A., Aryaksama, T., Zheng, M. & Jagota, A. Quantification of DNA/SWCNT solvation differences by aqueous two-phase separation. Langmuir 34, 1834–1843 (2018).
Zheng, Y., Bachilo, S. M. & Weisman, R. B. Quenching of single-walled carbon nanotube fluorescence by dissolved oxygen reveals selective single-stranded DNA affinities. J. Phys. Chem. Lett. 8, 1952–1955 (2017).
Tu, X., Manohar, S., Jagota, A. & Zheng, M. DNA sequence motifs for structure-specific recognition and separation of carbon nanotubes. Nature 460, 250–253 (2009).
Vens, C., Rosso, M.-N. & Danchin, E. G. J. Identifying discriminative classification-based motifs in biological sequences. Bioinformatics 27, 1231–1238 (2011).
Frank, E., Hall, M. A. & Witten, I. H. The WEKA Workbench. Online Appendix for “Data Mining: Practical Machine Learning Tools and Techniques”, Morgan Kaufmann, Fourth Edition (2016).
Cox, D. R. The regression analysis of binary sequences. J. Roy. Stat. Soc. Ser. B (Methodol.) 20, 215–242 (1958).
Murtagh, F. Multilayer perceptrons for classification and regression. Neurocomputing 2, 183–197 (1991).
Zhang, Y. & Ling, C. A strategy to apply machine learning to small datasets in materials science. npj Comput. Mater. 4, 25 (2018).
Ao, G. & Zheng, M. Current Protocols in Chemical Biology 7, 43−51 (John Wiley & Sons Inc., New York, 2015).
Srinivasan, S. M., Vural, S., King, B. R. & Guda, C. Mining for class-specific motifs in protein sequence classification. BMC Bioinforma. 14, 96 (2013).
Vinga, S. & Almeida, J. Alignment-free sequence comparison—a review. Bioinformatics 19, 513–523 (2003).
Cessie, S. Le & Van Houwelingen, J. C. Ridge estimators in logistic regression. Appl. Stat. 41, 191 (1992).
Platt, J. Fast Training of Support Vector Machines Using Sequential Minimal Optimization, Advances in Kernel Methods - Support Vector Learning (MIT Press, 1998).
Kotthoff, L., Thornton, C., Hoos, H. H., Hutter, F. & Leyton-Brown, K. Auto-WEKA 2.0: Automatic model selection andhyperparameter optimization in WEKA. J. Mach Learning Res. 18, 1–5 (2017).
Aiello, S., Eckstrand, E., Fu, A., Landry, M. & Aboyoun, P. Machine Learning with R and H 2 O. http://h2o.ai/resources/ (2018).
Acknowledgements
We would like to thank Dr. Arun Jagota for helpful discussion and suggestions. Y.Y. was supported by a Dean’s Fellowship. This work is part of the NHI Initiative at Lehigh University.
Author information
Authors and Affiliations
Contributions
Y.Y. carried out the majority of the modeling and experimental work, analyzed the data, co-wrote the manuscript, and jointly with co-authors made decisions about progress of the research. M.Z. designed experimental protocols used, contributed to several aspects of the machine learning model including analysis of results, and co-wrote the manuscript. A.J. designed modeling approaches, jointly analyzed the results, co-wrote the manuscript and provided overall supervision for the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yang, Y., Zheng, M. & Jagota, A. Learning to predict single-wall carbon nanotube-recognition DNA sequences. npj Comput Mater 5, 3 (2019). https://doi.org/10.1038/s41524-018-0142-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-018-0142-3
This article is cited by
-
Machine learning for the discovery of molecular recognition based on single-walled carbon nanotube corona-phases
npj Computational Materials (2022)