Abstract
The discovery of high-performance functional materials is crucial for overcoming technical issues in modern industries. Extensive efforts have been devoted toward accelerating and facilitating this process, not only experimentally but also from the viewpoint of materials design. Recently, machine learning has attracted considerable attention, as it can provide rational guidelines for efficient material exploration without time-consuming iterations or prior human knowledge. In this regard, here we develop an inverse design model based on a deep encoder-decoder architecture for targeted molecular design. Inspired by neural machine language translation, the deep neural network encoder extracts hidden features between molecular structures and their material properties, while the recurrent neural network decoder reconstructs the extracted features into new molecular structures having the target properties. In material design tasks, the proposed fully data-driven methodology successfully learned design rules from the given databases and generated promising light-absorbing molecules and host materials for a phosphorescent organic light-emitting diode by creating new ligands and combinatorial rules.
Similar content being viewed by others
Introduction
Historically, the discovery of new functional materials has led to major technological advancements, and it remains an important objective to meet the ever-growing demand for various applications, such as semiconductors, displays, and batteries. To develop new materials, the stepwise procedure of molecule design, property prediction, chemical synthesis, and experimental evaluation is usually repeated until satisfactory performance is achieved. As this trial-and-error approach is time-consuming and expensive, more efficient in silico techniques, such as high-throughput computational screening (HTCS),1,2,3,4,5 have emerged during the past two decades. In HTCS, the construction of a virtual chemical library by combinatorial enumeration6,7,8 is followed by large-scale property prediction using first-principle simulation9 or machine learning,10,11 which allows efficient sorting of potential candidates for subsequent chemical synthesis. However, the success of HTCS depends on the quality of the chemical library built on the basis of researcher experience and intuition. If the virtual material pool has no solution from the beginning, the target materials cannot be found. Moreover, another chemical library should be built by modifying previous enumeration rules or adopting new fragments. Therefore, it generally suffers from a low hit rate. In addition, there is no certainty as to whether the correct chemical space is being explored.
The only way to overcome the above-mentioned issues is to devise a methodology for directly designing the target materials. In this regard, new approaches were proposed to extract latent knowledge from molecular databases, such as PubChem12 and ZINC,13 and generate the target molecules.14,15,16,17,18,19 However, they required additional incorporation of chemical knowledge in terms of design rules and predefined molecular fragments in order to construct molecular structures, and the deduced candidates were not free from heuristic instructions. Thus, we cannot be confident that the latent information in the training dataset is fully used and reflected in the outputs. In this regard, we propose an inverse design method that operates in a fully data-driven manner for targeted molecular design as illustrated in Fig. 1a. This method aims to design organic molecules that are expected to meet the given target properties in a direct manner, whereas the conventional approach designs materials first and predicts their properties subsequently. The inverse design approach extracts the molecular design knowledge hidden in the molecular database and generates new molecules on the basis of its own knowledge, thereby allowing systematic materials exploration without the need for researcher experience or intuition.
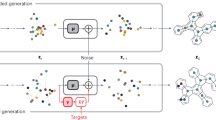
Data-driven inverse design. a Concept of inverse design: hidden knowledge for molecular design is extracted from a given molecular database in a fully data-driven manner using deep-learning, and new molecules with the target properties are generated subsequently. b Deep encoder-decoder architecture of inverse design model: the encoding and property prediction functions are obtained by a DNN using the molecular descriptor as an input, and the decoding function is obtained by an RNN using the encoding function as an input to generate the molecular identifier
The inverse design model was implemented with a deep encoder-decoder architecture inspired by neural machine language translation.20,21,22,23,24 As it is extremely difficult to directly reconstruct molecular structures from molecular descriptors used for property prediction, we had to translate the molecular descriptors into molecular structure identifiers for designing new molecules. In the proposed model, a deep neural network (DNN) and a recurrent neural network (RNN) were adopted as the encoder and the decoder, respectively.23,24,25,26 The DNN identifies the relationship between molecular structures and their material properties, and it encodes the molecular descriptors that are expected to meet the target properties. Then, the RNN reconstructs the encoded molecular descriptors into molecular structure identifiers that we can recognize as real molecular structures.27 The performance of the proposed model was evaluated by performing two design tasks for light-absorbing organic molecules and host materials for a blue phosphorescent organic light-emitting diode (OLED), followed by experimental verification. The results showed that the proposed model is effective in suggesting prominent molecular structures.
Results and discussion
Inverse design model
Figure 1b shows the conceptual framework of the inverse design model. The model predicts the molecular structure identifier y and the corresponding property t = (t1, t2,∙∙∙, tl) from an arbitrary molecular descriptor x. A DNN is used as the encoder to obtain the encoding function e(∙) and the property prediction function f(∙) by encoding the relationship between x and t; consequently, it selects the encoded vectors of the molecular descriptors z that are expected to satisfy the target properties. The encoding function is an abstraction of x regarding t with the functional relationship f(e(x)) = f(z) = t. An RNN is employed as the decoder to obtain the decoding function d(∙) in order to derive y conditioned on z as d(z) = y; consequently, it translates the encoded vectors of the molecular descriptors z into real chemicals that can be recognized by humans.
The molecular descriptor vector x is the collection of structural features of a given molecule for predicting the molecular properties t, and the molecular structure identifier vector y describes the molecular structure in an arbitrarily chosen notation. In this study, extended-connectivity fingerprint (ECFP)28 was used as the molecular descriptor to express the structural feature of a molecule as an m-dimensional bit vector, which indicates the presence or absence of particular substructures. As ECFP is widely used for molecular characterization and can be expressed in fixed-length bit string form, it is suitable for our purpose of molecular property prediction and random search (refer to the next section). As for the molecular structure identifier, we employed the simplified molecular-input line-entry system (SMILES),29 which represents chemical species as a sequence in a single-line notation form using ASCII strings. Such a notation can be generated by simple vocabulary and grammar rules, and its uniqueness in representing a certain molecule is guaranteed by the canonicalization.30
The interrelations among the above-mentioned molecular feature vectors are modeled by the functions e(∙), f(∙), and d(∙). The encoder function extracts a vector of hidden factors by identifying the relationship between x and t, followed by the estimation of molecular properties from these hidden factors by f(∙). Finally, d(∙) is used to derive y from the hidden factors. Hence, with a specific dataset consisting of x, t, and y for each molecule, e(∙), f(∙), and d(∙) are trained to capture the inherent relations. To obtain f(∙), a DNN with three hidden layer functions, namely h1, h2, and h3, and an output layer function, namely o(∙), is constructed, i.e., f(e(x)) = f(z) = o(h3(h2(h1(x))). Further, the function e(∙) is defined as the output of the third hidden layer function h3 to capture the encoded representation of fingerprints. In our preliminary test for the model architecture, extracting the encoded representations from the higher DNN layer provided better decoding performance and the percentage of valid SMILES was close to 90% for the third hidden layer when the SMILES strings were inspected by RDKit library (RDKit: Open-source cheminformatics. https://www.rdkit.org). In general, it is known that more abstract representation of the structural features and higher predictive accuracy can be achieved by adding more hidden layers.31,32 Specifically, for a given molecular descriptor x, e(x) is determined by sigmoid(W(3)h(2) + b(3)), where W(3) is the weight for the third hidden layer, h(2) is the output of the previous hidden layer, b(3) is the bias for the third hidden layer, and sigmoid(∙) is a nonlinear activation function. To determine the decoding function d(∙), an RNN with two hidden layers of long short-term memory (LSTM) units33 is used. The RNN is capable of dealing with variable-length sequences as input and output by passing the information across time steps using recurrent connections. Furthermore, the LSTM units provide better learning performance for the long-term dependency in the sequences. The decoding function is defined to predict the identifier vector y = (y1, y2,∙∙∙, yT) from z as a single-step moving window sequence of three-character substrings, where the sequence length T can vary and the last two characters of yt - 1 are equivalent to the first two characters of yt. To learn the SMILES generation rule, the RNN is constructed in the form of a language model.34 The first substring y1 is predicted given a start token and z, and the output yt at each time step t becomes the next input to predict the next output yt + 1 until an end token is predicted with the constraint of ensuring the continuity of the sequence, where the last two characteristics of yt are equivalent to the first two characteristics of yt + 1. The substring yt in the sequence for each time step t is predicted according to the probability distribution p(yt|z, y1, y2,∙∙∙, yt - 1) conditioned on the previous substrings and z.
Automated workflow of inverse design
The flowchart of the molecular design process using the inverse design model is shown in Fig. 2. To generate new molecules, an arbitrary fingerprint vector is first generated by random enumeration of an m-dimensional bit vector x, and it is provided as an input to the model. The fingerprint is then selected if its estimated property vector f(z) satisfies the target condition. The search for x vectors that satisfy the target conditions can be performed by combinatorial optimization among 2m possible combinations. In this regard, meta-heuristic optimization algorithms, such as the genetic algorithm and particle swarm optimization, are useful options.35 Nonetheless, random search was sufficiently effective in our case, as the required time was relatively short in the overall workflow. Next, the selected fingerprint x is fed into the encoding function to obtain the hidden factor vector z. The decoding function subsequently predicts the identifier vector y = (y1, y2,∙∙∙, yT) that maximizes the likelihood \({\mathrm{p}}\left( {{\boldsymbol{y}}|{\mathbf{z}}} \right){\mathrm{ = {\Pi}}}_{t = 1}^T{\mathrm{p}}(y_t|{\mathbf{z}},{\mathrm{y}}_1 \cdots y_{t - 1})\) to constitute a SMILES string. The validity of the decoded SMILES strings is inspected in terms of grammatical correctness with RDKit library (RDKit: Open-source cheminformatics. http://www.rdkit.org.), such as extra opening/closing parentheses, unclosed rings, and Kekulization feasibility. Finally, the properties of the generated molecules are predicted by density functional theory (DFT) simulation to reconfirm the fulfillment of the target.
Inverse design of light-absorbing organic molecules
The effectiveness of the inverse design model was verified by deriving molecules having specific maximum light-absorbing wavelengths (λmax). The model was trained with a chemical library that was constructed by randomly sampling 50,000 molecules from the PubChem database,12 whose molecular weights were between 200 and 600 g/mol. First, to assess the performance of the DNN in property prediction, each molecule was labeled with molecular orbital energies (HOMO, LUMO) and excitation energies (lowest singlet (S1) and triplet (T1) excited states at the optimized singlet ground state) by the DFT calculation. The trained DNN accurately predicted the calculated values of the DFT simulation with correlation coefficients (R) of 0.938−0.965 in tenfold cross-validation (Fig. S1.1 in the Supplementary Information).
Then, we conducted inverse design for three target λmax ranges: 200−300 nm (S1 = 4.13−6.20 eV), 300−400 nm (S1 = 3.10−4.13 eV), and 400−500 nm (S1 = 2.48−3.10 eV). Figure 3 shows the distribution of the simulated wavelengths for the designed molecules (500 molecules per target) and indicates that the property goals were well satisfied with a considerable hit rate. Remarkably, approximately 10% of the designed molecules were found in the PubChem database, even though they were not included in the randomly selected training library. This implies that the inverse design model can efficiently propose molecules similar to those that chemists have developed over a long period of time on the basis of their extensive experience and knowledge, and it is capable of suggesting practically meaningful molecules in terms of properties, chemical validity, and synthetic feasibility.
Results of inverse design for generating light-absorbing molecules. Distribution of the simulated maximum light-absorbing wavelength values of the inverse-designed molecules. Target for inverse design: a λmax = 200–300 nm. b λmax = 300–400 nm. c λmax = 400–500 nm. 82.6%, 64.8%, and 45.6% of the designed molecules were within the target ranges for the cases of a, b, and c, respectively. Note that the hit rates reached 96.0%, 95.0%, and 80.8% when the acceptance criteria were relaxed by ± 50 nm
In the visible spectrum range, several molecules were found to have moieties that are often observed in well-known dyes, some of which can be classified as derivatives of anthraquinone, azobenzene, and isoindoline (Fig. 4a−c, respectively). This implies that the inverse design model can generate new molecules through a combination of existing moieties in the training library with suitable modifications. Some design cases were beyond simple modification, as shown in Fig. 4d, where the squaraine dye moiety, which is widely used for organic photovoltaic materials, was inverse-designed even though no squaraine dyes were included in the training library. Thus, our model possesses the ability to expand the accessible chemical space beyond the span of the training set via deep-learning and can hence produce new molecules.
Inverse design of host materials for blue phosphorescent OLED
As a second verification, the inverse design model was applied to a more practical design problem of blue OLED host to investigate the efficacy in addressing one of long-standing challenges associated with efficiency and lifetime of OLED devices. An OLED undergoes electroluminescence with low driving voltages, yielding highly efficient illuminants in full-color display applications.36 The device is usually fabricated with several organic layers, each with a specific function, such as charge injection, transport, and recombination, followed by the emission of light of a specific color. In the emitting layer (EML), a guest-host system is widely adopted, where emissive dopants are dispersed in suitable host materials. To fully harvest the electro-generated excitons in the EML for light emission, organometallic complexes containing heavy metal ions, such as iridium or platinum, in which the internal heavy atom effect leads to complete conversion into triplet excitons for light emission as phosphorescence, are employed.37 In this case, the energy differences in the triplet energies of the host and guest materials are crucial for the confinement of the triplet excitons in the dopant by preventing back energy transfer from the dopant to the host. For deep-blue OLEDs, host materials with high triplet energy (> 2.8 eV) are required; however, it is not straightforward to find a suitable host for high-energy triplet emitters. Thus, the inverse design model carried out the design of host materials having sufficient triplet energy.
An in-house materials library was built for model training by combinatorial enumeration and property labeling with DFT calculations. In particular, 9 linker fragments (L) and 57 terminal fragments (R), such as carbazole, indolocarbazole, and fluorine, which are frequently employed in OLED hosts, and their derivatives, were chosen as ingredients for the enumeration. For each linker fragment, two substitution sites were assigned to symmetric positions and two identical terminal fragments were assembled with R-L-R type enumeration. Further, two identical terminal fragments were linked in R-R type without linkers. Consequently, around 6000 symmetric molecules were included in the library (the details of the fragments are summarized in Table S2.1 of the Supplementary Information).
Considering the efficient blue emission and the available energy levels of the guest materials reported in the literature, we employed a target condition of T1 ≥ 3.00 eV. The inverse design model successfully decoded 36,581 valid SMILES strings (91.5%) from 40,000 random trials. After removing duplicated and existing SMILES in the training data, 3205 unique molecules were obtained and their properties were calculated with DFT simulation. The correlation coefficient between the T1 values estimated by the DNN and the simulated T1 values was 0.881 in tenfold cross-validation (Fig. S2.1 in the Supplementary Information). Figure 5 shows the distribution of the simulated T1 energy levels for the host materials. Assessment based on the simulation results showed that the fraction of the inverse-designed hosts that satisfied the target (T1 ≥ 3.00 eV) was 58.7% (Fig. 5b), while only 36.2% of the molecules in the training library had T1 values greater than 3.00 eV (Fig. 5a). Thus, the inverse design model worked properly as expected. For reference, we generated 3497 molecules without a specific target, and the corresponding fraction was 26.9%, which was significantly lower than that in the training library (Fig. 5c).
Distribution of simulated T1 (eV) energy levels for blue phosphorescent OLED hosts. a For the training library (mean = 2.94, std = 0.15). b For the targeted (T1 ≥ 3.00 eV) inverse-designed molecules (mean = 3.02, std = 0.10). c For the untargeted inverse-designed molecules (mean = 2.92, std = 0.13). The fractions of hosts possessing T1 values greater than 3.00 eV were 36.2%, 58.7%, and 26.9% in the cases of a, b, and c, respectively (std denotes standard deviation)
The inverse-designed molecules were also analyzed in terms of modifications in the fragments or linking positions. Among the 3205 molecules, 2091 molecules (65.2%) possessed the same fragments as the training library but their connection rules were different from the symmetric R-L-R or R-R type enumeration. Further, the remaining 1114 molecules (34.8%) contained at least one new fragment that was not present in the training library. Some typical examples, classified into three groups, are shown in Fig. 6 with their T1 values. The first group (Fig. 6a) consists of the given fragments in the training library, connected in asymmetric fashion. The molecules in the second group (Fig. 6b) have new fragments that are connected in symmetric positions. The last group (Fig. 6c) has asymmetric molecules with at least one new fragment. Thus, we could confirm again that the inverse design model can propose new fragments and combinatorial rules to create new materials to meet the target properties (see Fig. S2.3 in the Supplementary Information for more detailed classification of the inverse-designed molecules).
Examples of inverse-designed host materials and their T1 values (ML: predicted value from DNN model; DFT: simulated value from DFT calculation). a Asymmetric molecules having given fragments in the training library. b Symmetric molecules where at least one fragment is different from those in the training library. c Asymmetric molecules where at least one fragment is different from those in the training library
Among the above-mentioned inverse-designed host materials, three molecules, namely a1, b1, and c1, were selected for subsequent experimental evaluation based on their structural novelty, synthetic feasibility, and expected stability. The procedures for synthesis and characterization are detailed in Section 3 of the Supplementary Information, and the measured HOMO, LUMO, S1, and T1 energy levels are summarized in Table S3.1. As can be seen from Fig. S3.4−6, the a1 and c1 molecules showed T1 energies of 3.01 and 2.91 eV, respectively, which were in good agreement with the values predicted by the DNN and those obtained by the DFT simulation, whereas the predicted T1 energy for the b1 molecule was overestimated by roughly 0.4 eV. The latter result can be ascribed to the vibrational broadening of the phosphorescence spectrum, leading to a red-shifted peak maximum assigned as the T1 energy. In this case, the assignment of the T1 energies as the onset of the spectrum is more appropriate, showing better agreement with the predicted values; the onset values of 3.06, 2.93, and 2.97 eV were obtained for the a1, b1, and c1 molecules, respectively. Thus, we successfully designed and discovered new high-T1 host molecules by using the inverse design method.
In this paper, a fully data-driven inverse design method was developed for accelerated and rational exploration of high-performance organic molecules. The inverse design model was embodied on the basis of an encoder-decoder structure consisting of heterogeneous deep neural networks for extracting the latent materials design rules and proposing the target molecular structures. The DNN identified the relationship between the structural features and their material properties, and the RNN reconstructed the recognizable molecular structures from the hidden relationship. By designing light-absorbing molecules using the PubChem database, we verified the basic performance in terms of the accuracy of the DNN in predicting the material properties, the validity of the generated molecules, and the ratio satisfying the given targets. Further, a more substantive design task was effectively conducted, followed by experimental evaluation to search for blue phosphorescent OLED host materials with a target of T1 ≥ 3.00 eV. Although the number of molecules that satisfy the target was low in the training library, the inverse design model successfully proposed new candidates in the target range by not only modifying the assembly rules but also creating new fragments. From these results, we concluded that the inverse design model can provide prominent molecular candidates without any external intervention. The quality and quantity of the training libraries are obviously as important as in other deep-learning applications. However, the proposed methodology learns the molecular design rules inherent in the libraries by itself, and it can reduce the effort required by researchers to analyze prior knowledge and experience. In addition, successively iterating the inverse design and updating the deep-learning model would probably enhance the molecular properties in an evolutionary manner. In summary, we expect our model to not only facilitate the discovery of new materials, but also support chemists by complementing the conventional heuristic design approach.
Methods
Deep-learning
For the DNN, each hidden layer consisted of 256 nodes, and the number of nodes in the output layer was equal to the number of properties of interest. Further, the DNN had an 8192-dimensional bit input. All the hidden layers used a logistic sigmoid activation function, while the output layer used a linear function. As for the RNN, each hidden layer consisted of 256 LSTM memory cells. The output layer was a softmax activation function for the probability distribution of the substrings, and the input layer used 256-dimensional embedding. Regarding the deep-learning model architecture, the number of hidden layers of the DNN and RNN has been changed from two to four and from one to three respectively. Also, the number of nodes in the DNN and LSTM memory cells in the RNN changed to 128, 256, and 512. As the validation loss did not vary significantly depending on each model, our model setting was within the sufficient performance range.
Given a set of instances for n molecules, \(\left\{ {\left( {x_i,t_i,y_i} \right)} \right\}_{i = 1}^n\), the DNN was trained on \(\left\{ {\left( {x_i,t_i} \right)} \right\}_{i = 1}^n\) to minimize the mean squared error between t and f(z), and the RNN was subsequently trained using \(\left\{ {\left( {{\mathrm{e}}(x_i),y_i} \right)} \right\}_{i = 1}^n\) to minimize the cross entropy of predicting the output vector (y1, y2, ∙∙∙, yT, <end>) from the input vector (<start>, y1, y2,∙∙∙, yT) conditioned on z. Note that <start> and <end> are special tokens indicating the start and the end of a sequence, respectively. All the neural networks were trained using the Adam optimization algorithm38 with a mini-batch size of 128. The numbers of training epochs for the DNN and RNN were 256 and 1024, respectively. We also tested different learning parameters by varying the mini-batch size to 64, 128, and 256 and the number of training epochs to 256, 512, and 1024. Although smaller mini-batch size and longer epochs generally showed lower validation loss, there was no significant change in the model accuracy. Therefore, we employed the learning parameters in consideration of model accuracy and training time together. The neural networks were implemented using the Keras library,39 which is based on GPU-accelerated Theano40 written in Python.
Quantum chemistry
All the calculations were performed using Gaussian09, Revision E.01.41 The molecular geometry of the ground singlet state (S0) was optimized by DFT simulation using the hybrid version of the Becke three-parameter exchange functional42 and the Lee-Yang-Parr correlation functional (B3LYP).43 All-electron atom-centered Gaussian basis sets (6-31 G**) were used for all the atoms. Time-dependent DFT calculation was performed for this geometry to obtain the vertical excitation energies of the excited singlets and triplets. No symmetry constraints were imposed in all the calculations.
Data availability
All data in this work are available from the corresponding author on reasonable request.
References
Pyzer-Knapp, E. O., Suh, C., Gómez-Bombarelli, R., Aguilera-Iparraguirre, J. & Aspuru-Guzik, A. What is high-throughput virtual screening? A perspective from organic materials discovery. Annu. Rev. Mater. Res. 45, 195–216 (2015).
Schneider, G. Virtual screening: An endless staircase? Nat. Rev. Drug Discov. 9, 273–276 (2010).
Gómez-Bombarelli, R. et al. Design of efficient molecular organic light-emitting diodes by a high-throughput virtual screening and experimental approach. Nat. Mater. 15, 1120–1127 (2016).
Shoichet, B. K. Virtual screening of chemical libraries. Nature 432, 862–865 (2004).
Curtarolo, S. et al. The high-throughput highway to computational materials design. Nat. Mater. 12, 191–201 (2013).
Foscato, M., Occhipinti, G., Venkatraman, V., Alsberg, B. K. & Jensen, V. R. Automated design of realistic organometallic molecules from fragments. J. Chem. Inf. Model. 54, 767–780 (2014).
Mauser, H. & Stahl, M. Chemical fragment spaces for de novo design. J. Chem. Inf. Model. 47, 318–324 (2007).
Yu, M. J. Natural product-like virtual libraries: Recursive atom-based enumeration. J. Chem. Inf. Model. 51, 541–557 (2011).
Hautier, G., Jain, A. & Ong, S. P. From the computer to the laboratory: Materials discovery and design using first-principles calculations. J. Mater. Sci. 47, 7317–7340 (2012).
Varnek, A. & Baskin, I. Machine learning methods for property prediction in chemoinformatics: Quo vadis? J. Chem. Inf. Model. 52, 1413–1437 (2012).
Ramakrishnan, R., Dral, P. O., Rupp, M. & von Lilienfeld, O. A. Big data meets quantum chemistry approximations: The Δ-machine learning approach. J. Chem. Theory Comput. 11, 2087–2096 (2015).
Bolton, E. E., Wang, Y., Thiessen, P. A. & Bryant, S. H. PubChem: Integrated platform of small molecules and biological activities. Annu. Rep. Comput. Chem. 4, 217–241 (2008).
Irwin, J. J., Sterling, T., Mysinger, M. M., Bolstad, E. S. & Coleman, R. G. ZINC: A free tool to discover chemistry for biology. J. Chem. Inf. Model. 52, 1757–1768 (2012).
De Vleeschouwer, F., Yang, W., Beratan, D. N., Geerlings, P. & De Proft, F. Inverse design of molecules with optimal reactivity properties: Acidity of 2-naphthol derivatives. Phys. Chem. Chem. Phys. 14, 16002–16013 (2012).
Brown, N., McKay, B. & Gasteiger, J. A novel workflow for the inverse QSPR problem using multiobjective optimization. J. Comput. Aided Mol. Des. 20, 333–341 (2006).
Nicolaou, C. A., Apostolakis, J. & Pattichis, C. S. De novo drug design using multiobjective evolutionary graphs. J. Chem. Inf. Model. 49, 295–307 (2009).
Miyao, T., Arakawa, M. & Funatsu, K. Exhaustive structure generation for inverse‐QSPR/QSAR. Mol. Inf. 29, 111–125 (2010).
Miyao, T., Kaneko, H. & Funatsu, K. Inverse QSPR/QSAR analysis for chemical structure generation (from y to x). J. Chem. Inf. Model. 56, 286–299 (2016).
Martin, S. Lattice enumeration for inverse molecular design using the signature descriptor. J. Chem. Inf. Model. 52, 1787–1797 (2012).
Ñeco, R. P. & Forcada, M. L. Asynchronous translations with recurrent neural nets. Proc. Int. Conf. Neural Netw. 4, 2535–2540 (1997).
Bengio, Y., Ducharme, R., Vincent, P. & Jauvin, C. A neural probabilistic language model. J. Mach. Learn. Res. 3, 1137–1155 (2003).
Kalchbrenner, N. & Blunsom, P. Recurrent continuous translation models. In Proc. Empirical Methods in Natural Language Processing 1700–1709 (Association for Computational Linguistics, Seattle, Washinton, USA, 2013).
Sutskever, I., Vinyals, O. & Le, Q. V. Sequence to sequence learning with neural networks. Proc. Adv. Neural Inf. Process. Syst. 27, 3104–3112 (2014).
Cho, K. et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation. In Proc. Empirical Methods in Natural Language Processing 1724–1734 (Association for Computational Linguistics, Doha, Qutar, 2014).
LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).
Lipton, Z. C., Berkowitz, J. & Elkan, C. A critical review of recurrent neural networks for sequence learning. Preprint at http://arXiv.org/abs/1506.00019 (2015).
Gómez-Bombarelli, R. et al. Automatic chemical design using a data-driven continuous representation of molecules. ACS Cent. Sci. 4, 268–276 (2018).
Rogers, D. & Hahn, M. Extended-connectivity fingerprints. J. Chem. Inf. Model. 50, 742–754 (2010).
Weininger, D. SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. J. Chem. Inf. Comput. Sci. 28, 31–36 (1988).
Weininger, D., Weininger, A. & Weininger, J. L. SMILES. 2. Algorithm for generation of unique SMILES notation. J. Chem. Inf. Comput. Sci. 29, 97–101 (1989).
Bengio, Y., Courville, A. & Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 35, 1798–1828 (2013).
Ma, J., Sheridan, R. P., Liaw, A., Dahl, G. E. & Svetnik, V. Deep neural nets as a method for quantitative structure–activity relationships. J. Chem. Inf. Model. 55, 263–274 (2015).
Hochreiter, S. & Schmidhuber, J. Long short-term memory. Neural Comput. 9, 1735–1780 (1997).
Mikolov, T., Karafiát, M., Burget, L., Cernocký, J. & Khudanpur, S. Recurrent neural network based language model. In Proc. INTERSPEECH, 1045−1048 (International Speech Communication Association, Makuhari, Chiba, Japan, 2010).
Gendreau, M. & Potvin, J. Y. Metaheuristics in combinatorial optimization. Ann. Oper. Res. 140, 189–213 (2005).
Brütting, W. & Adachi, C. Physics of Organic Semiconductors (John Wiley & Sons, 2012).
Yersin, H. Highly Efficient OLEDs with Phosphorescent Materials (John Wiley & Sons, 2008).
Kingma, D. & Ba, J. Adam: A method for stochastic optimization. Preprint at http://arXiv.org/abs/1412.6980 (2014).
Chollet, F. et al. Keras. https://keras.io (2018)
Al-Rfou, R. et al. Theano: A python framework for fast computation of mathematical expressions. Preprint at https://arxiv.org/abs/1605.02688 (2016)
Frisch, M. J. et al. in Gaussian 09, Revision E.01 Fox. (D. J. Gaussian, Inc., Wallingford CT, 2009)..
Becke, A. D. J. Density-functional thermochemistry. III. The role of exact exchange. Chem. Phys. 98, 5648–5652 (1993).
Lee, C., Yang, W. & Parr, R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 37, 785–789 (1988).
Acknowledgements
Computational resources were provided by the supercomputing center at Samsung Advanced Institute of Technology.
Author information
Authors and Affiliations
Contributions
S.K.1, K.K., and J.Y. devised and implemented the inverse design methodology with contributions from Y.K. and Y.-S.C., S.K.1, and K.K. applied the inverse design model to the light-absorbing materials and OLED host materials, respectively. Y.K. developed the databases. Y.N. and I.K. constructed the workflow for high-throughput simulation. D.L. and Y.N. performed DFT simulations to build the molecular libraries and predict the properties of the inverse-designed molecules. D.L. and Y.J. selected the fragments for the training library of the OLED host materials. D.L., Y.J., S.K.2, W.-J.S., and J.S.1 assessed the inverse-designed molecules in terms of their novelty, synthetic feasibility, and stability. S.K.2 synthesized and experimentally characterized the OLED host molecules. S.K.1 wrote the first version of the manuscript, and all the authors contributed toward the discussion and editing of the manuscript. Y.-S.C. and H.S.L. supervised the research, and S.K.3, J.S.2, and S.H. conceived and organized the project. Kyungdoc Kim (K.K.), Seokho Kang (S.K.1), Jiho Yoo (J.Y.), Youngchun Kwon (Y.K.), Youngmin Nam (Y.N.), Dongseon Lee (D.L.), Inkoo Kim (I.K.), Youn-Suk Choi (Y.-S.C.), Yongsik Jung (Y.J.), Sangmo Kim (S.K.2), Won-Joon Son (W.-J.S.), Jhunmo Son (J.S.1), Hyo Sug Lee (H.S.L.), Sunghan Kim (S.K.3), Jaikwang Shin (J.S.2), Sungwoo Hwang (S.H.)
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kim, K., Kang, S., Yoo, J. et al. Deep-learning-based inverse design model for intelligent discovery of organic molecules. npj Comput Mater 4, 67 (2018). https://doi.org/10.1038/s41524-018-0128-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-018-0128-1
This article is cited by
-
Airfoil Inverse Design Using a Deep Neural Net with an Explainable Attention Mechanism
International Journal of Aeronautical and Space Sciences (2024)
-
For chemists, the AI revolution has yet to happen
Nature (2023)
-
AI powered, automated discovery of polymer membranes for carbon capture
npj Computational Materials (2023)
-
Efficient enumeration-selection computational strategy for adaptive chemistry
Scientific Reports (2022)
-
Artificial intelligence: machine learning for chemical sciences
Journal of Chemical Sciences (2022)