Abstract
The ReaxFF reactive force-field approach has significantly extended the applicability of reactive molecular dynamics simulations to a wide range of material properties and processes. ReaxFF parameters are commonly trained to fit a predefined set of quantum-mechanical data, but it remains uncertain how accurately the quantities of interest are described when applied to complex chemical reactions. Here, we present a dynamic approach based on multiobjective genetic algorithm for the training of ReaxFF parameters and uncertainty quantification of simulated quantities of interest. ReaxFF parameters are trained by directly fitting reactive molecular dynamics trajectories against quantum molecular dynamics trajectories on the fly, where the Pareto optimal front for the multiple quantities of interest provides an ensemble of ReaxFF models for uncertainty quantification. Our in situ multiobjective genetic algorithm workflow achieves scalability by eliminating the file I/O bottleneck using interprocess communications. The in situ multiobjective genetic algorithm workflow has been applied to high-temperature sulfidation of MoO3 by H2S precursor, which is an essential reaction step for chemical vapor deposition synthesis of MoS2 layers. Our work suggests a new reactive molecular dynamics simulation approach for far-from-equilibrium chemical processes, which quantitatively reproduces quantum molecular dynamics simulations while providing error bars.
Similar content being viewed by others
Introduction
The reactive molecular dynamics (RMD) method has enabled large-scale simulations of chemical events in complex materials involving multimillion atoms.1,2 In particular, RMD simulations based on first principles-informed reactive force fields (ReaxFF)3 describe chemical reactions (i.e., bond breakage and formation) through a bond-order/distance relationship that reflects each atom’s coordination change. ReaxFF–RMD simulations describe full dynamics of chemical events at the atomic level with significantly reduced computational cost compared with quantum-mechanics (QM) calculations.4 ReaxFF consists of a number of empirical force-field parameters in its functional form, which are optimized mainly against a QM-based training set using a single-parameter parabolic search scheme.5 In addition to such a well-established optimization technique, several ReaxFF optimization frameworks have been developed recently using multiobjective genetic algorithms (MOGA) and other evolutionary optimization methods.6,7 QM data points in a training set include not only energies of small clusters (e.g., full bond dissociation, angle distortion and torsion energies) and reaction energies/barriers for key chemical reactions, but also bulk properties of crystal systems (e.g., equations of state, bulk modulus and cohesive energies).8,9 As a result, ReaxFF has shown its ability to successively study chemical, physical and mechanical properties of a wide range of complex materials such as hydrocarbon,10 high energy materials11 and metal/transition-metal systems.12,13
Despite these successes, the transferability of ReaxFF to highly non-equilibrium processes such as high-temperature reactions remains to be established. This is because the QM data points used in force-field optimization are mainly static quantities like ground/intermediate/transition-state structures and energies. For more accurate RMD simulations of far-from-equilibrium reaction dynamics, we here propose a dynamic approach, where ReaxFF parameters are calibrated by directly fitting RMD trajectories against quantum molecular dynamics (QMD)14,15,16,17 trajectories on the fly. This dynamic approach is implemented using MOGA to optimize the ReaxFF model in terms of multiple quantities of interest (QoI). MOGA uses a non-dominated sorting algorithm18,19 to sort out a population of ReaxFF models into different sets called Pareto optimal fronts, such that every set contains models non-dominated by each other in terms of accuracy of the QoI. Further information regarding the implementation of this algorithm is provided in the Methods section and Supplementary Information.
While significantly extending the applicability of ReaxFF to a wider range of reactions and processes, the above dynamic approach poses a challenge in estimating uncertainties in the force-field parameters and propagating them to those in model predictions. Such uncertainty quantification (UQ) has become central to most computational sciences.20 In particular, Bayesian-ensemble approaches have been applied successfully to UQ of force-field parameters21,22 in molecular dynamics (MD) simulations and the exchange-correlation functional in density functional theory (DFT) for QMD simulations.23,24 These approaches are typically employed within the conventional training of model parameters so as to minimize a weighted sum of errors against given ground-truth values in a training set. While multiobjective training like MOGA makes the application of standard Bayesian-ensemble UQ nontrivial, it also brings in a natural ensemble for UQ, i.e., Pareto optimal front. In this paper, we introduce a MOGA-based UQ approach for RMD, in which model uncertainties are estimated using an ensemble of Pareto-optimal ReaxFF models.
Recent years have shown an increase in datacentric approaches to design of new materials and force fields. Machine learning methods in particular have been significant in identification of defects25 and designing of new composite26 and polymeric materials.27,28 The utility of these methods have been greatly enhanced by the availability of open source databases, associated useful frameworks29,30, and their contributed importance to in-situ data analysis. Considering the high-throughput nature of these workflows involving in-situ data analysis, we propose a scalable workflow which eliminates the file I/O bottleneck using inter-process communications. We have previously implemented a MOGA workflow based on file-based communications between RMD, QMD and genetic-algorithm (GA) computations. However, the file-based approach was not scalable for high-throughput workflows involving hundreds of concurrent RMD simulations. In this paper, we utilize the above mentioned scalable in situ MOGA (iMOGA) workflow that eliminates the file I/O bottleneck but with minimal modification of the original parallel RMD code.31 We employ the iMOGA workflow to refine the ReaxFF description of Mo/O/S/H elements. Specifically, our focus is computational synthesis of layered transition metal dichalcogenide (TMDC) materials by chemical vapor deposition (CVD). We aim to optimize the ReaxFF description for sulfidation of MoO3 flakes using H2S precursors, which is an elementary reaction step for CVD growth of MoS2 layers at high temperatures.32,33
Results
In this section, we describe the optimization of ReaxFF parameters using iMOGA.
Multiobjective genetic algorithm for optimizing ReaxFF parameters
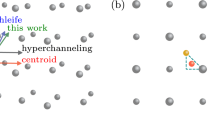
As a specific example, we studied high-temperature sulfidation of MoO3 flakes with H2S precursors during CVD synthesis of MoS2 monolayers.34 The goal was to train ReaxFF parameters against QMD simulations. For ReaxFF training, both QMD and RMD simulations were performed using a 128 atom MoO3–H2S system, with exactly the same simulation schedule. The simulation schedule and other details are described in the Methods section. Figure 1a, b shows the initial (at time 0.0 ps) and final (4.2 ps) configurations of QMD simulations, respectively. In the QMD simulations, it was observed that H transfers occur from H2S molecules to O-termination sites on MoO3 flakes, leading to H2O and Mo–S bond formation. It is essential that the time evolution of those key reaction events by the QMD simulations be quantitatively reproduced by RMD simulations. For this purpose, reaction dynamics were investigated by estimating the numbers of H–S, Mo–O and Mo–S bonds as a function of time during the QMD simulations. We then compared these QoI with those in the RMD simulations.
As shown in Fig. 2, RMD simulations using the initial force-field parameters for Mo/O/S/H elements (previously published by Hong et al.35 and recently extended to H2O/H2S systems) qualitatively describe the overall trends in the numbers of H–S bonds (Fig. 2a), Mo–S bonds (Fig. 2c) and Mo–O bonds (Fig. 2e). However, the RMD results still exhibit significant quantitative differences from the QMD results. To improve the accuracy of RMD simulations, we have used the iMOGA workflow to reoptimize ReaxFF parameters on the fly during RMD simulations. In this approach, we first compared the time series of the H–S, Mo–O and Mo–S bond populations in RMD simulations with the ground-truth QMD results (blue lines in Fig. 2). We then reoptimized four ReaxFF parameters using the iMOGA workflow: H–S, Mo–O and Mo–S sigma-bond dissociation energies, \(D_e^\sigma\), as well as H–S van der Waals dissociation energy, \(D_{{\mathrm{vdw}}}\). Details of these ReaxFF parameters are described by Chenoweth et al.10 These four parameters primarily affect bond strengths of H–S, Mo–O and Mo–S interactions, which in turn dictate key reaction events during sulfidation of MoO3 flakes using H2S precursors.
Time evolution of the numbers of H–S a, b, Mo–S c, d and Mo–O e, f bonds, where the blue and red lines show the ground-truth QMD and RMD results, respectively. The RMD results with the initial ReaxFF parameters are shown in a, c, and e, whereas those with the reoptimized ReaxFF parameters by MOGA training are shown in b, d, and f. g–i show the ratio of the number of bonds—for the optimal (\(N_{ReaxFF}^{optimal}\)) and initial (\(N_{ReaxFF}^{initial}\)) force fields—to the ground-truth QMD value (\(N_{QMD}\)). The optimal force-field result is closer to 1 as compared to the initial force-field result, notably around 4 ps in h and 2 ps in i, demonstrating the improved accuracy by the force-field optimization
In this specific example, each “gene” in GA is a quadruplet of real numbers (a general gene would be an n-tuple composed of n of the ReaxFF parameters). For MOGA training, we used the NSGA-II approach18,19,36 with blended crossover37 and random mutation of ReaxFF parameters.19 The cost functions are the squared differences between QMD and RMD results on the H–S, Mo–O and Mo–S time series. The mutation and crossover probabilities were set as 0.1 and 0.9, respectively, and the population size was set to 128. Mutation and crossover operations on ReaxFF parameters were combined with the roulette wheel selection operator to train the parameters to better fit the ground-truth QMD values. Further implementation details of the algorithm are discussed in the Methods section.
The algorithm converged to the Pareto optimal front within 140 generations, after which no further improvement was observed until 260th generations. Figure 3 shows the convergence of the Pareto optimal front in the population of ReaxFF models over various generations. Figure 2b, d, f compares the time evolution of the numbers of bonds between the ground-truth QMD and final RMD results (i.e., with reoptimized force-field parameters) in the 260th generation. After the MOGA training, the RMD results quantitatively agree with the QMD results based on the ratio plots of H–S, Mo–S, and Mo–O bonds in Fig. 2g–i.
Evolution of the Pareto optimal front solution (red) in a 10th generation, b 50th generation and c 260th generation, compared with the local Pareto optimal solution in 1st generation (blue). The solution converges to the global Pareto optimal solution in 260 generations as shown in c. Each of the Mo–O, H–S and Mo–S bond errors is calculated as \(\mathop {\sum}\nolimits_{i = 1}^{N{\mathrm{frames}}} {(BondCount_{{\mathrm{RMD}}}\left[ i \right] - BondCount_{{\mathrm{QMD}}}[i])^2}\), where BondCountRMD[i] and BondCountQMD[i] are the number of bonds in the ith time frame estimated using RMD and QMD simulations, respectively (N frames is the total number of time frames). Convergence is quantified in d, e and f, where the sum of errors (divided by 10,000) is plotted for all the points in each generation. The dashed blue lines show the average error in the first generation, whereas the dashed red lines show the average error in 10th, 50th and 260th generations, respectively. Lowering of the dashed red lines with successive generations shows convergence of the proposed scheme
As shown in Fig. 2, MOGA reoptimization of ReaxFF parameters has significantly improved the RMD description of key reaction behaviors that are essential for CVD synthesis. Supplementary Fig. S1 shows that the re-optimization has not degraded the agreement between ReaxFF and QM calculations that were included in the original (static) training dataset.
While the new iMOGA workflow has eliminated the I/O bottleneck in a previous MOGA workflow,31 the remaining bottleneck is the sequential execution of the GA procedure. This may be circumvented by incorporating a divide-and-conquer GA algorithm38 into our iMOGA workflow, which can result in an additional improvement of 40–70% (Fig. S2).
Uncertainty quantification of calculated quantities of interest
The MOGA method provides us with a local Pareto optimal solution set in every generation, which converges towards the global Pareto optimal set. Since the solutions (or ReaxFF models) in the global Pareto optimal set are non-dominated with respect to each other, all the models in the global Pareto optimal front are equally acceptable. We employ the non-dominated set to quantify the errors in RMD simulation results. In Fig. 4, the blue bands show the standard deviations for the calculated numbers of bonds within an ensemble of RMD simulations corresponding to the global Pareto optimal set involving 12 ReaxFF models. It should be noted that the error bar can be estimated for any quantity by using the same Pareto optimal ensemble of ReaxFF models. While we have used QMD simulation as the ground-truth, its accuracy in fact depends on the approximate density functional used in DFT calculation.39 For absorption energies, for example, typical uncertainty among various functionals is estimated to be around 3.2 kcal/mol.24
Uncertainty quantification of RMD simulations. a–c The blue bands show time evolution of the standard deviation in the numbers of a H–S, b Mo–O and c Mo–S bonds calculated by RMD simulations, which are overlaid with the ground-truth QMD values (red lines). d–f Error bars scaled by the corresponding ground-truth QMD bond values for d H–S, e Mo–O and f Mo–S bonds
Discussion
In addition to ReaxFF-RMD simulations, the iMOGA workflow provides a viable approach for training and UQ of general force-field parameters with minimal modifications of any existing molecular-dynamics code. Our previous 786,432-process RMD simulation on 786,432 Blue Gene/Q cores2 forced us to employ collective I/O by grouping data from 192 MPI ranks into one file, so that the number of total files was reduced to 4096.40 While such code modification was possible in the case of a monolithic in-house application, many scientific-computing tasks are formulated as a complex workflow, in which a number of legacy applications are glued together using a scientific-workflow system like Pegasus,41 while communicating with each other via file I/O. As the scale of these simulation and data-analytics components continue to increase, in situ analysis42,43 of simulation data (rather than file-based post-processing) such as iMOGA will become progressively more important.
Methods
Molecular dynamics simulations
As discussed above, we used the same simulation schedule for the RMD and QMD simulations, starting with the same initial positions and velocities of atoms at a temperature of 900 K. We first ran MD simulation in the canonical (or NVT) ensemble at 900 K for 1.2 ps. Subsequently, the system was heated first to 3500 K in 0.3 ps, then to 4500 K in 3.7 ps. The equations of motion were integrated numerically with a unit time step of 0.3 fs. The numbers of H–S, Mo–O and Mo–S bonds were sampled every 12 fs at 900 K, and every 6 fs at 3500 K and 4500 K. The numbers of bonds were calculated as a function of time for the RMD and QMD simulations, and their deviation was used as cost functions to train the ReaxFF parameters using MOGA as discussed below.
Multiobjective genetic algorithm
The goal of MOGA is to find a set of solutions (or genes) that are not dominated by any other solution, i.e., no other solution is better than it in all objectives. At each generation, all solutions are ranked according to the non-domination level, i.e., the number of objectives for which the solution is not dominated. Members at the same level dominate each other in at least one objective, and all members at level k are dominated by all solutions at levels k-2, k-3, …, 1. To sort the current solutions into different non-domination levels, we first find all solutions that are not dominated by any other solution in at least one objective. We place these solutions in level 1. Subsequently, we apply the same procedure for the remaining solutions that have not been sorted yet and place them in level 2. The procedure is applied recursively until all solutions are ranked (pseudo code for the sorting is discussed in supplementary information). The fitness of the solution is chosen to be a decreasing function of the non-domination level thus calculated (pseudocode for ranking is provided in supplementary information). The MOGA algorithm repeats rounds of generations to iteratively push the gene population towards a set of non-dominated solutions, i.e., Pareto front.
Scalable parallel in situ MOGA (iMOGA) workflow
In the original MOGA workflow in Fig. 5a, GA procedures and a population of RMD-simulation processes communicated by writing and reading files. The workflow, implemented as a combination of Python and distributed shell scripts, perform the following procedures: Given an input set of N parameter n-tuples (corresponding to a population of N genes), the procedure first creates N force-field parameter files. These parameter files are read by N concurrent RMD simulations, one for each gene, where each RMD simulation is a message passing interface (MPI) process.1,2 Each RMD process simulates the MoO3–H2S system using the assigned variant of ReaxFF parameters, and outputs three bond time-series files containing, respectively, the numbers of H–S, Mo–O and Mo–S bonds as a function of time. Next, another Python function reads these bond time-series files along with the ground-truth time series from QMD simulation to calculate the squared error (or the cost) associated with each ReaxFF parameter n-tuple. The error values for the N parameter n-tuples are written in a single error file. The error information is used by a GA function that combines blended crossover and mutation operations to generate the next generation of N genes based on the roulette wheel selection operator. This constitutes one generation of GA iteration, which is repeated until the results converge within a prescribed tolerance or the number of GA generations reaches the prescribed maximum value.
a Original MOGA workflow for re-optimizing ReaxFF parameters to reproduce the ground-truth QMD trajectory. This workflow creates N different force-field files corresponding to N different RMD simulations. It then produces the equal number of bond time-series files for H–S, Mo–O and Mo–S, which are compared against the ground-truth QMD time series. b The iMOGA workflow produces N different force-field n-tuples, corresponding to which N different RMD simulations are run, which in turn generates the equal number of bond time-series and compares them with the QMD ground-truth
The most serious bottleneck of the MOGA workflow discussed above is the number of files and directories generated during the runtime. For a population of size N, the original implementation first creates N directories to run N RMD simulations concurrently at each round of GA optimization. Within each directory, the workflow creates one ReaxFF parameter file and each RMD simulation generates 3 bond time-series files as outputs. This amounts to a total of 4N files. While this was manageable for the simple example of N = 128 (or 512 files) explained above, we anticipate need for much larger MOGA optimizations in near future. Instead of just four of the total of several hundred ReaxFF parameters in the above example, we need to optimize more parameters for more complex chemical reactions. The resulting higher-dimensional optimization would require a drastically larger population size N, for which the required 4N files would become a serious bottleneck.
To eliminate the file I/O bottleneck, we here utilize a scalable in situ MOGA (iMOGA) workflow (Fig. 5b), which is based on interprocess communications but with minimal modification of the original parallel RMD code.2 The iMOGA workflow uses a client-server model, where the main workflow script runs on the head node and acts as the server. The server then computes the bond populations corresponding to every client process and finally estimates the error with respect to the ground-truth QMD values. The server then writes all the error values to a file and executes a GA procedure written in C. The output from the GA procedure is a set of N ReaxFF parameter n-tuples for the next round of ReaxFF simulations, which is written into another file. The workflow script reads this file and starts the next GA round by spawning MPI jobs for RMD simulations, one per each gene, by communicating ReaxFF parameter n-tuples as command line arguments.
The entire iMOGA workflow creates only two files per GA generation (instead of 4N files in the original MOGA workflow), i.e., the input and output of the GA procedure. Each instance of the RMD simulations reads a single identical initial-configuration file. It also reads an identical ReaxFF parameter file that contains several hundred parameters, out of which only four parameters are replaced by the values read as command line arguments. Since the total number of files does not depend on the population size, the iMOGA workflow is expected to be much more scalable than the original MOGA workflow.
Data avilability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Nomura, K., Kalia, R. K., Nakano, A. & Vashishta, P. A scalable parallel algorithm for large-scale reactive force-field molecular dynamics simulations. Comput. Phys. Commun. 178, 73–87 (2008).
Nomura, K., Small, P. E., Kalia, R. K., Nakano, A. & Vashishta, P. An extended-Lagrangian scheme for charge equilibration in reactive molecular dynamics simulations. Comput. Phys. Commun. 192, 91–96 (2015).
van Duin, A. C. T., Dasgupta, S., Lorant, F. & Goddard, W. A. ReaxFF: a reactive force field for hydrocarbons. J. Phys. Chem. A 105, 9396–9409 (2001).
Senftle, T. P. et al. The ReaxFF reactive force-field: development, applications and future directions. npj Comput. Mat. 2, 15011 (2016).
van Duin, A. C. T., Baas, J. M. & de Graaf, B. Delft molecular mechanics: a new approach to hydrocarbon force fields. Inclusion of a geometry-dependent charge calculation. J. Chem. Soc. Faraday Trans. 90, 2881–2895 (1994).
Jaramillo-Botero, A., Naserifar, S. & Goddard, W. A. General multiobjective force field optimization framework, with application to reactive force fields for silicon carbide. J. Chem. Theory Comput. 10, 1426–1439 (2014).
Larentzos, J. P., Rice, B. M., Byrd, E. F. C., Weingarten, N. S. & Lill, J. V. Parameterizing complex reactive force fields using multiple objective evolutionary strategies (MOES). part 1: ReaxFF models for cyclotrimethylene trinitramine (RDX) and 1,1-diamino-2,2-dinitroethene (FOX-7). J. Chem. Theory Comput. 11, 381–391 (2015).
Raymand, D., van Duin, A. C., Baudin, M. & Hermansson, K. A reactive force field (ReaxFF) for zinc oxide. Surf. Sci. 602, 1020–1031 (2008).
Hong, S. & van Duin, A. C. Atomistic-scale analysis of carbon coating and its effect on the oxidation of aluminum nanoparticles by ReaxFF-molecular dynamics simulations. J. Phys. Chem. C. 120, 9464–9474 (2016).
Chenoweth, K., van Duin, A. C. T. & Goddard, W. A. ReaxFF reactive force field for molecular dynamics simulations of hydrocarbon oxidation. J. Phys. Chem. A 112, 1040–1053 (2008).
Strachan, A. et al. Shock waves in high-energy materials: the initial chemical events in nitramine RDX. Phys. Rev. Lett. 91, 098301 (2003).
Hong, S. & van Duin, A. C. T. Molecular dynamics simulations of the oxidation of aluminum nanoparticles using the ReaxFF reactive force field. J. Phys. Chem. C. 119, 17876–17886 (2015).
Ostadhossein, A. et al. ReaxFF reactive force-field study of molybdenum disulfide (MoS2). J. Phys. Chem. Lett. 8, 631–640 (2017).
Car, R. & Parrinello, M. Unified approach for molecular-dynamics and density-functional theory. Phys. Rev. Lett. 55, 2471–2474 (1985).
Payne, M. C., Teter, M. P., Allan, D. C., Arias, T. A. & Joannopoulos, J. D. Iterative minimization techniques for ab initio total-energy calculations - molecular-dynamics and conjugate gradients. Rev. Mod. Phys. 64, 1045–1097 (1992).
Shimojo, F. et al. A divide-conquer-recombine algorithmic paradigm for multiscale materials modeling. J. Chem. Phys. 140, 18A529 (2014).
Shimamura, K. et al. Hydrogen-on-demand using metallic alloy nanoparticles in water. Nano. Lett. 14, 4090–4096 (2014).
Deb, K., Agrawal, S., Pratap, A. & Meyarivan, T. A fast and elitish multiobjective genetic algorithm. Proc. ICPPN 6, 849–858 (2000).
Deb, K., Pratap, A., Agarwal, S. & Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE T Evolut. Comput. 6, 182–197 (2002).
Karniadakis, G. E. & Glimm, J. Uncertainty quantification in simulation science. J. Comput. Phys. 217, 1–4 (2006).
Frederiksen, S. L., Jacobsen, K. W., Brown, K. S. & Sethna, J. P. Bayesian ensemble approach to error estimation of interatomic potentials. Phys. Rev. Lett. 93, 165501 (2004).
Rizzi, F. et al. Uncertainty quantification in MD simulations. part Ii: Bayesian inference of force-field parameters. Multiscale Model. Sim. 10, 1460–1492 (2012).
Mortensen, J. J. et al. Bayesian error estimation in density-functional theory. Phys. Rev. Lett. 95, 216401 (2005).
Medford, A. J. et al. Assessing the reliability of calculated catalytic ammonia synthesis rates. Science 345, 197–200 (2014).
Cubuk, E. D. et al. Identifying structural flow defects in disordered solids using machine-learning methods. Phys. Rev. Lett. 114, 108001 (2015).
Gu, G. X., Chen, C.-T. & Buehler, M. J. De novo composite design based on machine learning algorithm. Ext. Mech. Lett. 18, 19–28 (2018).
Sharma, V. et al. Rational design of all organic polymer dielectrics. Nat. Commun. 5, 4845 (2014).
Ramprasad, R., Batra, R., Pilania, G., Mannodi-Kanakkithodi, A. & Kim, C. Machine learning in materials informatics: recent applications and prospects. npj Comput. Mat. 3, 54 (2017).
Jain, A. et al. Commentary: the materials project: a materials genome approach to accelerating materials innovation. Appl. Phys. Lett. Mat. 1, 011002 (2013).
Huck, P. et al. User applications driven by the community contribution framework MPContribs in the materials project. Concurr. Comput. Prac. Exp. 28, 1982–1993 (2016).
Cheng, H. C. et al. A high-throughput multiobjective genetic-algorithm workflow for in situ training of reactive molecular-dynamics force fields. Proc SpringSim HPC2016 (SCS, Pasadena, CA, 2016).
Kim, Y., Bark, H., Ryu, G. H., Lee, Z. & Lee, C. Wafer-scale monolayer MoS2 grown by chemical vapor deposition using a reaction of MoO3 and H2S. J. Phys. Cond. Matter 28, 184002 (2016).
Dumcenco, D. et al. Large-area MoS2 grown using H2S as the sulphur source. 2D Mater. 2, 044005 (2015).
Salazar, N., Beinik, I. & Lauritsen, J. V. Single-layer MoS2 formation by sulfidation of molybdenum oxides in different oxidation states on Au (111). Phys. Chem. Chem. Phys. 19, 14020–14029 (2017).
Hong, S. et al. Computational synthesis of MoS2 layers by reactive molecular dynamics simulations: initial sulfidation of MoO3 surfaces. Nano. Lett. 17, 4866–4872 (2017).
Srinivas, N. & Deb, K. Multi-objective function optimization using non-dominated sorting genetic algorithms. Evol. Comput. 2, 221–248 (1995).
Eshelman, L. J. & Schaffer, J. D. Real-coded genetic algortihms and interval-schemata. Found. Genet. Algorithms 2, 187–202 (1993).
Liu, Y. Y. & Wang, S. W. A scalable parallel genetic algorithm for the generalized assignment problem. Par. Comput. 46, 98–119 (2015).
Medvedev, M. G., Bushmarinov, I. S., Sun, J., Perdew, J. P. & Lyssenko, K. A. Density functional theory is straying from the path toward the exact functional. Science 355, 49–52 (2017).
Nomura, K. et al. Metascalable quantum molecular dynamics simulations of hydrogen-on-demand. Proc SC14, 661–673 (IEEE/ACM, New Orleans, LA, 2014).
Deelman, E. et al. Pegasus, a workflow management system for science automation. Future Gener. Comp. Sys. 46, 17–35 (2015).
Nakano, A. et al. Divide-conquer-recombine: an algorithmic pathway toward metascalability. Beowulf ‘14, 17–27 (ACM, Annapolis, MD, 2014).
Romero, N. A. et al. Quantum molecular dynamics in the post-petaflops era. IEEE Comput. 48, 33–41 (2015).
Acknowledgements
This work was supported as part of the Computational Materials Sciences Program funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, under Award Number DE-SC0014607. The simulations were performed at the Argonne Leadership Computing Facility under the DOE INCITE program and the Center for High Performance Computing of the University of Southern California.
Author information
Authors and Affiliations
Contributions
R.K., A.N. and P.V. designed the research. P.R. designed the multi-objective genetic algorithm, and S.H. applied it to the optimization of reactive force-field parameters, which were fitted to quantum molecular dynamics simulations performed by C.S. A.M. implemented the entire framework and executed it, with the help of K.N. on software. All authors participated in writing the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mishra, A., Hong, S., Rajak, P. et al. Multiobjective genetic training and uncertainty quantification of reactive force fields. npj Comput Mater 4, 42 (2018). https://doi.org/10.1038/s41524-018-0098-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-018-0098-3