Abstract
Catalytic activity of the hydrogen evolution reaction on nanoclusters depends on diverse adsorption site structures. Machine learning reduces the cost for modelling those sites with the aid of descriptors. We analysed the performance of state-of-the-art structural descriptors Smooth Overlap of Atomic Positions, Many-Body Tensor Representation and Atom-Centered Symmetry Functions while predicting the hydrogen adsorption (free) energy on the surface of nanoclusters. The 2D-material molybdenum disulphide and the alloy copper–gold functioned as test systems. Potential energy scans of hydrogen on the cluster surfaces were conducted to compare the accuracy of the descriptors in kernel ridge regression. By having recourse to data sets of 91 molybdenum disulphide clusters and 24 copper–gold clusters, we found that the mean absolute error could be reduced by machine learning on different clusters simultaneously rather than separately. The adsorption energy was explained by the local descriptor Smooth Overlap of Atomic Positions, combining it with the global descriptor Many-Body Tensor Representation did not improve the overall accuracy. We concluded that fitting of potential energy surfaces could be reduced significantly by merging data from different nanoclusters.
Similar content being viewed by others
Introduction
Due to their remarkable properties, nanoclusters have gained attention in heterogeneous catalysis.1,2,3 Nanoclusters differ from bulk metal behaviour, and their catalytic properties are sensitive to changes in size and morphology.4,5,6,7 For example, gold clusters with a diameter of a few nanometres exhibit non-metallic properties due to quantum size effects.8 Scientists have advanced significantly in producing nanoparticles with defined composition, size and morphology in the last decade.1,9,10,11,12 These developments mean a tremendous combinatorial and structural space has opened up for rational catalyst design, where nanoscale experiments and computational screening can be used to optimize catalyst design.13
In this context, the development of new materials for the scalable production of hydrogen is a key challenge, with massive impact in clean-energy technologies.14,15,16 At the cathode of electrolytic water splitting into hydrogen and oxygen, the hydrogen evolution reaction (HER) takes place. As part of the process, the currently used expensive noble metals, especially platinum group metals (PGM), categorised as critical by the European Commission,17 need to be replaced to make the production of hydrogen competitive to other energy storage technologies. Some bimetallic alloy nanoclusters, such as copper–titanium18 exhibit catalytic activity towards HER, thus binary combinations of metals are of high interest, particularly if the fraction of PGMs can be significantly reduced.19 Beyond metals, one candidate to replace PGMs are MoS2 nanoclusters. Recent studies of single-layer MoS2 have shown that its electronic band structure can be fine-tuned at the nanoscale.20 On the otherwise semiconducting material, the edges of triangular- to hexagonal-shaped nanoclusters demonstrate metallic character and these are likely to be the active site for HER.20,21,22
The configurational space offered by the wide variety of nanocluster materials, active sites and environmental conditions means that a conventional approach to catalyst optimization, using ab initio methods, is particularly challenging. Hence, very recently there has been a surge in attempts to apply machine learning (ML) approaches to modelling catalytic systems.23,24,25,26,27,28
In this work, we begin by considering the latest developments in descriptors for ML in materials science, as yet untested in nanocatalytic systems, and compare them in terms of accuracy and efficiency for characterizing a particular catalytic reaction, HER:
This stands out as a relatively simple reaction with one intermediate state—adsorbed hydrogen on the catalyst surface. The rate of the reaction on a catalyst surface (denoted below as *) is determined by the hydrogen adsorption free energy ΔGH of the elementary Volmer step:
According to the Sabatier principle, hydrogen should neither bind too weakly nor too strongly. This general principle explains why ΔGH can reasonably describe catalytic activity. Optimally, nanoclusters should have adsorption sites with ΔGH ≈ 0 to be considered catalyst candidates.29,30 Since this quantity is accessible by ab initio methods, directly from the adsorption energy of hydrogen, materials can be pre-screened computationally. Our approach is to build a large data set of hydrogen adsorption energies on a variety of nanoclusters, characterize this with appropriate structural descriptors, and then train a model to predict these energies for an arbitrary site based on its description.
Results
Potential energy scan of sample clusters
As initial data sets, we started by mapping out the energy landscape of hydrogen adsorbed on the surface of one sample cluster for each system, MoS2 and AuCu.
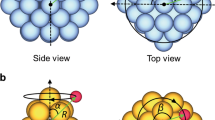
The two nanoclusters were fully scanned with respect to the hydrogen position and are depicted in Fig. 1. Figure 1a shows a potential energy scan of a triangular-shaped sample MoS2 cluster with molybdenum-terminated edges (Fig. 1b). The cluster Au40Cu40-H had a flatter potential energy surface (Fig. 1c) than MoS2-H and no patterns were clearly apparent. On the other hand, MoS2-H had three distinct global minima at the edges where hydrogen bound to molybdenum. Since the cluster had a near-C3-symmetry the local environments of the 3 minima were equivalent. When hydrogen was bound at corner-sites, ΔEH increased, while the highest energy positions were observed on the surface sulphur atoms. Even though the C3-symmetry of the cluster was broken, ΔEH remained similar at different edges and corners.
Machine learning on single clusters
The data sets MoS2(single) and Au40Cu40(single) contained 10,000 DFT-based ΔEH single-point calculations of hydrogen positioned on the surface of the same cluster. We were interested in how many points were needed to predict the potential energy surface by interpolation. However, we did not conduct this interpolation in real space, but feature space with KRR. Thus, two points far away from each other in real space were close in feature space if the structures were similar. The feature space was spanned by the descriptors Atom-Centered Symmetry Functions (ACSF), Many-Body Tensor Representation (MBTR) or Smooth Overlap of Atomic Positions (SOAP). The goal was to reach an accuracy of 0.1 eV, which would allow us to make reasonable predictions of ΔEH for an arbitrary system.
Figure 2a shows learning curves predicting ΔEH at random positions around the triangular MoS2 cluster (Fig. 1b). In this example only, we included the results for the Coulomb Matrix (CM) descriptor in order to see how it fares with respect to adsorption energy prediction. As we transformed the global descriptor into a local CM, we observed an improved accuracy. This was due to the strong dependence of ΔEH on the local environment. In general, the CM had a significantly higher MAE, which might be due to its values ranging over many orders of magnitude,31 see also Fig. 3. To do justice to CM, it is possible to increase the accuracy a bit by randomly sorting it, and thus smoothening the feature space.32 ACSF performs comparably to ACSFH and MBTR with a training set larger than 3000, and reached the threshold of 0.1 eV at about 900 training points. ACSFH required only about 400 training points. SOAP and MBTR, on the other hand, had a MAE of 0.1 eV with only 300 training points, while SOAP also performed best at large training set sizes.
Mean of data point pairs on the axes of Δ(ΔEH) and (dis)similarity defined by d = \(\left\| {Descriptor} \right\|_2\) within bins of size 0.1. The coloured area highlights the standard deviation in those bins. The data set MoS2(multi) was used to compare the descriptors CM (cyan, offset 1.0 eV), SOAP (red, offset 0.7 eV), MBTR (blue, offset 0.3 eV) and ACSF (green)
Figure 2b shows learning curves predicting ΔEH at random positions around a medium-sized AuCu cluster. SOAP and MBTR again performed equally well reaching the threshold of 0.1 eV with about 300 training points. Remarkably, ACSFH reached 0.1 eV MAE with only 100 training points, but it exhibited a shallow learning curve. Although ACSF had a lower accuracy with small training set sizes, it overtook ACSFH and MBTR with a training set larger than 3000. The low error with a large training set makes ACSF an excellent choice for Molecular Dynamics simulations where high accuracy is needed, for example simulations over many time steps where even small errors can propagate rapidly. A machine learning potential fitted to a large DFT data set provides energies close to the reference method.31 SOAP showed a similarly steep learning curve compared to ACSF, however was offset to a lower accuracy at all training set sizes.
To summarise the results for both test systems, ACSF needed a large training set, but then it was as good or even better than MBTR. This was due to the many symmetry functions used. If symmetry functions were eliminated by feature selection the performance of ACSF at lower training set sizes would likely be better.
Indeed, a principal component analysis revealed that 130 components for both data sets could explain 99% of the variance. A sensible choice was to restrict the features to ACSFH, the local version of ACSF. Expectedly, ACSFH performed better than global ACSF for smaller training set sizes. Systematic feature selection using e.g., mutual information could further reduce the MAE for small training set sizes. Eventually, ACSFH, MBTR and SOAP showed comparable MAE with smaller training set sizes.
Machine learning on multiple clusters
In the next step, we were interested if it was possible to interpolate between hydrogen adsorption sites on different clusters. The data sets MoS2(multi) and AuCu(multi) contained around 10,000 DFT-based ΔEH single-point calculations. The data set MoS2(multi) consisted of hydrogen positioned on the surface of 91 MoS2 clusters. A total of 110 points were randomly chosen for each cluster.
Figure 2c shows the learning curve predicting ΔEH at random positions around multiple MoS2 clusters. The descriptor SOAP reached a MAE of 0.1 eV with a training set size of 4000 (or 44 per cluster). It was estimated before that learning on the potential energy surface of a single cluster required 300 training points (MoS2(single)). This comparison clarified that learning on different clusters simultaneously was beneficial and interpolation in compound space was possible with similar nanoclusters. MBTR got as low as 0.13 eV with a training set size of 9000. The size of ACSF depended on the number of atoms in the system. Since the nanoclusters had different sizes and different compositions, it did not make sense to compare atoms other than hydrogen with each other. Hence, the local version of ACSF, ACSFH was taken. Similar to MBTR it did not reach the threshold of 0.1 eV, but got as close as 0.11 eV with 9000 training points. Since SOAP (here a local descriptor) and MBTR (here a global descriptor) were designed in such a way that they might contain information which the other did not, we tried to combine both. In this case, however, the combined and equally weighted features of MBTR and SOAP did not improve the overall accuracy.
To verify that the results were independent of the system, we repeated the analysis with the data set AuCu(multi) containing 24 small copper–gold clusters with a fixed size of 13 atoms, but different compositions. A total of 420 hydrogen positions were randomly chosen on the surface of each cluster.
Figure 2d shows the learning curve predicting ΔEH at random positions around multiple AuCu clusters. A MAE of around 0.11 eV was reached at 9000 training points with MBTR and ACSFH. With SOAP, only 2000 training points or 80 per cluster were needed to achieve a MAE lower than 0.1 eV. It was estimated before that learning on the potential energy surface of a single-copper–gold cluster required around 300 training points. Again, this comparison confirmed that learning on different clusters was possible, which indicated that it should be possible on any nanocluster system. Furthermore, the fact that MBTR and SOAP combined did not improve the overall accuracy, strongly suggests that the relevant information is contained around the adsorption site. Since SOAP outperformed the other descriptors even though it only contained information about the local environment around hydrogen, it became apparent that size effects of nanoclusters play a minor role (<0.1 eV in our model) in defining ΔEH.
The log–log plots of Fig. 2 emphasize the empirical linear relationship log(MAE) = a–b log(N) for large N in agreement with ref. 33. The linear relationship of our data sets started at around N = 500–2000 where different error decay rates became apparent. The global descriptor ACSF and SOAP displayed their superiority over ACSFH and MBTR in this regime.
The purpose of the above data sets was to compare descriptors as well as to investigate the benefit of merging data from diverse structures. The generalization error of the best performing descriptor should be estimated higher, though only slightly, since the test sets acted as validation sets to pick the best descriptor. An estimate of the generalization error will be presented for MoS2 in Fig. 5.
To visualise that similar local environments indeed do not give vastly different ΔEH, 1000 data point pairs were selected with the lowest (dis)similarity d = \(\left\| {Descriptor} \right\|_2\), descriptor being SOAP, MBTR or ACSF. In Fig. 3, a histogram plot shows pairs of local environments at a certain (dis)similarity d (taken from the data set MoS2(multi)) and the mean of their difference in energy Δ(ΔEH). The mean difference in ΔEH at any given d increased monotonously. As depicted by the increasing standard deviation, the more dissimilar the data points were the wider the spread of ΔEH, which indicated that the property changed smoothly in feature space. On average, MBTR had a slightly higher Δ(ΔEH) than SOAP or ACSF. For comparison, CM exhibits a much less smooth feature space. In summary, SOAP outperformed MBTR and ACSFH and the information to explain adsorption energies is contained in the local environment. The property of interest, ΔEH, changed smoothly in feature space spanned by SOAP even though clusters of different sizes were present.
As depicted in Fig. 3 similar adsorption sites have similar ΔEH. In order to achieve predictive power with as few training points as possible, clustered data points should be avoided, but instead selected as such that they are approximately evenly spaced. The data set MoS2(single) is a good example to show that the accuracy depends on whether the training points are chosen randomly or are identically distributed. Since significantly more data points were sampled on the sulphur surface of MoS2 than on its Mo-terminated edges we suspected a biased data set. Descriptors can be used to select an identically distributed data set with respect to feature space (spanned by the descriptor).
The greedy algorithm farthest point sampling (FPS) was exerted to get a set of the most dissimilar training points.34 In Fig. 4, the MAE of random training and test sets were plotted and contrasted against FPS-sampled training and test sets. Using FPS improved the overall accuracy significantly at smaller training set sizes but the effect soon became less apparent. The choice of the test set did not significantly affect the MAE. At a large enough training set size of 500–1500, selecting training points did not make a difference any more. However, when the training set size was in the range of interest (MAE around 0.1 eV) the difference was significant. We interpreted this result as such that the randomly selected data set was biased and not identically distributed. In order to reduce data set size, descriptors could be used to scan local environments and represent them evenly without bias towards more abundant structural patterns.
Prediction of energy distribution of potential energy scan
Next, we investigated to which degree the potential energy surface of a single cluster can be inferred from a data set of multiple clusters. The data set MoS2(multi) was used as a training set to predict ΔEH on the surface of the sample cluster MoS2(single), where a large test set was available. It should be mentioned that the sample MoS2 cluster was part of the data set MoS2(multi) with 110 data points.
Figure 5a shows the parity plot of ΔEH of the test set MoS2(multi). Here, SOAP was chosen as the descriptor. An overall MAE of 0.13 eV was reached. In the sparsely sampled high-energy region, the error was significantly higher than average. In the sparsely sampled low-energy region, however, the error was much lower. Since stable adsorption sites will not be found in the high-energy region, the accuracy of predictions could further be improved by sampling more in the low-energy region. As can be seen from the dashed line errors introduced predicting ΔEH with descriptors were statistical and not systematic since the predictions were centered around y = x. Figure 5a also shows the distribution of ΔEH of the test set MoS2(multi). When focusing on global rather than local properties, the MAE does not have to be as low as 0.1 eV rather should the energy distribution be predicted accurately. The predicted energy distribution was in good agreement with the DFT energy distribution. Depending on the desired accuracy, smaller data sets than the ones we used might be enough to reliably predict the energy distribution.
Parity plot of predicted against calculated ΔEH/ΔGH together with a histogram of predicted (red) and calculated (black) energy distributions. a The data set of multiple clusters MoS2(multi) was used as a training set and the data set MoS2(single) cluster was used as the displayed test set. b The data set of multiple clusters MoS2(multi) was used as a training set and a data set of local minima on frozen clusters was used as the displayed test set
Finally, we tested whether ΔGH of local minima on the potential energy surface could be predicted accurately from single-point calculations only going from ΔEH to ΔGH by adding a constant shift. Hydrogen on top of around 1000 MoS2 surface atoms of the data set MoS2(multi) was relaxed while the cluster itself was kept frozen. SOAP descriptors were created at the relaxed positions. The data set MoS2(multi) was used as a training set to predict ΔGH of the relaxed hydrogen adsorption sites. Figure 5b shows the resulting parity plot. Again, an overall MAE of 0.12 eV was reached. However, it showed several outliers. This was probably due to the fact that local environments of the low-energy region were under-represented in the data set MoS2(multi). Higher sampling in the region of interest could alleviate the probability of outliers and further reduce MAE.
Figure 5b also shows the distribution of ΔGH of the sampled hydrogen adsorption sites. The predicted energy distribution was in good agreement with the DFT energy distribution. There seemed to be no systematic over- or under-estimation of the property. KRR failed to predict the lowest-energy adsorption sites under ΔGH = −0.4 eV. This was again due to poor sampling in the low-energy region. Even though only random positions were taken on the surface of several nanoclusters, a combined database could extrapolate to the local minima with a satisfactory accuracy. A smarter selection of points in feature space spanned by a descriptor opens up a new way of finding adsorption sites on similar systems.
To show the limitation of this method, we greedily extrapolated from the data set AuCu(multi), containing 13-atom clusters to predict ΔEH on the surface of the sample cluster Au40Cu40. Figure 6 shows a parity plot using the previously best performing descriptor SOAP.
SOAP showed learning tendency with a slight under-estimation. However, the MAE at 0.25 was too high, especially due to the under-estimation of the high-energy regime. Also, it can be noted that the parity plot featured two clusters which indicated that only part of the local environments of Au40Cu40 were represented in the training set.
Discussion
We analysed the performance of state-of-the-art atomic structural descriptors (SOAP, MBTR and ACSF) when used to predict the hydrogen adsorption (free) energy on the surface of nanoclusters. As expected, we found that none of the descriptors which had been designed for molecules and crystals are optimized for nanoclusters. In general, we observed that learning on one cluster at a time required unnecessarily large training sets to achieve good accuracy—this can be improved by merging data from many different nanoclusters in the training set. Since SOAP performed significantly better, we deem it a good choice for adsorption energy predictions. Our data sets did not make it necessary to include global information as could be seen upon the combination of SOAP and MBTR, so the local environment dominates the influence on the adsorption energy. It is, however, possible that a global addition improves the learning when e.g., dopants or defects are added. Descriptor improvements might be possible by combining other descriptors, optimising the weighting functions or other parameters of MBTR and SOAP, or even by constructing a new descriptor encompassing the special structural features of nanoclusters like size, shape and surface morphology. Recently, a multi-scale SOAP kernel has been developed which could incorporate missing information while still retaining the local nature of the descriptor.34 This new approach will be subject to future work. Nevertheless, given sufficient training, all descriptors except CM performed satisfactorily when used as features in KRR.
We identified a few shortcomings of ACSF, MBTR and SOAP with respect to the description of nanoclusters. SOAP in the implementation used here only considers the local environment of hydrogen within a certain cutoff. There are, however, global SOAP descriptors which take into account local environments of all atoms—its performance on nanoclusters will be investigated in the future. ACSF, in order to be size-consistent, was feature selected to be a local descriptor ACSFH, and the accuracy improves slowly with increasing training set size. Better performance with smaller training set sizes could be achieved by feature-selecting symmetry functions. MBTR as a global, size-consistent descriptor could not exhibit its conceptual advantage over the local descriptors, the local environment mostly determined ΔEH.
Many interesting studies could build upon the presented results. In the future, we plan to make more complex databases where the compound space is enlarged by defects or dopants. Ternary metallic clusters, with increased compositional space are particularly challenging for conventional ab initio approaches and could be systems of interest for ML optimization. In terms of the DFT data generation itself, by including information about local similarity encoded in the descriptors it should also be possible to reduce the number of relaxation steps needed to find the local minimum. In conclusion, our results demonstrate that the approach of predicting properties based on descriptors alleviates redundancy in a batch of similar nanocluster calculations—the near-symmetric structures with repeating patterns offer many similar local environments perfectly suited to descriptor methods.
Methods
Density functional theory calculations
All electronic calculations were performed with the CP2K package35 at the density functional theory (DFT) level, where orbitals and electron density were represented by Gaussian and planewave (GPW) basis sets. The exchange-correlation energy was approximated using the spin-polarized GGA-functional by Perdew–Burke–Ernzerhof (PBE).36 Short-ranged double-ζ valence plus polarization molecularly optimized basis sets (MOLOPT-SR-DZVP)37 and norm-conserving Goedecker-Teter-Hutter (GTH) pseudopotentials38,39,40 were assigned to all atom types. Van der Waals interactions were taken into account with the D3 method of Grimme et al. with Becke-Johnson damping (DFT-D3(BJ)).41,42 The energy cutoff for the auxiliary PW basis was set to 550 Ry and the cutoff of the reference grid was set to 60 Ry. Atomic positions were optimised using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm until the maximum force component reached 0.02 eV/Å. A gap of at least 8 Å vacuum was added in all cartesian directions of the simulation box. The crystal structures of bulk gold, copper and MoS2 obtained at this DFT-level were in good agreement with experiments. In Supplementary Information, it is shown that the double-ζ basis set performs in good agreement with TZV2P.
Regarding relaxed hydrogen structures, we calculated the Gibbs free energy of adsorbed hydrogen ΔGH as
where ECluster+H, ECluster and \(E_{H_2}\) denote the total energy of adsorbed hydrogen, the solitary cluster and molecular hydrogen in the gas phase. The term EBSSE corrected for basis-set-superposition error. The term ΔEZPE − TΔSH was approximated by values from literature at standard conditions; in the case of MoS2, the zero-point energy minus the entropic term was estimated as 0.29 eV in ref. 43. Considering the system AuCu, ΔSH was approximated by \(\frac{1}{2}{\mathrm{\Delta }}S_{H_2}^0\), the entropy of H2 in the gas phase at standard conditions as in ref. 43; The zero-point-energies of copper (0.17) and gold (0.14) from ref. 44 differed only a little and were averaged as an approximation, which resulted in ΔEZPE − 298 KΔSH ≈ 0.22 eV. This approximation resulted in a constant shift in adsorption energy.
Nanocluster data sets
We created several DFT data sets based on nanoclusters of the 2D-material MoS2 and the metal alloy AuCu. Two nanoclusters were fully scanned with respect to the hydrogen position. They are as follows:
-
a triangular MoS2 cluster with Mo-terminated edges
-
a medium-sized near-spherical Au40Cu40 cluster
The structures are depicted in Fig. 1. The single-cluster data sets, named hereafter MoS2(single) and Au40Cu40(single), comprised of 10,000 single-point calculations of single-hydrogen atoms adsorbed on the surface. Hydrogen was positioned randomly at a distance of 130–220 pm from the cluster, where the random points were at least 0.1 Å from each other. Furthermore, data sets containing hydrogen adsorbed on different nanoclusters were produced in a similar fashion. Small-sized AuCu clusters containing 13 atoms ranged from 4 to 9 gold atoms. We wanted to analyse clusters of the same size, but with different compositions. For each of those 24 clusters, we calculated 420 data points of adsorbed hydrogen. The combined data set, named hereafter AuCu(multi), had a size of around 10,000 points. Analogously, the data set MoS2(multi) comprised of 91 different MoS2 nanoclusters, so that it also contained around 10,000 data points. MoS2 clusters of different size (ranging from 4 to 11 Mo atoms at the edge), shape and edge-termination were chosen based on ref. 22. In order to create clusters of different shapes, ranging from triangular to hexagonal, corners were capped, leaving behind 3 additional sulphur-terminated edges. First, one Mo atom was capped, then 3, then 6, until the cluster had a hexagonal shape. Different edge types were also present in the data set, with sulphur coverages of 0, 25, 50 and 100% equally represented. A few examples are shown in Fig. 7, otherwise edge structures can be found here.22
Structural descriptors
In general, with a large enough data set containing nanocluster structures, the location of the hydrogen adsorption site and their corresponding ΔGH, it is fairly straightforward to develop a predictive model with the help of ML. ab initio calculations require only atomic types and relative positions of atoms as input. Hence, cartesian coordinate or Z-matrix formats contain all information in order to calculate the total energy of a nanocluster and then derive ΔGH. Those formats, however, have a disadvantage when it comes to interpolation of data or ML. The same structure can be constructed in many different ways—as a result, similar structures might not be treated as similar by the ML algorithm, and discontinuities appear. ML in general requires the input data to be in compact form and in a smooth feature space.
Another structural representation (descriptor) is needed which fulfils several criteria, summarised here.45 A good structural descriptor is:
-
invariant with respect to rotation, translation and homo-nuclear permutation
-
unique—there should be only one way to construct a descriptor for any given structure
-
non-degenerate—no two sets of descriptor features are identical for structures with different relevant properties
-
continuous in the spanned feature space
Efforts to develop efficient descriptors in materials science have led to a family of approaches successfully applied to molecules and crystals.46,47 In particular, we consider the following popular descriptors (a detailed description of each of the descriptors is available in Supplementary Information):
-
CM is a global descriptor based on pairwise coulomb repulsion of the nuclei.48
-
ACSF49—for each atom in a system, ACSF express distance and angular interactions with neighbour atoms in symmetry functions.
-
SOAP47,50—SOAP represents the local environment around a center atom by gaussian-smeared neighbour atom positions made rotationally invariant.
-
MBTR51—MBTR is a global descriptor which groups interactions by atomic type and puts them into a tensor.
Descriptor hyper-parameters
The structural descriptors CM, ACSF, MBTR and SOAP have method-specific parameters which can be fitted to the investigated system. A few performance tests showed that the mean absolute error (MAE) was sensitive to a few of those hyper-parameters. The radial cutoff of the local CM was optimised to 6 Å. The rows and columns of the matrix were sorted with respect to the L2-norm. Regarding ACSF, only the radial cutoff Rc was optimised. For other parameters, all combinations of sensible values inspired by Behler,49 were used to construct symmetry functions. Table 1 shows the values used for the parameters ζ, κ, η, λ and Rs, which in combination formed symmetry functions from Supplementary Eqs. (S2)–(S5). ACSFH denotes the symmetry functions with hydrogen as the center atom.
The performance of MBTR depended on several hyper-parameters, namely the gaussian broadening parameters σ(k2), σ(k3) as well as the decay exponent d. The other parameters, such as σ(k1) = 5 Å and the grid fineness n(k1) = 100, n(k2) = 900, n(k3) = 360 were kept constant for all data sets. SOAP can in principle be made global by matching local environments with each other, but we used it only locally in this work. The performance of the SOAP descriptor was to a small degree sensitive to the radial cutoff Rc. Other parameters, such as the highest angular contribution lmax = 9 and the highest radial contribution nmax = 10 were kept constant. The aforementioned descriptor parameters were scanned and evaluated on around 1000 data points, a subset of the training set. The optimal parameters are listed in Table 2.
Kernel ridge regression
For medium-sized data sets (1000–10,000) kernel ridge regression is a fast and accurate ML method. In ref. 52, KRR performed best with the descriptor HDAD (histograms of distances, angles and dihedrals) at predicting atomization energies, a conceptually similar descriptor to the ones we used which supported our choice of KRR. Of the ML models in ref. 52, graph convolution neural networks were not applicable to the descriptors, hence only random forest regression was another sensible choice. However, as shown in Supplementary Information, its performance is significantly worse than KRR in our case. In order to predict the properties of new data points, the descriptor features of the training set x are compressed into the kernel matrix K
where x1, …, xN are feature vectors of N training points and K(xi, xj) is a symmetric positive semi-definite kernel function (e.g., Gaussian kernel). The property y of a new data point xpred is predicted by inverting the kernel matrix
and regularising it by λ. The vector ytrain consists of the properties y1, …, yN of the training set. The kernel vector kpred is defined as:
The method benefits from a continuous feature space and a unique descriptor-property relation. It is worth mentioning that it works well even with large descriptor sizes and small training sets. The computational cost, however, scales with \({\cal O}\left( {N^3} \right)\), which makes it computationally expensive or infeasible for large data sets (>10,000).
The calculated adsorption energies of the training sets were interpolated by kernel ridge regression using the radial basis function kernel
Based on a comparison of different kernels in Supplementary Information, the RBF kernel performs on par with the SOAP-kernel.50 The resulting kernel matrices were used to predict the (free) adsorption energies of the test sets. The exponent of the radial distribution function γ and regularization parameter α were optimised by fivefold cross-validation.
When the features of MBTR and SOAP were combined to a new descriptor, they were weighted within the kernel:
where \(q = \frac{{n_{{\rm MBTR}}}}{{n_{{\rm SOAP}}}}\) is the quotient of the number of features in MBTR and SOAP. This accounted for different descriptor sizes and thus ensured equal weigthing of the descriptors.
Data availability
The DFT data that support the findings of this study are available in the NOMAD repository with the identifiers https://doi.org/10.17172/NOMAD/2018.06.12-2 and https://doi.org/10.17172/NOMAD/2018.06.12-1.53,54 The structures and adsorption energies of the data sets can be found as Supplementary Material.
References
Wang, D. et al. Shape control of CoO and LiCoO2 nanocrystals. Nano Res. 3, 1–7 (2010).
Liu, Y., Zhao, G., Wang, D. & Li, Y. Heterogeneous catalysis for green chemistry based on nanocrystals. Natl Sci. Rev. 2, 150–166 (2015).
Yang, F., Deng, D., Pan, X., Fu, Q. & Bao, X. Understanding nano effects in catalysis. Natl Sci. Rev. 2, 183–201 (2015).
Zhou, K. & Li, Y. Catalysis based on nanocrystals with well-defined facets. Angew. Chem. - Int. Ed. 51, 602–613 (2012).
Nan, C. et al. Size and shape control of LiFePO4 nanocrystals for better lithium ion battery cathode materials. Nano Res. 6, 469–477 (2013).
Sayle, D. C., Maicaneanu, S. A. & Watson, G. W. Atomistic models for CeO2(111), (110), and (100) nanoparticles, supported on yttrium-stabilized zirconia. J. Am. Chem. Soc. 124, 11429–11439 (2002).
Fan, Z., Huang, X., Tan, C. & Zhang, H. Thin metal nanostructures: synthesis, properties and applications. Chem. Sci. 6, 95–111 (2015).
Valden, M. Onset of catalytic activity of gold clusters on titania with the appearance of nonmetallic properties. Science 281, 1647–1650 (1998).
Cuddy, M. J. et al. Fabrication and atomic structure of size-selected, layered MoS2 clusters for catalysis. Nanoscale 6, 12463–12469 (2014).
Hu, J. et al. Engineering stepped edge surface structures of MoS2 sheet stacks to accelerate the hydrogen evolution reaction. Energy Environ. Sci. 10, 593–603 (2017).
Fu, G. et al. Synthesis and electrocatalytic activity of Au@Pd core-shell nanothorns for the oxygen reduction reaction. Nano Res. 7, 1205–1214 (2014).
Zhang, Z.-c, Xu, B. & Wang, X. Engineering nanointerfaces for nanocatalysis. Chem. Soc. Rev. 43, 7870–7886 (2014).
Seh, Z. W. et al. Combining theory and experiment in electrocatalysis: Insights into materials design. Science 355, eaad4998 (2017).
Walter, M. G. et al. Solar water splitting cells. Chem. Rev. 110, 6446–6473 (2010).
Lewis, N. S. & Nocera, D. G. Powering the planet: chemical challenges in solar energy utilization. Proc. Natl Acad. Sci. USA 103, 15729–15735 (2006).
Roger, I., Shipman, M. A. & Symes, M. D. Earth-abundant catalysts for electrochemical and photoelectrochemical water splitting. Nat. Rev. Chem. 1, 0003 (2017).
European Commission. Report on Critical Raw Materials for the EU, Ad hoc Working Group on defining critical raw materials. Tech. Rep. (2014).
Lu, Q. et al. Highly porous non-precious bimetallic electrocatalysts for efficient hydrogen evolution. Nat. Commun. 6, 6567 (2015).
Nørskov, J. K., Bligaard, T., Rossmeisl, J. & Christensen, C. H. Towards the computational design of solid catalysts. Nat. Chem. 1, 37–46 (2009).
Sørensen, S. G., Füchtbauer, H. G., Tuxen, A. K., Walton, A. S. & Lauritsen, J. V. Structure and electronic properties of in situ synthesized single-layer MoS2 on a gold surface. ACS Nano 8, 6788–6796 (2014).
Bruix, A. et al. In situ detection of active edge sites in single-layer MoS2 catalysts. ACS Nano 9, 9322–9330 (2015).
Walton, A. S., Lauritsen, J. V., Topsøe, H. & Besenbacher, F. MoS2 nanoparticle morphologies in hydrodesulfurization catalysis studied by scanning tunneling microscopy. J. Catal. 308, 306–318 (2013).
Ma, X., Li, Z., Achenie, L. E. K. & Xin, H. Machine-learning-augmented chemisorption model for CO2 electroreduction catalyst screening. J. Phys. Chem. Lett. 6, 3528–3533 (2015).
Takigawa, I., Shimizu, K.-i, Tsuda, K. & Takakusagi, S. Machine-learning prediction of d-band center for metals and bimetals. RSC Adv. 6, 52587–52595 (2016).
Ma, X. Orbitalwise coordination number for predicting adsorption properties of metal nanocatalysts. Phys. Rev. Lett. 118, 036101 (2017).
Li, Z., Ma, X. & Xin, H. Feature engineering of machine-learning chemisorption models for catalyst design. Catal. Today 280, 232–238 (2017).
Ulissi, Z. W., Medford, A. J., Bligaard, T., Nørskov, J. K. & Nørskov, J. K. To address surface reaction network complexity using scaling relations machine learning and DFT calculations. Nat. Commun. 8, 14621 (2017).
Li, Z., Wang, S., Chin, W. S., Achenie, L. E. & Xin, H. High-throughput screening of bimetallic catalysts enabled by machine learning. J. Mater. Chem. A 5, 24131–24138 (2017).
Parsons, R. The rate of electrolytic hydrogen evolution and the heat of adsorption of hydrogen. Trans. Faraday Soc. 54, 1053 (1958).
Nørskov, J. K. et al. Trends in the exchange current for hydrogen evolution. J. Electrochem. Soc. 152, J23 (2005).
Behler, J. Perspective: machine learning potentials for atomistic simulations. J. Chem. Phys. 145, 170901 (2016).
Hansen, K. et al. Assessment and validation of machine learning methods for predicting molecular atomization energies. J. Chem. Theory Comput. 9, 3404–3419 (2013).
Huang, B. & von Lilienfeld, O. A. Communication: understanding molecular representations in machine learning: the role of uniqueness and target similarity. J. Chem. Phys. 145, 161102 (2016).
Bartók, A. P. et al. Machine learning unifies the modeling of materials and molecules. Sci. Adv. 3, e1701816 (2017).
Hutter, J., Iannuzzi, M., Schiffmann, F. & VandeVondele, J. CP2K: atomistic simulations of condensed matter systems. Wiley Interdiscip. Rev.-Comput. Mol. Sci. 4, 15–25 (2014).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
VandeVondele, J. & Hutter, J. Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases. J. Chem. Phys. 127, 114105 (2007).
Goedecker, S., Teter, M. & Hutter, J. Separable dual-space Gaussian pseudopotentials. Phys. Rev. B 54, 1703–1710 (1996).
Krack, M. Pseudopotentials for H to Kr optimized for gradient-corrected exchange-correlation functionals. Theor. Chem. Acc. 114, 145–152 (2005).
Hartwigsen, C., Goedecker, S. & Hutter, J. Relativistic separable dual-space Gaussian pseudopotentials from H to Rn. Phys. Rev. B 58, 3641–3662 (1998).
Grimme, S., Antony, J., Ehrlich, S. & Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132, 154104 (2010).
Grimme, S., Ehrlich, S. & Goerigk, L. Effect of the damping funtion in dispersion corrected density functional theory. J. Comput. Chem. 32, 1456–1465 (2011).
Hinnemann, B. et al. Biomimetic hydrogen evolution: MoS2 nanoparticles as catalyst for hydrogen evolution. J. Am. Chem. Soc. 127, 5308–5309 (2005).
Greeley, J. & Mavrikakis, M. Surface and subsurface hydrogen: adsorption properties on transition metals and near-surface alloys. J. Phys. Chem. B 109, 3460–3471 (2005).
Faber, F., Lindmaa, A., Von Lilienfeld, O. A. & Armiento, R. Crystal structure representations for machine learning models of formation energies. Int. J. Quantum Chem. 115, 1094–1101 (2015).
Ghiringhelli, L. M., Vybiral, J., Levchenko, S. V., Draxl, C. & Scheffler, M. Big data of materials science: critical role of the descriptor. Phys. Rev. Lett. 114, 105503 (2015).
De, S., Bartók, A. P., Csányi, G. & Ceriotti, M. Comparing molecules and solids across structural and alchemical space. Phys. Chem. Chem. Phys. 18, 1–18 (2016).
Rupp, M. et al. Fast and accurate modeling of molecular atomization energies with machine learning. Phys. Rev. Lett. 108, 58301 (2012).
Behler, J. Atom-centered symmetry functions for constructing high-dimensional neural network potentials. J. Chem. Phys. 134, 074106 (2011).
Bartók, A. P., Kondor, R. & Csányi, G. On representing chemical environments. Phys. Rev. B - Condens. Matter Mater. Phys. 87, 1–19 (2013).
Huo, H. & Rupp, M. Unified Representation of Molecules and Crystals for Machine Learning. Preprint at https://arxiv.org/pdf/1704.06439.pdf.
Faber, F. A. et al. Prediction errors of molecular machine learning models lower than hybrid DFT error. J. Chem. Theory Comput. 13, 5255–5264 (2017).
Jäger, M. O. J., Morooka, E. V., Canova, F. F., Himanen, L. & Foster, A. S. Machine learning hydrogen adsorption on nanoclusters through structural descriptors. MoS2 dataset. NOMAD Repository (2018).
Jäger, M., Morooka, E. V., Federici Canova, F., Himanen, L. & Foster, A. S. Machine learning hydrogen adsorption on nanoclusters through structural descriptors. AuCu dataset. NOMAD Repository (2018).
Acknowledgements
We acknowledge the generous computing resources from CSC—IT Center for Scientific Computing and the computational resources provided by the Aalto Science-IT project. The work was supported by the World Premier International Research Center Initiative (WPI), MEXT, Japan and the European Union’s Horizon 2020 research and innovation program under grant agreement no. 676580 NOMAD, a European Center of Excellence and no. 686053 CRITCAT.
Author information
Authors and Affiliations
Contributions
M.O.J.J. and E.V.M. created the data, performed machine learning and wrote the manuscript. M.O.J.J., E.V.M., F.F.C., L.H. implemented and tested descriptors. M.O.J.J., E.V.M. and F.F.C. analyzed the results. All authors reviewed and commented on the manuscript. A.S.F. supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jäger, M.O.J., Morooka, E.V., Federici Canova, F. et al. Machine learning hydrogen adsorption on nanoclusters through structural descriptors. npj Comput Mater 4, 37 (2018). https://doi.org/10.1038/s41524-018-0096-5
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-018-0096-5
This article is cited by
-
A computational approach for mapping electrochemical activity of multi-principal element alloys
npj Materials Degradation (2023)
-
CEGANN: Crystal Edge Graph Attention Neural Network for multiscale classification of materials environment
npj Computational Materials (2023)
-
Machine learning-enabled exploration of the electrochemical stability of real-scale metallic nanoparticles
Nature Communications (2023)
-
Identification of chemical compositions from “featureless” optical absorption spectra: Machine learning predictions and experimental validations
Nano Research (2023)
-
Machine Learning-Assisted Low-Dimensional Electrocatalysts Design for Hydrogen Evolution Reaction
Nano-Micro Letters (2023)