Abstract
The question of material stability is of fundamental importance to any analysis of system properties in condensed matter physics and materials science. The ability to evaluate chemical stability, i.e., whether a stoichiometry will persist in some chemical environment, and structure selection, i.e. what crystal structure a stoichiometry will adopt, is critical to the prediction of materials synthesis, reactivity and properties. Here, we demonstrate that density functional theory, with the recently developed strongly constrained and appropriately normed (SCAN) functional, has advanced to a point where both facets of the stability problem can be reliably and efficiently predicted for main group compounds, while transition metal compounds are improved but remain a challenge. SCAN therefore offers a robust model for a significant portion of the periodic table, presenting an opportunity for the development of novel materials and the study of fine phase transformations even in largely unexplored systems with little to no experimental data.
Similar content being viewed by others
Introduction
Reliably accurate first-principles stability calculations are critical to the studies of materials synthesis,1 reactivity2,3 and properties,4 and essential for both the exploration of new chemical spaces and the study of difficult-to-observe phases. For known materials, the question of solids stability can be resolved experimentally through a variety of calorimetric techniques, which yield the enthalpy of formation (∆H f ), defined as the energy released when a compound is formed out of the elemental constituents in their standard states. In the prediction of new materials however, the formation enthalpy must be calculated from first-principles, which is most commonly done using density functional theory (DFT)5,6,7,8 with the well-established Perdew–Burke–Ernzerhof (PBE)9 density functional. Furthermore, in the evaluation of solids differing in structure, but not chemistry, the differences between the formation enthalpies of competing phases often lie on a very fine energy scale, and are very difficult to measure experimentally, motivating their calculation from first-principles.10
Due to the diversity of chemical degrees of freedom, from subtle structural differences to changes in bonding characteristics, it is challenging for first-principles methods to tackle both facets of the stability problem at a reasonable computational cost. The chemical accuracy of ∆H f , typically quoted as 1 kcal/mol (0.04 eV/atom), can be achieved in experiments, usually limited by sample quality and measurement uncertainties. High-level wavefunction methods11 (e.g., the configuration interaction or quantum Monte Carlo approaches) can achieve such accuracy, but they are limited to systems having a relatively small number of electrons per periodic unit cell due to their high computational cost. DFT5,6,7,8 with the PBE9 generalized gradient approximation (GGA) to its exchange–correlation energy currently is the dominant calculation approach due to its relatively cheap computational cost and reasonable accuracy. Unfortunately, errors in formation enthalpy predicted by PBE are usually at the level of ~0.2 eV/atom, which leads to significant errors in predicting phase stability among dissimilar chemistries. While error cancellation reduces the magnitude of enthalpy error when considering chemically similar phases, the remaining errors still result in difficulties in selecting the ground state structure among chemically similar phases (see Fig. 1). The three major sources of error in PBE are the self-interaction error, the incomplete error cancellation between the target compound and the elemental references, and the absence of van der Waals (vdW) interactions. Attempts have been made to improve upon PBE at the GGA level using non-empirical derivations, including the Wu-Cohen,12 PBEsol13 and AM0514 GGAs. A GGA referred to as PBEfe has been specifically optimized for the formation enthalpies of solids.15 However, none of the GGAs improve over PBE systematically and replace PBE as a general-purpose functional. For example, those GGAs such as PBEsol that are better than PBE for the lattice constants of solids are typically worse than PBE for the binding energies of molecules (relevant to the formation energy).
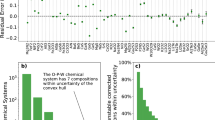
SCAN provides a significant improvement over PBE in computing the absolute and relative stability of main group compounds, approaching the chemical accuracy of 0.04 eV/atom in formation enthalpy and providing reliable structure selection as an indicator of accurate relative stability. a The formation enthalpy of main group compounds, and oxides in particular. b The probability that the computed energy of a predicted structure with respect to that of the experimental ground state structure lies below a threshold energy or tolerance across main group compounds for a range of tolerances
Moving beyond pure GGA functionals, the GGA+U approximation16,17 is a common method which improves the representation of transition (with valence d electrons) metal elements at marginal extra computational cost. DFT+U is an empirical method for modeling electron correlation effects in which one complements DFT with a model Hamiltonian by adding an on-site interaction given by the Hubbard U term. In the commonly used implementations, U is treated as an empirical scalar parameter to reduce the self-interaction error in the underlying density functional.18 The DFT+U scheme reduces the self-interaction error by linearizing the electronic energy with respect to the occupation of a set of selected (for example, d or f) orbitals and helps localize the associated electronic states, and improves energetic descriptions for many compounds involving transition metal elements.19 However, the U parameter used in this approach is typically determined empirically and is system and property dependent, such that the simultaneous representation of, for example, chemical and structural stability would require different and non-generalizable U values.20,21
Similarly, an array of vdW corrections22,23,24 have been proposed to PBE to improve the description of the vdW interactions. The vdW-corrected PBE is useful for systems where vdW interactions are important, which however faces the problem of double counting of the vdW interaction from both PBE (and in general the underlying density functional) and the vdW correction.25 Furthermore, the vdW corrections are usually not helpful for dealing with the other two sources of error.
To deal with the imperfect error cancellation of PBE, a number of different approaches have been developed, such as the fitted elemental-phase reference energies (FERE) scheme,26,27 and other schemes with fitted corrections to elemental and molecular reference states.28,29 These corrections assume that most of the error in compound formation enthalpy depends only on the overall composition, and attempt to eliminate this error by using the total energies of elemental phases as fitting parameters. In the case of FERE, with about 30 fitting parameters, the PBE mean absolute error (MAE) is reduced from 0.250 eV/atom to 0.052 eV/atom for a set of 110 main-group binary solids that largely overlap our testing set to be discussed here. However, neither FERE nor the other composition-based schemes can provide the correction to PBE needed to predict the relative stability of different phases of a compound, which is critically important for structure selection, and by extension the prediction of properties that depend on local structural changes rather than simply the average composition. Furthermore, fitting schemes, based on common structures and thus common geometries and oxidation states, are difficult to generalize outside of their initial fitting data, especially to situations where rare electronic configurations may give rise to unexpected errors not accounted for by the fitted correction.29
The corrections mentioned above were developed or motivated to solve one of the three major error sources of PBE. As a result, broad benchmarks across GGA-based functionals targeting solid formation enthalpies, crystal structure selection and various material properties continue to rely on PBE as a representative general-purpose GGA, offering a balanced performance in the representation of various characteristics of a solid.
Compared to GGAs, which are built using only the electron density and its gradient, meta-GGAs30,31,32,33,34,35,36,37,38,39,40 add the electronic kinetic energy density as an additional ingredient. The kinetic energy density is semilocal in the occupied orbitals, immediately available from common DFT calculations, and thus only adds moderate extra computational cost. While a number of different meta-GGAs have been proposed based on both non-empirical derivations30,32,33,35,36,37 and fitting schemes,31,34,38,39,40 the strongly constrained and appropriately normed (SCAN) meta-GGA30 is unique in that it satisfies all known (17) exact constraints applicable to a meta-GGA. In contrast, the PBE GGA only satisfies 11 of the 17 exact constraints. By correctly building the kinetic energy density into a dimensionless orbital-overlap indicator, SCAN distinguishes between density regions characterizing different chemical bonds (including covalent, ionic, metallic, hydrogen and vdW), and treats them properly through appropriate GGA constructions, allowing SCAN to address diverse types of bonding in materials and systematically improve over PBE in general.41 SCAN has been tested for different properties and systems with excellent performance in comparison with GGAs and other meta-GGAs, including molecules,42 liquids,43,44 surfaces45 and solids.46,47,48 For cohesive energies of solids tested in refs. 25 and 46 which might not be a good indicator for testing density functionals,49 SCAN slightly improves over PBE,25,46 while SCAN demonstrates significantly better accuracy than PBE and PBE-based density functionals for energetics and structures of a small set of binary oxides,47 which is more relevant to experimental measurements. The unique and non-empirical derivation of SCAN suggests transferability in reproducing chemical and structural stability of compounds across the periodic table, as compared to PBE, motivating the present study.
Here, we show that the SCAN30 semilocal density functional halves the errors of PBE in predicting formation enthalpies of about 200 binary solids,15 taking a significant step towards chemical accuracy while retaining a comparable efficiency to PBE. Remarkably, SCAN also yields a significant improvement in the reliability of crystal structure selection, consistently halving the error rate in ground state selection accuracy and reducing the error in the relative energies of crystal structures. While the computational cost of SCAN is modestly greater than (usually 2–3 times) that of PBE, it is much less (in general by an order of magnitude in plane-wave codes) than that of hybrid functionals, and very much less than that of wavefunction methods. We believe that this development is a very significant step for the ab initio prediction of novel compounds and their properties and one that will lend more credibility to such predictions when experimental efforts are needed to realize them.
Results and discussion
To systematically compare the performance of SCAN and PBE, we group chemistries by how they are affected by known errors in semilocal density functionals. Self-interaction error, one of the three major error sources in PBE, is intrinsic to all computationally semilocal density functionals, among which are PBE and SCAN. Self-interaction error manifests itself in transition metal compounds, especially in semiconducting and insulating oxides, more than in main group compounds due to the presence of valence d electrons that localize more than valence sp electrons.50 The late 3d elements Cr, Mn, Fe, Co, and Ni, are especially problematic. To resolve self-interaction error in a true first-principles spirit, nonlocal corrections are necessary, which are typically computationally expensive and scale poorly with system size. Therefore, we first address the behavior of main group compounds so as to characterize the performance of PBE and SCAN as efficient semilocal functionals largely in the absence of self-interaction error.
As shown in Fig. 1a, the MAE of SCAN in the formation enthalpy of 102 main group compounds is 0.084 eV/atom, about 2.5 times lower than that of PBE, while the MAE of SCAN for the 21 main group oxides (shown in the inset) is 0.038 eV/atom, impressively within the typically quoted chemical accuracy of 0.04 eV/atom. MAE is used here to characterize the accuracy of functionals, while further discussions about metrics for characterizing the accuracy can be found in refs. 51 and 52 The reduction in error afforded by SCAN relative to PBE originates from the fact that PBE is not able to simultaneously and accurately treat the different types of chemical bonds30,41 found in a compound and its constituent elemental phases, leading to the well-known imperfect error cancellation, e.g., between the molecular O2 reference and metal oxides.28 SCAN, on the other hand, is able to capture the behavior of all such interactions41 by introducing the Kohn–Sham kinetic energy density into the functional in a way that satisfies all known limiting behaviors and constraints on electronic interaction appropriate to semilocal functionals.30 This construction leads to a widely predictive functional.53 In particular, without being fitted to any bonded system, SCAN captures even the intermediate-range vdW attraction between neighboring atoms in a solid, which PBE largely neglects. Furthermore, PBE underestimates the chemical stabilities of most solids, for example erroneously making InN chemically unstable, an error which SCAN avoids. These errors arise largely from PBE over-stabilization of reference molecules, and could not be fixed by simply adding a vdW correction to PBE.
An even stronger indication of the general reliability of SCAN for stability calculations is its superior performance in identifying ground state crystal structures. Here the intermediate-range vdW interaction, present in SCAN but not in PBE, can play a particularly important role, for example, by stabilizing the correct CsCl structure in the heavy halides CsCl, CsBr and CsI.54 Based on 190 stoichiometric main group binary compounds with 1627 experimentally reported and predicted crystal structures, we identify the most stable low-temperature, low-pressure phases within PBE and SCAN. We then evaluate the frequency with which PBE or SCAN stabilizes an incorrect ground state structural polymorph in comparison to the experimental structure. The zero-temperature ground state crystal structure is thermodynamically defined as the phase with the lowest enthalpy, as, under these conditions, enthalpy is exactly equal to the system Gibbs free energy. Thus, the relative energies of competing crystal structures computed from DFT provide a nearly complete representation of their relative Gibbs free energies under these conditions. The missing terms in the Gibbs free energy difference are the change in zero-point vibrational energy, which is in the scale of 0.005 eV/atom,55,56,57,58 ambient pressure effects, which lie in the scale of 0.001 eV/atom, and other contributions of smaller magnitudes. To account for these effects, as well as other potential noise in the calculations, we introduce a tolerance on structure selection ∆Etol, and count the frequency with which PBE or SCAN erroneously stabilize a crystal structure by more than ∆Etol with respect to the experimental ground state structure.. As can be seen in Fig. 1b, SCAN provides a significant improvement over PBE in selecting the correct ground state structure, reducing the frequency of structure prediction error from 12% to just 3% at a 0.01 eV/atom tolerance, where the improvement in structure selection accuracy likely originates from the more accurate physical model provided by SCAN relative to PBE. Notably, the energy scale of competing crystal structures59,60,61 and the associated tolerances are far below the average error suggested by total formation enthalpy statistics discussed earlier, which confirms the consensus that density functionals work better in predicting energy difference between chemically similar systems than that of dissimilar systems. Thus, it is evident that reliable structure selection is a sensitive indicator of how well a functional captures fine details in the relative stability of chemically similar phases.
Our structure selection results highlight the difficulty of reliable structure prediction by first-principles calculations. While we find that PBE yields close to a 21% error rate in structure selection in absolute terms and a 12% error rate with a 0.01 eV/atom tolerance, this error rate is likely a lower bound as no method that we are aware of can guarantee that no other crystal structures exist with a lower energy for any given chemistry. Conversely, experimental uncertainties in the ground state crystal structure originating from difficult-to-observe low-temperature phase transitions, small off-stoichiometries and other errors mean that even the exact functional would likely not be able to achieve complete agreement with experiment. In this light, the 3% error rate of SCAN within the 0.01 eV/atom tolerance is remarkable. The impact of this improvement is immediately visible—for example, in SiO2, SCAN is able to reproduce the correct α-quartz low-temperature, low-pressure ground state structure and, correspondingly, the pressure–temperature phase diagram, as PBE over-stabilizes the high-temperature β-cristobalite polymorph. The intermediate-range vdW interaction in SCAN stabilizes the correct, higher-density quartz phase of this earth-abundant material. Taken together with the promising performance in predicting formation enthalpy, these results suggest that SCAN is highly reliable for both the absolute and relative stability of the main group compounds.
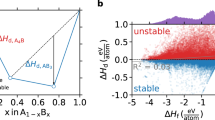
We now turn to transition metal compounds, where self-interaction error poses a fundamental limitation on the performance of semilocal density functionals. For the formation enthalpies of 98 transition metal binaries (where we consider compounds consisting of a transition metal and an electronegative anion, excluding intermetallic compounds), Fig. 2a shows that SCAN still has an MAE of 0.122 eV/atom, which is significantly larger than that of the main group compounds. However, SCAN improves over PBE by about 0.08 eV/atom, or 40% of the total PBE error, for the transition metal compounds. Similarly, as can be seen in Fig. 2b, based on 106 transition metal binary compounds with 1336 experimental and predicted structures, SCAN also gives a significant improvement relative to PBE in structure selection accuracy, although the absolute performance of both functionals is much worse than that in the main group compounds, both in the frequency of structure selection errors and their energetic magnitude. The fact that this discrepancy persists even at a 0.02 eV/atom tolerance, where the SCAN error rate in main group chemistries approaches zero, suggests that further improvements in functional performance would require a fundamentally different approach, moving to non-local functional forms or explicit self-interaction corrections.62,63,64,65
SCAN considerably reduces the average error in formation enthalpy and structure selection error frequency relative to PBE in transition metal compounds that are more difficult to represent than the main group compounds due to an increased contribution of self-interaction error. a The enthalpy of formation of transition metal binary compounds, and oxides in particular. b The probability of incorrect structure selections by PBE or SCAN across transition metal compounds, for a range of tolerances
The development of semilocal exchange–correlation functionals in DFT has been driven by the promise of these approximations to efficiently evaluate the stability and properties of both known and predicted solid phases. As summarized in Table 1, the SCAN functional, without any fitted corrections, now approaches experimental accuracy in both total energy and the relative stability of solid phases across main group compounds, and the remaining challenges to DFT functionals appear to be self-interaction error dominated systems. Correspondingly, future improvement in general-purpose functional performance will require a solution to the self-interaction problem and a representation of non-local phenomena.
Methods
The calculations of enthalpy of formation are performed for 196 binary compounds with 101 main group systems (the chemistries are listed in Table S1 in Supplementary Information) and 95 systems containing transition metals (see Table S2). The structures and reference formation energies for these 196 compounds are based on the dataset reported by Sarmiento-Pérez et al,15 neglecting any potentially lower energy structures predicted by PBE or SCAN. The analysis of structure selection accuracy is based on 296 binary chemistries, of which 190 are main group compositions and 106 contain transition metals (see Table S4). In the choice of chemistries, we choose only compositions for which the low-temperature, low-pressure ground state crystal structure can be identified from experimental data to the best of our ability. The chemistries included in this sample are comprised of compositions previously chosen to benchmark formation enthalpy,15 AB-type compounds and a selection of binary compositions previously enumerated in crystal structure prediction studies.66 To the best of our knowledge, this selection of chemistries does not introduce any bias in the likelihood of structure selection error not present more generally in binary main group and transition metal compounds. For each chemistry, we consider experimentally reported crystal structures from the Inorganic Crystal Structure Database,67 as well as likely structures predicted by data mined elemental substitution methods,66 giving a total of 2963 crystal structures. All structures considered are available in POSCAR format in the supplementary materials, relaxed with PBE or SCAN. Finally, to determine whether or not a DFT-relaxed crystal structure matches the experimentally reported structure, we rely on a distortion-tolerant affine map, implemented as the StructureMatcher algorithm in the Pymatgen package.68
All calculations are performed using the Vienna Ab Initio Simulation Package (VASP)69,70 using the projector augmented wave (PAW) method71,72 with a reciprocal space discretization of 25 K-points per Å−1 and a plane wave energy cutoff of 520 eV. Both the semilocal GGA in the standard form of the PBE9,73 and the SCAN30,41 meta-GGA74 exchange–correlation functionals are used (with VASP PAW potential version “PAW 52”). In magnetically active systems, the energy is taken as the lowest of a ferromagnetic and a sample of small-unit-cell antiferromagnetic orderings. For the structure selection, the calculations are converged to 10−6 eV in total energy and 0.01 eV/Å on atomic forces. For computing formation enthalpies, all calculations are converged to 10−7 eV on total energy and 0.01 eV/Å on atomic forces. Molecular reference states are used for H2, N2, O2, F2 and Cl2, where the isolated molecule is represented by a dimer in a 15 × 15 × 15 Å3 box. Experimental standard enthalpies of formation used to determine the error in formation energy are defined at 298 K and 1 atm of pressure.
Data availability
All structures considered in the structure selection dataset, and experimental reference structures, as well as their relative energies computed in PBE and SCAN, are available in POSCAR format in the supplementary information. All structures considered in the enthalpy of formation dataset are available in previous datasets referred to in the main text.
References
Kitchaev, D. A. & Ceder, G. Evaluating structure selection in the hydrothermal growth of FeS2 pyrite and marcasite. Nat. Commun. 7, 13799 (2016).
Oganov, A. R. & Glass, C. W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 124, 244704 (2006).
Woodley, S. M. & Catlow, R. Crystal structure prediction from first principles. Nat. Mater. 7, 937–946 (2008).
Robinson, D. M. et al. Photochemical water oxidation by crystalline polymorphs of manganese oxides: structural requirements for catalysis. J. Am. Chem. Soc. 135, 3494–3501 (2013).
Kohn, W. Nobel Lecture: Electronic structure of matter–wave functions and density functionals. Rev. Mod. Phys . 71, 1253 (1999).
Burke, K. Perspective on density functional theory. J. Chem. Phys. 136, 150901 (2012).
Becke, A. D. Perspective: Fifty years of density-functional theory in chemical physics. J. Chem. Phys. 140, 18A301 (2014).
Yu, H. S., Li, S. L. & Truhlar, D. G. Perspective: Kohn-Sham density functional theory descending a staircase. J. Chem. Phys. 145, 130901 (2016).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Kitchaev, D. A., Dacek, S. T., Sun, W. & Ceder, G. Thermodynamics of phase selection in MnO2 framework structures through alkali intercalation and hydration. J. Am. Chem. Soc. 139, 2672–2681 (2017).
Booth, G. H., Grüneis, A., Kresse, G. & Alavi, A. Towards an exact description of electronic wavefunctions in real solids. Nature 493, 365–370 (2013).
Wu, Z. & Cohen, R. E. More accurate generalized gradient approximation for solids. Phys. Rev. B 73, 235116 (2006).
Perdew, J. P. et al. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100, 136406 (2008).
Armiento, R. & Mattsson, A. E. Functional designed to include surface effects in self-consistent density functional theory. Phys. Rev. B 72, 085108 (2005).
Sarmiento-Pérez, R., Botti, S. & Marques, M. A. Optimized exchange and correlation semilocal functional for the calculation of energies of formation. J. Chem. Theory Comput. 11, 3844–3850 (2015).
Liechtenstein, A., Anisimov, V. & Zaanen, J. Density-functional theory and strong interactions: orbital ordering in Mott-Hubbard insulators. Phys. Rev. B 52, R5467 (1995).
Dudarev, S., Botton, G., Savrasov, S., Humphreys, C. & Sutton, A. Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA + U study. Phys. Rev. B 57, 1505 (1998).
Cococcioni, M. & De Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA + U method. Phys. Rev. B 71, 035105 (2005).
Peng, H. & Perdew, J. P. Synergy of van der Waals and self-interaction corrections in transition metal monoxides. Phys. Rev. B 96, 100101(R) (2017).
Kitchaev, D. A. et al. Energetics of MnO2 polymorphs in density functional theory. Phys. Rev. B 93, 045132 (2016).
Curnan, M. T. & Kitchin, J. R. Investigating the energetic ordering of stable and metastable TiO2 polymorphs using DFT + U and hybrid functionals. J. Phys. Chem. C. 119, 21060–21071 (2015).
Grimme, S., Antony, J., Ehrlich, S. & Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132, 154104 (2010).
Tkatchenko, A. & Scheffler, M. Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data. Phys. Rev. Lett. 102, 073005 (2009).
Vydrov, O. A. & Van Voorhis, T. Nonlocal van der Waals density functional: the simpler the better. J. Chem. Phys. 133, 244103 (2010).
Peng, H., Yang, Z.-H., Perdew, J. P. & Sun, J. Versatile van der Waals density functional based on a meta-generalized gradient approximation. Phys. Rev. X 6, 041005 (2016).
Stevanović, V., Lany, S., Zhang, X. & Zunger, A. Correcting density functional theory for accurate predictions of compound enthalpies of formation: fitted elemental-phase reference energies. Phys. Rev. B 85, 115104 (2012).
Lany, S. Semiconductor thermochemistry in density functional calculations. Phys. Rev. B 78, 245207 (2008).
Wang, L., Maxisch, T. & Ceder, G. Oxidation energies of transition metal oxides within the GGA + U framework. Phys. Rev. B 73, 195107 (2006).
Persson, K. A., Waldwick, B., Lazic, P. & Ceder, G. Prediction of solid-aqueous equilibria: scheme to combine first-principles calculations of solids with experimental aqueous states. Phys. Rev. B 85, 235438 (2012).
Sun, J., Ruzsinszky, A. & Perdew, J. P. Strongly constrained and appropriately normed semilocal density functional. Phys. Rev. Lett. 115, 036402 (2015).
Zhao, Y. & Truhlar, D. G. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys. 125, 194101 (2006).
Tao, J. & Mo, Y. Accurate semilocal density functional for condensed-matter physics and quantum chemistry. Phys. Rev. Lett. 117, 073001 (2016).
Sun, J., Xiao, B. & Ruzsinszky, A. Communication: Effect of the orbital-overlap dependence in the meta generalized gradient approximation. J. Chem. Phys. 137, 051101 (2012).
Sun, J. et al. Semilocal and hybrid meta-generalized gradient approximations based on the understanding of the kinetic-energy-density dependence. J. Chem. Phys. 138, 044113 (2013).
Tao, J., Perdew, J. P., Staroverov, V. N. & Scuseria, G. E. Climbing the density functional ladder: nonempirical meta-generalized gradient approximation designed for molecules and solids. Phys. Rev. Lett. 91, 146401 (2003).
M. del Campo, J., Gázquez, J. L., Trickey, S. B. & Vela, A. A new meta-GGA exchange functional based on an improved constraint-based GGA. Chem. Phys. Lett. 543, 179–183 (2012).
Sun, J., Perdew, J. P. & Ruzsinszky, A. Semilocal density functional obeying a strongly tightened bound for exchange. Proc. Natl. Acad. Sci. USA 112, 685–689 (2015).
Wellendorff, J., Lundgaard, K. T., Jacobsen, K. W. & Bligaard, T. mBEEF: an accurate semi-local Bayesian error estimation density functional. J. Chem. Phys. 140, 144107 (2014).
Yu, H. S., He, X. & Truhlar, D. G. MN15-L: a new local exchange-correlation functional for Kohn–Sham density functional theory with broad accuracy for atoms, molecules, and solids. J. Chem. Theory Comput. 12, 1280–1293 (2016).
Mardirossian, N. & Head-Gordon, M. Mapping the genome of meta-generalized gradient approximation density functionals: the search for B97M-V. J. Chem. Phys. 142, 074111 (2015).
Sun, J. et al. Accurate first-principles structures and energies of diversely bonded systems from an efficient density functional. Nat. Chem. 8, 831–836 (2016).
Goerigk, L. et al. A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions. Phys. Chem. Chem. Phys. 19, 32184–32215 (2017).
Remsing, R. C., Klein, M. L. & Sun, J. Dependence of the structure and dynamics of liquid silicon on the choice of density functional approximation. Phys. Rev. B 96, 024203 (2017).
Chen, M. et al. Ab initio theory and modeling of water. Proc. Natl. Acad. Sci. USA 114, 10846–10851 (2017).
Patra, A., Bates, J., Sun, J. & Perdew, J. P. Properties of real metallic surfaces: effects of density functional semilocality and van der Waals nonlocality. Proc. Natl. Acad. Sci. USA 114, E9188–E9196 (2017).
Tran, F., Stelzl, J. & Blaha, P. Rungs 1 to 4 of DFT Jacob’s ladder: extensive test on the lattice constant, bulk modulus, and cohesive energy of solids. J. Chem. Phys. 144, 204120 (2016).
Hinuma, Y., Hayashi, H., Kumagai, Y., Tanaka, I. & Oba, F. Comparison of approximations in density functional theory calculations: energetics and structure of binary oxides. Phys. Rev. B 96, 094102 (2017).
Zhang, Y., Sun, J., Perdew, J. P. & Wu, X. Comparative first-principles studies of prototypical ferroelectric materials by LDA, GGA, and SCAN meta-GGA. Phys. Rev. B 96, 035143 (2017).
Perdew, J. P., Sun, J., Ruzsinszky, A., Mezei, P. D. & Csonka, G. I. Why density functionals should not be judged primarily by atomization energies. Period. Polytech. Chem. Eng. 60, 2 (2016).
Chevrier, V. L., Ong, S. P., Armiento, R., Chan, M. K. & Ceder, G. Hybrid density functional calculations of redox potentials and formation energies of transition metal compounds. Phys. Rev. B 82, 075122 (2010).
Pernot, P., Civalleri, B., Presti, D. & Savin, A. Prediction uncertainty of density functional approximations for properties of crystals with cubic symmetry. J. Phys. Chem. A 119, 5288–5304 (2015).
Lejaeghere, K., Van Speybroeck, V., Van Oost, G. & Cottenier, S. Error estimates for solid-state density-functional theory predictions: an overview by means of the ground-state elemental crystals. Crit. Rev. Solid State Mater. Sci. 39, 1–24 (2014).
Medvedev, M. G., Bushmarinov, I. S., Sun, J., Perdew, J. P. & Lyssenko, K. A. Response to Comment on “Density functional theory is straying from the path toward the exact functional”. Science 356, 496–496 (2017).
Zhang, F., Gale, J., Uberuaga, B., Stanek, C. & Marks, N. Importance of dispersion in density functional calculations of cesium chloride and its related halides. Phys. Rev. B 88, 054112 (2013).
Robie, R. A. Debye temperatures of selected silicate minerals. US Geological Survey, 1988. https://pubs.er.usgs.gov/publication/ofr88663.
Anderson, O. L., Schreiber, E., Liebermann, R. C. & Soga, N. Some elastic constant data on minerals relevant to geophysics. Rev. Geophys. 6, 491–524 (1968).
Bachmann, K., Hsu, F., Thiel, F. & Kasper, H. Debye temperature and standard entropies and enthalpies of compound semiconductors of the type I-III-VI2. J. Electron. Mater. 6, 431–448 (1977).
Tanaka, I. Impacts of first principles calculations in engineering ceramics. J. Ceram. Soc. Jpn. 124, 791–795 (2016).
Navrotsky, A. Nanoscale effects on thermodynamics and phase equilibria in oxide systems. ChemPhysChem 12, 2207–2215 (2011).
Sun, W. et al. The thermodynamic scale of inorganic crystalline metastability. Sci. Adv. 2, e1600225 (2016).
Curtarolo, S., Morgan, D. & Ceder, G. Accuracy of ab initio methods in predicting the crystal structures of metals: a review of 80 binary alloys. Calphad 29, 163–211 (2005).
Li, C., Zheng, X., Cohen, A. J., Mori-Sánchez, P. & Yang, W. Local scaling correction for reducing delocalization error in density functional approximations. Phys. Rev. Lett. 114, 053001 (2015).
Jaramillo, J., Scuseria, G. E. & Ernzerhof, M. Local hybrid functionals. J. Chem. Phys. 118, 1068–1073 (2003).
Perdew, J. P. & Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 23, 5048 (1981).
Pederson, M. R., Ruzsinszky, A. & Perdew, J. P. Communication: Self-interaction correction with unitary invariance in density functional theory. J. Chem. Phys. 140, 121103 (2014).
Fischer, C. C., Tibbetts, K. J., Morgan, D. & Ceder, G. Predicting crystal structure by merging data mining with quantum mechanics. Nat. Mater. 5, 641–646 (2006).
Belsky, A., Hellenbrandt, M., Karen, V. L. & Luksch, P. New developments in the Inorganic Crystal Structure Database (ICSD): accessibility in support of materials research and design. Acta Crystallogr. Sect. B Struct. Sci. 58, 364–369 (2002).
Ong, S. P. et al. Python Materials Genomics (pymatgen): a robust, open-source python library for materials analysis. Comput. Mater. Sci. 68, 314–319 (2013).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Perdew, J. P., Burke, K. & Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 54, 16533 (1996).
Sun, J. et al. Density functionals that recognize covalent, metallic, and weak bonds. Phys. Rev. Lett. 111, 106401 (2013).
Acknowledgements
Y.Z., H.P., J.P.P. and J.S. acknowledge the support from the Center for the Computational Design of Functional Layered Materials, an Energy Frontier Research Center funded by the US Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES), under award No. DE-SC0012575. D.A.K., T.C., S.T.D. and G.C. acknowledge support from the Center for Next-Generation of Materials by Design, an Energy Frontier Research Center funded by the US DOE, Office of BES. J.Y. acknowledges support from the Department of Defense (DoD) through the National Defense Science & Engineering Graduate Fellowship (NDSEG) Program. Y.Z. and J.S. acknowledge support in the form of computer time from the National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility. D.A.K. acknowledges computational resources sponsored by the Department of Energy’s Office of Energy Efficiency and Renewable Energy and located at the National Renewable Energy Laboratory. M.A.L.M. acknowledges partial support from the DFG though project MA-6786/6.
Author information
Authors and Affiliations
Contributions
J.S., H.P., J.P.P. and G.C. designed the project. Y.Z., D.A.K. and J.S. performed the calculations. Y.Z., J.S., R.A.S.-P. and M.A.L.M. constructed the formation enthalpy dataset. D.A.K., J.Y., T.C. and S.T.D. constructed the structure selection dataset. J.S., D.A.K. and Y.Z. wrote the paper. J.P.P. and G.C. edited the manuscript. All authors have discussed the results.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, Y., Kitchaev, D.A., Yang, J. et al. Efficient first-principles prediction of solid stability: Towards chemical accuracy. npj Comput Mater 4, 9 (2018). https://doi.org/10.1038/s41524-018-0065-z
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-018-0065-z
This article is cited by
-
In situ formed partially disordered phases as earth-abundant Mn-rich cathode materials
Nature Energy (2023)
-
DFT estimation of structural parameters and band gaps of III–V (GaP, AlP, InP, BP) and II–VI (BeX, MgX, CdX: X\(=\)O, S, Se, Te) semiconductors
Pramana (2023)
-
Superconductivity in antiperovskites
npj Computational Materials (2022)
-
A flexible and scalable scheme for mixing computed formation energies from different levels of theory
npj Computational Materials (2022)
-
Creating superconductivity in WB2 through pressure-induced metastable planar defects
Nature Communications (2022)