Abstract
The recent studies on nanotwinned (NT) and hierarchical nanotwinned (HNT) face-centered cubic (FCC) metals are presented in this review. The HNT structures have been supposed as a kind of novel structure to bring about higher strength/ductility than NT counterparts in crystalline materials. We primarily focus on the recent developments of the experimental, atomistic and theoretical studies on the NT and HNT structures in the metallic materials. Some advanced bottom-up and top-down techniques for the fabrication of NT and HNT structures are introduced. The deformation induced HNT structures are available by virtue of severe plastic deformation (SPD) based techniques while the synthesis of growth HNT structures is so far almost unavailable. In addition, some representative molecular dynamics (MD) studies on the NT and HNT FCC metals unveil that the nanoscale effects such as twin spacing, grain size and plastic anisotropy greatly alter the performance of NT and HNT metals. The HNT structures may initiate unique phenomena in comparison with the NT ones. Furthermore, based on the phenomena and mechanisms revealed by experimental and MD simulation observations, a series of theoretical models have been proposed. They are effective to describe the mechanical behaviors of NT and HNT metals within the applicable scope. So far the development of manufacturing technologies of HNT structures, as well as the studies on the effects of HNT structures on the properties of metals are still in its infancy. Further exploration is required to promote the design of advanced materials.
Similar content being viewed by others
Introduction
Nanocrystallization of polycrystalline metals characterizes a dramatic growth of the volume fraction of grain boundaries (GBs) in nanocrystalline (NC) metals, which significantly changes the physical, mechanical and chemical properties in comparison with the coarse-grained (CG) counterparts. Such nanostructuring process usually generates metals with high strength, low ductility and work hardening due to the suppression of dislocation activities by trivial crystallites.1, 2 The plastic deformation of NC metals is always dominated by GB-mediated activities such as GB sliding, diffusion and grain rotation.3,4,5,6,7 The yield strength of NC metals always increases along with the decrease of grain size due to the dislocation pile-up at GBs, well-known as the Hall–Petch strengthening mechanism.8 Nevertheless, there exists a critical grain size for achieving the optimal yield strength. The softening stage appears with excessive refinement of grains due to the inverse Hall–Petch effect.9 Grain refinement induced substantial increase of GBs can well impede the dislocation motion during plastic deformation. Such behavior plays a significant role in achieving ultrahigh strength. However, it is always accompanied by a severe decline of ductility. GB in crystalline materials is a quintessential high-dimensional structure with great complexity.10 Some new interesting efforts have been made to develop the fundamental understanding of its physical characteristics such as analyzing physical “building blocks” in GBs by machine learning,10 a three-dimensional polyhedral unit model developed for GB structure,11 tailoring the stability of GB by Mo segregation12 and the hydrogen embrittlement of GBs.13
Although nanocrystallization failed to surmount the common sense that strength and ductility are mutually exclusive, many other efforts have been made to explore strategies for simultaneously improving the strength and ductility of NC metals by designing the tunable nanostructures of materials in recent years.14 Several approaches have been proposed, such as bimodal or multimodal grain-size distribution,15,16,17,18 second-phase particle hardening,19,20,21 dual-phase nanostructuring,22 fabricating high dislocation density in deformation-induced martensitic transformation system,23 introducing NT structures into nanosized grains14,24,25 and the construction of gradient/hierarchical structures via surface mechanical grinding treatment (SMGT),26,27 surface mechanical attrition treatment (SMAT),28,29 pre-torsion30 and uniaxial tension.31 Inspired by the fact that strain localization can be suppressed in NC metal films adhesion with a ductile substrate under tension,32,33 the delocalized effect induced fracture toughening is realized in multilayered steel sheets.34 The materials with a gradient grain size distribution, which is elastically homogeneous but plastically gradient, exhibit good ductility by restraining the strain localization during plastic deformation.26,27,28 Interestingly, when the NT structures are introduced into the crystalline metals, which means that a high density of twin boundaries (TBs) is embedded in the grains, this kind of special nanostructure can act as coherent boundaries to improve the mechanical and physical properties of metals.14,24,25,35,36,37,38,39,40,41,42,43,44 The unique mechanical properties of NT materials derive from dislocation-TBs interactions which are different from dislocation-GBs and dislocation-dislocation interactions. Owing to the complicated dislocation-TBs reactions, NT materials breakthrough the conventional dilemma of strength and ductility, realizing significant strengthening and good ductility. TBs act as the efficient barriers for dislocation propagation inside the grains, different from the twin-free NC counterparts. Besides, TBs firstly can be the containers for dislocation aggregation and then become dislocation sources after losing coherency during plastic deformation,45,46 which relieves local stress concentration and make further plasticity into reality. So the perfection of TBs is critical to the strengthening effect of NT materials.47 Therefore, a new kind of hierarchical nanostructured materials called NT materials has been developed to concurrently achieve high strength and high ductility. NT materials have attracted worldwide attention due to the favorable mechanical and physical properties. Experimental studies have uncovered that NT metals have ultrahigh strength/hardness,24,25,38,48,49,50 good ductility25,51,52 and great strain hardening.25,51,53 Corresponding to these experimental outcomes, a large quantity of theoretical studies are available, such as the intrinsic size effects and plastic anisotropy, the stability of NT structures,54,55 the effect of surface stress56,57 and NT structures in CG system on the mechanical properties of metals.58,59,60,61 Moreover, the electrical conductivity of NT bulk metals is similar to the conventional CG counterpart but much higher than NC metals.22 NT structures lead to a significant variation of the electronic and optical properties of nanowires.38,39,40,41,42 And they are also able to strengthen the face-centered diamond-cubic materials such as silicon, diamond and cubic boron nitride which has a crystal structure analogous to that of diamond.62,63,64,65 In addition, multiple twins are available in ferromagnetic shape memory alloys, which can be used to control the properties of ferromagnetic, ferroelastic, and ferroelectric materials.66,67
Research on the mechanical performance of materials with NT structures is still an extremely popular topic and many progresses have been reported in last few years. The in-depth vision on the formation, structure and deformation of NT metals has been conducted.68,69,70,71,72,73,74 According to the molecular dynamics (MD) simulation results, the brittle/ductile deformation modes of NT metals can be affected by the thickness of materials and environmental temperature.75,76 The plastic anisotropy has also been validated.77,78,79,80 The exceptional torsion capability of nanowires is accessible by domino detwinning.81 Also, both the experimental and computational studies on various properties of materials, such as friction,82 fracture,83,84,85 fatigue,83,85,86,87,88,89,90 creep85,91 and corrosion,92 are promoting the understanding of NT materials. The experimental93,94,95,96,97 and MD studies98,99,100 of NT structures have demonstrated that they are also beneficial to the adsorption of irradiation-induced defects, and thus can effectively reduce the irradiation hardening effect and keep good ductility. Crystal plasticity models have been developed to describe the mechanical behaviors of irradiated face-centered cubic (FCC) metals with and without NT structures.101,102 Also, many theoretical models have been proposed to improve the fundamental understanding of the deformation mechanisms of NT metals,103,104,105,106,107,108,109,110,111 some of which will be introduced in this review. In addition to the superior mechanical properties, it has also been reported that NT structures alter the electronic and optical properties of semiconductor nanowires.39,40,41,42 Hence, NT structures are suggesting promising applications in various material fields such as high-performance mechanical structures, nano-devices in optical systems, biological sensing and nano-electromechanical materials.
The construction of hierarchical nanostructures has been demonstrated as a novel approach to enhance the strength of metals by controlling the microstructure instead of changing chemical composition. Some strategies of hierarchy design such as subnanometer intragranular solute cluster, two geometries of nanometer-scale solute structures and nanoscale refinement of grains can increase the strength of aluminum alloy.112 In addition, polycrystalline metals with hierarchical nanotwinned (HNT) structures can tremendously change the mechanical performance compared with that of the NT counterparts, which could be particularly suitable for the metals in which NT structures can be formed easily. Specifically, HNT structures imply that there coexist primary twins, secondary twins, tertiary twins or even higher ordered NT structures in a single grain. The HNT structures have already been observed during martensitic transformation.66,113,114 It is found that the secondary twins form in the primary twins and the tertiary twins are generated from the secondary ones. These HNT structures play an important role in the mechanical behaviors of materials.115 Based on some modern techniques such as surface mechanical grinding treatment (SMGT) and equal-channel angular pressing (ECAP), HNT structures have been observed in ultrafine/NC Cu and Cu–Al alloys.116,117 Zhu et al. have pioneeringly predicted that these HNT structures are beneficial to the optimization of the strength and ductility of materials. They have proposed the related plasticity models for HNT materials.118,119 Furthermore, HNT structures are observed in twinning-induced plasticity (TWIP) steels during the process of surface mechanical attrition treatment (SMAT) and subsequent tensile deformation. HNT structures are supposed to be an essential factor for obtaining high performance TWIP steels.120 More recently, the gradient HNT structures are discovered during the tensile test on pre-torsioned TWIP steel,30 clearly showing the distribution of HNT structures and the effect of stacking faults (SFs) and dislocations on the formation of TBs. The researchers demonstrate that HNT structures can contribute to fantastic improvement of strength without sacrifice of ductility. Besides, some MD simulation efforts for the understanding of the intrinsic size effect of HNT structures have also been reported,121,122,123,124 trying to understand the relationship between the nanostructures and the mechanical properties. Thus, HNT structures have received sustained attention in the context of achieving even higher strength and better ductility by designing the nanostructures of metals.
As mentioned above, the mechanical and physical properties of NT materials gradually become an issue of great concern in the last decades. Significant progresses have been made to understand the superiorities of NT and HNT structures through large quantity of experiments, computational simulations and theoretical studies. Introducing NT and HNT structures into materials have been proved as a new effective approach to produce mechanically and physically high-performance crystalline materials. In this paper, we review the NT and HNT structures fabricated by some frequently used experimental technologies. The discussions on the important issues such as deformation mechanisms and mechanical properties will be presented based on the findings from the experimental tests, MD simulations and theoretical studies. Note that we will only give introductions to the fabrication techniques of NT and HNT structures, the theoretical studies applicable for the description and analysis of the deformation mechanisms of NT and HNT FCC metals. Here we also refer readers to some existing review articles on NT structures for a more thorough understanding of the fundamentals and details of previous researches. Comprehensive coverage of the NT structures are available, mainly about the growth twinning, deformation twinning, detwinning in FCC, hexagonal close-packed (HCP), and body-centered cubic (BCC) materials.116,125,126,127,128,129,130,131
Figure 1 shows some remarkable approaches to achieve the extraordinary overall mechanical properties with the associated strategies of structure design in metal materials. The two nanostructures highlighted by red color (nanotwins and hierarchical nanotwins) are reviewed in this paper. Specifically, this review is composed of the review of the representative fabrication technologies, MD simulation outcomes and theoretical models of NT and HNT FCC metals. A brief perspective is also given for the future studies on the HNT structures. It is essential to clarify the effects of such structures on the mechanical properties of materials, shedding light on the design of higher-performance materials.
Flow chart of selected outstanding structures to improve the overall mechanical properties of metal materials. The two nanostructures highlighted by red color (nanotwins and hierarchical nanotwins) are reviewed in this paper (the inset of gradient structure is reproduced with permission from ref.26 Copyright (2017) The American Association for the Advancement of Science)
NT FCC metals
Fabrication of NT structures
Nucleation of NT structures in FCC metals is closely related to the nucleation and propagation of partial dislocations in the {111} <112> slip systems. Since NT structure is a monolayer of HCP atoms with a symmetric arrangement on both sides, the glide of partials, which changes the local stacking sequence from FCC to HCP structure, is critical for the formation of NT structures. The propagation of partials always results in the formation of SFs, which could be the precursors of NT structures. Thus the SF energy, defined as the energy per unit area of this fault, is considered as the primary intrinsic material property that affects twinning probability.132 Low SF energy always promotes the formation of NT structures in FCC metals and alloys. For instance, higher density of NT structures can be observed with the decrease of SF energy of NC Cu-Al, Cu-Zn and Cu-Al-Zn alloys.133,134,135,136,137,138 The SF energies of some selected FCC metals are shown in Table 1. Metals with low SF energy preferentially nucleate NT structures, whereas those with high SF energy have difficulty with the nucleation and propagation of partials. Consequently, the nucleation of NT structures in materials with high SF energies, such as Al or Ni, is difficult. Exactly, NT Al is firstly predicted by MD simulation139 and observed in experiments by cryogenic ball milling.140 Only limited work reported the successful fabrication of growth and deformation twins in Al currently.141 A more common option to synthesize NT structures in high SF energy materials is, to introduce intermediate layers of another kind of materials. For example, the TiN layers are successfully used for the fabrication of NT structures in Al.142 NT Al has also been fabricated in sputtered Al/Ag multilayers.143,144,145 In addition, NT Ni layers are nucleated in highly textured Cu/Ni multilayer structures.146 Furthermore, SF energy can be adjusted by alloying, which could be beneficial to the formation of NT structures. For example, the increase of Co content in Co/Ni alloy shows a continuous decrease of SF energy.147 On the other hand, the strain rate of top-down severe plastic deformation (SPD) techniques, such as SMAT, may significantly affect the evolution of nanostructures including grain refinement and deformation twinning behaviors.148,149,150,151
Growth NT structures
The amazing discovery of NT structures for achieving ultrastrong metals with good ductility has greatly promoted the fabrication techniques of NT metals. One of the optional strategies is to control the atomic arrangement of metals during the bottom-up fabrication of metals. Such NT structures are called growth twins. The main synthesis techniques include magnetron sputtering deposition,48,50,78,86,110,130 chemical vapor deposition (CVD),152 electrodeposition,14,24,25,82,83,88,89,91 hybrid physical-chemical vapor deposition (HPCVD),153 electroplating154 etc. However, the growth HNT structures have not been well developed nowadays. A brief introduction about the synthesis of growth NT structures in bulk materials, films, nanowires and nanopillars is given below.
Equiaxed NT Cu with ultrahigh strength and high electrical conductivity is fabricated by electrodeposition (Fig. 2a).24 The electrical resistivity of TBs is lower than that of the conventional high angle GBs. In addition, the resistivity increases due to the propagation of scattering dislocations during tensile deformation. Columnar-grained Cu with preferentially oriented nanoscale twins, which is also obtained by means of electrodeposition, exhibits inhomogeneous deformation behaviors (Fig. 2b).155 The plastic anisotropy of NT materials is not negligible at nanoscale due to the effect of spatial orientations of the nanotwins and the applied forces. Using magnetron sputtering deposition technique, Cu foils with preferred orientation of growth twins are successfully synthesized,48 providing an alternative for the synthesis of ultrahigh-strength, ductile pure metals via the control of twin spacing and twin orientation (Fig. 2c). Epitaxial Ag films synthesized by magnetron sputter-deposited method show greatly enhanced hardness in comparison to bulk Ag (Fig. 2d).50 The key factor, which results in such hardness enhancement, is the relation of the angle between the indentation direction and the twin orientation. NT Cu nanopillars in the absence of GBs and initial dislocations through electroplating template fabrication exhibit brittle-to-ductile transition as the twin spacing decreases below a critical value (Fig. 2e).156 The mechanism of brittle fracture might be intrinsic brittleness of TBs when the twin spacing is large. However, ductile failure appears with the decrease of twin spacing. The nucleation of twinning dislocations on the TBs near the crack tip leads to a cascade of dislocation activities. In addition, the loading axis corresponding to the twin lamellae also greatly affect the deformation modes of nanopillars, finding two different deformation mechanisms: (1) TB-dislocation interaction dominated strain localization in orthogonal samples; (2) detwinning in slanted ones. Single crystalline Au nanowires with angstrom scale twins (synthesized by the reduction of HAuCl4 in oleic acid and oleylamine) achieve near-ideal theoretical strength,157 giving rise to the nucleation of homogeneous dislocations and plastic shear localization. This mechanism is opposite to the heterogeneous slip mechanism in single crystalline or low density NT nanowires (Fig. 2f).
Growth twins fabricated in bulk, film, nanopillar and nanowire materials. a Electrodeposited equiaxed NT Cu (adapted with permission from ref.24 Copyright (2017) The American Association for the Advancement of Science). b Electrodeposited columnar grained Cu with preferentially oriented NT structures (adapted with permission from ref.155 Copyright (2017) Elsevier). c Magnetron sputtering deposited Cu foils with preferred orientation of NT structures (adapted with permission from ref.48 Copyright (2017) AIP Publishing LLC). d Epitaxial NT Ag films by magnetron sputtering deposition (adapted with permission from ref.50 Copyright (2017) Elsevier). e Free-standing Cu nanopillar with densely spaced NT structures by electroplating (adapted with permission from ref.156 Copyright (2017) Springer Nature). f Ultrahigh-density twins distributed along the nanowire axis by reduction of HAuCl4 in oleic acid and oleylamine (adapted with permission from ref.157 Copyright (2017) Springer Nature)
The bottom-up synthesis methods provide a path to attaining quantitatively tunable growth NT materials by designing the geometry, intrinsic sizes and twin distribution etc. With the optimization of the manageable aspects, NT materials can simultaneously exhibit high strength and good ductility, the characteristics that are thought to be mutually exclusive. Besides, they also display high-performance on electrical conductivity37,49 and thermal stability etc.158,159,160 Thus, the development of synthesis techniques for growth NT structures in metals is increasingly a fascinating issue. In the meantime, the fabrication of growth HNT metals in experiments is still a significantly challenging topic which deserves extensive attention in order to develop novel materials with better performance beyond NT materials.
Deformation-induced NT structures
Bulk nanostructured materials processed by various SPD techniques161,162 have attracted the growing interest in materials science owing to the merits of grain refinement and deformation twinning. The methods such as high-pressure torsion (HPT),163 dynamic plastic deformation (DPD),164,165 SMAT,116,66,167 SMGT116,168 and ECAP117,169,170 have been manifested powerful for the construction of NT structures in crystalline materials.
During HPT processing of NC Cu, twinning becomes a dominant deformation mechanism under low strain rate and at room temperature. Twins and SFs are formed through the emission of partial dislocations from GBs.163 In addition to the single twins, multiple twins such as the so-called fivefold twins171 are observed in NT materials (Fig. 3a), indicating that the complicated deformation-induced NT structures can be synthesized via top-down SPD techniques. The formation of NT structures in Cu is investigated by DPD at high strain rates and cryogenic temperatures (Fig. 3b).165 The higher density of deformation twins is always consistent with higher strains. Figure 3c exhibits the TEM image of Cu-Al SMATed alloy with NT structures.167 It has been found that a high density of NT structures in Cu-Al alloy could keep the accumulated dislocations easily slip along the TBs and lower the exhaustion of mobile dislocation. Nanotwins have also been produced in a Fe–20Mn–3Al–3Si transformation-induced plasticity (TRIP) steel by SMGT (Fig. 3d).168 This steel shows TWIP characteristics during the SMGT process, indicating that the steel may undergo a transition from TRIP to TWIP under high-strain-rate deformation. In addition, deformation twins are widely observed in polycrystalline Cu with grain sizes varying from micrometers to nanometers during the process of ECAP at room temperature and low strain rate (Fig. 3e).169 It is demonstrated when the grain size is at nanoscale, twinning takes place via the emission of partial dislocations from GBs and GB junctions. The plastic deformation of metals is always dominated by slip dislocations. For example, the slip of perfect dislocations accounts for the plastic deformation. However, deformation twinning can occur in addition to the slip in metals especially with low or medium SF energy. In these metals, twinning prefers to nucleate at low temperatures164 and/or high strain rates.172 Moreover, both the thickness and heterogeneity of metals vary the nucleation of NT structures. NT structures always nucleate at the locations showing stress concentration or defectiveness. This is because the partial dislocations are easy to emit from such locations and form NT structures.
Deformation induced NT metals. a The fivefold NT structures produced in Cu by HPT (adapted with permission from ref.163 Copyright (2017) AIP Publishing LLC). b NT bundles formed in Cu by DPD (adapted with permission from ref.165 Copyright (2017) Elsevier). c A bright-field TEM image of Cu-4.5Al SMATed sample with NT structures (adapted with permission from ref.167 Copyright (2017) Elsevier). d TEM morphology of the twinned bundles in SMGTed Fe-20Mn-3Al-3Si TRIP steel (adapted with permission from ref.168 Copyright (2017) Elsevier). e TEM micrograph of deformation twins in grain interior of the ECAPed Cu with nanotwins indicated by arrows (adapted with permission from ref.169 Copyright (2017) Elsevier)
MD studies on the deformation mechanisms of NT FCC metals
NT structures in metals have been identified to be a kind of desirable planar defects which can improve the mechanical and physical properties. However, it is challenging to observe the dynamic behaviors of deformation and defect evolutions in experiments. Therefore, it would be charming to combine MD simulations and experimental observations to investigate the deformation mechanisms of NT materials. On the one hand, experimental results can provide the guidance for atomistic modeling and validate the accuracy of the results obtained from MD simulations. On the other hand, the in-depth observation of microstructure evolution during MD simulations is beneficial to unveil the effect of NT structures on the deformation mechanisms. By the way, we chiefly review the microstructure evolution in NT metals during plastic deformation instead of the twinning mechanisms in NC metals which has been reviewed in detail in Zhu et al.’s work.127
Interactions between dislocations and TBs
TBs can act as barriers to impede dislocation motion. Some experimental work on the atomic level observations reveals the effect of grain size,173,174 dislocation density,175 twin thickness176 on the interactions between dislocations and TBs, and the dislocation-TB reaction induced detwinning behaviors.177,178 The development of in situ atomic scale experimental techniques promotes the investigation of dynamic dislocation-TB interaction modes.176,179,180,181,182,183,184 Actually, the detailed interactions between dislocations and TBs are also widely investigated by means of MD simulations. Owing to the significant merit of MD simulation that the microstructure evolution can be tracked perfectly, the simulation studies on dislocation-TB interaction in NT metals have been comprehensively discussed in recent years.
It has been revealed that there always exist four kinds of slip systems in FCC metals: (1) partial dislocations inclined to TBs; (2) partial dislocations parallel to TBs; (3) perfect dislocations inclined to TBs and (4) screw perfect dislocations.127 When a dislocation propagates along one slip plane inclined to the TB, the interaction between dislocation and TBs can be generally classified into three types: (1) the gradual accumulation and absorption of dislocations into TBs; (2) the decomposition of dislocations with one residing on TBs and the other transmit across TBs into the adjacent mirror domain; (3) the transfer of dislocations through TBs. Note that the occurrence of these interactions strongly depends on the high applied stress in the appropriate orientation. The large geometric misorientation between both sides of TBs leads to high energetic barriers to the transmission of inclined dislocations across TBs. Absorption of a dislocation followed by dissociation of dislocation in TBs and eventually emitting a dislocation into the mirror domain is a typical dislocation nucleation and propagation process during plastic deformation. Based on MD simulations, the transmission of dislocations is investigated in NT Ni,185 the applied shear with respect to a resolved shear stress up to 1.77 GPa gives rise to the transmission of dislocation across TBs. Jin et al.’s MD simulation studies clarify the interaction mechanisms of both screw and non-screw dislocations with TBs in different FCC metals.186,187 For instance, the screw dislocation transmits across TBs through three steps: (1) leading partial is forced to enter TBs; (2) nucleation of full dislocation at TBs with the combination of trailing and leading partials; (3) Shockley partials nucleate at TBs and propagate into the other side of TBs. The critical stress for dislocation to overcome the energy barrier of TBs is also measured, about 465–510 MPa for screw dislocation and 1.2 GPa for non-screw dislocation in Cu. Furthermore, the interface-mediated slip transfer mechanism accounts for the strengthening and toughening processes at the later stages of plastic deformation in NT Cu.188
Twin spacing and twin orientation effects
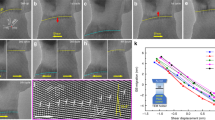
In recent years, the effects of twin spacing inside the nanograins and twin orientation with respect to external loading direction are revealed by MD simulations. For instance, the MD results indicate that there exists a critical twin spacing for achieving the maximum strength of NT Cu.189 With the decrease of twin spacing, the strengthening mechanism of dislocation cutting through TBs induced dislocation pile-up transfers to the softening mechanism of dislocation nucleation parallel to TBs induced TB migration (Fig. 4a,b). In addition, the maximum strength also depends on the grain size. The critical twin spacing is proportional to the grain size. The smaller the grain size, the higher the maximum strength of NT Cu in the Hall–Petch strengthening regime.189 Plastic anisotropy is discovered in columnar-grained Cu with preferentially orientated NT structures (Fig. 4c-e).190 By changing the loading direction with respect to TBs, the dominant deformation mechanisms appear three totally different behaviors corresponding to the external loading direction with respect to TBs, (1) dislocations glide in between the twins; (2) dislocations transfer across TBs; and (3) dislocation-mediated TB migration. The similar deformation behaviors are also observed in NT Cu films and totally alter the tensile strength and failure modes.77 Near-ideal strength of Au nanowires is achieved owing to the heterogeneous to homogeneous transition of the nucleation behavior of dislocations. Because the well-aligned ultrahigh density NT structures with twin spacing λ < 2.8 nm leads to a remarkable ductile-to-brittle transition (Fig. 4f).157 This finding is exactly opposite to the observation in Jang et al.’s study on NT Cu nanopillar.156 The distinct behaviors may result from the difference of SF energies of Au and Cu and the large repulsive force on the gliding dislocations induced by the small diameter of Au nanowires. In the case of external stress parallel to TBs, the transition of threading to jogged dislocations nucleation with the decrease of twin spacing is uncovered in columnar-grained NT Cu (Fig. 4g).191 This newly discovered deformation mechanism involves the collective behavior of multiple extended jogged dislocations bounded by the adjacent TBs with reduced twin spacing, leading to the continuous strengthening instead of the softening phenomenon, without a critical twin spacing for strengthening to softening transition observed in equiaxed NT metals.25,189
a, b Two plastic deformation mechanisms under different twin spacing in equiaxed NT Cu (adapted with permission from ref.189 Copyright (2017) Springer Nature). a Partial dislocations gliding parallel to twin planes. b Dislocations cutting across twin planes. c–e Three plastic deformation mechanisms depending on twin orientations with respect to the compression direction in columnar-grained NT Cu (adapted with permission from ref.190 Copyright (2017) Elsevier). c Dislocations transfer across TBs under 90° compression. d Dislocations glide in between the twins under 0° compression. e Dislocation-mediated TB migration under 45° compression. f Homogeneous dislocation dominated deformation mechanism in well-aligned ultrahigh density NT Au nanowires (adapted with permission from ref.157 Copyright (2017) Springer Nature). g Jogged dislocation governed continuous strengthening with decrease of twin spacing in columnar-grained NT Au under external stress parallel to TBs (adapted with permission from ref.191 Copyright (2017) American Chemical Society)
Theoretical models applicable for the mechanical behaviors of NT FCC metals
The development of theoretical models to describe various mechanical behaviors of NT FCC metals is very useful for the precise understanding of physical mechanisms, effectively predicting important phenomena and conveniently acting as guidance for the design of high-performance materials. However, excellent theoretical modeling is very challenging because any analytical description of deformation mechanisms in NT FCC metals should be based on the physical phenomena in experimental and/or reliable atomistic studies. The most important quality of a theoretical model is to effectively describe physical mechanisms instead of fitting experimental data. Because only the models taking deformation physics into consideration can predict comprehensive experimental phenomena. We will introduce some representative theoretical models and discuss their advantages and limitations in this section.
There mainly exist two kinds of theoretical studies on the NT structures in metals. One is the theoretical models for the description of deformation twinning processes in NC FCC metals. In brief, under what conditions can NT structures be generated. The other is the mechanism-based theoretical models developed to describe the mechanical behaviors of NT metals. To identify the deformation twinning mechanisms in NC metals, dislocation based model is a representative to depict the twinning behavior of NT structures in FCC metals,192,193 which is primarily determined by SF energies, showing an optimum grain size for twinning. However, SF energies alone are not sufficient to explain the observed twinning behaviors. It has been identified that the generalized planar fault energy (GPFE) also significantly affects the partial-dislocation-mediated deformation process which has close relation to the twinning propensity of NC metals.103,194 To compensate this shortage, GPFE based models have also been developed to explain the deformation twinning process. Zhu et al.’s review work has clearly elucidated these theoretical studies on the deformation twinning process of NC metals.127 In this review, we mainly focus on the introduction of mechanism-based plasticity models developed to investigate the effects such as grain size and twin spacing on the mechanical behaviors of NT metals.
Both two- and three-dimensional mechanism-based crystal plasticity models for NT metals have been proposed, taking the effect of nanoscale twins into consideration.104,105 For example, similar to the model of GB-affected zone (GBAZ),195 the rate-dependent crystal plasticity model of NT Cu is developed based on the concept of TB-affect zone (TBAZ).104 It is modified from the theories which primarily focus on the deformation of microcrystalline metals.196,197,198 The plastic anisotropy is taken into account by distinguishing shear deformation parallel to or across TBs. The rate form of the constitutive relation is described as:
where \({\dot{\boldsymbol \gamma }}_{\boldsymbol{\alpha }}\) is the shear rate on the slip system α, L represents the velocity gradient of the single crystal, \({\dot{\boldsymbol E}}\) is the Green strain rate, X α is related to the slip direction and its slip plane normal. Details of Eq. (1) can be found in the work by Dao et al.104
This model is developed to simulate the mechanical behaviors of metals by finite element method. It successful reveals the strong plasticity and rate-sensitivity anisotropy of NT metals. The model shows reasonable agreement with the experimental findings. Besides, with the consideration of out-of-plane slip, cross-slip and grain rotation, three dimensional NT models of NC metals are developed to predict the dependence of stress-strain response under different twin densities and estimate the ductility by means of a failure criterion.105 Although the models can reasonably explain some experimental observations, the softening behavior with the excessive decrease of twin spacing is not considered in this theoretical models.
According to the softening behavior observed in MD simulations, the softening arises from the nucleation of source-governed preferential dislocations in the vicinity of TBs while the strengthening arises from the dislocation pile-up at TBs, which critically depends on the twin spacing.189 For the sake of the shortcoming of the above models, a discrete twin crystal plasticity (DT-CP) model is established with a focus on modeling the strengthening-softening yield transition below a critical twin spacing in NT Cu.106 And it is applied to study the TB emigration behavior in NT FCC metals.108 This model qualitatively captures the transition of the mechanical behavior from strengthening to softening as a function of twin spacing. However, it has been demonstrated that the critical twin spacing for the transition of yield strength is sensitive to grain size.189 Whereas the grain size effect on the critical twin spacing for strengthening to softening transition is not taken into consideration in this DT-CP model. Thus, the theoretical model needs further development.
Accordingly, by analyzing two competitive plastic deformation mechanisms: (1) strengthening dominated by inclined dislocations with respect to twin planes; and (2) detwinning-induced softening, a scale law of the maximum strength of the NT metals is explored to describe the transition of deformation mechanisms.199 The Eshelby’s shear transformation idea200 is adopted to approximate the increase of strain energy by detwinning. The critical resolved shear stress for triggering the nucleation of partial dislocations is described by previous works.103,201,202 The maximum strength occurs when both twinning and the inclined dislocation slip are active. In addition, it is found that the maximum strength gradually increases when the critical twin spacing for the strengthening to softening transition decreases along with the decrease of grain size. The specific relations are described as:
Maximum strength τmax vs. grain size d:
Transitional twin spacing λT vs. grain size d:
where γsf is the SF energy, n is a geometrical parameter, b and b(c) are the magnitudes of the Burgers vectors of partial and complete dislocations, respectively, and μ is the shear modulus.
where α is a coefficient on the order of unit, v is the Poisson’s ratio, and eT is the characteristic shear strain which is equal to 0.707 in FCC metals.
It is apparent that there exist two relationships, \(\tau _{\mathrm{max}} \propto d^{ - 1{\mathrm{/}}2}\) and \(\lambda _{\mathrm{T}} \propto d^{1{\mathrm{/}}2}\). Such scale law shows exceptional agreement with the experimental and large-scale MD simulation results.25,189
In spite of the fact that the effects of twin spacing and grain size on the yield strength have been captured by these continuum models, taking into account the strengthening and softening behaviors of NT metals. The quantitative description on strain hardening and ductility, both of which should also be sensitive to these nanostructures, remains unexplored by these models. Thus, a mechanism-based plasticity model is developed, based on the strain gradient plasticity theory,203,204 by introducing the role of dislocation pile-up zones near the TBs and GBs (TBDPZ and GBDPZ), as well as twinning partial dislocations into strengthening and work hardening.107 Besides, a local fracture criterion has also been proposed to estimate the tensile ductility of NT metals. The mechanism-based plasticity model is described as follows:
The relationship between flow stress and dislocation density is
where ρ = ρ I + ρTB + ρGB is the total dislocation density in crystal interior, TBDPZ and GBDPZ, respectively; α is the Taylor constant; μ is the shear modulus; M is the Taylor factor, which can be used to characterize the local anisotropy. Note that the Taylor factor in this model is averaged, ignoring the effect of plastic anisotropy. σ0 denotes the lattice friction stress and σb is the back stress, taking twinning partial dislocations into account for kinematic hardening.
To determine the tensile ductility of NT metals, Asaro and Suresh103 give a formula:
where \({\boldsymbol{K}}_{{\boldsymbol{\mathrm{II}}}}\) is the stress intensity factor, τcrit is the critical stress for nucleation of dislocations, d* represents the twin spacing for TBs or grain size for GBs. Thus, with an additional failure criterion τflow ≥ τcrit, the ductility of NT metals can be evaluated.
In addition, the relationship between critical twin spacing and grain size can be obtained as follow:107
where ρTB is the dislocation density in the TBDPZ. kTB = 12dTBDPZ/φTBπdTB, \(\tilde \eta ^{\mathrm{TB}} = \eta ^{\mathrm{TB}} - \eta _{\mathrm{P}}{\mathrm{/}}d_{\mathrm{TB}}\) and ηP = √3πφPb/12dTBDPZ. \(\tilde \eta ^{\mathrm{TB}}\) denotes the effective local strain gradient in the TBDPZ. ηTB = η1dTB + η0 is the local mean strain gradient in the TBDPZ with \(\eta _1 = \phi ^{\mathrm{TB}}N_0b/(d_{\mathrm{TBDPZ}}d_{\mathrm{G}}^2)\) and \(\eta _0 = \phi ^{\mathrm{TB}}n_{\mathrm{p}}^\prime b{\mathrm{/}}(d_{\mathrm{TBDPZ}}d_{\mathrm{G}}\sqrt 3 )\). N0 is a constant standing for the maximum number of inclined dislocations in a grain. \(n_{\mathrm{p}}^\prime\) is the number of initial twinning partials in the TBDPZ, which is independent of the twin spacing. dG represents the grain size, b is the magnitude of Burgers vector, φTB and φP are geometric factors, dTB is the twin spacing and dTBDPZ is the thickness of TBDPZ. Note that ηP and η0 are the parameters independent of the twin spacing.
Differentiate Eq. (7) with respect to twin spacing and set equal to zero, the critical twin spacing for maximum strength can be obtained as:
Substitute the formula for ηP and η0 into Eq. (8), the linear relationship between the critical twin spacing and grain size can be obtained as:
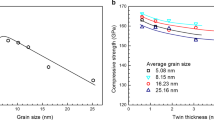
The predicted results are well consistent to the MD results (Fig. 5)114 and experimental observations.5,25,189,205 The properties of strength, ductility and work hardening are verified both sensitive to grain size and twin spacing. Thus, this mechanism-based plasticity model can effectively describe the variation of strength, strain hardening and the ductility of NT metals corresponding to various grain sizes and twin spacings. However, the effect of plastic anisotropy is ignored in this model.
a A snapshot of 3-D dislocation structures at a total strain of 22.1%, showing that TB has become a wall accumulated high dislocation density. b Distribution of dislocation density across the twin plane showing the characteristic thickness of the TBDPZ to be around 2.5–3.5 nm on each side of the TB. c The local strain gradient and density of dislocations in the TBDPZ as a function of twin spacing. d The predicted yield stress of NT copper as a function of twin spacing in comparison with the corresponding experimental results. e The critical twin spacing as a function of grain size in the NT copper (adapted with permission from ref.107 Copyright (2017) Elsevier)
The crystal plasticity finite element (CPFE) models have been developed to study polycrystalline materials with great success.206 One main advantage of CPFE models lies in their ability to describe crystal mechanical behaviors under complicated boundary conditions. They also have great flexibility when including various constitutive formulations for plastic flow and hardening at the elementary shear system level.206 Three dimensional CPFE model has been established to study the evolution of grains and GB structures.207 However, the limitation of most CPFE models is that they are not applicable for understanding the behavior of nanostructured metals in which individual dislocations can be resolved and the amount of slips affected by the grain size and twin spacing. To solve this problem, a constitutive model is developed for NC metals in which plasticity occurs with discrete slips from GBs.208 Then it is incorporated in the CPFE model and can catch the effect of the texture, grain-grain and twin-twin interactions during plastic deformation.111 The plastic anisotropy exhibited in columnar-grained NT metals are well described by the CPFE model.
Also, some other analytical models have been developed to predict the strengthening mechanism of NT metals. For instance, the strength of NT metals is determined by the resistance of dislocations to transmit across boundaries which is affected by averaged twin spacing.109,160,209 And a semi-analytical grain aggregate model is proposed. This model can successfully explain the strain hardening in NT Pd film owing to the effect of twins, grain size and the presence of a thin surface layer.110 Hence, various versatile theoretical models have been proposed to characterize the specific NT systems. However, the theoretical studies on the HNT structures have received almost no attention.
HNT FCC metals
Fabrication of HNT structures
The fabrication of growth HNT metals in experiments is still a significantly challenging topic which deserves extensive attention. HNT structures are only observed during martensitic transformation and fabricated in Ni-Mn-Ga ferromagnetic shape memory alloy.66 On the other hand, deformation-induced HNT structures have been observed in some materials treated by ECAP, surface treatment methods, stretching after pre-torsion and tensile deformation,30,31,116,117,120 demonstrating that the existence of HNT structures in materials can simultaneously improve the strength and ductility.30,31,117, 120 In particular, the viewpoint paper introduces that the formation of secondary twins is one of the mechanisms during the nanoscale structural refinement via deformation twinning (Fig. 6a).116 The HNT structures are embedded in Cu-Al alloys by using ECAP, leading to a finer twin network (Fig. 6b).117 The strength and ductility can be simultaneously improved by decreasing the SF energy in Cu–Al alloys, which can be attributed to the formation of HNT structures as one important influence. Also, the HNT structures have been observed in TWIP steel cylinder by torsion treatment and uniaxial tension (Fig. 6c).30 The evasion of strength-ductility trade-off is due to the formation of gradient HNT structures. Besides, multiply twinned nanostructure is obtained from martensitic transformation in a Ni-Mn-Ga ferromagnetic shape memory alloy (Fig. 6d,e).66 The HNT structures with both straight and “step” interfaces are successfully synthesized. Recently, three ordered HNT structures have formed during uniaxial tensile deformation in the CrCoNi medium-entropy alloy (MEA) (Fig. 6f).31 The HNT structures simultaneously serve as the conventional TB strengthening, the pathways for dislocation glide along, and cross-slip between, intersecting TB-matrix interfaces. Also, three ordered HNT structures have successfully been processed in SMATed TWIP steel (Fig. 6g-i).120 The materials display an extraordinary relationship between yield strength and the uniform elongation. In view of the innovative prediction for the extraordinary performance of HNT materials done by Zhu et al.’s theoretical studies,118,119 more and more attention has been paid to the development of technologies to fabricate HNT structures. The formation of HNT structures in crystalline materials could be a novel strategy to maintain higher strength and better ductility compared with the NT counterparts.
HNT structures in some metal materials. a Formation of HNT structures in Cu by SMGT (adapted with permission from ref.116 Copyright (2017) Elsevier). b HNT structures embedded in Cu–Al alloys by ECAP (adapted with permission from ref.117 Copyright (2017) Elsevier). c HNT structures observed in TWIP steel cylinder by pre-torsion treatment and uniaxial tension.30 d, e Multiply twinned nanostructure obtained from martensitic transformation in a Ni–Mn–Ga ferromagnetic shape memory alloy (adapted with permission from ref.66 Copyright (2017) Elsevier). d Two groups of different oriented twin lamellae with straight interface. e Two groups of different oriented twin lamellae with interface in “step” configuration. f Bright-field TEM image showing the three ordered HNT structure formed during uniaxial tensile deformation in CrCoNi MEA. Scale bar, 1 μm.31 g–i Morphology and a schematic diagram showing HNT structures in SMATed TWIP steel (adapted with permission from ref.120 Copyright (2017) John Wiley and Sons).120 g Secondary twins inside of primary twins. h Tertiary twins inside of secondary twins. i The overall schematic orientation of HNT structures corresponding to the experimental observations
MD studies on the deformation mechanisms of HNT FCC metals
Basic configuration of HNT structures
Although the atomistic modeling of NT structures in FCC metals is extensively available, HNT structure modeling for MD simulation is a little more complicated. Thus, a brief introduction about HNT structure is given in this section. The fundamental definition of HNT structure is that there exist TBs along different directions in the same grain. Although the microstructure of HNT metals has been uncovered by experimental studies, it is essential to determine the atomic distribution to realize the atomistic-level study on HNT structures. The distribution of HNT structures in experiments (Fig. 6) can be used to validate the accuracy of HNT structures built in the atomistic models. We can observe the theoretical distribution of primary, secondary, and tertiary TBs (Fig. 7b) by simplifying the experimental results from Fig. 7a. Note that the HNT structures in Fig. 7a are intermittent, lack of integrity. Based on the lattice structure of FCC metals, it is found that the TBs2nd are generated inside of TBs1st with locally disordered, split segments in TBs1st. Thus, the formation of high ordered TBs inevitably need to tailor the integrity of low ordered TBs. The atomistic model of HNT metals with both primary and secondary TBs is shown in Fig. 7c.121,122 The primary TBs are split into TBs1st and GBs1st. Since one of the important deformation twinning mechannisms is closely related to the emission of successive partial dislocations from GBs, these GBs may play a key role in the nucleation of high ordered HNT structures during plastic deformation. In addition, TBs3rd are not constructed in the atomistic model, which may appear by deformation twinning during plastic deformation as indicated by the green line in Fig. 7c. The formation of TBs3rd may also induce the rupture of TBs2nd. To construct HNT structures, two totally different domains named TGTG- and TTTT-regions, the former is surrounded by both TBs and GBs while the latter is only surrounded by TBs, are classified in the model. The effects of these microstructures on the deformation behaviors of HNT metals need to be discussed. Basically speaking, the theoretical distribution is well consistent with the experimental observation in Fig. 7a. However, the TBs3rd are parallel to the TBs1st as mentioned in Wei et al.’s work.30 We think these tertiary twins are still the primary twins, which can only reduce the primary twin spacing. On the contrary, we can find the position of real TBs3rd from Fig. 7b which could be formed in the TGTG-regions along the green line in Fig. 7c. Such distribution can be verified by the experimental results shown in Fig. 6g-i, in which the distribution of three ordered HNT structures are in three different directions.
The basic configuration of HNT structures in FCC metals. a The experimental observation of HNT structures in TWIP steel cylinder.30 b Theoretical distribution of HNT structures. “//” represents the locally disordered, split segments. c The local atomistic configuration of HNT metals (adapted with permission from ref.122 Copyright (2017) Taylor & Francis)
Primary and secondary twin spacings
When HNT structures are introduced into metals, the effects such as grain size, twin spacing, dislocation density and twin orientation on the strength and ductility require further discussions. Nowadays, only quite limited computational studies are available, mainly focusing on the effect of twin spacing.121,122,123,124
In order to uncover the relationship between the twin spacing and strength of HNT metals, several MD simulations are conducted to reveal the effect of primary and secondary twin spacings on the strength separately.121,122 For the same grain size and spacing of primary twins, the average flow stress first increases then decreases with the decrease of secondary twin spacing, existing a critical secondary twin spacing achieving maximum strength (Fig. 8a).121 The smaller the primary twin spacing is, the smaller the critical secondary twin spacing becomes. The travel of partials emitting from GBs and TBs across other TBs and GBs accounts for the strengthening mechanism. Detwinning of secondary twins and migration of primary twins result in softening. Interestingly, for the same grain size and secondary twin spacing, two softening and one strengthening stages are discovered with the decrease of primary twin spacing.122 Two critical primary twin spacings with one for local minimum and the other for maximum strength are achieved accompanied by the reduction of primary twin spacing. The different microstructural evolution processes are observed, exposing three totally different deformation mechanisms by MD simulations: (1) the transition from full dislocation to partial dislocation propagation—softening; (2) from partial dislocation propagation to dislocation blockage—strengthening; (3) from dislocation blockage to partial induced twin migration and detwinning—softening. Note that such unique phenomenon, which is unavailable in NT structures, is consistent to the prediction by Zhu et al.’s dislocation-based theoretical model.118 Thus, HNT structures in metals may subvert our knowledge of NC metals and would be beneficial to broaden the design strategy and further reinforce the mechanical properties of metals.
The strength of HNT Cu affected by twin spacing. a The decrease of secondary twin spacing results in rise to fall of strength, existing a critical secondary twin spacing achieving maximum (adapted with permission from ref.121 Copyright (2017) AIP Publishing LLC). b Two critical primary twin spacings corresponding to the local maximum and minimum strength (adapted with permission from ref.122 Copyright (2017) Taylor & Francis)
The fracture behaviors along TBs in NT and HNT metals are also studied by MD simulations.75,123 The propagation of cracks can be affected by the thickness of metals, location and the shape of cracks. The HNT structures can highly enhance the crack resistance. Smaller secondary twin spacing leads to higher fracture toughness, effective to impede crack propagation. On the other hand, the effect of twin spacing on shock response and spallation behaviors is studied in HNT Ag, uncovering the similar critical secondary twin spacing for achieving maximum strength under shock conditions.124 It is found that in addition to the partial dislocation propagation, formation of tertiary twins is discovered as another strengthening factor. However, detwinning and partial induced coherency loss of TBs dominate the softening process when the secondary twin spacing is smaller than the critical value. But HNT structures have no contribution to improve spallation strength because more nucleation sources of voids exist in HNT metals compared with the twin-free counterparts. In particular, GBs are the main source for void nucleation, while the formation of HNT structures inevitably introduce more GBs into metals (Fig. 7c).
The study on the mechanical and physical properties of HNT metals is still in its infancy due to the constraint of synthesis techniques. MD method, which has been demonstrated as a powerful instrument to analyze the deformation mechanisms of NT metals, is gradually adopted to predict the effect of hierarchical structures in HNT metals. The computational outcomes may provide insights into the relationship between HNT structures and the performance of various aspects, acting as benchmark for the design of metals exhibiting fascinating mechanical properties.
Theoretical description of the mechanical behaviors of HNT FCC metals
Similar to the MD simulation studies, the theoretical work on the mechanical behaviors of HNT FCC metals is also seldom. However, seldom does not mean insignificant. Since the HNT structures have been demonstrated to be more beneficial to the improvement of strength, crack propagation resistance and shock response compared with NT counterparts through experimental observations and MD simulations,30,120,123,124 the theoretical study on this topic is also essential to describe the relationship between HNT structures and the mechanical behaviors of metals. Based on the experimental and MD simulation phenomena, Zhu et al.118,119 have started some pioneering mechanism-based theoretical work on the effect of HNT structures in FCC metals recently. As shown in Fig. 9a, the TBDPZ is classified into primary and secondary TBDPZs, the total density of dislocations in TBDPZs is equal to \(\rho _{\mathrm{TB}} = \rho _{\mathrm{TB}}^1 + \rho _{\mathrm{TB}}^2\). Note that the framework of this mechanism-based plasticity model for HNT metals is a development of their previous work for NT metals.107 Thus, the HNT structures are taken into account and some predictions can be made. As mentioned above, one interesting prediction is that the variation of primary twin spacing results in two softening stages in HNT FCC metals (Fig. 9b) which is not observed in NT FCC metals. This special phenomenon is verified and the related mechanism is uncovered through MD simulation studies conducted by Sun et al.122
a Schematics of HNT structures in a grain with primary and secondary twins. The TBDPZ and GBDPZ are introduced to develop mechanism-based plasticity model for HNT metals. b The variation of the flow stress of HNT Cu as a function of primary twin spacing (adapted with permission from ref.118 Copyright (2017) AIP Publishing LLC)
To further improve the applicability of the mechanism-based theoretical model, it has been extended to study the twin spacing and grain size dependence of the yield strength and ductility for the case of HNT FCC metals with higher twin order.119 The total dislocation density is revised as:
where N represents the twin order. Thus, the effect of tertiary or even higher ordered twins can be depicted.
In addition, the deformation twinning behavior of HNT FCC metals is developed with the well-known twin nucleation criterion τtwin < τtrail, taking GPFE effect into account.127 Thus, the proposed mechanism-based plasticity model is capable of capturing the dependence of the strength and ductility on the grain size and twin spacing of HNT FCC metals. However, these models do not consider the split effect of TBs during the formation of HNT structures (Fig. 7). The induced variation of density of TBs and GBs should be taken into consideration in order to evaluate the dislocation density more accurately. Hence, more efficient theoretical models need to be developed to predict the effects of HNT structures in the future work.
Perspective for the studies on HNT structures
HNT structures open up a new possibility to further improve the mechanical properties of crystalline materials. Here we put forward some potential future efforts on this attractive topic. Experimentally, bottom-up growth of HNT structures is challenging in view of the complicated stacking configuration of atoms. Based on top-down techniques, only up to tertiary twins have been observed in experiments with questionable density nowadays. It should be noted that due to the limitation of two dimensional TEM imaging to reflect the three-dimensional HNT structures, the order of HNT structures could be underestimated. Thus, it is also essential to study the way to comprehensively characterize the three-dimensional HNT structures or build the relationship between three-dimensional structures and two-dimensional images. Anyway, achieving higher ordered HNT structures and the improvement of the density of HNT structures still need more efforts. Moreover, the synthesis of HNT structure with gradient nanograined structure could be a more novel way to enhance deformability of metallic materials.
On the other hand, the formability of hierarchical twins with respect to the order of HNT structures remains ambiguous. Generally speaking, the difficulty of formation of HNT structures may gradually arise with the increase of twin order. The synergy of low ordered twin spacings on the formability of high ordered twins is important for achieving high ordered HNT structures. Although high ordered HNT structures could be favorable, here remains a question that if there exists a limit for strength and ductility when increasing the order of HNT structures. Are HNT structures always beneficial for mechanical performance with the increase of twin order? These issues are critical for researchers to decide whether making efforts on achieving high ordered HNT structures or focusing on the optimization of double twins and the three-order twins. With the increase of the order of HNT structures, the twin spacing generally decreases (Higher order, smaller twin spacing). Since the inverse Hall–Petch effect appears with the decrease of twin spacing in NT materials, it should be investigated if high ordered HNT structures with very small twin spacing have an adverse effect on the mechanical properties. Also, the effect of split induced GBs during the formation of HNT structures need to be clarified. Although it has been verified that the NT structures exhibit very good stability, it is still ambiguous that if HNT structures have similar good stability.
Furthermore, reliable theoretical models need to be developed to describe the deformation behaviors with the consideration of the influential factors uncovered from experimental and atomistic studies. From our point of view, at least the split effect and the synergy of twin spacings instead of twin spacing alone need to be taken into account for the HNT system, whether to describe the hierarchical twinning behaviors or the deformation mechanisms. In addition, it has been widely known that the back stresses arise from geometrically necessary dislocations, which play an important role on work hardening while lack of studies for HNT structures.
Conclusion
At last, we summarize some of the representative experimental and MD results about the effects of grain size, twin spacing and twin orientation on the mechanical properties of NT and HNT metals under different loading modes and strain rates (Table 2) for easier comparison by readers.
In summary, NC metals with NT and HNT structures have very delightful mechanical properties in comparison with the twin-free counterparts. In this review, the main experimental techniques for the fabrication of NT and HNT structures in FCC metals have been introduced. Both the configuration of growth and deformation-induced NT structures can be controlled during the synthetic processes. However, growth HNT structures are only observed in martensitic transformation, which is not well implemented for synthesis, while deformation-induced HNT structures has been successfully fabricated by means of some SPD based techniques. However, the quantitative control of the intrinsic parameters in HNT metals is still challenging.
On the other hand, a large quantity of key factors, such as twin spacing, twin density, grain size and plastic anisotropy are uncovered by MD simulations, which greatly affect the mechanical characteristics of NT and HNT metals. Furthermore, the phenomena observed in experimental and MD studies become the foundation of mechanism-based theoretical modeling. Many theoretical models have been proposed to explain the extraordinary plastic deformation behaviors caused by the particular nanostructures in NT and HNT metals. The models are also employed to predict the conditions for achieving metals with distinguished performance.
Therefore, this review provides a clear framework for the studies of NT and HNT FCC metals through three aspects: (1) experiments for the fabrication of NT and HNT structures, (2) atomistic simulations for the mechanism exploration and (3) theoretical models as benchmarks for the prediction and microstructural design. In particular, the studies on HNT structures in metals remains in the initial stage and waiting for systematic investigation.
References
Koch, C. C., Morris, D. G., Lu, K. & Inoue, A. Ductility of nanostructured materials. MRS Bull. 24, 54–58 (1999).
Meyers, M. A., Mishra, A. & Benson, D. J. Mechanical properties of nanocrystalline materials. Prog. Mater. Sci. 51, 427–556 (2006).
Lu, L., Sui, M. L. & Lu, K. Superplastic extensibility of nanocrystalline copper at room temperature. Science 287, 1463–1466 (2000).
Schiøtz, J., Di Tolla, F. D. & Jacobsen, K. W. Softening of nanocrystalline metals at very small grain sizes. Nature 391, 561–563 (1998).
Schiøtz, J. & Jacobsen, K. W. A maximum in the strength of nanocrystalline copper. Science 301, 1357–1359 (2003).
Yamakov, V., Wolf, D., Phillpot, S. R. & Gleiter, H. Grain-boundary diffusion creep in nanocrystalline palladium by molecular-dynamics simulation. Acta Mater. 50, 61–73 (2002).
Shan, Z. W. et al. Grain boundary-mediated plasticity in nanocrystalline nickel. Science 305, 654–657 (2004).
Nieh, T. G. & Wadsworth, J. Hall-Petch relation in nanocrystalline solids. Scr. Metall. Et. Mater. 25, 955–958 (1991).
EI-Sherik, A. M., Erb, U., Palumbo, G. & Aust, K. T. Deviations from hall-petch behavior in as-prepared nanocrystalline nickel. Scr. Metall. Et. Mater. 27, 1185–1188 (1992).
Rosenbrock, C. W., Homer, E. R., Csányi, G. & Hart, G. L. W. Discovering the building blocks of atomic systems using machine learning: application to grain boundaries. npj Comput. Mater. 3, 29 (2017).
Banadaki, A. D. & Patala, S. A three-dimensional polyhedral unit model for grain boundary structure in fcc metals. npj Comput. Mater. 3, 13 (2017).
Hu, J., Shi, Y. N., Sauvage, X., Sha, G. & Lu, K. Grain boundary stability governs hardening and softening in extremely fine nanograined metals. Science 355, 1292–1296 (2017).
Huang, S., Chen, D., Song, J., McDowell, D. L. & Zhu, T. Hydrogen embrittlement of grain boundaries in nickel: an atomistic study. npj Comput. Mater. 3, 28 (2017).
Lu, K., Lu, L. & Suresh, S. Strengthening materials by engineering coherent internal boundaries at the nanoscale. Science 324, 349–352 (2009).
Wang, T. M., Chen, M. W., Zhou, F. H. & Ma, E. High tensile ductility in a nanostructured metal. Nature 419, 912–915 (2002).
Zhu, L. L., Shi, S. Q., Lu, K. & Lu, J. A statistical model for predicting the mechanical properties of nanostructured metals with bimodal grain size distribution. Acta Mater. 60, 5762–5772 (2012).
Zhu, L. L. & Lu, J. Modelling the plastic deformation of nanostructured metals with bimodal grain size distribution. Int. J. Plast. 30-31, 166–184 (2012).
Zhu., L. L., Guo, X., Ruan, H. H. & Lu, J. Prediction of mechanical properties in bimodal nanotwinned metals with a composite structure. Compos. Sci. Technol. 123, 222–231 (2016).
Horita, Z., Ohashi, K., Fujita, T., Kaneko, K. & Langdon, T. G. Achieving high strength and high ductility in precipitation-hardened alloys. Adv. Mater. 17, 1599–1602 (2005).
Zhao, T. H., Zhu, Y. T. & Lavernia, E. J. Strategies for improving tensile ductility of bulk nanostructured materials. Adv. Eng. Mater. 12, 769–778 (2010).
Jiao, Z. B. et al. Synergistic effects of Cu and Ni on nanoscale precipitation and mechanical properties of high-strength steels. Acta Mater. 61, 5996–6005 (2013).
Wu, G., Chan, K., Zhu, L., Sun, L. & Lu, J. Dual-phase nanostructuring as a route to high-strength magnesium alloys. Nature 80, 80–83 (2017).
He, B. B. et al. High dislocation density-induced large ductility in deformed and partitioned steels. Science 357, 1029–1032 (2017).
Lu, L., Shen, Y. F., Chen, X. H., Qian, L. H. & Lu, K. Ultrahigh strength and high electrical conductivity in copper. Science 304, 422–426 (2004).
Lu, L., Chen, X., Huang, X. & Lu, K. Revealing the maximum strength in nanotwinned copper. Science 323, 607–610 (2009).
Lu, K. Making strong nanomaterials ductile with gradients. Science 345, 1455–1456 (2014).
Fang, T. H., Li, W. L., Tao, N. R. & Lu, K. Revealing extraordinary intrinsic tensile plasticity in gradient nano-grained copper. Science 331, 1587–1590 (2011).
Wu, X. L., Jiang, P., Chen, L., Yuan, F. P. & Zhu, Y. T. Extraordinary strain hardening by gradient structure. Proc. Natl. Acad. Sci. U. S. A. 111, 7197–7201 (2014).
Chen, A. Y., Liu, J. B., Wang, H. T., Lu, J. & Wang, Y. M. Gradient twinned 304 stainless steels for high strength and high ductility. Mater. Sci. Eng. A 667, 179–188 (2016).
Wei, Y. et al. Evading the strength- ductility trade-off dilemma in steel through gradient hierarchical nanotwins. Nat. Commun. 5, 3580 (2014).
Zhang, Z. et al. Dislocation mechanisms and 3D twin architectures generate exceptional strength-ductility-toughness combination in CrCoNi medium-entropy alloy. Nat. Commun. 8, 14390 (2017).
Xiang, Y., Li, T., Suo, Z. G. & Vlassak, J. J. High ductility of a metal film adherent on a polymer substrate. Appl. Phys. Lett. 87, 161910 (2005).
Lu, N. S., Wang, X., Suo, Z. G. & Vlassak, J. J. Failure by simultaneous grain growth, strain localization, and interface debonding in metal films on polymer substrates. J. Mater. Res. 24, 379–385 (2009).
Chen, A. Y., Li, D. F., Zhang, J. B., Song, H. W. & Lu, J. Make nanostructured metal exceptionally tough by introducing non-localized fracture behaviors. Scr. Mater. 59, 579–582 (2008).
Wu, Z. X., Zhang, Y. W. & Srolovitz, D. J. Deformation mechanisms, length scales and optimizing the mechanical properties of nanotwinned metals. Acta Mater. 59, 6890–6900 (2011).
Bezares, J. et al. Indentation of nanotwinned fcc metals: Implications for nanotwin stability. Acta Mater. 60, 4623–4635 (2012).
Chen, X. H., Lu, L. & Lu, K. Electrical resistivity of ultrafine-grained copper with nanoscale growth twins. J. Appl. Phys. 102, 083708 (2007).
Anderoglu, O. et al. Epitaxial nanotwinned Cu films with high strength and high conductivity. Appl. Phys. Lett. 93, 083108 (2008).
Algra, R. E. et al. Twinning superlattices in indium phosphide nanowires. Nature 456, 369–372 (2008).
Caroff, P. et al. Controlled polytypic and twin-plane superlattices in III-V nanowires. Nat. Nanotechnol. 4, 50–55 (2008).
Arbiol, J. et al. Triple-twin domains in Mg doped GaN wurtzite nanowires: structural and electronic properties of this zinc-blende-like stacking. Nanotechnology 20, 145704 (2009).
Spirkoska, D. et al. Structural and optical properties of high quality zinc-blende/wurtzite GaAs nanowire heterostructures. Phys. Rev. B 80, 245325 (2009).
Wang, J. & Zhang, X. Twinning effects on strength and plasticity of metallic materials. MRS Bull. 41, 274–281 (2016).
Sansoz, F., Lu, K., Zhu, T. & Misra, A. Strengthening and plasticity in nanotwinned metals. MRS Bull. 41, 292–297 (2016).
Wang, Y. B., Wu, B. & Sui, M. L. Dynamical dislocation emission processes from twin boundaries. Appl. Phys. Lett. 93, 041906 (2008).
Konopka, K., Mizera, J. & Wyrzykowski, J. W. The generation of dislocations from twin boundaries and its effect upon the flow stresses in FCC metals. J. Mater. Process. Technol. 99, 255–259 (2000).
Wang, Y. M. et al. Defective twin boundaries in nanotwinned metals. Nat. Mater. 12, 697–702 (2013).
Zhang, X. et al. High-strength sputter-deposited Cu foils with preferred orientation of nanoscale growth twins. Appl. Phys. Lett. 88, 173116 (2006).
Anderoglu, O., Misra, A., Ronning, F., Wang, H. & Zhang, X. Significant enhancement of the strength-to-resistivity ratio by nanotwins in epitaxial Cu films. J. Appl. Phys. 106, 024313 (2009).
Bufford, D., Wang, H. & Zhang, X. High strength, epitaxial nanotwinned Ag films. Acta Mater. 59, 93–101 (2011).
Ma, E. et al. Strain hardening and large tensile elongation in ultrahigh-strength NT copper. Appl. Phys. Lett. 85, 4932–4934 (2004).
Wang, G. et al. The origin of the ultrahigh strength and good ductility in nanotwinned copper. Mater. Sci. Eng. A 527, 4270–4274 (2010).
Idrissi, H., Wang, B., Colla, M. S. & Raskin, J. P. Ultrahigh strain hardening in thin Palladium films with nanoscale twins. Adv. Mater. 23, 2119–2122 (2011).
Wang, J., Li, N. & Misra, A. Structure and stability of Σ3 grain boundaries in face centered cubic metals. Philos. Mag. 93, 315–327 (2013).
Wright, T. W., Daphalapurkar, N. P. & Ramesh, K. T. Stability of ideal fcc twin boundaries. J. Mech. Phys. Solids 73, 228–241 (2014).
Zhu, L. L., Guo, X. & Lu, J. Surface Stress Effects on the Yield Strength in Nanotwinned Polycrystal Face-Centered-Cubic Metallic Nanowires. J. Appl. Mech. 81, 101002 (2014).
Cao, R., Deng, Y. & Deng, C. Ultrahigh plastic flow in Au nanotubes enabled by surface stress facilitated reconstruction. Acta Mater. 86, 15–22 (2015).
Zhu, Y. T., Liao, X. Z., Wu, X. L. & Narayan, J. Grain size effect on deformation twinning and detwinning. J. Mater. Sci. 48, 4467–4475 (2013).
Guo, X., Ji, R., Weng, G. J., Zhu, L. L. & Lu, J. Computer simulation of strength and ductility of nanotwin-strengthened coarse-grained metals. Model. Simul. Mater. Sci. Eng. 22, 075014 (2014).
Yang, G., Guo, X., Weng, G. J., Zhu, L. L. & Ji, R. Simulation of ballistic performance of coarse-grained metals strengthened by nanotwinned regions. Model. Simul. Mater. Sci. Eng. 23, 085009 (2015).
Guo, X., Ouyang, Q. D., Weng, G. J. & Zhu, L. L. The direct and indirect effects of nanotwin volume fraction on the strength and ductility of coarse-grained metals. Mater. Sci. Eng. A 657, 234–243 (2016).
Wang, Y. Q., Smirani, R. & Ross, G. G. Nanotwinning in silicon nanocrystals produced by ion implantation. Nano Lett. 4, 2041–2045 (2004).
Tian, Y. J. et al. Ultrahard nanotwinned cubic boron nitride. Nature 493, 385–388 (2013).
Li, B., Sun, H. & Chen, C. F. Large indentation strain stiffening in nanotwinned cubic boron nitride. Nat. Commun. 5, 4965 (2014).
Huang, Q. et al. Nanotwinned diamond with unprecedented hardness and stability. Nature 510, 250–253 (2014).
Cong, D. Y. et al. Microstructural and crystallographic characteristics of interpenetrating and non-interpenetrating multiply twinned nanostructure in a Ni-Mn-Ga ferromagnetic shape memory alloy. Acta Mater. 59, 7070–7081 (2011).
Kauffmann-Weiss, S. et al. Magnetic nanostructures by adaptive twinning in strained epitaxial films. Phys. Rev. Lett. 107, 206105 (2011).
Jung, J. et al. Continuum understanding of twin formation near grain boundaries of FCC metals with low stacking fault energy. npj Comput. Mater. 3, 21 (2017).
Pei, Z. et al. Atomic structures of twin boundaries in hexagonal close-packed metallic crystals with particular focus on Mg. npj Comput. Mater. 3, 6 (2017).
Bufford, D., Liu, Y., Wang, J., Wang, H. & Zhang, X. In situ nanoindentation study on plasticity and work hardening in aluminium with incoherent twin boundaries. Nat. Commun. 5, 4864 (2014).
Kobler, A. et al. Nanotwinned silver nanowires: structure and mechanical properties. Acta Mater. 92, 299–308 (2015).
Tucker, G. J. & Foiles, S. M. Quantifying the influence of twin boundaries on the deformation of nanocrystalline copper using atomistic simulations. Int. J. Plast. 65, 191–205 (2015).
Lu, N., Du, K., Lu, L. & Ye, H. Q. Transition of dislocation nucleation induced by local stress concentration in nanotwinned copper. Nat. Commun. 6, 7648 (2015).
Xu, S., Xiong, L., Chen, Y. & McDowell, D. L. Sequential slip transfer of mixed-character dislocations across Σ3 coherent twin boundary in FCCmetals: a concurrent atomistic-continuum study. npj Comput. Mater. 2, 15016 (2016).
Sun, L. G., He, X. Q., Wang, J. B. & Lu, J. Deformation and failure mechanisms of nanotwinned copper films with a pre-existing crack. Mater. Sci. Eng. A 606, 334–345 (2014).
Pei, L. Q. et al. Brittle versus ductile behaviour of nanotwinned copper: a molecular dynamics study. Acta Mater. 89, 1–13 (2015).
Sun, L. G., He, X. Q. & Lu, J. Atomistic simulation study on twin orientation and spacing distribution effects on nanotwinned Cu films. Philos. Mag. 95, 3467–3485 (2015).
Ott, R. T. et al. Optimization of strength and ductility in nanotwinned ultra-fine grained Ag: twin density and grain orientations. Acta Mater. 96, 378–389 (2015).
Borovikov, V., Mendelev, M. I., King, A. H. & LeSar, R. Effect of stacking fault energy on mechanism of plastic deformation in nanotwinned FCC metals. Model. Simul. Mater. Sci. Eng. 23, 055003 (2015).
Borovikov, V., Mendelev, M. I., King, A. H. & LeSar, R. Effects of Schmid factor and slip nucleation on deformation mechanism in columnar-grained nanotwinned Ag and Cu. J. Appl. Phys. 117, 085302 (2015).
Zhou, H. F. et al. Torsional detwinning domino in nanotwinned one-dimensional nanostructures. Nano Lett. 15, 6082–6087 (2015).
Singh, A., Dao, M., Lu, L. & Suresh, S. Deformation, structural changes and damage evolution in nanotwinned copper under repeated frictional contact sliding. Acta Mater. 59, 7311–7324 (2011).
Singh, A., Tang, L., Dao, M., Lu, L. & Suresh, S. Fracture toughness and fatigue crack growth characteristics of nanotwinned copper. Acta Mater. 59, 2437–2446 (2011).
Zeng, Z., Li, X. Y., Lu, L. & Zhu, T. Fracture in a thin film of nanotwinned copper. Acta Mater. 98, 313–317 (2015).
Li, X. Y., Dao, M., Eberl, C., Hodge, A. M. & Gao, H. J. Fracture, fatigue, and creep of nanotwinned metals. MRS Bull. 41, 298–304 (2016).
Shute, C. J. et al. Detwinning, damage and crack initiation during cyclic loading of Cu samples containing aligned nanotwins. Acta Mater. 59, 4569–4577 (2011).
Zhang, Z. J., Zhang, P., Li, L. L. & Zhang, Z. F. Fatigue cracking at twin boundaries: Effects of crystallographic orientation and stacking fault energy. Acta Mater. 60, 3113–3127 (2012).
Pan, Q. S., Lu, Q. H. & Lu, L. Fatigue behavior of columnar-grained Cu with preferentially oriented nano scale twins. Acta Mater. 61, 1383–1393 (2013).
Pan, Q. S. & Lu, L. Strain-controlled cyclic stability and properties of Cu with highly oriented nanoscale twins. Acta Mater. 81, 248–257 (2014).
Zhou, X. L., Li, X. Y. & Chen, C. Q. Atomistic mechanisms of fatigue in nanotwinned metals. Acta Mater. 99, 77–86 (2015).
Yang, X. S. et al. Time-, stress-, and temperature-dependent deformation in nanostructured copper: Creep tests and simulations. J. Mech. Phys. Solids 94, 191–206 (2016).
Zhao, Y., Cheng, I. C., Kassner, M. E. & Hodge, A. M. The effect of nanotwins on the corrosion behavior of copper. Acta Mater. 67, 181–188 (2014).
King, A. H. & Smith, D. A. On the mechanisms of point-defect absorption by grain and twin boundaries. Philos. Mag. A 42, 495–512 (1980).
Yu, K. Y. et al. Removal of stacking-fault tetrahedra by twin boundaries in nanotwinned metals. Nat. Commun. 4, 1377 (2013).
Li, J. et al. In situ study of defect migration kinetics and self-healing of twin boundaries in heavy ion irradiated nanotwinned metals. Nano Lett. 15, 2922–2927 (2015).
Chen, Y. et al. Damage-tolerant nanotwinned metals with nanovoids under radiation environments. Nat. Commun. 6, 7036 (2015).
Chen, Y. et al. In situ studies on radiation tolerance of nanotwinned Cu. Acta Mater. 111, 148–156 (2016).
Niewczas, M. & Hoagland, R. G. Molecular dynamics studies of the interaction of a/6 <112> Shockley dislocations with stacking fault tetrahedra in copper. Part I: intersection of SFT by an isolated Shockley. Philos. Mag. 89, 623–640 (2009).
Demkowicz, M. J., Anderoglu, O., Zhang, X. & Misra, A. The influence of ∑3 twin boundaries on the formation of radiation-induced defect clusters in nanotwinned Cu. J. Mater. Res. 26, 1666–1675 (2011).
Mendelev, M. I. & King, A. H. The interactions of self-interstitials with twin boundaries. Philos. Mag. 93, 1268–1278 (2013).
Xiao, X. Z., Song, D. K., Xue, J. M., Chu, H. J. & Duan, H. L. A self-consistent plasticity theory for modeling the thermo-mechanical properties of irradiated FCC metallic polycrystals. J. Mech. Phys. Solids 78, 1–16 (2015).
Xiao, X. Z., Song, D. K., Chu, H. J., Xue, J. M. & Duan, H. L. Mechanical behaviors of irradiated FCC polycrystals with nanotwins. Int. J. Plast. 59, 664601 (2016).
Asaro, R. J. & Suresh, S. Mechanistic models for the activation volume and rate sensitivity in metals with nanocrystalline grains and nano-scale twins. Acta Mater. 53, 3369–3382 (2005).
Dao, M., Lu, L., Shen, Y. F. & Suresh, S. Strength, strain-rate sensitivity and ductility of copper with nanoscale twins. Acta Mater. 54, 5421–5432 (2006).
Jerusalem, A., Dao, M., Suresh, S. & Radovitzky, R. Three-dimensional model of strength and ductility of polycrystalline copper containing nanoscale twins. Acta Mater. 56, 4647–4657 (2008).
Mirkhani, H. & Joshi, S. P. Crystal plasticity of nanotwinned microstructures: a discrete twin approach for copper. Acta Mater. 59, 5603–5617 (2011).
Zhu, L. L. et al. Modeling grain size dependent optimal twin spacing for achieving ultimate high strength and related high ductility in nanotwinned metals. Acta Mater. 59, 5544–5557 (2011).
Mirkhani, H. & Joshi, S. P. Mechanism-based crystal plasticity modeling of twin boundary migration in nanotwinned face-centered-cubic metals. J. Mech. Phys. Solids 68, 107–133 (2014).
Gu, P., Dao, M., Asaro, R. J. & Suresh, S. A unified mechanistic model for size-dependent deformation in nanocrystalline and nanotwinned metals. Acta Mater. 59, 6861–6868 (2011).
Colla, M. S. et al. High strength-ductility of thin nanocrystalline palladium films with nanoscale twins: On-chip testing and grain aggregate model. Acta Mater. 60, 1795–1806 (2012).
Yuan, R., Beyerlein, I. J. & Zhou, C. Z. Statistical dislocation activation from grain boundaries and its role in the plastic anisotropy of nanotwinned copper. Acta Mater. 110, 8–18 (2016).
Liddicoat, P. V. et al. Nanostructural hierarchy increases the strength of aluminium alloys. Nat. Commun. 63, 1–7 (2010).
Saburi, T., Wayman, C. M., Takala, K. & Nenno, S. The shape memory mechanism in 18R martensitic alloys. Acta Metall. 28, 15–32 (1980).
Müllner, P., Chernenko, V. A. & Kostorz, G. A microscopic approach to the magnetic-field-induced deformation of martensite (magnetoplasticity). J. Magn. Magn. Mater. 267, 325–334 (2003).
Müllner, P. & King, A. H. Deformation of hierarchically twinned martensite. Acta Mater. 58, 5242–5261 (2010).
Tao, N. R. & Lu, K. Nanoscale structural refinement via deformation twinning in face-centered cubic metals. Scr. Mater. 60, 1039–1043 (2009).
Qu, S. et al. Microstructural evolution and mechanical properties of Cu-Al alloys subjected to equal channel angular pressing. Acta Mater. 57, 1586–1601 (2009).
Zhu, L., Kou, H. & Lu, J. On the role of hierarchical twins for achieving maximum yield strength in nanotwinned metals. Appl. Phys. Lett. 101, 081906 (2012).
Zhu, L. L., Qu, S. X., Guo, X. & Lu, J. Analysis of the twin spacing and grain size effects on mechanical properties in hierarchically nanotwinned face-centered cubic metals based on a mechanism-based plasticity model. J. Mech. Phys. Solids 76, 162–179 (2015).
Kou, H. N., Lu, J. & Li, Y. High-strength and high-ductility nanostructured and amorphous metallic materials. Adv. Mater. 26, 5518–5524 (2014).
Yuan, F. P. & Wu, X. L. Size effects of primary/secondary twins on the atomistic deformation mechanisms in hierarchically nanotwinned metals. J. Appl. Phys. 113, 203516 (2013).
Sun, L. G., He, X. Q., Zhu, L. L. & Lu, J. Two softening stages in nanotwinned Cu. Philos. Mag. 94, 4037–4052 (2014).
Yuan, F. P. & Wu, X. L. Atomistic scale fracture behaviours in hierarchically nanotwinned metals. Philos. Mag. 93, 3248–3259 (2013).
Yuan, F. P., Chen, L., Jiang, P. & Wu, X. L. Twin boundary spacing effects on shock response and spall behaviors of hierarchically nanotwinned fcc metals. J. Appl. Phys. 115, 063509 (2014).
Christian, J. W. & Mahajan, S. Deformation twinning. Prog. Mater. Sci. 39, 1–157 (1995).
Yoo, M. H., Morris, J. R., Ho, K. M. & Agnew, S. R. Nonbasal deformation modes of HCP metals and alloys: role of dislocation source and mobility. Metall. Mater. Trans. A 33, 813–822 (2002).
Zhu, Y. T., Liao, X. Z. & Wu, X. L. Deformation twinning in nanocrystalline materials. Prog. Mater. Sci. 57, 1–62 (2012).
Mahajan, S. Critique of mechanisms of formation of deformation, annealing and growth twins: face-centered cubic metals and alloys. Scr. Mater. 68, 95–99 (2013).
Beyerlein, I. J., Zhang, X. & Misra, A. Growth twins and deformation twins in metals. Annu. Rev. Mater. Res. 44, 329–363 (2014).
Velasco, L. & Hodge, A. M. The mobility of growth twins synthesized by sputtering: tailoring the twin thickness. Acta Mater. 109, 142–150 (2016).
Wang, J. et al. Detwinning mechanisms for growth twins in face-centered cubic metals. Acta Mater. 58, 2262–2270 (2010).
Hirth, J. P., Lothe, J. (eds). Theory of Dislocations. (Krieger Publishing Company, Malabar, FL, 1992).
Zhang, Y., Tao, N. R. & Lu, K. Effect of stacking-fault energy on deformation twin thickness in Cu-Al alloys. Scr. Mater. 60, 211–213 (2009).
Zhao, Y. H., Zhu, Y. T., Liao, X. Z., Horita, Z. & Langdon, T. G. Tailoring stacking fault energy for high ductility and high strength in ultrafine grained Cu and its alloy. Appl. Phys. Lett. 89, 121906 (2006).
Wang, Z. W. et al. Influence of stacking fault energy on deformation mechanism and dislocation storage capacity in ultrafine-grained materials. Scr. Mater. 60, 52–55 (2009).
Balogh, L. et al. Influence of stacking-fault energy on microstructural characteristics of ultrafine-grain copper and copper-zinc alloys. Acta Mater. 56, 809–820 (2008).
Zhao, Y. H., Horita, Z., Langdon, T. G. & Zhu, Y. T. Evolution of defect structures during cold rolling of ultrafine-grained Cu and Cu-Zn alloys: Influence of stacking fault energy. Mater. Sci. Eng. A 474, 342–347 (2008).
Youssef, K., Sakaliyska, M., Bahmanpour, H., Scattergood, R. & Koch, C. Effect of stacking fault energy on mechanical behavior of bulk nanocrystalline Cu and Cu alloys. Acta Mater. 59, 5758–5764 (2011).
Yamakov, V., Wolf, D., Phillpot, S. R. & Gleiter, H. Deformation twinning in nanocrystalline Al by molecular dynamics simulation. Acta Mater. 50, 5005–5020 (2002).
Liao, X. Z., Zhou, F., Lavernia, E. J., He, D. W. & Zhu, Y. T. Deformation twins in nanocrystalline Al. Appl. Phys. Lett. 83, 5062–5064 (2003).
Xue, S. et al. The formation mechanisms of growth twins in polycrystalline Al with high stacking fault energy. Acta Mater. 101, 62–70 (2015).
Bhattacharyya, D. et al. Heterotwin formation during growth of nanolayered Al-TiN composites. Appl. Phys. Lett. 96, 093113 (2010).
Bufford, D., Bi, Z., Jia, Q. X., Wang, H. & Zhang, X. Nanotwins and stacking faults in high-strength epitaxial Ag/Al multilayer films. Appl. Phys. Lett. 101, 223112 (2012).
Bufford, D. et al. Formation mechanisms of high-density growth twins in aluminum with high stacking-fault energy. Mater. Res. Lett. 1, 51–60 (2013).
Yu, K. Y. et al. Basic criteria for formation of growth twins in high stacking fault energy metals. Appl. Phys. Lett. 103, 181903 (2013).
Liu, Y., Bufford, D., Wang, H., Sun, C. & Zhang, X. Mechanical properties of highly textured Cu/Ni multilayers. Acta Mater. 59, 1924–1933 (2011).
Sun, P. L. et al. Effect of stacking fault energy on strength and ductility of nanostructured alloys: An evaluation with minimum solution hardening. Mater. Sci. Eng. A 525, 83–86 (2009).
Wang, K., Tao, N. R., Liu, G., Lu, J. & Lu, K. Plastic strain-induced grain refinement at the nanometer scale in copper. Acta Mater. 54, 5281–5291 (2006).
Chan, H. L., Ruan, H. H., Chen, A. Y. & Lu, J. Optimization of the strain rate to achieve exceptional mechanical properties of 304 stainless steel using high speed ultrasonic surface mechanical attrition treatment. Acta Mater. 58, 5086–5096 (2010).
Chen, A. Y. et al. The influence of strain rate on the microstructure transition of 304 stainless steel. Acta Mater. 59, 3697–3709 (2011).
Zhu, K. Y., Vassel, A., Brisset, F., Lu, K. & Lu, J. Nanostructure formation mechanism of α-titanium using SMAT. Acta Mater. 52, 4101–4110 (2004).
Kim, C. et al. Copper nanowires with a five-twinned structure grown by chemical vapor deposition. Adv. Mater. 20, 1859–1863 (2008).
Brom, J. E. et al. Structural and electrical properties of epitaxial Bi2Se3 thin films grown by hybrid physical-chemical vapor deposition. Appl. Phys. Lett. 100, 162110 (2012).
Burek, M. J. & Greer, J. R. Fabrication and microstructure control of nanoscale mechanical testing specimens via electron beam lithography and electroplating. Nano Lett. 10, 69–76 (2010).
You, Z. S., Lu, L. & Lu, K. Tensile behavior of columnar grained Cu with preferentially oriented nanoscale twins. Acta Mater. 59, 6927–6937 (2011).
Jang, D. C., Li, X., Gao, H. & Greer, J. R. Deformation mechanisms in nanotwinned metal nanopillars. Nat. Nanotechnol. 7, 594–601 (2012).
Wang, J. et al. Near-ideal theoretical strength in gold nanowires containing angstrom scale twins. Nat. Commun. 4, 1742 (2013).
Anderoglu, O., Zhang, X. & Misra, A. Thermal stability of sputtered Cu films with nanoscale growth twins. J. Appl. Phys. 103, 094322 (2008).
Zhao, Y. F., Furnish, T. A., Kassner, M. E. & Hodge, A. M. Thermal stability of highly nanotwinned copper: the role of grain boundaries and texture. J. Mater. Res. 27, 3049–3057 (2012).
Bufford, D., Wang, H. & Zhang, X. Thermal stability of twins and strengthening mechanisms in differently oriented epitaxial nanotwinned Ag films. J. Mater. Res. 28, 1729–1739 (2013).
Valiev, R. Z., Islamgaliev, R. K. & Alexandrov, I. V. Bulk nanostructured materials from severe plastic deformation. Prog. Mater. Sci. 45, 103–189 (2000).
Estrin, Y. & Vinogradov, A. Extreme grain refinement by severe plastic deformation: A wealth of challenging science. Acta Mater. 61, 782–817 (2013).
Liao, X. Z. et al. Deformation twinning in nanocrystalline copper at room temperature and low strain rate. Appl. Phys. Lett. 84, 592–594 (2004).
Li, Y. S., Tao, N. R. & Lu, K. Microstructural evolution and nanostructure formation in copper during dynamic plastic deformation at cryogenic temperatures. Acta Mater. 56, 230–241 (2008).
Zhang, Y., Tao, N. R. & Lu, K. Mechanical properties and rolling behaviors of nano-grained copper with embedded nano-twin bundles. Acta Mater. 56, 2429–2440 (2008).
Ruan, H. H., Chen, A. Y., Chan, H. L. & Lu, J. Characterization of plastically graded nanostructured material: Part II. The experimental validation in surface nanostructured material. Mech. Mater. 42, 698–708 (2010).
Yin, Z., Sun, L., Yang, J., Gong, Y. & Zhu, X. Mechanical behavior and deformation kinetics of gradient structured Cu-Al alloys with varying stacking fault energy. J. Alloy. Compd. 687, 152–160 (2016).
Xie, P. et al. A nanotwinned surface layer generated by high strain-rate deformation in a TRIP steel. Mater. Des. 80, 144–151 (2015).
Huang, C. X. et al. Deformation twinning in polycrystalline copper at room temperature and low strain rate. Acta Mater. 54, 655–665 (2006).
Zhu, C. F. et al. Microstructure and strength of pure Cu with large grains processed by equal channel angular pressing. Mater. Des. 52, 23–29 (2013).
Liao, X. Z., Huang, J. Y. & Zhu, Y. T. Nanostructures and deformation mechanisms in a cryogenically ball-milled Al-Mg alloy. Philos. Mag. 83, 3065–3075 (2003).
Gray, G. T. High-strain-rate deformation: mechanical behavior and deformation substructures induced. Annu. Rev. Mater. Res. 42, 285–303 (2012).
Wu, X. L. & Zhu, Y. T. Inverse grain-size effect on twinning in nanocrystalline Ni. Phys. Rev. Lett. 101, 025503 (2008).
Ni, S. et al. Effect of grain size on the competition between twinning and de-twinning in nanocrystalline metals. Phys. Rev. B 84, 235401 (2011).
Ni, S. et al. The effect of dislocation density on the interactions between dislocations and twin boundaries in nanocrystalline materials. Acta Mater. 60, 3181–3189 (2012).
Wang, L. H. et al. Dynamic and atomic-scale understanding of the twin thickness effect on dislocation nucleation and propagation activities by in situ bending of ni nanowires. Acta Mater. 90, 194–203 (2015).
Cao, Y. et al. De-twinning via secondary twinning in face-centered cubic alloys. Mater. Sci. Eng. A 578, 110–114 (2013).
Cao, Y. et al. Grain boundary formation by remanent dislocations from de-twinning of thin nano-twins. Scr. Mater. 100, 98–101 (2015).
Wang, Y. B., Sui, M. L. & Ma, E. In situ observation of twin boundary migration in copper with nanoscale twins during tensile deformation. Philos. Mag. Lett. 87, 935–942 (2007).
Wang, Y. B. & Sui, M. L. Atomic-scale in situ observation of lattice dislocations passing through twin boundaries. Appl. Phys. Lett. 94, 021909 (2009).
Han, X. D., Wang, L. H., Yue, Y. H. & Zhang, Z. In situ atomic scale mechanical microscopy discovering the atomistic mechanisms of plasticity in nano-single crystals and grain rotation in polycrystalline metals. Ultramicroscopy 151, 94–100 (2015).
Yue, Y. H. et al. Quantitative evidence of crossover toward partial dislocation mediated plasticity in copper single crystalline nanowires. Nano Lett. 12, 4045–4049 (2012).
Wang, L. H. et al. Plastic deformation through dislocation saturation in ultrasmall pt nanocrystals and its in situ atomistic mechanisms. Nano Lett. 17, 4733–4799 (2017).
Wang, L. H. et al. In situ atomic-Scale observations of continuous and reversible lattice deformation far beyond the elastic limit. Nat. Commun. 4, 2413 (2013).
Zhang, X. et al. Nanoscale-twinning-induced strengthening in austenitic stainless steel thin films. Appl. Phys. Lett. 84, 1096–1098 (2004).
Jin, Z. H. et al. The interaction mechanism of screw dislocations with coherent twin boundaries in different face-centred cubic metals. Scr. Mater. 54, 1163–1168 (2006).
Jin, Z. H. et al. Interactions between non-screw lattice dislocations and coherent twin boundaries in face-centered cubic metals. Acta Mater. 56, 1126–1135 (2008).
Zheng, Y. G., Lu, J., Zhang, H. W. & Chen, Z. Strengthening and toughening by interface-mediated slip transfer reaction in nanotwinned copper. Scr. Mater. 60, 508–511 (2009).
Li, X., Wei, Y., Lu, L., Lu, K. & Gao, H. Dislocation nucleation governed softening and maximum strength in nano-twinned metals. Nature 464, 877–880 (2010).
You, Z. et al. Plastic anisotropy and associated deformation mechanisms in nanotwinned metals. Acta Mater. 61, 217–227 (2013).
Zhou, H., Li, X., Qu, S., Yang, W. & Gao, H. A jogged dislocation governed strengthening mechanism in nanotwinned metals. Nano Lett. 14, 5075–5080 (2014).
Zhu, Y. T. et al. Nucleation and growth of deformation twins in nanocrystalline aluminum. Appl. Phys. Lett. 85, 5049–5051 (2004).
Zhu, Y. T., Liao, X. Z., Srinivasan, S. G. & Lavernia, E. J. Nucleation of deformation twins in nanocrystalline face-centered-cubic metals processed by severe plastic deformation. J. Appl. Phys. 98, 034319 (2005).
Van Swygenhoven, H., Derlet, P. M. & Froseth, A. G. Stacking fault energies and slip in nanocrystalline metals. Nat. Mater. 3, 399–403 (2004).
Schwaiger, R., Moser, B., Dao, M., Chollacoop, N. & Suresh, S. Some critical experiments on the strain-rate sensitivity of nanocrystalline nickel. Acta Mater. 51, 5159–5172 (2003).
Asaro, R. J. & Rice, J. R. Strain localization in ductile single crystals. J. Mech. Phys. Solids 25, 309–338 (1977).
Dao, M., Kad, B. K. & Asaro, R. J. Deformation and fracture under compressive loading in lamellar TiAl microstructures. Philos. Mag. A 74, 569–591 (1996).
Dao, M. & Asaro, R. J. Loacalized deformation modes and non-schmid effects in crystalline solids. part II. deformation patterns. Mech. Mater. A 23, 103–132 (1996).
Wei, Y. Scaling of maximum strength with grain size in nanotwinned fcc metals. Phys. Rev. B 83, 132104 (2011).
Eshelby, J. D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. A 241, 376–396 (1957).
Zhu, B., Asaro, R. J., Krysl, P. & Bailey, R. Transition of deformation mechanisms and its connection to grain size distribution in nanocrystalline metals. Acta Mater. 53, 4825–4838 (2005).
Wei, Y. J., Su, C. & Anand, L. A computational study of the mechanical behavior of nanocrystalline fcc metals. Acta Mater. 54, 3177–3190 (2006).
Huang, Y., Qu, S., Hwang, K. C., Li, M. & Gao, H. A conventional theory of mechanism-based strain gradient plasticity. Int. J. Plast. 20, 753–782 (2004).
Qu, S., Huang, Y., Pharr, G. P. & Hwang, K. C. The indentation size effect in the spherical indentation of iridium: a study via the conventional theory of mechanism-based strain gradient plasticity. Int. J. Plast. 22, 1265–1286 (2006).
Yip, S. Nanocrystals: the strongest size. Nature 391, 532–533 (1998).
Roters, F. et al. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: theory, experiments, applications. Acta Mater. 58, 1152–1211 (2010).
Knezevic, M., Drach, B., Ardeljan, M. & Beyerlein, I. J. Three dimensional predictions of grain scale plasticity and grain boundaries using crystal plasticity finite element models. Comput. Methods Appl. Mech. Eng. 277, 239–259 (2014).
Yuan, R., Beyerlein, I. J. & Zhou, C. Emergence of grain-size effects in nanocrystalline metals from statistical activation of discrete dislocation sources. Acta Mater. 90, 169–181 (2015).
Gu, P., Dao, M. & Suresh, S. Analysis of size-dependent slip transfer and inter-twin flow stress in a nanotwinned fcc metal. Acta Mater. 67, 409–417 (2014).
Acknowledgements
J. L. acknowledges the supports from the National Key R&D Program of China (Project No. 2017YFA0204403), Research Grants Council of the Hong Kong Special Administrative Region (Grant No. CityU-11247516), the Hong Kong Collaborative Research Fund (CRF) Scheme (C4028-14G), Guangdong Science and Technology Department (Ref: 2014B050504003) and SZSTI (Ref: ZDSYS201602291653165). X. H. is grateful for the support from the Research Grants Council of the Hong Kong Special Administrative Region (Grant No. CityU-11204414).
Author information
Authors and Affiliations
Contributions
J. L. conceived the project and provided guidance for the literature review. L. S. organized the reference materials and wrote the review paper. J. L. and X. H. reviewed and revised the paper and offered helpful suggestions during the work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sun, L., He, X. & Lu, J. Nanotwinned and hierarchical nanotwinned metals: a review of experimental, computational and theoretical efforts. npj Comput Mater 4, 6 (2018). https://doi.org/10.1038/s41524-018-0062-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-018-0062-2
This article is cited by
-
Role of geometry and coherent twin boundaries in mechanical response of Cu〈110〉 nanopillars under tensile loading: insights from molecular dynamics simulations
Journal of Materials Science (2024)
-
Formation and impact of nanoscopic oriented phase domains in electrochemical crystalline electrodes
Nature Materials (2023)
-
Effect of Aluminum Addition on Microstructure, Recrystallization and Work Hardening of MnCrCoFeNi High-Entropy Alloy
Transactions of the Indian Institute of Metals (2023)
-
Work Hardening and Kinetics Analysis of Al0.3MnCrCoFeNi High-Entropy Alloy
JOM (2023)
-
Role of planar faults in martensite formation in nano-polycrystalline iron by molecular dynamics simulation
Journal of Materials Science (2022)