Abstract
Although high-entropy alloys (HEAs) are attracting interest, the physical metallurgical mechanisms related to their properties have mostly not been clarified, and this limits wider industrial applications, in addition to the high alloy costs. We clarify the physical metallurgical reasons for the materials phenomena (sluggish diffusion and micro-twining at cryogenic temperatures) and investigate the effect of individual elements on solid solution hardening for the equiatomic CoCrFeMnNi HEA based on atomistic simulations (Monte Carlo, molecular dynamics and molecular statics). A significant number of stable vacant lattice sites with high migration energy barriers exists and is thought to cause the sluggish diffusion. We predict that the hexagonal close-packed (hcp) structure is more stable than the face-centered cubic (fcc) structure at 0 K, which we propose as the fundamental reason for the micro-twinning at cryogenic temperatures. The alloying effect on the critical resolved shear stress (CRSS) is well predicted by the atomistic simulation, used for a design of non-equiatomic fcc HEAs with improved strength, and is experimentally verified. This study demonstrates the applicability of the proposed atomistic approach combined with a thermodynamic calculation technique to a computational design of advanced HEAs.
Similar content being viewed by others
Introduction
High-entropy alloys (HEAs) are attracting an academic interest for their promising properties as structural materials.1 Particularly, the equiatomic CoCrFeMnNi HEAs have been reported to possess a wide-range of promising properties such as good high-temperature structural stability2,3 and an excellent balance between strength and ductility, particularly at cryogenic temperatures, typically 77 K, the liquid nitrogen temperature.4 Even though most HEAs have equiatomic or near equiatomic compositions, it is believed that the equiatomic composition would not be the optimum composition for a wide range of material properties.5,6,7,8,9,10 To improve a specific material property, one may have to change the alloy composition from the equiatomic composition. Indeed, there have been many efforts to improve the face-centered cubic (fcc) single-phase stability or mechanical properties of the CoCrFeMnNi HEAs by adjusting the composition.5,6,7,8,9 However, for an efficient alloy design, one would need to understand the reason for the typical HEA properties and the effect of individual elements on them.
Sluggish diffusion,11,12,13 severe lattice distortion14 and micro-twinning2,3,4,8,15 have been mentioned as probable reasons for the typical HEA properties. However, exact mechanisms for such structural reasons are not clearly known yet. For example, the variety of the surrounding atoms of each lattice site and the existence of low-energy sites that may serve as vacancy trap sites have been mentioned as a probable reason for the sluggish diffusion.11 However, the distribution and amount of such trap sites need further investigation. Similarly, the quantitative effect of severe lattice distortion on solid solution hardening is not known yet and the reason why the micro-twinning is activated, particularly at 77 K, has not been explained yet either. The fact that the physical metallurgical mechanisms related to individual properties are mostly not clarified limits wider industrial applications of HEAs, in addition to the high alloy costs, even with the good combination of engineering properties.
The diffusion, strengthening and plastic deformation are all atomic-level materials phenomena that have origins on an atomic scale. Experimental analyses of atomic-level materials phenomena are not trivial, while large-scale atomistic simulation techniques based on semi-empirical interatomic potentials can be an efficient tool for atomic-scale analyses. A bottleneck in the atomistic simulation approach would be the availability of reliable interatomic potential for the relevant alloy systems.
An atomistic simulation on a multicomponent alloy system requires at least interatomic potentials for all the constituent binary alloy systems. Recently, interatomic potentials for all constituent binary systems of the CoCrFeMnNi HEA system became available with a second nearest-neighbor modified embedded-atom method (2NN MEAM) potential formalism,16 as a result of a long-term research effort of the present authors’ group. The necessary unary and binary potential parameters were determined by fitting to known fundamental material properties of relevant materials and already published.17,18,19,20,21,22,23,24 Ternary parameters were given default assumed values in the present work to complete the interatomic potential for the five-component alloy system. Therefore, using atomistic simulation techniques based on the 2NN MEAM potential, the goal in the present study was to clarify fundamental reasons for sluggish diffusion and micro-twining at cryogenic temperatures and to investigate the effect of individual elements on those properties as well as on solid solution hardening. We used a Canonical Monte Carlo (CMC) simulation, molecular dynamics (MD) simulation and a 0 K molecular statics simulation to examine the equilibrium atomic configuration, stability of lattice structure and mechanical properties of the equiatomic CoCrFeMnNi HEA. We derived an empirical equation to predict the critical resolved shear stress (CRSS) from the simulation results, designed non-equiatomic CoCrFeMnNi HEAs with improved strength and experimentally confirmed their strength.
Results and discussion
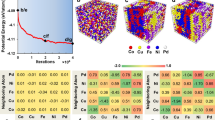
Before starting the computation of any specific materials properties, we examined whether the present interatomic potential yields a stable fcc random solid solution for the equiatomic CoCrFeMnNi HEA (designated CoCrFeMnNi HEA hearafter) in the typical process temperature range (1073–1473 K), as has been reported experimentally.11,14,15 To obtain the equilibrium atomic configuration, we performed a CMC simulation for 10,000 MC steps using a sample with 5760 atoms at 1073 K. Periodic boundary conditions were applied to all directions, and atomic vibration and change in sample dimensions were allowed during the simulation. The results are presented in Fig. 1a together with atomic distribution of individual element atoms. The results show that all five element atoms are uniformly distributed as has been known experimentally. The randomness was checked by calculating short-range order (SRO) parameters for all possible nearest neighbor bonds and comparing them with SRO values for reference model alloys with various degree of ordering. The details of the analysis are provided in the supplementary information of this manuscript.
Atomic configuration and distribution of vacancy migration energy barriers. a atomic configuration and distribution of Co, Cr, Fe, Mn, Ni atoms in the CoCrFeMnNi HEA, obtained by a Canonical Monte Carlo simulation at 1073 K. b schematic diagram of a sample involving a vacancy. c the relative change in energy as the vacancy repeatedly moves to neighboring lattice sites. d the average value of the migration energy barrier for each element. e the size distribution of the calculated migration energy barrier
In addition to the uniform atomic distribution, we wanted to confirm whether the fcc lattice structure is maintained in the CoCrFeMnNi HEA from 1073 K up to the melting temperature. For this, we performed a MD simulation using the sample obtained from the CMC simulation, increasing the temperature by 200 K from 1073 K and equilibrating at a given temperature for 50 ps. Through an analysis of the lattice structure of the sample rapidly cooled to 0 K from each equilibration temperature, we could confirm that the fcc structure is maintained from 1073 K up to the melting. According to the present interatomic potential, the lattice parameter of the CoCrFeMnNi HEA was 3.595 Å at 0 K, which is close to the experimental values, 3.59 (ref. 25) and 3.592 Å (ref. 26). The experimental values must be room temperature (RT) data and it may not be suitable to compare the 0 K calculations with RT data. It should be mentioned here that the unary model parameter that determines the lattice parameter of pure elements at 0 K was optimized by fitting to RT experimental data, assuming that the thermal expansion between 0 K and RT may be small. Our work mentioned above confirmed that the present potential correctly describes the fundamental materials properties of the CoCrFeMnNi HEA and is ready for calculation of other specific materials properties.
Reason for the sluggish diffusion in the CoCrFeMnNi HEA
Previous studies11,12,13 experimentally reported that the CoCrFeMnNi HEA shows the slowest diffusion compared to fcc Fe–Cr–Ni alloys or fcc elements at equal homologous temperatures. Among the five elements, Ni and Co are the most slowly diffusing elements while Mn is the fast diffusing element.11,12 As we noted earlier, the vacancy trapping effect of low-energy sites that may exist due to the variety of surrounding atoms of each lattice site has been mentioned as the reason for the sluggish diffusion.11 However, the distribution and amount of such low-energy sites have not been investigated quantitatively, so one cannot yet conclude whether the sluggish diffusion is a phenomenon that happens to be observed in the CoCrFeMnNi HEA or a phenomenon that can always be expected from multicomponent alloys.
To prove the existence and estimate the number of low-energy sites with high vacancy migration energy barriers, we examined the variety of the vacancy migration energy barriers and their distribution. For this, initially, we introduced a vacancy on a lattice site (numbered “0” in Fig. 1b) of the sample obtained from the CMC with relaxation and moved a nearest neighboring atom straightly to the vacant site step-by-step. At each step of the movement, we allowed relaxation of neighboring atoms, while fixing the position of the moving atom and far distanced atoms (to prohibit the shift of the whole sample). The energy difference between the initial step and each step during the movement was plotted, and the maximum difference was chosen as the vacancy migration energy. The relative change of energy from the initial step as the vacancy repeatedly moves to neighboring lattice site is presented in Fig. 1c. Since the movement of a vacancy into a neighboring site corresponds to a movement of a real atom in the opposite direction, each energy barrier of the vacancy migration could be associated with the energy barrier for the migration of a real atom by the vacancy mechanism. The type (element) of atom associated with each migration energy barrier is designated in Fig. 1c.
As expected, the calculated energy barriers were all different for different migrations, which must have come from the variety of surrounding atoms of each lattice site. We also found that the energy barrier for the migration of Mn atoms is generally lower than those of Co and Ni. To clarify the tendency of the level of migration energy of individual atoms more quantitatively, the average value of migration energy barrier for each element was calculated out of a total of 390 migration energy barriers considered. The results are presented in Fig. 1d. Indeed, the average migration energy barrier of Ni and Co was higher than that of Mn, which means that the diffusion of Ni and Co would be slower than that of Mn. The order in the calculated migration energy barrier was Ni > Co > Cr > Fe > Mn which is close to the order in the experimentally observed diffusivity of individual element atoms, Ni < Co < Fe < Cr < Mn.11
It has been shown that there is a wide spectrum in the migration energy of individual atomic jumps. To estimate the fraction of a so-called low-energy site11 that can serve as a vacancy trapping site, the size distribution of the calculated migration energy barrier was examined as shown in Fig. 1e. The element that has the highest vacancy migration energy barrier among the five elements was Ni, and its value was 1.47 eV according to the present interatomic potential.19 Figure 1e shows that about 9% of the migrations (35 among the 390 migrations) in the CoCrFeMnNi HEA have larger energy barriers than pure Ni. Those lattice sites with the large migration energy barrier can be thought to serve as a strong vacancy trap that blocks the diffusion and eventually be the origin of the sluggish diffusion in the multicomponent CoCrFeMnNi HEA. Based on our results, we believe the sluggish diffusion is a general phenomenon in highly alloyed multicomponent materials that yield a variety of surrounding environments for individual lattice points, not a special phenomenon that occurs only in the CoCrFeMnNi HEA.
Micro-twining mechanism at cryogenic temperatures
Micro-twins have been experimentally observed in most HEAs during deformation,2,3,4,8,15 particularly at 77 K, and are regarded as a probable reason for excellent tensile properties at 77 K. Previous studies claimed that the low stacking fault energy (SFE) of HEAs is one of the probable reasons for the micro-twinning.27,28 However, it is not fully understood why HEAs have a low SFE.
First, we wanted to confirm whether our potential indeed reproduces the formation of micro-twins during low temperature deformation and to investigate the fundamental reason for the micro-twinning. For this, we performed a uniaxial tensile simulation on a single crystal nanowire, which was a simple way to observe both slip and twinning in alloys according to the authors’ experience. For this, an fcc single crystal sample was prepared by depositing (110) atomic layers along the y-axis as shown in Fig. 2a. The sample size was 72 Å × 254 Å × 64 Å, with 100,000 atoms. The top and bottom regions, marked in gray, were set as rigid blocks of immobile atoms. A rigid displacement was applied to both blocks along the y-axis toward opposite directions (see Fig. 2a), followed by a molecular statics simulation at 0 K. The rigid displacement and molecular statics simulation was repeated while the total amount of uniaxial strain was increased, and a stress–strain curve was obtained as shown in Fig. 2b. This simulation was also performed for two binary alloys, Co-50at%Ni and Fe-50at%Ni (designated Co-50Ni and Fe-50Ni hereafter) and for pure Ni as well as the CoCrFeMnNi HEA. All alloy samples were obtained by assuming a random mixing between individual elements.
Uniaxial tensile simulation. a schematic diagram of the uniaxial tensile simulation on a single crystal nanowire. b the simulated stress–strain curves of 100Ni, Co-50Ni, Fe-50Ni and CoCrFeMnNi HEA at 0 K. c–d plastic deformation in the CoCrFeMnNi HEA and Fe-50Ni alloy at 0.02, 0.03, 0.04, 0.05 and 0.06 strain
Figure 2b shows the simulated stress–strain curves of all the alloys considered. It shows that the stress increases monotonically with strain in all the materials and shows an abrupt change which looks similar to the yield point in ordinary stress–strain curves. However, it should be emphasized that the abrupt change does not represent the yielding but the formation of a dislocation in the initially perfect, single crystalline sample. It is also shown that the dislocations form most easily (at the lowest stress or strain level) in the CoCrFeMnNi HEA, rather than in the binary or unary alloys. Another point that needs attention is the further, remarkable drop in stress in the stress–strain curve. This drop in stress, marked by an arrow in Fig. 2b, represents the formation of a twin, as shown in Fig. 2c, d.
From the simulation results shown in Fig. 2, one can confirm that our potential indeed reproduces the formation of micro-twins during the low temperature deformation. During uniaxial extension of nanowires, dislocations were generated in the CoCrFeMnNi HEA most easily and the resultant slip yielded the formation of micro-twins. A question raised here was why dislocations formed most easily in the CoCrFeMnNi HEA rather than in other binary or unary alloys. We believe the easy formation of dislocation came from the severe lattice distortion (which is associated with local stresses and irregular alignment of atoms) in the HEA. According to our potential, the interatomic distance of the Co, Cr, Fe, Mn and Ni in fcc structures were 2.50, 2.58, 2.55, 2.61 and 2.49 Å, respectively. The lattice distortion in the HEA that contains all five different elements should be the largest. The lattice distortion in the Fe-50Ni alloy should also be larger than that in the Co-50Ni alloy, because the size difference between Fe and Ni is larger than that between Co and Ni. The dislocation formation behavior (easiness) in the different materials shown in Fig. 2b can be well explained from the degree of lattice distortion that can be qualitatively estimated from size differences among elements. Even though the atomic size difference would not be the only factor that can explain the lattice distortion, it has been reported that larger atomic size difference usually causes a larger lattice distortion in HEA.29
The next question that may be raised from the simulation results in Fig. 2 is why the formation of dislocations and the resultant slip yields the twins in the HEA and binary alloys. As already mentioned, low SFE can be the factor that leads to micro-twins, and it is necessary to estimate the SFE of the alloys considered. A simple way to estimate the SFE is to calculate the energy difference between hexagonal close-packed (hcp) and fcc structures since the hcp/fcc energy difference is the dominant factor that determines the SFE value.28 The calculated hcp/fcc energy difference (∆Efcc→hcp) in the CoCrFeMnNi HEA is −814 J/mol at 0 K, which means that hcp is a more stable structure than fcc for the CoCrFeMnNi HEA at absolute zero temperature. We believe the higher stability of hcp than fcc yields a low SFE and eventually leads to the easy formation of micro-twins in the HEA during deformations at 77 K. The same quantity (∆Efcc→hcp) for the other alloys, Fe-50Ni, Co-50Ni and 100Ni, are 239, 794 and 1930 J/mol, respectively. One can see that the micro-twining tendency shown in Fig. 2 can be well explained by the calculated hcp/fcc energy difference in the individual alloys. In the present study, the hcp/fcc energy difference is calculated by comparing the 0 K energy of randomly generated hcp and fcc alloys using the molecular statics. It is hard to estimate the error range of the calculation for the five component alloys. However, it can be noted here that the present interatomic potential reproduces the hcp/fcc energy differences for pure elements well. The calculated ∆Efcc→hcp for Co, Cr, Fe Mn and Ni by the present potential is −349, −2711, −1797, −735, + 1996 J/mol, respectively, while the CALPHAD thermodynamic calculation30 yields −428, −2846, −2243, −1000 and +1046 J/mol for the same quantities. Since the heat of mixing of solid solution phases in the constituent ten binary systems are also reasonably reproduced,17,18,19,20,21,22,23,24 it is expected that the accuracy level in the calculation for the five component alloys would be reasonable. It should be noted here that a negative value of ∆Efcc→hcp for the CoCrFeMnNi HEA has been also reported from an ab initio calculation.31,32
Solid solution hardening—effect of individual elements
The CoCrFeMnNi HEA is a highly alloyed material, and a severe lattice distortion and high solid solution hardening effect have been expected.14,33 However, the effect of individual elements on the strength, which is highly necessary for an alloy design of HEAs with an improved strength, is insufficiently known. One study presented a systematic report for the effect of individual elements on the strength of this alloy: the yield strength (YS) of the CoCrFeNi, CoCrMnNi, CoFeMnNi HEA as well as the CoCrFeMnNi HEA.34 The former three alloys are equiatomic quaternary alloys obtained by removing Mn, Fe and Cr one by one from the CoCrFeMnNi HEA. The YS of two binary alloys, Fe-50Ni and Co-50Ni, was also presented in the same study.34 According to this work, the YS of the alloys decreased in the following order: CoCrMnNi > CoCrFeNi > CoCrFeMnNi > Fe-50Ni > CoFeMnNi > Co-50Ni.
In this study, we wanted to confirm whether our potential reproduces well the above mentioned order in YS among the alloys considered and to analyze the effect of alloying elements on the YS in more detail by calculating the CRSS of individual alloys. For this, we used the method proposed by Osetsky and Bacon,35 inserting a single straight edge dislocation in a perfect fcc crystal, as shown in Fig. 3a. The initial, perfect fcc crystal was prepared by depositing (111) atomic layers along the y-axis. The sample size was 305 Å × 622 Å × 13 Å, with 215,100 atoms. The simulation method was similar to that described above for the tensile simulation, but the direction of rigid displacement was along the x-axis, not the y-axis. Periodic boundary conditions were applied along x-axis and z-axis and the change in sample dimension along the y-axis was allowed during the simulation. The stress–strain curves obtained for individual alloys are presented in Fig. 3b. Since our simulation was performed with a single crystal sample with a sufficient size involving one dislocation, there could be no work hardening effect (as shown in the simulated stress–strain curves). Therefore, the CRSS values were determined as the average of flow stresses after yielding in the stress–strain curves. According to our calculation, the CRSS of the alloys had the following order: CoCrFeNi > CoCrMnNi > CoCrFeMnNi > Fe-50Ni > CoFeMnNi > Co-50Ni. The agreement with an experiment, CoCrMnNi > CoCrFeNi > CoCrFeMnNi > Fe-50Ni > CoFeMnNi > Co-50Ni,34 was good even though it was not perfect. We could not perform the same calculation for the CrFeMnNi and CoCrFeMn alloys, which are the quaternary alloys obtained by removing Co and Ni one by one from the CoCrFeMnNi HEA because the CoCrFeMnNi HEA becomes unstable when Co or Ni is removed, which we believe is also the reason there is no experimental information on those quaternary alloys. Instead of removing Co or Ni, we changed the content by 10at% and calculated the CRSS to investigate the influence of Co and Ni. The resultant stress–strain curves are compared with that of CoCrFeMnNi HEA in Fig. 3c, d.
Simulation of shear deformation. a schematic diagram for the simulation of shear deformation. b simulated shear stress–strain curves of the 0Cr, 0Fe, 0Mn, Co-50Ni, Fe-50Ni alloys and the CoCrFeMnNi HEA at 0 K. c simulated shear stress–strain curves of the 10Co and 30Co alloys at the same temperature compared to the CoCrFeMnNi HEA. d simulated shear stress–strain curves of the 10Ni and 30Ni alloys at the same temperature compared to the CoCrFeMnNi HEA
It should be mentioned here that the simulated CRSS values (order of GPa) are much higher than experimental YS values (order of 100 MPa). This is because of the simulation temperature and strain rate which are far from experimental conditions. The present simulation was performed at 0 K, while the experimental values were obtained at finite temperatures. Although it would be more natural to perform the simulation at finite temperatures, the strain rate in the present type of MD simulations is unrealistically high (order of 107–109) compared to the experiments (order of 10−4–10−2). Since significant strain rate dependence is often observed at finite temperature simulations, a method that does not consider the thermal activation and is less sensitive to strains rate is necessary. Therefore, in order to avoid probable artifacts that may come from the high strain rate, 0 K or a very low temperature is usually chosen in this type of MD simulation. In this study, a 0 K molecular statics simulation with a conjugate-gradient scheme was used. An important point here is that all the alloys were simulated under the same conditions.
It should be further mentioned here that there is a theoretical work on the solid solution strengthening based on an effective matrix scheme from Curtin and coworkers,36 which accurately predicts the absolute values of YS. However, this work is applicable only to the solution hardening, while atomistic simulations that utilize the present interatomic potential can cover much wider range of material properties with an accuracy level applicable to real alloy design, as described in the next section.
Non-equiatomic HEAs with higher strength—design and experimental confirmation
The CoCrFeMnNi HEA has an excellent balance of strength and ductility, especially at 77 K. The low temperature ductility (elongation of over 70% at 77 K) looks sufficient, while a further increase in strength would extend the application range. Therefore, we attempted to design non-equiatomic HEAs stronger than the equiatomic CoCrFeMnNi alloy. Since the present atomistic simulation proved to predict the effect of alloying elements on the solid solution hardening correctly, we intended to fully utilize the simulation results on the CRSS. For this, we derived an empirical equation that predicts the CRSS value for a given composition in the following form:
Here, “3.0” is the CRSS of the CoCrFeMnNi equiatomic HEA, and the numeric values of the coefficients for individual elements (0.1195, 0.1203, etc.) were determined by fitting the calculated CRSS values for various compositions (as shown in Fig. 3). More details of the fitting procedure and fitting results are presented in the supplementary information of this manuscript.
We used Eq. (1) to estimate the relative (not absolute) strength of solid solution hardening effect in non-equiatomic HEAs at arbitrary compositions. Its validity would remain only in quaternary and quinary alloys because the data points used in fitting were for those alloys. However, we emphasize here that Eq. (1) predicts the well-known fact that the CoCrNi ternary alloy is stronger than other quaternary or quinary alloys in this alloy system.37
Concerning the mechanical strength, in the present work, we focused only on the solid solution hardening effect without considering other strengthening mechanisms that come from the existence of a second phase. Therefore, we confined the alloy design only to fcc single phase alloys. It was necessary to predict the fcc single phase region on the phase diagram of the quinary alloy system. For this, we used the CALPHAD computational thermodynamic approach.38 The software Thermo-Calc39 and the thermodynamic database TCFE2000 and its upgraded version40,41 have been used for thermodynamic calculations on HEAs.42,43 Recently, this thermodynamic database was further upgraded in a way that improved the description for the sigma phase and was used in the present work. Details of the upgrade of the thermodynamic database will be reported separately, later on (Choi, W.-M. and Lee, B.-J., 2017, POSTECH, unpublished work).
Figure 4 shows the present strategy for the alloy design of non-equiatomic HEAs stronger than the equiatomic CoCrFeMnNi alloy. Here, calculated equilibrium phase diagrams at 1023 K based on 20Co-20Cr, 10Co-25Cr, 20Co-25Cr (at%) and the variable fractions of Fe, Mn, Ni overlap with the predicted CRSS contour lines. The yellow area indicates the fcc single phase region and alloys with compositions in this region are expected to have fcc single phase microstructures from 1023 K to the melting temperature. The “●” mark in each diagram represents the alloy composition selected in the present study for experimental verification. For example, the alloy marked in Fig. 4a corresponds to the equiatomic CoCrFeMnNi HEA, and the predicted CRSS is around 3 GPa. The other alloys, designated HEA1 and HEA2 in Fig. 4b, c, respectively, are non-equiatomic alloys predicted to be stronger than the equiatomic alloy while the fcc single phase microstructure is maintained.
Alloy Design of Non-equiatomic HEAs with higher strength. a-c equilibrium phase diagrams at 1023 K obtained when mole fractions of Fe, Mn, Ni are varied in an alloy containing 20Co-20Cr, 10Co-25Cr and 20Co-25Cr (at%), respectively, overlapped with the predicted CRSS. The yellow area represents the fcc single-phase region
For the selected alloys (equiatomic HEA, HEA1 and HEA2), we performed a series of experimental examinations to confirm if both of the non-equiatomic alloys have an fcc single phase microstructure and higher strength than the equiatomic alloy. For the X-ray diffraction (XRD) analysis, we used samples annealed at 1173 K. However, for the tensile test, we had to control the annealing temperature (1073~1223 K) to maintain a similar grain size in each sample and minimize the grain size effect on the strength of individual alloys. Fig. 5a shows the XRD patterns of all the selected alloys annealed at 1173 K. Only fcc peaks are observed, which indicates that all the selected alloys indeed had a fcc single phase microstructure in the present process temperature range. Fig. 5b, c show stress–strain curves at RT and the microstructures of the alloys annealed at various temperatures to control the grain size, as mentioned above. The designed alloy composition and predicted CRSS, annealing temperature, measured YS and grain size are listed in Table 1. As expected, both the HEA1 and HEA2 have higher YS than the CoCrFeMnNi HEA, and HEA2 is stronger than HEA1. Although there are still some differences in the grain size among the alloys even with the controlled annealing, its effect on the YS does not appear to be decisive in these alloys within the present grain size range. The YS of the HEA1 varies between 466 and 470 MPa for the grain size in the range of 2.61–5.44 μm. The difference among alloys in the tensile strength is shown more clearly in Fig. 5b. The fcc single phase microstructure and increased strength of the designed alloys indicate the validity of the present atomistic approach as an alloy design tool of the HEAs, in combination with the CALPHAD thermodynamic calculation technique.
XRD patterns, tensile properties and microstructures of selected alloys. a XRD patterns of the HEAs annealed at 1173 K. b room-temperature stress–strain curves of HEAs annealed at various temperatures to maintain similar grain sizes. c EBSD IPF maps of HEAs annealed at various temperatures to maintain similar grain sizes
In summary, we used an atomistic simulation technique to clarify fundamental reasons for the sluggish diffusion and micro-twining at cryogenic temperatures (typically 77 K) and to investigate the effect of individual elements on solid solution hardening. The vacancy migration energy barrier in the CoCrFeMnNi HEA showed a large scattering in the peak height, and a significant amount of stable vacancy sites probably caused the sluggish diffusion. For the equiatomic CoCrFeMnNi HEA, the hcp structure was predicted to be more stable than the fcc structure at 0 K, which is expected to yield a low SFE and to activate the micro-twinning at cryogenic temperatures. The predicted alloying effect on the CRSS was used to design non-equiatomic fcc HEAs with improved strength over the equiatomic CoCrFeMnNi HEA, and the validity of the computational approach was proved experimentally. The proposed atomistic approach reproduced fundamental structural properties (lattice parameter, structural stability and diffusion) of the CoCrFeMnNi HEA in good agreement with experimental information, as well as the alloying effect on the solid solution hardening (CRSS). This approach can be further utilized for more elaborate alloy and process design of new HEAs with advanced properties.
Methods
The CoCrFeMnNi quinary interatomic potential
Completion of 2NN MEAM potential for the CoCrFeMnNi quinary system requires potential parameter sets for constituent unary, binary and ternary systems. The potentials of all the unary elements, Co,21 Cr,17,23 Fe,17 Mn,20 Ni19 and all the binary systems, Co–Cr,23 Co–Fe,23 Co–Mn,23 Co–Ni,22 Cr–Fe,18 Cr–Mn,23 Cr–Ni,24 Fe–Mn,20 Fe–Ni,24 Mn–Ni23 have already been published. Since the Cr–Fe–Ni ternary potential was also available,24 the remaining task for the completion of the quinary potential was to complete the potential parameter sets for the other nine ternary systems. For the completion of a ternary potential parameter set, three Cmin(i–j–k) and three Cmax(i–j–k) parameter values should be determined in addition to constituent unary and binary potential parameters. Those parameters represent the degree of screening by a third element atom (j) to the interaction between two neighboring atoms (i and k) of different types. Mechanically derived, assumed values have been assigned to those parameters,44,45,46 taking a kind of an average concept. In the present work, a similar approach was used to determine the Cmin and Cmax parameter values. Numerical values of the ternary parameters and the assumption made for each system is given as supplementary information (SI) of this manuscript. All potential parameters are also provided in a LAMMPS47 format in the SI. All calculations were performed with a radial cutoff distance of 4.5 Å.
Fabrication of the CoCrFeMnNi HEA, HEA1 and HEA2
We used compact vacuum induction melting equipment (model; MC100V, Indutherm, Walzbachtal-Wossingen, Germany) in an argon atmosphere to fabricate the CoCrFeMnNi HEA, HEA1 and HEA2 from commercially pure elements (the purity of each raw material was at least 99.9%). The alloying of the raw elements was carried out in a ZrO2—coated Al2O3 ceramic crucible of a vacuum induction melting furnace. Before putting the Al2O3 crucible into the furnace, we removed the water vapor by heating it at 873 K for 1 h. We melted approximately 150 g of master alloys and poured it into a rectangular graphite module with a length of 100 mm, width of 35 mm, and thickness of 8 mm. Before melting the samples, we evacuated the furnace chamber to 6 × 10−2 Pa and backfilled it with high-purity argon gas to 0.06 MPa. Then, we homogenized the ingots at 1373 K for 6 h, pickled in 20% HCl and milled to a thickness of 7 mm, and rolled the pickled ingots to a thickness of 2 mm at RT (reduction ratio; 75%). We obtained fully recrystallized microstructures by annealing the sheets at 1073, 1173 and 1223 K for 10 min and water quenched.
Microstructure characterization and mechanical property tests
We used an XRD (Cu Kα radiation, scan rate; 2 deg min−1, scan step size; 0.02 deg) technique to identify the phases present in the alloy sheets. We also conducted an EBSD analysis (step size; 0.12 μm) by a field emission scanning electron microscope (Quanta 3D FEG, FEI Company, USA), after performing a mechanical and electro-polishing on the EBSD specimens at RT in a solution of CH3COOH (92%) and HClO4 (8%) with an operating voltage of 32 V. We used an orientation imaging microscopy analysis software (TexSEM Laboratories, Inc.) to interpret the EBSD data. The mechanical property tests were carried out using a universal testing machine (model; 8801, Instron, Canton, MA, USA) of 100 kN capacity. The crosshead speed was 6.4 × 10−3 mm/s. and the tests were performed at RT on plate-type sub-sized tensile specimens with a gage length of 6.4 mm, gage width of 2.5 mm and gage thickness of 1.5 mm.
Data availability
The authors declare that the data supporting the findings of this study are available within the paper, and the specific information for evaluation of the randomness of atomic distribution and empirical equation for the prediction of CRSS are available in its supplementary information file. 2NN MEAM library/parameter files are also available in supplementary information in the LAMMPS format.
References
Miracle, D. B. et al. Exploration and development of high entropy alloys for structural applications. Entropy 16, 494–525 (2014).
Otto, F. et al. The influences of temperature and microstructure on the tensile properties of a CoCrFeMnNi high-entropy alloy. Acta Mater. 61, 5743–5755 (2013).
Gali, A. & George, E. P. Tensile properties of high-and medium-entropy alloys. Intermetallics 39, 74–78 (2013).
Gludovatz, B. et al. A fracture-resistant high-entropy alloy for cryogenic applications. Science 345, 1153–1158 (2014).
Yao, M. J., Pradeep, K. G., Tasan, C. C. & Raabe, D. A novel, single phase, non-equiatomic FeMnNiCoCr high-entropy alloy with exceptional phase stability and tensile ductility. Scr. Mater. 72–73, 5–8 (2014).
Pradeep, K. G. et al. Non-equiatomic high entropy alloys: approach towards rapid alloy screening and property-oriented design. Mater. Sci. Eng. A 648, 183–192 (2015).
Li, Z., Pradeep, K. G., Deng, Y., Raabe, D. & Tasan, C. C. Metastable high-entropy dual-phase alloys overcome the strength–ductility trade-off. Nature 534, 277–230 (2016).
Jo, Y. H. et al. Cryogenic strength improvement by utilizing room-temperature deformation twinning in a partially recrystallized VCrMnFeCoNi high-entropy alloy. Nat. Commun. 8, 15719 (2017).
Li, Z. & Raabe, D. Strong and ductile non-equiatomic high-entropy alloys: design, processing, microstructure, and mechanical properties. JOM 69, 2099–2106 (2017).
Tsai, M.-H. Three strategies for the design of advanced high-entropy alloys. Entropy 18, 252–265 (2016).
Tsai, K.-Y., Tsai, M.-H. & Yeh, J.-W. Sluggish diffusion in Co–Cr–Fe–Mn–Ni high-entropy alloys. Acta Mater. 61, 4887–4897 (2013).
Chen, W. & Zhang, L. High-throughput determination of interdiffusion coefficients for Co-Cr-Fe-Mn-Ni high-entropy alloys. J. Phase Equilibria Diffus. 38, 457–465 (2017).
Vaidya, M., Trubel, S., Murty, B. S., Wilde, G. & Divinski, S. V. Ni tracer diffusion in CoCrFeNi and CoCrFeMnNi high entropy alloys. J. Alloys Compd. 688, 994–1001 (2016).
Yeh, J.-W. Physical metallurgy of high-entropy alloys. JOM 67, 2254–2261 (2015).
Laplanche, G., Kostka, A., Horst, O. M., Eggeler, G. & George, E. P. Microstructure evolution and critical stress for twinning in the CrMnFeCoNi high-entropy alloy. Acta Mater. 118, 152–163 (2016).
Lee, B.-J. & Baskes, M. I. Second nearest-neighbor modified embedded-atom method potential. Phys. Rev. B. 62, 8564–8567 (2000).
Lee, B.-J., Baskes, M. I., Kim, H. & Cho, Y. K. Second nearest-neighbor modified embedded atom method potentials for BCC transition metals. Phys. Rev. B 64, 184102 (2001).
Lee, B.-J., Shim, J.-H. & Park, H. M. A semi-empirical atomic potential for the fe-cr binary system. Calphad 25, 527–534 (2001).
Lee, B.-J., Shim, J.-H. & Baskes, M. I. Semi-empirical atomic potentials for the FCC metals Cu, Ag, Au, Ni, Pd, Pt, Al and Pb based on first and second nearest-neighbor modified embedded atom method. Phys. Rev. B 68, 144112 (2003).
Kim, Y.-M., Shin, Y.-H. & Lee, B.-J. Modified embedded-atom method interatomic potentials for pure Mn and Fe-Mn system. Acta Mater. 57, 474–485 (2009).
Dong, W.-P., Kim, H.-K., Ko, W.-S., Lee, B. M. & Lee, B.-J. Atomistic modeling of pure Co and Co-Al system. Calphad 38, 7–16 (2012).
Kim, Y.-K., Jung, W.-S. & Lee, B.-J. Modified embedded-atom method interatomic potentials for the Ni-Co binary and the Ni-Al-Co ternary systems. Model. Simul. Mater. Sci. Eng. 23, 055004 (2015).
Choi, W.-M., Kim, Y. M., Seol, D. H. & Lee, B.-J. Modified embedded-atom method interatomic potentials for the Co-Cr, Co-Fe, Co-Mn, Cr-Mn and Mn-Ni binary systems. Comput. Mater. Sci. 130, 121–129 (2017).
Wu, C., Lee, B.-J. & Su, X. Modified embedded-atom interatomic potential for Fe-Ni, Cr-Ni and Fe-Cr-Ni systems. CALPHAD 57, 98–106 (2017).
Bhattacharjee, P. P. et al. Microstructure and texture evolution during annealing of equiatomic CoCrFeMnNi high-entropy alloy. J. Alloys Compd. 587, 544–552 (2014).
Stepanov, N. D. et al. Effect of V content on microstructure and mechanical properties of the CoCrFeMnNiVx high entropy alloys. J. Alloys Compd. 628, 170–185 (2015).
Zaddach, A. J., Niu, C., Koch, C. C. & Irving, D. L. Mechanical properties and stacking fault energies of NiFeCrCoMn high-entropy alloy. JOM 65, 1780–1789 (2013).
Huang, S. et al. Temperature dependent stacking fault energy of FeCrCoNiMn high entropy alloy. Scr. Mater. 108, 44–47 (2015).
Song, H. et al. Local lattice distortion in high-entropy alloys. Phys. Rev. Mater. 1, 023404 (2017).
Dinsdale, A. T. SGTE data for pure elements. Calphad 15, 317–425 (1991).
Ma, D., Grabowski, B., Körmann, F., Neugebauer, J. & Raabe, D. Ab initio thermodynamics of the CoCrFeMnNi high entropy alloy: Importance of entropy contributions beyond the configurational one. Acta Mater. 100, 90–97 (2015).
Li, Z., Kormann, F., Grabowski, B., Neugebauer, J. & Raabe, D. Ab initio assisted design of quinary dual-phase high-entropy alloys with transformation-induced plasticity. Acta Mater. 136, 262–270 (2017).
Oh, H. S. et al. Lattice distortions in the FeCoNiCrMn high entropy alloy studied by theory and experiment. Entropy 18, 321–329 (2016).
Wu, Z., Bei, H., Pharr, G. M. & George, E. P. Temperature dependence of the mechanical properties of equiatomic solid solution alloys with face-centered cubic crystal structures. Acta Mater. 81, 428–441 (2014).
Osetsky, Y. N. & Bacon, D. J. An atomic-level model for studying the dynamics of edge dislocations in metals. Model. Simul. Mater. Sci. Eng. 11, 427–446 (2003).
Varvenne, C., Luque, A. & Curtin, W. A. Theory of strengthening in fcc high entropy alloys. Acta Mater. 118, 164–176 (2016).
Gludovatz, B. et al. Exceptional damage-tolerance of a medium-entropy alloy CrCoNi at cryogenic temperatures. Nat. Commun. 7, 10602 (2016).
Lukas, H. L., Fries, S. G. & Sundman, B. Computational Thermodynamics: The Calphad Method (Cambridge University Press, 2007).
Sundman, B., Jansson, B. & Andersson, J. O. The thermo-calc databank system. Calphad 9, 153–190 (1985).
TCFE2000: The Thermo-Calc Steels Database. Upgraded by B.-J. Lee, B. Sundman at KTH (KTH, Stockholm, 1999).
Chin, K. G., Lee, H. J., Kwak, J. H., Kang, J. Y. & Lee, B.-J. Thermodynamic calculation on the stability of (Fe,Mn)3AlC carbide in high aluminum steels. J. Alloys Compd. 505, 217–223 (2010).
Choi, W.-M., Jung, S., Jo, Y. H., Lee, S. & Lee, B.-J. Design of new face-centered cubic high entropy alloys by thermodynamic calculation. Met. Mater. Int. 23, 839–847 (2017).
Park, N., Lee, B.-J. & Tsuji, N. The phase stability of equiatomic CoCrFeMnNi high-entropy alloy: Comparison between experiment and calculation results. J. Alloys Compd. 719, 189–193 (2017).
Kim, H.-K., Jung, W.-S. & Lee, B.-J. Modified embedded-atom method interatomic potentials for the Fe-Ti-C and Fe-Ti-N systems. Acta Mater. 57, 3140–3147 (2009).
Ko, W.-S. & Lee, B.-J. Modified embedded-atom method interatomic potentials for pure Y and the V–Pd–Y ternary system. Model. Simul. Mater. Sci. Eng. 21, /8 (2013).
Dong, W.-P., Lee, B.-J. & Chen, Z. Atomistic modeling for interfacial properties of Ni-Al-V ternary system. Met. Mater. Int. 20, 423–429 (2014).
Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19 (1995).
Acknowledgements
This research was supported by the Future Material Discovery Program of the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT of Korea (2016M3D1A1023383).
Author information
Authors and Affiliations
Contributions
B.-J.L. and S.L. designed the research, W.-M.C. performed the simulation, and Y.H.J. and S.S.S. performed the experimental study. All authors analyzed and interpreted the data. W.-M.C., Y.H.J. and B.-J.L. drafted the manuscript, and all authors edited the final submission.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Choi, WM., Jo, Y.H., Sohn, S.S. et al. Understanding the physical metallurgy of the CoCrFeMnNi high-entropy alloy: an atomistic simulation study. npj Comput Mater 4, 1 (2018). https://doi.org/10.1038/s41524-017-0060-9
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-017-0060-9
This article is cited by
-
Serrated plastic flow in deforming complex concentrated alloys: universal signatures of dislocation avalanches
Journal of Materials Science: Materials Theory (2024)
-
Unlocking enhanced thermal conductivity in polymer blends through active learning
npj Computational Materials (2024)
-
Lattice distortion enabling enhanced strength and plasticity in high entropy intermetallic alloy
Nature Communications (2024)
-
Active learning of ternary alloy structures and energies
npj Computational Materials (2024)
-
Local Nanostructure in Multicomponent High-Entropy Materials
High Entropy Alloys & Materials (2024)