Abstract
Element sulfur in nature is an insulating solid. While it has been tested that one-dimensional sulfur chain is metallic and conducting, the investigation on two-dimensional sulfur remains elusive. We report that molybdenum disulfide layers are able to serve as the nanotemplate to facilitate the formation of two-dimensional sulfur. Density functional theory calculations suggest that confined in-between layers of molybdenum disulfide, sulfur atoms are able to form two-dimensional triangular arrays that are highly metallic. As a result, these arrays contribute to the high conductivity and metallic phase of the hybrid structures of molybdenum disulfide layers and two-dimensional sulfur arrays. The experimentally measured conductivity of such hybrid structures reaches up to 223 S/m. Multiple experimental results, including X-ray photoelectron spectroscopy (XPS), transition electron microscope (TEM), selected area electron diffraction (SAED), agree with the computational insights. Due to the excellent conductivity, the current density is linearly proportional to the scan rate until 30,000 mV s−1 without the attendance of conductive additives. Using such hybrid structures as electrode, the two-electrode supercapacitor cells yield a power density of 106 Wh kg−1 and energy density ~47.5 Wh kg−1 in ionic liquid electrolytes. Our findings offer new insights into using two-dimensional materials and their Van der Waals heterostructures as nanotemplates to pattern foreign atoms for unprecedented material properties.
Similar content being viewed by others
Introduction
Element sulfur in nature is an insulating solid consisting of rings of S atoms.1 However, at high pressures (e.g., exceeding 90 GPa), it transforms from an insulator to a metallic phase accompanied by a crystallographic change to a base-center orthorhombic structure.1,2,3,4 At 93 GPa and below a critical temperature (e.g., 10 K), the metallic phase sulfur could even transform into a superconductor.5 These phenomena indicate that the metallic property of sulfur is highly related to its crystallographic morphology.
Base-centered orthorhombic crystal could be considered as an assembly of layers of atoms that are arranged in a triangular pattern. Hypothetically, one could consider each layer as an array of one-dimensional (1D) linear or zigzag atomic chains. In the case of sulfur, this 1D crystallographic morphology renders a finite electronic density of states (DOS) near the Fermi level. Therefore 1D atomic sulfur chains have been predicted as metallic phase.6,7,8 However, the experimental synthesis of metallic phase 1D atomic sulfur has not been reported until decades after the theoretical prediction, largely because of the difficulties to stabilize 1D chains without any physical confinements. Experimentally metallic phase 1D atomic sulfur chain has been realized inside a carbon nanotube.9 The steric constraints from carbon nanotubes with diameter of ~1 nm makes them the suitable candidate as host materials. Nevertheless, to the best of our knowledge, to date the theoretical and experimental reports on the electronic properties of two-dimensional (2D) atomic sulfur remain elusive. Compared with 1D case, experimentally it is even more challenging to identify a suitable host material to preserve the atomic sulfur in a 2D form.
Molybdenum disulfide (MoS2) has a crystal structure with weakly coupled layers where a layer of Mo atoms is sandwiched between two layers of S atoms. These S atoms are triangularly patterned within each layer with an atomic spacing around 0.32 nm. Since each S atom has a Van der Waals interaction equilibrium radius10 around 0.4 nm, above which attraction dominates and below which repulsion dominates, the triangularly patterned S atoms induce triangularly distributed spatial locations of Van der Waals interaction equilibrium over the surface of MoS2. It is thus promising to take advantage of these spatial locations to trap and confine another layer of S atoms. In this paper, density functional theory (DFT) calculations indicate that highly conducting and metallic 2D atomic S layers are able to exist by using MoS2 as nanotemplate. Confined in-between MoS2 layers, S atoms are arranged into a two-dimensional triangular array, inheriting the intrinsic triangular pattern of atomic S layer of MoS2. We have further experimentally synthesized the proposed hybrid structures composed of alternating MoS2 layers and 2D atomic S layers. Multiple experimental measurements confirm the computational predictions. The as-prepared samples exhibit exceptional conductivity up to 223 S/m. The application of our sample to supercapacitor has yielded an impressive high scan rate without the attendance of conductive additives.
Results and discussion
We first investigate the electronic properties of two-dimensional triangular array of S atoms with the atomic spacing (0.32 nm) comparable to the Mo–Mo in-plane spacing in MoS2. From the electronic band structure and electronic DOS calculation (Fig. 1a), it is interesting to realize that two-dimensional triangular array of S atoms displays highly metallic feature. The DOS near Fermi level is contributed from the p orbitals of S atoms (Supplementary Figure 1). We next calculate the band structure and DOS of monolayer 2H phase Molybdenum disulfide (2H–MoS2) with Mo–Mo spacing of 0.32 nm. It is well known that 2H–MoS2 is a semiconductor, in accordance with Fig. 1b which shows that it has a band gap about 1.8 eV, agreeing well with literature reported data.11 Figure 1c shows the geometry optimized structure of a triangular array of S atoms positioned on a monolayer 2H-MoS2 and its associated band structure and DOS. It is immediately found that the entire hybrid structure becomes metallic. The triangularly patterned S atoms contribute a significant amount to the DOS near Fermi level. Compared with the DOS of pure atomic S layer as shown in Fig. 1a, the DOS of atomic S layer templated by 2H-MoS2 has preserved key features around the Fermi level. For example, its peak DOS is still positioned quite close to the Fermi level, although there is a tiny shift (about −0.1 eV) below Fermi energy. In addition, there is still a peak at around 0.6 eV although there is a new peak emerging near the peak DOS. Nevertheless, it again indicates clearly that the metallicity of the array of triangularly patterned S atoms could be still in effect in the presence of monolayer 2H–MoS2. Hereinafter we refer to such structure as monolayer 2H–MoS2–S, and the triangularly patterned S atom as S1 atom, the other S atoms from MoS2 as S2 and S3 atom, as labeled in Fig. 1c. The vertical distance between S1 and S2 atom determined from structure optimization is around 0.31 nm, which is much longer than the typical S–S covalent bond length (around 0.2 nm),12 suggesting a non-bonded interaction type between S1 and S2 atom. Charge analysis suggests that in the current configuration S1 atom has a small negative charge of −0.015\(\left| e \right|\), while −0.092\(\left| e \right|\) for atom S2, −0.102\(\left| e \right|\) for atom S3 and 0.209\(\left| e \right|\) for atom Mo (Supplementary Figure 2). Atom Mo has roughly about twice the magnitude of charge than that of S2 (or S3), indicating that the structural integrity of 2H–MoS2 remains almost intact. It also indicates that the S1 atom has taken away some electrons from the monolayer 2H–MoS2 which is initially charge neutral. Such charge transfer results in a similar effect as p-type doping for monolayer 2H–MoS2. As a result, in the band structure (Fig. 1c), the Fermi level shifts downwards to the valence bands of 2H–MoS2. This is also manifested in the DOS where the Fermi level shifts left towards to the filled states of 2H–MoS2. The shifting of Fermi level allows the contribution from the atoms of 2H–MoS2 (e.g., d orbitals of Mo atom and p orbitals of S2 atom, Supplementary Figure 2) to the DOS near Fermi level. On the other hand, the array of S1 atoms, which is initially charge neutral, received electrons, which causes the Fermi level to shift towards the unfilled states of S1 atoms. Nevertheless in current configuration, such a shift is not as significant as that for 2H–MoS2. We further extend our calculation to hybrid structures composed of alternating 2H-MoS2 layers and 2D atomic S layers (Fig. 1d). Hereinafter we refer to such hybrid structure as layered 2H-MoS2-S. Similarly, the DOS plot and band structure suggest that arrays of S1 atoms are the dominating factor for the overall metallicity of the hybrid structure. In addition, d orbitals of Mo atom and p orbitals of S2 and S3 atoms contribute to the DOS near Fermi level (Supplementary Figure 3). Charge density contour plots confirm that the interactions between S1 atoms and S2 (S3) atoms are not covalent type (Supplementary Figure 3).
Top view, side view, band structure and Density of States (DOS) of four structures. The dashed line indicates the Fermi level. a Array of triangularly-patterned S atoms. S–S distance is fixed to be 0.32 nm. It is found that such a structure is highly metallic. b Monolayer 2H–MoS2. Mo–Mo distance is fixed to be 0.32 nm. It is found that such a structure has a bandgap ~1.8 eV. c Triangularly-patterned S atoms positioned on monolayer 2H phase MoS2. Mo–Mo distance is fixed to be 0.32 nm. The vertical distance between S1 and S2 is 0.31 nm, which is determined from structure optimization. It is found that near Fermi level the S1 atom contributes most to the DOS. d Hybrid structure of alternating 2H–MoS2 layers and 2D atomic S layers. Mo–Mo distance is fixed to be 0.32 nm. It is found that near Fermi level the atom S1 contributes most to the DOS
The arrays of S1 atoms are metallic on a range of inter-atomic spacing that is potentially compatible with the MoS2 nanotemplate (Fig. 2a and Supplementary Figure 4). To account for the influence of inter-atomic spacing on the electronic properties of arrays of S1 atoms in the presence of layers of 2H–MoS2, we further calculate the DOS and band structures of layered 2H–MoS2–S for a variety of external hydrostatic pressures ranging from 15 to 35 GPa. The Mo–Mo out-of-plane distance decreases from about 0.77 to 0.735 nm while the Mo–Mo in-plane distance decreases from about 0.305 to 0.295 nm as the pressure increases (Fig. 2b). The associated DOS and band structures (Fig. 2c and Supplementary Figure 5) show that these 2H–MoS2–S structures are metallic. The arrays of S1 atoms are still the dominating factor for the overall metallicity. Charge analysis suggests that the magnitude of the negative charge on S1 atom decreases as the pressure increases (Supplementary Figure 5). Such observation suggests that the pressure-induced mechanical deformation could make the S1 atom layers be closer to “pure atomic sulfur arrays”, which in principle do not carry charge. The pressure-induced decrease in the magnitude of charge of S1 atom is closely related to anti-bonding molecular orbitals between S1 and S2 (S3) layers, since it is not favorable for the formation of strong covalent interactions between S1 and S2 (S3) layers. As the spacing between S1 and S2 (S3) layers decreases, the increase in the magnitude of negative charge of S1 layers implies more electrons are shared between S1 and S2 (S3) layers and thus a stronger covalent interactions between S1 and S2 (S3) layers, which is not true. Compared with the case with zero pressure (Fig. 1d), the Fermi level shifts further towards the filled states of 2H–MoS2. As a result, the Mo and S atoms in 2H–MoS2 are contributing a lot more to the available states for occupation near Fermi level with increased pressure. On the other hand, with increased pressure the Fermi level shifts a noticeable amount (compared with Fig. 1d) further towards the unfilled states of S1 atoms.
a DOS demonstrating metallicity of array of triangularly patterned S atoms with varying inter-atomic spacing. b The variation of Mo-Mo out-of-plane and in-plane distance in hybrid structures of alternating 2H-MoS2 layers and 2D atomic S layers as a function of external hydrostatic pressure. c DOS showing metallicity of hybrid structures of alternating 2H–MoS2 layers and 2D atomic S layers with varying external hydrostatic pressure. d The variation of Mo–Mo out-of-plane and in-plane distance in hybrid structures of alternating 1T-MoS2 layers and 2D atomic S layers as a function of external hydrostatic pressure. e DOS showing metallicity of arrays of hybrid structures of alternating 1T-MoS2 layers and 2D atomic S layers with varying external hydrostatic pressure
It is reported that there could exist phase transition of MoS2 from stable semiconductor 2H–MoS2 to meta-stable metallic 1T–MoS2 through the sliding of S plane.13 In addition, experimentally and computationally it has demonstrated that external high pressure (~19 to 40 GPa) could induce the semiconducting to metallic transition.14 Since the surface S atoms in 1T–MoS2 are also triangularly patterned, it could therefore also possibly template an additional layer of S1 atoms. To account for the electronic properties of arrays of S1 atoms in the presence of layers of meta-stable 1T–MoS2, we also calculate the DOS and band structures of layered 1T–MoS2-S for a variety of external hydrostatic pressures ranging from 15 to 35 GPa. The Mo-Mo out-of-plane distance decreases from about 0.71 to 0.68 nm while the Mo–Mo in-plane distance decreases from about 0.315 to 0.305 nm as the pressure increases (Fig. 2d). Compared with 2H–MoS2–S case, the Mo–Mo out-of-plane distance of 1T–MoS2–S is relatively smaller. Since 1T–MoS2 itself is metallic, the layered 1T–MoS2–S under pressure is calculated to be metallic (Fig. 2e) as expected. Charge analysis suggests that the magnitude of the negative charge on S1 atom decreases as the pressure increases (Supplementary Figure 6). Compared with Mo atom, the S1 atom contributes almost the same amount to the DOS near Fermi level. A further comparison between the DOS of layered 1T–MoS2–S with layered 1T–MoS2 shows that for each atom type the shifting of Fermi level does not change significantly the DOS near Fermi level (Supplementary Figure 7). This means that the presence of S1 atoms provides extra available states for occupation at Fermi level in addition to the already existing states contributed from 1T–MoS2.
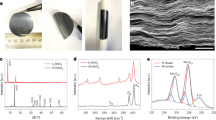
We have made experimental efforts to synthesize the predicted materials MoS2–S. We have successfully isolated these materials in the transitional period from MoS3 to MoS2 by carefully controlling the reaction time and reductant quantity. The synthesis involves high pressure treatment in autoclave. The preparation method is described in detail in the experimental section. We find that the as-prepared MoS2–S possesses high conductivity that is five orders of magnitude higher than that of semiconducting 2H–MoS2, confirming the exceptional metallicity contributed from the two-dimensional triangular array of sulfur atoms. Excellent conductivity of 223 S/m is obtained using four-probe measurement on 200 nm thickness of MoS2–S film (Fig. 3a). The conductivity is five orders of magnitude higher than that of semiconducting phase 2H–MoS2 15 as the counterpart semiconducting phase 2H–MoS2 has almost zero current due to its intrinsic insolating nature. X-ray photoelectron spectroscopy spectra of MoS2–S is presented in Fig. 3b and Supplementary Figure 8. We find the ratio of Mo to S is 1:3 by X-ray photoelectron spectroscopy (XPS). This ratio has an excellent agreement with our computational model. Furthermore this ratio is consistent with EDX (energy dispersive X-Ray spectroscopy) by HRTEM (high resolution transmission electronic microscopy) (Supplementary Figure 9), which has an excellent agreement with our computational structure model. Furthermore, as shown in Fig. 3c, the MoS2–S film possesses metallic luster. The material can work as a metallic mirror coating and clear “Huskies” picture could be reflected in this film (Fig. 3d and Supplementary Figure 10). These superior metallic features with high electrical conductivity and metallic luster of the MoS2–S, which are quite different from that of semiconducting phase MoS2, are attributed to the metallic two-dimensional sulfur arrays.
The property of as-prepared MoS2–S. a I-V curve of MoS2–S film measured by four probe measurement (film thickness 200 nm). b Sulfur spectrum in XPS of MoS2–S. c Film of MoS2-S presenting metallic luster. d “Huskies” picture reflected in this MoS2–S film. e UV-vis absorption spectroscopy of MoS2–S and 2H–MoS2. f Tyndall effect
The absorption spectrum of MoS2–S does not show salient absorption peaks but a monotonic change in visible light range, indicating its metallic property (Fig. 3e), which is different from that of semiconducting phase MoS2 in water.16, 17 Semiconducting phase MoS2 has two feature absorption peaks at 440 and 612 nm associated with the energy split from the valence band spin-orbital coupling in semiconducting MoS2 (Fig. 3e). We find that our as-prepared MoS2–S is able to exist as stable colloidal solution. As shown in Supplementary Figure 11, the as-prepared MoS2–S can be dispersed uniformly in water after sonication. The colloidal property is well illustrated by the Tyndall effect (Fig. 3f). Furthermore, zeta potential is measured in pure water and shows −51 mV for 0.25 mg ml−1 MoS2–S solution, indicating that the solution has good stability.
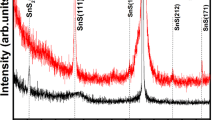
The unique structure and morphology of MoS2–S are confirmed with high resolution scan electronic microscopy (SEM) and atomic resolution spherical aberration–corrected transmission electron microscopy. Figure 4a shows that the as-prepared MoS2–S has a morphological feature of wrinkles and curvature, suggesting the 2D morphology. Figure 4b, c are low magnification TEM images further showing the nanosheets morphology and layered structure of the as-prepared MoS2-S. Figure 4d is the High resolution TEM image which shows the crystal lattice clearly (Supplementary Figure 12). We also observe the polycrystalline feature, which is consistent with SAED data showing the emerging of multiple rings and X-ray powder diffraction (XRD) with wide peak (Supplementary Figure 13). As shown in Fig. 4e, f, the Mo atoms are rather uniformly distributed along three directions and the Mo–Mo in-plane distance is measured to be around 0.265 and 0.3 nm, depending on the direction. We have also measured 0.27 and 0.32 nm in some other regions. Mo–Mo out-of-plane distance (the spacing between the Mo planes) in as-prepared MoS2–S is measured to be around 0.66 nm (Supplementary Figure 14). Based on these experimental measured distances, we are able to identify a 2H–MoS2–S structure that matches well with SAED (Fig. 4g, h and Supplementary Figure 15), further supporting the existence of our proposed structure in our as-prepared sample. Figure 4g shows the experimental measured diffraction pattern (SAED) of our as-prepared sample. Figure 4h shows the calculated diffraction intensities from the proposed structure with respect to the plane spacing. We can see that they are in good agreement since both are showing reflections at plane spacing at ~0.27 and ~0.16 nm. We believe there is possible residue compressive pressure in our locally crystalized MoS2–S structure, since the experimental measured Mo–Mo in-plane distance of as-prepared MoS2–S is on average much smaller than the typical Mo–Mo in-plane distance of MoS2.
The morphology and structure of conducting MoS2–S. a SEM image of MoS2–S. b Low magnification TEM image showing nanosheet morphology. c Low magnification TEM image displaying layered structure. d High resolution TEM image. e Crystal lattice is observed. Three directions marked by three arrows indicate the triangular atomic arrangement of Mo atoms of the region labeled by white box. f Magnified high resolution TEM image of the region labeled by the white box in e. The measured Mo–Mo distance along direction 1 and 2 is ~0.3 nm, and ~0.265 nm along direction 3. g TEM selected area electron diffraction (SAED) pattern. h Simulated diffraction pattern for 2H-MoS2-S structure. Scar bars: a 300 nm, b 100 nm, c 20 nm, d 2 nm, e 2 nm, f 1 nm
In addition to the excellent conductivity, as-prepared MoS2–S is hydrophilic and contact angle measurement is conducted using water droplet (Supplementary Figure 16). We also find that the contact angle in organic solvent is as small as 10 degrees, which demonstrates that MoS2–S has excellent compatibility with the electrolyte. The outstanding hydrophilic nature is conducive to obtain high performance for capacitance, while the other key factor is high conductivity. Therefore our prepared sample is promising to be used for supercapacitor application. On the other hand, recent study on graphene wrinkling has indicated that presence of wrinkling makes the surface of 2D materials hydrophobic.18 Therefore our current as-prepared sample has exhibited unexpected behaviors to this end. It might be possible that if more wrinkles appear on the sample surface, it becomes hydrophobic. Nevertheless, future work on the systematic investigation of effect of wrinkling topology is needed to gain thorough understanding.
The quest for both high power density and energy density is perpetual in energy storage; unfortunately, capacitance and scan rate are generally mutually exclusive. It is a huge challenge to obtain high rate and high capacitance simultaneously.19 To investigate the capacitive performance of MoS2-S, classical three-electrode system is conducted in aqueous 0.5 M H2SO4 electrolyte. MoS2–S solution is drop-cast on the glassy carbon without binder and conducting additive. Note that the MoS2-S firmly sticks on the glassy carbon due to the static electricity. Typical cyclic voltammetry (CVs) shows nearly rectangular shape until an ultrafast scan rate 100,000 mV s−1 with the absence of appreciable change (Supplementary Figure 17). Discharge current density preserves a linear relationship within 10 -100,000 mV s−1 (Supplementary Figure 18). To the best of our knowledge, the upper limit scan rate is the best even comparable to carbon nanotube and graphene.20, 21 This high rate result indicates that MoS2–S is indeed highly conductive. The metallic property and electrochemical impedance spectroscopy further confirm its practical use in capacitive application with low internal overall impedance within a wide range of frequency (Supplementary Figure 19). Considering the practical application of supercapacitor, we investigate symmetrical two electrode capacitors based on this conducting MoS2–S. The sample is directly loaded onto three dimensional highly compressible graphene foam electrodes (14 mm in diameter, 0.4 mg) without additives and binder, and two identical electrode are separated by porous glassy fiber paper. The capacitance contribution from graphene foam is negligible compared to MoS2–S for supercapacitor (Supplementary Figure 20). The physical composition itself acts as both working electrode and current collector. We adopt 1-Ethyl-3methylimidazolium tetrafluoroborate ([EMIM][BF4]) as electrolyte because it offers larger voltage window (2 V). From the CV curves, we find a perfect overlapping from the first to the tenth cycle shown in Supplementary Figure 21. Near perfect rectangular shapes (Fig. 5a–d) maintain until another ultra-high 30,000 mV s−1 scan rate is employed. This high scan rate property is mainly from MoS2–S other than graphene foam since we find the same high scan rate property without graphene foam in three electrodes measurement. A maximum specific capacitance of 200 F g−1 is reached under 10 mV s−1. Increasing the scan rate abruptly in a magnitude of 1000 -100,000 mV s−1, the cell could surprisingly sustain a high specific capacitance around 50 F g−1. This high rate performance maintains until 30,000 mV s−1, beyond which the capacitive property cannot maintain any more (Fig. 5e). It is obvious that as the sweep rate increased by a factor of 1000 (from 10 to 10,000 mV s−1), the specific capacitance could still maintain a high value of 84 F g−1, which is 43% of the retention of the maximum one under 10 mV s−1 scan rate. The high rate capability of MoS2–S based supercapacitor is also confirmed by galvanostatic charge-discharge (GCD, Fig. 5f). GDC curves display a symmetric shape, with small capacitance drop from a current density of 1 A g−1 to a high 10 A g−1, confirming good rate performance in cell application (Fig. 5g). Moreover, the typical cell cycled under 5 A g−1 retains 75.6% capacity retention after 10,000 cycles (Fig. 5h). The merit of MoS2-S in supercapacitor is evaluated in Ragone plot for symmetric electrochemical cells on the electrode mass basis. A maximum power density close to 106 W kg−1 is achieved, while a high energy density 47.5 Wh kg−1 is also expected (Fig. 5i). The high energy density coupled with high power density open possibility to further engineer better supercapacitor based on this conducting MoS2–S material. In addition to the efficient performance, smooth preparation method holds promising anticipation for large-scale production in the near future.
Supercapacitor performance in [EMIM][BF4]/AN electrolyte. CV curve for scan rate of a 500 mV s−1, b1000 mV s−1, c 10,000 mV s−1, d 30,000 mV s−1, e Relationship between scan rate vs. current density, f Galvanostatic charge/discharge curves under different current density. g Relationship between scan rate vs. specific capacitance, inset image shows the lower scan rate. h Stability performance after 10,000 cycles, inset image shows charge/discharge curves from 2500th to 2505th cycles. i Ragone plots based on electrode mass
In summary, we computationally and experimentally investigate metallic hybrid structures of alternating layers of molybdenum disulfide and atomic sulfur. We discover that confined in between layers of molybdenum disulfide, sulfur atoms are able to form two-dimensional arrays of metallic phase, and render the MoS2–S metallic phase and exceptional conductivity of 223 S/m. The MoS2–S structure predicted from computation fits the selected area electron diffraction (SAED) quite well. Further evidences are from spherical aberration corrected TEM experimental measurements. High conductivity of MoS2-S allows the rapid electronic transfer. Using this MoS2–S as active materials for supercapacitor results in high scan rate and excellent performance in an ionic liquid electrolyte with no conductive additive attended. The current study offers insights into using two-dimensional materials and their Van der Waals heterostructures as nanotemplates to pattern foreign atoms to achieve unprecedented material properties.
Methods
DFT calculation
We perform first-principle DFT calculations by utilizing the SIESTA code.22 The generalized gradient approximation in the framework of Perdew–Burke–Ernzerhof (PBE) is adopted for the exchange-correlation potential. The effect of Van der Waals interaction is accounted for by using the dispersion corrected DFT (optB88-vdW functional).23, 24 Numerical atomic orbitals with double zeta plus polarization are used for the basis set, with a plane-wave energy cutoff of 500 Ry. Geometric structures are relaxed until the force on each atom is less than 0.01 eV A˚−1 and the convergence criteria for energy is 10−5 eV. The settings for Monkhorst–Pack k-points are 26 × 26 × 6 for layered structures (e.g., Fig. 1d) and 26 × 26 × 1 for slab structure (e.g., Fig. 1a–c). For electronic structure calculation, ten times denser K-points are used and self-consistent field tolerance is 10−6. The electronic smearing temperature during all calculations is 300 K. See section “Discussions on interpretation of computational results” in SI for further details including: (I) Computations in Fig. 1; (II) Computations in Fig. 2; (III) The nature of mechanical effect from extra S layer on MoS2.
Experimental section
Tweleve milligram MoO3 and 24 mg Thioacetamide (Fisher Scientific, US) were added into 10 mL deionized (DI) water, followed with 1 h magnetic stirring at 500 r.p.m. Then the well mixed solution was transferred to autoclave (Parr Instrument Cop.) and kept in furnace at 200 °C for 18 h. The autoclave was cooled down after 18 h in room temperature. The as prepared MoS2–S was washed with DI water and ethanol individually and stabilized in the mixture of DI water and ethanol with volume ratio of 1:1.
Sample characterization
Four probe electrical conductivity test
The electrical conductivity of the material is measured by a four point probe method using the Janis probe station under room temperature and 20 mTorr conditions. Ti (5 nm)/Au(60 nm) electrodes were deposited by e beam evaporator. The spacing between the electrodes is 0.5 mm, and the length of the electrodes is 6 mm. The film thickness is 200 nm.
Ultraviolet–visible-IR spectroscopy
UV-vis-IR absorption spectroscopy of the dispersion of the MoS2–S in water were recorded with a Perkin Elmer Lambda 25 spectrophotometer.
Transmission electron microscopy observations
TEM and HRTEM imaging and electron diffraction were performed on a FEI Tecnai G2 F20 S-Twin microscope operated at an accelerating voltage of up to 100 kV. The TEM samples were prepared by sonication at 500 W for ~5 min, and 25 µL supernatant was dropped onto holey carbon grids.
Scanning electron microscopy observations
Morphology and composition of the as-prepared MoS2–S was characterized by an ultra-high resolution scanning electron microscopy (Hitachi S4800), which has an optimum resolution of 1.4 nm. The MoS2–S film was first coated with 5 nm platinum and then imaged under ultra-high resolution mode at 3 kV accelerating voltage to reveal the morphology. For composition analysis, uncoated samples were analyzed by the accessorily equipped EDX spectroscopy at 15 kV accelerating voltage.
X-ray photoelectron spectroscopy
XPS was conducted using an Axis Ultra DLD (Kratos) system. The vacuum of the chamber was 1 × 10−9 Torr. A monochromatic aluminum Kα source with a source power of 150 W (15 kV × 10 mA) was used. The pass energy was 160 eV for wide scans and 40 eV for narrow scans.
XRD patterns
The XRD patterns of MoS2–S was recorded for two theta values ranging from 4° to 18° to characterize the interlayer spacing. The characterization was performed on a Bruker AXS-D8 Advance powder X-ray diffractometer using Cu/Ka radiation (λ = 1.5406 Å) with a step size of 0.02° and a dwell time of 3.0 s.
Surface area measurement
In order to measure the surface area of MoS2–S, UV-vis spectroscopy (cary 4000i, Agilent, America) with methylene blue (MB) dye as a probe was used here. At first, three different concentrations of MB aqueous solution (5, 10, and 20 mg L−1) were used to make a standard plot. Then, 4.5 mg MoS2–S was added into 8 mL MB solution with concentration of 80 mg L−1, followed by magnetic stirring until achieving the adsorption/desorption equilibrium in darkness. Subsequently, the MoS2–S was filtrated and the concentration of MB was soon measured by UV-vis spectroscopy relative to standard concentrations. In this study, the assumption was made that all the MB molecules were laying flat, so the reported value of 1.30 nm2 per molecule of MB was employed. The surface area of MoS2–S is calculated to be 383 m2 g−1. Moreover, when the reported value of 2.54 m2 (one mg covered surface) was used in the calculation, close surface area value of MoS2–S was obtained.
Electrochemical analysis
Electrochemical measurements were conducted on Biologic SP150. For tests in three-electrode cell configuration, 0.5 M H2SO4 was used as electrolyte solution, saturated AgCl/Ag and platinum mesh were used as reference and counter electrode, respectively. Cyclic data was collected between −0.25 – 0.55 V vs. AgCl/Ag with scan rates ranging from 10 to 300,000 mV s−1. this voltage window was chosen to avoid hydrogen and evolution and oxidation beyond the scope. Impedance spectra was measured for a 0.01 Hz to 100 KHz frequency range with a 5 mV amplitude. Typically, prior to drop-casting MoS2–S onto the surface of glassy carbon working electrode, MoS2–S was sonicated for at least 20 mins. Usually 8–10 ug active material was cast on and dried in air.
Electrochemical measurements in organic electrolyte: The measurement in organic electrolyte was performed using a two-electrode configuration. Organic electrolyte was prepared using 1 M [EMIM][BF4] dissolved in acetonitrile (AC), and a higher potential window of 2 V was applied. Specifically, active material MoS2-S was loaded onto inactive graphene foam here to work as a composite electrode and electric conductive current collector without any additive, while graphene capacitance could be subtracted. The 3D highly compressive graphene substrate helps to build mechanically indetachable integral.
Calculation of gravimetric capacitances of electrodes
Gravimetric capacitance was calaculated from cyclic voltammetry and galvonastatic charging discharging plots using the following formula:
Using Cg: gravimetric capacitance (F g−1); I: current (A); v-scan rate (V s−1); m: mass of MoS2–S (g) t: discharge time (s); V: potential range.
The mass of MoS2–S was calibrated by homogeneous membrane weighing before and after.
The energy density and power density of the capacitor were calculated according to the following equations:
Here the C is total capacitance of two-electrode supercapacitor, ΔV is effective potential window during discharge process, tdischarge is the discharge time (s). E (unit: \({\rm{Wh/Kg}}\)) represents the energy density and P (unit: \({\rm{W/Kg}}\)) power density, M represents the weight of whole electrode.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
References
Steudel, R. & Eckert, B. Solid sulfur allotropes. Top. Curr. Chem. 230, 1–79 (2003).
Amaya, K., Shimizu, K., Eremets, M., Kobayashi, T. & Endo, S. Observation of pressure-induced superconductivity in the megabar region. J. Phys. Condens. Matter 10, 11179–11190 (1998).
Akahama, Y., Kobayashi, M. & Kawamura, H. Pressure-Induced structural phase-transition in sulfur at 83-Gpa. Phys. Rev. B 48, 6862–6864 (1993).
Luo, H., Desgreniers, S., Vohra, Y. & Ruoff, A. High-pressure optical studies on sulfur to 121 Gpa - optical evidence for metallization. Phys. Rev. Lett. 67, 2998–3001 (1991).
Struzhkin, V., Hemley, R., Mao, H. & Timofeev, Y. Superconductivity at 10-17 K in compressed sulphur. Nature 390, 382–384 (1997).
Springborg, M. & Jones, R. Energy surfaces of polymeric sulfur - structure and electronic-properties. Phys. Rev. Lett. 57, 1145–1148 (1986).
Springborg, M. & Jones, R. Sulfur and selenium helices - structure and electronic-properties. J. Chem. Phys. 88, 2652–2658 (1988).
Okano, S. & Tomanek, D. Effect of electron and hole doping on the structure of C, Si, and S nanowires. Phys. Rev. B 75, 195409 (2007).
Fujimori, T. et al. Conducting linear chains of sulphur inside carbon nanotubes. Nat. Commun. 4, 2162 (2013).
Rappe, A., Casewit, C., Colwell, K., Goddard, W. & Skiff, W. Uff, a full periodic-table force-field for molecular mechanics and molecular-dynamics simulations. J. Am. Chem. Soc. 114, 10024–10035 (1992).
He, Z. & Que, W. Molybdenum disulfide nanomaterials: Structures, properties, synthesis and recent progress on hydrogen evolution reaction. Appl. Mater. Today 3, 23–56 (2016).
Hibble, S. & Wood, G. Modeling the structure of amorphous MoS3: A neutron diffraction and reverse Monte Carlo study. J. Am. Chem. Soc. 126, 959–965 (2004).
Lin, Y., Dumcencon, D., Huang, Y. & Suenaga, K. Atomic mechanism of the semiconducting-to-metallic phase transition in single-layered MoS2. Nat. Nanotechnol. 9, 391–396 (2014).
Nayak, A. et al. Pressure-induced semiconducting to metallic transition in multilayered molybdenum disulphide. Nat. Commun. 5, 3731 (2014).
Eda, G. et al. Photoluminescence from chemically exfoliated MoS2. Nano. Lett. 11, 5111–5116 (2011).
Li, J. et al. MoS2-reduced graphene oxide composites synthesized via a microwave-assisted method for visible-light photocatalytic degradation of methylene blue. RSC Adv. 4, 9647–9651 (2014).
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically thin MoS 2: a new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010).
Chen, P. et al. Multiscale graphene topographies programmed by sequential mechanical deformation. Adv. Mater. 28, 3564–3571 (2016).
Acerce, M., Voiry, D. & Chhowalla, M. Metallic 1T phase MoS2 nanosheets as supercapacitor electrode materials. Nat. Nanotechnol. 10, 313–318 (2015).
Sheng, K., Sun, Y., Li, C., Yuan, W. & Shi, G. Ultrahigh-rate supercapacitors based on eletrochemically reduced graphene oxide for ac line-filtering. Sci. Rep. 2, 247 (2012).
Dinh, T., Armstrong, K., Guay, D. & Pech, D. High-resolution on-chip supercapacitors with ultra-high scan rate ability. J. Mater. Chem. A 2, 7170–7174 (2014).
Soler, J. M. et al. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter 14, 2745–2779 (2002).
Klimeš, J., Bowler, D. R. & Michaelides, A. Chemical accuracy for the van der Waals density functional. J. Phys. Condens. Matter 22, 022201 (2009).
Klimeš, J., Bowler, D. R. & Michaelides, A. Van der Waals density functionals applied to solids. Phys. Rev. B 83, 195131 (2011).
Acknowledgements
H.Z. acknowledges the financial startup support and Tier 1 award from Northeastern University. We also thank Dr. Kar Swastic in Department of Physics in Northeastern University for sharing their Raman spectroscopy. We thank Alolika Mukhopadhyay for helping test UV-vis absorption spectroscopy. We also thank Center for Nanoscale System (CNS) in Harvard University for using their facilities.
Author information
Authors and Affiliations
Contributions
H.Z. supervised and conceived this project. S.Z. performed DFT calculations. S.Z. and H.Z. analyzed computational results, experimental results, and wrote the manuscript. X.G. led the material preparation, experimental characterization, and contributed to the writing on the experimental part of the manuscript. X.G., J.L., and L.C. contributed to the material preparation, experimental characterization, and collected and analyzed the data. Y.H. helped the supercapacitor performance test. I.B. did the conductivity characterization. M.B. performed TEM and SAED. All of the authors commented the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhu, S., Geng, X., Han, Y. et al. Metallic and highly conducting two-dimensional atomic arrays of sulfur enabled by molybdenum disulfide nanotemplate. npj Comput Mater 3, 41 (2017). https://doi.org/10.1038/s41524-017-0041-z
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-017-0041-z
This article is cited by
-
Atomic structure and electrical property of ionic liquids at the MoS2 electrode with varying interlayer spacing
Journal of Molecular Modeling (2021)
-
Origin of ultrafast growth of monolayer WSe2 via chemical vapor deposition
npj Computational Materials (2019)