Abstract
A large body of experimental work has established that athermal colloid/polymer mixtures undergo a sequence of transitions from a disordered fluid state to a colloidal crystal to a second disordered phase with increasing polymer concentration. These transitions are driven by polymer-mediated interparticle attraction, which is a function of both the polymer density and size. It has been posited that the disordered state at high polymer density is a consequence of strong interparticle attractions that kinetically inhibit the formation of the colloidal crystal, i.e., the formation of a non-equilibrium gel phase interferes with crystallization. Here we use molecular dynamics simulations and density functional theory on polymers and nanoparticles (NPs) of comparable size and show that the crystal-disordered phase coexistence at high polymer density for sufficiently long chains corresponds to an equilibrium thermodynamic phase transition. While the crystal is, indeed, stabilized at intermediate polymer density by polymer-induced intercolloid attractions, it is destabilized at higher densities because long chains lose significant configurational entropy when they are forced to occupy all of the crystal voids. Our results are in quantitative agreement with existing experimental data and show that, at least in the nanoparticle limit of sufficiently small colloidal particles, the crystal phase only has a modest range of thermodynamic stability.
Similar content being viewed by others
Introduction
Over five decades of experimental, theoretical and simulation work1,2,3,4,5,6,7,8,9,10,11,12,13 have led to the knowledge that polymer-induced depletion attractions between colloids in solution can cause them to crystallize even at low polymer concentrations. For large colloids, both face centered cubic (FCC) and hexagonally closed packed (HCP) structures tend to form, since the free energy difference between these two polymorphs is very small.14 In the nanoparticle limit, when the colloids and chains become comparable in size, we13 recently showed that colloids preferentially crystallize into the HCP structure in the presence of a dilute concentration of long enough polymers, in preference to the FCC morphology. This preference is driven by the difference in the free energy cost of confining individual polymer chains within the voids of the two different colloidal crystal morphologies. Specifically, polymers prefer to occupy the octahedral voids (OV), which are ~6 times larger in volume than the tetrahedral voids (TVs). The HCP structure features connected OVs, while in the FCC OVs are completely surrounded by TVs. Therefore, because a sufficiently long polymer chain must spread across multiple connected voids, it has significantly lower free energy in a HCP crystal than in the FCC analog. Further increasing the polymer density ϕ p, however, experimentally leads to disordered structures, and the formation of apparently kinetically arrested states (diffusion limited or reaction limited aggregations) that has generally been attributed to the increasing pairwise attractions between colloids.7
In this work we show that, at least in the nanoparticle limit (~10 nm), there is an equilibrium phase transition between the crystal and a disordered phase at high polymer densities—just as the relative stability of the crystal polymorphs at intermediate polymer concentrations is controlled by the nature of the chains partitioned into the crystal phase, this transition is also driven by the unfavorable entropic cost associated with confining a long polymer chain into the TVs of a periodic colloidal crystal, which become necessary at higher polymer concentrations.15 We thus conclude that the colloidal crystal phase in the nanoparticle limit only has a limited range of thermodynamic stability.9
Results
Bulk phase behavior
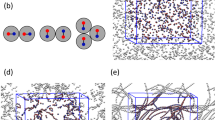
To illustrate the surprising thermodynamic stability of the high-polymer-density disordered phase, colloid-polymer mixtures are simulated using the molecular dynamics method for several different polymer volume fractions at a fixed colloid loading (see “Methods”). At each state point, we performed two simulations – one where the colloids begin in a HCP structure that is stable at moderate polymer fraction ϕ p and another in which they are in a disordered structure, specifically the one that is stable at high ϕ p (Fig. 1). These simulations verify that the states resulting from the simulations are not kinetically trapped, and the structural transitions that we report are reversible. Figure 2 shows the radial distribution function of colloids, g(r), and the time evolution of the global bond order parameter Q 6, at three different ϕ p and a colloid volume fraction ϕ c ~ 0.1 for polymer chain length M = 10. At ϕ p = 0.81, the final radial distribution functions exhibit crystal-like behavior characterized by multiple sharp peaks persisting to large radial distances (Fig. 2c). Closer examination shows that each g(r) has well defined characteristics of the HCP (e.g. a split peak at ~2σc) rather than the FCC structure, as expected by our previous work.13 Both the initially amorphous and initially crystalline states converge to the same g(r), as do the global bond order parameter (a measure of crystallinity, Fig. 2f). At ϕ p = 0.91, the g(r) in Fig. 2a has an unusually large contact peak but there is an absence of any long-range order. After visually inspecting the snapshots from simulations (Fig. 1b), this g(r) corresponds to the aggregation of colloids into a disordered “open” structure. There are many pairwise colloid contacts, but an absence of any higher-order closed packed structures. (We cannot determine if these structures are quasi-crystalline due to system size limitations.) The reduced crystallinity in this case is clearly shown by the Q 6 (Fig. 2d), and the results are again independent of the initial configuration. Simulations at ϕ p = 0.86 produced two temporally persistent structures, depending on the initial states (“hysteresis”). Both the crystal-like structure and the “open” structure persist over long simulations (Fig. 2b) as do the corresponding Q 6 values. We conclude that the disordered and crystalline states are at equilibrium at high and low polymer concentrations, respectively, and imply that there is a first-order phase transition occurring between an ordered HCP crystal and a disordered structure in the vicinity of ϕ p = 0.86.
a–c colloidal radial distribution function g(r), and d–f the global bond order parameter Q6, obtained from bulk simulations at three polymer densities ϕ p = 0.81 (bottom), 0.86 (middle) and 0.91 (top). The polymer chain length is M = 10 and the colloid volume fraction ϕ C = 0.1. The blue and red points represent results obtained from using two different initial states for simulations, namely an ordered HCP crystal and a disordered structure, respectively. The black dashed lines in c indicate the g(r) of a perfect HCP crystal
The “boundaries” between the disordered structure and the HCP crystal derived in this manner are shown in Fig. 3. (Note that we report results for two different polymer-colloid size ratios q = 2R g /σ c = 0.6 and 0.8, where R g is the chain radius of gyration.) In the ϕ c−ϕ p phase diagram we note that boundaries from our simulations agree well with the “gelation” boundaries widely reported for polymer-colloid mixtures over this modest q range. Limited dynamics studies (not shown) illustrate that the disordered state is not an “arrested” structure; in the framework of our simulations this implies that the crystal-disordered boundary does not correspond to a non-ergodicity transition. This conclusion is well supported by the reversibility studies that are the focus of Fig. 2. Instead, as we shall show below, the transition from the HCP to the disordered structure is an equilibrium phase transition; at higher polymer loadings the HCP is shown to be thermodynamically less stable than the disordered state. One thing worth mentioning is that the ϕ c−P phase boundary, where P is the pressure of the system (see method section), indicates that transition occurs at P ≈ 2~2.5ε/σ 3 independent of colloid volume fraction. This allows the proposed potential of mean force simulations (discussed in the next) to be conducted at conditions that are comparable to the bulk simulations.
The ϕ c− ϕ p phase diagram showing the regions where the disordered (open symbols) and the HCP structure (filled symbols) are obtained from bulk simulations. The blue and red symbols represent simulations with chain length M = 10 and 20, corresponding to the colloid-polymer aspect ratio q ~ 0.6 and 0.8, respectively. Boundaries predicted by the density functional theory are marked by the solid lines for chain length of 10 (blue), 20 (red) and 40 (green). The “gelation” boundaries adopted from Ref. [7] for corresponding q values are also included for comparison: open stars are the gel phase while filled stars are crystals
Void occupation
To understand the molecular basis of these results we conduct simulations (see “Methods”) to study the polymer occupation of the OV and TV of rigid HCP colloidal crystals with increasing polymer density. Results for FCC crystals are qualitatively similar and are not shown here. We reiterate that an OV has a volume that is ~6 times larger than a TV (Figure 4a).13 Figure 4(b) and 4(c)show the radial distribution function of chain monomer segments around the centers of OVs and TVs inside a HCP structure (held fixed) at ϕ c = 0.1 and M = 10 with varying ϕ p. It is seen that OVs are occupied by polymers at all ϕ p investigated, which forms the basis for the increased relative thermodynamic stability of this polymorph over the FCC at low to modest polymer concentrations, as previously reported.13 However, while the TVs are mostly vacant at (and presumably up to) ϕ p ~ 0.81, a sudden increase in occupancy, indicated by an increase in the magnitude of g TV (r ~ 0), is observed at ϕ p ~ 0.86. The occupancy stays relatively unchanged with further increases in P. This result unambiguously shows that at low pressure (polymer density), where the HCP crystal is stable, polymer chains avoid the TVs because they have much smaller volume than OVs. However, with increasing pressure (polymer density) the polymers are forced to overcome the entropic penalty associated with confinement into the smaller TVs. As we show next, this is responsible for the destabilization of the crystal phase.
a Schematic illustrations of the A-B layer, and the “HCP- contacts” and “FCC-contacts” defined in text.13 Radial distributions of polymer segments (color symbols) and colloids (black circles and dashed vertical lines) about centers of the b TV and c OV voids inside a HCP structure. ϕ p = 0.73 (cyan), 0.81 (magenta), 0.86 (blue), 0.91 (green) and 0.95 (red)
Free energies
It is inherently difficult to calculate the free energy of high-density systems. So, rather than using methods such as umbrella sampling, Widom test particle insertion, or the Gibbs ensemble,16,17,18,19 which have been applied with difficulty to the simpler case of hard sphere mixtures with size disparity, we have devised a hybrid approach that uses inputs from the molecular dynamics simulations (such as the radial distribution function, and potentials of mean force (POMF),20, 21 “Methods”) in conjunction with the density functional theory22 to evaluate the free energy of both the crystal and the disordered phase.23, 24 Validation of the phase boundaries calculated using this approach against the bulk simulations then provides a validating test of its accuracy. (Recent work by Dijkstra25 appears to allow for a facile means of exactly enumerating phase equilibria.)
This approach requires knowledge of the polymer-mediated g(r) between the colloids, and also two-body and higher order POMF that are representative of the crystal and the disordered phases. The pairwise POMFs, \({{\psi }}_{{\rm{pair}}}\), are shown in Fig. 5a at different pressures; data over much broader ranges of pressure show the same trends. The depth of the first minimum of \({{\psi }}_{{\rm{pair}}}\) generally decreases with increasing P, as expected. However, the conventional reasoning that colloids become kinetically arrested at high P (ϕ p) due to much stronger effective attractions is not supported by our results. Thus, \({{\psi }}_{{\rm{pair}}}\), which only changes marginally with polymer loading, provides little justification for any possible changes in the phase behavior of colloid-polymer mixtures with increasing polymer densities.
a Two-body potential of mean force Ψ pair measured from simulations with chain length M = 10, and P = 0.15ε/σ 3 (red), 0.20 ε/σ 3 (blue), 0.25 ε/σ 3 (black) and 0.30 ε/σ 3 (magenta). b “Surface” potential of mean force Ψ surface with chain length M = 10 at P = 1.5ε/σ 3. The filled symbols are results directly measured from simulations, and the open symbols are values calculated from Ψ pair using the pair-additive assumption. The Ψ tri and Ψ HCP are shown in black and magenta, respectively. c Same as b, but at P= 2.5ε/σ 3. d The free energy per colloid as a function of ϕ p, of the HCP colloidal crystal (filled symbol and solid line), the “open” colloidal structure (open symbol and solid line), and the hypothetical HCP colloidal crystal in absence of many-body effects (filled symbol dotted line)
To quantify higher-order effects we measure the free energy cost of bringing a test colloid particle from an infinite distance to being “in contact” with an existing colloid layered structure (see “Methods”). Since the contact is between a colloid and a structured surface, there are numerous ways for the “contact” to occur. We focus on the POMF of two types of “contacts” (Fig. 5b and 5c): (a) \({\bar{{\psi }}}_{{\rm{hcp}}}\) when the test colloid forms a TV by coming into a three-fold hollow created by three surface sites; and (b) \({\bar{{\psi }}}_{{\rm{tri}}}\) of the “tri-contact” where the test colloid forms a equilateral triangular with two neighboring colloids on the surface. This latter choice is motivated by the examination of the bulk disordered structures (Fig. 1b), which shows the formation of such triangles, but not closed packed structures, is the norm for the high density disordered structure. For most of the relevant polymer densities, we found that \({\bar{{\psi }}}_{{\rm{tri}}}\) agrees well with 3 × \({{\psi }}_{{\rm{pair}}}\), i.e., the pair-wise additive assumption is followed; however, the \({\bar{{\psi }}}_{{\rm{hcp}}}\) shows much complicated behavior (Fig. 5c).
The resulting relative free energy (per colloid) of the disordered and crystalline colloidal phases (Fig. 5c) clearly illustrates a phase transition from a crystal to a disordered phase at a polymer concentration of P≈1.8ε/σ 3. For the sample with ϕ c = 0.1 and M = 10, our MD bulk simulations suggest a transition from the crystal to a disordered phase in the vicinity of P≈2.0ε/σ 3(ϕ p ≈0.86), which is consistent with this estimate. More to the point, Fig. 2 shows that this free energy evaluation using DFT correctly predicts the transition observed in MD and/or experiments for the three q values that we have considered. (The results at q = 1 are only qualitatively correct.) Our results clearly illustrate that the transition observed is an equilibrium phase transition that is driven by the fact that, at high enough polymer densities, the chains lose free energy when they are confined into the TVs that are characteristic of close-packed colloidal crystals. This free energy loss no longer occurs when the colloids are still in close contact but do not form a closed packed structure, i.e., the disordered phase (Fig. 1). While this gel-like structure is very reminiscent of one formed, for example, by irreversible attraction, it is in fact an equilibrium structure.
Discussion
Several important issues need to be stressed in this context. First, while we have taken considerable care in simulating q values that closely match experiment, the actual sizes of the colloids and the polymers in the experiment and the simulations are quite different. For example, the experimental results of Lekkerkerker7 use colloids that are ~200–300 nm in diameter. Our simulations are typically constructed for a colloid that is 6.45 times the size of a chain monomer—assuming a monomer size of ~1 nm then suggests that our colloids are ~50 times smaller than the experiments. The nearly quantitative agreement of the crystal-disordered solid boundary predicted by the theory and those found in the experiments imply that q might be the single relevant parameter that defines these physical situations. More experimental work, especially those using NPs, can go to verifying this conjecture. Regardless, our previous work on the increased stability of the HCP crystal in the presence of such polymers, independent of colloid size,13 suggest that our results might continue to hold for more experimentally accessible scales.
Given the importance of chain confinement in TVs as the driving force for the crystal to disorder transition, we postulate that short enough chains (or small enough q) would yield no such transition, much in the same way these chains do not impose a polymorphic preference for the HCP crystal over the FCC since they do not stretch across multiple voids when confined.13 Indeed, simulations for q = 0.25 show no such transition, suggesting that this equilibrium transition will only occur for large enough q values. Delineating the precise value of q above which this transition occurs is an open question that needs to be pursued, which we defer for future work. However, it is important to stress that small q values do not fall in the regime where this crystal-disordered phase transition is predicted to occur—the observation of gelation phenomena that have been found experimentally thus may indeed be purely a non-ergodicity transition in this limit.
It has been argued that gelation occurs because the contact value of the effective intercolloid potential becomes strongly favorable. While this result might be true for small enough q values, in general it is apparent that the contact value of the POMF only changes marginally with polymer density (Fig. 5a) and is ~−4kT for all the pressures considered. These numbers are much more favorable than the −3kT that has been postulated as necessary to form colloidal gels. Hence we conclude that the formation of the disordered phase is not only related to the two-body POMF but is primarily driven by higher-order contributions.
At last, by keeping interaction potentials being purely repulsive (see “Methods”) the systems investigated in this study resemble athermal systems, for which temperature only plays insignificant role in determining systems’ phase behavior.
Methods
Simulations
In our simulations, polymer chains are represented by the Kremer–Grest bead-spring model.23 All chain monomers are chemically identical and have a mass m and diameter σ. Beads along the chain are connected by a finitely extensible nonlinear elastic potential with k = 30ε/σ 2 and R 0 = 1.5σ.26 NPs are represented as uniform spheres of diameter σ NP and mass m NP. We focus on “athermal” systems, where all non-bonded pair interactions are purely repulsive and represented by the “expanded” Lennard-Jones potential: \({U}_{i,j}(r)=4{\epsilon }[{(\frac{\sigma }{r-{\Delta }_{i,j}})}^{12}-{(\frac{\sigma }{r-{\Delta }_{i,j}})}^{6}],\,r < {r}_{c}\), where ε is the well depth of the potential and i,j = monomer or NP. The cut-off distance r c = Δ i,j +21/6 σ is chosen for all pair interactions. The shift, \({\Delta }_{i,j}=[\frac{({\sigma }_{i}+{\sigma }_{j})}{2}]-1.0\), where σ i refers the diameter of particle i, ensures that U i,j ((σ i +σ j )/2) = 0 and \(\frac{d{U}_{i,j}(r)}{dr}\,({\rm{for}}\,r > {\Delta }_{i,j})\), or “the hardness”, is same for all non-bonded pair potentials. Following refs 13, 27, 28 we consider colloids of diameter σ C = 6.45σ and vary the polymer chain length M = 10, 20 or 40 in a series of simulations corresponding to a polymer-colloid aspect ratio q = 0.6, 0.8 and 1.0, respectively. (Our previous work suggests that the free energy difference of confining a polymer chain in a tetrahedral versus octahedral void settles to a limiting value of ~2k BT with increasing nanoparticle–monomer aspect ratio. We therefore expect that at other aspect ratios occupying a TV is still going to destabilize the crystal phase, but for progressively larger chain lengths, M. If our logic is correct, then the monomer thickness is not relevant—rather it is the q parameter, which is the ratio of the R g of the chains to the radius of the NP.)
All simulations are performed using the LAMMPS parallel molecular dynamics package, under the isothermal–isobaric (NPT) conditions with temperature T = 1.0ε/k B and a pressure range of P = 1 to 3ε/σ 3. (Some limited simulations at T = 1.2ε/k B gave similar results.) The Nose–Hoover thermostat and barostat are used to maintain temperature and pressure at prescribed values with damping constants Γ = 1.0 and 5τ−1, respectively where τ = σ(m/ε)1/2. The time step in all simulations is set to be δt = 0.01τ.
Periodic boundary conditions are used in all three dimensions in bulk simulations, which only considered M = 10 and 20 chains. For each chain length, simulations are first run at the two pressures P = 1 and 3ε/σ 3 using random initial configurations. These were created by first randomly placing a desired number of colloids in the simulation box, followed by growing polymer chains as described by Auhl et al.29 with the additional restriction that no monomers overlap the colloids. Overlapping monomers were pushed off each other using a soft potential14 until they are far enough apart for the LJ interaction to be switched on. After 5 × 106 τ, the resulting configurations at the two pressures are then used as starting points for simulations at incrementally lower and higher pressures (1, 1.5, 2.0, 2.5 and 3.0ε/σ 3, respectively). At each pressure, colloid radial distribution functions and global bond order parameters from both initial states are calculated and compared to check the reversibility of the simulations. Three colloid volume fractions \({\eta }_{{\rm{C}}}=\frac{\pi {\sigma }_{{\rm{C}}}^{3}{N}_{{\rm{C}}}}{6V}\) are investigated. N C = 80, 160 and 240 colloids are mixed, respectively, with 56700, 48600, and 42300 monomers in a simulation box whose volume V varies in the range 453−493 σ 3, yielding η C ~ 0.1, ~0.2 and ~0.3.
In the potential of mean force (POMF) simulations, we follow the force integration method in ref. 28 to obtain the POMF. In the two-body POMF measurements, two colloids of diameter σ C are placed at (x, 0, 0) and (−x, 0, 0) in a simulation box mixed with polymer chains of the desired length (so that the simulations have 4000 monomers). The volume of the box varies from 5600 ~ 8000 σ 3 depending on the pressure, and the aspect ratio of simulation box is fixed at 5:3:3. The inter-colloid separation 2x increases from σ C to a distance where no interactions between the two colloids are observed (up to simulation uncertainties). The measured forces are then integrated to obtain the two-body POMF Ψ pair. In the surface POMF simulations, forces are measured between a colloid and a colloidal structure that is made of two layers of 16 hexagonally packed colloids. The two colloidal layers that span the x−y dimension of the simulation box are stacked in the same way as the A-B layer structure seen in both the HCP and FCC crystals (Fig. 4a). There are 13,000 monomers in each simulation, and the pressure is controlled by varying only the z dimension of the simulation box between 40 ~ 46σ. We are particularly interested in the POMF of forming two types of “contacts” between an “incoming” colloid and the A-B layer: the “tri-contact” POMF, Ψ tri, which measures the free energy cost for the incoming colloid forming an equilateral triangle with two colloids in the A-layer and the “HCP-contact”, Ψ HCP, which measures the free energy cost for the incoming colloid forming a tetrahedron with three colloids in the A-layer (Fig. 4a). Forces exerted on the incoming colloid are measured at a set of distances along paths that are perpendicular to the surface of A-B layer.
Finally, to relate to the experiments in bulk simulations, the reduced polymer density \({\phi }_{{\rm{p}}}\equiv \frac{4}{3}\pi {R}_{{\rm{g}}}^{3}{N}_{{\rm{S}}}/MV\) is used for discussions in place of simulation pressure, where N S is the number of monomers in simulations, and R g is the radius of gyration of polymer chains measured at the corresponding ϕ p.
Free energy calculations
To compare the relative stability of the colloidal crystal and disordered phase, free energies of the two phases are calculated. For the crystal phase, the “Baxter sticky sphere model”30 is used with the assumption that colloids move independently inside crystal lattice cells, while interacting via the square-well potential with their neighbors. The free energy per colloid is given by
where β = 1/k B T, Z is the coordination number of crystal lattice, δ is the potential width and ∈ sq is the depth of the square well. The values of δ and ε sq are estimated by analyzing the Ψ HCP measured at a given pressure, such as Fig. 4b, c. ε sq is taken to be the minimum of Ψ HCP, and δ is estimated as the distance over which an increase of ~k B T in Ψ HCP occurs. In our calculations, δ varies between 0.1 ~ 0.15σ depending on the pressure. The coordination number of a HCP lattice Z = 12.
Density functional theory22 is invoked for calculating the free energy of the disordered phase where colloids are assumed to interact with each other through the two-body POMF Ψ pair. According to the density functional theory, the free energy of a system consists of an ideal part F id and an excess part F ex:
The formula for the ideal free energy is exact, given by:
where Ψ(r) is the external potential, and ρ(r) is the density of colloids at r. In a spherical coordinate system, the system becomes radially symmetric subject to an external potential Ψ(r) of form:
where σ c is the colloid diameter. Also, ρ(r) becomes ρ(r) = ρ b g(r) where g(r) is the colloidal radial distribution function. Thus,
with both g(r) and Ψ pair(r) to be obtained from simulations. In practice, the integration is performed to a distance r max, where ρ(r max) = ρ b . The per-colloid free energy is thus
The excess free energy accounts for the interactions between colloids. In our calculations, short-range repulsions between colloids (“expanded” Lennard–Jones potential) are approximated by Hard-Sphere interactions, and the long-range attractions are described by the two-body POMF Ψ pair. Thus the excess free energy can be decomposed into two contributions:
where \({F}_{{\rm{hs}}}^{ex}\) and \({F}_{{\rm{dep}}}^{ex}\) are, respectively, the excess free energy due to hard-sphere repulsions and depletion attractions. \({F}_{{\rm{dep}}}^{ex}\) can be approximately calculated using the colloid configurations obtained during simulations. That is
where N C is the number of colloids in simulation box, and 〈 〉 stands for an average over all saved configurations. In practice, 5 × 104~105 configurations are used in calculations with each configuration being generated every 1000τ during simulations. The per-colloid free energy due to depletion attraction is thus \({f}_{{\rm{dep}}}^{ex}={F}_{{\rm{dep}}}^{ex}/{N}_{{\rm{C}}}\).
The framework of fundamental measure theory (FMT) is followed for calculating \(\beta {F}_{{\rm{hs}}}^{ex}=\int d{\bf{r}}[{\Phi }^{{\rm{hs}}}({\bf{r}})]\), where Φhs(r) is the excess free energy density at r. For detailed discussion of the FMT, readers are referred to ref. 22. A brief account of implementation of this method in this study is provided in the Supporting materials. The per-colloid excess free energy due to hard sphere interactions is finally calculated as \({f}_{{\rm{hs}}}^{ex}={F}_{{\rm{hs}}}^{ex}/{\int }_{0}^{{r}_{{\rm{\max }}}}4\pi \rho (r)\,{r}^{2}dr\), where r max is the radial distance from the origin where bulk colloid density ρ b is recovered.
The total free energy per colloid for the disordered phase is thus \(\beta f=\beta {f}^{id}+\beta {f}_{{\rm{hs}}}^{ex}+\beta {f}_{{\rm{dep}}}^{ex}\).
References
Asakura, S. & Oosawa, F. On interaction between two bodies immersed in a solution of macromolecules. J. Chem. Phys. 22, 1255–1256 (1954).
Asakura, S. & Oosawa, F. Interaction between particles suspended in solutions of macromolecules. J. Polym. Sci. 33, 183–192 (1958).
Anderson, V. J. & Lekkerkerker, H. N. W. Insights into phase transition kinetics from colloid science. Nature 416, 811–815 (2002).
Frenkel, D. Entropy-driven phase transitions. Phys. A 263, 26–38 (1999).
Lekkerkerker, H. N. W., Poon, W. C. K., Pusey, P. N., Stroobants, A. & Warren, P. B. Phase-behavior of colloid plus polymer mixtures. Europhys. Lett. 20, 559–564 (1992).
Poon, W. C. K. The physics of a model colloid-polymer mixture. J. Phys. Condens. Matter. 14, R859–R880 (2002).
Lekkerkerker, H. N. & Tuinier, R. Colloids and the depletion interaction. Vol. 833 (Springer, 2011).
Chin, W. C., Orellana, M. V. & Verdugo, P. Spontaneous assembly of marine dissolved organic matter into polymer gels. Nature 391, 568–572 (1998).
Feng, L., Laderman, B., Sacanna, S. & Chaikin, P. Re-entrant solidification in polymer-colloid mixtures as a consequence of competing entropic and enthalpic attractions. Nat. Mater. 14, 61–65 (2015).
Pham, K. N. et al. Multiple glassy states in a simple model system. Science 296, 104–106 (2002).
Mahynski, N. A., Kumar, S. K. & Panagiotopoulos, A. Z. Tuning polymer architecture to manipulate the relative stability of different colloid crystal morphologies. Soft Matter 11, 5146–5153 (2015).
Mahynski, N. A., Kumar, S. K. & Panagiotopoulos, A. Z. Relative stability of the FCC and HCP polymorphs with interacting polymers. Soft Matter 11, 280–289 (2015).
Mahynski, N. A., Panagiotopoulos, A. Z., Meng, D. & Kumar, S. K. Stabilizing colloidal crystals by leveraging void distributions. Nat. Commun. 5, 5472 (2014).
Frenkel, D. & Ladd, A. J. C. New Monte-Carlo method to compute the free-energy of arbitrary solids - application to the FCC and HCP phases of hard-spheres. J. Chem. Phys. 81, 3188–3193 (1984).
Lu, B. & Denton, A. R. Crowding of polymer coils and demixing in nanoparticle-polymer mixtures. J. Phys. Condens. Matter. 23, 285102 (2011).
Ashton, D. J., Wilding, N. B. & Sollich, P. Fluid phase coexistence and critical behavior from simulations in the restricted Gibbs ensemble. J. Chem. Phys. 132, 074111 (2010).
Liu, J., Wilding, N. B. & Luijten, E. Simulation of phase transitions in highly asymmetric fluid mixtures. Phys. Rev. Lett. 9, 115705 (2006).
Virnau, P. & Muller, M. Computer simulation studies in condensed-matter physics XVI In Springer Proceedings in Physics Vol. 103 (eds Landau, D. P., Lewis, S. P., & Schuttler, H. B.) 151–154 (Springer, 2006).
Wilding, N. B. & Sollich, P. A Monte Carlo method for chemical potential determination in single and multiple occupancy crystals. Europhys Lett. 101, 10004 (2013). p1–6.
Ashton, D. J., Sanchez-Gil, V. & Wilding, N. B. Monte Carlo methods for estimating depletion potentials in highly size-asymmetrical hard sphere mixtures. J. Chem. Phys. 139, 144102 (2013).
Ashton, D. J., Wilding, N. B., Roth, R. & Evans, R. Depletion potentials in highly size-asymmetric binary hard-sphere mixtures: comparison of simulation results with theory. Phys. Rev. E 84, 061136 (2011).
Rosenfeld, Y. Free-energy model for the inhomogeneous hard-phere fluid mixture and density-functional theory of freezing. Phys. Rev. Lett. 63, 980–983 (1989).
Schmidt, M., Lowen, H., Brader, J. M. & Evans, R. Density functional for a model colloid-polymer mixture. Phys. Rev. Lett. 85, 1934–1937 (2000).
Wu, J. & Li, Z. Density functional theory for complex fluids. Annu. Rev. Phys. Chem. 58, 85–112 (2007).
Edison, J. R., Dasgupta, T., Dijkstra, M. Stabilizing the hexagonal close packed structure of hard spheres with polymers: phase diagram, structure, and dynamics. Preprint at arXiv:1605 00586 (2016).
Grest, G. S. & Kremer, K. Molecular-Dynamics simulation for polymers in the presence of a heat bath. Phys. Rev. A 33, 3628–3631 (1986).
Meng, D., Kumar, S. K., Lane, J. M. D. & Grest, G. S. Effective interactions between grafted nanoparticles in a polymer matrix. Soft Matter 8, 5002–5010 (2012).
Meng, D., Kumar, S. K., Cheng, S. & Grest, G. S. Simulating the miscibility of nanoparticles and polymer melts. Soft Matter 9, 5417–5427 (2013).
Auhl, R., Everaers, R., Grest, G. S., Kremer, K. & Plimpton, S. J. Equilibration of long chain polymer melts in computer simulations. J. Chem. Phys. 119, 12718–12728 (2003).
Charbonneau, P. & Frenkel, D. Gas-solid coexistence of adhesive spheres. J. Chem. Phys. 126, 196101 (2007).
Acknowledgements
This research used resources of the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231 and the Advanced Scientific Computing Research (ASCR) Leadership Computing Challenge (ALCC). This work was performed, in part, at the Center for Integrated Nanotechnologies, a U.S. Department of Energy, Office of Basic Energy Sciences user facility. Sandia National Laboratories is a multi-program laboratory managed and operated by Sandia Corporation, a wholly owned subsidiary of Lockheed Martin Corporation, for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-AC04-94AL85000. Financial support was received from the National Science Foundation (Collaborative Research Award CBET-1403049 at Columbia and CBET-1402166 at Princeton) is gratefully acknowledged.
Author contributions
D.M. and N.M. performed this research, S.K.K., A.Z.P. and G.S.G. designed the research. All five authors wrote the paper.
Competing interests
The authors declare no competing interests.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Meng, D., Kumar, S.K., Grest, G.S. et al. Reentrant equilibrium disordering in nanoparticle–polymer mixtures. npj Comput Mater 3, 3 (2017). https://doi.org/10.1038/s41524-016-0005-8
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-016-0005-8