Abstract
Laser-driven plasma accelerators provide tabletop sources of relativistic electron bunches and femtosecond x-ray pulses, but usually require petawatt-class solid-state-laser pulses of wavelength λL ~ 1 μm. Longer-λL lasers can potentially accelerate higher-quality bunches, since they require less power to drive larger wakes in less dense plasma. Here, we report on a self-injecting plasma accelerator driven by a long-wave-infrared laser: a chirped-pulse-amplified CO2 laser (λL ≈ 10 μm). Through optical scattering experiments, we observed wakes that 4-ps CO2 pulses with < 1/2 terawatt (TW) peak power drove in hydrogen plasma of electron density down to 4 × 1017 cm−3 (1/100 atmospheric density) via a self-modulation (SM) instability. Shorter, more powerful CO2 pulses drove wakes in plasma down to 3 × 1016 cm−3 that captured and accelerated plasma electrons to relativistic energy. Collimated quasi-monoenergetic features in the electron output marked the onset of a transition from SM to bubble-regime acceleration, portending future higher-quality accelerators driven by yet shorter, more powerful pulses.
Similar content being viewed by others
Introduction
Since Tajima and Dawson proposed the idea of accelerating charged particles by surfing them on light-speed plasma waves1, plasma-based wakefield accelerators (WFAs) have fueled a worldwide quest for more compact, less expensive alternatives to conventional radio-frequency (rf) accelerators2,3. Tabletop laser-driven WFAs (LWFAs) have accelerated high-quality electron bunches to nearly 10 GeV within a few centimeters4. LWFAs underlie femtosecond X-ray sources5, and are part of mainstream planning for 21st century accelerator science in the U.S.6, Europe7 and the U.K.8. Chirped-pulse amplified (CPA) lasers9 that produce light pulses powerful and short enough to drive the high-amplitude, near-light-speed plasma waves needed to capture and accelerate electrons drove LWFA development for a quarter-century. But only solid-state CPA lasers at wavelengths λL ~ 1 μm have done so, except for a recent demonstration of an LWFA driven by a mid-wave-infrared laser (λL = 3.9 μm)10. Long-wave-infrared (LWIR, 8 < λL < 15 μm) CPA lasers producing pulses with terawatt peak power11,12 open new opportunities for LWFAs13. Here, we demonstrate an LWFA driven by picosecond λL ~ 10 μm pulses from a CPA carbon-dioxide (CO2) laser, and diagnose the properties of the laser-driven plasma waves and relativistic electrons that these waves capture and accelerate.
In their original proposal1, Tajima and Dawson envisioned a laser (L) pulse of duration τL < π/ωp impulsively exciting a collective electron-density (Langmuir) wave at the natural plasma frequency \({\omega }_{p}={[{n}_{e}{e}^{2}/{\epsilon }_{0}{m}_{e}]}^{1/2}\). Here, ne is the plasma’s unperturbed electron density, e and me denote electron charge and mass, respectively, and ϵ0 is the permittivity of free space. Such a pulse launches a plasma wave resonantly by expelling plasma electrons from within its sub-period envelope by exerting ponderomotive pressure14, equivalent to the gradient \(\nabla ({\epsilon }_{0}{E}_{L}^{2}/2)\) of the pulse’s cycle-averaged electromagnetic energy density, where EL is the optical field strength. To drive waves to their full amplitude, the pulse must impart relativistic momentum eEL/ωL ≳ mec to plasma electrons within each optical cycle \({\omega }_{L}^{-1}\)2, i.e. the momentum ratio a0 ≡ eEL/ωLmec, often called the dimensionless field amplitude or normalized vector potential, must exceed 1. This in turn necessitates peak intensity IL [W/cm2] \(\gtrsim {({a}_{0}/{\lambda }_{L}[\mu {{{{{{{\rm{m}}}}}}}}])}^{2}\times 1{0}^{18}\), and yields longitudinal electrostatic fields Ez [V/cm] ≈ (ne [cm−3])1/2 within the driven waves. In order for Ez to exceed accelerating fields in conventional rf accelerators ( ~ 106 V/cm) by an interesting factor of ≳ 102, plasma of density ne ≳ 1016 cm−3, and drive pulses of duration τL ≲ 1 ps with \({I}_{L}\gtrsim {({a}_{0}/{\lambda }_{L}[\mu {{{{{{{\rm{m}}}}}}}}])}^{2}\times 1{0}^{18}\) W/cm2 are needed. While today’s λL ~ 1μm CPA lasers routinely provide such pulses, CPA lasers available in the 1990s did not.
Instead, researchers at that time discovered two alternative LWFA drive schemes that circumvented these requirements. In one, the drive laser (coincidentally CO2) operated at two closely-spaced frequencies whose beat frequency matched ωp of ne ≈ 1016 cm−3 plasma. The dual-wavelength pulses thus drove plasma waves resonantly to high-amplitude at this specific density, and accelerated small numbers of externally-injected electrons, despite its sub-relativistic IL and multi-λp/c duration15,16. In the second scheme, researchers focused CPA pulses with λL ~ 1μm and τL ≫ λp/c into near atmospheric density plasma (ne ~ 1019 cm−3), since shorter duration pulses were not yet available. Nevertheless, strong wakes were generated and copious self-injected tens-of-MeV electrons produced17 when the peak power PL of the drive pulse exceeded the critical power18,19
for relativistic self-focusing (RSF), which is favored at high ne. Here, \({n}_{cr}={\epsilon }_{0}{m}_{e}{\omega }_{L}^{2}/{e}^{2}=(1.1\times 1{0}^{21})/{({\lambda }_{L}[\mu {{{{{{{\rm{m}}}}}}}}])}^{2}\) cm−3 is the critical plasma density at which ωL = ωp. Because of RSF, the drive pulse reached, and self-guided at, higher a0 inside the plasma than it had upon entering the plasma, enabling it to drive forward Raman instabilities18,19,20. These instabilities broke up the pulse into a train of sub-pulses spaced by λp, each of length cτL ≲ λp and relativistic strength a0 ≳ 1. Consequently they drove a wake beyond the wave-breaking limit, triggering self-injection of plasma electrons, as Stokes and anti-Stokes sidebands at ± nωp(n = 1, 2, 3, . . . ) appeared on the transmitted drive pulse spectrum. Although these self-modulated (SM) LWFAs yielded electron bunches of lower energy, and wider energy and angular spread, than today’s impulsively-excited bubble-regime LWFAs21, their decade-long (1995-2004) study uncovered much LWFA physics relevant to the latter regime, and drove short-pulse CPA technology needed to realize it. Moreover, SM-LWFAs remain of contemporary interest as strong betatron x-ray emitters22 and as models for self-modulated proton-driven plasma-based accelerators23.
For LWFA applications, today’s CPA CO2 lasers (pulse energy \({{{{{{{{\mathcal{E}}}}}}}}}_{L}\lesssim 10\) J, duration τL ≈ 2 ps12) have developed to a stage analogous to 1990s-era 1-μm CPA lasers. The duration of their shortest pulses still exceeds an oscillation period (λp/c ≈ 1 ps) of ne = 1016 cm−3 plasma, preventing bubble-regime excitation. Nevertheless, simulations24 indicate that the bubble regime is within reach with only 4 (2.5)-fold improvement in τL (\({{{{{{{{\mathcal{E}}}}}}}}}_{L}\)), offering the prospect of bubble structures of unprecedented size λp ≈ 300μm, along with better control of LWFA and higher e-beam quality. Meanwhile, ~ 10-μm CPA pulses available here provided nominally \({P}_{L}\approx {{{{{{{{\mathcal{E}}}}}}}}}_{L}/{\tau }_{L}\approx 2\) TW, which exceeds Pcr for ne as low as 1017 cm−3 [see Eq. (1)]. This enables SM-LWFA at > 100 × lower ne, via wakes of 10 × larger λp, than was possible with 1-μm CPA lasers of equivalent PL or demonstrated with mid-wave-infrared CPA lasers10. Equivalently, at fixed ne current 10-μm CPA pulses can trigger SM-LWFA at 100 × lower PL than 1-μm pulses: e.g., a recent study of SM-LWFA at ne = 3 × 1017 cm−3 used 1-μm pulses of PL ≈ 170 TW25. Simulations26,27 have borne out these general expectations for ~ 10-μm CPA pulses. Here, we demonstrate them in the laboratory for the first time. We first characterize SM-LWFA structures generated by 2 J, 4 ps pulses at PL > Pcr, but below the threshold of electron self-injection. Then, following a laser upgrade nominally to ~ 4 J, 2 ps pulses, with occasional more powerful pulses available, we characterized MeV electrons generated at PL > Pcr. But unexpectedly, we also observed electrons for PL as low as 0.3Pcr (i.e. ne down to 3 × 1016 cm−3), indicating that self-focusing was no longer essential to exciting plasma wakes or to capturing and accelerating plasma electrons. Moreover, collimated, quasi-monoenergetic electrons accompanied the divergent, thermal electrons traditionally generated by SM-LWFA, indicating that we had entered a transitional LWFA regime intermediate between SM and bubble-regime LWFA28. The results thus represent a steppingstone toward bubble-regime LWFAs of unprecedented spatial scale in ne ~ 1016 cm−3 plasma, which offer the possibilities of precisely injecting synchronized low-energy-spread, low-emittance bunches from conventional linacs into LWFAs. Large bubbles in turn offer excellent prospects for preserving high beam quality during acceleration, and thus for driving the next generation’s coherent X-ray sources29.
Results
Generation of self-modulated wakes
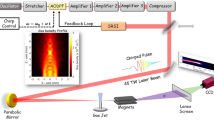
Experiments were carried out at Brookhaven National Laboratory’s (BNL’s) Accelerator Test Facility (ATF)30. To generate SM wakes, an off-axis parabola (OAP) mirror focused linearly-polarized drive pulses from ATF’s CPA CO2 laser11,12 to Gaussian spot radius w0 ≈ 27.5 μm at a focal plane located 1 ± 0.1 mm before the center of a supersonic hydrogen gas jet with an axially symmetric profile of 2 mm diameter. The dashed curve in Fig. 1a shows an idealized electron density profile ne(z) of the ionized gas jet along the laser propagation axis, here with plateau density ne = 5 × 1017 cm−3, that we used for simulations. In simulations the laser focal plane was at z = 0.1 mm, near the beginning of the density plateau (see Methods/Simulations for further discussion). The laser focal spot matched half a plasma wavelength λp/2 = π/kp (where kp = 2π/λp is the plasma wavenumber) for plateau density ne = 4 × 1017 cm−3, and thus satisfied a transverse near-resonant excitation condition kpw0 ~ π to within a factor of two over the density range 1017 ≲ ne ≲ 1018 cm−3 of interest here, even though the pulses were mismatched to the longitudinal resonant condition ωpτL ~ π by factors ranging from 7 (for ne = 4 × 1016 cm−3, τL = 2 ps) to 100 (for ne = 2 × 1018 cm−3, τL = 4 ps). This contributed to efficient excitation of stable longitudinally-propagating plasma waves, and contrasts with most previous SM-LWFA experiments17, in which λL ≈ 1 μm drive pulses were focused to spot sizes w0 ≫ λp/2 well outside the transverse resonant condition, subjecting the drive pulse to filamentation.
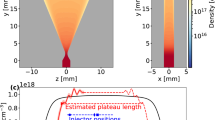
a Electron density ne(z) profile (black dashed curve) of unperturbed, fully-ionized 2 mm gas jet with ne = 5 × 1017 cm−3 plateau and 0.25 mm exit ramp used for simulations. Vacuum field envelopes of right-propagating 2 J, 4 ps (0.5 TW, yellow) and 4 J, 2 ps (2 TW, blue) pulses, which vacuum-focused at z = 0.1 mm (marked by star), are shown at z = 1.7 mm. Remaining panels: 2D wake profiles δne(x, z)/ne when b 0.5 TW or d 2 TW pulses reach z = 1.7 mm, and simultaneous normalized 2D electron momentum profiles pz(x, z)/mec for c 0.5 TW and e 2 TW excitation, i.e. below and above self-injection threshold, respectively. Black curves in (c) and (e): longitudinal electric field Ez(z) profiles on the laser propagation axis, referenced to right-hand vertical scales. f Projection onto a plane of ≥10 MeV electrons at a later instant, after the 2-TW-laser-driven wake accelerated them into vacuum.
To generate wakes that did not capture and accelerate electrons, the ATF laser delivered drive pulses of 4 ps (FWHM) duration and up to 2 J energy (i.e. PL ≲ 0.5 TW) at wavelength λL = 10.3 μm. Focused pulses thus had peak vacuum intensity up to I0 ≈ 4 × 1016 W/cm2, or vacuum laser strength parameter \({a}_{0}^{(vac)}\approx 1.8\). Since here a0 ≳ 1, the interaction was mildly relativistic. Simulations of the interaction that include tunneling ionization, exemplified by Fig. 1b–c, show that under these conditions, the wings of a focused Gaussian CO2 laser pulse self-ionize a hydrogen column of radius Rp ~ 50 μm (see Fig. 1b). Non-Gaussian (e.g. Lorentzian, aberrated) pulses of the same FWHM would ionize an even wider column because of their more intense wings. Regardless of the exact Rp, the drive pulse generated wakes of transverse radius Rw ≈ w0 ≈ 20 μm that lay entirely within the self-ionized plasma column. Thus pre-ionization was not essential to produce a plasma wide enough to support the wake oscillations. By adjusting backing pressure of the gas jet nozzle, electron density ne of the resulting plasma was varied over the range 1017 cm−3 < ne < 2 × 1018 cm−3, which corresponded to a range 1.7 > Pcr > 0.08 TW of critical powers [see Eq. (1)] that straddled the maximum available incident peak power \({P}_{L}^{(max)}\approx 0.5\) TW. Experiments discussed below detected wakes only for PL > Pcr, i.e. for ne > 3.5 × 1017 cm−3. Their wavelengths λp ranged from 56 μm at this threshold to 24 μm at ne = 2 × 1018 cm−3. This threshold ne was nearly 100 × lower than densities at which λL = 1 μm laser pulses of similar PL generated detectable SM wakes17. Panels b and c of Fig. 1 show simulated temporal snapshots of the electron density ne(x, z) (b) and longitudinal momentum pz(x, z) (c) profiles of wake oscillations for plateau density ne = 5 × 1017 cm−3, after the λL = 10 μm, 0.5 TW drive pulse propagated to the end (z = 1.6 mm) of the gas jet’s density plateau (see Methods for details of simulations). Our simulations presented in ref. 27 show a strong influence of the dynamic ionization model on the structure and evolution of the SM wakes compared to the pre-ionized plasma approximation. In dynamically ionized gas the laser pulse modulates more strongly, and stronger wakes form earlier because of the stronger ponderomotive force. Likewise, including ion motion in simulations leads to the formation of ionization channels (Fig. 1b,d), which are largely suppressed in simulations using the fixed ion approximation, as shown in Supplementary Fig. 1. ref. 27 further discusses the role of dynamic ionization and ion motion in wake formation.
Even though wakes formed for PL > Pcr, the pz(x, z) profile in Fig. 1c shows only momenta attributable to the wake oscillations themselves. The additional z-momentum that would be expected if the wake had trapped and accelerated electrons is not present. This means that at PL = 0.5T´W and ne = 5 × 1017 cm−3 we are above the self-focusing threshold needed to form wake structures, but below the self-injection threshold. This absence of self-injected, trapped electrons accelerating along the wake propagation direction in these simulations corroborates our observation of no accelerated electrons.
To generate strongly nonlinear SM wakes that captured and accelerated plasma electrons to produce a collimated beam, the CO2 laser was upgraded (see Methods) to deliver nominally 2 ps, λL = 9.2 μm pulses with energy up to 4 J to the jet with the same focus. Occasional individual pulses with τL as small as 1.8 ps, \({{{{{{{{\mathcal{E}}}}}}}}}_{L}\) has high as 6 J, and PL approaching ~ 3 TW, with only slightly degraded focus (see Methods), were measured at the vacuum interaction region. With the upgraded pulses, we observed relativistic electron production at densities down to ne ≈ 3 × 1016 cm−3. Vacuum peak intensity now reached I0 ≈ 2.5 × 1017 W/cm2 (a0 ≈ 3.9) for 6 J pulses. As a result, the interaction became strongly relativistic, and the forward Raman instability grew more rapidly than for the 0.5 TW pump. Panels d and e of Fig. 1 show simulations of the corresponding ne(x, z) (d) and pz(x, z) (e) profiles of SM wakes that 2 TW pulses drive in self-ionized plasma of plateau density ne = 5 × 1017 cm−3. Compared to the ne(x, z) profile in Fig. 1b, the self-ionized plasma column is twice as wide, relativistic self-focusing is stronger and wake oscillations reach wave-breaking amplitude (see Fig. 1d). In contrast to the pz(x, z) profile in Fig. 1c, copious electrons with relativistic pz are now evident. In Fig. 1e, electron bunches accelerated to pz/mec ~ 40 (red) are distributed among the multiple accelerating bins of the wake that the drive pulse overlapped. Moreover they are distributed randomly throughout each bin because the plasma waves had broken, injecting plasma electrons at uncontrolled initial locations and times prior to their trapping in the wake’s accelerating potential. This wave-breaking and injection, once started in mid-jet, continued through the end of the interaction, since they are the culmination of the forward Raman instability. Figure 1f shows a subset of the accelerated electrons with Ee > 10 MeV after they had propagated into vacuum. The simulated angular and energy distributions of these electrons are shown later in comparison with experimental data.
Characterization of self-modulated wakes
Figure 2 a shows the schematic setup for probing wakes generated under the conditions of Fig. 1b,c via forward collective Thomson scatter (CTS)31,32. When the CO2 pump drove wake oscillations δne(x, t) above the level of thermal fluctuations, they appeared to a green (λpr = 0.532 μm) co-propagating probe pulse of duration τpr = 4 ps \( > {\omega }_{p}^{-1}\) (see Methods) as a refractive index grating δη(x, t) ≈ δne(x, t)/2ncr moving at phase velocity ωp/kp33. This grating scattered probe light at frequencies ωpr ± ωp and wave vectors kpr ± kp, over and above background Thomson scatter at ωpr from uncorrelated individual electrons. A lens (not shown) collected forward CTS probe light, and relayed it to the entrance slit of a spectrometer through a notch interference filter that blocked frequencies within the bandwidth of the incident probe, but transmitted its Stokes and anti-Stokes sidebands. When the delay Δt between the green probe and CO2 pulses was 0, the overlapped pump and probe pulses also generated difference- and sum-frequency signals at ωpr ± ωL. The raw spectrometer data in Fig. 2b, taken at Δt = 0, shows both Stokes/anti-Stokes and difference-/sum-frequency generation (DFG/SFG) signals for seven different values of plasma density in the range 0.57≤ne≤1.69 × 1018 cm−3, calibrated by independent optical measurements of the density profile ne(z) of the ionized gas jet with ± 10% accuracy using an ionization-induced plasma grating technique34. The magnitude \({\omega }_{p} \sim {n}_{e}^{1/2}\) of the Stokes/anti-Stokes shifts increased as expected with ne, whereas the DFG/SFG peaks remained at ne-independent frequencies and helped to calibrate the spectrometer’s frequency scale.
a Schematic experimental setup with green probe pulse co-propagating at delay Δt behind CO2 pump pulse. b Spectra of forward-scattered probe light for PL = 0.5 TW and Δt ≈ 0, for seven indicated plasma densities ne, showing ne-dependent anti-Stokes/Stokes sidebands due to CTS from wake and ne-independent difference- and sum-frequency-generation (DFG/SFG) peaks at ωpr ± ωL.
Figure 3 a compares the seven measured Stokes and anti-Stokes shifts ∣ΔλCTS(ne)∣ (data points) from Fig. 2b quantitatively with λp(ne). The right-hand vertical scale gives the corresponding frequency shifts ΔfCTS(ne). The agreement is excellent. Because of the low ne, these frequency shifts are much smaller — 7 < ∣ΔλCTS∣ < 12 nm — than those observed by LeBlanc et al.35 — namely ∣ΔλCTS∣ = 45 nm, ∣ΔfCTS(ne)∣ = 48 THz — by probing SM wakes driven by λL = 1 μm pulses in ne = 3 × 1019 cm−3 plasma using the same λpr (see e.g. Fig. 1 of ref. 35). Moreover, in the previous experiment DFG and SFG peaks could not be observed because their shift from λpr was beyond the range of the CTS spectrometer. The green-shaded region of Fig. 3a corresponds to Stokes/anti-Stokes shifts for ne < 4 × 1017 cm−3, but was notch-filtered. Nevertheless, by rotating this interference filter slightly we could leak light from the blocked spectral window 525 < λ < 537 nm into the CTS spectrometer. Through such measurements we confirmed, as shown in Fig. 3b, that sideband intensity within this window, was vanishingly weak or absent for ne < 4 × 1017 cm−3 for excitation at PL. From Eq. (1), this turn-on density corresponds to Pcr = PL = 0.5 TW. The red-shaded region in Fig. 3a corresponds to ne > 2 × 1018 cm−3, i.e. densities within a factor of 5 of the critical density for λL = 10 μm light. At these densities, back-reflections of the incident CO2 laser light from the gas jet became strong enough to endanger upstream optics in the CO2 laser system. We therefore avoided densities in this range.
a Spectral Stokes/anti-Stokes shift vs. ne. Data points: observed shifts for the seven ne values in Fig. 2b. Solid curve: plasma wavelength vs. ne. Green shading: no sidebands observed. Red shading: no measurements attempted because of strong pump back-reflections from ionized gas jet. b Probe sideband intensity vs. ne for PL = 0.5 TW and Δt ≈ 0. Black data points: measured average probe Stokes/anti-Stokes intensities. Colored data points and connecting lines: simulated pump Stokes (blue) and anti-Stokes (orange) sideband intensities at ne = 5, 7, 9 and 10 × 1017 cm−3. Error bars in both a and b: 1 standard deviation of variation among repeated runs.
The data points in Fig. 3b illustrate how side-band intensity varied as ne increased from the lower to upper threshold described above, with PL fixed at 0.5 TW and Δt ≈ 0. Each data point represents an average over several shots and over the Stokes and anti-Stokes sidebands. Sideband intensity rose sharply as ne increased from 4 × 1017 cm−3 to 7 × 1017 cm−3, then fell off equally sharply at higher ne. There is no single explanation for this trend. The main factors governing sideband intensity are: i) wake amplitude; ii) wake lifetime within the 4 ps probe longitudinal envelope; iii) wake location within that envelope; iv) dephasing between co-propagating wake and probe. Generally, strong sidebands occur when a high-amplitude wake filling a large fraction of the most intense portion of probe’s longitudinal envelope co-propagates with the probe for approximately one coherence length31. As ne increased from zero, wakes began to form when PL ≈ Pcr, here at ne ≈ 4 × 1017 cm−3. As ne increased further, Pcr decreased, causing stronger self-focusing near the jet exit. Initially, this simply increased wake amplitude, causing stronger CTS. Eventually, however, the pump over-focused, generating wakes that decayed and become chaotic faster, and formed earlier both within the probe profile, where intensity was weaker, and within the jet, resulting in stronger dephasing. These factors combined to weaken CTS. These results emphasize that sideband intensity is not simply proportional to wake amplitude.
To emulate the observed trend in probe CTS intensity at minimal computation cost, we simulated the corresponding trend in pump CTS, which requires tracking only a single light frequency. Qualitatively similar ne-dependence is expected, since the pump coincided temporally with the probe at Δt ≈ 0. We therefore self-consistently simulated wake formation/propagation and pump spectral evolution at four ne within the measured range27. Blue and red data points in Fig. 3b show the results. We applied an overall vertical shift to simulated pump Stokes (blue) and anti-Stokes (red) intensities to optimize the fit to relative probe sidebands, since absolute sideband intensities could not be measured accurately. The simulations qualitatively reproduced the observed trend of an initial increase in sideband intensity followed by a decrease at higher density.
Figure 4 a illustrates how the intensity and spectral shape of the first Stokes sideband varied as PL/Pcr increased from ~ 0.2 to 2.5 at fixed density ne = 1.3 × 1018 cm−3 and delay Δt ≈ 0. Spectra of the probe pulse (λpr = 0.532 μm), a small portion of which was leaked into the spectrometer by rotating the notch interference filters, and of the difference-frequency signal (λDFG ≈ 0.560 μm) are shown for comparison. For PL/Pcr < 1, no sidebands were observed. Then within the narrow range 1 < PL/Pcr < 1.2 sideband intensity grew quickly. For PL/Pcr > 1.2 it fluctuated erratically from shot-to-shot around an average, but nearly PL-independent, value. The solid red curve in Fig. 4a summarizes these trends, which mirrored those of the anti-Stokes sideband. DFG signals were observed at normalized power down to PL/Pcr ≈ 0.5, then strengthened gradually with increasing PL. RMS fluctuations of both CTS sideband and DFG signals significantly exceeded those of the probe power Ppr itself, as is evident from the leaked probe signals in Fig. 4a.
a 1st Stokes intensity vs. PL/Pcr at ne = 1.3 × 1018 cm−3. Notch filter is rotated slightly to leak a small fraction of 532 nm probe light. 1st Stokes peaks at ~ 542 nm appear only for PL/Pcr > 1; pump-probe difference-frequency-generation (DFG) peaks at ~ 560 nm are detectable down to PL ≈ 0.5 Pcr. b Examples of forward CTS spectra at same ne for two rare shots showing 2nd-order anti-Stokes (blue curve) or Stokes (dashed red curve) peaks along with corresponding 1st-order peaks. Weak spectral lines between 1st and 2nd anti-Stokes peaks originate from aluminum in gas nozzle that was vaporized by wings of the CO2 pulse. Partial peak at ~ 505 nm is the pump-probe sum-frequency signal.
To understand these trends, we must take into account the influence of wave vector mismatch on both forward CTS and DFG/SFG signals. Forward-scattered power PS,AS of first-order Stokes (S) or anti-Stokes (AS) sidebands, normalized to the portion of probe power Ppr that overlaps the wake of amplitude δne over interaction length L, is given by31,32
where r0 is the classical electron radius, \(F\equiv {\sin }^{2}(\Delta kL)/{(\Delta kL)}^{2}\) is the wave vector mismatch factor and Δk = kpr − kS,AS ± kp is the mismatch of the z-components of the wave vectors. Here, kpr is the z-component of the wave vector of incident probe light, kS,AS of forward-scattered sidebands and kp = ωp/vp of the plasma wave, the phase velocity vp of which equals pump group velocity vg, and the sign of which is taken as + ( − ) for S (AS). For the conditions of Fig. 4a, one finds Δk ≈ 150 cm−1, implying coherence length Lcoh = π/(4∣Δk∣) ≈ 50μm, i.e. CTS signals grow only over propagation distances ~ 50μm, < 5% of the plasma density plateau length (see Fig. 1a), before de-phasing from, and destructively interfering with, previously generated CTS light. Thus fluctuations in L of only 50μm, which we cannot control, can cause Ps to fluctuate between 0 and its maximum value. This explains why shot-to-shot fluctuations in PS,AS exceed those in Ppr. A factor of the same form as F, with \(\Delta {k}^{{\prime} }={k}_{{{{{{{{\rm{DFG}}}}}}}}/{{{{{{{\rm{SFG}}}}}}}}}-{k}_{pr}\pm {k}_{pu}\) replacing Δk, governs DFG/SFG. One finds \({L}_{{{{{{{{\rm{coh}}}}}}}}}^{{{{{{{{\rm{DFG}}}}}}}}/{{{{{{{\rm{SFG}}}}}}}}}\approx 10\,\mu {{{{{{{\rm{m}}}}}}}}\), implying even greater sensitivity to fluctuations in L.
Normalized wake amplitude δne/ne was difficult to estimate accurately from Eq. (2), since an absolute measurement of PS/AS was required, and the fraction of the probe that overlaps the wake was not accurately known. Moreover, L was not well-characterized, and F varied rapidly with L. However, on occasional shots for which second-order Stokes and/or anti-Stokes signals were visible — see e.g. Fig. 4b — a more accurate estimate was possible. Harmonics of δne/ne, and thus of first-order S/AS sidebands, appear as δne/ne increases because the wave steepens36,37,38. Harmonic analysis for a cold plasma yields the ratio37,38,39
where \(\delta {n}_{e}^{(m)}\) (m = 1, 2) denotes the mth Fourier component of the wake oscillations and ne the uniform background plasma density. The amplitude \({P}_{S,AS}^{(2)}\) of the 2nd-order S/AS sideband is related to \(\delta {n}_{e}^{(2)}\) by an equation of the form (2), with \({P}_{S,AS}^{(2)},\delta {n}_{e}^{(2)},\Delta {k}^{(2)}\) and L(2) replacing their first-order counterparts. In the approximations that L(2) ≈ L and 1st- and 2nd-order wave vector matching factors average to similar values over multiple shots, the right-hand side of (3) can be approximated by \({[{P}_{S,AS}^{(2)}/{P}_{S,AS}^{(1)}]}^{1/2}\), i.e. the square-root of the 2nd-to-1st-order S/AS power ratio. The data in Fig. 4b, which is representative of a multi-shot average, shows \({P}_{S,AS}^{(2)}/{P}_{S,AS}^{(1)}\approx .01\), implying \(\delta {n}_{e}^{(1)}/{n}_{e}\approx 0.1\) using Eq. (3). Since 2nd-order sidebands appeared on only ~ 5% of shots, we infer that \(\delta {n}_{e}^{(1)}/{n}_{e} < 0.1\) for most shots driven by 0.5 TW pulses.
Figure 5 a shows how the Stokes and anti-Stokes sideband profiles varied with pump-probe delay Δt in increments of 0.33 ps at fixed ne = 1.5 × 1018 cm−3 and PL = 0.5 TW. Both sidebands rise and fall within times close to the width of the pump-probe cross-correlation (see Fig. 5c). High-amplitude sidebands at Δt ≈ 0 were spectrally multi-peaked (see Fig. 5b). Their strongest peaks occurred at the same frequency ωpr ± ωp as the single peak of lower-amplitude wakes (red curve, Fig. 5b), but satellite peaks at smaller Stokes/anti-Stokes shifts accompanied them. We attribute this spectral structure to transient ne gradients within the pump envelope due to its ponderomotive force on plasma electrons, which can lead to a distribution of Stokes/anti-Stokes shifts at Δt ≈ 0. Cross-phase modulation of the probe by the strong pump may have also contributed40. Figure 5d shows results of a SPACE simulation that included a continuous-wave (CW) probe beam (λpr = 2.5 μm) co-propagating with the 10 μm, 4 ps drive pulse, shown by the red dashed curve. Using a CW probe saved computational time, because the time response could be deduced in a single computational run from the CTS response at different locations within the probe with respect to the pump. The ~ 1 ps relaxation is consistent with the dephasing time of the inhomogeneously broadened Raman-shifted lines. The resulting plot (data points and blue connecting lines in Fig. 5d), however, is not convolved with the 4 ps probe used in the experiments. Including this probe convolution yields the dotted green curve in panel c). It is slightly broader than the pump-probe autocorrelation, shown by the red-dashed curve in panel c), but slightly narrower than the measured response. A weak component of both sidebands persisted out to Δt ≈ 30 ps, suggesting a slower decay mechanism for low-amplitude wakes. The simulation could not capture this feature because of numerical noise. We have ruled out the possibility that post-pulses caused this delayed feature since autocorrelation measurements12 do not detect any post-pulses in the interval 0 < Δt < 25 ps, and those detected at longer Δt are too weak to generate wakefields detectable by CTS. Its ~ 30 ps relaxation is, however, consistent with the decay time of electron plasma waves into ion acoustic waves41.
a 1st Stokes and anti-Stokes sideband intensity profiles vs. pump-probe delay Δt at ne = 1.5 × 1018 cm−3 and PL = 0.5 TW. b Example of spectrally-structured sideband at Δt ≈ 0 (blue curve), in contrast to simpler single-peaked sideband observed at ∣Δt∣ > 0 (red dashed curve). c Blue data points: Plot of sideband intensity vs. Δt for a different data run than a, but under identical conditions, averaged over first Stokes/anti-Stokes peaks and multiple shots. Blue dashed lines connect data points. Red dashed curve: pump-probe cross-correlation. Green dotted curve: simulated response from d convolved with pump-probe autocorrelation. d Simulated average Stokes/anti-Stokes sideband amplitude on continuous-wave probe (λpr = 2.5 μm, field amplitude Epr = EL/200, focus \({w}_{0}^{pr}=40\,\mu {{{{{{{\rm{m}}}}}}}}\)) co-propagating with a 2 J, 4 ps pump (λL = 10.6 μm, w0 = 20 μm), with profile shown by red dashed curve, in ne = 1018 cm−3 plasma at selected delays Δt. Error bars: 1 SD of variation among repeated experimental c or simulation d runs.
Measurements of accelerated electrons
Upon decreasing CO2 laser pulse duration to τL ≈ 2 ps and increasing energy \({{{{{{{{\mathcal{E}}}}}}}}}_{L}\) to ≲ 4 J (i.e. PL ≲ 2 TW), with occasional pulses up to PL ~ 3 TW, we observed collimated MeV electrons from plasmas of ne down to 3 × 1016 cm−3, 13 times lower than the threshold ne ≈ 4 × 1017 cm−3 observed at lower PL by CTS. Electron yield peaked with the vacuum laser focus shifted forward toward the center, rather than exactly at the entrance, of the gas jet. We adjusted the exact vacuum focus location empirically with each run to maximize yield, but generally it lay between the entrance and center for experiments.
Figure 6 a plots total charge yield (determined from integrated luminescence from a calibrated42 downstream scintillating screen) vs. PL/Pcr for ~ 100 shots of power 0.2 ≲ PL ≲ 3.3 TW driving plasmas of four different ne, indicated in the legend. Approximately half of these shots, shown by green diamonds, used pulses of power 0.2 ≲ PL ≲ 1.5 TW to drive ne ≈ 4 × 1017 cm−3 plasma, for which Pcr = 0.5 TW. At PL/Pcr < 0.7 we observed only the detector noise floor at this ne. But yield rose sharply for PL ≳ 0.7Pcr, and exceeded 100 pC for PL > Pcr. Remaining data points show yield for shots up to 3.3 TW peak power driving less dense plasma: ne = 1.6 × 1017 cm−3 (Pcr = 1.5 TW, inverted black triangles); 0.9 × 1017 cm−3 (Pcr = 2.6 TW, filled blue squares; 0.4 × 1017 cn−3 (Pcr = 5.9 TW, filled red circles). At all four ne, the threshold power \({P}_{L}^{({{{{{{{\rm{thr}}}}}}}})}\) for generating detectable charge, indicated by color-coded arrows along the upper horizontal axis of Fig. 6(a), was less than Pcr. At ne = 1.6 × 1017 cm\({}^{-3},{P}_{L}^{({{{{{{{\rm{thr}}}}}}}})}\) reaches as low as 0.3Pcr, more than 3 × smaller than the wake formation threshold observed by CTS for longer, less powerful pulses in denser plasma (Fig. 1d–e). Such sub-Pcr appearance thresholds indicate that self-focusing was no longer the principal mechanism triggering wake formation or acceleration at these low ne.
a Total charge of > 1 MeV electrons vs. normalized peak power PL/Pcr of ~ 2 ps laser pulses driving LWFA in plasma of 4 densities in the range 0.4 × 1017≤ne≤4 × 1017 cm−3 as per key. b Data from a re-plotted as a function of \({a}_{0}^{(vac)}\). Color-coded arrows at top of a, b: electron appearance thresholds for each ne.
To help understand these sub-Pcr thresholds, Fig. 6b re-plots data in Fig. 6a as a function of vacuum focused \({a}_{0}^{(vac)}\) for each ne. Now there are four ne-dependent appearance thresholds at \({a}_{0}^{(vac)}=\) 1.35 (for ne = 4 × 1017 cm−3), 1.9 (for ne = 1.6 × 1017 cm−3), 2.5 (for ne = 0.9 × 1017 cm−3), and 3.4 (for ne = 0.4 × 1017 cm−3). Moreover, all are relativistic. Evidently in this regime, a0 is high enough to trigger wake formation without self-focusing. Indeed exponentially-growing self-modulated wakes driven by relativistically intense laser pulses with PL/Pcr as small as 0.25 have been seen in computer simulations (see e.g. Fig. 4 of43), but not, to our knowledge, previously realized in experiments. In contrast, under the conditions of e.g. Fig. 4a (ne = 1.3 × 1018 cm−3, Pcr = 0.15 TW), \({a}_{0}^{(vac)}=0.89\) at PL = Pcr. Thus for \({P}_{L} < {P}_{cr},{a}_{0}^{(vac)}\) was sub-relativistic, insufficient to drive growth of the forward Raman and self-modulation instabilities rapidly enough to produce a detectable wake.
Figure 7 a shows a simulated e-beam profile 27 cm downstream of the accelerator for the conditions of Fig. 1d–f (ne = 5 × 1017 cm−3). The approximately Gaussian profile with ΔθHWHM ≈ 75 mrad typified most observed profiles at this ne. At lower ne, on the other hand, about 90% of electron-producing shots revealed, in addition to a near-Gaussian background of similar HWHM, an intense core with divergence 40 ≳ ΔθHWHM ≳ 12 mrad. Figure 7b–d shows examples of luminescence images recorded on a LANEX screen at z = 27 cm for ne = 1.6, 0.9, and 0.4 × 1017 cm−3. The narrowest such peaks had half-widths ΔθHWHM ≈ 12 mrad. The centroids of these narrow beamlets exhibited RMS shot-to-shot pointing fluctuations of ~ 5 mrad.
a Simulated e-beam profile at z = 27 cm for conditions of Fig. 1d-f, and b–d luminescence images for the 3 lowest ne in Fig. 6 recorded on LANEX screen at z = 27 cm. White arrows: paths of line-outs displayed around periphery. Black dots: line-out data; long-dashed pink curves: fits of each lineout to sum of a wide (w) Gaussian \(A{e}^{-{({\theta }_{i}-{\theta }_{0i})}^{2}/{\sigma }_{wi}^{2}}\) (green, i = x, y), one or more narrow (n) Gaussians \({B}_{j}{e}^{-{({\theta }_{i}-{\theta }_{0ij})}^{2}/{\sigma }_{nij}^{2}}\) (red, j = peak label), and background count C, assumed constant for each panel. Non-zero parameter values are listed inside each panel in units of nC/sR (A, Bj) or mrad (θ0i, σwi,nij). C = 2 nC/sR for b and c and 0.1 for d.
To characterize the energy of electrons contributing to each part of this angular distribution, the intense core and a slice of the diffuse background passed through the 2 mm-wide vertical entrance slit of a magnetic spectrometer. The left-hand column of Fig. 8 shows energy- (horizontal) and angle- (vertical) resolved luminescence images recorded on LANEX screens at the spectrometer’s detection plane, from electrons accelerated at ne = 2.4 × 1017 cm−3 (a1) and 4.1 × 1017 cm−3 (a2-a5). The right-hand column shows corresponding electron energy distribution curves, obtained by vertically integrating the raw data and re-scaling the horizontal axis to be linear in Ee. For the data in Fig. 8a, the LANEX screen was positioned diagonally across the spectrometer’s dispersion plane, as shown by the green line in the inset of panel b1. Here, it recorded electrons of energies 0 < Ee < 7 MeV. Beyond Ee ~ 1 MeV, electron yield decreased exponentially and angular spread narrowed with energy, mirroring thermal electron spectra typically observed from SM-LWFAs at higher ne17. Similarly-shaped electron spectra were observed in this energy-range for nearly all electron-yielding shots.
LANEX luminescence images from magnetic spectrometer (left column) and corresponding energy distribution plots (right column). Row 1: Data taken with LANEX screen in position 1 (see inset of panel b1: solid green line) and ne = 2.4 × 1017 cm−3 to record electrons with energy 0 < Ee < 7 MeV. Rows 2-5: Data taken with LANEX screen in position 2 (see inset of panel b2: solid green line) and ne = 4.1 × 1017 cm−3 to record electrons with energy 7 < Ee < 15 MeV. In left column, horizontal Ee scale at bottom applies only to Rows 2-5. Arrows in a3 thru a5 highlight quasi-monoenergetic features. Black dots in b1 and b2 are fits of the exponential tail of the energy distribution curve to functions \(\exp (-{E}_{e}/{k}_{B}{T}_{e})\), with kBTe = 1.2(0.62) MeV for b1 (b2). Open black squares in b5 show the energy distribution of electrons from the simulation in Fig. 1d–f, for conditions (ne = 5 × 1017 cm−3, 4.0 J pump) close to those of the measured distribution in this panel.
When the LANEX screen was re-positioned at the back of the spectrometer (green line at the top of the inset of panel b2), it recorded electrons of energies 7 < Ee < 15 MeV, as rows 2-5 of Fig. 8 exemplify. Figure 8a2 displays an exponential distribution, possibly the high-energy tail of a distribution similar to the one shown in Fig. 7a1. Black dots in panels b1 and b2 show fits of the high-energy tail of these energy distributions to exponential functions \(\exp (-{E}_{e}/{k}_{B}{T}_{e})\), where kB is Boltzmann’s constant, and Te is an effective electron temperature.
Remaining rows of Fig. 8 uniquely exhibit spectral peaks, which were observed on approximately 90 % of ~ 70 electron-yielding shots characterized with the spectrometer in its higher energy configuration. Supplementary Fig. 2 presents additional examples of electron spectra with both exponential and peaked spectra. Panels a3 and b3 present a sharp peak at Ee ≈ 7.7 MeV (superposed on a broader background) containing ~ 0.1 pC charge with an angular half-width ΔθHWHM ≈ 2 mrad in the vertical direction and a fractional horizontal width (HWHM) ΔEe/Ee of only 0.03 (i.e. Ee = 7.7 ± 0.2 MeV). Our observations of spectrally-integrated luminescence images such as Fig. 7b–d consistently show vertical and horizontal divergences of similar magnitude. Thus on the reasonable assumption that they are equal, this beamlet’s inherent divergence is responsible for ~ 2/3 of the horizontal width of the recorded feature. When divergence is de-convolved, we obtain fractional energy spread ΔEe/Ee ≈ 0.01 (i.e. Ee = 7.7 ± 0.07 MeV), which rivals the smallest fractional energy spreads reported for bubble-regime LWFAs44. Panels a4 and b4 show a spectrum with two quasi-monoenergetic peaks, possibly due to electrons trapped in separate accelerating buckets of the wake. One is centered at Ee ≈ 7 MeV with ~ 100 pC charge and ΔEe/Ee ≈ 0.15, the other at Ee ≈ 8.5 MeV with ~ 0.5 pC and ΔEe/Ee ≈ 0.01 when de-convolved as described earlier. At the other extreme, in panels a5 and b5 we see a peak centered at Ee = 9 MeV with θ ≈ 7 mrad containing 50 pC with ΔEe/Ee ≈ 0.35. For comparison, the open black squares show the qualitatively similar peaked spectrum of electrons emerging from the simulated accelerator in Fig. 1d–f for similar conditions. This comparison shows that simulations reproduce peaked (as opposed to exponential) spectra observed on the high-energy screen with close to the observed peak energy, but do not capture the exceptionally narrow features shown in rows 3 and 4 of Fig. 8. Spectral peaks on other shots had energy/angular widths and charges in between these extremes. Quasi-monoenergetic peaks observed on the high-energy screen were narrower in angular spread than the exponential distributions observed on the low-energy screen, suggesting that they correspond to the bright cores of the images in Fig. 7b–d. The angular width of the quasi-monoenergetic peaks scaled approximately in proportion to its energy width.
Discussion
The appearance of quasi-monoenergetic, collimated-electron spectral features on ~ 90% of electron-yielding shots suggests that for ne≤4 × 1017 cm−3 and PL > 0.5 TW, we have entered a transitional regime between SM-LWFA and “forced"28 or bubble-regime21 LWFA in which the number Np = ωpτL/2π of plasma periods within the drive pulse envelope is small, enabling drive pulse energy to channel preferentially into a single plasma period as it self-steepens. Here, Np ranges from ~ 10 for the conditions of rows 2 thru 5 of Fig. 8 (ne ≈ 4 × 1017 cm−3) to ~ 3 for the conditions of Fig 7d (ne ≈ 4 × 1016 cm−3). Although we have so far observed unambiguous quasi-monoenergetic spectral peaks only at the higher density (Fig. 8), where yield is higher, we observe the correlated intense beam cores down to the lower density (Fig. 7d). Importantly, here we observe signatures of this transitional regime at ~ 100 × lower ne than in its original discovery using λL ≈ 1 μm lasers28 or in more recent experiments using λL = 3.9 μm lasers10. Forced LWFA at λL ≈ 1 μm was a precursor of strongly nonlinear bubble-regime LWFA at the same λL, which for the first time provided plasma-based accelerating and focusing fields capable of preserving low ΔEe/Ee and emittance, and which awaited only the development of shorter, more powerful λL ≈ 1 μm drive pulse lasers a couple of years later. Similarly here, shorter (τL < 1 ps), more powerful (PL ≳ 20 TW) λ ≈ 10 μm drive pulse laser technology capable of supporting bubble-regime LWFA at ne as low as 1016 cm−324 now appears within reach (see Methods)45,46. The importance of achieving the bubble regime at ne ~ 1016 cm−3 is two-fold: (1) high-quality, near-fully-blown-out bubbles can be generated with little or no uncontrolled background injection from the surrounding plasma24, the principal origin of > 1 % energy spreads and spin depolarization that currently limit applications of LWFA as e.g. free-electron-laser drivers or nuclear probes; (2) these bubbles are then large enough (e.g. bubble radius Rb ≈ πλp ≈ 0.3 mm at ne ≈ 1016 cm−347) to accommodate precise, reproducible injection of sub-percent ΔEe/Ee, spin-polarized, high-charge electron bunches from a small conventional MeV linac, given current tolerances on pointing and timing jitter and bunch compression48.
In summary, we have demonstrated SM and forced laser wakefield excitation and acceleration using a LWIR drive laser for the first time. Long-wave (λL ≈ 10 μm) excitation enables SM-LWFA at plasma densities 0.3 × 1017 ≲ ne ≲ 1018 cm−3 that are ≳ 100 × lower, and with wavelengths λp that are ~ 10 × larger, than previous SM-LWFA experiments using λL ≈ 1 μm laser drive pulses. Although SM wakes are by definition excited non-resonantly (i.e. cτL > > λp/2) in the longitudinal dimension, here for the first time we have excited them near-resonantly in the transverse dimension (i.e. w0 ≈ λp/2), generating stable SM wakes that can be accurately simulated. Accordingly our fully 3D PIC simulations have accurately modeled four key observables: (1) the SM-wake excitation threshold PL ≈ Pcr for ne > 4 × 1017 cm−3 (see Fig. 1b–c); (2) the onset of self-injection for wakes excited by 2 TW pulses (see Fig. 1d–f); (3) the dependence of CTS sideband intensity (which is related to wake amplitude) on ne at fixed PL and Δt (see Fig. 3b) and on (4) Δt at fixed PL and ne (see Fig. 4a). This quantitative agreement, however, was obtained only when ionization and motion of hydrogen ions was taken into account. The quantitative agreement between measurements and simulations achieved here for SM-LWFA lends confidence to simulations24 that predict efficient LWIR excitation of fully blown-out bubble regime wakes of unprecedented size (λp ≈ 300 μm) in ne ≈ 1016 cm−3 plasma — enabling unprecedented control over e-beam energy spread, emittance and polarization — if CO2 lasers can be scaled to pulse durations τL < 1 ps and peak powers PL > 20 TW. Recent progress with CPA CO2 laser technology suggests that this goal is within reach45.
Methods
CO2 laser
The terawatt CO2 laser system at ATF is based on a master oscillator - power amplifier design with CPA11,12. An optical parametric amplifier (Quantronix Palitra) following a Ti:Sapphire oscillator- amplifier system generates 15 μJ, 350 fs seed pulses. A grating stretcher chirps these to 140 ps and filters out a 0.8 THz wide part of their spectra sufficient for compression to 2 ps. Stretched pulses are transmitted to a 10 bar, mixed-isotope, discharge-pumped CO2 regenerative amplifier (SDI Lasers, Ltd. HP-5) through a Faraday Isolator (Innovation Photonics FIO-5-9). After 16 double passes, a semiconductor switch, consisting of a Brewster-angle germanium plate activated by synchronized Nd:YAG laser pulses inside an optical cavity49, couples out 10 mJ, 70 ps amplified pulses of high beam quality and transmits them through a 4-cm-thick NaCl window into an 8 bar final CO2 amplifier (Optoel Co., PITER-I) that is also mixed-isotope and discharge-pumped. After propagating through a 5-meter, multi-pass gain length using nine intra-vessel mirrors, amplified pulses exit the power amplifier through a 10-cm-thick NaCl window with 10 cm clear aperture. An unfolded, mirror-less four-grating configuration with 100 lines/mm gratings and 70 % transmission temporally compresses them. Compressed 2 ps pulses of > 5 TW peak power were demonstrated. Peak power delivered to the interaction point is, however, presently limited to ~ 2 TW because of partially-in-air laser beam transport. Nonlinear optical interactions in these air-filled regions caused occasional pulses delivered with PL > 2 TW to focus less tightly. This limitation will be eliminated in the near future after the installation of a vacuum compressor chamber and the completion of the vacuum transport line. See refs. 11,12 for further details.
The Supplementary Information presents measurements of the vacuum-focused spatial profiles, spectra, and duration of the CO2 laser pulses. Supplementary Fig. 3 shows images of the vacuum-focused intensity profiles and their intensity-dependence. Supplementary Fig. 4 shows spectra of the CO2 laser pulses in the 0.5 TW configuration used in initial wake generation experiments. These can be compared and contrasted with spectra in the 2 TW configuration, shown in Fig. 4 of ref. 12, used to accelerate electrons. Supplementary Fig. 5 shows how the duration τL of the CO2 laser pulses, determined from single-shot autocorrelation measurements, varies with pulse energy.
Pulse energy was monitored by measuring the 8% reflection from a tilted uncoated NaCl input window of the vacuum system with a 95 mm diameter pyroelectric joule-meter (Gentec-EO, Model QE95LP). Laser pulse energy varied typically ± 20% shot-to-shot. This natural variation combined with stepwise adjustment of the gain of the CO2 laser amplifier (controlled by the voltage of the pumping discharge) was used for collecting pulse-energy statistics. The laser operates in a single-shot regime. The minimum time delay between shots, dictated by the capacitor charging time of the Marx generator powering the discharge in the final amplifier, is approximately 20 seconds. However, we deliberately extend this interval to at least 1.5 minutes between shots to allow adequate cooldown of the spark gaps (high voltage switching components). This practice helps to prolong their operational lifetime.
A research and development effort is presently underway aimed at CO2 laser parameters needed for generating the blown-out bubble regime wakes (τL < 1 ps, PL > 20 TW). This goal can be achieved using a combination of two techniques45: 1) maximizing the bandwidth of the amplified pulses by simultaneous use of 9R and 9P branches of CO2 gain spectrum, and 2) post-compression of the pulse. According to simulations backed up by recent proof-of-principle experiments46 pulse durations in the order of 100 fs (3 optical cycles) with several joules of energy can be achieved with this approach in a system based on ATF’s final amplifier. We are also in the initial stages of research and development aimed at increasing the laser repetition rate to 1 Hz and beyond. Currently, we are of the view that this increase would require a shift from electric-discharge to optical pumping methods50.
Probe laser
CTS probes originated as few mJ, 14 ps pulses of wavelength 1.06 μm from a mode-locked Nd:YAG laser. After amplification in two passes to ~ 30 mJ, a polarizing beam-splitter divided them into orthogonally polarized sub-pulses, which passed through independent delay arms. They were re-combined with adjustable delay at a second polarizing beam splitter, and co-propagated into a potassium dihydrogen phosphate (KDP) crystal as ordinary (o) and extraordinary (e) pulses with different group velocities. Because of their group-velocity mismatch, the o and e pulses drifted through one another, during which time they underwent pump-depleted Type II second-harmonic generation. This effectively limited their overlap duration to 4 ps, creating a compressed probe pulse of wavelength λpr = 0.532 μm, duration τpr = 4 ps, and energy \({{{{{{{{\mathcal{E}}}}}}}}}_{pr}\approx 3\) mJ51. A lens focused these pulses with f/62.5 through a 5 mm-diameter hole in the pump OAP to a beam waist w0 ≈ 50 μm centered on the focal spot of the CO2 pump pulse at the gas jet entrance.
Probe and CO2 laser pulses were synchronized by phase-locking mode-locked pulse trains from the Nd:YAG and Ti:S oscillators at the front ends of the probe and CO2 laser systems, respectively, to a common frequency-divided RF reference frequency. Fast photodiodes monitored small portions of each oscillator output, delivered via piezoelectrically-controlled mirrors. These signals were sent to phase-locked-loops, which compared them to the RF reference signal and fed back error signals to the piezo-mirrors. This feedback adjusted the mirror positions to ensure phase locking of the pump and probe laser oscillators with the RF reference signal. The electronic synchronization loops at ATF are designed to operate with sub-picosecond timing jitter, a level that is negligible under the conditions of this work. The best evidence for this is that the rise time of pump-probe data in our experiments (e.g. Fig. 5c, blue data points) closely matched the pump-probe cross-correlation (dashed red curve) determined from single-shot autocorrelation measurements.
A delay arm within the CO2 laser controlled pump-probe delay Δt at the interaction region. We identified Δt = 0 using a silicon optical switch, i.e. we temporarily replaced the gas jet with a thin silicon plate, oriented so that probe and attenuated CO2 pulses were near-normally incident. With the probe blocked, or trailing the CO2 pulse, the latter passed through the plate, since its photon energy lies below the silicon band gap. When the probe led the CO2 pulse, its above-gap photons generated a short-lived dense electron-hole plasma that reflected and absorbed the CO2 pulse. A detector monitoring the transmitted CO2 pulses as Δt varied observed the sharp change in transmission at Δt = 0.
After the probe co-propagated through the gas jet with the 0.5 TW pump pulse, a BK7 vacuum chamber window blocked the pump. A lens collected transmitted green probe light and delivered it to a series combination of two notch interference filters (Alluxa, Inc.), each with optical density 6 within a 14 nm (FWHM) spectral window centered at λpr = 0.532 μm. Remaining probe light outside this window then entered an imaging spectrometer (SPEX model 270M) equipped with a charge-coupled device (CCD) camera (Princeton Instruments ProEM1024B) that detected a spectral region spanning 37 nm centered at 532 nm.
Accelerated electron characterization
We characterized accelerated electrons generated with the vacuum laser focus between the entrance and the center of the gas jet, where we observed maximum electron yield. For energy-integrated measurements, the beam illuminated a scintillating screen (Kodak Lanex Regular) covered with a 20 μm-thick aluminium laser shield located 27 cm downstream of the gas jet, close enough to capture the entire beam profile, but far enough to avoid saturation. Cathodoluminescence from the back of the screen was imaged to a CCD camera. We extracted total charge from integrated luminescence, using the calibration of42.
For energy-resolved measurements, we constructed an in-vacuum magnetic electron spectrometer. Electrons entered the spectrometer through a 2 mm slit that limited their cone angle to 9 mrad. They passed through one of two cylindrical regions filled with uniform axial magnetic fields: 1) B = 0.25 T, diameter 5 cm, followed by a Lanex screen that allowed measurement of > 5 MeV electrons with 40 % resolution; 2) B = 0.3 T, diameter 10 cm, followed by a Lanex screen configured to measure either 0 - 7 MeV electrons with 10 % resolution or 7-15 MeV electrons with 10 % resolution at 10 MeV. The cited magnetic fields and their associated fringe fields were profiled with a Hall probe, and the measured fields used in calculating electron trajectories through the spectrometer. The 9 mrad cone angle of electrons entering the magnetic fields was, however, the main factor limiting energy resolution to 10%.
Simulations
Simulations were performed using the 3D, parallel, relativistic PIC code SPACE52. The electromagnetic module of SPACE utilizes Yee’s finite-difference time domain method for solving field equations53 and the Boris-Vay pusher for advancing macroparticles54,55. SPACE also includes algorithms for atomic physics processes induced by high-energy laser- and beam-plasma interactions27,52. The algorithm for laser-induced tunneling ionization is based on ADK formalism56. The code computes ionization and recombination rates on the grid and transfers them to particles, rather than using a Monte Carlo approach. In contrast to simulations reported in ref. 27, which assumed stationary ions, the simulations in Fig. 1 (and ref. 24) take ion motion fully into account. This dampened wake amplitudes and raised self-injection thresholds compared to immobile-ion simulations. It also brought simulated injection thresholds into closer agreement with observed thresholds for relativistic electron production.
All simulations were performed in a 3D Cartesian geometry using a static window in the laboratory frame. The computational box has a transverse size of 600 μm and a longitudinal size of 3 − 5 mm, with a transverse resolution of dx = dy = 2.0 μm and a longitudinal resolution of dz = 0.5 μm. This corresponds to approximately 20 cells per laser wavelength (λL) in the longitudinal direction and 10 cells per beam waist w0 in the transverse direction. Simulations use a minimum of 32 macro-particles per cell. Numerical convergence studies confirmed that this resolution is sufficient for the study of the problems targeted here.
Test simulations were carried out to optimize gas jet shape, laser pulse profile, and vacuum laser focus location used in presented simulation runs. These tests balanced four criteria: 1) best match to known experimental conditions, within measurement uncertainty; 2) best match to experimental results (sideband intensities, electron yield and spectrum); 3) best simulation efficiency; 4) least sensitivity to small changes in input parameters. Simulations of CTS experiments (Fig. 1b, c; Fig. 3b; Fig. 5d) came close to meeting all four criteria simultaneously. Simulations of electron acceleration experiments (Fig. 1d–f; Fig. 7a; Fig. 8b5) required some compromise. We made the following decisions:
-
Gas jet: Simulation results were insensitive to entrance (exit) ramp length over the range 0≤Lent ≲ 0.4 mm (0.2≤Lexit ≲ 0.4 mm. Here, we present results with Lent = 0 (in the interests of simulation efficiency) and Lexit = 0.25 mm (close to measured ramp). Overall jet length (including ramps) was fixed at the measured length of 2 mm.
-
Laser pulse profile: A Gaussian vacuum spatial (temporal) profile with w0 = 27.5 μm (τL = 4 or 2 ps) was used because it closely matched vacuum focus spot profile (autocorrelation) measurements (Supplementary Fig. 3c, inset; Supplementary Fig. 5 and ref. 12). These measurements provided no clear guidance for exploring deviations from Gaussian profiles.
-
Vacuum laser focus position: In test simulations of CTS experiments, results were insensitive to small changes in vacuum focus location over the range 0 < z < 0.1 mm (referring to the horizontal scale of Fig. 1a). In test simulations of electron acceleration experiments, for which the vacuum focus was shifted toward the gas jet center (z = 1 mm), results best matched experimental electron yield and energy for z = 0.1 mm. Thus, as a compromise, we used a vacuum focus at z = 0.1 mm for simulations of all experiments. This is smaller than the average z used in electron acceleration experiments. We attribute the discrepancy tentatively to the highly nonlinear nature of the interaction in those experiments, as a result of which small deviations of gas jet and laser pulse profiles from their ideal shapes can play an outsized role in the results of the experiment.
Data availability
Experimental data were generated at BNL’s Accelerator Test Facility. The authors declare that all data supporting the findings of this study are available within the paper and its Supplementary Information. Additional inquiries about the data should be directed to the corresponding author.
Code availability
The authors declare that the computer code SPACE supporting the findings of this study is fully documented within the paper, its references, and its Supplementary Information. Additional inquiries about the codes should be directed to R. S.
References
Tajima, T. & Dawson, J. M. Laser electron accelerator. Phys. Rev. Lett. 43, 267 (1979).
Esarey, E., Schroeder, C. B. & Leemans, W. P. Physics of laser-driven plasma-based electron accelerators. Rev. Mod. Phys. 81, 1229 (2009).
Albert, F. et al. 2020 roadmap on plasma accelerators. N. J. Phys. 23, 031101 (2021).
Gonsalves, A. J. et al. Petawatt laser guiding and electron beam acceleration to 8 GeV in a laser-heated capillary discharge waveguide. Phys. Rev. Lett. 122, 084801 (2019).
Corde, S. et al. Femtosecond X-rays from laser-plasma accelerators. Rev. Mod. Phys. 85, 1–48 (2013).
U. S. Dept. of Energy, Office of Science, Washington, DC. Advanced Accelerator Development Strategy Report: DOE Advanced Accelerator Concepts Research Roadmap Workshop. https://doi.org/10.2172/1358081 (2016).
Cros, B. and Muggli, P. Towards a Proposal for an Advanced Linear Collider: Report on the Advanced and Novel Accelerators for High Energy Physics Roadmap Workshop, CERN, Geneva. https://cds.cern.ch/record/2298632 (2017).
Hidding, B. et al. Plasma wakefield accelerator research 2019-2040: a community-driven UK roadmap compiled by the Plasma Wakefield Accelerator Steering Committee. Preprint at https://doi.org/10.48550/arXiv.1904.09205 (2019).
Strickland, D. & Mourou, G. Compression of amplified chirped optical pulses. Opt. Commun. 56, 219 (1985).
Woodbury, D. et al. Laser wakefield acceleration with mid-IR laser pulses. Opt. Lett. 43, 1131–1134 (2018).
Polyanskiy, M. N., Babzien, M. & Pogorelsky, I. V. Chirped-pulse amplification in a CO2 laser. Optica 2, 675–681 (2015).
Polyanskiy, M. H., Pogorelsky, I. V., Babzien, M. & Palmer, M. A. Demonstration of a 2 ps, 5 TW peak power, long-wave infrared laser based on chirped-pulse amplification with mixed-isotope CO2 amplifiers. OSA Contin. 3, 459–472 (2020).
Pogorelsky, I. V., Polyanskyi, M. N. & Kimura, W. D. Mid-infrared lasers for energy frontier plasma accelerators. Phys. Rev. Accel. Beams 19, 091001 (2016).
Kruer, W.L. The Physics of Laser-Plasma Interactions. (Addison-Wesley, Redwood City, 1988).
Kitagawa, Y. et al. Beat-wave excitation of plasma wave and observation of accelerated electrons. Phys. Rev. Lett. 68, 48 (1992).
Clayton, C. E. et al. Ultrahigh-gradient acceleration of injected electrons by laser-excited relativistic electron plasma waves. Phys. Rev. Lett. 70, 37 (1993).
Modena, A. et al. Electron acceleration from the breaking of relativistic plasma waves. Nat. (Lond.) 377, 606–608 (1995).
Antonsen, T. M. & Mora, P. Self-focusing and Raman scattering of laser pulses in tenuous plasmas. Phys. Rev. Lett. 69, 2204 (1992).
Sprangle, P., Esarey, E., Krall, J. & Joyce, G. Propagation and guiding of intense laser pulses in plasmas. Phys. Rev. Lett. 69, 2200 (1992).
Andreev, N. E., Gorbunov, L. M., Kirsanov, V. I., Pogosova, A. A. & Ramazashviili, R. R. Resonant excitation of wakefields by a laser pulse in a plasma. JETP Lett. 55, 571 (1992).
Pukhov, A. & Meyer-ter-Vehn, J. Laser wake field acceleration: the highly non-linear broken-wave regime. Appl. Phys. B 74, 355 (2002).
Albert, F. et al. Observation of betatron x-ray radiation in a self-modulated laser wakefield accelerator driven with picosecond laser pulses. Phys. Rev. Lett. 118, 134801 (2017).
Adli, E. et al. Acceleration of electrons in the plasma wakefield of a proton bunch. Nat. (Lond.) 561, 363 (2018).
Kumar, P. et al. Evolution of the self-injection process in long-wavelength infrared laser-driven wakefield accelerators. Phys. Plasmas 28, 013102 (2021).
King, P. et al. Predominant contribution of direct laser acceleration to high-energy electron spectra in a low-density self-modulated laser wakefield accelerator. Phys. Rev. Accel. Beams 24, 011302 (2021).
Andreev, N. E., Kuznetsov, S. V., Pogosova, A. A., Steinhauer, L. C. & Kimura, W. D. Modeling of laser wakefield acceleration at CO2 laser wavelengths. Phys. Rev. ST Accel. Beams 6, 041301 (2003).
Kumar, P. et al. Simulation study of CO2 laser-plasma interactions and self-modulated wakefield acceleration. Phys. Plasmas 26, 083106 (2019).
Malka, V. et al. Electron acceleration by a wake field forced by an intense ultraashort laser pulse. Science 298, 1596–1600 (2002).
Wang, W. et al. Free-electron lasing at 27 nanometres based on a laser wakefield accelerator. Nature 595, 516–520 (2021).
Pogorelsky, I. V. & Ben-Zvi, I. Brookhaven National Laboratory’s Accelerator Test Facility: research highlights and plans. Plasma Phys. Control. Fusion 56, 084017 (2014).
Slusher, R. E. & Surko, C. M. Study of density fluctuations in plasmas by small-angle CO2 laser scattering. Phys. Fluids 23, 472 (1980).
Villenueve, D. M., Baldis, H. A., Bernard, J. E. & Benesch, R. Collective Thomson scattering in a laser-produced plasma resolved in time, space, frequency or wave number. J. Opt. Soc. Am. B 8, 895 (1991).
Froula, D. H., Glenzer, S. H., Luhmann, Jr., N. C. and Sheffield, Plasma Scattering of Electromagnetic Radiation, 2nd. ed. (Academic Press, New York, 2011).
Zhang, C. et al. Ionization-induced plasma grating and its applications in strong-field ionization measurements. Plasma Phys. Control. Fusion 63, 095011 (2021).
LeBlanc, S. P. et al. Temporal characterization of a self-modulated laser wakefield. Phys. Rev. Lett. 77, 5381–5384 (1996).
Dawson, J. M. Nonlinear electron oscillations in a cold plasma. Phys. Rev. 113, 383 (1959).
Jackson, E. A. Nonlinear oscillations in a cold plasma. Phys. Fluids 3, 831 (1960).
Koch, P. & Albritton, J. Nonlinear evolution of stimulated Raman backscatter in cold homogeneous plasma. Phys. Rev. Lett. 34, 1616 (1975).
Umstadter, D., Williams, R., Clayton, C. & Joshi, C. Observation of steepening in electron plasma waves driven by stimulated Raman backscattering. Phys. Rev. Lett. 59, 292–295 (1987).
Chen, S., Rever, M., Zhang, P., Theobald, W. & Umstadter, D. Observation of relativistic cross-phase modulation in high-intensity laser-plasma interactions. Phys. Rev. E 74, 046406 (2006).
Ting, A. et al. Temporal evolution of self-modulated laser wakefields measured by coherent Thomson scattering. Phys. Rev. Lett. 77, 5377–5380 (1996).
Kurz, T. et al. Calibration and cross-laboratory implementation of scintillating screens for electron bunch charge determination. Rev. Sci. Instrum. 89, 093303 (2018).
Esarey, E., Kroll, J. & Sprangle, P. Envelope analysis of intense laser pulse self-modulation in plasmas. Phys. Rev. Lett. 72, 2887 (1994).
Rechatin, C. et al. Controlling the phase-space volume of injected electrons in a laser-plasma accelerator. Phys. Rev. Lett. 102, 164801 (2009).
Polyanskiy, M. N. et al. High-peak-power long-wave infrared lasers with CO2 amplifiers. Photonics 8, 101 (2021).
Polyanskiy, M. N. et al. Post-compression of long-wave infrared 2 picosecond sub-terawatt pulses in bulk materials. Opt. Express 29, 31714–31725 (2021).
Lu, W. et al. Generating multi-GeV electron bunches using single stage laser wakefield acceleration in a 3D nonlinear regime. Phys. Rev. ST - Accel. Beams 10, 061301 (2007).
Marchetti, B., Assmann, R., Dorda, U. & Zhu, J. Conceptual and technical design aspects of accelerators for external injection in LWFA. Appl. Sci. 8, 757 (2018).
Alcock, A. J. & Corkum, P. B. Ultra-fast switching of infrared radiation by laser-produced carriers in semiconductors. Can. J. Phys. 57, 1280–1290 (1979).
Tovey, D. et al. Multi-atmosphere picosecond CO2 amplifier optically pumped at 4.3 μm. Appl. Opt. 58, 5756–5763 (2019).
Umbrasas, A., Diels, J.-C., Jacob, J., Valiulis, G. & Piskarskas, A. Generation of femtosecond pulses through second-harmonic compression of the output of a Nd:YAG laser. Opt. Lett. 20, 2228–2230 (1995).
Yu, K., Kumar, P., Yuan, S., Cheng, A. & Samulyak, R. SPACE: 3D parallel solvers for Vlasov-Maxwell and Vlasov-Poisson equations for relativistic plasmas with atomic transformations. Computer Phys. Commun. 277, 108396 (2022).
Yee, K. S. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 14, 302–307 (1966).
Boris, J. P. Relativistic plasma simulation-Optimization of a hybrid code. in Proceedings of 4th Conference on Numerical Simulation of Plasmas (Naval Research Laboratory, Washington D. C., 1970), pp. 3-67.
Vay, J. L. Simulation of beams or plasmas crossing at relativistic velocity. Phys. Plasmas 15, 056701 (2008).
Ammosov, M. V., Delone, N. B. & Krainov, V. P. Tunnel ionization of complex atoms and of atomic ions in electromagnetic field. Sov. Phys. JETP 64, 1191–1194 (1986).
Acknowledgements
This work was supported by grant DE-SC0014043 from the U.S. Department of Energy (DoE), Office of Science, High Energy Physics (V.N.L. and N.V.-N., principal investigators; M.C.D. and C.J., sub-awardees). U. Texas-Austin authors acknowledge additional support from Air Force Office of Scientific Research grant FA9550-16-1-0013 and DoE grant DE-SC0011617 (M.C.D., principal investigator). Brookhaven National Lab co-authors acknowledge additional support from DoE grant DE-SC0012704.
Author information
Authors and Affiliations
Contributions
R.Z. designed and installed the apparatus for optical wake probing and accelerated electron characterization, with assistance from J.W., Y.C., D.L.A., A.G., P.I., and I.P., and led the acquisition and analysis of all experimental data. N.V.-N. coordinated experimental activity with BNL staff and M.C.D., P.K. and A.C. carried out SPACE simulations under the supervision of R.S., who coordinated with R.Z. and M.C.D. on interpreting experimental results. D.L.A. and C.Z. contributed additional simulation support. M.B., M.F., R.K., K.K., M.N.P., and C.S. operated, maintained and upgraded the CO2 laser system under the leadership of I.V.P. and M.A.P., M.C.D. conceived the experiments, inspired by theoretical work by I.V.P. on CO2 laser-driven wakefield acceleration13, led contributions of the U. Texas-Austin team and wrote the paper, in consultation with R.Z., R.S., C.J. and N.V.-N., V.N.L. acquired funding for the experiment, and contributed to discussions of procedure and analysis. C.J. contributed frequent advice and guidance based on years of experience with CO2 laser experiments. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
: Nature Communications thanks Hans-Peter Schlenvoigt and the other, anonymous, reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zgadzaj, R., Welch, J., Cao, Y. et al. Plasma electron acceleration driven by a long-wave-infrared laser. Nat Commun 15, 4037 (2024). https://doi.org/10.1038/s41467-024-48413-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-024-48413-y
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.