Abstract
Empowering independent control of optical and acoustic modes and enhancing the photon-phonon interaction, integrated photonics boosts the advancements of on-chip stimulated Brillouin scattering (SBS). However, achieving acoustic waveguides with low loss, tailorability, and easy fabrication remains a challenge. Here, inspired by the optical anti-resonance in hollow-core fibers and acoustic anti-resonance in cylindrical waveguides, we propose suspended anti-resonant acoustic waveguides (SARAWs) with superior confinement and high selectivity of acoustic modes, supporting both forward and backward SBS on chip. Furthermore, this structure streamlines the design and fabrication processes. Leveraging the advantages of SARAWs, we showcase a series of breakthroughs for SBS within a compact footprint on the silicon-on-insulator platform. For forward SBS, a centimeter-scale SARAW supports a large net gain exceeding 6.4 dB. For backward SBS, we observe an unprecedented Brillouin frequency shift of 27.6 GHz and a mechanical quality factor of up to 1960 in silicon waveguides. This paradigm of acoustic waveguide propels SBS into a new era, unlocking new opportunities in the fields of optomechanics, phononic circuits, and hybrid quantum systems.
Similar content being viewed by others
Introduction
Brillouin nonlinearities arise from the coupling of photons and phonons1,2,3,4. Due to its unique characteristics derived from acoustic phonons, SBS has found widespread applications in the realms of signal generation and processing5,6,7,8,9,10,11,12,13,14,15,16,17,18, such as narrow linewidth laser16,17, microwave photonic filters5,6,7,8, slow and fast light9,10,11, distributed sensing13,14,15, and optical non-reciprocal devices18. Recently, integrated photonics has enabled better confinement and manipulation of optical and acoustic modes19,20,21,22,23,24,25,26,27, ushering in a new era of photon-phonon interaction.
While optical mode confinement methods are well established, how to confine acoustic modes is still evolving, which now primarily relies on three strategies. The first approach is acoustic total internal reflection, which is generally applied in materials with low stiffness19,20, such as chalcogenides. Nonetheless, these materials are difficult to integrate with standard silicon photonic circuits. The second solution, based on acoustic impedance, involves isolating waveguides from the substrate to effectively prevent acoustic leakage21,22. Whereas, this approach has difficulty in flexibly selecting acoustic frequencies, and necessitates complex fabrication processes. The third strategy utilizes phononic bandgaps to obstruct the spread of acoustic waves28,29,30,31. However, its complex structures pose difficulties for design and manufacturing and result in low robustness.
Emerging anti-resonant reflection offers an alternative approach to achieve field confinement32,33,34,35,36. This approach has been successfully applied in hollow-core fibers32,33,34, effectively confining optical modes within the lower-refractive-index air core. Compared with photonic bandgap hollow-core fibers32, anti-resonant hollow-core fibers have a simpler structure and lower loss. Anti-resonant reflection has been theoretically proposed to confine acoustic modes of both forward and backward SBS in cylindrical waveguides35. However, they are not compatible with integrated photonic platforms.
In this paper, we transfer the concept of anti-resonant reflection to integrated platforms and demonstrate a novel suspended anti-resonant acoustic waveguide (SARAW), proving its effectiveness in the confinement of phonons. By designing the anti-resonant structures, we can flexibly control the acoustic modes without affecting optical modes. This characteristic enables us to manipulate the acoustic mode distribution, select the eigenfrequency, and optimize the mechanical quality factor Qm. Consequently, SARAWs can support both forward and backward SBS and achieve a series of extraordinary results of SBS on the silicon-on-insulator (SOI) platform. For forward SBS, we attain a Brillouin gain coefficient GB of 3530 W−1m−1, over 2000 times larger than that of standard single-mode fibers. The threshold for achieving Brillouin net gain is remarkably low (<5 mW). Under a modest pump power, a large net gain of up to 6.4 dB can be realized with a compact footprint. These results highlight that SARAWs can significantly enhance the coupling strength of optical and acoustic waves. For backward SBS, we observe a record-high Brillouin frequency shift of 27.6 GHz and an unprecedented Qm of 1960 in integrated silicon waveguides. These breakthroughs show that acoustic waves in SARAWs can operate at frequencies extending to millimeter-wave bands, and exhibit extremely low propagation loss. In terms of fabrication and design, SARAWs eliminate the need for overlay exposure in the fabrication processes, thus suppressing the harmful inhomogeneous broadening of Brillouin resonance. It also allows for a simplified waveguide design process utilizing genetic algorithms37,38.
Results
Design and fabrication of SARAWs
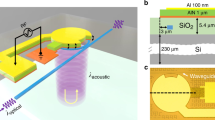
We first introduce the principle of acoustic anti-resonant reflection with the planar waveguide, as depicted at the top of Fig. 1a. To confine the acoustic field within the middle layer, the side layers with slower acoustic velocities are incorporated as anti-resonant reflecting layers, which can be conceptualized as Fabry-Pérot cavities. By manipulating cavities thicknesses, the anti-resonance states can be achieved. Consequently, the acoustic wave is unable to traverse the side layers and is reflected to the middle layer, leading to the acoustic field distribution outlined by the black line in Fig. 1a. Generally, different velocity layers are composed of distinct materials32,35, such as silicon and silica. However, implementing this transverse multilayer structure on the chip is challenging. Here, we propose a new approach to address this issue. Considering the situation in the suspended solid membrane, as illustrated at the bottom of Fig. 1a, slots with width t are etched onto both sides of the central waveguide. In the slot regions, the boundary between air and solid geometrically softens the structural response of solid film3, thus lowering its effective acoustic velocity and achieving anti-resonant reflecting layers.
a The principle of anti-resonant reflection and its implementation on chip. b Schematic of the SARAW. c Cross-section of the SARAW and its geometric parameters. These parameters are axisymmetric. Wi (i = 1, 2, 3) corresponds to the width of the unetched region, ti corresponds to the width of the etched slot, and di corresponds to the etching depth of the etched slot. Benefiting from the loading-effect etching process, wherein a wider ti corresponds to a deeper di, we can control the etching depth di by adjusting the slot width ti. t3 is set to sufficiently large to achieve overetching, which enables the hydrofluoric acid solution to remove the silica substrate. Consequently, the waveguides are fully suspended in air. d The electric field of the optical mode. e The x component of the electrostrictive force. f The elastic displacement field of the optimized acoustic mode. Here, slot width t1 meets the anti-resonance condition. Figure (e, f ) use the optimized parameters for the forward SBS with a waveguide width W1 of 700 nm. The detailed geometric parameters are shown in Supplementary Section III. g, h The elastic displacement field when acoustic mode under the resonance condition. In Fig. (f–h), the color bar corresponds to the magnitude of the x component of the elastic displacement field. The deformations depict the cross-sectional displacement fields. i, j Top-down SEM image of the fabricated SARAW (i) and a magnified view (j). k Cross-sectional SEM image of the fabricated SARAW. Scale bars, 10 μm (i); 2 μm (j); and 1 μm (k).
Following this approach, we propose the suspended anti-resonant acoustic waveguide as shown in Fig. 1b, c. The device consists of a central waveguide flanked by two sets of etched slots, and the entire suspended structure is supported by a series of tethers. Since silicon exhibits excellent optical and acoustic properties, such as a high refractive index and a low acoustic loss, and is compatible with complementary metal-oxide-semiconductor (CMOS) technology, it becomes a conducive medium for robust photon-phonon interactions. We deploy SARAWs on the SOI platform and demonstrate its improvement and tailorability on Brillouin nonlinearities.
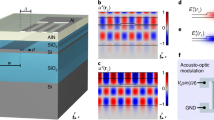
We first investigate the properties of the SARAWs using forward SBS, which has a larger gain coefficient GB than backward SBS. Through the meticulous adjustment of anti-resonant structures using a genetic algorithm37,38 (see “Methods”), SARAWs can be optimized to achieve the largest GB. We showcase the SARAW with a central waveguide width W1 of 700 nm, see Supplementary Section III for detailed parameters. The SARAW supports a fundamental transverse electric-like optical mode (Fig. 1d), and the corresponding electrostrictive force is depicted in Fig. 1e. The acoustic mode of SARAWs, compared to the rib waveguides22, is squeezed towards the central waveguide, as shown in Fig. 1f, indicating the effectiveness of anti-resonant reflection in acoustic mode confinement. Furthermore, the similar distribution of the electrostrictive force and acoustic mode suggests a large photon-phonon overlap, closing to that of the fully suspended rectangular waveguide. To further demonstrate the effect of anti-resonant reflection, we introduce a variation (t/t1 = 20%) to the slot width (t1), making SARAWs to operate in resonance conditions. As shown in Fig. 1g, h, the acoustic intensity at the central waveguide decreases sharply, and a significant portion of the acoustic energy leakages into the slot region, inducing a significant increase in the deformation. This results in a reduction in photon-phonon overlap. Hence, by adjusting the geometric parameters, SARAWs can be flexibly switched between the anti-resonance and resonance states, effectively manipulating the acoustic confinement and the photon-phonon coupling strength. Moreover, this manipulation does not influence the optical mode and can be performed independently.
SARAWs also streamline the fabrication processes and play a significant role in reducing the inhomogeneous broadening of Brillouin resonance. Previous suspended SBS waveguides typically necessitate overlay exposure22,29, involving at least two exposure steps and two etching steps, and all steps call for exceptional alignment precision. Furthermore, the alignment mismatches in the overlay exposure process would introduce inhomogeneous broadening of Brillouin resonance, exacerbating SBS performance. Particularly, the degradation of alignment mismatches is significantly magnified in spiral waveguides (see Supplementary Section VIII). Here, for the first time, we innovatively propose an etching technique based on the loading effect to fabricate the whole structure via a single exposure and etching step (see “Methods” and Supplementary Section IV). The loading effect39, where the etch rate depends on pattern width in etching processes, generally acts as a barrier to achieving depth uniformity. Yet, this property provides the opportunity to attain different etching depths in a single etching step. Given the distinctive structure of the SARAW, which requires different slots depths (d1 ~ d3), the loading-effect etching technique can be effectively applied, avoiding the costs and yield losses caused by multiple fabrication cycles. By excluding the overlay exposure requirement, the loading-effect etching technique can accommodate high fabrication precision (<5 nm), and mitigate the inhomogeneous broadening. By introducing rectangle spiral waveguides (see Supplementary Section VIII), we can achieve centimeter-scale-long waveguides in a compact footprint with improved consistency, yielding higher Qm and GB compared to straight waveguides. On top of these design and fabrication processes, the SARAWs are analyzed by scanning electron microscopy (SEM) (Fig. 1i–k), which demonstrate excellent structural stability and uniformity. Benefiting from the streamlined fabrication process and compatibility with CMOS technology, these results exhibit great reproducibility and scalability, facilitating the large-scale integration of Brillouin-based devices.
Demonstration of anti-resonance with SARAWs
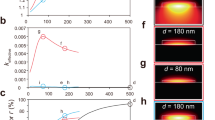
Initially, we validate the tailorability of SARAWs through simulation in terms of the acoustic frequency and mode distribution. For the anti-resonant structure, the slot width t1 can effectively control the anti-resonance state and influence the acousto-optic interaction strength. Therefore, we varied the slot width t1 of the SARAW from 200 to 400 nm, with the other parameters kept the same as in Fig. 1f. Through the simulation (see “Methods” and Supplementary Section III), we tracked the acoustic frequency and coupling factor GB/Qm, which reflects the photon-phonon overlap. The simulation results, shown in Fig. 2b, indicate a decrease in the frequency of the Brillouin-active acoustic mode from 6.8 GHz to 5.9 GHz as the width t1 increases. This trend results from the influence of another acoustic mode (see Supplementary Section III). During the sweep, three resonance conditions are met (t1 = 225, 325, and 388 nm), with two anti-resonance conditions in between. When slot width t1 meets the resonance condition, avoided mode crossing40 is observed. This phenomenon arises from the strong coupling between the acoustic mode in the central waveguide and the shear modes in the slot regions, leading to a significant decrease in photon-phonon overlap. The uneven appearance of resonance conditions when t1 increases is mainly attributed to the consideration of the loading effect in the simulations (see Supplementary Section III).
a Diagram of the heterodyne FWM experiment. Two continuous-wave (C.W.) lasers operate at frequencies ν1 and ν2 (corresponding to wavelengths of 1550 and 1552 nm). The upper laser generates sidebands (ν1 ± fm/2) via an intensity modulator (IM) with the modulation signal (fm/2) provided by a vector network analyzer (VNA). After amplified by an erbium-doped fiber amplifier (EDFA), these sidebands serve as the pump light for the device under test (DUT). The second C.W. laser is split into two paths by a coupler. The upper branch is amplified by an EDFA as the probe light. The lower branch undergoes a frequency shift of Δf via an acousto-optic modulator (AOM) as a reference signal. Within the DUT, the pump light (ν1 ± fm/2) and the probe light (ν2) generate two sidebands at ν2 ± fm through FWM (the gray area beneath the DUT). To measure the intensity variations of the FWM-generated sidebands when fm scans over the Brillouin frequency shift, ν2 ± fm are filtered out via a cavity band-pass filter (BPF) (the dark gray trapezoidal box on the right below the DUT), and then mixed with ν2 + Δf on a photodetector (PD), yielding signals at fm ± Δf. The corresponding FWM variation curves can be obtained on the VNA, corresponding to Stokes (fm + Δf) and anti-Stokes (fm − Δf) components. b The influence of resonance/anti-resonance condition on Brillouin frequency shift and coupling factor GB/Qm with different slot width (t1). To facilitate observation, the linewidth of the acoustic modes is set to 50 kHz. c–e Experimental and simulated results show the impact of anti-resonant reflection on Brillouin frequency shift, GB/Qm, and Qm,, respectively. The elastic displacement magnitude (top) and measurement results (bottom) of the heterodyne FWM experiment (anti-Stokes sideband, ν2 + fm) in SARAWs under the anti-resonance (f) and resonance (g) condition. The waveguide width W1 = 700 nm. The a.u. denotes arbitrary units. h The experimental attained GB and Qm of optimized SARAWs for W1 = 450, 700, and 1200 nm, with the acoustic eigenfrequency of 8.6, 5.9, and 3.6 GHz, respectively.
Using the parameters in the simulation, we fabricated a series of 5-mm-long SARAWs and conducted the heterodyne four-wave mixing (FWM) experiment22,29. This experimental setup, shown in Fig. 2a, provides excellent sensitivity and avoids the impact of coupling loss fluctuations, thus ensuring robust and reliable results. We extract Brillouin frequency shift, GB, and Qm by fitting the obtained asymmetric Fano-like spectral lines (see Supplementary Section V). In order to clearly compare the simulation and experimental results, acoustic frequency and coupling factor GB/Qm are depicted in Fig. 2c, d respectively. Avoided mode crossing and decrease of coupling factor GB/Qm under resonance conditions are observed, showing good agreement with the simulation. As shown in Fig. 2e, the dips and peaks of mechanical quality factor Qm illustrate the noticeable difference between resonance and anti-resonance conditions for the acoustic confinement effect. The difference is further illustrated by Brillouin spectra obtained by the heterodyne FWM experiment under corresponding conditions (Fig. 2f, g). Under the anti-resonance condition (Fig. 2f), the fitted GB and Qm reach up to 3530 W−1m−1 and 680, indicating that the acoustic mode is effectively confined within the central waveguide. While under the resonance condition (Fig. 2g), both GB and Qm decrease dramatically by over 80%, reaching 540 W−1m−1 and 120, respectively, as the acoustic mode energy disperses into the slot regions. The above simulation and experimental results solidly validate the effectiveness of SARAWs for acoustic confinement and manipulation. Compared to suspended rectangular waveguides without anti-resonant structures41, SARAWs can compress the acoustic mode into the central waveguide, thereby mitigating the impact of sidewall roughness on the Qm, resulting in a larger GB. Moreover, the presence of the anti-resonant structure can isolate the optical mode from the supporting tethers, reducing optical mode mismatch loss. These attributes underscore the comprehensive superiority and inherent flexibility of SARAWs.
Utilizing the manipulating ability and frequency selectivity of anti-resonance, we optimize and fabricate 5-mm-long SARAWs with different central waveguide widths (W1 = 450, 700, and 1200 nm) to obtain the respective maximum GB. The experimentally attained Brillouin frequency shift, GB, and Qm are shown in Fig. 2h. As the waveguide width increases, the waveguide acquires a larger mode field area and becomes less sensitive to sidewall roughness. Therefore, the eigenfrequency and coupling factor GB/Qm decrease gradually, while Qm increases accordingly. The 450-nm SARAW exhibits the highest GB/Qm of 8.57, but suffers more from the inhomogeneous broadening caused by sidewall roughness, resulting in a low Qm. The 700-nm SARAW achieve a remarkable GB of 3530 W−1m−1 in silicon waveguides with a balance of GB/Qm and Qm. And the 1200-nm SARAW shows a higher Qm of up to 850. Consequently, SARAWs can be flexibly extended to different waveguide widths, allowing for the attainment of distinct acoustic frequencies, GB and Qm.
Large Brillouin net gain in SARAWs
The Brillouin net gain, which takes the Brillouin gain coefficient GB and optical loss into account, is typically a comprehensive figure of merit for Brillouin-based applications. Hence, we conducted further design and experiment to illustrate the potential of SARAWs in achieving large Brillouin net gain. Benefiting from the properties of low optical loss and minimal inhomogeneous broadening, SARAWs with a central waveguide width of 1200 nm are suitable for attaining large net gain. We examine Brillouin interactions in a 2.5-cm-long rectangular spiral SARAW with a compact footprint of 1900 μm × 460 μm.
We carried out a three-tone direct gain experiment29 (see Supplementary Section VI) to obtain the net gain, owing to its simpler setup compared to traditional small-signal gain experiment. Figure 3a shows three Brillouin gain spectra measured for pump powers of 12, 22, and 36 mW. These gain spectra, which illustrate the relative change in the probe intensity, reveal a Brillouin resonance with a high mechanical quality factor (Qm = 660, see Supplementary Section VI for a detailed fitting process) at 3.63 GHz. The probe intensity is significantly amplified by approximately 10 dB under 36 mW pump power. There is a slight discrepancy between the experimental results and the fittings, which could be attributed to the phase drift of the modulator and the acoustic eigenfrequency drift. Figure 3b shows the Stokes gain at Brillouin resonance as a function of pump power. To satisfy the small signal approximation, the pump power is kept below 40 mW. By numerically solving the three-tone coupling equations (see Supplementary Section VI), the fitted GB is determined as 1700 W−1m−1 (Fig. 3b). It is of great consistency with the independent measurement of the same waveguide performed through heterodyne FWM measurement (GB = 1670 W−1m−1, Qm = 650), as is shown in Fig. 3c. Compared to the 5-mm-long SARAW with the same structure parameters (Fig. 2h, central waveguide width W1 = 1200 nm), Brillouin gain coefficient GB and mechanical quality factor Qm here are slightly reduced due to the inhomogeneous broadening under long waveguide length. Based on the results from the above experiments (Fig. 3b, c), the small-signal Stokes gain and the net gain are numerically calculated (see Supplementary Section VI) and shown in Fig. 3d. Benefiting from the low optical loss (0.3 dB/cm, see Supplementary Section I) and large Brillouin gain, the threshold for net gain is below 5 mW. Considering the maximum on-chip pump power of 57 mW constrained by EDFA and coupling loss (single-sideband 5.4 dB), SARAWs can support a net gain of up to 6.4 dB and an on-off gain of 8.7 dB. These results mark the present apex of Brillouin gain levels in silicon waveguides and can be further improved with higher on-chip power and longer waveguide length. However, it should be noted that, on the SOI platform, further increases in pump power may lead to notable nonlinear absorption losses (see Supplementary Section I). This factor would become the primary constraint for achieving larger Brillouin net gain. The introduction of pump light in far-infrared wavelengths or the free-carrier suppression techniques42 could potentially overcome this limitation.
Backward SBS in SARAWs
Backward SBS, mediated by the interaction of two counter-propagating optical waves with a phase-matched longitudinal acoustic wave, exhibits distinct characteristics compared to forward SBS. Acoustic modes in backward SBS exhibit higher acoustic frequency and quality factor. The longitudinal wave nature of the backward SBS acoustic mode necessitates an extensive waveguide length to build up to its full strength. However, existing suspended waveguides inevitably introduce periodic supporting structures22,43, leading to the dissipation of acoustic waves. Meanwhile, the material property of the photoelastic coefficient makes it challenging to observe backward SBS in silicon waveguides2. The maximum on-off gain, GB, and Brillouin frequency shift for backward SBS in silicon waveguides achieved so far are only 0.2 dB, 359 W−1m−1, and 13.7 GHz21, respectively. However, in SARAWs, the anti-resonant structures separate the acoustic wave from the periodic supporting tethers. This separation enables the acoustic wave to build up to its full strength, thereby facilitating robust support for backward SBS.
We designed and fabricated 2-cm-long SARAWs with central waveguide widths W1 = 450, 700, and 1200 nm. Utilizing the setup in Supplementary Section VII, we observed a bell-shaped acoustic mode under all three waveguide widths (Fig. 4a–c). Same as the trends in forward SBS, as the central waveguide width W1 increases, the photon-phonon overlap decreases and the mechanical quality factor increases. With a balance of GB/Qm and Qm, the 700 nm SARAW achieves a backward Brillouin gain coefficient GB of 600 W−1m−1 (Fig. 4b), nearly doubling the current record observed in silicon waveguides21. And surprisingly, the 1200-nm SARAW (Fig. 4c) attains an unprecedented Qm of up to 1960 in integrated waveguides, significantly exceeding that of forward SBS acoustic modes. Furthermore, a record-high acoustic frequency of 27.6 GHz is observed in another acoustic mode (Fig. 4d) utilizing a 450-nm SARAW. The geometric parameters used here have been meticulously optimized for this specific acoustic mode, distinguishing from the parameters used in Fig. 4a. It underscores the selectivity of SARAWs for specific acoustic modes and frequencies. However, this acoustic mode exhibits lower GB of 480 W−1m−1 and Qm of 380. It may be attributed to the fact that a significant portion of the acoustic mode is distributed near the waveguide boundaries, which results in a smaller acousto-optic overlap and makes it more vulnerable to surface roughness. Thus this mode has not been observed in SARAWs with central waveguide widths W1 of 700 and 1200 nm.
a–d The elastic displacement magnitude of the corresponding acoustic mode field (upper gray region) and backward SBS gain spectra (lower). Figures (a–c) correspond to the optimized acoustic modes with central waveguide width W1 = 450, 700, and 1200 nm, using the genetic algorithm. Figure (d) illustrates the outcomes obtained through optimization for higher-order acoustic modes within a 450-nm SARAW. The values of Brillouin gain coefficient GB (W−1m−1) and mechanical quality factor Qm are: (530, 470); (600, 1300); (430, 1960); (480, 380), corresponding to figure (a–d), respectively.
The record-breaking results above demonstrate that SARAWs can flexibly enhance and manipulate acoustic modes for backward SBS. As a result, SARAWs support acoustic modes with high group velocity (>3000 m/s), and the corresponding acoustic decay length of over 50 μm, offering a low-loss and long-distance transmission platform for acoustic waves. However, the observation of backward SBS net gain remains hindered by the limitation imposed by the intrinsic photoelastic coefficient of silicon. Promising avenues for overcoming this challenge include transplanting SARAWs onto a chalcogenide glass platform or selecting SOI wafers with diverse crystal orientations44.
Discussion
Leveraging genetic-algorithm-based optimization scheme and loading-effect-based fabrication technique, SARAWs can be rapidly designed and fabricated. For design scheme, the genetic algorithm eliminates the need for time-consuming parameter sweep and greatly simplifies the SARAW design process. Moreover, it allows for the rapid and specific optimization of various merit figures in SBS. This versatility is crucial for SBS-based applications with different requirements depending on the use-case. For instance, SBS-based microwave photonic filters5,6,7,8 with different center frequencies, bandwidths, and out-of-band suppression ratios demand diverse Brillouin frequency shift, mechanical quality factor Qm, and Brillouin gain coefficient GB. Meanwhile, the innovative loading-effect-based etching technique minimizes the manufacturing cost while maintaining excellent fabrication precision. It lessens the degradation of Brillouin resonance caused by inhomogeneous broadening while minimizing the overall footprint. Furthermore, this scheme is portable to other material platforms, rendering it highly suitable for integrated acousto-optic devices.
In our work, the net gain in SARAWs is mainly constrained by the coupling loss and the roughness of the waveguide sidewall, which are limited by our fabrication capabilities. These limitations hinder further increases in on-chip pump power and mechanical quality factor Qm, and impede further reductions in optical propagation loss. However, referring to previous work21, the utilization of CMOS pilot line in the foundry could potentially yield lower coupling loss, higher Qm, and lower optical loss. These advancements promise a performance enhancement of more than twofold for current net gain results.
We would like to emphasize that SARAWs exhibit exceptional characteristics in backward SBS. The backward SBS acoustic mode exhibits a significantly larger group velocity and an extended phonon lifetime than the forward SBS, resulting in a large acoustic decay length. This is also a crucial characteristic for the acoustic waveguides, making SARAWs a promising candidate for supporting the burgeoning field of phononic circuits45. Furthermore, the promotions in acoustic mode eigenfrequency and Qm underscore the potential of SARAWs. A maximum Qm of 1960 and an unprecedented acoustic eigenfrequency of 27.6 GHz are particularly advantageous for microwave photonics and signal processing devices for 5G and future communication systems, including microwave generations12 and acoustic wave filters46. In addition, the acoustic frequency of 19.6 GHz and Qm of 1960 indicate a product of frequency and quality factor f × Qm exceeding 3.8 × 1013 Hz, which is important for quantum systems. It is expected to be further improved in phonon lasers47 based on SARAWs.
In summary, SARAWs incorporate innovations in acoustic anti-resonance theory, intelligent algorithm empowered design, and nanofabrication technique, offering a comprehensive solution for integrated photon-phonon interaction platforms. It heralds a new era for SBS, paving the way for breakthroughs in optomechanics48, phononic circuits45, and hybrid quantum systems49.
Methods
Device fabrication
The SARAW was fabricated from the 220 nm silicon layer of a SOI wafer with the 〈100〉 crystal orientation utilizing electron-beam lithography (EBL) and inductively coupled plasma (ICP) etching. With loading-effect-based etching technique, SARAW can be fabricated with one exposure step and one etching step. Whereafter, the oxide undercladding was then released by immersion in 10% hydrofluoric acid. The SARAW employs a rectangular spiral for long waveguides. The 2.5-cm-long waveguide has a footprint of 1900 μm × 460 μm (see Supplementary Section IV).
Genetic algorithm and finite element simulation
First, we developed the main program and invoked the Genetic Algorithm Toolbox in MATLAB. Then, we simulated acoustic and optical modes through the finite element solver COMSOL, calculating the total GB/Qm produced by electrostrictive force and radiation pressure. Subsequently, the obtained GB/Qm was further iterated by the genetic algorithm until the algorithm converged. It should be noted that due to the loading effect, slot width ti dictates the slot depth di (Fig. 1c). Therefore, we measured the relationship curve between ti and di caused by the loading effect through separate experiments, and then compensated it into the main program, ensuring that our optimization results were consistent with the actual fabricated waveguides (see Supplementary Section III).
Data availability
The data that supports the plots within this paper and other findings of this study have been deposited in the Zenodo database (https://zenodo.org/doi/10.5281/zenodo.10946980). All other data used in this study are available from the corresponding author upon request.
Code availability
The codes that support the findings of this study are available from the corresponding author upon request.
References
Merklein, M., Kabakova, I. V., Zarifi, A. & Eggleton, B. J. 100 years of Brillouin scattering: Historical and future perspectives. Appl. Phys. Rev. 9, 041306 (2022).
Eggleton, B. J., Poulton, C. G., Rakich, P. T., Steel, M. J. & Bahl, G. Brillouin integrated photonics. Nat. Photonics 13, 664–677 (2019).
Safavi-Naeini, A. H., Van Thourhout, D., Baets, R. & Van Laer, R. Controlling phonons and photons at the wavelength scale: integrated photonics meets integrated phononics. Optica 6, 213–232 (2019).
Wiederhecker, G. S., Dainese, P. & Mayer Alegre, T. P. Brillouin optomechanics in nanophotonic structures. APL Photonics 4, 071101 (2019).
Garrett, M. et al. Integrated microwave photonic notch filter using a heterogeneously integrated Brillouin and active-silicon photonic circuit. Nat. Commun. 14, 7544 (2023).
Jiang, H. et al. Wide-range, high-precision multiple microwave frequency measurement using a chip-based photonic Brillouin filter. Optica 3, 30–34 (2016).
Marpaung, D. et al. Low-power, chip-based stimulated Brillouin scattering microwave photonic filter with ultrahigh selectivity. Optica 2, 76–83 (2015).
Gertler, S. et al. Narrowband microwave-photonic notch filters using Brillouin-based signal transduction in silicon. Nat. Commun. 13, 1947 (2022).
Zhu, Z., Gauthier, D. J. & Boyd, R. W. Stored light in an optical fiber via stimulated brillouin scattering. Science 318, 1748–1750 (2007).
Merklein, M., Stiller, B. & Eggleton, B. J. Brillouin-based light storage and delay techniques. J. Opt. 20, 083003 (2018).
McKay, L. et al. Brillouin-based phase shifter in a silicon waveguide. Optica 6, 907–913 (2019).
Li, J., Lee, H. & Vahala, K. J. Microwave synthesizer using an on-chip Brillouin oscillator. Nat. Commun. 4, 2097 (2013).
Galindez-Jamioy, C., López-Higuera, J. & Bernini, R. Brillouin distributed fiber sensors: An overview and applications. J. Sens. 2012, 204121 (2012).
Thévenaz, L. Brillouin distributed time-domain sensing in optical fibers: state of the art and perspectives. Front. Optoelectron. China 3, 13–21 (2010).
Bao, X. & Chen, L. Recent progress in brillouin scattering based fiber sensors. Sensors 11, 4152–4187 (2011).
Loh, W. et al. Operation of an optical atomic clock with a brillouin laser subsystem. Nature 588, 244–249 (2020).
Gundavarapu, S. et al. Sub-hertz fundamental linewidth photonic integrated Brillouin laser. Nat. Photonics 13, 60–67 (2019).
Kittlaus, E. A., Otterstrom, N. T., Kharel, P., Gertler, S. & Rakich, P. T. Non-reciprocal interband Brillouin modulation. Nat. Photonics 12, 613–619 (2018).
Morrison, B. et al. Compact Brillouin devices through hybrid integration on silicon. Optica 4, 847–854 (2017).
Song, J. et al. Stimulated brillouin scattering in Low-Loss Ge25Sb10S65 chalcogenide waveguides. J. Lightwave Technol. 39, 5048–5053 (2021).
Van Laer, R., Kuyken, B., Van Thourhout, D. & Baets, R. Interaction between light and highly confined hypersound in a silicon photonic nanowire. Nat. Photonics 9, 199–203 (2015).
Kittlaus, E. A., Shin, H. & Rakich, P. T. Large Brillouin amplification in silicon. Nat. Photonics 10, 463–467 (2016).
Sohn, D. B., Kim, S. & Bahl, G. Time-reversal symmetry breaking with acoustic pumping of nanophotonic circuits. Nat. Photonics 12, 91–97 (2018).
Liu, Q., Li, H. & Li, M. Electromechanical Brillouin scattering in integrated optomechanical waveguides. Optica 6, 778–785 (2019).
Kim, D.-G. et al. Universal light-guiding geometry for on-chip resonators having extremely high Q-factor. Nat. Commun. 11, 5933 (2020).
Gyger, F. et al. Observation of Stimulated Brillouin Scattering in Silicon Nitride Integrated Waveguides. Phys. Rev. Lett. 124, 013902 (2020).
Poulton, C. G., Pant, R. & Eggleton, B. J. Acoustic confinement and stimulated brillouin scattering in integrated optical waveguides. JOSA B 30, 2657–2664 (2013).
Gertler, S., Kittlaus, E. A., Otterstrom, N. T., Kharel, P. & Rakich, P. T. Microwave filtering using forward brillouin scattering in photonic-phononic emit-receive devices. J. Lightwave Technol. 38, 5248–5261 (2020).
Wang, K. et al. Demonstration of forward brillouin gain in a hybrid photonic-phononic silicon waveguide. ACS Photonics 8, 2755–2763 (2021).
Zurita, R. O., Wiederhecker, G. S. & Alegre, T. P. M. Designing of strongly confined short-wave Brillouin phonons in silicon waveguide periodic lattices. Opt. Express 29, 1736–1748 (2021).
Laude, V. et al. Phononic band-gap guidance of acoustic modes in photonic crystal fibers. Phys. Rev. B 71, 045107 (2005).
Fokoua, E. N., Mousavi, S. A., Jasion, G. T., Richardson, D. J. & Poletti, F. Loss in hollow-core optical fibers: mechanisms, scaling rules, and limits. Adv. Opt. Photonics 15, 1–85 (2023).
Jasion, G. T. et al. 0.174 dB/km hollow core double nested antiresonant nodeless fiber (DNANF). In 2022 Optical Fiber Communications Conference and Exhibition (OFC), 1–3 https://ieeexplore.ieee.org/abstract/document/9748272 (IEEE, 2022).
Amrani, F. et al. Low-loss single-mode hybrid-lattice hollow-core photonic-crystal fibre. Light Sci. Appl. 10, 7 (2021).
Schmidt, M. K., O’Brien, M. C., Steel, M. J. & Poulton, C. G. ARRAW: anti-resonant reflecting acoustic waveguides. N. J. Phys. 22, 053011 (2020).
Litchinitser, N., Abeeluck, A., Headley, C. & Eggleton, B. Antiresonant reflecting photonic crystal optical waveguides. Opt. Lett. 27, 1592–1594 (2002).
Ruano, P. N. et al. Genetic optimization of Brillouin scattering gain in subwavelength-structured silicon membrane waveguides. Opt. Laser Technol. 161, 109130 (2023).
Lei, P. et al. Optimization of Suspended Phononic Crystal Brillouin Waveguides Using Genetic Algorithm. In 2022 Asia Communications and Photonics Conference (ACP), 1629–1632 https://ieeexplore.ieee.org/abstract/document/10088893 (IEEE, 2022).
Yeom, J., Wu, Y., Selby, J. C. & Shannon, M. A. Maximum achievable aspect ratio in deep reactive ion etching of silicon due to aspect ratio dependent transport and the microloading effect. J. Vac. Sci. Technol. B: Microelectron. Nanometer Struct. Process., Meas., Phenom. 23, 2319–2329 (2005).
Stern, I., Carosi, G., Sullivan, N. & Tanner, D. Avoided mode crossings in cylindrical microwave cavities. Phys. Rev. Appl. 12, 044016 (2019).
Lei, P., Xu, M., Bai, Y., Chen, Z. & Xie, X. Loading-effect-based three-dimensional microfabrication empowers on-chip brillouin optomechanics. Opt. Lett. 49, 1465–1468 (2024).
Turner-Foster, A. C. et al. Ultrashort free-carrier lifetime in low-loss silicon nanowaveguides. Opt. Expr. 18, 3582–3591 (2010).
Shin, H. et al. Tailorable stimulated Brillouin scattering in nanoscale silicon waveguides. Nat. Commun. 4, 1944 (2013).
Diallo, S., Aubry, J.-P. & Chembo, Y. K. Effect of crystalline family and orientation on stimulated brillouin scattering in whispering-gallery mode resonators. Opt. Expr. 25, 29934–29945 (2017).
Madiot, G. et al. Optomechanical generation of coherent GHz vibrations in a phononic waveguide. Phys. Rev. Lett. 130, 106903 (2023).
Ruppel, C. C. Acoustic wave filter technology–a review. IEEE Trans. Ultrason. Ferroelectr .Freq. Control 64, 1390–1400 (2017).
Grudinin, I. S., Lee, H., Painter, O. & Vahala, K. J. Phonon laser action in a tunable two-level system. Phys. Rev. Lett. 104, 083901 (2010).
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391 (2014).
Clerk, A., Lehnert, K., Bertet, P., Petta, J. & Nakamura, Y. Hybrid quantum systems with circuit quantum electrodynamics. Nat. Phys. 16, 257–267 (2020).
Acknowledgements
This work is funded by National Natural Science Foundation of China (62071010 X.X.).
Author information
Authors and Affiliations
Contributions
P.L., M.X., Z.C., and X.X. jointly proposed the design of the anti-resonant acoustic waveguide. P.L. and M.X. fabricated the waveguide devices. P.L. developed the etching technique and optimization algorithm, performed the experiments and analyzed the results. P.L., M.X., Y.B., and X.X. wrote the manuscript. All co-authors contributed by providing their valuable feedback and comments. X.X. supervised the work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Benjamin J. Eggleton, David Marpaung and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lei, P., Xu, M., Bai, Y. et al. Anti-resonant acoustic waveguides enabled tailorable Brillouin scattering on chip. Nat Commun 15, 3877 (2024). https://doi.org/10.1038/s41467-024-48123-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-024-48123-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.