Abstract
Faraday rotation is a fundamental effect in the magneto-optical response of solids, liquids and gases. Materials with a large Verdet constant find applications in optical modulators, sensors and non-reciprocal devices, such as optical isolators. Here, we demonstrate that the plane of polarization of light exhibits a giant Faraday rotation of several degrees around the A exciton transition in hBN-encapsulated monolayers of WSe2 and MoSe2 under moderate magnetic fields. This results in the highest known Verdet constant of -1.9 × 107 deg T−1 cm−1 for any material in the visible regime. Additionally, interlayer excitons in hBN-encapsulated bilayer MoS2 exhibit a large Verdet constant (VIL ≈ +2 × 105 deg T−1 cm−2) of opposite sign compared to A excitons in monolayers. The giant Faraday rotation is due to the giant oscillator strength and high g-factor of the excitons in atomically thin semiconducting transition metal dichalcogenides. We deduce the complete in-plane complex dielectric tensor of hBN-encapsulated WSe2 and MoSe2 monolayers, which is vital for the prediction of Kerr, Faraday and magneto-circular dichroism spectra of 2D heterostructures. Our results pose a crucial advance in the potential usage of two-dimensional materials in ultrathin optical polarization devices.
Similar content being viewed by others
Introduction
The Faraday effect is crucial for numerous scientific and technological advancements in astronomy, biology, chemistry, physics, and materials science. For instance, it is used for investigating the magnetic domain structure in solids1,2, nuclear magnetic resonance in fluids via optical detection3,4, paramagnetic gas molecule detection5, determination of magnetic fields6 and electron-density distribution in outer space and celestial objects7, probing spin coherence in cold atoms8, quantum spin fluctuation measurements9, biochemical and biomolecular detection10, stabilization of laser frequency11, optical current sensing12, optical Hall effect13, and optical isolators14.
In recent years, extraordinary progress has been made in exploring the unique physical phenomena in atomically thin transition metal dichalcogenide (TMDC) semiconductors15,16,17,18,19,20,21. In two-dimensional TMDCs, Coulomb-bound electron–hole composite quasiparticles such as neutral and charged excitons possess large binding energies and giant oscillator strengths19,21, when compared to the traditional group III–V or II–VI quantum wells22,23. These exceptional properties enable investigating 2D quantum effects even at room temperature. Furthermore, the corners of the Brillouin zone i.e. the K± valleys in TMDCs selectively couple to circularly polarized light21,24. The magnetic moments associated with the neighboring K+ and K− valleys are opposite to each other. This property leads to effects unique to atomically thin TMDCs, such as valley polarization24, valley coherence25, valley Zeeman splitting26,27, the valley Hall effect28, the valley-selective optical Stark effect29, and magnetic-field-induced valley polarization30,31,32,33,34,35,36,37. From the magneto-optics perspective, TMDCs have been extensively studied using magneto-photoluminescence, magneto-reflectance and magneto-transmittance21. However, the classic magneto-optical phenomena such as the Faraday and Kerr effect still remain to be explored experimentally due to major challenges involved in these measurements on the microscopic level38,39,40.
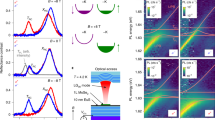
For 2D materials, the Faraday and Kerr effects can provide crucial information on the valley-related processes, such as valley Zeeman splitting38 and magnetic-field-induced valley polarization38. While Faraday rotation is generally accompanied with ellipticity when light passes through an absorbing medium (Fig. 1), a measurement of only Faraday rotation is sufficient for obtaining all the magneto-optical information about the sample1.
Here, we show that the giant oscillator strength and large valley Zeeman splitting of excitons in WSe2 and MoSe2 monolayers result in the highest known Verdet constant (Faraday rotation per unit length per unit magnetic field) in a material in the visible regime31,32,33,34,35,36,41,42,43,44,45,46,47,48. We measure giant Faraday rotations on the order of degrees under a small magnetic field of around 1 T.
Faraday rotation arises from the non-zero off-diagonal term of the complex dielectric tensor of a material. For light incident along the z-direction perpendicular to the sample plane with B||z, (i.e. Faraday geometry), the complex dielectric tensor for the xy plane can be written as1,49,50,51
The diagonal components are responsible for the conventional optical response of materials in reflectance, transmittance, and absorption. For materials with a high degree of in-plane symmetry, such as monolayer MX2 (M = Mo, W; X = S, Se), the diagonal components are equal i.e. \({\widetilde{\epsilon }}_{{xx}}={\widetilde{\epsilon }}_{{yy}}\). Normally, in semiconductors, off-diagonal terms \({\widetilde{\epsilon }}_{{xy}}\) are zero in the absence of a magnetic field49. But these components reach very large values around the exciton resonances under magnetic fields, due to the exciton Zeeman splitting39. We note that in two-dimensional electron/hole gases in the quantum Hall regime, \({\widetilde{\epsilon }}_{{xy}}\) also rises sharply around inter-Landau level transition energies52. However, usually, the magnetic field to reach the quantum Hall regime is much higher compared to the one required for large Faraday effects around Zeeman-split exciton energies1,53. Far from the exciton lines, \({\widetilde{\epsilon }}_{{xy}}\) are smaller by many orders of magnitude. \({\widetilde{\epsilon }}_{{xy}}\) is given as49,54
where \({\widetilde{n}}_{{xx}}=n+{ik}=\sqrt{{\widetilde{\epsilon }}_{{xx}}}=\sqrt{{\epsilon }_{{xx}1}+{i\epsilon }_{{xx}2}}\) is the complex refractive index, and \(\widetilde{V}={V}_{{FR}}+i{V}_{{FE}}\) is the complex Verdet constant with its components \({V}_{{FR}}\) and \({V}_{{FE}}\). The complex Verdet constant is related to the complex Faraday rotation \({\widetilde{\phi }}_{F}={\phi }_{F}+i{\eta }_{F}\) as \(\widetilde{V}={\widetilde{\phi }}_{F}/({d\; B})\) where \({\phi }_{F}\) and \({\eta }_{F}\) are Faraday rotation and Faraday ellipticity, respectively, d is the sample thickness, B is the magnetic field. We note that \({\widetilde{\epsilon }}_{{xy}}\) is related to the popularly defined “Voigt constant” Q as \(Q=i{\widetilde{\epsilon }}_{{xy}}/{\widetilde{\epsilon }}_{{xx}}\)50.
Results
Excitonic Faraday rotation in MoSe2 and WSe2 monolayers
We measure the Faraday rotation (the real component of \({\widetilde{\phi }}_{F}\), i.e., \({\phi }_{F}\)) of light around the neutral and charged A exciton transitions in a hBN-encapsulated MoSe2 monolayer, and the neutral A exciton transition in a hBN-encapsulated WSe2 monolayer. The substrates are c-cut double-side polished sapphire, which enable optical transmission measurements. Details about our experimental setup are described in ref. 38 and are briefly summarized in the supporting information. Here, we first discuss the case of the MoSe2 sample, and extend our conclusions to the WSe2 sample afterwards. Figure 2a shows the measured optical transmittance spectrum of an hBN-encapsulated MoSe2 monolayer in the spectral region of the neutral and charged exciton (trion) at a temperature of T = 10 K. The measured spectrum (solid spheres) is modeled using the transfer-matrix method (lines) to incorporate the effects of optical interference due to multiple layers of the sample on the spectral line shape55,56. The excitonic contribution to the dielectric function is described as a complex Lorentzian
where, \({A}_{j},{E}_{0j},\) and \({\gamma }_{j}\) are the oscillator strength, transition energy and full-width at half-maximum (FWHM) linewidth of the \({j}^{th}\) resonance. \({n}_{b}+i{k}_{b}\) is the complex background dielectric function of monolayer MoSe2 without excitonic contributions57. The exciton and trion resonances A and T are at 1.634 eV and 1.607 eV, respectively (Fig. 2a). Narrow FWHM linewidths (2.7 meV and 4.0 meV, respectively) approaching the homogeneous linewidth limit indicate the excellent quality of our samples58,59,60.
a Optical transmission spectrum of hBN/1L MoSe2/hBN (left panel) and f hBN/1L WSe2/hBN (right panel) around the exciton and trion resonances A and T in the MoSe2 sample and A exciton in the WSe2 sample. A strong dip is observed around the neutral A exciton resonance. b, g Experimental (spheres) and modeled (solid lines) Faraday rotation spectra of resonances in magnetic fields ranging from \(B=0.2\,{{{{{\rm{T}}}}}}-1.4\,{{{{{\rm{T}}}}}}\) for the two samples. The spectra are vertically shifted by 0.5° successively for clarity. The shift is mentioned along with the respective plots. Characteristic Faraday rotation spectral line shapes are revealed around the resonance energies. The exciton transition exhibits a large peak Faraday rotation of 2.2° and 1.7°, respectively, for the MoSe2 and WSe2 cases at \(B=1.4\,{{{{{\rm{T}}}}}}\). c, h Real and imaginary parts of the off-diagonal dielectric function of the two materials at B = 1.4 T derived from our measurements, as explained in the main text and the supporting information. d, i Zeeman splittings of the resonances derived from line shape modeling. Linear fits (solid lines) are used to derive the effective g-factors \({g}_{A}\) and \({g}_{T}\). e, j Measured peak Faraday rotation of the resonances as a function of the magnetic field. Peak rotation is fitted linearly for deriving the Verdet constants VA = −(2.3 ± 0.2) × 107 deg T−1 cm−1 and VT = −(0.9 ± 0.2) × 106 deg T−1 cm−1 for the MoSe2 and VA = −(1.9 ± 0.2) × 107 deg T−1 cm−1 for the WSe2 sample.
Faraday rotation ϕF is measured in this spectral region under moderate out-of-plane applied magnetic fields ranging from B = 0.2–1.4 T. We observe characteristic Faraday rotation line shapes with a dip around the exciton and trion energies. From our data, we determine the real and imaginary components (\({\epsilon }_{{xy}1}\) and \({\epsilon }_{{xy}2}\)) of the off-diagonal dielectric constant \({\widetilde{\epsilon }}_{{xy}}\) of monolayer MoSe2 following Eq. (2). An example of \({\epsilon }_{{xy}1}\) and \({\epsilon }_{{xy}2}\) for \(B=1.4\,{{{{{\rm{T}}}}}}\) is shown in Fig. 2c. As required by Eq. (2), the procedure involves a calculation of Faraday ellipticity using a Kramers–Kronig analysis of our data in Fig. 2b61, as well as the complex diagonal dielectric function \({\widetilde{\epsilon }}_{{xx}}\). Details of the calculation are provided in the supporting information.
The Faraday rotation line shapes in Fig. 2b are modeled using the transfer-matrix method to determine the Zeeman splittings of A and T as a function of magnetic field (Fig. 2d)38,55,56. First, the transmittance spectrum is modeled as described before. The complex transmission Fresnel coefficients for left and right circular polarizations σ± are given as
They are identical in the absence of an external magnetic field. \({\widetilde{t}}_{\pm }\) are obtained from modeling the transmission spectrum. In the presence of a magnetic field, excitons and trions undergo a valley Zeeman splitting, leading to different \({\widetilde{t}}_{\pm }\), and thereby different ϕ±. The Faraday rotation of polarized light under a magnetic field is related to ϕ± as
Solid lines in Fig. 2b are the fits to the Faraday rotation spectra using this procedure. The modeling provides the valley Zeeman splittings of the excitons and trions as a function of magnetic field, which are plotted in Fig. 2d. The absolute value of the Zeeman splitting increases linearly as a function of the magnetic field. The Zeeman splitting of an exciton resonance X is given as \(\Delta E={g}_{{{{{{\rm{X}}}}}}}{\mu }_{B}B\), where \({g}_{{{{{{\rm{X}}}}}}}\) is the effective exciton g-factor and \({\mu }_{B}=5.788\times {10}^{-5}{{{{{\rm{eV}}}}}}{{{{{{\rm{T}}}}}}}^{-1}\) is the Bohr’s magneton. By fitting the data in Fig. 2d using this relation, we obtain the exciton and trion g-factors as \({g}_{A}=-4.3\pm 0.3\) and \({g}_{T}=-4.8\pm 0.6\). These values are in excellent agreement with literature values21,33,45,46. Figure 2f–j presents the results for an hBN-encapsulated WSe2 monolayer around the A exciton, yielding similar results as for MoSe2.
We find that around the A exciton, the magnitude of the Faraday rotation relative to the flat spectral background (i.e., 0° rotation) is 2.2° for monolayer MoSe2, and 1.7° for monolayer WSe2 at \(B=1.4\,{{{{{\rm{T}}}}}}\). The magnitude of Faraday rotation for the A and T transitions in MoSe2 are plotted as a function of the magnetic field in Fig. 2e, and for the A exciton in WSe2 in Fig. 2j. The rotation increases linearly with the magnetic field for all resonances. The Faraday rotation (real part) around a resonance X at a magnetic field B is given as
where \({V}_{{{{{{\rm{X}}}}}}}\) is the Verdet constant of the resonance, and d is the layer thickness. Fitting the data in Figs. 2e, j using this relation yields Verdet constants of A and T, respectively as VA = −(2.3 ± 0.2) × 107 deg T−1 cm−1 and VT = −(0.9 ± 0.2) × 106 deg T−1 cm−1 for monolayer MoSe2, and VA = −(1.9 ± 0.2) × 107 deg T−1 cm−1 for monolayer WSe2.
Faraday rotation around interlayer excitons in a MoS2 bilayer
As an example of a material with a positive Verdet constant, we perform Faraday rotation spectroscopy of interlayer excitons (IL) in a hBN-encapsulated MoS2 bilayer (Fig. 3). Interlayer excitons in bilayer and bulk TMDCs are known to have a positive g-factor which is opposite in sign to the intralayer excitons21,62,63. However, interlayer excitons have a much smaller oscillator strength and a larger line width compared to the intralayer excitons62,63,64. Therefore, their Verdet constant is expected to be smaller. The measured transmittance (for B = 0) and the Faraday rotation spectra (under \(B=0.4-1.4\,{{{{{\rm{T}}}}}}\)) of the hBN-encapsulated MoS2 bilayer sample are shown in Fig. 3a. Clear signatures corresponding to the intralayer exciton (A) at 1.930 eV, intralayer trion (T) at 1.909 eV, and a split interlayer exciton (IL1 at 1.994 eV and IL2 at 2.004 eV) are visible in the Faraday rotation spectra. The assignment of the features are performed on the following grounds: A and T resonances have similar g-factors, nearly equal to −4, suggesting their intralayer character21,63. T polarizes strongly under magnetic field, with its valley polarization approaching ≈ +14% (Fig. 3c). Furthermore, A polarizes only weakly (valley polarization ≈ −2%). The large polarization of T with an opposite sign compared to A is characteristic for the appearance of a trion–exciton pair65. We notice that the binding energy of the trion in the MoS2 bilayer is about 21 meV. In comparison, the reported value in a non-encapsulated bilayer is 27 meV66. A smaller value in our work signifies the effect of an increased dielectric constant around the trion, due to hBN encapsulation. The split IL exciton lines are identified due to their positive g-factors (\({g}_{{{{{{\rm{IL}}}}}}1}=+ 6.6\pm 0.3\) and \({g}_{{{{{{\rm{IL}}}}}}2}=+ 7.2\pm 0.3\))21,62,63 in Fig. 3d. In previous works, one IL resonance has been observed in optical reflectance spectra21,63. In our transmittance spectra, we also notice one (broad) IL line (Fig. 3a), while Faraday rotation spectroscopy is able to resolve two close-lying IL features due to the high sensitivity of the technique (Fig. 3b). We believe that the reason for the appearance of the two IL features is the Stark effect splitting of the IL exciton due to a static electric field67,68, which can be created by charge transfer from impurities in the substrate69. The Verdet constant of the interlayer excitons are VIL1 = +(1.9 ± 0.5) × 105 deg T−1 cm−1 and VIL2 = +(2.2 ± 0.5) × 105 deg T−1 cm−1 (Fig. 3e). In contrast, the intralayer exciton in this sample has a Verdet constant of VA = −(1.5 ± 0.2) × 106 deg T−1 cm−1.
a Optical transmission spectrum of hBN/2 L MoS2/hBN displaying trion T, intralayer exciton A, and a pair of interlayer excitons IL1 and IL2. b Experimental (spheres) and modeled (solid lines) Faraday rotation spectra of resonances in magnetic fields ranging from \(B=0.4\,{{{{{\rm{T}}}}}}-1.4\,{{{{{\rm{T}}}}}}\). The spectra are vertically shifted by 0.1° successively for clarity. The shift is mentioned along with the respective plots. The characteristic line shapes of the T, A, and IL resonances are used for their assignment explained in the main text. c Magnetic-field-induced valley polarization of A and T derived from modeling in (b). d Valley Zeeman splittings deduced for the four resonances from the line shape modeling in (b). Linear fits (solid lines) are used to derive the effective g-factors \({g}_{A}\) and \({g}_{T}\). e Measured peak Faraday rotation of the resonances as a function of the magnetic field. Peak rotation is fitted linearly for deriving the Verdet constants VA = −(1.5 ± 0.2) × 106 deg T−1 cm−1, VIL1 = +(1.9 ± 0.5) × 105 deg T−1 cm−1 and VIL2 = +(2.2 ± 0.5) × 105 deg T−1 cm−1.
Discussion
In Table 1, we compare the derived Verdet constants for our non-magnetic atomically thin semiconductors with conventional semiconductors, diluted magnetic semiconductors (DMSs), and magneto-optical elements used in optical isolators, covering the visible to infrared wavelength range14,70. Most importantly, we find that the Verdet constants for monolayer MoSe2 and WSe2 are larger by many orders of magnitude compared to other materials in this wavelength region14,70. A comparable magnitude is only known in the far-infrared (Terahertz) region, where graphene has a Verdet constant of 2.7 × 107 deg T−1 cm−1 (see ref. 52), which is due to inter-Landau-level transitions (in the low-doping regime) or cyclotron resonances (high-doping regime) in the Terahertz region52.
In general, for the case of an ultrathin dielectric material with the thickness of our monolayer samples, Faraday rotation is expected to be negligibly small for energies far away from excitonic resonances. For example, the Faraday rotation of a 0.65 nm (typical thickness of a TMDC monolayer) thick InSb crystal in the sub-bandgap region at 0.23 eV under a magnetic field of B = 1.4 T (maximum applied field in this work) would be of the order of 10−7 deg71. However, close to an excitonic resonance, Faraday rotation is enhanced by many orders of magnitude. For instance, Faraday rotation for InAs at the exciton resonance is expected to be about 10−3 deg at the abovementioned conditions, which is four orders of magnitude larger71. In the case of TMDC monolayers, this value is enhanced even further by another 2–3 orders of magnitude leading to a giant Faraday effect. This is explained as follows. In general, Faraday rotation around exciton resonances occurs if both oscillator strength and Zeeman splitting of the exciton transition are non-zero. A large oscillator strength implies strong dips in transmission amplitudes t± for the σ± transitions (Eq. (4)). This results in an appreciable phase difference \({\phi }_{+}-{\phi }_{-}\) and thereby a strong Faraday effect around the exciton transition. This enhancement of up to four orders of magnitude in the Verdet constant around the exciton transitions, compared to the sub-bandgap region, has been confirmed earlier in III–V and II–VI semiconductors1. The observed giant excitonic Faraday rotation in TMDC monolayers is however due to a combined effect of (i) a giant exciton oscillator strength21,72,73,74,75, and (ii) a large exciton g-factor (≈ −421,27,44,76), when compared to conventional III–V and II–VI semiconductors1,56,77. The giant exciton oscillator strength in TMDCs is both due to the small excitonic spatial extent (≈1 nm) and the character of the electron and hole wavefunctions (localized in d-orbitals of the transition metals)72,73,74,75,78. Furthermore, considering the Wannier model, TMDCs are expected to have a large joint density of states at the van-Hove singularity at the K point due to a large exciton reduced mass21,79,80, which is about 5–10 times larger compared to a typical III–V semiconductor such as GaAs77,81. This results in a giant exciton oscillator strength. The exciton g-factor of ≈ −4 in TMDC monolayers is mainly due to the contributions of d-orbitals at the top of the valence bands at the K point, with modifications due to electron–hole interactions21,27,76,78. This is a large value compared to exciton g-factors in typical III–V 2D semiconductors i.e. quantum wells. For instance, the heavy-hole exciton g-factor in a GaAs/AlGaAs quantum well varies from −2 to +1 for well widths increasing from 2 to 25 nm56,82. The large exciton g-factor in a TMDC monolayer results in an appreciable lifting of the energetic degeneracy of the σ± polarized exciton transitions under a magnetic field. As a result, a strong Faraday effect is observed around the exciton resonance due to a large phase difference ϕ± under a magnetic field (Eq. 5)83. We note that in the present work, Landau quantization effects84,85,86,87 can be neglected due to the following reasons: (i) the large exciton binding energy (>150 meV) in hBN-encapsulated monolayers strongly dominates the magnetic quantization energy scale (i.e., \({\hslash }{{{{{\rm{eB}}}}}}/{{2}{{{{{\rm{m}}}}}}}^{*}\) ≈ 0.3 meV at \(B=1.4\,{{{{{\rm{T}}}}}}\)) at the magnetic fields used19,21,53. This situation is unlike the case of graphene, where such Coulomb interactions are absent, and low magnetic fields (<5 T) are sufficient to observe Landau quantization in the THz regime52. (ii) Our hBN-encapsulated samples are not in the highly-doped regime, as evidenced by low (high) trion (exciton) oscillator strengths (Figs. 2 and 3). Inter-Landau transition effects in TMDCs have only been observed previously under high-doping conditions and large magnetic fields85.
In conclusion, we have measured giant Faraday rotation around the A exciton transitions in hBN-encapsulated MoSe2 and WSe2 monolayers, as well as interlayer excitons in a MoS2 bilayer. The Verdet constants are many orders of magnitude larger than those observed in conventional III–V or II–VI semiconductors and the well-known Faraday rotators used in optical isolators.
The Faraday rotation in monolayer TMDCs could be further enhanced by optimizing the multilayer structure of hBN and the TMDC monolayer by enhancing the dip in the transmittance in Figs. 2a and 3a. Furthermore, a heterostructure of a TMDC with a 2D ferromagnet could further raise the Verdet constant20,88,89. In such a heterojunction, strong magnetic exchange interaction effects between the ferromagnetic layer and the excitons in the TMDC are expected90. Finally, our work paves the way for a new generation of ultrathin optical polarization devices based on 2D materials.
Methods
Experimental setup for Faraday rotation spectroscopy on 2D materials
Broadband light from a Xe-arc lamp is collimated, and is linearly polarized, as shown in Fig. S1 of the Supplementary Information. It is focused on the sample mounted on the cold finger of a continuous-flow cryostat. The cold finger hangs between the pole pieces of an electromagnet, with a maximum magnetic field of B = 1.4 T applied perpendicular to the sample surface. The light undergoes a Faraday rotation \({\phi }_{F}\), and is reflected from a mirror. It is collimated after passing through a 10× long-working-distance infinity-corrected objective lens. The collimated light is focused on a 20 μm diameter pinhole, which selects light from a spot of about 4 μm diameter on the sample surface. The light is again collimated and passes through a beam displacer, which spatially separates the linear polarization components. The two components are focused on the input slit of a 0.3 m focal length monochromator, are wavelength dispersed, and are collected simultaneously using a Peltier-cooled CCD detector. A Jones matrix analysis of the setup is performed to obtain the Faraday rotation as discussed in ref. 38.
Determination of the complex dielectric tensor of hBN-encapsulated atomically thin semiconductors
The complex magneto-optical dielectric tensor is
Diagonal elements of the dielectric tensor
There are four unknowns in this matrix i.e. \({\epsilon }_{{xx}1},{\epsilon }_{{xx}2},{\epsilon }_{{xy}1}\) and \({\epsilon }_{{xy}2}\). Out of these, \({\epsilon }_{{xx}1}\) and \({\epsilon }_{{xx}2}\) can be determined by measuring reflectance \(R({\widetilde{\epsilon }}_{{xx}})\) and transmittance \(T({\widetilde{\epsilon }}_{{xx}})\) of the materials. The measured \(R({\widetilde{\epsilon }}_{{xx}})\) and \(T({\widetilde{\epsilon }}_{{xx}})\) spectra are shown in Fig. S2a, e for hBN-encapsulated MoSe2 and WSe2 monolayers in the Supplementary Information. Essentially, the experimentally measured \(R({\widetilde{\epsilon }}_{{xx}})\) and \(T({\widetilde{\epsilon }}_{{xx}})\) are simultaneously a function of the two unknowns \({\epsilon }_{{xx}1}\) and \({\epsilon }_{{xx}2}\)55. A transfer-matrix-based approach is used to numerically calculate \({\epsilon }_{{xx}1}\) and \({\epsilon }_{{xx}2}\) with \(R({\widetilde{\epsilon }}_{{xx}})\) and \(T({\widetilde{\epsilon }}_{{xx}})\) spectra as inputs to the calculation55. The results of the calculation are presented in Fig. S2c, g of the Supplementary Information, respectively for the two materials.
Off-diagonal elements of the dielectric tensor
The real and imaginary parts of the off-diagonal element \({\widetilde{\epsilon }}_{{xy}}\) can be determined from the measured Faraday rotation spectrum \({\phi }_{F}(E)\) as follows. \({\phi }_{F}(E)\) is the real part of the complex Faraday rotation spectrum \({\widetilde{\phi }}_{F}(E)={\phi }_{F}+i{\eta }_{F}\) where \({\eta }_{F}\) is the Faraday ellipticity. Both \({\phi }_{F}\) and \({\eta }_{F}\) are functions of complex diagonal and off-diagonal components of the dielectric tensor, i.e., \({\widetilde{\epsilon }}_{{xx}}\) and \({\widetilde{\epsilon }}_{{xy}}\) (see Eq. (2)) which are four unknowns considering their real and imaginary parts. Since \({\widetilde{\epsilon }}_{{xx}}\) is already determined above (Fig. S2c, g of the Supplementary Information) for hBN-encapsulated MoSe2 and WSe2 monolayers, respectively, we are left with two unknowns, i.e., \({\epsilon }_{{xy}1}\) and \({\epsilon }_{{xy}2}\). The knowledge of \({\phi }_{F}\) and \({\eta }_{F}\) enable us now to calculate \({\epsilon }_{{xy}1}\) and \({\epsilon }_{{xy}2}\). Experimentally we measure only \({\phi }_{F}\). To determine \({\eta }_{F}\), we make use of the Kramers–Kronig analysis61. The real and imaginary parts of the complex Faraday effect given by \({\widetilde{\phi }}_{F}(E)={\phi }_{F}+i{\eta }_{F}\) are related to each other through Kramers–Kronig dispersion relations for small values (i.e., \(\tan {\eta }_{F} \sim {\eta }_{F}\)) as follows:
Here P is the principal value, \(\omega\) and \(\omega {\prime}\) are the frequencies given as \(E/\hslash\). An application of Eq. (9) on \({\phi }_{F}(E)\) spectra as input (solid lines in Fig. S2b, f of the Supplementary Information) yields Faraday ellipticity spectra \({\eta }_{F}(E)\) (dashed orange lines in Fig. S2b, f) for our samples. To test the applicability of our method, we use these dashed orange lines as input \({\eta }_{F}(E)\) spectra to calculate \({\phi }_{F}(E)\) using Eq. (8) (dashed blue lines) and compare with the experimentally measured \({\phi }_{F}(E)\) spectra (solid lines). The respective dashed blue and solid plots are in good agreement with each other, providing us confidence in our method. Finally, Eq. (2) is used to calculate the real and imaginary parts of the off-diagonal dielectric tensor, \({\epsilon }_{{xy}1}\) and \({\epsilon }_{{xy}2}\). These are shown in Fig. S2d, h of the Supplementary Information and also in Figs. 2c and 3c of the main text for hBN-encapsulated MoSe2 and WSe2 respectively.
Data availability
The minimum data sets that support the findings of this work have been deposited in the Figshare repository under the accession code https://figshare.com/s/06c6748220460582f8ff. Further requests for materials should be addressed to ashish.arora@iiserpune.ac.in.
References
Piller, H. Chapter 3 Faraday rotation. Semicond. Semimetals 8, 103–179 (1972).
Černe, J., Schmadel, D. C., Rigal, L. B. & Drew, H. D. Measurement of the infrared magneto-optic properties of thin-film metals and high temperature superconductors. Rev. Sci. Instrum. 74, 4755–4767 (2003).
Savukov, I. M., Lee, S.-K. & Romalis, M. V. Optical detection of liquid-state NMR. Nature 442, 1021–1024 (2006).
Pagliero, D., Dong, W., Sakellariou, D. & Meriles, C. A. Time-resolved, optically detected NMR of fluids at high magnetic field. J. Chem. Phys. 133, 154505 (2010).
Lewicki, R., Doty, J. H., Curl, R. F., Tittel, F. K. & Wysocki, G. Ultrasensitive detection of nitric oxide at 5.33 m by using external cavity quantum cascade laser-based Faraday rotation spectroscopy. Proc. Natl. Acad. Sci. USA 106, 12587–12592 (2009).
Dreher, J. W., Carilli, C. L. & Perley, R. A. The Faraday rotation of Cygnus A—magnetic fields in cluster gas. Astrophys. J. 316, 611 (1987).
Longair, M. S. High Energy Astrophysics (Cambridge University Press, 2011).
Swar, M., Roy, D., Bhar, S., Roy, S. & Chaudhuri, S. Detection of spin coherence in cold atoms via Faraday rotation fluctuations. Phys. Rev. Res. 3, 043171 (2021).
Chen, S.-W. & Liu, R.-B. Faraday rotation echo spectroscopy and detection of quantum fluctuations. Sci. Rep. 4, 4695 (2015).
Murdock, R. J. et al. High‐throughput, protein‐targeted biomolecular detection using frequency‐domain Faraday rotation spectroscopy. Small 13, 1602862 (2017).
Quan, W. et al. Far off-resonance laser frequency stabilization using multipass cells in Faraday rotation spectroscopy. Appl. Opt. 55, 2503 (2016).
Ning, Y. N., Wang, Z. P., Palmer, A. W., Grattan, K. T. V. & Jackson, D. A. Recent progress in optical current sensing techniques. Rev. Sci. Instrum. 66, 3097–3111 (1995).
Ikebe, Y. et al. Optical Hall effect in the integer quantum Hall regime. Phys. Rev. Lett. 104, 256802 (2010).
Stadler, B. J. H. & Mizumoto, T. Integrated magneto-optical materials and isolators: a review. IEEE Photonics J. 6, 1–15 (2014).
Wang, Q. H., Kalantar-Zadeh, K., Kis, A., Coleman, J. N. & Strano, M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 7, 699–712 (2012).
Geim, A. K. & Grigorieva, I. V. Van der Waals heterostructures. Nature 499, 419–425 (2013).
Schaibley, J. R. et al. Valleytronics in 2D materials. Nat. Rev. Mater. 1, 16055 (2016).
Mueller, T. & Malic, E. Exciton physics and device application of two-dimensional transition metal dichalcogenide semiconductors. NPJ 2D Mater. Appl. 2, 29 (2018).
Wang, G. et al. Colloquium: excitons in atomically thin transition metal dichalcogenides. Rev. Mod. Phys. 90, 021001 (2018).
Gibertini, M., Koperski, M., Morpurgo, A. F. & Novoselov, K. S. Magnetic 2D materials and heterostructures. Nat. Nanotechnol. 14, 408–419 (2019).
Arora, A. Magneto-optics of layered two-dimensional semiconductors and heterostructures: progress and prospects. J. Appl. Phys. 129, 120902 (2021).
Miller, R. C. & Kleinman, D. A. Excitons in GaAs quantum wells. J. Lumin. 30, 520–540 (1985).
Chemla, D. S. Quantum wells for photonics. Phys. Today 38, 56–64 (1985).
Behnia, K. Condensed-matter physics: polarized light boosts valleytronics. Nat. Nanotechnol. 7, 488–489 (2012).
Jones, A. M. et al. Optical generation of excitonic valley coherence in monolayer WSe2. Nat. Nanotechnol. 8, 634–638 (2013).
Urbaszek, B. & Marie, X. Valleytronics: divide and polarize. Nat. Phys. 11, 94–95 (2015).
Deilmann, T., Krüger, P. & Rohlfing, M. Ab initio studies of exciton g factors: monolayer transition metal dichalcogenides in magnetic fields. Phys. Rev. Lett. 124, 226402 (2020).
Mak, K. F., McGill, K. L., Park, J. & McEuen, P. L. The valley Hall effect in MoS2 transistors. Science 344, 1489–1492 (2014).
Sie, E. J. et al. Valley-selective optical Stark effect in monolayer WS2. Nat. Mater. 14, 290–294 (2014).
Li, Y. et al. Valley splitting and polarization by the Zeeman effect in monolayer MoSe2. Phys. Rev. Lett. 113, 266804 (2014).
Aivazian, G. et al. Magnetic control of valley pseudospin in monolayer WSe2. Nat. Phys. 11, 148–152 (2015).
Mitioglu, A. A. et al. Optical investigation of monolayer and bulk tungsten diselenide (WSe2) in high magnetic fields. Nano Lett. 15, 4387–4392 (2015).
Wang, G. et al. Magneto-optics in transition metal diselenide monolayers. 2D Mater. 2, 034002 (2015).
MacNeill, D. et al. Breaking of valley degeneracy by magnetic field in monolayer MoSe2. Phys. Rev. Lett. 114, 037401 (2015).
Arora, A. et al. Valley Zeeman splitting and valley polarization of neutral and charged excitons in monolayer MoTe2 at high magnetic fields. Nano Lett. 16, 3624–3629 (2016).
Plechinger, G. et al. Excitonic valley effects in monolayer WS2 under high magnetic fields. Nano Lett. 16, 7899–7904 (2016).
Nagler, P. et al. Giant magnetic splitting inducing near-unity valley polarization in van der Waals heterostructures. Nat. Commun. 8, 1551 (2017).
Carey, B. et al. High‐performance broadband Faraday rotation spectroscopy of 2D materials and thin magnetic films. Small Methods 6, 2200885 (2022).
Have, J., Peres, N. M. R. & Pedersen, T. G. Excitonic magneto-optics in monolayer transition metal dichalcogenides: from nanoribbons to two-dimensional response. Phys. Rev. B 100, 045411 (2019).
Das, D., Jindal, V., Sugunakar, V. & Ghosh, S. Landé g-factor of excitons from circularly polarized low-field magnetomodulated reflectance spectroscopy: application to bulk 2H-MoS2. Phys. Rev. Appl. 19, 064073 (2023).
Yang, S. et al. Layer-dependent electrical and optoelectronic responses of ReSe2 nanosheet transistors. Nanoscale 6, 7226 (2014).
Srivastava, A. et al. Valley Zeeman effect in elementary optical excitations of monolayer WSe2. Nat. Phys. 11, 141–147 (2015).
Mitioglu, A. A. et al. Magnetoexcitons in large area CVD-grown monolayer MoS2 and MoSe2 on sapphire. Phys. Rev. B 93, 165412 (2016).
Koperski, M. et al. Optical properties of atomically thin transition metal dichalcogenides: observations and puzzles. Nanophotonics 6, 1289–1308 (2017).
Arora, A. et al. Zeeman spectroscopy of excitons and hybridization of electronic states in few-layer WSe2, MoSe2 and MoTe2. 2D Mater. 6, 015010 (2018).
Koperski, M. et al. Orbital, spin and valley contributions to Zeeman splitting of excitonic resonances in MoSe2, WSe2 and WS2 monolayers. 2D Mater. 6, 015001 (2018).
Schmidt, R. et al. Magnetic-field-induced rotation of polarized light emission from monolayer WS2. Phys. Rev. Lett. 117, 077402 (2016).
Jiang, C. et al. Zeeman splitting via spin-valley-layer coupling in bilayer MoTe2. Nat. Commun. 8, 802 (2017).
Fowles, G. R. Introduction to Modern Optics (Dover Publications, Inc., 1989).
You, C.-Y. & Shin, S.-C. Generalized analytic formulae for magneto-optical Kerr effects. J. Appl. Phys. 84, 541 (1998).
Zak, J., Moog, E. R., Liu, C. & Bader, S. D. Magneto-optics of multilayers with arbitrary magnetization directions. Phys. Rev. B 43, 6423–6429 (1991).
Crassee, I. et al. Giant Faraday rotation in single- and multilayer graphene. Nat. Phys. 7, 48–51 (2011).
Miura, N. Physics of Semiconductors in High Magnetic Fields (Oxford University Press Inc., 2008).
Fronk, M. et al. Determination of the Voigt constant of phthalocyanines by magneto-optical Kerr-effect spectroscopy. Phys. Rev. B 79, 235305 (2009).
Hecht, E. Optics (Pearson Addison Wesley, 2001).
Arora, A., Mandal, A., Chakrabarti, S. & Ghosh, S. Magneto-optical Kerr effect spectroscopy based study of Landé g-factor for holes in GaAs/AlGaAs single quantum wells under low magnetic fields. J. Appl. Phys. 113, 213505 (2013).
Li, Y. et al. Measurement of the optical dielectric function of monolayer transition-metal dichalcogenides: MoS2, MoSe2, WS2, and WSe2. Phys. Rev. B 90, 205422 (2014).
Wierzbowski, J. et al. Direct exciton emission from atomically thin transition metal dichalcogenide heterostructures near the lifetime limit. Sci. Rep. 7, 12383 (2017).
Cadiz, F. et al. Excitonic linewidth approaching the homogeneous limit in MoS2-based van der Waals heterostructures. Phys. Rev. X 7, 021026 (2017).
Ajayi, O. A. et al. Approaching the intrinsic photoluminescence linewidth in transition metal dichalcogenide monolayers. 2D Mater. 4, 031011 (2017).
Kielar, P. Magneto-optical polar Kerr effect and dispersion relations. J. Opt. Soc. Am. B 11, 854 (1994).
Arora, A. et al. Interlayer excitons in a bulk van der Waals semiconductor. Nat. Commun. 8, 639 (2017).
Slobodeniuk, A. O. et al. Fine structure of K-excitons in multilayers of transition metal dichalcogenides. 2D Mater. 6, 025026 (2019).
Deilmann, T. & Thygesen, K. S. Interlayer excitons with large optical amplitudes in layered van der Waals materials. Nano Lett. 18, 2984–2989 (2018).
Kossacki, P. Optical studies of charged excitons in II VI semiconductor quantum wells. J. Phys. Condens. Matter 15, R471–R493 (2003).
Pei, J. et al. Exciton and trion dynamics in bilayer MoS2. Small 11, 6384–6390 (2015).
Leisgang, N. et al. Giant Stark splitting of an exciton in bilayer MoS2. Nat. Nanotechnol. 15, 901–907 (2020).
Peimyoo, N. et al. Electrical tuning of optically active interlayer excitons in bilayer MoS2. Nat. Nanotechnol. 16, 888–893 (2021).
Grzeszczyk, M. et al. Exposing the trion’s fine structure by controlling the carrier concentration in hBN-encapsulated MoS2. Nanoscale 13, 18726–18733 (2021).
Srinivasan, K. & Stadler, B. J. H. Review of integrated magneto-optical isolators with rare-earth iron garnets for polarization diverse and magnet-free isolation in silicon photonics [Invited]. Opt. Mater. Express 12, 697 (2022).
Pidgeon, C. R. & Brown, R. N. Interband magneto-absorption and Faraday rotation in InSb. Phys. Rev. 146, 575–583 (1966).
Qiu, D. Y., da Jornada, F. H. & Louie, S. G. Optical spectrum of MoS2: many-body effects and diversity of exciton states. Phys. Rev. Lett. 111, 216805 (2013).
Qiu, D. Y., da Jornada, F. H. & Louie, S. G. Screening and many-body effects in two-dimensional crystals: monolayer MoS2. Phys. Rev. B 93, 235435 (2016).
Drüppel, M., Deilmann, T., Krüger, P. & Rohlfing, M. Diversity of trion states and substrate effects in the optical properties of an MoS2 monolayer. Nat. Commun. 8, 2117 (2017).
Gjerding, M. N. et al. Recent progress of the computational 2D materials database (C2DB). 2D Mater. 8, 044002 (2021).
Woźniak, T., Faria Junior, P. E., Seifert, G., Chaves, A. & Kunstmann, J. Exciton g factors of van der Waals heterostructures from first-principles calculations. Phys. Rev. B 101, 1–29 (2020).
Klingshirn, C. F. Semiconductor Optics (Springer Berlin Heidelberg, 2012).
Kormányos, A. et al. k·p theory for two-dimensional transition metal dichalcogenide semiconductors. 2D Mater. 2, 022001 (2015).
Goryca, M. et al. Revealing exciton masses and dielectric properties of monolayer semiconductors with high magnetic fields. Nat. Commun. 10, 4172 (2019).
Zipfel, J. et al. Spatial extent of the excited exciton states in WS2 monolayers from diamagnetic shifts. Phys. Rev. B 98, 075438 (2018).
Singh, J. Electronic and Optoelectronic Properties of Semiconductor Structures (Cambridge University Press, 2003).
Snelling, M. J., Blackwood, E., McDonagh, C. J., Harley, R. T. & Foxon, C. T. B. Exciton, heavy-hole, and electron g factors in type-I GaAs/AlxGa1−xAs quantum wells. Phys. Rev. B 45, 3922–3925 (1992).
Wu, M., Li, Z., Cao, T. & Louie, S. G. Physical origin of giant excitonic and magneto-optical responses in two-dimensional ferromagnetic insulators. Nat. Commun. 10, 2371 (2019).
Ho, Y.-H., Chiu, C.-W., Su, W.-P. & Lin, M.-F. Magneto-optical spectra of transition metal dichalcogenides: a comparative study. Appl. Phys. Lett. 105, 222411 (2014).
Wang, Z., Shan, J. & Mak, K. F. Valley- and spin-polarized Landau levels in monolayer WSe2. Nat. Nanotechnol. 12, 144–149 (2017).
Marinov, K., Avsar, A., Watanabe, K., Taniguchi, T. & Kis, A. Resolving the spin splitting in the conduction band of monolayer MoS2. Nat. Commun. 8, 1938 (2017).
Nguyen, C. V. et al. Magneto-optical transport properties of monolayer MoS2 polar substrates. Phys. Rev. B 96, 125411 (2017).
Liu, S. et al. Two-dimensional ferromagnetic superlattices. Natl. Sci. Rev. 7, 745–754 (2020).
Huang, B. et al. Emergent phenomena and proximity effects in two-dimensional magnets and heterostructures. Nat. Mater. 19, 1276–1289 (2020).
Zhong, D. et al. Van der Waals engineering of ferromagnetic semiconductor heterostructures for spin and valleytronics. Sci. Adv. 3, e1603113 (2017).
Balkanski, M. & Amzallag, E. Band parameters determination from Faraday rotation measurements. Phys. Status Solidi 30, 407–439 (1968).
Gabriel, C. J. & Piller, H. Determination of the optical Verdet coefficient in semiconductors and insulators. Appl. Opt. 6, 661 (1967).
Dudziak, E., Bożym, J., Pruchnik, D. & Wasilewski, Z. R. Faraday rotation in multiple quantum wells of GaAs/AlGaAs. Acta Phys. Pol. A 90, 1022–1026 (1996).
Zvára, M., Žaloudek, F. & Prosser, V. Interband Faraday effect in CdTe single crystals. Phys. status Solidi 16, K21–K24 (1966).
Stramska, H., Bachan, Z., Byszewski, P. & Kołsodziejczak, J. Interband Faraday rotation and ellipticity observed at the absorption edge in silicon. Phys. Status Solidi 27, K25–K28 (1968).
Güntherodt, G., Schoenes, J. & Wachter, P. Optical constants of the Eu chalcogenides above and below the magnetic ordering temperatures. J. Appl. Phys. 41, 1083–1084 (1970).
Gong, C. et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 546, 265–269 (2017).
Hwang, Y., Chung, S. & Um, Y. Giant Faraday rotation in Cd1-xMnxTe (0<x<0.82) crystals. Phys. Status Solidi 4, 4453–4456 (2007).
Kuroiwa, T. et al. Faraday rotation of ferromagnetic (Ga, Mn). As. Electron. Lett. 34, 190 (1998).
Onodera, K., Masumoto, T. & Kimura, M. 980 nm compact optical isolators using Cd1–x–yMnxHgyTe single crystals for high power pumping laser diodes. Electron. Lett. 30, 1954–1955 (1994).
Nakano, T., Yuri, H. & Kihara, U. Magneto-optical properties of YIG single crystal by TSFZ method. IEEE Trans. Magn. 20, 986–988 (1984).
Bi, L., Hu, J., Dionne, G. F., Kimerling, L. & Ross, C. A. Monolithic integration of chalcogenide glass/iron garnet waveguides and resonators for on-chip nonreciprocal photonic devices. In Integrated Optics: Devices, Materials, and Technologies XV (eds Broquin, J. E. & Nunzi Conti, G.) Vol. 7941, 794105 (SPIE Publications, 2011).
Fakhrul, T. et al. High figure of merit magneto‐optical Ce‐ and Bi‐substituted terbium iron garnet films integrated on Si. Adv. Opt. Mater. 9, 2100512 (2021).
Srinivasan, K. et al. High-gyrotropy seedlayer-free Ce:TbIG for monolithic laser-matched SOI optical isolators. ACS Photonics 6, 2455–2461 (2019).
Acknowledgements
The authors acknowledge the financial support from the German Research Foundation (DFG project nos. AR 1128/1-1 and AR 1128/1-2), the Alexander von Humboldt Foundation, and NM-ICPS of the DST, Government of India through the I-HUB Quantum Technology Foundation (Pune, India), Project No. CRG/2022/007008 of SERB (Government of India), and MoE-STARS project No. MoE-STARS/STARS-2/2023-0912 (Government of India). Fruitful discussions with Thorsten Deilmann and Mukul Kabir are gratefully acknowledged.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
A.A. conceived the idea of the project. B.C. and A.A. performed the experiments and analyzed the data. N.K.W. and P.S. fabricated the samples. N.K.W., B.C., and A.A. built the setup. A.A. wrote the manuscript with contributions and suggestions from all authors. R.S., S.M.V., R.B., and A.A. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Carey, B., Wessling, N.K., Steeger, P. et al. Giant Faraday rotation in atomically thin semiconductors. Nat Commun 15, 3082 (2024). https://doi.org/10.1038/s41467-024-47294-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-024-47294-5
This article is cited by
-
Ultrathin 2D materials rotate visible light
Nature India (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.