Abstract
Magnetic noise of atomic nuclear spins is a major source of decoherence in solid-state spin qubits. In theory, near-unity nuclear spin polarization can eliminate decoherence of the electron spin qubit, while turning the nuclei into a useful quantum information resource. However, achieving sufficiently high nuclear polarizations has remained an evasive goal. Here we implement a nuclear spin polarization protocol which combines strong optical pumping and fast electron tunneling. Nuclear polarizations well above 95% are generated in GaAs semiconductor quantum dots on a timescale of 1 minute. The technique is compatible with standard quantum dot device designs, where highly-polarized nuclear spins can simplify implementations of qubits and quantum memories, as well as offer a testbed for studies of many-body quantum dynamics and magnetism.
Similar content being viewed by others
Introduction
The capability of initializing a quantum system into a well-defined eigenstate is one of the fundamental requirements in quantum science and technology. This has been demonstrated for individual and dilute nuclear spins in the solid state1,2, but remains a long-standing challenge for dense three-dimensional lattices of nuclear spins. For the quantum ground state of a spin ensemble the polarization degree is PN = ± 100%, which is equivalent to absolute zero spin temperature. Very high polarizations, PN ≈ 95–99%, can be reached through brute-force cooling in certain bulk materials, but the cooling cycle may take hours or even days3,4. More scalable approaches seek to use individual or dilute electron spins to polarize the dense nuclear ensembles. Microwave pumping of paramagnetic impurities in bulk solids5,6 provides polarizations up to PN ≈ 80–90%. In semiconductor nanostructures, PN ≈ 50–80% is achieved either through electronic transport7 or optical excitation8. However, polarizations much closer to unity are needed to suppress the electron spin qubit dephasing, whose rate scales as \(\sqrt{1-{P}_{{{{{{{{\rm{N}}}}}}}}}^{2}}\)9, or reduce the nuclear ensemble entropy, which scales as \(\frac{1-{P}_{{{{{{{{\rm{N}}}}}}}}}}{2}(1-\ln (\frac{1-{P}_{{{{{{{{\rm{N}}}}}}}}}}{2}))\)10. Therefore, different techniques are needed to approach a fully-polarized nuclear state.
Extensive theoretical studies have been conducted to understand what limits nuclear spin pumping in a central-spin scenario, where the electron can be polarized on demand, while the ensemble of N nuclei can only be accessed through hyperfine (magnetic) coupling with that central electron (Fig. 1a). The formation of coherent “dark” states11 has been shown to suppress the transfer of polarization from the electron to nuclei12. Thus an open question remains – is it possible, even in principle, to reach a fully-polarized nuclear state in a real central-spin system?
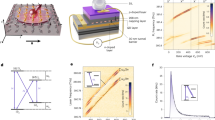
a Schematic of a central electron spin and an ensemble of nuclear spins coupled through hyperfine interaction with constants aj. The nuclei are coupled through dipolar interactions with pairwise constants bj,k (see Supplementary Note 2). b Schematic cross-section of a p − i − n diode with embedded epitaxial GaAs quantum dots. Laser excitation, photoluminescence collection and the external magnetic field are directed along the sample growth axis z. Doped semiconductor layers are used to apply the gate bias VGate, resulting in a tunable electric field along z. c Typical photoluminescence spectra of a negatively charged trion X− in an individual QD. The spectral splitting ΔEPL depends both on magnetic field Bz and the helicity (σ+ or σ−) of the optical pumping due to the buildup of the nuclear spin polarization. d Experimental cycle consisting of nuclear spin optical pumping, nuclear magnetic resonance (NMR) excitation, and optical probing of the photoluminescence spectrum. VGate is switched between an arbitrary level VPump and the levels that tune the QD into the electron-charged (1e) and neutral (0e) states.
We work with GaAs/AlGaAs quantum dots (QDs) and use optical excitation to polarize nuclear spins. While the optical method is well known13, achieving near-unity polarizations and understanding the underlying physics proved challenging. Here, we show that the solution is to combine strong optical excitation with fast carrier tunneling, which resolves the main bottleneck of slow optical recombination. Moreover, no “dark”-state limitation occurs, which we also attribute to the extremely short lifetime of the electron spin. As a result, we achieve nuclear polarization degrees well above PN > 95%. The maximum polarizations vary between individual QDs, which we ascribe to slight fluctuations in QD shapes and partial relaxation of the optical selection rules. For the best dots we derive PN ≳ 99%, limited only by the accuracy of the existing measurement techniques. These high polarizations surpass the predicted PN ≳ 90% threshold for achieving extended electron spin qubit coherence14,15, quantum memory operation15,16, superradiant electron-nuclear spin dynamics17,18, as well as magnetic-ordering phase transition19,20.
Results
The semiconductor device, sketched in Fig. 1b, is a p − i − n diode with epitaxial GaAs QDs embedded into the AlGaAs barrier layers (see Supplementary Note 1). By changing the gate bias VGate it is possible to charge the QD with individual resident electrons21,22 and apply a tunable electric field. Each individual QD contains N ≈ 105 nuclei, with the three abundant isotopes 75As, 69Ga and 71Ga, all possessing spin momentum I = 3/2. The sample is cooled to ≈4.25 K and placed in a magnetic field Bz parallel to the electric field and sample growth direction (see Supplementary Note 3). Thanks to the selection rules13, optical excitation creates spin-polarized electron-hole pairs; σ± polarized photons with ±1 angular momentum (in units of ℏ) generate electrons with spin projection sz = ∓ 1/2. Owing to the electron-nuclear hyperfine interaction (Fig. 1a), a polarized electron can transfer its spin to one of the nuclei and, through repeated optical pumping, induce a substantial polarization ∣PN∣. Conversely, the energy of the photon emitted from electron-hole recombination depends on the mutual alignment of the electron spin and the total magnetic field, which is a sum of Bz and the effective field of the polarized nuclei. The resulting optical spectrum is a doublet (Fig. 1c), whose splitting ΔEPL is used as a sensitive probe of the nuclear spin polarization state. We define the exciton hyperfine shift Ehf = − (ΔEPL − ΔEPL,0), where ΔEPL,0 is the splitting measured for depolarized nuclei (PN ≈ 0).
The high resolution optical spectra (Fig. 1c), required to measure Ehf, can only be observed for a narrow range of gate biases and optical excitation powers. Therefore, we use a pump-probe technique (Fig. 1d), where the nuclear spins are polarized by an optical pump with an arbitrary set of parameters, while the optical probe parameters are fixed and optimized for the readout of Ehf. Conducting experiments at high magnetic field Bz = 10 T, we maximize the hyperfine shift ∣Ehf∣ by optimizing the following parameters: the elliptical polarization of the optical pump, its power PPump, photon energy EPump and the bias VPump during pumping. The results are interpreted with reference to photoluminescence data. Figure 2a shows low power luminescence spectra, which reveal a well-known bias-controlled charging of the ground state (s-shell) exciton in a QD22. High optical power (Fig. 2b) broadens the spectra, also populating the higher shells p, d, etc.23,24. (See additional data in Supplementary Note 4).
a Bias-dependent photoluminescence spectra of an individual dot QD1 measured at Bz = 10 T at low excitation power PExc = 0.5 nW and excitation photon energy EExc = 1.96 eV. Labels show neutral (X0), positively (Xn+) and negatively (Xn−) multi-charged QD excitons. Broad spectral features at higher energies arise from the AlGaAs layers. b Photoluminescence spectra at an increased power PExc = 20 μW reveal saturated emission from higher QD exciton shells, labeled s, p, d. c Hyperfine shift measured in a pump-probe experiment (Fig. 1d) on QD1 as a function of gate bias VPump and the photon energy EPump of the σ+ polarized optical pump with power PPump = 1.5 mW. Parameter regions where no data has been measured are shown in gray. Excitonic spectral features are labeled up to the h shell. The dashed ellipse highlights the parameters that result in the most efficient nuclear spin polarization. d Schematic of the conduction and valence band edges along the z direction, as well as confined electron (full circles) and hole (open circles) states. The three stages of the cyclic nuclear spin pumping process are shown schematically. Source data for a–c are provided as a Source Data file.
The dependence of nuclear-induced shift Ehf on EPump and VPump, shown in Fig. 2c, reveals spectral bands that match the excitonic shells in Fig. 2b, demonstrating that nuclear spin pumping proceeds through resonant optical driving of the QD exciton transitions. The largest ∣Ehf∣ is observed when the pump is resonant with the s shell (EPump ≈ 1.565 eV), and at a large reverse bias VPump = −2.3 V, where photoluminescence is completely quenched. Moreover, the optimal pump laser power PPump = 1.5 mW is five orders of magnitude higher than the saturation power of the s-shell luminescence. Based on these observations, the nuclear spin pumping effect can be understood as a cyclic process sketched in Fig. 2d. First, circularly-polarized resonant optical excitation creates a spin-polarized electron-hole pair in the quantum dot. Then, the electron has a small but finite probability to undergo a flip-flop with one of the nuclei, increasing the ensemble polarization ∣PN∣. Finally, in order to proceed to the next cycle, the electron is removed through tunneling. The tunneling time, estimated from bias-dependent photoluminescence in Supplementary Note 4, is ≲ 0.1 ps, much shorter than the ≈ 300 ps radiative recombination time25. The combination of high-power optical pumping and fast tunneling escape results in rapid cycling. This in turn leads to a high rate of nuclear spin pumping, which helps to outpace the inevitable nuclear spin relaxation. The cycling time is also much shorter than the period of coherent electron precession ≳ 20 ps, ensuring the spin-flipped electrons are removed before they can undergo a reverse flip-flop26. The ultimate result is a large steady-state nuclear hyperfine shift ∣Ehf∣ > 110 μeV, exceeding ∣Ehf∣ observed previously8,27.
Although Ehf scales linearly with nuclear polarization degree PN, its absolute value depends on the QD structure. The electron wavefunction leaks into the barriers where the fraction of Ga atoms replaced with Al atoms is not known precisely. A more reliable measurement of the PN is achieved through nuclear magnetic resonance (NMR) spin thermometry (see Supplementary Note 5 for details). The method assumes Boltzmann probability distribution pm ∝ emβ for each nucleus to occupy a state with spin projections m, where β is the dimensionless inverse spin temperature. For spin I = 1/2, where m = ± 1/2, any statistical distribution has the Boltzmann form. By contrast, for I > 1/2, the Boltzmann distribution expresses the non-trivial nuclear spin temperature hypothesis28, verified for epitaxial GaAs quantum dots previously8.
In order to perform spin thermometry, we first measure the single-QD NMR spectra29, as exemplified in Fig. 3a for 69Ga spins. The three magnetic-dipole transitions of the 3/2 spins are well resolved thanks to the quadrupolar shifts νQ, which originate from the lattice mismatch of GaAs and AlGaAs. Compared to the Larmor frequency νL ≈ 100 MHz, these strain-induced quadrupolar effects ∣νQ∣ ≲ 100 kHz are still too small to impede nuclear spin pumping. This is a significant advantage over the highly-strained Stranski–Krastanov QDs29, where ∣νQ∣ ≈ 1–10 MHz so that large ∣PN∣ is prohibited simply because nuclear eigenstates are not aligned along the magnetic field30 (the misalignment is characterized by the ratio \(\propto {({\nu }_{{{{{{{{\rm{Q}}}}}}}}}/{\nu }_{{{{{{{{\rm{L}}}}}}}}})}^{2}\)). The resolved NMR triplet is essential, as it allows β to be derived from the Boltzmann exponent, which then relates to PN through the standard Brillouin function. Qualitatively this is demonstrated in Fig. 3b with simple saturation NMR spectroscopy31. At moderate polarization PN ≈ −0.6 (dashed line) all three magnetic-dipole transitions m ↔ m + 1 are observed, and their amplitudes are proportional to the differences ∣pm+1 − pm∣ (Fig. 3c). At the maximum positive polarization (solid line) a single NMR peak +1/2 ↔ +3/2 is observed, indicating that nearly all spins have been cooled to the m = + 3/2 state.
a High-resolution spectrum of 69Ga measured in QD1 at Bz = 10 T using “inverse NMR” signal enhancement technique29. Inset shows the nuclear energy levels with spin projections m = ± 1/2, ± 3/2. The resonance between m = ± 1/2 is at a pure Larmor frequency νL, whereas the satellite transitions involving m = ± 3/2 are split off by the quadrupolar shifts ∓ νQ (for Ga nuclei the shifts are predominantly negative νQ < 0). b Low-resolution spectrum of the same QD1, but measured using the saturation technique in order to reveal the population probabilities of the nuclear spin levels. c Population probabilities of spin levels with different m, sketched for the same two nuclear polarization degrees as in b. d Hyperfine shift variation arising from selective NMR manipulation of the 69Ga nuclear spins plotted against the initial photoluminescence spectral splitting ΔEPL, varied by changing the optical pump wavelength and polarization. Squares show the total 69Ga hyperfine shift measured by broadband saturation of the entire NMR triplet, which equalizes populations pm for all m. Circles and triangles show the selective signals of the ± 1/2 ↔ ± 3/2 resonances measured via frequency-swept adiabatic inversion. Lines show fitting, from which nuclear spin polarization degree is derived and plotted in the top horizontal scale (see Supplementary Note 5). e Maximum positive and minimum negative nuclear spin polarization degrees PN derived for 69Ga (triangles) and 75As (circles) in individual dots QD1 - QD3 (indexed by numbers adjacent to the symbols) at Bz = 10 T (solid symbols) and Bz = 4 T (open symbols). Error bars are 95% confidence intervals. f Maximum positive and minimum negative hyperfine shifts measured on individual dots QD1–QD12 at Bz = 10 T. Source data for d and f are provided as a Source Data file. Source data for e can be found in Supplementary Information.
For quantitative spin thermometry we measure the peak areas of the −3/2 ↔ −1/2 and +1/2 ↔ +3/2 NMR transitions at different nuclear polarizations. The results are shown in Fig. 3d (circles and triangles), together with the total signal obtained by saturating all three NMR transitions (squares). We take into account the small overlaps of the NMR triplet components (see Supplementary Note 5) and use Boltzmann model fitting (lines) to derive the polarization degree PN (top axis). The model reproduces well both the linear dependence of the total NMR signal and the non-linear dependencies of the selective ± 1/2 ↔ ± 3/2 signals, revealing a close approach to PN ≈ −1. Qualitatively, at PN = −1 the m = +1/2, +3/2 states must be depopulated, resulting in a vanishing +1/2 ↔ +3/2 signal, as indeed observed experimentally. Moreover, at PN = −1 the −3/2 ↔ −1/2 signal must be 2/3 of the total NMR signal, also in good agreement with experiment. By switching from σ+ to σ− optical pumping we also approach PN ≈ +1. The largest positive and negative PN are shown in Fig. 3e for individual dots QD1–QD3, chosen for their highest ∣Ehf∣. At the highest static field Bz = 10 T the best-fit estimates for 69Ga are around ∣PN∣ ≈ 0.99, with somewhat lower ∣PN∣ ≈ 0.98 for 75As. With 95% confidence, ∣PN∣ exceeds 0.95, but the data is also compatible with ∣PN∣ = 1. It is thus possible that the actual polarization is much closer to unity – at present, the measurement accuracy is the main limitation. Spin thermometry on one of the QDs at Bz = 4 T yields similarly high polarizations ∣PN∣ ≳ 0.93, although the measurement accuracy is reduced due to the less efficient optical probing.
A simpler measurement of the largest positive and negative hyperfine shift Ehf is shown in Fig. 3f for 12 randomly chosen dots. For some QDs, nuclear polarization does not exceed ∣PN∣ ≈ 0.9. We also observe that for all studied QDs the optimal optical polarization of the pump is not circular, but is rather elliptical32, with a randomly-oriented linearly-polarized contribution ranging between 0 and 0.4 (see Supplementary Note 3). This points to heavy-light hole mixing, which is always present in QDs33 and is more pronounced under low-symmetry confinement34,35. In additional measurements, where the symmetry is reduced on purpose through uniaxial stress or tilting the magnetic field by ≈ 12∘, we indeed find a significant reduction in maximum ∣Ehf∣. Therefore, the dot-to-dot variation of PN is attributed to the randomness of the QD morphology.
The buildup dynamics, measured under optimal nuclear spin pumping, are shown in Fig. 4a. The approach to the steady state is non-exponential since the nuclei that are further away from the center of the QD are less coupled to the electron and take longer to polarize. It takes on the order of ≈ 60 s to reach the steady-state PN within the measurement accuracy. Once optical pumping is switched off, nuclear spins depolarize in the dark (squares in Fig. 4b) on a timescale of minutes, mainly through spin diffusion36. Such long lifetimes mean that a highly-polarized nuclear spin state can be prepared and used to extend electron spin qubit coherence over a large number of short (few nanoseconds) qubit operations. We further examine the effect of the initial PN on the relaxation dynamics by augmenting the optically-pumped nuclear state with a short partially-depolarizing NMR pulse (triangles and stars in Fig. 4b). When normalized by the initial polarization, the plot reveals accelerated nuclear spin relaxation under reduced initial polarization (inset in Fig. 4b). This is quantified in Fig. 4c, where at high polarization the nuclear spin relaxation half-lifetime T1,N is seen to be a factor of ≈ 2–3 longer than in case of low initial polarization (the lowest studied initial polarization is limited by the accuracy of the T1,N measurement). This is a non-trivial result: scaling of the initial PN should not change T1,N within the linear spin diffusion model.
a Nuclear spin buildup dynamics measured (symbols) in an individual dot QD2 at Bz = 10 T under σ+ (triangles) and σ− (squares) optical pumping. Lines show biexponential fitting. b Nuclear spin relaxation dynamics in the dark measured in a neutral QD state following σ+ optical pumping (squares). The same relaxation dynamics are also measured with partial NMR saturation after the optical pump, which reduces the initial PN (triangles and stars). Lines show fitting used to derive the nuclear spin half-lifetimes T1,N. Inset shows the same data, but normalized by the initial hyperfine shift at short dark times TDark. c Nuclear spin relaxation times T1,N as a function of the initial hyperfine shift Ehf. The corresponding approximate initial PN is shown on the top axis. Error bars are 95% confidence intervals. d Density of states calculated for N = 6 dipolar-coupled I = 3/2 nuclei (without the electron). Each band, broadened by dipolar couplings \(h{\nu }_{{{{{{{{\rm{dd}}}}}}}}}\propto \max | {b}_{j,k}|\), corresponds to a well-defined total spin projection M. The adjacent bands are split by the Zeeman energy hνL. e Population probability of the eigenstates, calculated for the spectrum in d and for two types of mixed states: Boltzmann distribution of Zeeman energies with high polarization PN ≈ 0.99 (red) and a narrowed Gaussian distribution with PN = 0 (blue). Source data for a–c are provided as a Source Data file.
In order to explain the non-linear diffusion, we consider the eigenspectrum of a nuclear spin ensemble, with an example shown in Fig. 4d for N = 6 spins I = 3/2. The adjacent bands are separated by the large Zeeman energy hνL (typical νL ≈ 100 MHz at Bz = 10 T), which corresponds to a flip of a single nucleus, accompanied by a ± 1 change in the total ensemble spin projection M. Each band consists of all possible superpositions with a given M, with degeneracy lifted by the small (νdd ≈ 1 kHz) nuclear-nuclear dipolar magnetic interaction. For M ≈ 0 (i.e. PN ≈ 0) the broadening of each band is maximal, characterized by the dipole-dipole energy hνdd. With ∣PN∣ approaching unity, the distribution of the available dipolar energies narrows, eventually vanishing for the two fully-polarized states with M = ± NI (i.e. PN = ± 1). The dipolar reservoir can act as a source or sink of energy for a flip-flop spin exchange between two nuclei whose energy gaps are slightly different (for example due to the inhomogeneity of the quadrupolar shifts νQ). Nuclear spin diffusion proceeds through such flip-flops. Therefore, the slow-down of diffusion at high initial ∣PN∣ is well explained by the narrowing of the dipolar reservoir.
The narrowing of the nuclear dipolar reservoir is conceptually similar to the state-narrowing technique, which aims to reduce the statistical dispersion of the nuclear Zeeman energies ∝ M in order to enhance the coherence of the electron spin qubit. An example of a narrowed mixed state is sketched in Fig. 4e for PN ≈ 0, but with uncertainty in M reduced down to a few units, as demonstrated experimentally previously37,38. The fundamental advantage of a polarized state (also sketched in Fig. 4e), is that it not only narrows the uncertainty in M by a factor \(\propto \sqrt{1-{P}_{{{{{{{{\rm{N}}}}}}}}}^{2}}\) (see derivation in Supplementary Note 4D and Supplementary Data 1 and 2), but also reduces the dipolar broadening. In other words, our scheme represents true cooling with ∣PN∣ → 1, whereas the narrowing schemes can be seen as partial cooling of certain degrees of freedom of the nuclear ensemble. The ultimate limit of PN = ± 1 corresponds to the only two non-degenerate nuclear states, for which the electron spin qubit coherence is predicted to be essentially non-decaying14,15. By contrast, even if the dispersion of M is reduced to zero, the dipolar energy uncertainty of a depolarized ensemble may still cause dynamics on the timescales of 1/νdd ≈ 1 ms, leading in turn to electron spin qubit decoherence. Investigation of electron spin coherence in a highly-polarized nuclear spin environment is an interesting subject for future work and may also provide a more sensitive tool for nuclear spin thermometry near ∣PN∣ ≈ 1. Alternatively, more accurate measurement of PN can be sought through “trigger” detection method28, relying on nuclear-nuclear interactions.
Discussion
Large nuclear polarizations are achieved here on a standard p − i − n diode device, fully compatible with high-quality electron spin qubit operation, as demonstrated recently in the same semiconductor structure39. The technique is simple to implement and robust – once optical pumping parameters are optimized for a certain QD, they do not require any correction over months of experiments. Even larger nuclear polarizations can be sought by combining QDs of high in-plane symmetry with biaxial strain in order to reduce the heavy-light hole mixing. Our nuclear spin cooling method uses the purity of the optical pump polarization as the final heat sink, ultimately limiting the achievable PN. This is different from the resonant “dragging” schemes40,41,42 where the ultimate heat sink is the photon number in the optical mode, offering in principle a much closer approach to ∣PN∣ ≈ 1, provided the dark-state bottleneck could be avoided. Combining the advantages of the two approaches in a two-stage cooling cycle can be a route towards the ultimate goal of initializing a nuclear spin ensemble into its fully-polarized quantum ground state. This would be a prerequisite for turning the enormously large Hilbert space of the N ≈ 105 QD nuclei into a high-capacity quantum information resource.
Data availability
The key data generated in this study are provided in the Source Data file SourceData.zip. The rest of the data that support the findings of this study are available from the corresponding author upon request. Source data are provided with this paper.
References
Jacques, V. et al. Dynamic polarization of single nuclear spins by optical pumping of nitrogen-vacancy color centers in diamond at room temperature. Phys. Rev. Lett. 102, 057403 (2009).
Falk, A. L. et al. Optical polarization of nuclear spins in silicon carbide. Phys. Rev. Lett. 114, 247603 (2015).
Reichertz, L. et al. Polarization reversal of proton spins in a solid-state target by superradiance. Nucl. Instrum. Methods Phys. Res. Sect. A 340, 278–282 (1994).
Knuuttila, T. A. et al. Polarized nuclei in normal and superconducting rhodium. J. Low. Temp. Phys. 123, 65–102 (2001).
Jacquinot, J. F., Wenckebach, W. T., Goldman, M. & Abragam, A. Polarization and NMR Observation of 43Ca Nuclei in CaF2. Phys. Rev. Lett. 32, 1096–1097 (1974).
Goldman, M. & Jacquinot, J. F. Measurement of 43Ca-19F Dipolar Energy in Antiferromagnetic CaF2. Phys. Rev. Lett. 36, 330–333 (1976).
Petersen, G. et al. Large nuclear spin polarization in gate-defined quantum dots using a single-domain nanomagnet. Phys. Rev. Lett. 110, 177602 (2013).
Chekhovich, E. A. et al. Measurement of the spin temperature of optically cooled nuclei and GaAs hyperfine constants in GaAs/AlGaAs quantum dots. Nat. Mater. 16, 982 (2017).
Kloeffel, C. & Loss, D. Prospects for spin-based quantum computing in quantum dots. Annu. Rev. Cond. Matt. Phys. 4, 51–81 (2013).
Wenckebach, W. T. The solid effect. Appl. Magn. Reson. 34, 227 (2008).
Imamoglu, A., Knill, E., Tian, L. & Zoller, P. Optical pumping of quantum-dot nuclear spins. Phys. Rev. Lett. 91, 017402 (2003).
Christ, H., Cirac, J. I. & Giedke, G. Quantum description of nuclear spin cooling in a quantum dot. Phys. Rev. B 75, 155324 (2007).
Urbaszek, B. et al. Nuclear spin physics in quantum dots: An optical investigation. Rev. Mod. Phys. 85, 79–133 (2013).
Khaetskii, A. V., Loss, D. & Glazman, L. Electron Spin Decoherence in Quantum Dots due to Interaction with Nuclei. Phys. Rev. Lett. 88, 186802 (2002).
Deng, C. & Hu, X. Electron-spin dephasing via hyperfine interaction in a quantum dot: An equation-of-motion calculation of electron-spin correlation functions. Phys. Rev. B 78, 245301 (2008).
Giedke, G., Taylor, J. M., D’Alessandro, D., Lukin, M. D. & Imamoğlu, A. Quantum measurement of a mesoscopic spin ensemble. Phys. Rev. A 74, 032316 (2006).
Kessler, E. M., Yelin, S., Lukin, M. D., Cirac, J. I. & Giedke, G. Optical superradiance from nuclear spin environment of single-photon emitters. Phys. Rev. Lett. 104, 143601 (2010).
Schuetz, M. J. A., Kessler, E. M., Cirac, J. I. & Giedke, G. Superradiance-like electron transport through a quantum dot. Phys. Rev. B 86, 085322 (2012).
Oja, A. S. & Lounasmaa, O. V. Nuclear magnetic ordering in simple metals at positive and negative nanokelvin temperatures. Rev. Mod. Phys. 69, 1–136 (1997).
Kotur, M. et al. Ultra-deep optical cooling of coupled nuclear spin-spin and quadrupole reservoirs in a GaAs/(Al,Ga)As quantum well. Commun. Phys. 4, 193 (2021).
Miller, B. T. et al. Few-electron ground states of charge-tunable self-assembled quantum dots. Phys. Rev. B 56, 6764–6769 (1997).
Warburton, R. J. et al. Optical emission from a charge-tunable quantum ring. Nature 405, 926–929 (2000).
Raymond, S. et al. Excitonic Energy Shell Structure of Self-Assembled InGaAs/GaAs Quantum Dots. Phys. Rev. Lett. 92, 187402 (2004).
Babinski, A., Potemski, M., Raymond, S., Lapointe, J. & Wasilewski, Z. R. Emission from a highly excited single InAs − GaAs quantum dot in magnetic fields: An excitonic Fock-Darwin diagram. Phys. Rev. B 74, 155301 (2006).
Schimpf, C. et al. Resolving the temporal evolution of line broadening in single quantum emitters. Opt. Express 27, 35290–35307 (2019).
Taylor, J. M., Marcus, C. M. & Lukin, M. D. Long-lived memory for mesoscopic quantum bits. Phys. Rev. Lett. 90, 206803 (2003).
Gammon, D. et al. Electron and nuclear spin interactions in the optical spectra of single GaAs quantum dots. Phys. Rev. Lett. 86, 5176–5179 (2001).
Goldman, M. Spin temperature and nuclear magnetic resonance in solids (Oxford University Press, Oxford, 1970).
Chekhovich, E. A. et al. Structural analysis of strained quantum dots using nuclear magnetic resonance. Nat. Nanotechnol. 7, 646 (2012).
Bulutay, C., Chekhovich, E. A. & Tartakovskii, A. I. Nuclear magnetic resonance inverse spectra of InGaAs quantum dots: Atomistic level structural information. Phys. Rev. B 90, 205425 (2014).
Bloch, F. Nuclear induction. Phys. Rev. 70, 460–474 (1946).
Koudinov, A. V., Akimov, I. A., Kusrayev, Y. G. & Henneberger, F. Optical and magnetic anisotropies of the hole states in Stranski-Krastanov quantum dots. Phys. Rev. B 70, 241305 (2004).
Luo, J.-W., Bester, G. & Zunger, A. Supercoupling between heavy-hole and light-hole states in nanostructures. Phys. Rev. B 92, 165301 (2015).
Huo, Y. H. et al. A light-hole exciton in a quantum dot. Nat. Phys. 10, 46–51 (2014).
Yuan, X. et al. Uniaxial stress flips the natural quantization axis of a quantum dot for integrated quantum photonics. Nat. Commun. 9, 3058 (2018).
Millington-Hotze, P., Manna, S., Covre da Silva, S. F., Rastelli, A. & Chekhovich, E. A. Nuclear spin diffusion in the central spin system of a GaAs/AlGaAs quantum dot. Nat. Commun. 14, 2677 (2023).
Xu, X. et al. Optically controlled locking of the nuclear field via coherent dark-state spectroscopy. Nature 459, 1105–1109 (2009).
Jackson, D. M. et al. Optimal purification of a spin ensemble by quantum-algorithmic feedback. Phys. Rev. X 12, 031014 (2022).
Zaporski, L. et al. Ideal refocusing of an optically active spin qubit under strong hyperfine interactions. Nat. Nanotechnol. 18, 257–263 (2023).
Latta, C. et al. Confluence of resonant laser excitation and bidirectional quantum-dot nuclear-spin polarization. Nat. Phys. 5, 758–763 (2009).
Högele, A. et al. Dynamic nuclear spin polarization in the resonant laser excitation of an InGaAs quantum dot. Phys. Rev. Lett. 108, 197403 (2012).
Gangloff, D. A. et al. Witnessing quantum correlations in a nuclear ensemble via an electron spin qubit. Nat. Phys. 17, 1247–1253 (2021).
Acknowledgements
P.M-H. and H.E.D. were supported by EPSRC doctoral training grants. E.A.C. was supported by a Royal Society University Research Fellowship and EPSRC award EP/V048333/1. A.R. acknowledges support of the Austrian Science Fund (FWF) via the Research Group FG5, I 4320, I 4380, I 3762, the Linz Institute of Technology (LIT), and the LIT Secure and Correct Systems Lab, supported by the State of Upper Austria, the European Union’s Horizon 2020 research and innovation program under Grant Agreements No. 899814 (Qurope), No. 871130 (Ascent+), the QuantERA II project QD-E-QKD and the FFG (grant No. 891366).
Author information
Authors and Affiliations
Contributions
S.M., S.F.C.S. and A.R. developed, grew, and processed the quantum dot samples. P.M-H. and E.A.C. conducted nuclear spin pumping experiments. H.E.D. and E.A.C. conducted supporting experiments on a stressed semiconductor sample. E.A.C. and P.M-H. analyzed the data. E.A.C. drafted the manuscript with input from all authors. E.A.C. coordinated the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Neelesh Kumar Vij, Edo Waks and the other, anonymous, reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Millington-Hotze, P., Dyte, H.E., Manna, S. et al. Approaching a fully-polarized state of nuclear spins in a solid. Nat Commun 15, 985 (2024). https://doi.org/10.1038/s41467-024-45364-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-024-45364-2
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.