Abstract
Spin defects in van der Waals materials offer a promising platform for advancing quantum technologies. Here, we propose and demonstrate a powerful technique based on isotope engineering of host materials to significantly enhance the coherence properties of embedded spin defects. Focusing on the recently-discovered negatively charged boron vacancy center (\({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\)) in hexagonal boron nitride (hBN), we grow isotopically purified h10B15N crystals. Compared to \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) in hBN with the natural distribution of isotopes, we observe substantially narrower and less crowded \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) spin transitions as well as extended coherence time T2 and relaxation time T1. For quantum sensing, \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) centers in our h10B15N samples exhibit a factor of 4 (2) enhancement in DC (AC) magnetic field sensitivity. For additional quantum resources, the individual addressability of the \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) hyperfine levels enables the dynamical polarization and coherent control of the three nearest-neighbor 15N nuclear spins. Our results demonstrate the power of isotope engineering for enhancing the properties of quantum spin defects in hBN, and can be readily extended to improving spin qubits in a broad family of van der Waals materials.
Similar content being viewed by others
Introduction
Optically-addressable spin defects in solid-state materials have emerged as one of the leading prospects for expanding the boundary of modern quantum technologies1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17. Recently, spin defects in atomically-thin van der Waals materials have attracted significant research interest for their innate ability to integrate with heterogeneous optoelectronic and nanophotonic devices18,19,20,21,22,23,24. Among a wide range of two-dimensional host materials, hexagonal boron nitride (hBN) stands out as a promising candidate owing to its large bandgap (~6 eV) and exceptional mechanical, thermal, and chemical stability25,26. Unlike established host materials such as diamond and silicon carbide, neither nitrogen nor boron has stable isotopes with zero nuclear spin, potentially to the detriment of spin defects in hBN. In particular, the presence of such a dense nuclear spin bath can substantially broaden electronic transitions and shorten the coherence time of spin defects. To this end, prior experimental works have focused on designing dynamical decoupling sequences to isolate spin defects from the local nuclear spin environment in hBN24,27.
In this work, we demonstrate isotope engineering of hBN as a more fundamental way of strengthening the capability of spin defects for quantum applications. By carefully optimizing the isotope species and preparing hBN samples with 15N and 10B, we drastically improve the spin coherent properties of the recently discovered negatively charged boron-vacancy defect (\({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\))18,19. We note that a prior study has investigated the effect of changing only boron isotopes in hBN and do not observe significant improvements in the spin properties of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) 28. Importantly, this technique of isotope engineering is fundamental because of its full compatibility with other ongoing \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) optimization efforts, making it a necessity for future \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) improvement and applications. Although here we focus on a specific spin defect in hBN, we would also like to highlight that the approach is exemplary for engineering other spin defects in general host materials.
Results
Optimal isotopes of hBN
We start with identifying the optimal isotope species in hBN for the embedded \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) defects. The \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) center harbors an electronic spin triplet ground state, \(\left|{m}_{s}=0,\pm 1\right\rangle\), which can be optically initialized and read out at room temperature18. The Hamiltonian of the system, including both the electronic degree of freedom and nearby nuclear spins, can be written as
where Dgs = (2π) × 3.48 GHz is the ground state zero-field splitting between \(\left|{m}_{s}=0\right\rangle\) and \(\left|{m}_{s}=\pm 1\right\rangle\), Bz is the external magnetic field aligned along the out-of-plane c axis of hBN (\(\hat{z}\) direction), S and Sz are the electronic spin-1 operators, Ij and \({I}_{z}^{j}\) are the spin operators for the jth nuclear spin (including both nitrogen and boron) with hyperfine tensors Aj, and γe = (2π) × 2.8 MHz/G and \({\gamma }_{n}^{j}\) are the electronic and nuclear spin gyromagnetic ratios (Fig. 1a, c). We note that, for nuclei with \({{{{{{{\mathcal{I}}}}}}}}\ge 1\), there is a small additional nuclear spin dependent energy shift corresponding to higher multipole moments. Nevertheless, this term only acts on the nuclear spin degree of freedom and thus has no effect on the measured electronic spin transitions to leading order.
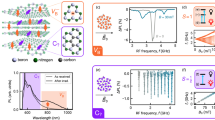
a Schematic of an individual \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) center (red spin) in an isotopically purified h10B15N crystal. \(\hat{z}\) is defined along the c-axis (perpendicular to the lattice plane) and \(\hat{x}\) and \(\hat{y}\) lie in the lattice plane, with \(\hat{x}\) oriented along one of the three \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) Nitrogen bonds. The table lists the nuclear spin quantum number (\({{{{{{{\mathcal{I}}}}}}}}\)), gyromagnetic ratio (γn), and overall electronic spin transition width (\(\propto 2| {\gamma }_{n}{{{{{{{\mathcal{I}}}}}}}}|\)) of the four stable atomic isotopes in hBN. b Energy level diagram of the \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) electronic ground state coupled to the three nearest-neighbor 15N nuclear spins (\({{{{{{{\mathcal{I}}}}}}}}=\frac{1}{2}\)) under an external magnetic field Bz. For each electronic spin transition \(\left|{m}_{s}=0\right\rangle \leftrightarrow \left|{m}_{s}=\pm 1\right\rangle\), the hyperfine interaction leads to four distinct resonances with total nuclear spin magnetic quantum number \(\sum {m}_{I}=\{-\frac{3}{2},-\frac{1}{2},\frac{1}{2},\frac{3}{2}\}\) of degeneracy {1, 3, 3, 1}. c Measured ESR spectra of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) in h10B15N and naturally abundant hBNnat at magnetic field Bz ≈ 87 G. Solid lines represent multi-peak Lorentzian fits, and shaded regions represent numerically simulated transitions considering the 36 nearest nuclear spins (18 nitrogen and 18 boron atoms; see Methods). Insets: ESR spectra at Bz = 0 G. Source data are provided as a Source Data file.
Throughout our experiment, we consistently operate within magnetic fields of Bz ≲ 760 G such that the energy splitting (Dgs ± γeBz) ≳ (2π) × 1.35 GHz between the electronic ground state levels \(\left|{m}_{s}=0\right\rangle\) and \(\left|{m}_{s}=\pm 1\right\rangle\) is much greater than the hyperfine interaction strength, i.e. ∣Aj∣ ≲ (2π) × 100 MHz. As a result, the hyperfine term can be approximated as \({\sum }_{j}{{{{{{{\bf{S}}}}}}}}{{{{{{{{\bf{A}}}}}}}}}^{j}{{{{{{{{\bf{I}}}}}}}}}^{j}\approx {\sum }_{j}{A}_{zz}^{j}{S}_{z}{I}_{z}^{j}=({\sum }_{j}{A}_{zz}^{j}{I}_{z}^{j}){S}_{z}\) to leading order, where all remaining terms are suppressed under the secular approximation. This term leads to an energy shift of the electronic spin transition that is dependent on the nuclear spin configuration; averaging across all different configurations gives rise to spectral crowding29,30 of the electronic spin transition with an overall width proportional to \(2| {\gamma }_{n}{{{{{{{\mathcal{I}}}}}}}}|\) (see Methods).
Figure 1a summarizes the nuclear spin quantum numbers and gyromagnetic ratios of the four stable atomic isotopes in hBN. Intuitively, a lower nuclear spin quantum number leads to fewer hyperfine states and contributes to less spectral crowding, with all other factors being equal. Accordingly, the nitrogen isotope 15N (\({{{{{{{\mathcal{I}}}}}}}}=1/2\)) induces a narrower transition linewidth of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) than its naturally abundant counterpart, 14N (\({{{{{{{\mathcal{I}}}}}}}}=1\)). However, we note that the gyromagnetic ratio is equally important in isotope engineering, and although 11B (\({{{{{{{\mathcal{I}}}}}}}}=3/2\)) has a lower spin quantum number compared to 10B (\({{{{{{{\mathcal{I}}}}}}}}=3\)), its gyromagnetic ratio is much larger, which results in a broader linewidth. Therefore, to minimize the spectral crowding of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\), we predict that h10B15N is the optimal host material.
Experimental characterization
To experimentally validate the effect of isotope engineering on the \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) center, we grow single h10B15N crystals with isotopically purified 15N and 10B sources (purity > 99.7% for 15N and > 99.2% for 10B, see Methods)31,32,33,34. We exfoliate the hBN crystal into thin flakes with thicknesses ranging from 20 to 70 nm. \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) defects are created via He+ ion implantation with energy 3 keV and dosage 1ion/nm2, resulting an estimated \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) concentration around 150 ppm24. In the experiment, the fluorescence signal of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) is collected using a home-built confocal microscope, and the microwave is delivered via a coplanar waveguide (see Supplementary Note 1). Most of the experiment in this work are performed at room temperature other than that specified (Fig. 2c).
a \({T}_{2}^{{{{{{{{\rm{E}}}}}}}}}\) spin echo measurements on samples S1 (h10B15N) and S4 (hBNnat). Insets: \({T}_{2}^{{{{{{{{\rm{XY}}}}}}}}}\) XY8 measurements on samples S1 and S4. Error bars represent 1 s.d. accounting statistical uncertainties. b Bottom: extracted spin coherence timescales \({T}_{2}^{{{{{{{{\rm{E}}}}}}}}}\) and \({T}_{2}^{{{{{{{{\rm{XY}}}}}}}}}\). Top: extracted spin relaxation timescales T1 for all six hBN samples investigated in this work. Error bars in time represent 1 s.d. accounting fitting error. c Relaxation timescales T1 for both h10B15N and hBNnat under different temperatures. Inset: T1 measurement comparison with temperature at 10 K. Error bars represent 1 s.d. accounting statistical uncertainties, and error bars in T1 represent 1 s.d. accounting fitting error. Source data are provided as a Source Data file.
The spin transitions of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) can be probed via electron spin resonance (ESR) spectroscopy: by sweeping the frequency of the applied microwave drive while monitoring the fluorescence signal of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\), we expect a fluorescence drop when the microwave is resonant with an electronic spin transition. Figure 1c compares the ESR spectra of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) in our isotopically engineered h10B15N and conventional naturally abundant hBNnat (99.6%/0.4% for 14N/15N and 20%/80% for 10B/11B) under a small external magnetic field (B ≈ 87 G). As expected, the ESR measurements for both \(\left|{m}_{s}=0\right\rangle \leftrightarrow \left|{m}_{s}=\pm 1\right\rangle\) transitions on h10B15N show much less crowded spectra than hBNnat. In particular, there are two striking features. First, instead of an ordinary 7-resonance spectrum observed in the naturally abundant sample18,35, we resolve 4 distinct hyperfine lines for \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) in h10B15N. This structure stems from the hyperfine interaction between \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) and the three nearest-neighbor 15N nuclear spins \((\mathop{\sum }\nolimits_{j=1}^{3}{A}_{zz}^{{}^{15}{{{{{{{\rm{N}}}}}}}}}{I}_{z}^{j}){S}_{z}\), where \({I}_{z}^{j}\) can take the values of \(\pm \frac{1}{2}\). Accounting for all nuclear spin configurations, there are a total of 4 hyperfine lines (split by \(| {A}_{zz}^{{}^{15}{{{{{{{\rm{N}}}}}}}}}|\)) with degeneracy {1:3:3:1} corresponding to the total nuclear spin number \(\sum {m}_{{{{{{{{\rm{I}}}}}}}}}=\{-\frac{3}{2},-\frac{1}{2},\frac{1}{2},\frac{3}{2}\}\) (Fig. 1b, c). By fitting the spectrum to the sum of four equally-spaced Lorentzians with amplitudes proportional to the aforementioned degeneracy ratio, we extract the hyperfine coupling \({A}_{zz}^{{}^{15}{{{{{{{\rm{N}}}}}}}}}=(2\pi )\times [-65.9\pm 0.9]\) MHz, where the negative sign originates from the negative gyromagnetic ratio of 15N. In comparison, the nearest-neighbor 14N hyperfine interaction strength in hBNnatis \({A}_{zz}^{{}^{14}{{{{{{{\rm{N}}}}}}}}}=(2\pi )\times [48.3\pm 0.5]\) MHz. The measured ratio \({A}_{zz}^{{}^{15}{{{{{{{\rm{N}}}}}}}}}/{A}_{zz}^{{}^{14}{{{{{{{\rm{N}}}}}}}}}\approx -1.36\) agrees well with the nuclear spin gyromagnetic ratios \({\gamma }_{n}^{{}^{15}{{{{{{{\rm{N}}}}}}}}}/{\gamma }_{n}^{{}^{14}{{{{{{{\rm{N}}}}}}}}}\approx -1.4\).
The second feature of the \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) spectrum in h10B15N is its dramatically narrower transitions. Specifically, the full width at half maximum (FWHM) linewidth for each hyperfine resonance is (2π) × [55 ± 2] MHz, almost a factor of two lower than that of the naturally abundant hBNnat sample, (2π) × [95 ± 2] MHz. The linewidth originates from the hyperfine couplings to boron and nitrogen nuclear spins beyond the three nearest-neighbor atoms. To quantitatively capture the measured ESR linewidth, we perform numerical simulations by summing over the couplings to the nearest 36 nuclear spins for four different kinds of isotopically distinct hBN samples (see Methods and Supplementary Information)36. The simulated spectra for h10B15N and hBNnat are in good agreement with the experimental data (Fig. 1c). Importantly, the narrower and less crowded hyperfine lines in h10B15N substantially boost the sensitivity of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) for quantum sensing applications37.
Enhanced quantum sensing
Taking magnetic field sensing as an example, we now evaluate the DC and AC magnetic field sensitivity enhancement of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) in h10B15N. The static magnetic field sensitivity of ESR measurement takes the form38,39
where R denotes the photon detection rate, C(ν) the ESR measurement contrast at microwave frequency ν, Cm the maximum contrast, and Δν the FWHM linewidth assuming a single Lorenztian resonance. If one directly compares the fitted FWHM from h10B15N and hBNnat, we find a factor of ~1.8 improvement in sensitivity. Moreover, the hyperfine transitions of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) in hBNnat significantly overlap with each other, while for \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) in h10B15N the resonances are individually resolvable. Therefore, a more accurate comparison instead takes the steepest slope, \(\max | \frac{\partial C(\nu )}{\partial \nu }|\), into consideration, with which we conclude a factor of ~4 improvement in sensitivity using isotope purified h10B15N. By optimizing the laser and microwave power, we estimate a static magnetic field sensitivity ηDC ≈ 10 μT \({{{{{{{{\rm{Hz}}}}}}}}}^{-\frac{1}{2}}\). We note that the sensitivities reported in this work are sample specific, and one can further optimize the sensitivity by increasing the number of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) defects used in experiment (see Supplementary Note 4).
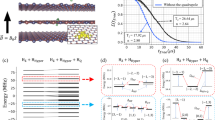
Next, we characterize the spin echo coherence of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) in h10B15N and hBNnat for AC field sensing. The spin echo coherent timescale, \({T}_{2}^{{{{{{{{\rm{E}}}}}}}}}\), of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) has been previously understood to be limited by the magnetic fluctuations from the nearby nuclear spin bath24,28,40, and the isotope engineering technique should precisely alleviate such decoherence. For a robust and systematic comparison, we prepare three h10B15N flakes (sample S1-S3) and three naturally abundant hBNnat flakes (sample S4-S6) onto the same microwave stripline (see Methods). Figure 2a shows the measured spin echo decays on h10B15N sample S1 and hBNnat sample S4, where the extension of spin echo timescales \({T}_{2}^{{{{{{{{\rm{E}}}}}}}}}\) exceeds twofold, from \({T}_{{{{{{{{\rm{2,S4}}}}}}}}}^{{{{{{{{\rm{E}}}}}}}}}=87\pm 9\) ns to \({T}_{{{{{{{{\rm{2,S1}}}}}}}}}^{{{{{{{{\rm{E}}}}}}}}}=186\pm 22\) ns. Figure 2b summarizes the experimentally measured spin echo coherence timescales \({T}_{2}^{{{{{{{{\rm{E}}}}}}}}}\) across all six hBN flakes, revealing a consistent improvement of coherence time in our isotopically purified samples. We also perform the spin echo measurement using h11B15N samples and find \({T}_{2}^{{{{{{{{\rm{E}}}}}}}}}\, \approx \,119\pm 6\) ns, lying in between h10B15N and hBNnat (see Supplementary Fig. 13).
The AC magnetic field sensitivity \({\eta }_{{{{{{{{\rm{AC}}}}}}}}}\propto {T}_{2}^{-1}\) exhibits improvement of more than a factor of 2 in our h10B15N samples. By employing an advanced dynamical decoupling sequence, XY8, which exploits a series of echo pulses with alternating phases, we further extend the coherence time of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) in h10B15N samples to \({T}_{2}^{{{{{{{{\rm{XY}}}}}}}}}\approx 500\) ns (Fig. 2b Inset). This improves the estimated AC magnetic field sensitivity to ηAC ≈ 7 μT \({{{{{{{{\rm{Hz}}}}}}}}}^{-\frac{1}{2}}\) for a signal at frequency ~ (2π) × 12 MHz (see Supplementary Note 4).
We now turn to investigate the spin relaxation time, T1, of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) in different isotopic samples. At room temperature, we find T1 of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) across all six samples to be comparable (T1 ≈ 15 μs) and nearly independent of isotope choice (Fig. 2b). To further explore the isotope effect on T1, we also explore the temperature-dependence of the \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) relaxation using an optical cryostat (Fig. 2c). The measured T1 in both h10B15N and hBNnat increases monotonically with decreasing temperatures. Interestingly, when the temperature goes below ~ 170 K, there is a clear improvement of T1 in the h10B15N sample compared to naturally abundant sample. At the lowest temperature 10 K, we find T1 = (1.00 ± 0.07) ms for \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) in h10B15N, around 50% longer than T1 = (0.63 ± 0.04) ms measured in hBNnat (Fig. 2c Inset). The current theoretical understanding of the spin relaxation process of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) identifies spin-phonon interaction as the main limitation19,41,42, which is consistent with the observed monotonic increase of T1 with decreasing temperature in both samples. One possible explanation for the improved T1 of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) in h10B15N is that the nearest-neighboring 15N nuclei are slightly heavier in mass, leading to a weaker spin-phonon coupling strength43,44. However, the detailed underlying mechanism of isotope and temperature dependences of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) spin lifetime invites more future studies. Nevertheless, the extension of T1 from isotope effect facilitates the use of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) as a noise magnetometer for diagnosing different phases of material, such as magnetic insulators and superconductivity at low temperature14,45,46,47.
Polarizing three nearest 15N Nuclear spins
Next, we demonstrate the polarization and coherent control of the three nearest-neighbor 15N nuclear spins using \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\). Nuclear spins feature exceptional isolation from external environments and offer long-lived systems for quantum simulation and computation applications. In contrast to \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) in naturally abundant hBN samples, our isotopically purified host h10B15N presents a unique advantage: the hyperfine levels are individually addressable with a much less crowded spectrum.
We start by dynamically polarizing the 15N nuclear spins at the electronic spin level anti-crossing (esLAC). Under an external magnetic field Bz ≈ 760 G, the \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) excited state levels \(\left|{m}_{s}=0\right\rangle\) and \(\left|{m}_{s}=-1\right\rangle\) are nearly degenerate48,49,50. In this regime, the secular approximation no longer holds, and we need to consider the full hyperfine interaction Hamiltonian,
To understand the nuclear spin polarization process, we can rewrite the hyperfine terms using ladder operators as
where \({A}_{1}^{j}=\frac{1}{4}({A}_{xx}^{j}+{A}_{yy}^{j})\), \({A}_{2}^{j}=\frac{1}{4}({A}_{xx}^{j}-{A}_{yy}^{j})+\frac{1}{2i}{A}_{xy}^{j}\), S± and I± are the ladder operators (see Supplementary Note 5).
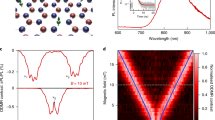
From Eq. (4), the nuclear spin polarization process at esLAC is made apparent. Specifically, the term \(({A}_{1}^{j}{S}_{+}{I}_{-}^{j}+h.c.)\) leads to electron-nuclear spin flip-flop, \(\left|{m}_{s}=0,{m}_{I}=\,\downarrow \right\rangle \leftrightarrow \left|{m}_{s}=-1,{m}_{I}=\,\uparrow \right\rangle\), while the term \(({A}_{2}^{j}{S}_{+}{I}_{+}^{j}+h.c.)\) connects the other two states, \(\left|{m}_{s}=0,{m}_{I}=\,\uparrow \right\rangle \leftrightarrow \left|{m}_{s}=-1,{m}_{I}=\,\downarrow \right\rangle\) (Fig. 3a). From previous ab-initio calculations35,36, \(| {A}_{1}^{j}| > | {A}_{2}^{j}|\) for the three nearest-neighbor 15N nuclear spins. Therefore, under the strong optical polarization that continuously pumps the electronic spin from \(\left|{m}_{s}=\pm 1\right\rangle\) to \(\left|{m}_{s}=0\right\rangle\) (while leaving the nuclear spin unchanged), each 15N will be preferentially polarized to \(\left|{m}_{I}=\,\uparrow \right\rangle\).
a Left: schematic of the nuclear spin polarization process of 15N spins at esLAC (Bz = 760 G). The hyperfine term (A1S+I− + h. c. ) (red) is much stronger than (A2S+I+ + h. c. ) (blue). Under laser pumping (green), which continuously polarizes the electronic spin to \(\left|{m}_{s}=0\right\rangle\), each nuclear spin will be preferentially polarized to \(\left|{m}_{I}=\,\uparrow \,\right\rangle\). Right: calculated excited state energy spectrum of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) as a function of magnetic field (see Supplementary Note 2). Inset: closeup of energy levels around esLAC (760 G). b Measured ESR spectra of the \(\left|{m}_{s}=0\right\rangle \leftrightarrow \left|{m}_{s}=+ 1\right\rangle\) transition at esLAC under different laser powers. Inset: ESR spectrum of the \(\left|{m}_{s}=0\right\rangle \leftrightarrow \left|{m}_{s}=-1\right\rangle\) transition at a laser power of ~ 10 mW. Dashed lines represent best fits assuming each 15N nucleus is independently polarized to \(\left|\uparrow \,\right\rangle\) with probability P. c Extracted \(P(\left|\uparrow \,\right\rangle )\) as a function of laser power. Inset: \(P(\left|\uparrow \,\right\rangle )\) as a function of the magnetic field alignment angle θ relative to the c-axis of hBN. Error bars represent 1 s.d. accounting fitting error. d Measured depolarization dynamics of nuclear spin as a function of wait time t. Inset: pulsed-ESR spectra at t = 2 μs and 10 μs, where PL is the fluorescence signal. Error bars represent 1 s.d. accounting fitting error. Source data are provided as a Source Data file.
To experimentally probe the nuclear spin polarization, we measure ESR spectra at a range of different laser powers. Here, we focus on the ESR transitions from \(\left|{m}_{s}=0\right\rangle\) to \(\left|{m}_{s}=+ 1\right\rangle\) to avoid any fluorescence modulation due to esLAC and thus accurately characterize the nuclear spin population51. At low laser power (0.3 mW), the ESR spectrum exhibits a symmetric four-peak structure with amplitudes {1:3:3:1}, similar to the low field measurement, indicating no nuclear spin polarization (Fig. 3b). Once the laser power, and hence the optical pumping rate, increases, the ESR spectrum manifests an asymmetry skewed toward the two resonances at lower frequencies. This indicates that the three nearest-neighbor 15N nuclear spins are significantly polarized to the \(\left|{m}_{I}=\,\uparrow \right\rangle\) state.
To quantify the nuclear spin polarization, we assume each nuclear spin is independently initialized to \(\left|{m}_{I}=\,\uparrow \right\rangle\) with probability \(P(\left|\uparrow \right\rangle )\) and \(\left|{m}_{I}=\,\downarrow \right\rangle\) with probability 1 − P. In this case, the population distribution of the four hyperfine resonances follows a ratio of {P3: 3P2(1 − P): 3P(1−P)2: (1−P)3} (See Methods). This model yields excellent agreement with the experimental data (Fig. 3b), allowing us to extract the nuclear spin polarization probability P at different laser powers. The nuclear polarization saturates at a laser power of around 10 mW, giving a maximum extracted nuclear spin polarization probability P = (63.2 ± 0.3)% (Fig. 3c). The nuclear spin polarization is also sensitive to the magnetic field alignment relative to the c-axis of the h10B15N, as a transverse magnetic field induces mixing between the nuclear spin states (Fig. 3c inset). We notice a small overall shift (~5 MHz) of the entire ESR spectrum at high laser power originating from the laser-induced heating effect of the sample37. Nevertheless, the well-resolved hyperfine lines in our isotopically purified h10B15N enable us to faithfully capture any temperature-induced shift that may have been previously difficult to distinguish in the spectrum of naturally abundant hBNnat.
We further study the nuclear spin depolarization dynamics via pulsed ESR measurements. After initializing the \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) electronic spin and the three 15N nuclear spins at esLAC with a 5 μs laser pulse, we wait for a time t before applying a microwave π-pulse with varying frequency to probe the hyperfine transitions, as shown in Fig. 3d. By fitting the ESR spectra, we observe that the nuclear spin population P exhibits almost no decay within 15 μs, the T1 time of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\). The longevity of nuclear spin polarization may serve as a vital attribute for future applications such as quantum registers52.
Coherent control of the nuclear spins
Next, we illustrate the direct control and detection of the three nearest-neighbor 15N nuclear spins. After polarizing the \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) to \(\left|{m}_{s}=0\right\rangle\) state via optical pumping, we apply a nuclear spin selective microwave π-pulse to transfer \(\left|{m}_{s}=0,\sum {m}_{I}=\frac{1}{2}\right\rangle\) population into \(\left|{m}_{s}=-1,\sum {m}_{I}=\frac{1}{2}\right\rangle\) followed by a radio-frequency (RF) π-pulse to drive the nuclear spin states (Fig. 4a). A final microwave π-pulse transfers \(\left|{m}_{s}=-1,\sum {m}_{I}=\frac{1}{2}\right\rangle\) back to \(\left|{m}_{s}=0,\sum {m}_{I}=\frac{1}{2}\right\rangle\) for nuclear spin detection.
a Experimental pulse sequence and schematic for the control and detection of nuclear spins. b Resulting 15N nuclear spin resonance spectra at 760 G and 210 G (Inset). Dashed lines represent simulated spectra using adjusted transverse hyperfine terms (see Supplementary Note 6.3). Error bars represent 1 s.d. accounting statistical uncertainties. c Measurement of nuclear spin Rabi oscillations. The dashed line corresponds to a cosine fit with exponentially decaying amplitude that takes the form \(A{e}^{-{(t/T)}^{\alpha }}\cdot \cos (2\pi t/\Omega )+c\). Error bars represent 1 s.d. accounting statistical uncertainties. Source data are provided as a Source Data file.
Figure 4b shows the measured 15N nuclear spin resonance spectrum obtained by sweeping the frequency of the RF pulse. The clear nuclear spin transition at around (2π) × 66.6 MHz is consistent with the sum of the measured 15N hyperfine interaction strength and the nuclear spin Zeeman shift \(| {A}_{zz}^{{}^{15}{{{{{{{\rm{N}}}}}}}}}+{\gamma }_{n}{B}_{z}|\, \approx \,(2\pi )\times 66.2\) MHz. By parking the RF pulse at this frequency and increasing the pulse duration, we obtain coherent Rabi oscillations of the nearest three 15N nuclear spins with Rabi frequency ΩN = (2π) × (1.67 ± 0.02) MHz (Fig. 4c).
Here, we would like to emphasize a few points. First, the nuclear spin Rabi signal contains a clear beating that does not fit to a single frequency oscillation. This originates from the interaction between nuclear spins which can be captured using a more sophisticated model containing \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) and three 15N nuclear spins (see Supplementary Note 6.3). Second, the transverse hyperfine interaction enhances the effective nuclear gyromagnetic ratio to35,53
enabling us to achieve a fast nuclear spin manipulation (see Supplementary Note 6.1). From our experiment, we estimate \({\gamma }_{n}^{{{{{{{{\rm{eff}}}}}}}}}/{\gamma }_{n}\approx 99\), suggesting \(\scriptstyle\sqrt{{A}_{xx}^{2}+{A}_{yy}^{2}+2{A}_{xy}^{2}}\approx (2\pi )\times 30\) MHz, a factor approximately 5 times lower than the values predicted by ab-initio calculations35,36 (see Supplementary Note 6.2). Another piece of evidence is that the measured nuclear spin resonance spectrum is consistent with the estimated transverse hyperfine parameters (Fig. 4b), while if we include the ab-initio predicted values, the simulated spectrum deviates from the measurement at B ≈ 760 G (Supplementary Fig. 9). Prior work using 14N nuclear spins in naturally abundant hBNnat has reported a ~ 30% discrepancy between experiment and the ab-initio calculated transverse hyperfine coefficients35. However, the measured 14N nuclear spin transitions contain multiple resonances and are much broader than what we have observed here using 15N nuclei. Future work is required to resolve such discrepancy between experiment and ab-initio results. For instance, one can perform high-resolution ESR spectroscopy near the ground-state anti-crossing (gsLAC) with magnetic field B ≈ 1200 G. At such field, the \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) electronic spin state \(\left|0\right\rangle\) and \(\left|-1\right\rangle\) are close to degenerate, and one expects the effect of transverse hyperfine coefficients to become evident.
Outlook
In conclusion, we present isotope engineering as a versatile and foundational tool to improve spin properties of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\). On the quantum sensing front, \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) centers in isotope-engineered h10B15N feature substantially narrower spin transitions and enhanced spin coherent time compared to conventional hBNnat, enabling a universal enhancement factor of ~ 4 (2) in DC (AC) magnetic field sensitivity. Additionally, we demonstrate the dynamical polarization and coherent control of the nearest neighboring three 15N nuclear spins.
Looking forward, our work also opens the door to a few highly promising directions. First, we believe that almost all previous works using \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) for sensing applications could greatly benefit from simply switching to our newly prepared h10B15N sample. The demonstrated sensitivity improvement is also fully compatible with other ongoing optimization efforts on \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) sensors, such as dynamical decoupling protocols to extend T224,27, coupling \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) to optical cavities54,55,56 and increasing \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) number and density24,57,58 to improve fluorescent signals. Second, the individual addressability of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) hyperfine transitions in h10B15N allows the utilization of nearby nuclear spins as valuable quantum resources and provides a promising platform to realize multi-qubit quantum registers in two-dimensional materials. Finally, we highlight that our isotope engineering method can be readily extended to other spin defects in hBN59,60 as well as the broader family of van der Waals materials61. For instance, the recent search for quantum spin defects in transition metal dichalcogenides62 will greatly benefit from a careful selection of host isotopes, which may even create a nuclear spin-free environment.
Methods
hBN device fabrication
Growth of isotopically purified h10B15N
High-quality h10B15N flakes are grown via precipitation from a molten Ni-Cr flux as detailed in a separate work34. Ni, Cr, and isotopically pure 10B powders in the mass ratio 12:12:1 [Ni:Cr:B] are first loaded into an alumina crucible, then heated at 1550 °C for 24 hr in a continuously flowing Ar/H2 atmosphere to melt all three components into a homogenous ingot and remove oxygen impurities. Next, this ingot is heated at 1550 °C for 24 hr in a static 15N2/H2 atmosphere to saturate the molten flux with 15N, then slowly cooled at 1∘C/hr to precipitate hBN from the solution. Since isotopically pure 10B (>99.2%) and 15N (>99.7%) are the only sources of boron and nitrogen in the system, the hBN single crystals that precipitated have the same isotopes.
Creation of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) defects
We first exfoliate hBN nanosheets using tapes and then transfer them onto the Si/SiO2 wafer. The wafer is pretreated with O2 plasma at 50 W for 1 min (flow rate 20sccm). The tapes and wafers are heated to 100 °C for 1 min before samples are carefully peeled off for maximum hBN flake yield63. The wafers with hBNnatand h10B15N are then sent to CuttingEdge Ions LLC for 4He+ ion implantation with energy 3 keV and dose density 1ion/nm2 to create \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) defects with estimated density ~ 150 ppm24. After implantation, the hBN flakes with thickness ranging from 20 to 70 nm are transferred onto the coplanar waveguide using polycarbonate (PC) stamps. Specifically, the temperature is raised in a stepwise manner to facilitate the transfer of hBN flakes. After successful transfer, the waveguide is immersed in chloroform for cleaning, removing any residual PC films. For a systematic comparison between \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) in isotopically purified h10B15N and naturally abundant hBNnat, we transfer three h10B15N flakes (S1-S3) and three hBNnat flakes (S4-S6) onto a single waveguide for measurement (Supplementary Fig. 1).
Fabrication of Coplanar Waveguide
An impedance-matched (50 Ω) coplanar waveguide is fabricated onto a 400 μm thick sapphire wafer for microwave delivery (Supplementary Fig. 1). Specifically, photoresist layers (LOR 1A/S1805) are first applied to the sapphire wafer at a spin rate 4000 rpm for 1 min. A carefully designed waveguide pattern with a 50 μm wide central line is then developed using a direct-write lithography system (Heidelburg DWL66+), followed by an O2 plasma cleaning process to remove resist residue. A 10 nm chromium adhesion layer and a 160 nm gold layer are deposited using thermal evaporation, followed by a lift-off process.
Comparison of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) in hBN with different isotopes
Simulation of ESR spectrum
To quantitatively capture the measured ESR spectra in hBN samples with different isotopes, we numerically simulate the \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) transitions by accounting for its hyperfine couplings to the nearest 36 nuclear spins. At small external magnetic fields, the hyperfine terms from main text Eq. (1), can be approximated as \({\sum }_{j}{{{{{{{\bf{S}}}}}}}}{{{{{{{{\bf{A}}}}}}}}}^{j}{{{{{{{{\bf{I}}}}}}}}}^{j}\approx {\sum }_{j}{A}_{zz}^{j}{S}_{z}{I}_{z}^{j}=({\sum }_{j}{A}_{zz}^{j}{I}_{z}^{j}){S}_{z}\), which leads to an effective energy shift of the electronic spin state depending on the nearby nuclear spin configurations. Considering the hyperfine interaction between \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) and an individual nuclear spin with spin number \({{{{{{{\mathcal{I}}}}}}}}\), the averaged spectrum for the electronic spin transition \(\left|{m}_{s}=0\right\rangle \leftrightarrow \left|{m}_{s}=\pm 1\right\rangle\) will exhibit \(2{{{{{{{\mathcal{I}}}}}}}}+1\) resonances with splitting Azz assuming the nuclear spin is in a fully mixed state (to be expected at room temperature). We note that the value of the hyperfine coupling is proportional to the gyromagnetic ratio of the nuclear spin, i.e. Azz ∝ γn; therefore, the overall bandwidth of the transition is proportional to \(2{{{{{{{\mathcal{I}}}}}}}}\times | {\gamma }_{n}|\). Supplementary Fig. 2 shows a schematic ESR spectrum assuming the \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) couples to a single 14N or 15N nuclear spin. To achieve a smaller overall linewidth of the \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) transitions, the value 2\(| {\gamma }_{n}{{{{{{{\mathcal{I}}}}}}}}|\) must be minimized for each atomic species in the host material (Fig. 1a).
Following this approximation, we proceed to compute the \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) ESR spectrum by summing over the hyperfine couplings to the 18 nearest nitrogen and 18 nearest boron nuclear spins. The values of Azz for 14N and 11B have been previously predicted using a Density Functional Theory (DFT) calculation36. To calculate Azz for 15N and 10B nuclear spins, we only need to account for the differences between gyromagnetic ratios. Direct summation of all nuclear configurations yields \({(2{{{{{{{{\mathcal{I}}}}}}}}}_{N}+1)}^{18}\times {(2{{{{{{{{\mathcal{I}}}}}}}}}_{B}+1)}^{18}\) individual resonances, where \({{{{{{{{\mathcal{I}}}}}}}}}_{N}\) and \({{{{{{{{\mathcal{I}}}}}}}}}_{B}\) represent the nuclear spin numbers of the corresponding nitrogen and boron isotopes, respectively. To mitigate the computational cost, we employ Fourier transformation to simplify the calculations (see Supplementary Note 2). The final ESR spectrum is obtained by binning transition frequencies with bin size 0.5 MHz. Supplementary Fig. 3 summarizes the simulated ESR spectra of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) centers in the four different types of isotopically purified hBN crystals (h10B14N, h10B15N, h11B14N, h11B15N), as well as naturally abundant hBN. As predicted, \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) centers in h10B15N has the least crowded spectrum with the narrowest individual transitions.
Coherence measurement of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) in other isotopically purified hBN
To further verify that h10B15N is the ideal host regarding the \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) coherence timescales, we prepare another sample with h11B15N, which is predicted to be the second best host material. Unsurprisingly, the ESR spectrum of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) in h11B15N exhibits a slightly broader transition linewidth in comparison with h10B15N (Supplementary Fig. 13a). By measuring the Spin Echo coherence time, \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) in h11B15N indeed shows \({T}_{2}^{{{{{{{{\rm{E}}}}}}}}}=119\pm 6\) ns, in between the values measured from h10B15N and h10B15N (Supplementary Fig. S13b). A previous work28 has also shown that \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) in h10B14N and h11B14N did not exhibit a clear improvement in spin echo T2 compared to naturally abundant hBN. Therefore, we believe that h10B15N is indeed the optimal isotope selection for improving the coherence time of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\).
Quantifying nuclear polarization
To quantify the nuclear spin polarization of the nearest three 15N, we assume each nuclear spin is individually prepared to \(\left|{m}_{I}=\,\uparrow \right\rangle\) with probability \(P(\left|\uparrow \right\rangle )\) and \(\left|{m}_{I}=\,\downarrow \right\rangle\) with probability \(1-P(\left|\uparrow \right\rangle )\). The energy sublevels accounting for the three 15N spins should effectively follow a binomial distribution with n = 3, the total number of a sequence of independent events. For a random variable X defined as the number of 15N nuclear spins being measured to be \(\left|{m}_{I}=\,\uparrow \right\rangle\) in a single observation, the probability mass function is
For example, the four possible nuclear spin configurations correspond to \(\sum {m}_{I}=-\frac{3}{2},-\frac{1}{2},\frac{1}{2},\frac{3}{2}\) and X = 0, 1, 2, 3. Therefore, the theoretical probability distribution follows \(\Bigg\{\left(\begin{array}{c}3\\ 3\end{array}\right){(1-P)}^{3}:\left(\begin{array}{c}3\\ 2\end{array}\right)P{(1-P)}^{2}:\left(\begin{array}{c}3\\ 1\end{array}\right){P}^{2}(1-P):\left(\begin{array}{c}3\\ 0\end{array}\right){P}^{3}\Bigg\}=\{{(1-P)}^{3}:3P{(1-P)}^{2}:3{P}^{2}(1-P):{P}^{3}\}\). When there is no nuclear spin polarization (P = 0.5), we obtain amplitudes {1: 3: 3: 1} for the ESR spectra.
To quantitatively extract the nuclear polarization, we first fit the ESR spectrum using the sum of four equally spaced Lorentzian distribution whose amplitude follows the aforementioned ratio. However, we note that the gyromagnetic ratio for 15N is negative, which reverses the order of the sublevels in the ESR spectrum. In this case, for the \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) transition between electronic \(\left|{m}_{s}=0\right\rangle\) and \(\left|{m}_{s}=+ 1\right\rangle\) states, the lowest-frequency resonance corresponds to \(\sum {m}_{I}=\frac{3}{2}\) or X = 3 (main text Fig. 3b).
We note here that previous studies have predicted a reduction of symmetry in the \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) excited state manifold from D3h to C2v due to Jahn–Teller effect35,36,64. This can lead to a different hyperfine interaction for one of the 15N nuclear spins compared to the other two. To this end, we also investigate the fitting of the experimental spectra assuming two of the 15N nuclear spins are polarized to \(\left|{m}_{I}=\,\uparrow \right\rangle\) with probability P1 and the third 15N is polarized with probability P2. The corresponding probability distribution for the four hyperfine resonances takes the form \(\{{(1-{P}_{1})}^{2}(1-{P}_{2}):{(1-{P}_{1})}^{2}{P}_{2}+2{P}_{1}(1-{P}_{1})(1-{P}_{2}):{P}_{1}^{2}(1-{P}_{2})+2{P}_{1}{P}_{2}(1-{P}_{1}):{P}_{1}^{2}{P}_{2}\}\). Supplementary Fig. 4 illustrates a comparison between the two different fitting methods, and we find that both models capture the experimental spectra almost identically well. Thus, the addition of the parameter P2 does not significantly enhance agreement with experiment. Furthermore, the two-parameter fit has much greater uncertainty in the extracted values of P1 and P2 compared to the single-parameter fit and the net nuclear spin polarization amount remains almost exactly the same between the two cases. Therefore, we utilize the first model with minimal fit parameters throughout the manuscript. Further studies are required to experimentally distinguish whether a parameter such as P2 is required.
Error analysis
The error bars for the measured fluorescence and contrast represent one standard deviation of the statistical error accounting for the photoluminescent counts from experiment. The errors on the measured photoluminescent counts are directly estimated assuming a Gaussian distribution with a mean value N and a standard deviation \(\sqrt{N}\), where N is the detected photon number. The error bars for the measured spin coherence time (T2), relaxation time (T1) and nuclear spin polarization represent one standard deviation from the fitting. We note that in our figures, some error bars are smaller than the data markers.
Data availability
Further data are available from the corresponding author upon request. Source data are provided with this paper.
References
Doherty, M. W. et al. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 528, 1–45 (2013).
Aharonovich, I., Englund, D. & Toth, M. Solid-state single-photon emitters. Nat. Photonics 10, 631–641 (2016).
Awschalom, D. D., Hanson, R., Wrachtrup, J. & Zhou, B. B. Quantum technologies with optically interfaced solid-state spins. Nat. Photonics 12, 516–527 (2018).
Atatüre, M., Englund, D., Vamivakas, N., Lee, S.-Y. & Wrachtrup, J. Material platforms for spin-based photonic quantum technologies. Nat. Rev. Mater. 3, 38–51 (2018).
Wolfowicz, G. et al. Quantum guidelines for solid-state spin defects. Nat. Rev. Mater. 6, 906–925 (2021).
Togan, E. et al. Quantum entanglement between an optical photon and a solid-state spin qubit. Nature 466, 730–734 (2010).
Pompili, M. et al. Realization of a multinode quantum network of remote solid-state qubits. Science 372, 259–264 (2021).
Degen, C. L., Reinhard, F. & Cappellaro, P. Quantum sensing. Rev. Modern Phys. 89, 035002 (2017).
Zu, C. et al. Emergent hydrodynamics in a strongly interacting dipolar spin ensemble. Nature 597, 45–50 (2021).
Koehl, W. F., Buckley, B. B., Heremans, F. J., Calusine, G. & Awschalom, D. D. Room temperature coherent control of defect spin qubits in silicon carbide. Nature 479, 84–87 (2011).
Nagy, R. et al. High-fidelity spin and optical control of single silicon-vacancy centres in silicon carbide. Nat. Commun. 10, 1954 (2019).
Hensen, B. et al. Loophole-free bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526, 682–686 (2015).
Randall, J. et al. Many-body–localized discrete time crystal with a programmable spin-based quantum simulator. Science 374, 1474–1478 (2021).
Hsieh, S. et al. Imaging stress and magnetism at high pressures using a nanoscale quantum sensor. Science 366, 1349–1354 (2019).
Thiel, L. et al. Probing magnetism in 2d materials at the nanoscale with single-spin microscopy. Science 364, 973–976 (2019).
Davis, E. et al. Probing many-body noise in a strongly interacting two-dimensional dipolar spin system. Nat. Phys. 19, 836–844 (2023).
He, G. et al. Quasi-floquet prethermalization in a disordered dipolar spin ensemble in diamond. Phys. Rev. Lett. 131, 130401 (2023).
Gottscholl, A. et al. Initialization and read-out of intrinsic spin defects in a van der waals crystal at room temperature. Nat. Mater. 19, 540–545 (2020).
Gottscholl, A. et al. Room temperature coherent control of spin defects in hexagonal boron nitride. Sci. Adv. 7, eabf3630 (2021).
Zhong, D. et al. Layer-resolved magnetic proximity effect in van der waals heterostructures. Nat. Nanotechnol. 15, 187–191 (2020).
Healey, A. et al. Quantum microscopy with van der waals heterostructures. Nat. Phys. 19, 87–91 (2023).
Broadway, D. A. et al. Imaging domain reversal in an ultrathin van der waals ferromagnet. Adv. Mater. 32, 2003314 (2020).
Vaidya, S., Gao, X., Dikshit, S., Aharonovich, I. & Li, T. Quantum sensing and imaging with spin defects in hexagonal boron nitride. Adv. Phys. X 8, 2206049 (2023).
Gong, R. et al. Coherent dynamics of strongly interacting electronic spin defects in hexagonal boron nitride. Nat. Commun. 14, 3299 (2023).
Caldwell, J. D. et al. Photonics with hexagonal boron nitride. Nat. Rev. Mater. 4, 552–567 (2019).
Naclerio, A. E. & Kidambi, P. R. A review of scalable hexagonal boron nitride (h-bn) synthesis for present and future applications. Adv. Mater. 35, 2207374 (2023).
Rizzato, R. et al. Extending the coherence of spin defects in hbn enables advanced qubit control and quantum sensing. Nat. Commun. 14, 5089 (2023).
Haykal, A. et al. Decoherence of \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) spin defects in monoisotopic hexagonal boron nitride. Nat. Commun. 13, 4347 (2022).
Bourassa, A. et al. Entanglement and control of single nuclear spins in isotopically engineered silicon carbide. Nat. Mater. 19, 1319–1325 (2020).
Waldherr, G. et al. Quantum error correction in a solid-state hybrid spin register. Nature 506, 204–207 (2014).
Liu, S. et al. Large-scale growth of high-quality hexagonal boron nitride crystals at atmospheric pressure from an Fe–Cr flux. Crystal Growth Design 17, 4932–4935 (2017).
Liu, S. et al. Single crystal growth of millimeter-sized monoisotopic hexagonal boron nitride. Chem. Mater. 30, 6222–6225 (2018).
Li, J. et al. Single crystal growth of monoisotopic hexagonal boron nitride from a Fe–Cr flux. J. Mater. Chem. C 8, 9931–9935 (2020).
Janzen, E. et al. Boron and nitrogen isotope effects on hexagonal boron nitride properties. Adv. Mater. 2306033 https://doi.org/10.1002/adma.202306033 (2023).
Gao, X. et al. Nuclear spin polarization and control in hexagonal boron nitride. Nat. Mater. 21, 1024–1028 (2022).
Ivády, V. et al. Ab initio theory of the negatively charged boron vacancy qubit in hexagonal boron nitride. npj Comput. Mater. 6, 41 (2020).
Gottscholl, A. et al. Spin defects in hbn as promising temperature, pressure and magnetic field quantum sensors. Nat. Commun. 12, 4480 (2021).
Dréau, A. et al. Avoiding power broadening in optically detected magnetic resonance of single NV defects for enhanced dc magnetic field sensitivity. Phys. Rev. B 84, 195204 (2011).
Barry, J. F. et al. Sensitivity optimization for NV-diamond magnetometry. Rev. Modern Phys. 92, 015004 (2020).
Yang, W. & Liu, R.-B. Quantum many-body theory of qubit decoherence in a finite-size spin bath. Phys. Rev. B 78, 085315 (2008).
Durand, A. et al. Optically active spin defects in few-layer thick hexagonal boron nitride. Phys. Rev. Lett. 131, 116902 (2023).
Cambria, M. et al. Temperature-dependent spin-lattice relaxation of the nitrogen-vacancy spin triplet in diamond. Phys. Rev. Lett. 130, 256903 (2023).
Tang, H., Barr, A. R., Wang, G., Cappellaro, P. & Li, J. First-principles calculation of the temperature-dependent transition energies in spin defects. J. Phys. Chem. Lett. 14, 3266–3273 (2023).
Mondal, S. & Lunghi, A. Spin-phonon decoherence in solid-state paramagnetic defects from first principles. npj Comput. Mater. 9, 120 (2023).
Chatterjee, S., Rodriguez-Nieva, J. F. & Demler, E. Diagnosing phases of magnetic insulators via noise magnetometry with spin qubits. Phys. Rev. B 99, 104425 (2019).
Chatterjee, S. et al. Single-spin qubit magnetic spectroscopy of two-dimensional superconductivity. Phys. Rev. Res. 4, L012001 (2022).
Huang, M. et al. Wide field imaging of van der waals ferromagnet Fe3GeTe2 by spin defects in hexagonal boron nitride. Nat. Commun. 13, 5369 (2022).
Mathur, N. et al. Excited-state spin-resonance spectroscopy of spin defects in hexagonal boron nitride (Bulletin of the American Physical Society, 2022).
Baber, S. et al. Excited state spectroscopy of boron vacancy defects in hexagonal boron nitride using time-resolved optically detected magnetic resonance. Nano Lett. 22, 461–467 (2021).
Yu, P. et al. Excited-state spectroscopy of spin defects in hexagonal boron nitride. Nano Lett. 22, 3545–3549 (2022).
Zu, C. et al. Experimental realization of universal geometric quantum gates with solid-state spins. Nature 514, 72–75 (2014).
Bradley, C. E. et al. A ten-qubit solid-state spin register with quantum memory up to one minute. Phys. Rev. X 9, 031045 (2019).
Sangtawesin, S. et al. Hyperfine-enhanced gyromagnetic ratio of a nuclear spin in diamond. N. J. Phys. 18, 083016 (2016).
Fröch, J. E. et al. Coupling spin defects in hexagonal boron nitride to monolithic bullseye cavities. Nano Lett. 21, 6549–6555 (2021).
Mendelson, N. et al. Coupling spin defects in a layered material to nanoscale plasmonic cavities. Adv. Mater. 34, 2106046 (2022).
Qian, C. et al. Unveiling the zero-phonon line of the boron vacancy center by cavity-enhanced emission. Nano Lett. 22, 5137–5142 (2022).
Whitefield, B., Toth, M., Aharonovich, I., Tetienne, J.-P. & Kianinia, M. Magnetic field sensitivity optimization of negatively charged boron vacancy defects in hbn. Adv. Quantum Technol. 2300118 https://doi.org/10.1002/qute.202300118 (2023).
Zhou, F. et al. Dc magnetic field sensitivity optimization of spin defects in hexagonal boron nitride. Nano Lett. 23, 6209–6215 (2023).
Guo, N.-J. et al. Coherent control of an ultrabright single spin in hexagonal boron nitride at room temperature. Nat. Commun. 14, 2893 (2023).
Stern, H. L. et al. Room-temperature optically detected magnetic resonance of single defects in hexagonal boron nitride. Nat. Commun. 13, 618 (2022).
Li, S., Thiering, G., Udvarhelyi, P., Ivády, V. & Gali, A. Carbon defect qubit in two-dimensional WS2. Nat. Commun. 13, 1210 (2022).
Lee, Y. et al. Spin-defect qubits in two-dimensional transition metal dichalcogenides operating at telecom wavelengths. Nat. Commun. 13, 7501 (2022).
Huang, Y. et al. Reliable exfoliation of large-area high-quality flakes of graphene and other two-dimensional materials. ACS Nano 9, 10612–10620 (2015).
Reimers, J. R. et al. Photoluminescence, photophysics, and photochemistry of the \({{{{{{{{\rm{V}}}}}}}}}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) defect in hexagonal boron nitride. Phys. Rev. B 102, 144105 (2020).
Clua-Provost, T. et al. Isotopic control of the boron-vacancy spin defect in hexagonal boron nitride. Phys. Rev. Lett. 131, 126901 (2023).
Acknowledgements
We gratefully acknowledge Vincent Jacques, Cassabois Guillaume, Bernard Gil, Cong Su, Emily Davis, Weijie Wu, Wonjae Lee, Khanh Pham, Benchen Huang, Xingrui Song, Li Yang, Du Li, Xingyu Gao, and Joonhee Choi for helpful discussions. We thank Justin S. Kim, Zhihao Xu, and Sang-Hoon Bae for their assistance in experiment. This work is supported by the Startup Fund, the Center for Quantum Leaps, the Institute of Materials Science and Engineering, and the OVCR Seed Grant from Washington University. T.L. acknowledges support from the Gordon and Betty Moore Foundation grant 10.37807/gbmf12259. V.L., B.Y., and N.Y.Y. acknowledge support from the U.S. Department of Energy through BES grant no. DE-SC0019241 and through the DOE Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division and the Division of Chemical Sciences, Geosciences and Biosciences at LBNL under Contract no. DE-AC02-05-CH11231. Support of E. Janzen and J. H. Edgar for hBN crystal growth is provided by the Office of Naval Research, award number N00014-22-1-2582. X.D. and E.A.H. acknowledge support from the Moore Foundation Experimental Physics Investigators Initiative award no. 11560. Note added: During the completion of this work, we became aware of complementary work studying boron-vacancy centers in both nitrogen and boron isotopes purified hBN crystals (Vincent Jacques, private communication)65.
Author information
Authors and Affiliations
Contributions
C.Z. conceived the idea. R.G., X.D., Z.L. and G.H. performed the experiment. R.G., X.D., V.L., Z.L., B.Y., N.Y. and C.Z. developed the theoretical models and performed the numerical simulations. R.G., X.D., V.L., Z.L. and C.Z. performed the data analysis. E.J. and J.H.E. grew the hBN samples. R.G., X.D., T.L. and E.A.H. fabricated the microwave delivery system. E.A.H. and C.Z. supervised the project. R.G., X.D., V.L. and C.Z. wrote the manuscript with inputs from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Takeshi Ohshima, and the other, anonymous, reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gong, R., Du, X., Janzen, E. et al. Isotope engineering for spin defects in van der Waals materials. Nat Commun 15, 104 (2024). https://doi.org/10.1038/s41467-023-44494-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-023-44494-3
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.