Abstract
Understanding projected changes in flooding across the contiguous United States (CONUS) helps increase our capability to adapt to and mitigate against this hazard. Here, we assess future changes in flooding across CONUS using outputs from 28 global climate models and four scenarios of the Coupled Model Intercomparison Project Phase 6. We find that CONUS is projected to experience an overall increase in flooding, especially under higher emission scenarios; there are subregional differences, with the Northeast and Southeast (Great Plains of the North and Southwest) showing higher tendency towards increasing (decreasing) flooding due to changes in flood processes at the seasonal scale. Moreover, even though trends may not be detected in the historical period, these projected future trends highlight the current needs for incorporating climate change in the future infrastructure designs and management of the water resources.
Similar content being viewed by others
Introduction
Much of the existing infrastructure and water resources management are based on the assumption of stationarity, implying that the statistical properties observed in the past will persist into the future. While stationarity has been the cornerstone of most of the flood frequency studies aiming at water resources management and infrastructure design, this working assumption has been challenged due to changes in the climate system and in the way we manage our landscapes1. However, this signal of change has been hard to find in observational studies due to the variability in the flood records (i.e., small signal-to-noise ratio), complexity in the physical processes leading to flooding, and large uncertainties2,3. The Intergovernmental Panel on Climate Change (IPCC) states that “confidence about peak flow trends over the past decades on the global scale is low”3 even though there are areas, such as the northeastern and southwestern United States, that have been experiencing increasing and decreasing trends4, respectively.
While the detection of changes is scientifically interesting, it provides limited insight for the design of future infrastructures5. Much effort has been placed in detecting trends in the observed floods series6,7,8,9,10,11,12,13; however, the only way to extrapolate these findings into the future is by assuming that the detected trends will persist in the decades to come14,15. Moreover, if we do not detect a trend in the historical past, are we sure that it is not going to manifest itself in the future? Because of these issues, a much more robust approach for the design of future water-related structures and projects includes first an analysis of the historical discharge records not from the perspective of the detection of changes, but rather of the attribution of the major drivers responsible for the observed interannual variability10,16,17. By looking back at the observational records and understanding of how different mechanisms (e.g., rainfall, snowmelt) were responsible for flooding, we can then move forward by examining how these drivers are projected to change and their implications in terms of changes in flood magnitudes.
There are two broad approaches for the attribution of nonstationarity in flood magnitudes18, simulation- and regression-based approaches. The former has the advantage of the use of mathematical equations describing the physical processes in flood discharge19, despite a greater computational burden. On the other hands, the regression-based approach models the statistical relationships between flood discharge and its possible drivers such as climate variables20, large-scale climate indices21, and land cover22. The main advantages of the statistical models are the computational cost and the flexibility in incorporating different process-related predictors, making these models competitive with the simulation-based approach in terms of model performance23. Moreover, they allow for a probabilistic view of discharge, enabling the assessment of changes in different parts of the flood peak distribution. Many of the published studies about projected changes in floods across the contiguous United States (CONUS) tend to follow a simulation-based approach at the regional or basin scales24,25,26,27,28,29, while only a few studies used a regression-based approach for hundreds of streamgages distributed across CONUS23,30.
Here, we assess future changes in flood magnitude across CONUS by taking advantage of the strengths and skill by the regression-based approach and the dense network of thousands of streamgages by the U.S. Geological Survey (USGS). We build on the statistical modeling framework described in ref. 17, which allows the attribution of the observed interannual variability in the annual maximum discharge records to basin- and season-averaged precipitation and temperature (see Methods). These variables are available from many global climate models (GCMs) and were shown to drive the year-to-year changes in annual maximum flood peaks across large areas of CONUS. By projecting precipitation and temperature and using them as inputs for the selected statistical models17, we quantify the projected changes in flood hazard over the 21st century across multiple Shared Socioeconomic Pathways (SSPs) (see Methods). Besides its good performance in reproducing historical observations, we have selected this approach because it allows us to consider the projected changes in flooding for any annual exceedance probabilities (AEPs), providing a framework for nonstationary flood frequency analyses under different scenarios.
Results and discussion
As a preliminary step, we check whether the GCM outputs can reproduce what was observed during the historical period. We evaluate the suitability of basin- and season-averaged GCM outputs in reproducing the observed trends in annual maximum discharge (see Methods). Based on the results in Supplementary Fig. 1, there are 28 GCMs that were able to satisfactorily reproduce the observed trends over the historical period, and those are the ones we use for the projections.
Projected changes in flood extremes across CONUS
To assess future changes in flood hazard across scenarios, we test whether the AEP distribution tends to shift towards larger or smaller values compared to the past (i.e., 2071-2100 vs. 1985-2014) under four SSPs (Fig. 1). Across CONUS, there is a general shift towards larger extremes regardless of scenarios: for a 0.5 AEP (i.e., it corresponds to a 2-year event), there are 72.7%–74.3% of the sites showing a positive shift (i.e., the distribution of the 0.5-AEP discharge is projected to shift towards larger discharge values), with this number increasing to 76.7%–81.6% for the 0.002 AEP (i.e., it corresponds to a 500-year event). On the other hand, the negative shifts between the historical period and the last 30 years of the 21st century (i.e., the distribution is projected to shift towards smaller discharge values) are limited to ~8.3%–15.1% of the sites, while a lack of detectable shifts is limited to ~8.5%–17.0% of the records depending on the AEP. Overall, these results indicate that annual maximum peak discharge is projected to become more extreme, with a larger tendency towards larger peaks. This is particularly true as we move from smaller to larger flood peaks (i.e., from the 0.5 to the 0.002 AEPs).
The left (right) panel shows the percentage of sites with a significant increasing (decreasing) shift in peak discharges for CONUS at the 5% level. The middle panel shows the percentage of sites where there is no significant shift in peak discharges at the 5% level. In each panel, redder bars indicate higher emission scenarios from SSP1-2.6 to SSP 5-8.5. The error bars represent the 95% confidence intervals for multinomial proportions computed based on the Sison-Glaz method62.
There is also a dependence in terms of emission scenarios (Fig. 1). Under SSP1-2.6, the percentage of sites showing a positive shift increases 3.8% (from 73.3% to 77.1%) as AEP decreases (from 0.5 to 0.002). As we move from SSP1-2.6 to SSP5-8.5, the changing rate of the sites with a positive shift also increases (i.e., 5.2%, 6.8%, and 7.5% under SSP2-4.5, SSP3-7.0, and SSP5-8.5, respectively), indicating that, the higher the emission scenario, the more the flood hazard is projected to increase for the more extreme events. These changes are compensated by the changes in those sites that did not exhibit statistically significant shifts. Based on these results, efforts to reduce greenhouse gas emissions and towards sustainability are projected to decrease the flood hazard, especially for the more extreme events.
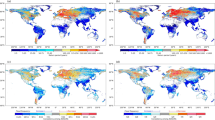
If we stratify the results across the seven subregions by the U.S. National Climate Assessment (Fig. 2), different parts of the country are expected to respond differently to climate change. Flooding is projected to increase in the northeastern and southeastern United States, with more than 86% of the streamgages in that region for which the distribution of the 0.01-AEP discharge is projected to shift towards larger values. The Northwest and Midwest also exhibit shifts in the distribution towards higher values (at more than 78% of the streamgages) compared to CONUS. The picture is different for the Southwest and the Great Plains, where the percentage of sites projected to increase is below 75%, and those projected to decrease ~16%. Moreover, these regions show more of a balance between increasing and decreasing flood hazards for larger AEPs (Supplementary Fig. 2).
a Blue (red) circles indicate the sites with a significant increasing (decreasing) shift in peak discharges, while the gray circles indicate the sites with no significant shift at the 5% level. Bold lines represent the boundaries of seven subregions. b The left (right) panel shows the percentage of sites with a 5%-significant increasing (decreasing) shift in peak discharges for CONUS and its seven subregions (see inset map for the definition of subregions). The middle panel shows the percentage of sites where there is no significant shift in peak discharges at the 5% level. The error bars represent the 95% confidence intervals for multinomial proportions computed based on the Sison-Glaz method62. The numbers in the legend represent the number of streamgages within each region. Notice that jitters are added to the x-axis to improve readability.
Our results illustrate that CONUS is projected to experience an overall increase in extreme flooding, even though the magnitude of this signal is not spatially homogeneous but varies sub-regionally. These findings expand on the recent literature on the projected changes in discharge for river basins within various subregions of the United States24,25,26,27,28,29, as well as CONUS30,31,32. Compared to existing studies, some of the strengths of these results are the large sample of streamgage stations, the use of CMIP6 GCM outputs, and multiple scenarios. By employing a statistical approach, we are able to project changes across different parts of the flood peak distributions, allowing accounting for the nonstationarities across different AEPs at any point in time during the 21st century. Moreover, by modeling the flood peak records by accounting for processes that are dominant during each of the four seasons (see Methods), we are moving closer to a process-driven flood frequency analysis, which is different from other regression-based modeling studies that model directly the annual maximum discharges23,30,33.
Role of seasonal climate drivers responsible for peak discharge
To shed some light on the possible physical mechanisms responsible for the detected shifts and their subregional variability, we examine the projected changes in seasonal precipitation and temperature (see Methods). All GCMs project increases in temperature with respect to the historical past, regardless of seasons, with the largest shifts as we move from SSP1-2.6 to SSP5-8.5 (Supplementary Fig. 3). On the other hand, precipitation exhibits a much more variable pattern of change in both seasonally and sub-regionally (Supplementary Fig. 4). In the Northwest, Great Plains of the North, and Midwest, there is an increasing shift in winter and spring precipitation, while there is a decreasing shift in summer precipitation at most sites, with a larger signal of change for higher emission scenarios. The Southwest shows a different seasonality, with a decreasing shift in spring precipitation and an increasing shift in winter precipitation. The Northeast and Southeast show an increasing shift in precipitation for all seasons and scenarios, except for few sites in the Southeast with a projected decreasing precipitation in the summer. One commonality among regions is the exacerbation of seasonal precipitation for increasing emissions: not only the absolute value of the projected changes in precipitation is expected to increase, but also its variability among the different sites and pointing to potentially larger climate swings within these regions.
To better understand the role of seasonal climate drivers in driving flood extremes, we investigate the seasonality of annual maximum discharge occurrence, given the good performance of our modeling framework in reproducing the historical flood seasonality (Supplementary Fig. 5). The seasonality of annual maximum discharge is projected to change, especially for increasing emissions, with differences depending on subregions (Supplementary Figs. 6, 7). If we focus on the main flood seasons, there is a distinct change in the seasonality of flooding across each of the seven subregions (Fig. 3). In the Northeast and Southeast, winter and spring are the main flood seasons, with winter being the dominant season for the higher emission scenarios. Therefore, the projected shift towards larger flood peaks can be interpreted through an increase in winter and spring precipitation28 (Supplementary Fig. 4). The winter and spring seasons are also the main flood seasons in the Northwest and Midwest, respectively, regardless of emission scenarios. The increasing shift in precipitation in those seasons (Supplementary Fig. 4) is consistent with the projected tendency towards increasing trends in flood peaks. In the Midwest, while spring is the dominant season, there is an increase in the number of sites for which winter’s contribution is projected to increase, especially for higher emissions, possibly due to the polarward shift of the tracks of extratropical cyclones34,35 (Supplementary Fig. 8). In the Southwest, the summer season, one of the main flood seasons in this area, is projected to contribute less to the annual maxima, particularly in the mountainous area such as the Rockies (Supplementary Fig. 7). Since snowmelt is the main flood process in this area36,37, spring precipitation and temperature play a crucial role in the magnitude of summer flood peaks17. Therefore, the decreasing (increasing) shifts in spring precipitation (temperature) can lead to the negative shifts in annual maximum discharge in this area (Fig. 2a). On the other hand, the positive shift in annual maximum discharge is likely associated with increases in precipitation in winter, the main flood season in the West Coast driven by atmospheric rivers38 (Supplementary Fig. 6). In the Great Plain of the North where snowmelt is the main driver of runoff potential39, spring and summer seasons are the main flood seasons40 (as also shown in Fig. 3). In addition to decreases in summer precipitation (Supplementary Fig. 4), the increases in temperature (Supplementary Fig. 3) can lead to negative shifts in annual maximum discharge by leading to snowpack decline41 and more rainfall than snow42. The Great Plain of the South shows the dominance of spring season for all scenarios. However, there is no consistency in the projected shifts in spring precipitation (Supplementary Fig. 4), consistent with the much larger degree of variability in the shift in flood extremes.
Projected changes in trends in flood extremes
Here we examine whether the historical trends in annual maximum discharge are expected to persist or not in the future. There is a significant change between historical and future trends depending on scenarios (Fig. 4). Under SSP1-2.6, trends in 0.01-AEP discharge are projected to remain not significant and/or to become smaller/more negative during the 2071–2100 period compared to 1985–2014. As we consider scenarios with higher emissions, however, trends are projected to be exacerbated over the future period, including trend-sign reversal from negative/not-significant to positive in the last 30 years of the 21st century compared to the historical past. This tendency is more intensified for larger flood peaks (i.e., smaller AEPs) (Supplementary Figs. 9, 10). The results are consistent with other studies whose results are derived from hydrological models43,44, reinforcing the message against extrapolating the observed historical trends in flood extremes directly to project future changes in the magnitude of extreme flooding. Likewise, the lack of statistically significant trends over the historical period should not be used as a justification for not taking climate change into account5.
Dependence of projected flood hazards on human-modified basins
The abovementioned results are based on 3,885 streamgages, regardless of the degree of anthropogenic modification that they experienced. To provide further evidence of the robustness of these findings as representative of a climate change signal, we stratified the basins into 752 reference and 2,989 non-reference sites according to the Geospatial Attributes of Gages for Evaluating Streamflow version II (GAGES-II) classification45. A reference site is defined as the least-disturbed watershed by human influences, while a non-reference site is identified as disturbed by anthropogenic activities (e.g., reservoirs and dams). Based on Supplementary Figs. 11–13, the results for the two classes of basins are similar (compare them to Figs. 1, 2 and 4 as well), pointing to the robustness of our results.
One way to interpret these results is that the most influential factor for extreme outflows of hydraulic structures is extreme inflow46, which in turn could be dominated by climate drivers. In addition, seasonal total precipitation is less sensitive to the lag effect of hydraulic structures and can be therefore a reasonable covariate for modeling flood extremes in a regulated basin33. These are possible reasons for the good performance of our statistical models, despite the use of only basin- and season-averaged climate drivers and the lack of hydraulic structures as predictors17. Although changes in the climate system play a dominant role in driving changes in flood hazard47, the role of hydraulic structures in mitigating flood risk under climate change should not be overlooked48,49. Therefore, future work should focus on modeling the annual maximum discharge records with additional dam or reservoir parameters and comparing the results to the existing model with only climate-related parameters to allow for a more accurate assessment of the impact of anthropogenic modification on the projected flood extremes.
The Fifth National Climate Assessment highlights the challenge of flood projections under climate change50. This challenge arises from the intricate interplay of multiple hydrological processes within flood-generating mechanisms, making it insufficient to extrapolate historical trends in the flood series. Our findings can provide valuable and direct information towards the detection, attribution, and projection of flooding by focusing on changes in climate drivers under different emission scenarios, not on historical trends of flood extremes. The main limitation of our climate-informed projections is the assumption that the statistical relationship between flood discharge and its climate drivers does not vary over time. This relationship could be modulated by non-climate drivers (e.g., urbanization51 and irrigation52), implying that our projections of flooding are limited to responses to changes in only climate drivers and may involve additional uncertainties.
Incorporating climate change into design decisions of water-related structures and projects still remains a major challenge in engineering practice53. Given that multiple emission scenarios are available, considering the worst-case scenario could represent a path forward, although scenario uncertainty is relatively small compared to other factors (e.g., GCMs and climate variability)54. Regarding design metrics, it has been suggested to replace the traditional measure (i.e., average return period) with other design concepts such as reliability or risk of failure over a planning horizon for better communicating under nonstationary conditions15. Because of its probabilistic nature, we have the entire statistical distribution of annual maximum discharge for any year, which can provide discharge values for different design metrics and scenarios over the 21st century. This feature can pave the way to supporting some of the most pressing needs in a robust design of the physical infrastructure55.
Methods
Statistical modeling of annual maximum discharge
We adopt the statistical attribution approach by Ref. 17, which showed good performance in reproducing the annual maximum mean daily discharge time series across the CONUS. For a given location, the method does not model directly the annual maximum discharge record, but it breaks it down into four seasonal models, reflecting different flood-generating mechanisms that comprise the population of the annual maxima. Therefore, the first step is to model the seasonal maximum mean daily discharge in terms of basin- and season-averaged precipitation and temperature using gamma regression models. Then, by means of Monte Carlo simulations, the four seasonal models are mixed to obtain the derived distribution of the annual maxima. In this study, we utilize the developed gamma regression models whose parameters were estimated for 3885 streamgages across CONUS in Ref. 17. We also follow their Monte Carlo approach to obtain annual maximum discharge with various annual exceedance probabilities (AEPs). Here, we iterate the simulation experiments 10,000 times to obtain more reliable extreme discharge series with lower AEPs; 0.5, 0.2, 0.1, 0.04, 0.02, 0.01, 0.004, and 0.002. See Ref. 17 for details on the statistical attribution methodology.
Post-processing of global climate model outputs
To assess future changes in flood extremes, we use the projected precipitation and temperature from GCMs part of the Coupled Model Intercomparison Project Phase 6 (CMIP6)56. We consider the GCMs that provide both precipitation (‘pr’) and near-surface air temperature (‘tas’) variables at a monthly time scale and nominal spatial resolutions of no more than 250 km. We obtain monthly mean ‘pr’ (kg m−2 s−1) and ‘tas’ (K) for 36 GCMs that have outputs under historical and four standard SSPs57: SSP1-2.6, SSP2-4.5, SSP3-7.0, and SSP5-8.5. The information about the 36 GCMs is summarized in Supplementary Table 1.
To use the projected variables as regression model inputs, we first convert monthly mean ‘pr’ and ‘tas’ into monthly total precipitation (mm) and monthly mean temperature (°C) and calculate the basin-averaged values based on the basin boundary data (USGS Streamgage NHDPlus Version 1 Basins 2011). We then bias-correct each GCM output and each month with respect to the Parameter-Elevation Regression on Independent Slopes Model (PRISM) data58 (i.e., reference data) for 1950–2014; we bias-correct the GCM outputs using empirical quantile mapping by the Santander Meteorology Group59. The bias-corrected monthly series are aggregated and averaged at the seasonal scale. Consequently, we obtain the basin- and season-averaged precipitation and temperature and use them as predictors for annual maximum discharge.
Evaluation of GCMs in reproducing trends in peak discharge
We use the basin- and season-averaged drivers derived from the GCMs as inputs to the abovementioned gamma regression models. To assess the suitability of the GCMs for projections, we first evaluate their capability in reproducing the observed trends over the historical period. More specifically, we compare the trend in annual maximum discharge series obtained when using the GCMs and the PRISM over the 1951–2014 period by means of the Mann-Kendall trend test60,61. Depending on the test results at the 5% significance level, streamgage stations are classified into “Match” and “Mismatch” groups as follows:
-
Match group: Both annual maximum discharge series derived from the GCM and PRISM have a statistically significant trend and of the same trend sign, or they are both not statistically significant.
-
Mismatch group: Annual maximum discharge series derived from the GCM (or PRISM) has modeled (observed) Kendall’s τ values that are not statistically significant, while observed (modeled) Kendall’s τ values are significant. Or both annual maximum discharge series derived from the GCM and PRISM have a significant trend, but of opposite sign.
Among the 36 GCMs we analyze, we select 28 GCMs in which the percentage of sites belonging to the match group is larger than 70% (Supplementary Fig. 1). For each selected GCM, we obtain annual maximum discharge series with various AEPs (i.e., 0.5, 0.2, 0.1, 0.04, 0.02, 0.01, 0.004, and 0.002) from the simulated series. Then we use the ensemble mean of the annual maximum discharge series for the selected GCMs to investigate how the magnitude and the trend of flood extremes could change in the future.
Detection of projected changes in flood extremes
We use a Monte Carlo approach to detect the significant increasing (or decreasing) projected changes in annual maximum discharge considering the uncertainties in the GCM ensemble mean. This simulation-based approach allows the detection of statistically significant changes in a given AEP based on the ensemble mean of the GCMs and their variability. The procedure for detecting projected changes is as follows:
-
(1)
For each year, estimate the sampling distribution parameters of the mean of the selected GCMs’ annual maximum discharge based on the central limit theorem.
-
(2)
From the sampling distribution, generate samples of the ensemble mean for historical and future periods.
-
(3)
Calculate the difference of median values between historical and future periods:
$$\Delta Q=\frac{{Q}_{{med}}^{{future}}-{Q}_{{med}}^{{hist}}}{{Q}_{{med}}^{{hist}}}$$(1)where \({Q}_{{med}}^{{hist}}\) and \({Q}_{{med}}^{{future}}\) are the median values of generated flood extremes for historical and future periods, respectively.
-
(4)
Iterate steps (2)–(3) 10,000 times and calculate 2.5%, 50%, and 97.5% quantiles of \(\Delta Q\) (i.e., \({\Delta Q}_{0.025}\), \({\Delta Q}_{0.5}\), and \({\Delta Q}_{0.975}\)).
-
(5)
Consider an increase (decrease) shift if the signs of all \({\Delta Q}_{0.025}\), \({\Delta Q}_{0.5}\), and \({\Delta Q}_{0.975}\) are positive (negative), while no shift if any signs of \({\Delta Q}_{0.025}\), \({\Delta Q}_{0.5}\), or \({\Delta Q}_{0.975}\) are different from the others.
For each site, the significant change of flood extreme for various AEPs and scenarios between historical (1985–2014) and future (2071–2100) periods is identified by conducting the simulation-based approach.
Projected changes in precipitation and temperature
To examine what climate drivers affect the projected shifts in flood extremes, we first obtain the ensemble mean of seasonal- and basin-averaged precipitation (\(P.{ens}\)) and temperature (\(T.{ens}\)) for all scenarios. Then we calculate the projected change in \(P.{ens}\) and \(T.{ens}\) as follows:
where \({P.{ens}}_{{med}}^{{hist}}\) (\({T.{ens}}_{{med}}^{{hist}}\)) and \({P.{ens}}_{{med}}^{{future}}\) (\({T.{ens}}_{{med}}^{{future}}\)) are the median values of \(P.{ens}\) (\(T.{ens}\)) for historical (1985–2014) and future (2071–2100) periods, respectively. For each corresponding season, we also calculate the relative change in the ensemble mean of seasonal maximum discharge (\(Q.{ens}\)):
where \({Q.{ens}}_{{med}}^{{hist}}\) and \({Q.{ens}}_{{med}}^{{future}}\) are the median values of \(Q.{ens}\) for historical (1985–2014) and future (2071–2100) periods, respectively.
Data availability
The USGS basin boundary data is available from the USGS Streamgage NHDPlus Version 1 Basins 2011 at https://water.usgs.gov/lookup/getspatial?streamgagebasins. The PRISM precipitation and temperature are obtained from the PRISM climate group58 and available at https://prism.oregonstate.edu/historical/. The historical and future projected precipitation and temperature from the CMIP6 GCMs are available at https://esgf-node.llnl.gov/search/cmip6/. The GAGES-II data is available at https://water.usgs.gov/GIS/metadata/usgswrd/XML/gagesII_Sept2011.xml.
Code availability
Codes that were used in this study are available upon request.
Change history
01 May 2024
A Correction to this paper has been published: https://doi.org/10.1038/s41467-024-48129-z
References
Milly, P. C. D. et al. Stationarity is dead: whither water management? Science 319, 573–574 (2008).
Serinaldi, F. & Kilsby, C. G. Stationarity is undead: uncertainty dominates the distribution of extremes. Adv. Water Resour. 77, 17–36 (2015).
IPCC. Climate Change 2021: The physical science basis. contribution of working group i to the sixth assessment report of the intergovernmental panel on climate change. (2021).
Hodgkins, G. A., Dudley, R. W., Archfield, S. A. & Renard, B. Effects of climate, regulation, and urbanization on historical flood trends in the United States. J. Hydrol. 573, 697–709 (2019).
Villarini, G. & Wasko, C. Humans, climate and streamflow. Nat. Clim. Change 11, 725–726 (2021).
Bertola, M., Viglione, A., Lun, D., Hall, J. & Blöschl, G. Flood trends in Europe: are changes in small and big floods different? Hydrol. Earth Syst. Sci. 24, 1805–1822 (2020).
Hecht, J. S. & Vogel, R. M. Updating urban design floods for changes in central tendency and variability using regression. Adv. Water Resour. 136, 103484 (2020).
Slater, L. et al. Global Changes in 20-Year, 50-Year, and 100-Year River Floods. Geophys. Res. Lett. 48, e2020GL091824 (2021).
Vogel, R. M., Yaindl, C. & Walter, M. Nonstationarity: flood magnification and recurrence reduction factors in the United States. JAWRA J. Am. Water Resour. Assoc. 47, 464–474 (2011).
Villarini, G. & Slater, L. in Oxford research encyclopedia of natural hazard science (2017).
Archfield, S. A., Hirsch, R. M., Viglione, A. & Blöschl, G. Fragmented patterns of flood change across the United States. Geophys. Res. Lett. 43, 10,232–210,239 (2016).
Merz, B. et al. Causes, impacts and patterns of disastrous river floods. Nat. Rev. Earth Environ. 2, 592–609 (2021).
Collins, M. J., Hodgkins, G. A., Archfield, S. A. & Hirsch, R. M. The occurrence of large floods in the united states in the modern hydroclimate regime: seasonality, trends, and large-scale climate associations. Water Resour. Res. 58, e2021WR030480 (2022).
Obeysekera, J. & Salas, J. D. Quantifying the uncertainty of design floods under nonstationary conditions. J. Hydrologic Eng. 19, 1438–1446 (2014).
Read, L. K. & Vogel, R. M. Reliability, return periods, and risk under nonstationarity. Water Resour. Res. 51, 6381–6398 (2015).
Merz, B., Vorogushyn, S., Uhlemann, S., Delgado, J. & Hundecha, Y. HESS Opinions ‘More efforts and scientific rigour are needed to attribute trends in flood time series’. Hydrol. Earth Syst. Sci. 16, 1379–1387 (2012).
Kim, H. & Villarini, G. On the attribution of annual maximum discharge across the conterminous United States. Adv. Water Resour. 171, https://doi.org/10.1016/j.advwatres.2022.104360 (2023).
Slater, L. J. et al. Nonstationary weather and water extremes: a review of methods for their detection, attribution, and management. Hydrol. Earth Syst. Sci. 25, 3897–3935 (2021).
Knoben, W. J. M., Freer, J. E., Peel, M. C., Fowler, K. J. A. & Woods, R. A. A Brief Analysis of Conceptual Model Structure Uncertainty Using 36 Models and 559 Catchments. Water Resources Research 56, https://doi.org/10.1029/2019WR025975 (2020).
Liu, J. et al. Global changes in floods and their drivers. J. Hydrol. 614, 128553 (2022).
Xu, P. C. et al. Multivariate hazard assessment for nonstationary seasonal flood extremes considering climate change. J. Geophys. Res-Atmos. 125, https://doi.org/10.1029/2020JD032780 (2020).
Woltemade, C. J., Hawkins, T. W., Jantz, C. & Drzyzga, S. Impact of changing climate and land cover on flood magnitudes in the Delaware River Basin, USA. J. Am. Water Resour. 56, 507–527 (2020).
Schlef, K. E., Francois, B. & Brown, C. Comparing flood projection approaches across hydro-climatologically diverse United States River Basins. Water Resour. Res. 57, https://doi.org/10.1029/2019WR025861 (2021).
Pal, S., Wang, J., Feinstein, J., Yan, E. & Kotamarthi, V. R. Projected changes in extreme streamflow and inland flooding in the mid-21st century over Northeastern United States using ensemble WRF-Hydro simulations. J. Hydrol.: Regional Stud. 47, 101371 (2023).
Dunne, K. B. J., Dee, S. G., Reinders, J., Munoz, S. E. & Nittrouer, J. A. Examining the impact of emissions scenario on lower Mississippi River flood hazard projections. Environ. Res. Commun. 4, https://doi.org/10.1088/2515-7620/ac8d53 (2022).
Gangrade, S., Kao, S. C. & McManamay, R. A. Multi-model hydroclimate projections for the alabama-coosa-tallapoosa river basin in the Southeastern United States. Sci. Rep-Uk 10, https://doi.org/10.1038/s41598-020-59806-6 (2020).
Queen, L. E., Mote, P. W., Rupp, D. E., Chegwidden, O. & Nijssen, B. Ubiquitous increases in flood magnitude in the Columbia River basin under climate change. Hydrol. Earth Syst. Sci. 25, 257–272 (2021).
Siddique, R., Karmalkar, A., Sun, F. Y. & Palmer, R. Hydrological extremes across the Commonwealth of Massachusetts in a changing climate. J. Hydrol-Reg. Stud. 32, https://doi.org/10.1016/j.ejrh.2020.100733 (2020).
Chegwidden, O. S., Rupp, D. E. & Nijssen, B. Climate change alters flood magnitudes and mechanisms in climatically-diverse headwaters across the northwestern United States. Environ. Res. Lett. 15, https://doi.org/10.1088/1748-9326/ab986f (2020).
Awasthi, C., Archfield, S. A., Ryberg, K. R., Kiang, J. E. & Sankarasubramanian, A. Projecting Flood Frequency Curves Under Near-Term Climate Change. Water Resour. Res. 58, https://doi.org/10.1029/2021WR031246 (2022).
Naz, B. S. et al. Effects of climate change on streamflow extremes and implications for reservoir inflow in the United States. J. Hydrol. 556, 359–370 (2018).
Villarini, G. & Zhang, W. Projected changes in flooding. a continental US Perspect. Ann. Ny. Acad. Sci. 1472, 95–103 (2020).
Swarnkar, S. & Mujumdar, P. Increasing flood frequencies under warming in the west-central himalayas. Water Resourc. Res. 59, https://doi.org/10.1029/2022wr032772 (2023).
Yin, J. H. A consistent poleward shift of the storm tracks in simulations of 21st century climate. Geophysical Res. Lett. 32, https://doi.org/10.1029/2005gl023684 (2005).
Clare, R. M., Desai, A. R., Martin, J. E., Notaro, M. & Vavrus, S. J. Extratropical cyclone response to projected reductions in snow extent over the great plains. Atmosphere 14, 783 (2023).
Berghuijs, W. R., Woods, R. A., Hutton, C. J. & Sivapalan, M. Dominant flood generating mechanisms across the United States. Geophys. Res. Lett. 43, 4382–4390 (2016).
McCabe, G. J. & Clark, M. P. Trends and variability in snowmelt runoff in the western United States. J. Hydrometeorol. 6, 476–482 (2005).
Payne, A. E. et al. Responses and impacts of atmospheric rivers to climate change. Nat. Rev. Earth Environ. 1, 143–157 (2020).
Welty, J. & Zeng, X. B. Characteristics and causes of extreme snowmelt over the conterminous United States. B Am. Meteorol. Soc. 102, E1526–E1542 (2021).
Villarini, G. On the seasonality of flooding across the continental United States. Adv. Water Resour. 87, 80–91 (2016).
Huning, L. S. & AghaKouchak, A. Mountain snowpack response to different levels of warming. P Natl Acad. Sci. USA 115, 10932–10937 (2018).
Marshall, A. M., Abatzoglou, J. T., Link, T. E. & Tennant, C. J. Projected changes in interannual variability of peak snowpack amount and timing in the Western United States. Geophys. Res. Lett. 46, 8882–8892 (2019).
Do, H. X. et al. Historical and future changes in global flood magnitude - evidence from a model-observation investigation. Hydrol. Earth Syst. Sci. 24, 1543–1564 (2020).
Mallakpour, I., Sadegh, M. & AghaKouchak, A. A new normal for streamflow in California in a warming climate: Wetter wet seasons and drier dry seasons. J. Hydrol. 567, 203–211 (2018).
Falcone, J. A. GAGES-II: Geospatial attributes of gages for evaluating streamflow. (Reston, VA, 2011).
Zhao, G., Bates, P. & Neal, J. The impact of dams on design floods in the conterminous US. Water Resour. Res. 56, https://doi.org/10.1029/2019WR025380 (2020).
Ficklin, D. L., Abatzoglou, J. T., Robeson, S. M., Null, S. E. & Knouft, J. H. Natural and managed watersheds show similar responses to recent climate change. Proc. Natl Acad. Sci. USA 115, 8553–8557 (2018).
Lazin, R., Shen, X., Moges, S. & Anagnostou, E. The role of renaissance dam in reducing hydrological extremes in the upper blue nile basin: current and future climate scenarios. J. Hydrol. 616, 128753 (2023).
Boulange, J., Hanasaki, N., Yamazaki, D. & Pokhrel, Y. Role of dams in reducing global flood exposure under climate change. Nat. Commun. 12, https://doi.org/10.1038/s41467-020-20704-0 (2021).
Payton, E. A. et al. Ch. 4. Water. (U.S. Global Change Research Program, Washington, DC, USA, 2023).
Skougaard Kaspersen, P., Høegh Ravn, N., Arnbjerg-Nielsen, K., Madsen, H. & Drews, M. Comparison of the impacts of urban development and climate change on exposing European cities to pluvial flooding. Hydrol. Earth Syst. Sci. 21, 4131–4147 (2017).
Huang, S., Krysanova, V., Zhai, J. & Su, B. Impact of intensive irrigation activities on river discharge under agricultural scenarios in the semi-arid Aksu River Basin, Northwest China. Water Resour. Manag. 29, 945–959 (2015).
Wasko, C. et al. Incorporating climate change in flood estimation guidance. Philos. Trans. R. Soc. A: Math., Phys. Eng. Sci. 379, 20190548 (2021).
Michalek, A. T., Villarini, G., Kim, T., Quintero, F. & Krajewski, W. F. Disentangling the sources of uncertainties in the projection of flood risk across the Central United States (Iowa). Geophys. Res. Lett. 50, e2023GL105852 (2023).
Lopez-Cantu, T., Prein, A. F. & Samaras, C. Uncertainties in future U.S. extreme precipitation from downscaled climate projections. Geophys. Res. Lett. 47, e2019GL086797 (2020).
Eyring, V. et al. Overview of the coupled model intercomparison project phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 9, 1937–1958 (2016).
O’Neill, B. C. et al. The scenario model intercomparison project (ScenarioMIP) for CMIP6. Geosci. Model Dev. 9, 3461–3482 (2016).
Daly, C., Gibson, W. P., Taylor, G. H., Johnson, G. L. & Pasteris, P. A knowledge-based approach to the statistical mapping of climate. Clim. Res. 22, 99–113 (2002).
Iturbide, M. et al. The R-based climate4R open framework for reproducible climate data access and post-processing. Environ. Model. Softw. 111, 42–54 (2019).
Mann, H. B. Nonparametric tests against trend. Econometrica 13, 245–259 (1945).
Kendall, M. G. Rank Correlation Methods. (Charles Griffin, 1975).
Sison, C. P. & Glaz, J. Simultaneous confidence-intervals and sample-size determination for multinomial proportions. J. Am. Stat. Assoc. 90, 366–369 (1995).
Acknowledgements
This work was supported in part by the USACE Institute for Water Resources and by the Princeton University Library Open Access Fund. Comments and suggestions by Gabriel Vecchi (Princeton University) and Enrico Scoccimarro (Centro Euro-Mediterraneo sui Cambiamenti Climatici) are gratefully acknowledged.
Author information
Authors and Affiliations
Contributions
H.K. processed the data, conducted the analyses, created the figures, interpreted the results, and prepared the manuscript. G.V. designed the study, interpreted the results, and prepared the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Naresh Devineni and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kim, H., Villarini, G. Higher emissions scenarios lead to more extreme flooding in the United States. Nat Commun 15, 237 (2024). https://doi.org/10.1038/s41467-023-44415-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-023-44415-4
This article is cited by
-
Floods across the eastern United States are projected to last longer
npj Natural Hazards (2024)
-
History, causes, and trend of floods in the U.S.: a review
Natural Hazards (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.