Abstract
The transformation of electromagnetic energy into matter represents a fascinating prediction of relativistic quantum electrodynamics that is paradigmatically exemplified by the creation of electron-positron pairs out of light. However, this phenomenon has a very low probability, so positron sources rely instead on beta decay, which demands elaborate monochromatization and trapping schemes to achieve high-quality beams. Here, we propose to use intense, strongly confined optical near fields supported by a nanostructured material in combination with high-energy photons to create electron-positron pairs. Specifically, we show that the interaction between near-threshold γ-rays and polaritons yields higher pair-production cross sections, largely exceeding those associated with free-space photons. Our work opens an unexplored avenue toward generating tunable pulsed positrons from nanoscale regions at the intersection between particle physics and nanophotonics.
Similar content being viewed by others
Introduction
The creation of massive particles from electromagnetic energy emerged as a prominent focus of attention in 1934, when the materialization of an electron and its antiparticle—the positron—was predicted to occur with nonvanishing probability by Breit and Wheeler (BW) from the scattering of two photons1, by Bethe and Heitler (BH) from the interaction of a photon and the Coulomb potential of a nucleus2, and by Landau and Lifshitz (LL) from the collision of two other massive particles3. A main difference between these processes relates to the real or virtual nature of the involved photons. While only real electromagnetic quanta lying inside the light cone (i.e., satisfying the light dispersion relation in vacuum, k = ω/c) participate in the BW mechanism for pair production, the LL process is mediated by two virtual photons, and both real and virtual photons play a role in BH scattering. Eventually, pair production was achieved by colliding energetic electrons and real photons delivered by high-power lasers4, and more recently using only real photons generated from atomic collisions5.
Besides the fundamental interest of these processes, the generation of positrons finds application in surface science6 through, for example, positron annihilation spectroscopy7,8,9 and low-energy positron diffraction10, as well as in the study of their interactions with atoms and molecules11,12. Positrons are also used to create antimatter, for example, antihydrogen13,14,15,16 and positronium17. In these studies, slow positrons are commonly obtained from beta decay, decelerated through metallic moderators18, and subsequently stored in different types of traps, from which they are extracted as low-energy, quasi-monochromatic pulses19,20,21,22.
Direct positron generation from light would not require nuclear decay and could further leverage recent advances in optics to produce ultrashort photon pulses. However, the cross-sections associated with the aforementioned processes are extremely small. As a possible avenue to increase the pair-production rate, we consider the replacement of free photons by confined optical modes in the hope that they alleviate the kinematic mismatch between the particles involved in BW scattering. In particular, surface polaritons, which are hybrids of light and polarization charges bound to material interfaces, can display short in-plane wavelengths compared with the free-space light wavelength. Such modes involve electromagnetic energy trapped at the interface between two media with different dielectric properties. For example, for a planar interface, when the sign of the real part of the permittivity of the two media is opposite, the associated optical fields decay exponentially away from the interface, but a similar behavior is observed when light is trapped by a thin metallic film23. Likewise, light can be trapped in polaritons sustained by more involved geometries24 (e.g., in a self-standing sphere, a polariton is defined by the condition that its permittivity is equal to −2 if one neglects retardation effects). Actually, a broad suite of two-dimensional (2D) materials has recently been identified to sustain long-lived, strongly confined polaritons25,26, including plasmonic23,27,28, phononic29,30, and excitonic31 modes that cover a wide spectral range extending from mid-infrared frequencies23,27,29,30 to the visible domain28,31. Specifically, modes bound to nanogaps32 feature large field confinement and enhancement (in vacuum regions) that boost light-mediated processes, such as surface-enhanced Raman scattering (SERS).
In this work, we calculate the pair-production cross section associated with the annihilation of γ-ray photons (γ-photons) and confined polaritons, leading to a substantial enhancement compared to free-space BW scattering. Part of this enhancement relates to the spatial confinement of surface polaritons, as the lack of translational invariance enables pair production for γ-photon energies just above the 2mec2 threshold (e.g., at the 60Co emission line ℏωγ ~1.17 MeV combined with a polariton energy ℏωp of a few eV), in contrast to free-space BW scattering, for which visible-range photons need to be paired with GeV photons such as those generated in astrophysical processes33,34. The latter include absorption of high-energy γ rays by extra-galactic background light35, by active galactic nuclei36, and during γ-ray bursts37, as well as plasma production in neutron-star magnetospheres38. For polaritonic nanogap modes confined in three dimensions, pairs can be produced by γ-photon scattering in the gap vacuum region, where polariton-mediated positron emission is not affected by the background of other emission processes such as BH scattering. By demonstrating the advantages of using deeply confined light, our work inaugurates an avenue in the exploration of nanophotonic structures as a platform for high-energy physics.
Results
Pair production from the scattering of a polariton and a γ-photon
Considering the general configuration illustrated in Fig. 1a, we study pair production by using the relativistic minimal coupling Hamiltonian39,40
where \(\hat{{{{{{{{\bf{j}}}}}}}}}({{{{{{{\bf{r}}}}}}}})=-ec:\overline{{{\Psi }}}({{{{{{{\bf{r}}}}}}}})\overrightarrow{\gamma }\hat{{{\Psi }}}({{{{{{{\bf{r}}}}}}}}):\) is the fermionic current, A(r, t) is the classical vector potential associated with the polariton and photon fields, and we adopt a gauge with vanishing scalar potential. Here, : ⋅ : denotes normal product concerning electron and positron annihilation (\({\hat{c}}_{{{{{{{{\bf{q}}}}}}}},s}\) and \({\hat{d}}_{{{{{{{{\bf{q}}}}}}}},s}\), respectively) and creation (\({\hat{c}}_{{{{{{{{\bf{q}}}}}}}},s}^{{{{\dagger}}} }\) and \({\hat{d}}_{{{{{{{{\bf{q}}}}}}}},s}^{{{{\dagger}}} }\)) operators (for fermions of momentum ℏq, spin s, and energy \(\hslash {\varepsilon }_{q}=c\sqrt{{m}_{{{{{{{{\rm{e}}}}}}}}}^{2}{c}^{2}+{\hslash }^{2}{q}^{2}}\)), and \(\hat{{{\Psi }}}({{{{{{{\bf{r}}}}}}}})={\sum }_{{{{{{{{\bf{q}}}}}}}},s}({u}_{{{{{{{{\bf{q}}}}}}}},s}{\hat{c}}_{{{{{{{{\bf{q}}}}}}}},s}{e}^{i{{{{{{{\bf{q}}}}}}}}\cdot {{{{{{{\bf{r}}}}}}}}}+{v}_{{{{{{{{\bf{q}}}}}}}},s}{\hat{d}}_{{{{{{{{\bf{q}}}}}}}},s}^{{{{\dagger}}} }{e}^{-i{{{{{{{\bf{q}}}}}}}}\cdot {{{{{{{\bf{r}}}}}}}}})\) is the fermionic field operator, with uq,s (vq,s) representing 4-component electron (positron) spinors.
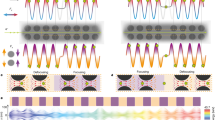
a We consider polaritons supported by a material structure. Energetic γ-rays interact with the polaritons, giving rise to electron–positron pairs. b Direct and time-reversed Feynman diagrams contributing to the investigated pair production. We indicate the energies and wave vectors of the polariton, the γ-photon, and the fermions by color-coordinated labels. Both polariton emission and absorption processes contribute to pair production, as indicated by orange arrows pointing toward the vertex or away from it, respectively.
We work in the continuous-wave regime and eventually normalize the resulting production rate to the number of polaritons and photons in the system. The vector potential is thus \({{{{{{{\bf{A}}}}}}}}({{{{{{{\bf{r}}}}}}}},\, t)=-(ic/{\omega }_{p})\,{\overrightarrow{{{{{{{{\mathcal{E}}}}}}}}}}_{p}({{{{{{{\bf{r}}}}}}}}){e}^{-i{\omega }_{p}t}-(ic/{\omega }_{\gamma })\,{{{{{{{{\mathcal{E}}}}}}}}}_{\gamma }\,{\hat{{{{{{{{\bf{e}}}}}}}}}}_{j}\,{e}^{i{k}_{\gamma }z-i{\omega }_{\gamma }t}+{{{{{{{\rm{c.c.}}}}}}}}\) (i.e., the sum of two monochromatic components), in which we consider two different polarizations \({\hat{{{{{{{{\bf{e}}}}}}}}}}_{j}=\hat{{{{{{{{\bf{x}}}}}}}}}\) or \(\hat{{{{{{{{\bf{y}}}}}}}}}\) (with j = 1 or 2) for the γ-ray field and take it to propagate along the z direction with the wave vector \({{{{{{{{\bf{k}}}}}}}}}_{\gamma }=\hat{{{{{{{{\bf{z}}}}}}}}}\,{\omega }_{\gamma }/c\). The polaritonic electric field \({{{{{{{\bf{E}}}}}}}}({{{{{{{\bf{r}}}}}}}},\, t)={\overrightarrow{{{{{{{{\mathcal{E}}}}}}}}}}_{p}({{{{{{{\bf{r}}}}}}}}){e}^{-i{\omega }_{p}t}+{{{{{{{\rm{c.c.}}}}}}}}\) incorporates a spatially localized amplitude \({\overrightarrow{{{{{{{{\mathcal{E}}}}}}}}}}_{p}({{{{{{{\bf{r}}}}}}}})\), for which we use expressions that describe modes in planar surfaces23 and nanostructures24. Such expressions have been extensively and successfully used in the explanation of nanophotonics experiments23,24,41.
The production rate for a state \({\hat{d}}_{{{{{{{{\bf{q}}}}}}}},s}^{{{{\dagger}}} }{\hat{c}}_{{{{{{{{{\bf{q}}}}}}}}}^{{\prime} },{s}^{{\prime} }}^{{{{\dagger}}} }\left|0\right\rangle\) comprising a positron (wave vector q, spin s) and an electron (wave vector \({{{{{{{{\bf{q}}}}}}}}}^{{\prime} }\), spin \({s}^{{\prime} }\)) is then calculated to the lowest (second) nonvanishing-order of time-dependent perturbation theory for the Hamiltonian in Eq. (1). This level of perturbation should be sufficient considering the low obtained cross sections (see below), while the renormalization group42,43 could be used to account for nonperturbative corrections. Following a standard procedure detailed in Supplementary Notes 1 and 2, the positron-momentum-resolved pair-production cross section associated with polariton and γ-photon scattering is found to be
where α ≈ 1/137 is the fine-structure constant, we average over γ-ray polarizations j, and a 4 × 4 matrix
is defined in terms of the Dirac γ matrices, the Feynman propagator40\({G}_{F}({{{{{{{\bf{q}}}}}}}},\, \omega )=[\omega {\gamma }^{0}-c\overrightarrow{\gamma }\cdot {{{{{{{\bf{q}}}}}}}}+({m}_{e}{c}^{2}/\hslash )]/({\omega }^{2}-{\varepsilon }_{q}^{2}+i{0}^{+})\), and the momentum representation of the polariton field \({\overrightarrow{{{{{{{{\mathcal{E}}}}}^{-}}}}}}_{p,{{{{{{{{\bf{k}}}}}}}}}_{p}}=\int\,{d}^{3}{{{{{{{\bf{r}}}}}}}}\,{\overrightarrow{{{{{{{{\mathcal{E}}}}}}}}}}_{p}({{{{{{{\bf{r}}}}}}}}){e}^{-i{{{{{{{{\bf{k}}}}}}}}}_{p}\cdot {{{{{{{\bf{r}}}}}}}}}\) and \({\overrightarrow{{{{{{{{\mathcal{E}}}}}}}}}}_{p,{{{{{{{{\bf{k}}}}}}}}}_{p}}^{+}=({\overrightarrow{{{{{{{{\mathcal{E}}}}}}}}}}^{-}_{p,{{{{{{{{\bf{k}}}}}}}}}_{p}})^{*}\). The cross-section in Eq. (2a) is normalized per polariton and incident γ-photon, and in particular, the denominator in front of the integral contains the number of polaritons Np sustained by the \({\overrightarrow{{{{{{{{\mathcal{E}}}}}}}}}}_{p}({{{{{{{\bf{r}}}}}}}})\) field (see Supplementary Notes 1 and 2 for details).
Equations (2a) and (2b) describes the annihilation of a γ-photon accompanied by the emission (upper signs) or absorption (lower signs) of a polariton, as indicated in the Feynman diagrams in Fig. 1b (orange arrows pointing away or toward the vertex, respectively), where a finite range of wave vectors kp is generally involved due to spatial confinement. Incidentally, we note that boson emission is forbidden in free-space BW scattering, whereas it contributes to the present polariton-mediated pair-production process. In addition, polariton absorption and emission processes lead to nearly identical contributions to the pair-production cross-section because the polariton energy and momentum are small compared with the total transferred amounts of these quantities.
Pair production assisted by surface polaritons
As an illustrative scenario, we consider surface polaritons (frequency ωp, wave vector \({{{{{{{{\bf{k}}}}}}}}}_{p}={k}_{{{{{{{{\rm{p}}}}}}}}}\hat{{{{{{{{\bf{x}}}}}}}}}\)) launched on a 2D material (z = 0 plane) by in-coupling a laser through a metallic tip (or, alternatively, a grating) (see Fig. 2a), producing a polariton field amplitude that can be generally written as (see, for example, ref. 44) \({\overrightarrow{{{{{{{{\mathcal{E}}}}}}}}}}_{p}({{{{{{{\bf{r}}}}}}}})\propto [i{\kappa }_{p}\hat{{{{{{{{\bf{x}}}}}}}}}-{k}_{p}{{{{{{{\rm{sign}}}}}}}}\{z\}\hat{{{{{{{{\bf{z}}}}}}}}}]\,{e}^{i{k}_{{{{{{{{\rm{p}}}}}}}}}x-{\kappa }_{p}| z| }\) with \({\kappa }_{p}=\sqrt{{k}_{p}^{2}-{\omega }_{p}^{2}/{c}^{2}}\), where we neglect material losses, γ-ray screening, and finite-thickness effects. Parallel momentum conservation leads to \({{{{{{{{\bf{q}}}}}}}}}_{\parallel \pm }^{{\prime} }=-{{{{{{{{\bf{q}}}}}}}}}_{\parallel }\, \mp \, {{{{{{{{\bf{k}}}}}}}}}_{p}\) for the in-plane electron wave vector components, while energy conservation determines the electron energy \({\varepsilon }_{{q}_{\pm }^{{\prime} }}={\omega }_{\gamma }\mp {\omega }_{p}-{\varepsilon }_{q}\) and out-of-plane wave vector \({q}_{z\pm }^{{\prime} }=\sqrt{{\varepsilon }_{{q}_{\pm }^{{\prime} }}^{2}/{c}^{2}-{m}_{{{{{{{{\rm{e}}}}}}}}}^{2}{c}^{2}/{\hslash }^{2}-{q}_{\parallel \pm }^{{\prime} \,2}}\), subject to the threshold-energy conditions \({\varepsilon }_{{q}_{\pm }^{{\prime} }}^{2} > \, {m}_{{{{{{{{\rm{e}}}}}}}}}^{2}{c}^{4}/{\hslash }^{2}-{c}^{2}{q}_{\parallel \pm }^{{\prime} \,2}\) and ωγ > ±ωp + εq. Calculating the Fourier transform of the surface polariton field and inserting it into Eqs. (2), we find (see Supplementary Note 4)
where \({{{{{{{{\bf{q}}}}}}}}}_{\mu \pm }^{{\prime} }={{{{{{{{\bf{q}}}}}}}}}_{\parallel \pm }^{{\prime} }+\mu {q}_{z\pm }^{{\prime} }\hat{{{{{{{{\bf{z}}}}}}}}}\) is the electron wave vector for upward (μ = 1) and downward (μ = − 1) emission contributions, while \({{{{{{{{\mathcal{N}}}}}}}}}_{j}^{\pm }({{{{{{{{\bf{q}}}}}}}}}^{{\prime} },\,{{{{{{{\bf{q}}}}}}}})\) is given by Eq. (2b) with \({\overrightarrow{{{{{{{{\mathcal{E}}}}}^{\pm }}}}}}_{p,{{{{{{{\bf{q}}}}}}}}+{{{{{{{{\bf{q}}}}}}}}}^{{\prime} }-{{{{{{{{\bf{k}}}}}}}}}_{\gamma }}\) replaced by a vector \({{{{{{{{\bf{f}}}}}}}}}_{\pm ({k}_{\gamma z}-{q}_{z}-{q}_{z}^{{\prime} })}\) defined in such a way that \({{{{{{{{\bf{f}}}}}}}}}_{{k}_{z}}=({\kappa }_{p}^{2}\,\hat{{{{{{{{\bf{x}}}}}}}}}+{k}_{{{{{{{{\rm{p}}}}}}}}}{k}_{z}\,\hat{{{{{{{{\bf{z}}}}}}}}})/({\kappa }_{p}^{2}+{k}_{z}^{2})\) encapsulates the out-of-plane momentum distribution of the polariton field.
a We consider surface modes excited in a 2D material by a coupling tip illuminated by laser pulses (red), while the γ-rays (dark gray) normally impinge on the surface. The positron emission direction (θ, φ) (purple) determines the electron direction (blue) by conservation of energy and in-plane momentum. b Comparison between the regions allowed by energy–momentum conservation in either Bethe–Wheeler (BW) photon–photon scattering (yellow) and polariton–photon scattering under the configuration of Fig. 1a (purple) as a function of polariton/photon energies. The BW threshold \({\hslash }^{2}{\omega }_{p}{\omega }_{\gamma }=2{m}_{{{{{{{{\rm{e}}}}}}}}}^{2}{c}^{4}/(1-\cos {\theta }_{p\gamma })\)39 is indicated for a relative photon-photon angle θpγ of π (absolute threshold) and π/2. c Pair-production cross sections for polariton-photon scattering (σpol, purple curves), BW scattering (σBW for θpγ = π/2, black curves; see Supplementary Note 5.3), and Bethe–Heitler (BH) scattering by a carbon atom (σBH, green curve; see Supplementary Note 5.1). We consider different polariton energies (see legend) with a fixed kp = 0.05 nm−1 in all cases. Solid vertical lines indicate the γ-photon BW threshold energies taken from the θpγ = π/2 curve in (a).
An immediate consequence of out-of-plane symmetry breaking is that the allowed kinematical space for which we obtain nonzero pair-production cross sections extends down to the infrared polariton regime even when using γ-photons just above the absolute energy threshold ≳ 2mec2 ≈ 1.02 MeV (Fig. 2b). In contrast, BW scattering with one of the photons in the optical regime requires the other photon to have energy exceeding ~0.1 TeV, which explains why free-space pair production has traditionally been observed only in its nonlinear version, where the energy–momentum mismatch is overcome by engaging a high number of photon exchanges45,46.
In Fig. 2c, we show that, for low-energy polaritons/photons (up to a few eV), the momentum-integrated polariton-assisted pair-production cross-section σpol = ∫ d3q (dσpol/dq), with dσpol/dq given by Eq. (3), takes substantial values at γ-photon energies far below the BW kinematical threshold (vertical solid lines). In addition, σpol is consistently several orders of magnitude higher than the BW cross section up to γ-photon energies in the TeV regime. Part of this enhancement can be attributed to the effect of spatial compression of polaritons relative to free-space photons.
Upon numerical examination of Eq. (3), we find positron emission to be dominated by contributions associated with an equal partition of kinetic energy between the two fermions, both for near-threshold (Supplementary Fig. 2) and GeV (Supplementary Fig. 3) emission, also displaying sharp angular profiles peaked around the forward direction defined by the γ-ray.
Unfortunately, the emission arising from scattering by surface polaritons is orders of magnitude smaller than that associated with BH scattering by the polaritonic material, as revealed by comparing their respective cross sections normalized per polariton and per atom (Fig. 3c). For example, for 1.17 MeV γ-photons traversing a highly doped graphene monolayer that supports 1 eV plasmons, the ratio between the emission from these two mechanisms is (npσpol)/(nCσBH), where np is the plasmon surface density, nC ~ 40/nm2 is the carbon atom density, and we have σpol ~ 10−13 barn (1 barn = 10−24 cm2) and σBH ~ 10−4 barn47 (see Supplementary Note 5.1). For the two signals to be comparable in magnitude, an unrealistically large plasmon density np > 1010/nm2 would be required.
a Sketch of the geometry under consideration, in which pairs are produced by γ-photons traversing a gap polariton. The latter can be excited by a laser pulse and is taken to have frequency ωp and uniform field \({\overrightarrow{{{{{{{{\mathcal{E}}}}}}}}}}_{p}\) confined to a spherical region of radius Rp (flanked by a polaritonic material). b Differential cross-section as a function of polar angle for polariton-assisted positron emission under the configuration in (a) (colored curves for different values of Rp and ωp, as indicated by labels), compared with the BH cross section for a gold atom (see Supplementary Note 5.1). We consider 1.17 MeV γ-photons in all cases.
Threshold pair-production assisted by gap polaritons
To reduce the effect of the BH background, we study pair production by scattering of γ-photons and gap polaritons (Fig. 3a). Besides the emission enhancement expected from the breaking of translational invariance in all directions, positrons produced by gap polaritons and γ-photons arise from the vacuum gap region, where no BH signal is generated, thus facilitating the identification of a polariton-assisted pair-production signal (see further discussion below). For simplicity, we consider a polariton field described by \({\overrightarrow{{{{{{{{\mathcal{E}}}}}}}}}}_{p}({{{{{{{\bf{r}}}}}}}})={E}_{p}\,\hat{{{{{{{{\bf{x}}}}}}}}}\,{{\Theta }}({R}_{p}-r)\), which has a uniform amplitude Ep polarized along x and extending within a sphere of radius Rp. This simple expression defines a confined mode of size Rp that allows us to obtain analytical expressions, while the details of the field in more complex structures24 should only produce minor modifications in the final results. Inserting this field in Eqs. (2a) and (2b), we obtain (see a detailed derivation in Supplementary Note 3)
where the value of \({q}_{\pm }^{{\prime} }\) is determined by the energy conservation condition \({\varepsilon }_{{q}_{\pm }^{{\prime} }}={\omega }_{\gamma }-{\varepsilon }_{q}\, \mp \, {\omega }_{p}\), the integral is restricted by the condition ωγ ∓ ωp ≥ mec2/ℏ + εq, and we define \({{{{{{{{\mathcal{P}}}}}}}}}_{j}^{\pm }({{{{{{{{\bf{q}}}}}}}}}^{{\prime} },\,{{{{{{{\bf{q}}}}}}}})={{{{{{{{\mathcal{M}}}}}}}}}_{j}^{\pm }({{{{{{{{\bf{q}}}}}}}}}^{{\prime} },\,{{{{{{{\bf{q}}}}}}}})/{E}_{p}\) [see Eq. (2b)]. The latter involves the normalized Fourier transform of the polariton field amplitude \({\overrightarrow{{{{{{{{\mathcal{E}}}}}}}}}}_{p}({{{{{{{\bf{r}}}}}}}})\), which reduces to
We use Eq. (4) to compute the results presented in Fig. 3b for different polariton sizes Rp and energies ℏωp after integrating over the azimuthal angle of positron emission. The differential cross section normalized per polariton and γ-photon exhibits a monotonic increase with decreasing Rp and ωp as well as a smooth dependence on polar angle θ.
Once more, we need to compare polariton-driven pair production to the background BH positron signal (i.e., γ-ray scattering by the nuclei of the polaritonic material). The complete suppression of BH scattering from the vacuum gap region could be leveraged by selecting positrons originating only in that region through the use of charged-particle optics elements (i.e., a positron analog of electron optics in an electron microscope), such that only positrons coming from the gap are collected, similarly to how photoemission electron microscopes collect electrons emitted within specimen regions spanning just a few nanometers48.
Even without resorting to positron microscopy, we argue next that spatial confinement in gap polaritons leads to a discernible positron emission signal under laser pulse irradiation when compared to the BH background, as the cross section per polariton undergoes an increase by several orders of magnitude when moving from confinement in one direction (surface polaritons, Fig. 2c) to full three-dimensional trapping (gap polaritons, Fig. 3b). For concreteness, we focus on low-energy (ℏωp = 0.1 eV) gap plasmons confined to an opening in a gold film with an effective mode volume assimilated to a sphere of radius Rp = 50 nm. These parameters can be obtained by engineering the morphology of the metal gap32. In practice, we envision an array of gaps such that the openings span a fraction η of the film surface. Under illumination with a laser peak amplitude of 108 V/m (a typical value below the damage threshold when using ultrafast pulses49) and a realistic polaritonic field enhancement of 102 (i.e., Ep ~ 1010 V/m), we have a number of polaritons \({N}_{p}\, \approx \, {E}_{p}^{2}{R}_{p}^{3}/3\hslash {\omega }_{p} \sim 3\times 1{0}^{7}\) per gap (i.e., a surface polariton density \({n}_{p}=\eta {N}_{p}/\pi {R}_{p}^{2} \sim 4\,\eta \times 1{0}^{3}/{{{{{{{{\rm{nm}}}}}}}}}^{2}\); see Supplementary Note 4), and therefore, the fraction of positrons generated per γ-photon is npσpol ~ η × 10−7, where we take σpol ~ 0.25 barn for the pair-production cross section per polariton (see Fig. 3b).
This fraction has to be compared to that of positrons associated with the BH mechanism. For a gold film of thickness L = 100 nm (much smaller than the positron escape depth; see Supplementary Note 5.2), as commonly employed in plasmonic studies, we combine the BH cross section for a gold atom at 1.17 MeV γ-photon energy (σBH ≈ 16 mbarn; see Fig. 3b) together with the volume per gold atom \({{{{{{{\mathcal{V}}}}}}}}\, \approx \, 17.0\) Å3 (i.e., a surface gold atom density \({n}_{{{{{{{{\rm{Au}}}}}}}}}=L/{{{{{{{\mathcal{V}}}}}}}} \sim 6\times 1{0}^{3}/{{{{{{{{\rm{nm}}}}}}}}}^{2}\)), to compute the fraction of BH positrons per incident photon, nAuσBH ~ 10−8. Under these conditions, the ratio of polariton-assisted emission to BH emission is ~10 η. For a realistic value of the opening fraction η ~ 10%, the noted ratio becomes ~1, and therefore, polariton-mediated pair production and BH scattering are comparable in magnitude.
We remark that this estimate assumes a synchronized detection, such that the signal is only collected within the duration of the optical pulses needed to sustain a large number of polaritons in the system. For example, with 1 g of 60Co, we have ~100 γ-photons overlapping in time with the duration of a 1 ps laser pulse (see Supplementary Note 4), which leads to the emission of npσpol ~ 10−6 positrons per pulse, half of them produced by polariton-assisted scattering. We thus predict a measurable signal when employing a high-repetition (~108 Hz) pulsed laser.
As an alternative geometry, one could rely on polaritons confined to nanoparticles (e.g., gold colloids24) of similar size as the gaps considered above and dispersed on a thin film (e.g., monolayer graphene), leading to similar estimates for the positron production yield and even higher ratios of polariton-driven to BH positron emission because of the reduction in polaritonic material volume.
Discussion
In conclusion, we advocate for the use of optical excitations confined to nanostructured materials in combination with γ-rays as a way of producing electron-positron pairs with higher efficiency than free-space BW scattering and requiring substantially lower photon energies. The breaking of translational invariance is responsible for the latter, whereas the spatial compression of the optical fields associated with surface polaritons facilitates the coupling to high-momentum products (the fermions). The proposed mechanism is still orders of magnitude weaker than BH scattering when the pairs are produced by γ-photons traversing polariton-supporting materials (e.g., graphene and planar waveguides). Isolation of the proposed mechanism could be achieved with the use of focused γ-photons targeted at the region in which the polariton has high strength, although such focusing represents a pending challenge in itself. Alternatively, we argue that gap polaritons confined to vacuum regions flanked by such materials can circumvent this problem by, for example, collecting positrons created at the gap using a positron microscope. In addition, when synchronizing positron detection with exposure of gap polaritons to ultrafast laser pulses, we show that the BH background becomes comparatively small thanks to the enhancement in the emission associated with strong polariton spatial confinement in all three dimensions. We remark that these conclusions are drawn from the study of positron emission produced by near-threshold γ-photons, such as those from 60Co.
Besides its fundamental interest, the proposed mechanism for polariton-driven positron emission opens exciting possibilities that are not accessible to other types of positron sources, such as the generation of positron pulses with ultrafast durations inherited from the incident laser pulses, as well as the nanoscale size of those sources when relying on confined gap polaritons. We envision the spatiotemporal modulation of the positron wave functions by shaping the employed laser field or by tailoring the spatial distribution and polarization of the polaritonic field (e.g., to create chiral positron beams or two-pulse positron states). We remark that the localized nature of the emission from regions in which strongly confined and intensity-enhanced polaritons are sustained renders this mechanism appealing for applications that demand spatially confined positron sources. Rough metal surfaces should also boost pair production due to the large optical enhancement that takes place at plasmonic hotspots32 in analogy to SERS, although positron emission via the BH mechanism would result in a large signal in such structures (see discussion on generation from gold films above) that could be reduced by resorting to ultrathin self-standing films or, alternatively, by synchronizing positron detection and laser pulse excitation of the polaritonic field. The inverse process of positron annihilation stimulated by polaritonic fields upon impact on a polariton-supporting material also bears interest as a possible source of localized γ-photons. Beyond these potential uses, antimatter production and annihilation assisted by collective optical excitations bear intrinsic interest as an example of a nanophotonics approach to high-energy physics.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
References
Breit, G. & Wheeler, J. A. Collision of two light quanta. Phys. Rev. 46, 1087–1091 (1934).
Bethe, H. & Heitler, W. On the stopping of fast particles and on the creation of positive electrons. Proc. R. Soc. Lond. Ser. A 146, 83–112 (1934).
Landau, L. D. & Lifschitz, E. M. On the production of electrons and positrons by a collision of two particles. Phys. Z. 6, 244 (1934).
Burke, D. L. et al. Positron production in multiphoton light-by-light scattering. Phys. Rev. Lett. 9, 1626–1629 (1997).
Adam, J. et al. Measurement of e+e− momentum and angular distributions from linearly polarized photon collisions. Phys. Rev. Lett. 127, 052302 (2021).
Schultz, P. J. & Lynn, K. G. Interaction of positron beams with surfaces, thin films, and interfaces. Rev. Mod. Phys. 60, 701–779 (1988).
Siegel, R. W. Positron annihilation spectroscopy. Annu. Rev. Mater. Sci. 10, 393–425 (1980).
Eijt, S. W. H. et al. Study of colloidal quantum-dot surfaces using an innovative thin-film positron 2d-acar method. Nat. Mater. 5, 23–26 (2006).
Tuomisto, F. & Makkonen, I. Defect identification in semiconductors with positron annihilation: experiment and theory. Rev. Mod. Phys. 85, 1583–1631 (2013).
Coleman, P. G. Surface physics with slow positron beams. Appl. Surf. Sci. 194, 264–270 (2002).
Surko, C. M., Gribakin, G. F. & Buckman, S. J. Low-energy positron interactions with atoms and molecules. J. Phys. B 38, R57–R126 (2005).
Gribakin, G. F., Young, J. A. & Surko, C. M. Positron-molecule interactions: resonant attachment, annihilation, and bound states. Rev. Mod. Phys. 82, 2557–2607 (2010).
Amoretti, M. et al. Production and detection of cold antihydrogen atoms. Nature 419, 456–459 (2002).
Gabrielse, G. et al. Background-free observation of cold antihydrogen with field-ionization analysis of its states. Phys. Rev. Lett. 89, 213401 (2002).
Andresen, G. B. et al. Trapped antihydrogen. Nature 468, 673–676 (2010).
Gabrielse, G. et al. Trapped antihydrogen in its ground state. Phys. Rev. Lett. 108, 113002 (2012).
Cassidy, D. B. & Mills Jr, A. P. The production of molecular positronium. Nature 449, 195–197 (2007).
Mills Jr, A. P. Sources and physics of positrons. Hyperfine Interact. 44, 105–123 (1988).
Gilbert, S. J., Kurz, C., Greaves, R. G. & Surko, C. M. Creation of a monoenergetic pulsed positron beam. Appl. Phys. Lett. 70, 1944–1946 (1997).
Gilbert, S. J. et al. Low-energy positron-matter interactions using trap-based beams. AIP Conf. Proc. 606, 24–34 (2002).
Cassidy, D. B., Deng, S. H. M., Greaves, R. G. & Mills Jr, A. P. Accumulator for the production of intense positron pulses. Rev. Sci. Instrum. 77, 073106 (2006).
Natisin, M. R., Danielson, J. R. & Surko, C. M. Formation mechanisms and optimization of trap-based positron beams. Phys. Plasmas 23, 023505 (2016).
García de Abajo, F. J. Graphene plasmonics: challenges and opportunities. ACS Photonics 1, 135–152 (2014).
Yu, R., Liz-Marzán, L. M. & García de Abajo, F. J. Universal analytical modeling of plasmonic nanoparticles. Chem. Soc. Rev. 46, 6710–6724 (2017).
Basov, D. N., Fogler, M. M. & García de Abajo, F. J. Polaritons in van der Waals materials. Science 354, aag1992 (2016).
Low, T. et al. Polaritons in layered two-dimensional materials. Nat. Mater. 16, 182–194 (2017).
Alcaraz Iranzo, D. et al. Probing the ultimate plasmon confinement limits with a van der Waals heterostructure. Science 360, 291–295 (2018).
Abd El-Fattah, Z. M. et al. Plasmonics in atomically thin crystalline silver films. ACS Nano 13, 7771–7779 (2019).
Li, P. et al. Infrared hyperbolic metasurface based on nanostructured van der Waals materials. Science 359, 892–896 (2018).
Caldwell, J. D. et al. Photonics with hexagonal boron nitride. Nat. Rev. Mater. 4, 552–567 (2019).
Li, Y. et al. Measurement of the optical dielectric function of monolayer transition-metal dichalcogenides: MoS2, MoSe2, WS2, and WSe2. Phys. Rev. B 90, 205422 (2014).
Álvarez-Puebla, R. A., Liz-Marzán, L. M. & García de Abajo, F. J. Light concentration at the nanometer scale. J. Phys. Chem. Lett. 1, 2428–2434 (2010).
Röser, S. Cosmic Matter (Wiley-VCH, New York, 2008).
Ruffini, R., Vereshchagin, G. & Xue, S.-S. Electron-positron pairs in physics and astrophysics: from heavy nuclei to black holes. Phys. Rep. 487, 1–140 (2010).
Biteau, J. & Williams, D. A. The extragalactic background light, the Hubble constant, and anomalies: conclusions from 20 years of TeV gamma-ray observations. Astrophys. J. 812, 60 (2015).
Abdalla, H. et al. Constraints on the emission region of 3C 279 during strong flares in 2014 and 2015 through VHE γ-ray observations with H.E.S.S. Astron. Astrophys. 627, A159 (2019).
Gill, R. & Granot, J. The effect of pair cascades on the high-energy spectral cut-off in gamma-ray bursts. Mon. Not. R. Astron. Soc. 475, L1–L5 (2018).
Voisin, G., Mottez, F. & Bonazzola, S. Electron-positron pair production by gamma-rays in an anisotropic flux of soft photons, and application to pulsar polar caps. Mon. Not. R. Astron. Soc. 474, 1436–1452 (2018).
Jauch, J. M. & Rohrlich, F. The Theory of Photons and Electrons (Springer, Berlin, 1976).
Mandl, F. & Shaw, G. Quantum Field Theory (Wiley, Hoboken, 2010).
Myroshnychenko, V. et al. Modelling the optical response of gold nanoparticles. Chem. Soc. Rev. 37, 1792–1805 (2008).
Barbiellini, B. & Nicolini, P. Enhancement of Compton scattering by an effective coupling constant. Phys. Rev. A 84, 022509 (2011).
Barbiellini, B., Joly, Y. & Tamasaku, K. Explaining the X-ray nonlinear susceptibility of diamond and silicon near absorption edges. Phys. Rev. B 92, 155119 (2015).
Dias, E. J. C. & García de Abajo, F. J. Fundamental limits to the coupling between light and 2D polaritons. ACS Nano 13, 5184–5197 (2019).
Reiss, H. R. Absorption of light by light. J. Math. Phys. 3, 59–67 (1961).
Ritus, V. I. Quantum effects of the interaction of elementary particles with an intense electromagnetic field. J. Russ. Laser Res. 6, 497–617 (1985).
Maximon, L. C. Simple analytic expressions for the total Born approximation cross section for pair production in a Coulomb field. J. Res. Natl Bur. Stand. 72B, 79–88 (1968).
Da̧browski, M., Dai, Y. & Petek, H. Ultrafast photoemission electron microscopy: imaging plasmons in space and time. Chem. Rev. 120, 2859–2870 (2020).
Feist, A. et al. Quantum coherent optical phase modulation in an ultrafast transmission electron microscope. Nature 521, 200–203 (2015).
Acknowledgements
This work has been supported in part by the European Research Council (Advanced Grant 789104-eNANO), the Spanish MICINN (PID2020-112625GB-I00 and Severo Ochoa CEX2019-000910-S), the Catalan CERCA Program, and Fundaciós Cellex and Mir-Puig.
Author information
Authors and Affiliations
Contributions
F.J.G.A. conceived the concept. V.D.G. and F.J.G.A. developed the theory and wrote the paper. V.D.G. performed the calculations and prepared the figures.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Ido Kaminer, Chen Mechel, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Di Giulio, V., García de Abajo, F.J. Nanophotonics for pair production. Nat Commun 14, 8189 (2023). https://doi.org/10.1038/s41467-023-43701-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-023-43701-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.