Abstract
Nonlinear damping, the change in damping rate with the amplitude of oscillations plays an important role in many electrical, mechanical and even biological oscillators. In novel technologies such as carbon nanotubes, graphene membranes or superconducting resonators, the origin of nonlinear damping is sometimes unclear. This presents a problem, as the damping rate is a key figure of merit in the application of these systems to extremely precise sensors or quantum computers. Through measurements of a superconducting resonator, we show that from the interplay of quantum fluctuations and the nonlinearity of a Josephson junction emerges a power-dependence in the resonator response which closely resembles nonlinear damping. The phenomenon can be understood and visualized through the flow of quasi-probability in phase space where it reveals itself as dephasing. Crucially, the effect is not restricted to superconducting circuits: we expect that quantum fluctuations or other sources of noise give rise to apparent nonlinear damping in systems with a similar conservative nonlinearity, such as nano-mechanical oscillators or even macroscopic systems.
Similar content being viewed by others
Introduction
Amplitude-dependent (nonlinear) damping is ubiquitous in nature. It was famously described mathematically by van der Pol1 in the context of his work on vacuum tube circuits2. Now, it is used to describe the physics of a diverse set of systems, such as the rolling of ships in waves3 or the nervous system4. It has attracted recent interest due to its appearance in novel experimental platforms such as nanoscale ferromagnets5, superconducting circuits6,7,8,9 and nanoelectromechanical systems (NEMS)10,11,12,13 made for example from carbon nanotubes, graphene14,15 or superconducting metal16. In some of these systems the nonlinearity is well explained17,18,19,20. Most notably the saturation of two-level systems in the environment can cause negative nonlinear damping: the damping rate decreases as the power injected into the system increases6,8,9,16. But the origin of an increase in damping with power in certain NEMS11,12,13,14 or superconducting resonators7 remains speculative. Understanding the origin of nonlinear damping in some of these systems is critical due to the importance of their energy damping rates in applications such as NEMS based mass sensing21 or spectrometry22, as well as quantum-limited amplification23,24 in superconducting quantum computers25.
We study a dephasing effect in superconducting circuits26, which phenomenologically appears as nonlinear damping when measuring the resonant response of a resonator. Central to the observed physics is the nonlinearity induced by a Josephson junction: that the resonance frequency varies with the oscillation amplitude, which can be further approximated as a Duffing or Kerr nonlinearity27. For this reason, the phenomena discussed here are applicable to all systems featuring a similar nonlinearity in their resonance frequency, for example the carbon-nanotubes mentioned above, or even a macroscopic mechanical pendulum. We focus on the regime where this nonlinearity is small, as in Josephson parametric amplifiers24, rather than the single-photon nonlinear regime used to construct artificial atoms in circuit quantum electrodynamics27. Because of their small nonlinearity, such systems are often thought to be completely described by the classical Kerr oscillator7,28.
Here however, we report on an effect that is not expected from the classical Kerr oscillator. More specifically, we present a phenomenon triggered by the interplay between the quantum noise and Kerr anharmonicity of the oscillator, which closely resembles nonlinear damping in the steady-state response of the oscillator. The apparent nonlinear damping is first experimentally characterized by probing the frequency response of the resonant circuit. Our observations are then accurately described by a quantum theory of a damped driven Kerr oscillator devoid of ad hoc nonlinear damping, but which takes into account the effect of quantum noise. Moreover, focusing on an oscillator steady-state below its bistability threshold, a Gaussian state approximation29 allows us to demonstrate that, in a close vicinity of the resonance, the expected amplitude of oscillations is akin to that of a driven classical Kerr oscillator with nonlinear damping. Finally, we provide an intuitive picture in which the phenomenon can be understood as the oscillator experiencing dephasing induced by its own photon shot noise.
Results
Experimental setup
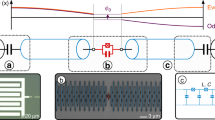
The circuit used in this experiment (Fig. 1) is constructed from an inductor, capacitor and superconducting quantum interference device, or SQUID. The SQUID is flux-biased to its sweet spot (integer flux quantum), and behaves as a single Josephson junction30. The junction induces an anharmonicity of strength K = 2π × 80 kHz five orders of magnitude smaller than the resonance frequency ωr = 2π × 5.17 GHz. The cosine potential of the junction is accurately described in this limit K ≪ ωr by the Kerr effect in the Hamiltonian31
where \(\hat{a}\) is the annihilation operator for photons in the circuit. Intuitively, the junction is acting as an inductor, with an inductance which increases with the number of photons \({\hat{a}}^{{{{\dagger}}} }\hat{a}\) in the circuit. As a consequence, the resonance frequency of the circuit is lowered with each added photon, labeled as the Kerr term in Eq. (1).
a The Kerr oscillator is constructed from an inductor, a capacitor and a SQUID (which behaves as and is depicted by a single Josephson junction), and is side-coupled to a transmission line with a coupling rate κext. The circuit undergoes internal damping at a rate κint. b Optical micrograph of the device, where light gray corresponds to superconducting molybdenum-rhenium, and dark gray to the insulating silicon substrate. An interdigitated capacitor on the right is connected to a meandering inductor on the left. The circuit couples to a transmission line (coplanar waveguide) at the top. c Scanning electron micrograph of the SQUID: two aluminum/aluminum-oxide Josephson junctions connected in parallel. As the flux threading the SQUID is fixed, it effectively behaves in this context as a single junction.
The circuit undergoes internal damping, losing energy at a rate κint = 2π × 186 kHz. This is typically due to losses in the different dielectric materials traversed by the electric fields32. Additionally, the circuit is coupled to a transmission line, through which we drive the circuit with a microwave signal. Conversely, the transmission line leads to energy leaking out of the circuit, which is characterized by an external damping rate κext = 2π × 2.1 MHz. As a consequence, the total damping rate and spectral linewidth κ = κint + κext is much larger than the shift in resonance frequency K due to an added photon: κ ≫ K. The circuit is thus far from the regime of superconducting qubits27. We will call it a Kerr oscillator and first attempt to describe its behavior following the classical equation for the steady-state amplitude of its oscillations a
Here Δ = ωr − ωd is the detuning of the driving frequency ωd to the resonance frequency ωr, and the strength of the drive \(\epsilon=\sqrt{{\kappa }_{{{{{{{{\rm{ext}}}}}}}}}{P}_{{{{{{{{\rm{in}}}}}}}}}/(2\hslash {\omega }_{{{{{{{{\rm{r}}}}}}}}})}\) is given by Pin the power of the drive impinging on the device.
The circuit is made by patterning a thin film of sputtered molybdenum–rhenium alloy on silicon, and subsequently fabricating the aluminum/aluminum-oxide tunnel junctions (see “Methods”). The device is thermally anchored to the ~20 milliKelvin stage of a dilution refrigerator, and the input (output) microwave wiring is attenuated (isolated) to lower its microwave mode temperature, such that the average number of photons nth excited by thermal energy is negligible. The transmission coefficient S21 = 1 − κexta/(2ϵ) is then measured using a vector network analyzer (VNA) for varying microwave power (see Fig. 2a).
a Measured transmission magnitude ∣S21∣ (dots) for different drive powers. While the shift in resonance frequency is expected from a classical analysis of the damped driven Kerr oscillator using Eq. (2), Min∣S21∣ is expected to remain constant (dashed line). b Measured Min∣S21∣ (dots) as a function of drive power. Eq. (2) yields Min∣S21∣ = ∣1 − κext/(κint + κext)∣, suggesting a damping rate which increases with power \({\kappa }_{{{{{{{{\rm{int}}}}}}}}}\to {\kappa }_{{{{{{{{\rm{int}}}}}}}}}^{{{{{{{{\rm{nl}}}}}}}}}(| a| )\) from \({\kappa }_{{{{{{{{\rm{int}}}}}}}}}^{{{{{{{{\rm{nl}}}}}}}}}=2\pi \times 193\) kHz to \({\kappa }_{{{{{{{{\rm{int}}}}}}}}}^{{{{{{{{\rm{nl}}}}}}}}}=2\pi \times 255\) kHz. Indeed, adding nonlinear damping \({\kappa }_{{{{{{{{\rm{int}}}}}}}}}^{{{{{{{{\rm{nl}}}}}}}}}(| a| )\) to Eq. (2) leads to theoretical predictions (solid lines in a) in good agreement with the data. At the three highlighted points, the expectation values of photon number ∣a∣2 (where the minimum of ∣S21∣ is achieved) are 1.1, 6.8 and 13.2.
Experimental data
We note an increase in both the detuning \({{{\Delta }}}_{\min }\) which minimizes transmission, and the value of the minimum Min∣S21∣. The classical prediction \({{{\Delta }}}_{\min }=K{\alpha }^{2}\) resulting from Eq. (2)—where α = 2ϵ/κ is the expected maximum amplitude—accurately matches the shift of the resonance. However, by plugging the maximum amplitude α into the expression for S21, we obtain a constant value for Min∣S21∣ = ∣1 − κext/κ∣ (dashed line in Fig. 2a), which disagrees with the measurement.
In a classical approach to the problem, a power-dependence of the internal damping rate therefore has to create this change. Since κext is determined by the geometry of the circuit, it should remain unchanged by the power of the drive. For κext/κ to vary and produce the observed change in Min∣S21∣ = ∣1 − κext/(κext + κint)∣, the internal damping should increase as the drive power increases. At the highest drive power for which data is displayed (Pin = − 124 dBm), the internal damping rises to 2π × 255 kHz. We note that this power lies below the bistability threshold (see Supplementary Notes 3 and 4F). Such nonlinear damping can be included in the model of Eq. (2) through \({\kappa }_{{{{{{{{\rm{int}}}}}}}}}\to {\kappa }_{{{{{{{{\rm{int}}}}}}}}}^{{{{{{{{\rm{nl}}}}}}}}}={\kappa }_{{{{{{{{\rm{int}}}}}}}}}+\gamma | a{| }^{2}\). We fit a solution of the resulting equation to the data (see Methods), observing good agreement (Fig. 2) for γ = 2π × 5.02 kHz.
While providing an accurate model for our observations, adding ad-hoc nonlinear damping offers no explanation as to the physical mechanism underlying the effect. Usually, the most prominent source of nonlinear damping in superconducting circuits is the saturation of two-level systems (TLSs) in the environment6,8,9. However, with increasing driving power, the saturation of TLSs will result in a decrease of the internal damping rate, while we observe the opposite. Here, we show that in our system this nonlinear damping behavior can be explained purely by dephasing triggered by the joint action of the intrinsic quantum noise and the Kerr anharmonicity of the oscillator.
Quantum mechanical simulation
We first show that approaching the problem quantum mechanically, without adding nonlinear damping, perfectly describes our measurements. The effect of quantum noise is included in the model through the steady-state Lindblad equation
where \(\hat{\rho }\) is the density matrix describing the steady-state of the oscillator. By numerically solving this equation for varying drive strengths and frequencies, the resulting amplitude \(\langle \hat{a}\rangle={{{{{{{\rm{Tr}}}}}}}}(\hat{a}\hat{\rho })\) is used to obtain S21. With only the circuit parameters as free variables, and notably a constant value for the internal damping, this model is fitted to all S21 traces (see “Methods” and Supplementary Note 2), revealing excellent agreement to the data (Fig. 3). Note that we recently became aware of an analytical solution to this Lindblad equation33,34, which may have simplified our approach.
The experimental results (dots) are compared here to a model with and without quantum noise (full and dashed line respectively). a Example of experimental and theoretical ∣S21∣ at the input power Pin = − 124 dBm. b As the power varies the model without quantum noise fails to capture the power-dependent depth of the response, which is accurately reproduced when quantum noise is introduced.
In Fig. 3, we compare this quantum model to the classical model: the solution to Eq. (2), which features neither nonlinear damping nor quantum noise. The only difference between the quantum model—which predicts the increase in Min∣S21∣—and that of Eq. (2)—which predicts a constant Min∣S21∣—lies in the value of the commutator \([\hat{a},\, {\hat{a}}^{{{{\dagger}}} }]\). In fact, by taking the trace Tr\((\hat{a}\,\cdot \,)\) of Eq. (3), and assuming the amplitude to be a complex number \(\hat{a}\to a\) such that [a, a*] = 0, we arrive at Eq. (2). Quantum noise can therefore lead to the entirety of the change in Min∣S21∣. Thermal noise could lead to a similar effect, but is expected to be negligible in our experiment (see Supplementary Note 7).
Beyond describing the data, this model can lead to a nonlinear damping equation for the expectation value \(\langle \hat{a}\rangle\). In the Supplementary Note 4, we derive an analytical formula that captures the behavior of the steady-state response that is in good agreement with the numerical simulations. We find that in a resonance scenario, whenever the Kerr effect and thermal noise have only a perturbative effect on the system, the corresponding steady-state expectation value for the amplitude \(\langle \hat{a}\rangle\) matches that of a classical non-linearly damped driven classical Kerr oscillator. That is, the steady-state amplitude is ruled by an equation resembling Eq. (2), but where the quantum and thermal noise lead to a nonlinear damping coefficient \(\kappa+\gamma | \langle \hat{a}\rangle {| }^{2}\) with
Here the familiar \(+\frac{1}{2}\) stems from quantum noise, which has the same effect as half a quantum of thermal noise. The fact that the nonlinear damping model and the quantum model are both able to describe our measurements is therefore not coincidental: while there is no microscopic process leading to nonlinear damping (i.e., loss of energy), there is apparent nonlinear damping in the equation for \(\langle \hat{a}\rangle\) when accounting for the presence of quantum noise. Similar results were derived for the classical35 and quantum36 spectrum of undriven oscillators, and also in work studying the spectrum of a probe field in the presence of a strong pump field37. The difference here is that we are instead interested in the power dependence of the scattering parameter S21.
Quantum mechanical interpretation
We now provide an intuitive explanation as to why there is a decrease in the amplitude of oscillations \(\langle \hat{a}\rangle\)—leading to an increase in the minimum of \(| \langle {\hat{S}}_{21}\rangle |=| 1-{\kappa }_{{{{{{{{\rm{ext}}}}}}}}}\langle \hat{a}\rangle /(2\epsilon )|\)—when quantum noise is considered. Because of the Kerr nonlinearity, the uncertainty in the photon number operator \({\hat{a}}^{{{{\dagger}}} }\hat{a}\), translates to uncertainty in the resonance frequency of the oscillator \({\omega }_{{{{{{{{\rm{r}}}}}}}}}-K{\hat{a}}^{{{{\dagger}}} }\hat{a}/2\) (see Hamiltonian of Eq. (1)). This has two consequences. Effect A: the signal leaking out of the oscillator into the transmission line inherits the frequency fluctuations of the oscillator. Since we are measuring a single frequency component with our VNA, we will measure a signal of smaller amplitude. Effect B: the driving is less effective at exciting the oscillator because the resonance frequency of the oscillator is fluctuating and no driving frequency will lead to resonant driving. The average number of photons in the oscillator will decrease.
This interpretation can be more thoroughly explored in phase space, by making use of the Wigner distribution and Wigner current38,39,40,41. We introduce \(\hat{x}=(\hat{a}+{\hat{a}}^{{{{\dagger}}} })/\sqrt{2}\) and \(\hat{p}=-i(\hat{a}-{\hat{a}}^{{{{\dagger}}} })/\sqrt{2}\), such that the amplitude \(\langle \hat{a}\rangle\) is given by the center of mass of the distribution through \(\langle \hat{a}\rangle=\sqrt{2}\iint {{{{{{{\rm{d}}}}}}}}x{{{{{{{\rm{d}}}}}}}}p(x+ip)W\). The Wigner current \(\overrightarrow{J}\), governs the dynamics of the Wigner function W through the continuity equation \({\partial }_{t}W+\overrightarrow{\nabla }\overrightarrow{J}=0\). It provides an intuitive visualization of the flow of quasi-probability in phase space.
As a pedagogical starting point, we show in Fig. 4a the distribution and different contributions to the current for a coherent state of amplitude α. This state corresponds to the steady-state that would be reached in our resonantly driven system without Kerr nonlinearity. The damping tends to bring each point of the distribution back to the origin. The drive however, is sensitive to phase and acts in a single direction. These two currents are balanced by the quantum noise, which creates a diffusion of the quasi-probability.
Here phase space operators are defined by \(\hat{a}=\left(\hat{x}+i\hat{p}\right)/\sqrt{2}\), see Supplementary Note 5A for further details. a Wigner distribution of the steady-state in absence of Kerr nonlinearity (driven at ωr with Pin = − 124 dBm). The balance between quantum noise, damping and drive is shown by vectors corresponding to Wigner currents. b Growth of phase uncertainty of a coherent state under Kerr nonlinearity. The amplitude-dependent resonance frequency (Kerr effect) translates to a radius-dependent rotation around the origin. The center of mass of the distribution rotates at a frequency Kα2. In a frame rotating at that frequency, the effect of the Kerr nonlinearity is to increase the uncertainty in phase (this is the frame adopted in (c)). The larger the uncertainty in phase (the extreme case being a ring around the origin), the closer the center of mass of the distribution gets to the origin (i.e., \(| \langle \hat{a}\rangle | \to 0\)). This is the first contribution (effect A) to a reduced resonant amplitude’s magnitude \(| \langle \hat{a}\rangle |\). c Wigner distribution of the steady-state with Kerr nonlinearity (at minimum ∣S21∣ with Pin = − 124 dBm). The Kerr effect is eventually balanced by the damping, quantum noise and drive. Since the drive now opposes both damping and Kerr effect, it is less effective at opposing the damping and driving the state away from the origin (compared to (a)). This brings the distribution closer to the origin, and constitutes the second contribution (effect B) to a reduced resonant amplitude’s magnitude \(| \langle \hat{a}\rangle |\). The center of mass (\(\langle \hat{a}\rangle\)) (white dot) is compared to the classical steady-state (white cross). Since the Wigner current of the Kerr effect grows with the amplitude squared \(| \langle \hat{a}\rangle {| }^{2}\propto {\epsilon }^{2}\) and the drive and dissipation currents grow with ϵ and \(| \langle \hat{a}\rangle |\) respectively, the reduction in \(| \langle \hat{a}\rangle |\) does not linearly follow the driving strength ϵ (see Supplementary Note 5B).
In Fig. 4b, we look at how the Kerr effect deforms the same coherent state, with the damping, driving, and noise temporarily inactive. We see the consequence of the amplitude-dependent resonance frequency of a damped driven quantum Kerr oscillator. In phase space, the resonance frequency sets the rate at which a point rotates around the origin. And the amplitude is given by the distance to the origin. The resulting deformation of the coherent state does not bring any point in phase space closer to the origin (total energy, or photon number, remains constant). The center of mass, however, will move closer to the origin. To be convinced of the latter, one can imagine the extreme case of the Kerr effect deforming the coherent state into a ring circling the origin, so that center of mass would be the origin, and \(| \langle \hat{a}\rangle |=0\). This mechanism for reducing \(| \langle \hat{a}\rangle |\) corresponds to Effect A previously discussed.
In the steady-state of our experiment, simulated in Fig. 4c, the evolution of the Kerr effect is eventually balanced by the other currents. Due to the large spread of the state in phase, the diffusion induced by quantum noise is weaker, and the damping current further misaligned with the drive compared to Fig. 4a. Since the drive is not parallel to the combined currents of damping and noise, it is less effective at countering them, so less effective at driving the system. Or in other words, in addition to countering the damping, the drive also has to counter the evolution of the Kerr effect. As a consequence, the average photon-number tends to decrease, which is the second contribution to a lower amplitude (Effect B). In the Supplementary Information (Supplementary Note 5B), we elaborate on why this decrease in amplitude is nonlinear with driving power.
Using a Gaussian state approximation (see Supplementary Note 4), we are able to weigh the influence of Effect A and Effect B in reducing the value of the resonant amplitude \(\langle \hat{a}\rangle\). We rely on an analytical comparison of the corresponding amplitude’s magnitude \(| \langle \hat{a}\rangle |\) and photon number \(\langle {\hat{a}}^{{{{\dagger}}} }\hat{a}\rangle\), and the fact that Effect A does not affect the photon number, whereas Effect B reduces the amplitude by reducing the photon number from its expected value for a coherent state \(\sqrt{\langle {\hat{a}}^{{{{\dagger}}} }\hat{a}\rangle }=| \langle \hat{a}\rangle |\). With respect to a coherent state of amplitude α, the reduction in \(\sqrt{\langle {\hat{a}}^{{{{\dagger}}} }\hat{a}\rangle }\) corresponds to half the reduction in \(| \langle \hat{a}\rangle |\) in our system (without thermal noise). This means that a reduction in photon number is responsible for only half of the observed effect, indicating that half of the increase in \({{{{{{{\rm{Min}}}}}}}}| {S}_{21}|\) can be attributed to Effect A, and half to Effect B. The same conclusions can be drawn with thermal noise (assuming nth ≪ α2).
While we have focused on the case nth ≪ α2, where the damping seems to increase with the amplitude of oscillations, the opposite regime nth ≫ α2 has already been explored experimentally42,43 and bears some common features with this work. When thermal fluctuations dominate, the state of the oscillator is well described as a statistical mixture of oscillatory amplitudes, each shifting the resonance frequency by a different amount given by the Duffing nonlinearity. This results in a broadening of the resonance line-shape when the oscillator is probed, which has been phenomenologically interpreted as an increase in damping, for example in carbon nanotubes42. This picture even extends to the case nth ≪ α2 where a residual broadening persists due to quantum heating of the oscillator by the driving field44.
Finally, we note that for all driving strengths featured in our measurements, quadrature squeezing occurs along an axis \(u=\cos (\theta )x+\sin (\theta )p\), rotated by an angle θ with respect the the x-axis. At the highest driving power (Figs. 3 and 4), the most highly squeezed quadrature is characterized by θ ≃ − 0.11π, where the uncertainty Δu is 83% of Δx for a coherent state.
Discussion
In conclusion, we have shown how the combination of Kerr nonlinearity and noise, and in particular quantum noise, leads to a dephasing that can manifest in the same way as nonlinear damping. Crucially, our findings are not limited to the case of superconducting resonators. Indeed, preliminary calculations based on our analytical model indicate that this effect has the correct order of magnitude to play a role in the nonlinear damping observed in NEMS systems14, however, driven by thermal rather than quantum noise. We are therefore confident that this phenomenon can play a valuable role in identifying the nature of nonlinear damping effects in a broader class of systems, such as NEMS or other Josephson circuits, which will be critical to their use in emerging technologies ranging from carbon nanotube sensors to superconducting quantum computing.
Methods
Device fabrication
The device shown in Fig. 1 is fabricated in two steps45. First, we fabricate the input/output waveguide structures, meandering inductor and capacitor. On a chip of high-resistivity silicon, cleaned in solutions of RCA-1, Piranha, and buffered hydrofluoric acid (BHF), we sputter 60 nm of molybdenum–rhenium (MoRe). A three layer mask (S1813/W(tungsten)/PMMA-950) is then patterned using electron-beam lithography, and is used in etching the MoRe by SF6/He plasma. The mask is finally stripped using PRS 3000.
Secondly, we fabricate the Josephson junctions using the Dolan bridge technique46. We first pattern a methyl-methacrylate (MMA)/polymethyl-methacrylate (PMMA) resist stack with e-beam lithography. After development of the resist, and to ensure a good contact between the aluminum of the junctions and the MoRe, we clean the sample with an oxygen plasma and BHF. Evaporation of two aluminum layers (30 nm and then 50 nm thick) under two angles (±11 degrees), interposed by an oxidization of the first aluminum layer, forms the junctions. Removal of the resist mask in N-methyl-2-pyrrolidone (NMP) at 80 degrees Celsius completes the sample fabrication.
Data analysis and fitting
Even at lowest driving power, the response of the device does not perfectly fit to a Lorentzian curve, indicating the presence of additional resonances in the measurement chain which could not be calibrated out experimentally. To eliminate these, as well as the change in phase length of the cabling with frequency, we subtract (divide) an affine function of frequency to the measured phase (amplitude).
The transformation between measured response S21,meas and fitted response S21,fit is thus given by
where A, B, C, and D are determined through a fit of a low-power response, where the nonlinearity does not come into play, and the response of the device alone S21,fit(ω) is assumed to be
We then reduce the amount of noise as well as the superfluous number of frequency points in the data-set by replacing blocks of 10 successive frequency data-points by their average. The reduction in number of data-points also facilitates the fitting. We were able to numerically compute S21 over the 500 frequency points of the data-set in a minimization routine. For each driving power of the data-set, the Python library QuTiP47,48 was used to solve the Lindblad equation of Eq. (3). For each power, the absolute difference between the 500 (complex) numerical and experimental points constitute a first contribution to the minimized cost function. The difference in the minimum of ∣S21∣, and the frequency at which ∣S21∣ is minimized, are also added to the cost-function each with a weight of 200 points. The function is minimized using a modified Powell algorithm49,50, with five free parameters: ωr, κint, κext, K, and the attenuation that the signal outputted at the VNA experiences before reaching the device. The attenuation is found to be 118.3 dB, consistent with the physical attenuation installed at room temperature and at the different stages of the dilution refrigerator. The device parameters converge to ωr = 2π × 5.172 GHz, κint = 2π × 186 kHz, κext = 2π × 2.12 MHz, K = 2π × 80 kHz.
Data availability
The data used in this study is available in a Zenodo database with the DOI identifier https://doi.org/10.5281/zenodo.4565179.
Code availability
The code used to analyze the data and generate all figures is available in a Zenodo database with the DOI identifier https://doi.org/10.5281/zenodo.4565179.
References
Van der Pol, B. Lxxxviii. On “relaxation-oscillations". Philos. Mag. 2, 978 (1926).
Cartwbight, M. Balthazar van der pol. J. London Math. Soc. 1, 367 (1960).
Taylan, M. The effect of nonlinear damping and restoring in ship rolling. Ocean Eng. 27, 921 (2000).
FitzHugh, R. Impulses and physiological states in theoretical models of nerve membrane. Biophys. J. 1, 445 (1961).
Barsukov, I. et al. Giant nonlinear damping in nanoscale ferromagnets. Sci. Adv. 5, eaav6943 (2019).
Gao, J., Zmuidzinas, J., Mazin, B. A., LeDuc, H. G. & Day, P. K. Noise properties of superconducting coplanar waveguide microwave resonators. Appl. Phys. Lett. 90, 102507 (2007).
Castellanos-Beltran, M. & Lehnert, K. Widely tunable parametric amplifier based on a superconducting quantum interference device array resonator. Appl. Phys. Lett. 91, 083509 (2007).
O’Connell, A. D. et al. Microwave dielectric loss at single photon energies and millikelvin temperatures. Appl. Phys. Lett. 92, 112903 (2008).
Gao, J. et al. Experimental evidence for a surface distribution of two-level systems in superconducting lithographed microwave resonators. Appl. Phys. Lett. 92, 152505 (2008).
Buks, E. & Yurke, B. Mass detection with a nonlinear nanomechanical resonator. Phys. Rev. E 74, 046619 (2006).
Zaitsev, S., Shtempluck, O., Buks, E. & Gottlieb, O. Nonlinear damping in a micromechanical oscillator. Nonlinear Dyn. 67, 859 (2012).
Imboden, M., Williams, O. A. & Mohanty, P. Observation of nonlinear dissipation in piezoresistive diamond nanomechanical resonators by heterodyne down-mixing. Nano Lett. 13, 4014 (2013).
Imboden, M. & Mohanty, P. Dissipation in nanoelectromechanical systems. Physics Reports 534, 89 (2014).
Eichler, A. et al. Nonlinear damping in mechanical resonators made from carbon nanotubes and graphene. Nat. Nanotechnol. 6, 339 (2011).
Singh, V., Shevchuk, O., Blanter, Y. M. & Steele, G. A. Negative nonlinear damping of a multilayer graphene mechanical resonator. Phys. Rev. B 93, 245407 (2016).
Yanai, S. et al. Mechanical dissipation in more superconducting metal drums. Appl. Phys. Lett. 110, 083103 (2017).
Atalaya, J., Kenny, T. W., Roukes, M. & Dykman, M. Nonlinear damping and dephasing in nanomechanical systems. Phys. Rev. B 94, 195440 (2016).
Shoshani, O., Shaw, S. W. & Dykman, M. I. Anomalous decay of nanomechanical modes going through nonlinear resonance. Sci. Rep. 7, 18091 (2017).
Güttinger, J. et al. Energy-dependent path of dissipation in nanomechanical resonators. Nat. Nanotechnol. 12, 631 (2017).
Dong, X., Dykman, M. I. & Chan, H. B. Strong negative nonlinear friction from induced two-phonon processes in vibrational systems. Nat. Commun. 9, 3241 (2018).
Chaste, J. et al. A nanomechanical mass sensor with yoctogram resolution. Nat. Nanotechnol. 7, 301 (2012).
Hanay, M. S. et al. Single-protein nanomechanical mass spectrometry in real time. Nat. Nanotechnol. 7, 602 (2012).
Vijay, R., Slichter, D. & Siddiqi, I. Observation of quantum jumps in a superconducting artificial atom. Phys. Rev. Lett. 106, 110502 (2011).
Aumentado, J. Superconducting parametric amplifiers: the state of the art in josephson parametric amplifiers. IEEE Microw. Mag. 21, 45 (2020).
Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505 (2019).
Vool, U. & Devoret, M. Introduction to quantum electromagnetic circuits. Int. J. Circuit Theory Appl. 45, 897 (2017).
Blais, A., Grimsmo, A. L., Girvin, S. & Wallraff, A. Circuit quantum electrodynamics. Rev. Mod. Phys. 93, 25005 (2021).
Beltran, M. A. C. Development of a Josephson Parametric Amplifier for the Preparation and Detection of Nonclassical States of Microwave Fields. Ph.D. thesis, University of Colorado Boulder (2010).
Degenfeld-Schonburg, P., Navarrete-Benlloch, C. & Hartmann, M. J. Self-consistent projection operator theory in nonlinear quantum optical systems: a case study on degenerate optical parametric oscillators. Phys. Rev. A 91, 053850 (2015).
Koch, J. et al. Charge-insensitive qubit design derived from the cooper pair box. Phys. Rev. A 76, 042319 (2007).
Gely, M. F. & Steele, G. A. Qucat: quantum circuit analyzer tool in python. New J. Phys. 22, 013025 (2020).
Wang, C. et al. Surface participation and dielectric loss in superconducting qubits. Appl. Phys. Lett. 107, 162601 (2015).
Drummond, P. & Walls, D. Quantum theory of optical bistability. I. Nonlinear polarisability model. J. Phys. Math. Gen. 13, 725 (1980).
Kheruntsyan, K. Wigner function for a driven anharmonic oscillator. J. Opt. B: Quantum Semiclass. Opt. 1, 225 (1999).
Dykman, M. I. & Krivoglaz, M. A. Classical theory of nonlinear oscillators interacting with a medium. Phys. Status Solidi B 48, 497 (1971).
Dykman, M. & Krivoglaz, M. Quantum theory of nonlinear oscillators interacting with a medium. Zh. Ehks. Teor. Fiz. 64, 993 (1973).
Dykman, M. I. in Fluctuating Nonlinear Oscillators: From nanomechanics to quantum superconducting circuits (ed. Dykman, M. I.) 165–197 (Oxford University Press, 2012).
Isar, A., Sandulescu, A. & Scheid, W. Phase space representation for open quantum systems within the lindblad theory. Int. J. Mod. Phys. B 10, 2767 (1996).
Stobińska, M., Milburn, G. & Wódkiewicz, K. Wigner function evolution of quantum states in the presence of self-kerr interaction. Phys. Rev. A 78, 013810 (2008).
Oliva, M. & Steuernagel, O. Quantum kerr oscillators’ evolution in phase space: Wigner current, symmetries, shear suppression, and special states. Phys. Rev. A 99, 032104 (2019).
Braasch Jr, W. F., Friedman, O. D., Rimberg, A. J. & Blencowe, M. P. Wigner current for open quantum systems. Phys. Rev. A 100, 012124 (2019).
Eichler, A., Moser, J., Dykman, M. & Bachtold, A. Symmetry breaking in a mechanical resonator made from a carbon nanotube. Nat. Commun. 4, 2843 (2013).
Maillet, O. et al. Nonlinear frequency transduction of nanomechanical brownian motion. Phys. Rev. B 96, 165434 (2017).
Dykman, M. I., Marthaler, M. & Peano, V. Quantum heating of a parametrically modulated oscillator: spectral signatures. Phys. Rev. A 83, 052115 (2011).
Yanai, S. & Steele, G. A. Observation of enhanced coherence in Josephson squid cavities using a hybrid fabrication approach. Preprint at https://arxiv.org/abs/1911.07119 (2019).
Dolan, G. Offset masks for lift-off photoprocessing. Appl. Phys. Lett. 31, 337 (1977).
Johansson, J. R., Nation, P. D. & Nori, F. Qutip: an open-source python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 183, 1760 (2012).
Johansson, J., Nation, P. & Nori, F. Qutip 2: a python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 184, 1234 (2013).
Virtanen, P. et al. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat. Methods 17, 261 (2020).
Powell, M. J. An efficient method for finding the minimum of a function of several variables without calculating derivatives. Comput. J. 7, 155 (1964).
Acknowledgements
We thank M. Kounalakis for discussions. This work was supported by the European Union’s Horizon 2020 research and innovation program under grant agreements 681476—QOM3D and 828826—Quromorphic, and by the research program of the Foundation for Fundamental Research on Matter (FOM), which was part of the Dutch Research Council (NWO).
Author information
Authors and Affiliations
Contributions
S.Y. performed the design and fabrication of the device, the measurements, and the initial data-analysis. D.B. and M.F.G. analyzed the data in the context of a classical nonlinear model. M.F.G. and R.v.d.S. analyzed the data using a quantum model, including fitting and the phase space interpretation, with A.S.M. carrying out the theoretical proof that the quantum model leads to the nonlinear damping equation. M.F.G. wrote the manuscript with contributions from all authors. G.A.S. supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Mark Dykman, Fabio Pistolesi, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gely, M.F., Sanz Mora, A., Yanai, S. et al. Apparent nonlinear damping triggered by quantum fluctuations. Nat Commun 14, 7566 (2023). https://doi.org/10.1038/s41467-023-43128-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-023-43128-y
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.