Abstract
Understanding the interplay between the inherent disorder and the correlated fluctuating-spin ground state is a key element in the search for quantum spin liquids. H3LiIr2O6 is considered to be a spin liquid that is proximate to the Kitaev-limit quantum spin liquid. Its ground state shows no magnetic order or spin freezing as expected for the spin liquid state. However, hydrogen zero-point motion and stacking faults are known to be present. The resulting bond disorder has been invoked to explain the existence of unexpected low-energy spin excitations, although data interpretation remains challenging. Here, we use resonant X-ray spectroscopies to map the collective excitations in H3LiIr2O6 and characterize its magnetic state. In the low-temperature correlated state, we reveal a broad bandwidth of magnetic excitations. The central energy and the high-energy tail of the continuum are consistent with expectations for dominant ferromagnetic Kitaev interactions between dynamically fluctuating spins. Furthermore, the absence of a momentum dependence to these excitations are consistent with disorder-induced broken translational invariance. Our low-energy data and the energy and width of the crystal field excitations support an interpretation of H3LiIr2O6 as a disordered topological spin liquid in close proximity to bond-disordered versions of the Kitaev quantum spin liquid.
Similar content being viewed by others
Introduction
Quantum spin liquids (QSLs) encompass a rich family of phases of matter with dynamically fluctuating and long-range entangled spins at zero temperature1,2. One particularly important QSL realization is the Kitaev model (KQSL). This exactly soluble model consists of highly-frustrated bond directional Ising-like interactions between spin-1/2 moments on the two-dimensional honeycomb lattice and can host topologically protected fractionalized excitations3. Material realizations of this model have been proposed in strong spin-orbit coupled 4d/5d transition metal (TM) compounds with edge-sharing TML6 (L = O, Cl) octahedra in a honeycomb lattice4. In this case, the Heisenberg, J, and symmetric off-diagonal, Γ, exchange terms between Jeff = 1/2 pseudospins are predicted to be suppressed in favor of finite anisotropic exchange, K5. However, the most heavily studied candidate Kitaev materials, α-Li2IrO3, Na2IrO36,7,8, and α-RuCl39,10, all magnetically order due to the existence of additional exchange interactions of comparable magnitude to ∣K∣, because of non-cubic distortions of the TML6 octahedra, and/or 4d/5d orbital extent11,12. Nonetheless, measurements of the excitation spectrum in these compounds have revealed high-energy magnetic continuum consistent with dominant Kitaev nearest-neighbor bond-directional interactions10,13,14,15,16.
H3LiIr2O6 is the most salient example of an emerging generation of Kitaev compounds. It is synthesized from the parent compound α-Li2IrO3 through the replacement of inter-honeycomb layer Li with H17. This leads to a reduction of inter-LiIr2O6 layer coordination from octahedral to linear and a consequent modification of the intra-layer Ir–O–Ir bond angles and Ir–Ir bond distance. As a result, superexchange pathways are modified with respect to those of α-Li2IrO3 and a different magnetic state is expected in H3LiIr2O617,18. Temperature-dependent measurements of the magnetic susceptibility in H3LiIr2O6 show no evidence for long-range magnetic order down to 5 mK, despite a Curie–Weiss temperature θCW ≈ −105 K, as confirmed by the NMR Knight shift19,20. The NMR relaxation rate rules out a spin glass in favor of dynamically fluctuating spins19. Raman spectroscopy21 finds a continuum of magnetic excitations similar to that in the proximate Kitaev magnet α-RuCl322,23. However, the observation of a non-zero NMR relaxation rate and T−1/2 C/T divergence indicate E = 0 spin excitations that are not consistent with expectations for a pure Kitaev QSL state19. Thus, the nature of the unconventional magnetic ground state and the associated collective excitations in H3LiIr2O6 remains unknown.
Achieving a microscopic description of the magnetic state in H3LiIr2O6 is complicated by disorder. Quasi-static H zero point motion20,24,25, present even in crystallographic pristine samples, can lead to local variations of the intra-layer exchange interactions26,27. Furthermore, the heavily faulted stacking structure due to the linear inter-layer O–H–O coordination might also result on random intra-layer magnetic exchanges17,18. It remains to be understood how the random distribution of magnetic exchanges modifies the magnetic Hamiltonian to render a state with no long-range magnetic order or frozen moments but with low-temperature low-energy spin excitations. One possibility is that bond-disorder brings H3LiIr2O6 away from the QSL regime26,27 into a state where the formation of a long-range magnetically order phase is inhibited but with short-range correlations remnant of ordered states in α-Li2IrO3 and Na2IrO313,15. A second possibility to account for the absence of frozen moments is that bond-disorder suppresses Kitaev exchange in favor of a random distribution of nearest neighbor J, promoting the formation of a random valence bond quantum paramagnet28. In these two scenarios, the low-energy excitations observed in H3LiIr2O6 could be explained by the presence of fluctuating unpaired spins that give rise to the C/T scaling29,30. Within a third alternative, the thermodynamic observations in H3LiIr2O6 can be explained by bond-disordered extensions of the pure (J = 0, Γ = 0) and extended Kitaev QSL (BD-KQSL). In this case, bond-disorder acts to pin a random distribution of flux degrees of freedom in the underlying KQSL and leads to the divergent low-energy density of states and associated T−1/2 low-temperature specific heat19,31,32,33,34,35,36. We remark that the disordered Kitaev state is proximal to the pristine KQSL, but it represents a disordered phase of topological matter. All of these models are distinct states that account for the absence of frozen moments and can explain the thermodynamic observations in H3LiIr2O6. However, they can be distinguished by their high-energy collective excitations that encode the dynamical spin-spin correlations, S(q, ω). For example, the proximity to magnetically ordered phases might lead to correlations on longer length scales than the nearest-neighbor-only of the BD-KQSL13,15,37,38. Similarly, singlet-triplet excitations at the scale of J in a random valence bond state lead to a characteristic momentum dependence of S(q, ω), with a maximum of intensity at the zone boundary and lack of intensity at the zone center39,40, distinct from the BD-KQSL32,41. A momentum-resolved spectroscopic measurement of the spin excitation spectrum is essential to distinguish between these two opposing views, discern the role of disorder, and reveal the magnetic ground state of H3LiIr2O6.
The small volume of available H3LiIr2O6 single crystals (see the Methods subsections “The sample growth and characterization” and “Resonant inelastic X-ray scattering (RIXS)”), high neutron absorption cross-section of Ir, and the incoherent scattering from H inhibits inelastic neutron scattering (INS) from accessing the magnetic spectrum in this compound10,42,43,44. Although RIXS remains limited by state-of-the-art energy resolution comparable to the theoretically predicted magnitude of K, high-resolution RIXS experiments at the Ir L3 edge have emerged as an alternative to access S(q, ω) in 5d Mott insulators13,14,16,45.
Here, we use RIXS to reveal that the low-energy collective magnetic excitations of H3LiIr2O6 are characterized by a broad momentum-independent continuum. The temperature evolution of these excitations indicates that they are distinct from the paramagnetic state, but there is no evidence for short-range correlations of a remnant-ordered state. While the low temperature collective magnetic excitations of H3LiIr2O6 are suggestive of calculations of S(q, ω) for KQSL, an exhaustive mapping of reciprocal space reveals a lack of a momentum dependence suggesting that H3LiIr2O6 is best understood as a proximal to a bond-disordered KQSL.
Results
Low-energy collective excitations
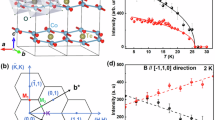
In Fig. 1a we show the RIXS intensity of single crystals of H3LiIr2O6 at the Ir L3 (Ei = 11.215 keV) with state-of-the-art energy resolution (full width half maximum FWHM = 20 meV) at high symmetry points of the pseudo-honeycomb lattice at T = 10 K following the experimental geometry sketched in Fig. 1b. Our measurement temperature is one order of magnitude smaller than θCW and below the ordering temperature of pristine α-Li2IrO38. The RIXS scans reveal a broad, σ = 40 ± 5 meV bandwidth, inelastic signal centered around E = 25 ± 5 meV. This signal resonates at the Ir L3 edge, confirming that these excitations arise from a direct RIXS process and pointing to a magnetic origin16 (see Supplementary Information) and is well described by an overdamped harmonic oscillator (DHO) weighted by a Bose factor (\(1/(1-{e}^{-E/{k}_{B}T})\)) and convolved with a Gaussian resolution46. The tail of the DHO extends into a high-energy magnetic continuum spanning up to E = 170 meV. Given the absence of any sharp features over a bandwidth that is 8 times larger than the energy resolution of our measurement, we attribute this signal to a continuum of magnetic excitations. The inelastic spectrum is remarkably similar at all high symmetry points, being of equal or comparable intensity to the elastic line and without an evident dispersion or intensity modulation. The absence of a momentum dependence is contrary to expectations for a random distribution of singlets in a valence bond solid with dominant nearest neighbor correlations39,40 and disordered Heisenberg AFM models47 that predict a vanishing intensity at Γ points. In Fig. 1d we show the RIXS spectra at the ordering vectors for the three 120° domains of the incommensurate spiral order in α-Li2IrO3 qα = [0.16, − 0.5], [0.16, 0.5], [0.32, 0]13. The inelastic data across all momentum points and azimuthal angles (see Supplementary Information) can be fit to the same functional form as for the high symmetry points in Fig. 1a without any additional broadening or energy shift to the DHO, and without the need to account for the gapless acoustic magnon at qα observed in α-Li2IrO3 below TN = 15 K13.
a (left) RIXS spectra at T = 10 K at high symmetry points of the Brillouin zone (BZ) (circular markers). The magnetic continuum extends up to 150 meV as shown in the right panel (right; data are scaled by a factor of 5). Spectra have been shifted vertically for clarity. b Sketch of the scattering geometry. The hexagonal arrangement of blue spheres represents a honeycomb layer of Ir4+ ions within the monoclinic crystal structure of H3LiIr2O6. The incident (ki) and outgoing (kf) radiation (orange arrows) define the scattering plane (gray), with momentum transfer Q (silver arrow). Green arrows show the polarization of the X-ray electric field (π: in-plane; \(\sigma,{\sigma }^{{\prime} }\): out-of-plane for the incoming and outgoing X-ray beam, respectively). φ is the azimuthal angle defined by the crystallographic a-axis and the scattering plane. c Schematic of the extended hexagonal BZ highlighting relevant symmetry points and directions (dashed lines follow the color scheme of Fig. 3) explored in this study. L varies between 5.91 and 5.95 r.l.u. d RIXS intensity at the wavevectors of the 120° spiral order of α-Li2IrO3. Solid lines in (a) and (d) are fit to the data, including a Voigt profile for the elastic line (dotted black line) and a damped harmonic oscillator (gray shading) centered at E0 = 25 meV, red bar of width 10 meV reflects the statistical uncertainty in determining E = 0 meV. All data were taken at φ = 180°.
Temperature-dependent RIXS spectra
The temperature-dependent RIXS intensity at Γ [Fig. 2a] is suggestive of a state that is intrinsically different from the high-temperature paramagnet. At room temperature, we find overdamped excitations with no discernible momentum dependence, as expected for the paramagnetic state [Fig. 2c] and consistent with previous high-temperature RIXS measurements in Na2IrO3 and α-Li2IrO316. Although the RIXS spectra of H3LiIr2O6 are characterized by overdamped excitations at all temperatures, the detailed temperature dependence reveals that the excitations for T ≲ θCW ≈ 105 K are distinct from those in the paramagnetic state. The DHO amplitude (A), monotonically increases as the temperature is lowered [square markers; Fig. 2b]. We observe a softening of the center energy of the magnetic continuum from E = 38 ± 5 meV with σ = 45 ± 5 meV bandwidth at T = 300 K ≈ 3θCW to E = 25 ± 5 at T < θCW [circular markers; Fig. 2b]. Between θCW and T ≈ 200 K the DHO is centered at E = 30 ± 5 meV; this temperature range corresponds to a hump of 130 K centered at 200 K seen in magnetic susceptibility measurements19 signifying the onset of nearest neighbor correlations in H3LiIr2O648,49. Note that the relatively coarse energy resolution of our measurements means that we cannot distinguish if this intensity and energy shift arises from the transfer of intensity between different modes above and below θCW or to a mode softening. While a direct comparison between the RIXS and Raman spin-flip process is complex, the evolution of the RIXS intensity with temperature resembles that seen in Raman spectroscopy measurements of Kitaev magnets21,23,50,51.
a High-resolution RIXS spectra at Γ (Q = [0, 0, 5.7]) and azimuthal angle φ = 0°, as a function of temperature. Spectra have been shifted vertically for clarity. b Circular markers indicate the center position of the damped harmonic oscillator (DHO) component as extracted from a fit to the data. Square markers are the extracted amplitude of the DHO normalized to the value at T = 10 K. The blue solid line indicates the Curie–Weiss temperature, θCW, and the dashed black lines are guides to the eye. Black error bars are the systematic error in determining E = 0 meV. Red error bars are the statistical uncertainty of RIXS intensity. c T = 300 K RIXS intensity (circular markers) at three high symmetry points (Γ, black, K, red, M, blue). The solid line is a fit to the data including a Voigt profile for the elastic line (dotted black line) and a damped harmonic oscillator (shading).
Momentum-independent excitations
One possible explanation for the excitations we observe is that bond-disorder and stacking faults act to inhibit an underlying magnetically ordered phase in H3LiIr2O626,27. In this scenario, remnant dynamical correlations reflecting a disorder limited short-range order should be present and give rise to a characteristic momentum dependence of S(q, ω)52. Good points of comparison are momentum-resolved measurements of magnetic X-ray scattering in α-Li2IrO3 and Na2IrO3 above their magnetic transition temperatures. For both compounds, the diffuse magnetic scattering is characterized by an intensity modulation that peaks at their respective ordering vectors and depends on the projection of the incident X-ray polarization on spins thermally-fluctuating about an average orientation13,15. Similar information can be extracted by examining the magnetic RIXS response as a function of momentum and azimuthal angle φ as sketched in Fig. 1c, d. We extract the inelastic RIXS intensity by subtracting the elastic line contribution determined from a fit to a resolution limited Voigt profile. Figure 2a shows the momentum dependence of inelastic magnetic intensity along high symmetry directions covering multiple zone center (Γ) and zone boundary (M, K, Y, and X) points with H ≤ 0 and φ = 0. Equivalent points with H ≥ 0 and φ = 180° are shown in Fig. 2b. For both azimuthal configurations, the excitation spectra has comparable intensity at the zone center and zone boundary, it is non-dispersive, and devoid of sharp coherent modes. These data, together with Fig. 1, rule out any short-range spiral order correlations as seen in α-Li2IrO313 or short-range zig-zag correlations as present in Na2IrO3 that lead to strong modulation of the magnetic diffuse scattering at M, Y, and X14,15. We thus rule out a disorder limited correlations remnant of an ordered state52 and conclude that the spin excitations in H3LiIr2O6 are intrinsically different to that of the parent compound or Na2IrO3. In Fig. 3a–d we plot the dependence of the center energy of the DHO along four additional high symmetry directions covering the totality of the BZ for three different values of φ. The inelastic intensity integrated after subtraction of the elastic line in the energy range E ∈ [−30, 170] meV is shown in Fig. 3e–h. We observe no dispersion of the broad continuum centered at E = 25 ± 10 meV (experimental resolution FHWM = 28 meV). The slight intensity modulation in our momentum-dependent data does not follow any of the structural symmetries of H3LiIr2O6 and it is correlated variations in the elastic line intensity that are difficult to decouple given our experimental resolution (see Supplementary Information). As such, we assign it to an experimental artifact possibly related to self-absorption effects16. Our RIXS measurements covering many Brillouin zones, azimuthal angles, and the full energy bandwidth of magnetic excitations in H3LiIr2O6 reveals dynamical correlations that are isotropic and with a featureless momentum dependence of the integrated intensity.
a High-resolution elastic-background-subtracted RIXS intensity along high symmetry paths with H ≤ 0, φ = 0° and, b, H ≥ 0, φ = 180°. Overlaid circular markers indicate the center position of the continuum of magnetic excitations as extracted from a fit to the data. Error bars are the systematic error in determining E = 0 meV. The colorbar applies to both (a) and (b). c–f Center energy of the continuum of magnetic excitations across the Brillouin zone as extracted from a fit to the inelastic RIXS intensity to a damped harmonic oscillator. The dashed line at E = 25 meV is the average momentum position of the continuum. The energy resolution was relaxed to a FWHM = 28 meV as indicated by the solid gray lines. Error bars are the systematic error in determining E = 0 meV. g–j Integrated elastic-background-subtracted RIXS intensity in the range E ∈ [−50, 170] meV. The gray-shaded rectangle represents the variation of the elastic intensity. error bars are the statistical uncertainty of RIXS intensity. Circular markers (φ = 0°), triangular markers (φ = 180°), and square markers (φ = 90°) show the azimuthal dependence.
Our data demonstrates the existence of magnetic excitations at high energies (25 meV) in addition to the low-energy divergence observed in C/T measurements in H3LiIr2O6. The appearance of two energy scales is suggestive of calculations of S(q, ω) for pure, extended, and bond-disorder gapless KQSL. Within these models the energy dependence of S(q, ω) is characterized by an intense low-energy (E ≈ 0) peak at the energy of the fractionalized fermionic excitations that decays exponentially into a high-energy continuum (up to 6J)32,37,38,41. The momentum dependence shows broad isotropic excitations with an intensity modulation that depends on the sign of K. For an antiferromagnetic K the q dependence of the broad magnetic continuum at \(E=\left|K\right|\) exhibits a shift of spectral weight from Γ to the zone boundary, while for the ferromagnetic (FM) Kitaev case a maximum of intensity is expected at Γ37,38,41,52. Calculations of the RIXS response for the Honeycomb Kitaev model distinguish between spin conserving (SC) and spin non-conserving (SNC) excitations channels which correspond to dispersive fractionalized fermionic excitations and bound gauge flux excitations, respectively. Within our experimental configuration (π incident polarization; 2θ = 90° scattering angle) the intensity is dominated by polarization-switching SNC channels leading to a nearly featureless excitation spectrum that resembles that accessible by inelastic neutron scattering measurements53. However, the lack of a clear peak of intensity at Γ and of any momentum dependence across the BZ is suggestive of broken translation invariance due to bond-disorder52. Thus, we assign the origin of the broad collective excitations centered at E = 25 ± 5 meV and high-energy continuum extending up to E = 170 meV to the existence of dominant bond-dependent nearest-neighbor spin-spin correlations with a FM Kitaev exchange, \(\left|K\right|\approx 25\) meV in a bond-disorderd background. While a random distribution of exchange values due to disorder hinder the exact determination of \(K,\left|K\right|\approx 25\) meV, is comparable to that of α-Li2IrO3 and Na2IrO313,14,15,16,54, to that extracted from the maximum of the continuum intensity in Raman scattering measurements at around ω ≈ 40 mev = 1.5K (K ≈ 26 meV)21, and to that from first principles calculations26,27. We remark that the energy resolution of our RIXS experiment E = 20 meV integrates over low-energy modes and prevents us from resolving the E ≈ 0 divergence predicted in the density of states for BD-KQSL models32. Similarly, we cannot exclude additional finite but comparable to kBT = 0.87 meV J, Γ or any other exchange terms in the magnetic Hamiltonian of H3LiIr2O626. Moreover, the observed redistribution of RIXS intensity across the onset temperature for magnetic correlations in a Kitaev model provides further evidence for a low-temperature collective excitation spectrum that reflects Kitaev physics in H3LiIr2O6 [Fig. 2]. Our RIXS data points to H3LiIr2O6 hosting a unique disordered topological state in close proximity to the KQSL resulting from the interplay of K and bond-disorder32,52.
Local Ir electronic structure
We finally comment on the specific effects of H on the local Ir electronic structure. While determining the position of the H atoms is not directly accessible in an X-ray experiment, measurements of the crystal field energies and width provide information about any local disorder on IrO6 octahedra55. In Fig. 4a we show the RIXS response of H3LiIr2O6 near the Ir L3 as a function of incident energy, Ei, and energy transfer, E. We focus our discussion on the 0.25 < E < 1.2 eV range corresponding to the intra-t2g excitations56. In this range, the RIXS spectrum is characterized by a set of four Gaussian peaks [Fig. 4b] (see Supplementary Information) of FWHMA-D = 75−120 meV, larger but comparable to that observed for α-Li2IrO356. We model the crystal field excitations in H3LiIr2O6 [Fig. 4b], by calculating the RIXS intensity from the exact diagonalization of a model Hamiltonian for an Ir4+ including nearest-neighbor hopping and local disorder55,57. Disorder is encoded by sampling the hopping parameters and the magnitude of the trigonal crystal field, δ, from a normal distribution. The data is well described by including an O mediating hopping with mean value tO = 440 meV. This value is well within the range of values extracted from density functional theory for an ideal C2/m structure26, and is 10% larger than that needed to account for the RIXS spectra of α-Li2IrO3 (see the Methods subsection “Exact diagonalization calculations”). The larger value of tO is suggestive of an increased Ir t2g-O 2p hybridization as a result of the introduction of H. This is substantiated by a qualitative comparison of the O-K edge XAS data between H3LiIr2O6 and α-Li2IrO3 (see the Methods subsection “O-K edge XAS”). The intensity and width of the α-peak at E = 529 eV reflects the degree of hybridization between O 2p and t2g states58, which is 1.16 times more intense and 1.4 times broader in H3LiIr2O6 than in α-Li2IrO3. Moreover, we find a comparable value of the mean δ between both compounds (δ = −48 meV in H3LiIr2O6 and δ = −50 meV in α-Li2IrO3), in agreement with the average <2% change in the Ir–O bond angles and <4% in Ir–Ir bond distance with respect to that of α-Li2IrO318. However, we find that a large distribution of δ values, as encoded by the standard deviation σδ = 20 meV, is needed to account for the broader crystal field excitations in H3LiIr2O6 and the relative intensity ratio between peaks A−B and C−D. This is consistent with the existence of slow H-ion motion at low temperature, which can generate variations of the local IrO6 environment20,24. Thus, our Ir crystal field RIXS data, O XAS measurements and analysis is consistent with the existence of local bond-disorder on IrO6 octahedra and points to an enhanced Ir–O hybridization as the leading mechanism favoring a dominant Kitaev-like exchange in H3LiIr2O6.
a RIXS intensity as a function of the incident X-ray energy near the Ir L3 edge. The intense inelastic feature centered at E ≈ 3.8 eV is from transitions between occupied t2g states and empty eg orbitals in a Ir4+ ion (see Supplementary Information). White dashed lines in (a) delineate the energy range shown in (b). b Intra-t2g RIXS excitations at Ei = 11.215 keV (circular markers) compared to the calculated RIXS intensity from exact diagonalization calculations. Blue solid line is a fit to the data including a Voigt peak, a DHO, four Gaussian peaks and an arctan step to account for the background (A–D). c O K-edge X-ray absorption spectroscopy data (μ(E)) and fit to the data in H3LiIr2O6 (circular markers; blue line) and α-Li2IrO3 (square markers; orange line). α and β highlight the two main features in the XAS data as discussed in the main text. Solid gray lines show the two Lorentzian and two Gaussian profiles included in the fit. Dashed line represents the arc tangent step to account for the electron hole continuum.
Discussion
In summary, the spin excitation spectrum of H3LiIr2O6 is characterized by broad isotropic excitations of comparable intensity to the elastic line without a momentum dependence of the integrated intensity. Altogether, our data support an interpretation of the magnetic excitation spectrum of H3LiIr2O6 as emerging from the interplay of disorder and dominant Kitaev-like nearest-neighbor bond-directional interactions between dynamically fluctuating spins. Of the theoretical proposals that have been put forward to explain the thermodynamic properties of H3LiIr2O6, bond-disorder KQSL models are the closest to describing our observations32,52. However, the lack of a clear intensity modulation across the BZ indicate that these excitations are of different nature to that of a pure KQSL despite being a magnetic state dominated by quantum fluctuations.
Methods
Sample growth and characterization
Precursor single crystals of α-Li2IrO3 were grown as described elsewhere59. 40 × 40 μm single crystals of H3LiIr2O6 were grown via a topotactic exchange by placing α-Li2IrO3 in an acidic environment for several hours18. Sample characterization including powder X-ray diffraction, specific heat, and magnetization measurements can be found in ref. 17.
Resonant inelastic X-ray scattering
RIXS measurements were performed at the 27 ID beamline of the Advance Photon Source using a horizontal scattering geometry with π-incident X-ray polarization. The low-energy RIXS spectra summing over π-\({\sigma }^{{\prime} }\) and π-\({\pi }^{{\prime} }\) polarization channels were collected with a fixed 2-m radius spherically diced Si(844) analyzer positioned to access a [−150, 200] meV energy window around the elastic line. All measurements utilized a high-heat-load diamond (1110) monochromator and an additional Si(844) upstream monochromator was used for the high-resolution measurements in order to obtain an overall energy transfer resolution of 20 meV. To minimize Thomson scattering the 2θ angle was fixed at 90°. This led to a small variation of the L values between 5.7 and 6 r.l.u. An iris analyzer mask was used to achieve a spectrometer momentum resolution of ±0.048 Å−1. RIXS data was collected using a photon-counting CdTe 2D detector tilted along the energy dispersion direction to provide an effective pixel size of 25 μm × 55 μm. Data was converted from pixels to energy by applying a calibration factor of epp = 4.5 meV/pixel. The uncertainty in determining E = 0 meV using incoherent scattering from an elastic line standard corresponds to ± 1 pixel. Each spectra shown are the average of 2–3 scans.
Exact diagonalization calculations
Crystal field excitations in H3LiIr2O6 and α-Li2IrO3 were modeled by considering a Hamiltonian including spin-orbit coupling (λ = 540 meV) in the large cubic crystal field limit H = HU + HCF + Ht including on-site Coulomb interactions (HU), trigonal distortions HCF and nearest-neighbors hopping Ht. Ht follows the form described in ref. 57 and ref. 55. The leading hopping integrals are t∣∣, that parameterizes hopping between parallel orbitals and tO that encodes hopping paths mediated by O 2p orbitals. These two hopping integrals were sampled from a normal distribution with standard deviations \({\sigma }_{{t}_{0}}=50\) meV, \({\sigma }_{{t}_{| | }}=10\) meV. For the magnitude of the trigonal fields, δ, the width of the normal distribution was allowed to vary between H3LiIr2O6,σδ = 20 meV, and α-Li2IrO3, σδ = 5 meV55. Our calculations explore the phase diagram given by the mean values (δ, tO, t∣∣) to find the best agreement with the data. For H3LiIr2O6 we found δ = −47 meV, tO = 440 meV, and t∣∣ = −50 meV. For α-Li2IrO3 this was δ = −50 meV, tO = 400 meV, and t∣∣ = −30 meV (see Supplementary Information).
O-K edge XAS
Low-temperature O-K edge XAS measurements were performed at the beamline 8 of the ALS in both partial fluorescence yield and total electron yield. We fit the data to a combination of two Lorentzians to account for the α peak, two Gaussians for the β peak and an arctan step.
Data availability
The RIXS data generated in this study have been deposited in the Zenodo database under accession code 816152260.
Code availability
The code used in this study is available from the authors upon reasonable request.
References
Savary, L. & Balents, L. Quantum spin liquids: a review. Rep. Prog. Phys. 80, 016502 (2017).
Broholm, C. et al. Quantum spin liquids. Science 367, eaay0668 (2020).
Kitaev, A. Anyons in an exactly solved model and beyond. Ann. Phys. 321, 2–111 (2006).
Jackeli, G. & Khaliullin, G. Mott insulators in the strong spin-orbit coupling limit: from Heisenberg to a quantum compass and Kitaev models. Phys. Rev. Lett. 102, 017205 (2009).
Rau, J. G., Lee, EricKin-Ho & Kee, Hae-Young Generic spin model for the honeycomb iridates beyond the Kitaev limit. Phys. Rev. Lett. 112, 077204 (2014).
Kobayashi, H., Tabuchi, M., Shikano, M., Kageyama, H. & Kanno, R. Structure, and magnetic and electrochemical properties of layered oxides, Li2IrO3. J. Mater. Chem. 13, 957–962 (2003).
Singh, Y. & Gegenwart, P. Antiferromagnetic Mott insulating state in single crystals of the honeycomb lattice material Na2IrO3. Phys. Rev. B 82, 064412 (2010).
Singh, Y. et al. Relevance of the Heisenberg-Kitaev model for the honeycomb lattice iridates A2IrO3. Phys. Rev. Lett. 108, 127203 (2012).
Plumb, K. W. et al. α−RuCl3: a spin-orbit assisted Mott insulator on a honeycomb lattice. Phys. Rev. B 90, 041112 (2014).
Banerjee, A. et al. Proximate Kitaev quantum spin liquid behaviour in a honeycomb magnet. Nat. Mater. 15, 733–740 (2016).
Rau, J. G., Lee, EricKin-Ho & Kee, Hae-Young Spin-orbit physics giving rise to novel phases in correlated systems: iridates and related materials. Annu. Rev. Condens. Matter Phys. 7, 195–221 (2016).
Takagi, H., Takayama, T., Jackeli, G., Khaliullin, G. & Nagler, S. E. Concept and realization of Kitaev quantum spin liquids. Nat. Rev. Phys. 1, 264–280 (2019).
Chun, SaeHwan et al. Optical magnons with dominant bond-directional exchange interactions in the honeycomb lattice iridate α−Li2IrO3. Phys. Rev. B 103, L020410 (2021).
Kim, J. et al. Dynamic spin correlations in the honeycomb lattice Na2IrO3 measured by resonant inelastic X-ray scattering. Phys. Rev. X 10, 021034 (2020).
Hwan Chun, S. et al. Direct evidence for dominant bond-directional interactions in a honeycomb lattice iridate Na2IrO3. Nat. Phys. 11, 462–466 (2015).
Revelli, A. et al. Fingerprints of Kitaev physics in the magnetic excitations of honeycomb iridates. Phys. Rev. Res. 2, 043094 (2020).
Bahrami, F., Abramchuk, M., Lebedev, O. & Tafti, F. Metastable Kitaev magnets. Molecules 27, 871 (2022).
Bette, S. et al. Solution of the heavily stacking faulted crystal structure of the honeycomb iridate H3LiIr2O6. Dalton Trans. 46, 15216–15227 (2017).
Kitagawa, K. et al. A spin-orbital-entangled quantum liquid on a honeycomb lattice. Nature 554, 341–345 (2018).
Lee, C. et al. Coexistence of random singlets and disordered Kitaev spin liquid in H3LiIr2O6. Phys. Rev. B 107, 014424 (2023).
Pei, S. et al. Magnetic Raman continuum in single-crystalline H3LiIr2O6. Phys. Rev. B 101, 201101 (2020).
Sandilands, L. J., Tian, Y., Plumb, K. W., Kim, Young-June & Burch, K. S. Scattering continuum and possible fractionalized excitations in α−RuCl3. Phys. Rev. Lett. 114, 147201 (2015).
Nasu, J., Knolle, J., Kovrizhin, D. L., Motome, Y. & Moessner, R. Fermionic response from fractionalization in an insulating two-dimensional magnet. Nat. Phys. 12, 912–915 (2016).
Geirhos, K. et al. Quantum paraelectricity in the Kitaev quantum spin liquid candidates H3LiIr2O6 and D3LiIr2O6. Phys. Rev. B 101, 184410 (2020).
Wang, S., Zhang, L. & Wang, F. Possible quantum paraelectric state in Kitaev spin liquid candidate H3LiIr2O6. Sci. China Phys., Mech. Astron. 63, 117411 (2020).
Li, Y., Winter, S. M. & Valentí, R. Role of hydrogen in the spin-orbital-entangled quantum liquid candidate H3LiIr2O6. Phys. Rev. Lett. 121, 247202 (2018).
Yadav, R. et al. Strong effect of hydrogen order on magnetic Kitaev interactions in H3LiIr2O6. Phys. Rev. Lett. 121, 197203 (2018).
Yamaguchi, H. et al. Randomness-induced quantum spin liquid on honeycomb lattice. Sci. Rep. 7, 16144 (2017).
Bhatt, R. N. & Lee, P. A. Scaling studies of highly disordered spin-\(\frac{1}{2}\) antiferromagnetic systems. Phys. Rev. Lett. 48, 344–347 (1982).
Kimchi, I., Sheckelton, J. P., McQueen, T. M. & Lee, P. A. Scaling and data collapse from local moments in frustrated disordered quantum spin systems. Nat. Commun. 9, 4367 (2018).
Slagle, K., Choi, W., Chern, Li. Ern & Kim, YongBaek Theory of a quantum spin liquid in the hydrogen-intercalated honeycomb iridate H3LiIr2O6. Phys. Rev. B 97, 115159 (2018).
Knolle, J., Moessner, R. & Perkins, N. B. Bond-disordered spin liquid and the honeycomb iridate H3LiIr2O6: abundant low-energy density of states from random Majorana hopping. Phys. Rev. Lett. 122, 047202 (2019).
Nasu, J. & Motome, Y. Thermodynamic and transport properties in disordered Kitaev models. Phys. Rev. B 102, 054437 (2020).
Kao, Wen-Han & Perkins, N. B. Disorder upon disorder: localization effects in the Kitaev spin liquid. Ann. Phys. 435, 168506 (2021).
Kao, Wen-Han, Knolle, J., Halász, G. áborB., Moessner, R. & Perkins, N. B. Vacancy-induced low-energy density of states in the Kitaev spin liquid. Phys. Rev. X 11, 011034 (2021).
Dantas, V. & Andrade, E. C. Disorder, low-energy excitations, and topology in the Kitaev spin liquid. Phys. Rev. Lett. 129, 037204 (2022).
Knolle, J., Kovrizhin, D.-L., Chalker, J.-T. & Moessner, R. Dynamics of a two-dimensional quantum spin liquid: signatures of emergent Majorana fermions and fluxes. Phys. Rev. Lett. 112, 207203 (2014).
Knolle, J., Kovrizhin, D. L., Chalker, J. T. & Moessner, R. Dynamics of fractionalization in quantum spin liquids. Phys. Rev. B 92, 115127 (2015).
Zhu, Z., Maksimov, P.-A., White, S. R. & Chernyshev, A.-L. Disorder-induced mimicry of a spin liquid in YbMgGaO4. Phys. Rev. Lett. 119, 157201 (2017).
Kimchi, I., Nahum, A. & Senthil, T. Valence bonds in random quantum magnets: theory and application to YbMgGaO4. Phys. Rev. X 8, 031028 (2018).
Knolle, J., Bhattacharjee, S. & Moessner, R. Dynamics of a quantum spin liquid beyond integrability: the Kitaev-Heisenberg- model in an augmented parton mean-field theory. Phys. Rev. B 97, 134432 (2018).
Mourigal, M. et al. Fractional spinon excitations in the quantum Heisenberg antiferromagnetic chain. Nat. Phys. 9, 435–441 (2013).
Han, Tian-Heng et al. Correlated impurities and intrinsic spin-liquid physics in the kagome material herbertsmithite. Phys. Rev. B 94, 060409 (2016).
Plumb, K. W. et al. Continuum of quantum fluctuations in a three-dimensional S = 1 Heisenberg magnet. Nat. Phys. 15, 54–59 (2019).
Kim, B. J. & Khaliullin, G. Resonant inelastic x-ray scattering operators for t2g orbital systems. Phys. Rev. B 96, 085108 (2017).
Lamsal, J. & Montfrooij, W. Extracting paramagnon excitations from resonant inelastic x-ray scattering experiments. Phys. Rev. B 93, 214513 (2016).
Shimokawa, T., Watanabe, K. & Kawamura, H. Static and dynamical spin correlations of the \(S=\frac{1}{2}\) random-bond antiferromagnetic Heisenberg model on the triangular and kagome lattices. Phys. Rev. B 92, 134407 (2015).
Nasu, J., Udagawa, M. & Motome, Y. Thermal fractionalization of quantum spins in a Kitaev model: temperature-linear specific heat and coherent transport of Majorana fermions. Phys. Rev. B 92, 115122 (2015).
Yamaji, Y. et al. Clues and criteria for designing a Kitaev spin liquid revealed by thermal and spin excitations of the honeycomb iridate Na2IrO3. Phys. Rev. B 93, 174425 (2016).
Glamazda, A., Lemmens, P., Do, S.-H., Kwon, Y. S. & Choi, K.-Y. Relation between Kitaev magnetism and structure in α−rucl3. Phys. Rev. B 95, 174429 (2017).
Li, G. et al. Probing the continuum scattering and magnetic collapse in single-crystalline α−Li2IrO3 by Raman spectroscopy. Phys. Rev. B 101, 174436 (2020).
Singhania, A., van den Brink, J. & Nishimoto, S. Disorder effects in the Kitaev-Heisenberg model. Phys. Rev. Res. 5, 023009 (2023).
Halász, G. áborB., Perkins, N. B. & van den Brink, J. Resonant inelastic X-ray scattering response of the Kitaev honeycomb model. Phys. Rev. Lett. 117, 127203 (2016).
Magnaterra, M. et al. RIXS observation of bond-directional nearest-neighbor excitations in the Kitaev material Na2IrO3. Prerpint at https://arxiv.org/abs/2301.08340 (2023).
de la Torre, A. et al. Electronic ground state of two nonmagnetic pentavalent honeycomb iridates. Phys. Rev. Mater. 6, 084406 (2022).
Gretarsson, H. et al. Crystal-field splitting and correlation effect on the electronic structure of A2IrO3. Phys. Rev. Lett. 110, 076402 (2013).
de la Torre, A. et al. Enhanced hybridization in the electronic ground state of the intercalated honeycomb iridate Ag3LiIr2O6. Phys. Rev. B 104, L100416 (2021).
Sohn, C. H. et al. Mixing between Jeff = 1/2 and 3/2 orbitals in Na2IrO3: a spectroscopic and density functional calculation study. Phys. Rev. B 88, 085125 (2013).
Freund, F. et al. Single crystal growth from separated educts and its application to lithium transition-metal oxides. Sci. Rep. 6, 35362 (2016).
de la Torre Duran, A. et al. kplumb/delatorre2022momentumindependent: v1.0.0 (2023).
Acknowledgements
We thank J. Knolle and P. A. Lee for useful discussions. Work performed at Brown University by A.d.l.T., B.Z., and K.P. was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award Number DE-SC0021265. Work carried out at Boston College by F.B. and F.T. was supported by the National Science Foundation under award number DMR-2203512. This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. This research used resources of the Advanced Light Source, which is a DOE Office of Science User Facility under contract no. DE-AC02-05CH11231.
Author information
Authors and Affiliations
Contributions
A.d.l.T. and B.Z. performed the X-ray spectroscopy measurements with support from M.H.U., J.K., G.F., G.-H.L., W.Y., and D.H. on samples synthesized by F.B. and F.T. A.d.l.T. and K.W.P. analyzed and interpreted the data. A.d.l.T. and K.W.P. wrote the paper with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
de la Torre, A., Zager, B., Bahrami, F. et al. Momentum-independent magnetic excitation continuum in the honeycomb iridate H3LiIr2O6. Nat Commun 14, 5018 (2023). https://doi.org/10.1038/s41467-023-40769-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-023-40769-x
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.