Abstract
CsV3Sb5 exhibits superconductivity at Tc = 3.2 K after undergoing intriguing two high-temperature transitions: charge density wave order at ~98 K and electronic nematic order at Tnem ~ 35 K. Here, we investigate nematic susceptibility in single crystals of Cs(V1-xTix)3Sb5 (x = 0.00-0.06) where double-dome-shaped superconducting phase diagram is realized. The nematic susceptibility typically exhibits the Curie‒Weiss behaviour above Tnem, which is monotonically decreased with x. Moreover, the Curie‒Weiss temperature is systematically suppressed from ~30 K for x = 0 to ~4 K for x = 0.0075, resulting in a sign change at x = ~0.009. Furthermore, the Curie constant reaches a maximum at x = 0.01, suggesting drastically enhanced nematic susceptibility near a putative nematic quantum critical point (NQCP) at x = ~0.009. Strikingly, Tc is enhanced up to ~4.1 K with full Meissner shielding realized at x = ~0.0075-0.01, forming the first superconducting dome near the NQCP. Our findings directly point to a vital role of nematic fluctuations in enhancing the superconducting properties of Cs(V1-xTix)3Sb5.
Similar content being viewed by others
Introduction
Metals with kagome lattices have drawn enormous attention due to their unique electronic structures, which can host Dirac points, flat bands, and saddle points in their crystal momentum space. Many of these peculiar features can lead to electronic instabilities associated with divergence in the density of states near the Fermi level. As such, it has been theoretically predicted that various emergent orders such as charge bond order1,2, charge density wave (CDW) order1, nematic order3, and superconductivity1,2,4 might appear. For instance, a functional renormalisation group study on the kagome-Hubbard model predicted that CDW order and unconventional d-wave superconductivity can arise near a van Hove singularity at an electron filling of 5/4 per band1.
Recently discovered V-based kagome metals AV3Sb5 (A = K, Rb, and Cs) represent experimental realisations of these various theoretical predictions; each member indeed exhibits signatures of the structural transition due to the CDW order below its CDW transition temperature TCDW, where TCDW = 80-104 K5,6,7, followed by the coexistence of superconductivity8,9,10. Within this material class, CsV3Sb5 has been most extensively studied due to its highest superconducting transition temperature (Tc = ~3.2 K) and the presence of multiple structural and electronic instabilities. For example, the CDW order found at TCDW = 98 K7 induces the first-order structural transition with a 2 × 2 modulation, showing a translational symmetry breaking in each kagome layer. Moreover, it was later found that the 2 × 2 modulation is accompanied by two kinds of out-of-plane modulations (i.e., 2 × 2 × 211 and 2 × 2 × 412). The structure in the CDW states with the c-axis modulation is compatible with the C2 rotational symmetry below TCDW13. However, it is known that the electronic rotational symmetry in each kagome layer is still maintained as C6 just below TCDW14. With a further decrease in temperature, the system finally reaches the electronic nematic transition at Tnem ~ 35 K, at which a rotational symmetry of the electronic state is continuously varied from C6 to C2 in the kagome layer, as evidenced by nuclear magnetic resonance (NMR), scanning tunnelling microscopy and elastoresistance measurements14.
Alongside the experimental progresses, recent theoretical studies based on the kagome-Hubbard model have successfully explained the multiple thermal phase transitions related to the CDW and the nematic orders in CsV3Sb53,15,16,17,18. Namely, the charge ordering at TCDW is understood as stemming from a triple-q-charge bond order, arising from the Fermi surface nesting at the van Hove singularity points in CsV3Sb53,15. Moreover, near the suppression of these charge bond orders, it has been predicted that bond order fluctuations can mediate sizable pairing glue for superconductivity, possibly resulting in the superconductivity of various symmetries including singlet s-wave17, triplet p-wave17, or d-wave superconductivity1.
However, in spite of extensive progress in both experiments and theories, the superconducting properties of CsV3Sb5 are still poorly understood. Firstly, no consensus has been reached on the pairing symmetry of CsV3Sb5. While unconventional superconductivity with the nodal gap structure has been suggested by thermal conductivity19 and scanning tunnelling microscopy data20, tunnel diode oscillator21 and muon spin resonance measurements22 support a nodeless s-wave gap with a sign-preserving order parameter. Secondly, an unusual superconducting phase diagram with a double-dome shape has been found independently either as a function of Sn doping in CsV3Sb5-xSnx polycrystals23 or that of pressure in a CsV3Sb5 single crystal24,25, of which physical mechanisms remain elusive.
Elastoresistance measurements, which is a direct probe of the even-parity nematic susceptibility, have been found to be quite useful in unravelling the pivotal role of nematic fluctuation in mediating Cooper pairing, particularly in several Fe-based superconductors26,27,28,29,30. To better understand the role of nematic order in the superconductivity of CsV3Sb5, we employ elastoresistance measurements to systematically study the nematic susceptibility in high-quality single crystals of Ti-doped CsV3Sb5, Cs(V1-xTix)3Sb5. It should be emphasised that such studies have not been available thus far, as both controlling the doping ratios and maintaining high quality in the doped single crystals of CsV3Sb5 have been quite challenging31,32.
Results
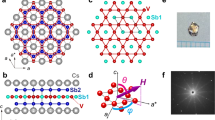
Figure 1a depicts the crystal structure of CsV3Sb5, forming the hexagonal P6/mmm space group with lattice constants of a = b = 5.508 Å and c = 9.326 Å. One unit cell comprises a V-Sb layer sandwiched by Cs planes, each of which consists of four Cs atoms. Within each V-Sb sheet, a kagome network of V atoms is interlaced with a hexagonal lattice of Sb. As the temperature is lowered below TCDW = 98 K, the V atoms rearrange themselves to form an inverse star-of-David pattern (2 × 2 charge order) in the kagome plane7,33. As the temperature is lowered further, an additional ordering is known to appear at Tnem ~ 35 K, below which the system forms a distinct nematic phase14 (Fig. 1b). Upon Ti doping, the titanium atoms can occupy the vanadium sites, resulting in progressive distortion of the vanadium kagome network.
a The crystal structure of CsV3Sb5. In the V3Sb5 layer, vanadium atoms form a kagome network within the ab plane. b Schematic illustration of the temperature-dependent evolution of the vanadium kagome net across the known phase transitions of CsV3Sb5. Here, the TCDW indicates the charge density wave (CDW) transition temperature, while Tnem indicates the nematic transition temperature. The red (orange) coloured vanadium atoms describe the maximum (minimum) of the local electron density of states in the nematic state, as observed from differential conductance maps from a recent scanning tunnelling microscopy experiment14. c Temperature dependence of the in-plane resistivity (ρab) normalised by the resistivity value of Cs(V1-xTix)3Sb5 single crystals at 300 K for 0 ≤ x ≤ 0.06. d dρab/dT curves of Cs(V1-xTix)3Sb5. The curves have been vertically shifted for clarity. The coloured arrows indicate TCDW. e Temperature dependence of the M/H of Cs(V1-xTix)3Sb5 measured at a constant external field of \({\mu }_{0}\)H = 1 T after zero-field cooling (ZFC). Here, M and H indicate the magnetisation and magnetic field, respectively. The inset depicts the temperature-dependent d(M/H)/dT plot of Cs(V0.95Ti0.05)3Sb5 near TCDW.
Figure 1c shows the in-plane resistivity ρab of Cs(V1-xTix)3Sb5 normalised by the resistivity at 300 K (ρab/ρab,300 K). The resistivity of the undoped CsV3Sb5, evidencing metallic behaviour near room temperature, exhibits a slight shoulder near 98 K due to the formation of the CDW order. With increasing x, the residual resistivity ratio (RRR) of Cs(V1-xTix)3Sb5 systematically decreases. This result implies increased impurity scattering within the kagome plane in proportion to x. Along with the decreased RRR value, Cs(V1-xTix)3Sb5 exhibits increasingly broadened CDW transitions with increasing x, which are well visualised in the dρab/dT curves (Fig. 1d). Furthermore, the anomalies in dρab/dT shift to lower temperatures, indicating the development of a lower TCDW at higher x, e.g., ~59 K at x = 0.04. The decreasing trend of TCDW is also confirmed by the dc magnetic susceptibility (M/H) data presented in Fig. 1e. A drop in the M/H curve observed in pristine CsV3Sb5, a Pauli paramagnet, indicates that depletion of the density of states has occurred due to the CDW gap opening at TCDW = 98 K. Consistent with the behaviour found in ρab, increasing x results in a shift in TCDW (the temperature of the M/H drop) to lower temperatures as well as a progressively decreased and broadened drop. This indicates that with progressive perturbation in the V atom arrangement by Ti doping, depletion of the electronic density of states at the long-range CDW transition is systematically reduced along with the decrease of the averaged TCDW and the increase of the TCDW distribution.
As the systematic suppression of TCDW is established with Ti doping, we now turn to the evolution of superconductivity to understand its interplay with the pre-existing CDW order. Figure 2 shows low-temperature ρab(T) and 4πχ(T) data of Cs(V1-xTix)3Sb5. Tc is clearly identified by either zero resistivity or the onset of diamagnetic behaviour in the χ(T) curves. Here, we define Tc from the transport data by the criterion of 0.5 ρN (ρN: normal-state resistivity)34. It is noted that Tc exhibits nonmonotonic behaviour with x. At x = 0.0075, Tc is maximised to 4.1 K from Tc = 3.2 K for the pristine compound. Moreover, in the doping range of x = 0.0–0.01, a full Meissner shielding of −4πχ ≅ 1 is realised. However, with a further increase of x towards x = 0.02, Tc is progressively suppressed to ~1.9 K, accompanied by decreased Meissner shielding of −4πχ ~ 0.3 at x = 0.015 and −4πχ ~ 0 around x = 0.02. At x > 0.02, Tc increases again to 3.8 K at x = 0.05 and recovers the full Meissner shielding. Thus, the evolution of the superconducting properties, i.e., Tc and Meissner shielding, reveals a double-dome feature.
Finding a superconducting region with a double-dome feature among CDW materials is unusual because the competition between CDW and superconductivity often leads to either a monotonically extended region of superconductivity after the collapse of the CDW order35, or a single superconducting dome stabilised at the putative CDW quantum critical point (QCP)36. While an increase in Tc at x = ~0.05 may be associated with the putative QCP of the CDW order, identifying another superconducting dome within the CDW order is truly uncommon. This finding strongly suggests that additional fluctuating orders could be present, enhancing the pairing interaction.
To investigate the origin of the unusual trend in Tc, the elastoresistance in Cs(V1-xTix)3Sb5 was investigated from 6 to 250 K. Figure 3a illustrates the experimental configuration for the elastoresistance measurements. It is known that nematic susceptibility \(\widetilde{n}\) can be obtained by measuring the electronic anisotropy induced by anisotropic strain. In other words, \(\widetilde{n}\) becomes linearly proportional to the anisotropic change in the resistance \(N\equiv {(\Delta R/R)}_{{xx}}-{(\Delta R/R)}_{{yy}}\) in response to anisotropic strain \(\left({\varepsilon }_{{xx}}-{\varepsilon }_{{yy}}\right)\), which results in \(\widetilde{n}=\alpha {{{{{\boldsymbol{\times }}}}}}\partial N/\partial ({\varepsilon }_{{xx}}-{\varepsilon }_{{yy}})\). Here, α is a proportionality constant depending on microscopic details of the electronic structure37 (See, Supplementary Note 8, for details). Therefore, \(\partial N/\partial ({\varepsilon }_{{xx}}-{\varepsilon }_{{yy}})\) reveals the essential temperature dependence of \(\widetilde{n}\) upon approaching a thermally driven nematic phase transition. According to the general definition of elastoresistance coefficients \({(\Delta R/R)}_{i}\equiv {\sum }_{j=1}^{6}{m}_{{i\, j}}{\varepsilon }_{j}\)37, \(\partial N/\partial ({\varepsilon }_{{xx}}-{\varepsilon }_{{yy}})\) can be expressed in terms of \({m}_{{ij}}\), where \({\varepsilon }_{j}\) represents the engineering strain, \({m}_{{ij}}\) are elastoresistance tensor components, and the subscripts i and j represent the Voigt notation (1 = xx, 2 = yy, 3 = zz, 4 = yz, 5 = zx, 6 = xy). For a crystal in the D6h point group with x measured along the [100] axis14, \(\partial N/\partial ({\varepsilon }_{{xx}}-{\varepsilon }_{{yy}})\) directly corresponds to the elastoresistance coefficient \(({m}_{11}-{m}_{12})\), representing the nematic susceptibility \(\widetilde{n}\) along the even-parity \({E}_{2g}\) symmetry channel (See, Supplementary Note 4).
a Schematic illustration of the elastoresistance measurement setup. Here, Vpiezo indicates the voltage applied on the piezo stack. b N vs. \(({\varepsilon }_{{xx}}-{\varepsilon }_{{yy}})\) plot of CsV3Sb5 at several representative temperatures, exhibiting a linear relationship; the nematic susceptibility \(\widetilde{n}\) can be obtained as \(\partial N/\partial ({\varepsilon }_{{xx}}-{\varepsilon }_{{yy}})\). c–i (top panel) Temperature dependence of \(\widetilde{n}\) in Cs(V1-xTix)3Sb5 for 0 ≤ x ≤ 0.02. A sharp jump in \(\widetilde{n}\) is observed near TCDW. Below and above this jump, the data can be clearly fitted to the Curie‒Weiss formula (Eq. (1)) (red and orange solid lines, respectively). The black dotted line indicates the deviation temperature from a Curie‒Weiss fit, while the blue arrow indicates the peak temperature of \(\widetilde{n}\), Tñ, peak. c–i (bottom panel) Temperature dependence of \({(\widetilde{n}-{\widetilde{n}}_{0})}^{-1}\) and \(\left(\widetilde{n}-{\widetilde{n}}_{0}\right)\left(T-{\theta }_{{{{{{\rm{nem}}}}}}}\right)\) below TCDW, represented by the pink and green open circles, respectively. The black dashed line refers to a linear guideline.
Figure 3b depicts the response of \(N\) to \(({\varepsilon }_{{xx}}-{\varepsilon }_{{yy}})\) for CsV3Sb5 at selected temperatures. \(N\) shows a linear relationship with \(({\varepsilon }_{{xx}}-{\varepsilon }_{{yy}})\), enabling a precise measurement of \(\widetilde{n}\) by obtaining \(N/({\varepsilon }_{{xx}}-{\varepsilon }_{{yy}})\) in a small strain limit of \(({\varepsilon }_{{xx}}-{\varepsilon }_{{yy}})\to 0\). This parameter is redefined as \(\widetilde{n}=\partial N/\partial ({\varepsilon }_{{xx}}-{\varepsilon }_{{yy}})\) (α is set to be 1), and the resulting \(\widetilde{n}\)(T) curve for CsV3Sb5 is presented in the top panel of Fig. 3c. A sharp jump in \(\widetilde{n}\) is found at TCDW = 98 K, implying that the first-order structural transition38 due to the charge bond order results in an abrupt offset change in the elastoresistance anisotropy. It is found that at temperatures above 36 K and below the sharp jump near TCDW, \(\widetilde{n}\) is well fitted by the Curie‒Weiss-type temperature dependence,
Here, \({\widetilde{n}}_{0}\) describes the intrinsic anisotropy in the piezoresistivity effect, unrelated to electronic nematicity, θnem is the mean-field nematic transition temperature, and C is the Curie constant of the corresponding nematic susceptibility. A good agreement of the experimental data to Eq. (1) can be confirmed by a fitted red solid line with \({\theta }_{{{{{{\rm{nem}}}}}}}\) = 30 K, \({\widetilde{n}}_{0}\) = 14.7, and C = 39 K. A good fit to Eq. (1) can also be verified by the plots of \({(\widetilde{n}-{\widetilde{n}}_{0})}^{-1}\) and \(\left(\widetilde{n}-{\widetilde{n}}_{0}\right)\left(T-{\theta }_{{{{{{\rm{nem}}}}}}}\right)\) at the bottom panel of Fig. 3c, which exhibit linear (pink open circles) and constant (green open circles) behaviours with temperature, respectively. The nearly constant value of \(\left(\widetilde{n}-{\widetilde{n}}_{0}\right)\left(T-{\theta }_{{{{{{\rm{nem}}}}}}}\right)\) should directly correspond to the C value.
It should be further noted in Fig. 3c that below 36 K as represented by a black dotted line, the experimental data clearly deviate from the trace predicted by Eq. (1). This deviation indicates that the nematic correlation goes beyond the mean-field description below this temperature located near the long-range ordering temperature Tnem. The temperature of 36 K is indeed close to Tnem ~ 35 K, as found by the previous work14. Therefore, our observation shows that a significant nematic correlation of even-parity type exists above Tnem up to TCDW and even above TCDW (vide infra).
Similar measurements and analyses were performed for Cs(V1-xTix)3Sb5 up to x = 0.06 (Fig. 3d–i) (for plots with x ≥ 0.03, see Supplementary Fig. 6). It is noted that the jump in \(\widetilde{n}\) at TCDW systematically decreases with increasing x, indicating weakened elastoresistance anisotropy at the CDW ordering. More importantly, we find that all the samples up to x = 0.03 exhibit the Curie‒Weiss temperature dependence of \(\widetilde{n}\) in broad temperature ranges above deviation temperatures represented by black dotted lines. For x = 0–0.0075, \(\widetilde{n}\) data clearly develop a peak at Tñ, peak. In previous work on the pristine sample14, Tnem identified by NMR and Tñ, peak determined by the \(\widetilde{n}\) measurements were indeed nearly the same as ~35 K. Therefore, Tñ, peak can be used as a good estimate of Tnem for each doping39. In our case, the resultant Tñ, peak = 34 K for x = 0 is indeed close to the known value of Tnem = ~35 K14. For other x, Tñ, peak shows a monotonous decrease; Tñ, peak = 18 K (x = 0.005) and 14 K (x = 0.0075). For x = 0.01, however, we did not identify any peak feature at least down to 6 K, except finding the deviation temperature from the Curie–Weiss behaviour at ~12 K. This observation indicates that for x = 0.01, the true long-range nematic ordering is located well below 6 K or might not even exist at a finite temperature. For x = 0.0125 and 0.015, \(\widetilde{n}\)(T) doesn’t show any peak feature either, and only the deviation from the Curie–Weiss behaviour is identified around ~8 K. This indicates that in x = 0.0125 and 0.015, only nematic correlation exists without the development of true long-range order at a finite temperature.
In order to understand quantitatively the evolution of \(\widetilde{n}\) over the broad doping ranges, we have tried to fit the experimental \(\widetilde{n}\)(T) of all the samples by Eq. (1) below TCDW. (see Supplementary Table 2 for detailed fit parameters). Firstly, we discuss the evolution of C for each doping. In contrast to the monotonic decrease in the jump of \(\widetilde{n}\)(T) and Tñ, peak with x, C is found to exhibit nonmonotonic behaviour, i.e. increasing trend with x for x = 0.0–0.01 and decreasing trend for x ≥ 0.0125; C, as indicated by the slope of \({(\widetilde{n}-{\widetilde{n}}_{0})}^{-1}\) or the value of \(\left(\widetilde{n}-{\widetilde{n}}_{0}\right)\left(T-{\theta }_{{{{{{\rm{nem}}}}}}}\right)\), increases with x from C = 39 K (x = 0) to 124 K (x = 0.0075), and exhibits a maximum value of C = ~ 157 K at critical doping of xc = 0.01. As a result, the highest value of \(\widetilde{n}\)(T = 6 K) ~ 23.8 can be found at xc. For x ≥ 0.0125, C decreases with x to exhibit C = 2 K at x = 0.03, resulting in a flattening of the \(\widetilde{n}\)(T) curve at higher doping ratios. For x ≥ 0.04, Eq. (1) cannot be fitted very well to the \(\widetilde{n}\)(T) curves due to the almost temperature-independent behaviour below and above the TCDW.
The fit to Eq. (1) strikingly reveals that θnem is systematically suppressed from 30.0 K (x = 0) to 3.6 K (x = 0.0075), and to eventually exhibit a sign change (x = ~0.009). At higher x, θnem is suppressed further, resulting in θnem = −42 K at x = 0.03. In general, a nematic quantum critical point (NQCP) is often located at the phase space where θnem goes to zero temperature and strongly enhanced nematic susceptibility exists. The systematic suppression of θnem to zero temperature at x = ~0.009, combined with the sharp maximum of the C value and the disappearance of Tñ, peak near xc, strongly suggests the presence of an NQCP near the doping level close to x ~ 0.009-0.01. Indeed, similar phenomena have been observed in numerous Fe-based systems having the NQCP, such as Ba(Fe1-xCox)2As227, Fe(Se1-xSx)28, LaFe1-xCoxAsO29, and Fe(Se1-xTex)30.
Another salient feature found in Fig. 3 is that the fit based on Eq. (1) below TCDW for each doping level can be successfully extended to explain \(\widetilde{n}\)(T) above TCDW with the same θnem and C but with a different \({\widetilde{n}}_{0}\) (orange solid line). This observation indicates that the even-parity nematic correlation might persist even above TCDW for CsV3Sb5 and Cs(V1-xTix)3Sb5 (x ≤ 0.03). As a result, the Curie‒Weiss tail above TCDW becomes clearly visible for 0 ≤ x ≤ 0.03, reaching at least up to the maximum investigated temperature of 250 K (see, Supplementary Fig. 6 for \(\widetilde{n}\)(T) plots up to 250 K and for x ≥ 0.03). Because of the most enhanced C value, the Curie–Weiss tail of \(\widetilde{n}\) becomes most conspicuous at xc = 0.01. It is striking that the enhanced \(\widetilde{n}\) up to at least 250 K is observed at xc = 0.01 where the actual nematic ordering temperature is close to zero. This directly suggests that large quantum fluctuation of even-parity nematic order near the NQCP could be responsible for the enhancement of \(\widetilde{n}\) at high temperatures.
Figure 4a, b summarises the phase diagram of Cs(V1-xTix)3Sb5 plotted on top of the colour contour of \(\widetilde{n}\); TCDW as derived from the data of ρab (orange circles), M/H (yellow octagons), and \(\widetilde{n}\) (brown crosses) are plotted for each x. Moreover, Tñ, peak (blue squares) and θnem (purple stars) obtained from \(\widetilde{n}\) in Fig. 3 are plotted with the Tnem (pink cross) of x = 0 determined in a previous work14. At x = 0, a jump in \(\widetilde{n}\)(T) near TCDW can be clearly identified by the abrupt change of colour in \(\widetilde{n}\) from blue at T > TCDW to green at T < TCDW. Near Tnem, the contour exhibits a yellow colour, indicating a local maximum of \(\widetilde{n}\) at Tñ, peak. With an increase in doping, the Tñ, peak shifts to low temperatures, resulting in the most intensified \(\widetilde{n}\) (6 K) indicated by the red colour near x = 0.0075-0.01. This behaviour is also confirmed by the maximum of the C value, indicated by the red diamonds.
a The orange circles, yellow octagons, and brown crosses represent TCDW obtained from ρab, M/H, and \(\widetilde{n}\) measurements. The pink cross in Tnem indicates the nematic transition temperature obtained from ref. 14. The blue squares and purple stars represent Tñ, peak and θnem obtained from the analysis of the nematic susceptibility \(\widetilde{n}\), respectively. A purple error bar is obtained by a standard deviation of the Curie‒Weiss fit. The overlaid colour contour represents the interpolated values generated from \(\widetilde{n}\) taken from the elastoresistance measurements. b The red diamonds show the Curie constant C obtained from the Curie‒Weiss fits of \(\widetilde{n}\) for 0 ≤ x ≤ 0.03. c Superconducting transition temperature Tc (green triangles) defined by the criterion of 0.5ρN (ρN: normal-state resistivity) determined from Fig. 2. The colour contour represents the Meissner volume fraction (−4πχ).
The superconducting phase diagram of Cs(V1-xTix)3Sb5 is also plotted in Fig. 4c. Here, the green triangles indicate the Tc obtained from transport measurements, while the Meissner volume fraction (−4πχ) is represented below the trace of Tc as a green colour contour. Surprisingly, it is found that Tc is optimised to 4.1 K (3.7 K) near this doping range of x = 0.0075 (0.01), when the nematic correlations indicated by the \(\widetilde{n}\) and C values are sharply enhanced near the NQCP. Our observation thus raises an intriguing possibility that fluctuation of the nematic order plays an important role in the pairing interaction to optimise superconductivity in the first superconducting dome of Cs(V1-xTix)3Sb5. At higher doping ratios of 0.01 ≤ x ≤ 0.02, Tc is monotonically suppressed with doping, which could be related to the reduced nematic fluctuations as indicated by the decreased \(\widetilde{n}\) and C values.
Based on our experimental findings and implications, the nematic fluctuations may be important in understanding the superconductivity in the AV3Sb5 family. A very small Tc ~ 0.0008 K in CsV3Sb5 has been indeed predicted based on the McMillan equation33, suggesting that electron-phonon coupling alone is not enough to explain the superconducting transition; nematic fluctuation should be considered as an essential ingredient to result in the relatively high Tc ~ 3.2 K in CsV3Sb5. In support of this scenario, it should be noted that the Tc values in KV3Sb5 (Tc = 0.93 K8) and in RbV3Sb5 (Tc = 0.92 K9) are lower than that in CsV3Sb5 (Tc = 3.2 K). In addition, unlike the Cs variant, a recent study of Sn doping in polycrystalline KV3Sb5 and RbV3Sb5 revealed single superconducting domes near the suppression of the CDW orders40. All these results, if interpreted correctly, potentially indicate that nematic order and its fluctuations might be absent in both compounds, motivating similar experiments for these materials. Furthermore, our scenario supports that nematic fluctuations should be also considered an important factor to understand the double superconducting domes reported in pressurised CsV3Sb524,25 and in CsV3Sb5-xSnx23 polycrystals.
It should be pointed out that the experimental results found here well resemble those found in the Fe-based superconductors, e.g., Ba(Fe1-xCox)2As227, LaFe1-xCoxAsO29 and Fe(Se1-xTex)30, where unconventional superconductivity is optimised near the NQCP. However, the microscopic origin for having the nematic order seems to be quite different; in contrast to the iron-based superconductors where the spin density wave order is closely coupled to the nematic order27,28,29,30,41, the nematic order in CsV3Sb5 is intertwined with the unconventional CDW order, possibly in a form of charge bond order3,14,18. Recent theoretical studies3,18 considering the kagome-Hubbard model have indeed shown that a triple-q-charge bond order is stabilised below TCDW, described by three complex CDW order parameters. Furthermore, those theories suggest that these CDW order parameters can undergo a continuous variation of their phases at Tnem from a triply-degenerate, isotropic phase of π/2 into two different values, without the change of the isotropic amplitude, thereby resulting in one-dimensional nematic modulation. Therefore, if the charge bond order developed in CsV3Sb5 is assumed to be still maintained over the significant doping level x, the enhanced nematic correlation might be linked to the quantum phase transition involving a continuous variation of the phases of the triple-q CDW order parameters, at which the charge bond order with anisotropic phases, thus called nematic charge bond order, develops from the one with a homogenous phase.
Several other theoretical investigations considering the kagome-Hubbard model have also predicted that CsV3Sb5 might have unconventional superconductivity with a superconducting gap function of s- or p- or d-wave type when the CDW state is melted1,17, possibly via suppression of the amplitudes in the three q-charge bond orders. Investigations on the superconducting order parameters at the doping level x = ~0.0075-0.01 near the NQCP (first dome) and x = ~0.05 (second dome) may thus provide an opportunity for studying comparative characteristics of superconductivity instigated by anisotropic phase fluctuations and amplitudes of the three q-charge bond orders, respectively.
In conclusion, our experimental findings coherently suggest that an NQCP is located near x = ~0.009-0.01. Moreover, a maximum Tc = ~4.1 K with full Meissner shielding is realised at x = ~0.0075-0.01, forming the first superconducting dome near the NQCP. This not only points out the vital role of nematic fluctuation in enhancing superconductivity but also provides important insights into understanding the link between the multiple orders and superconductivity in CsV3Sb5 and related kagome superconductors.
Methods
Single crystal growth
Cs(V1-xTix)3Sb5 (0 ≤ x ≤ 0.06) single crystals were grown by the Cs-Sb flux method. A mixture of Cs chunks (99.8%, Alfa Aesar), V powders (99.9%, Sigma Aldrich), Ti powders (99.99%, Alfa Aesar) and Sb shots (99.999%, Alfa Aesar) with a molar ratio of Cs: (V, Ti): Sb = 2: 1: 3 were put in an alumina crucible and were double-sealed in an evacuated quartz ampule with pressures less than 2 × 10−5 mbar. The sealed ampules were heated at a rate of 100 °C/h and kept at 1000 °C for 24 h to fully dissolve the V and Ti into the Cs-Sb eutectic mixture. Later, the ampoules were cooled down to 600 °C at a rate of 2 °C/h. At 600 °C, the ampules were centrifuged to separate the crystals from the molten flux. To avoid oxidation, all the sample preparation was done inside a glove box, which was kept in an Ar atmosphere with oxygen and moisture concentrations less than 1 ppm. Shiny plate-like crystals were obtained with a typical lateral area of 3 × 2 mm2. The CsV3Sb5 single crystals exhibited a residual resistivity ratio (RRR) value as high as 129.2.
In-plane resistivity and magnetisation measurements
In-plane resistivity measurements were performed in the PPMSTM using a conventional four-probe method. The electrical contacts were attached by silver paint (Dupont 4929 N). The M/H after zero-field cooling (ZFC) were obtained by MPMSTM (Quantum Design) at temperatures between 5 and 300 K, while the magnetic susceptibility χ between 1.8 and 5 K were measured by a vibrating sample magnetometer in a PPMSTM (Quantum Design). The demagnetisation factors in the M/H and χ measurements have been corrected after measuring the samples in a needle-like configuration.
Elastoresistance measurements
The elastoresistance was measured in a closed-cycle cryostat (Sumitomo RDK-101D) using a commercial piezoelectric actuator (Piezomechanik PSt 150) at various temperatures from 6 to 250 K. The samples were glued to the piezoelectric actuator by using an adhesive epoxy (Devcon 14250). Two samples were cut in rectangular shapes with a lateral size of ~1 × 0.2 mm2; the longer direction was parallel (perpendicular) to the a-axis for the Rxx (Ryy) sample. All the samples were cleaved to the thickness of ~20 μm to ensure efficient strain transmission to the entire sample. The electrical contacts were attached directly by silver paint (Dupont 4929 N) to the freshly cleaved surface. Two strain gauges were glued on the other side of the actuator with perpendicular orientation to each other.
X-ray diffraction and wavelength dispersive X-ray spectroscopy measurements
Cs(V1-xTix)3Sb5 single crystals were ground and inserted inside a quartz capillary tube with an inner diameter of 0.5 mm. The tube was measured by x-ray diffraction (XRD) θ−2θ scans using a high-resolution x-ray diffractometer (PANalytical Empyrean). Wavelength dispersive x-ray spectroscopy (WDS) were performed in a field emission electron probe microanalyzer (JEOL Ltd., JXA-8530F) by taking V (99.99%), Ti (99.9%) and Sb (99.99%) metals as standard specimens. The standard specimen data of Cs was taken from the JEOL database due to the high air sensitivity of the elemental Cs metal.
Data availability
Source data are provided with this paper. The data generated in this study have been deposited in the Figshare database42.
References
Wang, W.-S., Li, Z.-Z., Xiang, Y.-Y. & Wang, Q.-H. Competing electronic orders on kagome lattices at van Hove filling. Phys. Rev. B 87, 115135 (2013).
Kiesel, M. L., Platt, C. & Thomale, R. Unconventional Fermi surface instabilities in the kagome Hubbard model. Phys. Rev. Lett. 110, 126405 (2013).
Denner, M. M., Thomale, R. & Neupert, T. Analysis of charge order in the kagome metal AV3Sb5 (A = K, Rb, Cs). Phys. Rev. Lett. 127, 217601 (2021).
Yu, S. –L. & Li, J. –X. Chiral superconducting phase and chiral spin-density-wave phase in a Hubbard model on the kagome lattice. Phys. Rev. B 85, 144402 (2012).
Jiang, Y.-X. et al. Unconventional chiral charge order in kagome superconductor KV3Sb5. Nat. Mater. 20, 1353 (2021).
Shumiya, N. et al. Intrinsic nature of chiral charge order in the kagome superconductor RbV3Sb5. Phys. Rev. B 104, 035131 (2021).
Wang, Z. et al. Electronic nature of chiral charge order in the kagome superconductor CsV3Sb5. Phys. Rev. B 104, 075148 (2021).
Ortiz, B. R. et al. Superconductivity in the Z2 kagome metal KV3Sb5. Phys. Rev. Mater. 5, 034801 (2021).
Yin, Q. et al. Superconductivity and normal-state properties of kagome metal RbV3Sb5 single crystals. Chin. Phys. Lett. 38, 037403 (2021).
Ortiz, B. R. et al. CsV3Sb5: a Z2 topological kagome metal with a superconducting ground state. Phys. Rev. Lett. 125, 247002 (2020).
Liang, Z. et al. Three-dimensional charge density wave and surface-dependent vortex-core states in a kagome superconductor CsV3Sb5. Phys. Rev. X 11, 031026 (2021).
Ortiz, B. R. et al. Fermi surface mapping and the nature of charge-density-wave order in the kagome superconductor CsV3Sb5. Phys. Rev. X 11, 041030 (2021).
Miao, H. et al. Geometry of the charge density wave in the kagome metal AV3Sb5. Phys. Rev. B 104, 195132 (2021).
Nie, L. et al. Charge-density-wave-driven electronic nematicity in a kagome superconductor. Nature 604, 59–64 (2022).
Park, T., Ye, M. & Balents, L. Electronic instabilities of kagome metals: Saddle points and Landau theory. Phys. Rev. B 104, 035142 (2021).
Wu, X. et al. Nature of unconventional pairing in the kagome superconductors AV3Sb5 (A=K, Rb, Cs). Phys. Rev. Lett. 127, 177001 (2021).
Tazai, R., Yamakawa, Y., Onari, S. & Kontani, H. Mechanism of exotic density-wave and beyond-Migdal unconventional superconductivity in kagome metal AV3Sb5 (A = K, Rb, Cs). Sci. Adv. 8, eabl4108 (2022).
Tazai, R., Yamakawa, Y. & Kontani, H. Charge-loop current order and Z3 nematicity mediated by bond-order fluctuations in kagome metal AV3Sb5 (A = Cs, Rb, K). Preprint at https://doi.org/10.48550/arXiv.2207.08068 (2022).
Zhao, C. C. et al. Nodal superconductivity and superconducting domes in the topological Kagome metal CsV3Sb5. Preprint at https://doi.org/10.48550/arXiv.2102.08356 (2021).
Chen, H. et al. Roton pair density wave in a strong-coupling kagome superconductor. Nature 599, 222–228 (2021).
Duan, W. et al. Nodeless superconductivity in the kagome metal CsV3Sb5. Sci. China. Phys. Mech. Astron. 64, 107462 (2021).
Gupta, R. et al. Microscopic evidence for anisotropic multigap superconductivity in the CsV3Sb5 kagome superconductor. npj Quantum Mater. 7, 49 (2022).
Oey, Y. M. et al. Fermi level tuning and double-dome superconductivity in the kagome metal CsV3Sb5−xSnx. Phys. Rev. Mater. 6, L041801 (2022).
Chen, K. Y. et al. Double superconducting dome and triple enhancement of Tc in the kagome superconductor CsV3Sb5 under high pressure. Phys. Rev. Lett. 126, 247001 (2021).
Yu, F. H. et al. Unusual competition of superconductivity and charge-density-wave state in a compressed topological kagome metal. Nat. Commun. 12, 3645 (2021).
Chu, J.-H., Kuo, H.-H., Analytis, J. G. & Fisher, I. R. Divergent nematic susceptibility in an iron arsenide superconductor. Science 337, 710–712 (2012).
Kuo, H. –H., Chu, J. –H., Palmstrom, J. C., Kivelson, S. A. & Fisher, I. R. Ubiquitous signatures of nematic quantum criticality in optimally doped Fe-based superconductors. Science 352, 958–962 (2016).
Hosoi, S. et al. Nematic quantum critical point without magnetism in FeSe1−xSx superconductors. Proc. Natl Acad. Sci. USA 113, 8139 (2016).
Hong, X. et al. Evolution of the nematic susceptibility in LaFe1−xCoxAsO. Phys. Rev. Lett. 125, 067001 (2020).
Ishida, K. et al. Pure nematic quantum critical point accompanied by a superconducting dome. Proc. Natl Acad. Sci. USA 119, e2110501119 (2022).
Yang, H. et al. Titanium doped kagome superconductor CsV3-xTixSb5 and two distinct phases. Sci. Bull. 67, 2176 (2022).
Liu, Y. et al. Doping evolution of superconductivity, charge order and band topology in hole-doped topological kagome superconductors Cs(V1−xTix)3Sb5. Phys. Rev. Materials 7, 064801 (2023).
Tan, H., Liu, Y., Wang, Z. & Yan, B. Charge density waves and electronic properties of superconducting kagome metals. Phys. Rev. Lett. 127, 046401 (2021).
Kim, C. et al. Experimental signatures of nodeless multiband superconductivity in a 2H-Pd0.08TaSe2 single crystal. Sci. Rep. 11, 13383 (2021).
Wang, B. et al. Pressure-induced bulk superconductivity in a layered transition-metal dichalcogenide 1T-tantalum selenium. Phys. Rev. B 95, 220501 (R) (2017).
Gruner, T. et al. Charge density wave quantum critical point with strong enhancement of superconductivity. Nat. Phys. 13, 967–972 (2017).
Kuo, H. –H., Shapiro, M. C., Riggs, S. C. & Fisher, I. R. Measurement of the elastoresistivity coefficients of the underdoped iron arsenide Ba(Fe0.975Co0.025)2As2. Phys. Rev. B 88, 085113 (2013).
Luo, J. et al. Possible star-of-David pattern charge density wave with additional modulation in the kagome superconductor CsV3Sb5. npj Quantum Mater. 7, 30 (2022).
Eckberg, C. et al. Sixfold enhancement of superconductivity in a tunable electronic nematic system. Nat. Phys. 16, 346–350 (2020).
Oey, Y. M., Kaboudvand, F., Ortiz, B. R., Seshadri, R. & Wilson, S. D. Tuning charge density wave order and superconductivity in the kagome metals KV3Sb5−xSnx and RbV3Sb5−xSnx. Phys. Rev. Mater. 6, 074802 (2022).
Fernandes, R. M., Chubukov, A. V. & Schmalian, J. What drives nematic order in iron-based superconductors? Nat. Phys. 10, 97–104 (2014).
Sur, Y., Kim, K. –T., Kim, S. & Kim K. H. Optimized superconductivity in the vicinity of a nematic quantum critical point in the kagome superconductor Cs(V1-xTix)3Sb5 data sets. figshare https://doi.org/10.6084/m9.figshare.22808321 (2023).
Acknowledgements
Y.S., K.–T.K., S.K. and K.H.K. were financially supported by the Ministry of Science and ICT through the National Research Foundation of Korea (2019R1A2C2090648, 2022H1D3A3A01077468) and by the Ministry of Education (2021R1A6C101B418).
Author information
Authors and Affiliations
Contributions
Y.S. and K.H.K. initiated the project. Y.S., K.–T.K. and S.K. prepared the single crystalline samples. Y.S. characterised the samples and performed the measurements. Y.S. and K.H.K. analysed the data and wrote the manuscript. K.H.K. devised the project and advised the research. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sur, Y., Kim, KT., Kim, S. et al. Optimized superconductivity in the vicinity of a nematic quantum critical point in the kagome superconductor Cs(V1-xTix)3Sb5. Nat Commun 14, 3899 (2023). https://doi.org/10.1038/s41467-023-39495-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-023-39495-1
This article is cited by
-
AV3Sb5 kagome superconductors
Nature Reviews Materials (2024)
-
Evidence for an odd-parity nematic phase above the charge-density-wave transition in a kagome metal
Nature Physics (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.