Abstract
Broken symmetries play a fundamental role in superconductivity and influence many of its properties in a profound way. Understanding these symmetry breaking states is essential to elucidate the various exotic quantum behaviors in non-trivial superconductors. Here, we report an experimental observation of spontaneous rotational symmetry breaking of superconductivity at the heterointerface of amorphous (a)-YAlO3/KTaO3(111) with a superconducting transition temperature of 1.86 K. Both the magnetoresistance and superconducting critical field in an in-plane field manifest striking twofold symmetric oscillations deep inside the superconducting state, whereas the anisotropy vanishes in the normal state, demonstrating that it is an intrinsic property of the superconducting phase. We attribute this behavior to the mixed-parity superconducting state, which is an admixture of s-wave and p-wave pairing components induced by strong spin-orbit coupling inherent to inversion symmetry breaking at the heterointerface of a-YAlO3/KTaO3. Our work suggests an unconventional nature of the underlying pairing interaction in the KTaO3 heterointerface superconductors, and brings a new broad of perspective on understanding non-trivial superconducting properties at the artificial heterointerfaces.
Similar content being viewed by others
Introduction
The study of heterointerface superconductivity has been a central theme in condensed matter physics communities1. Due to the presence of inversion symmetry breaking and the particular interactions found at their interface between two constitute materials, the strong interplay between the electrons with Coulomb interaction and the interfacial electron-phonon coupling gives rise to novel superconducting behaviors, providing an ideal platform for understanding the underlying rich physical properties and developing the next-generation quantum technologies2,3,4. The archetypal heterointerface superconductivity has been experimentally observed at the heterointerface of crystalline (c)-LaAlO3/SrTiO3 with a superconducting transition temperature (Tc) of 250 mK5, which ignites the first fire in heterointerface superconductivity research. Strikingly, a variety of appealing quantum phenomena has also been revealed at the superconducting SrTiO3 heterointerfaces, such as the coexistence of ferromagnetism and superconductivity6,7,8 and the gate-tunable superconductivity9,10,11,12,13, indicative of a possible unconventional and non-trivial superconducting phase as the ground state14. Unfortunately, the extremely low Tc of SrTiO3 heterointerface superconductors is a critical challenge, preventing extensive attentions to further unveil the origin of these emergent quantum phases.
Very recently, unexpected superconductivity is experimentally observed at the heterointerface between polycrystalline (p)-EuO [or amorphous (a)-LaAlO3] and KTaO3 single-crystal substrates which shows a Tc ~ 2 K15,16, approximately one order of magnitude higher than that of c-LaAlO3/SrTiO35, evoking an exciting opportunity to study the physical properties of heterointerface superconductivity. Although KTaO3 shares many common features with SrTiO315,16,17,18, the superconductivity of KTaO3 heterointerfaces behaves in a quite different manner. Remarkably, the superconductivity of these heterointerfaces exhibits a strong dependence on the KTaO3 crystalline orientations by compared to the SrTiO3 crystalline orientation independence of superconductivity19,20,21,22,23,24. Furthermore, considering the fact that the strong spin-orbit coupling associated with the heavy Ta in 5d orbitals of KTaO3 heterointerfaces is comparable to the bandwidth and the accompanying strong on-site Coulomb repulsion25,26,27, the combination of strong spin-orbit coupling and the electron-electron interaction is theoretically expected to result in an unconventional superconductivity, including a mix of spin-singlet and spin-triplet components28 as a manifestation of rotational symmetry breaking. Experimentally, an indication of strong in-plane anisotropic electrical resistance in the normal state has been reported at the ferromagnetic heterointerface of p-EuO/KTaO3, implying a possible existence of “stripe”-like superconducting phase15. This anisotropy, however, is alternatively attributed to be an extrinsic property of the ferromagnetic p-EuO in theory29, leading to that a consensus on the rotational symmetry breaking of superconductivity in KTaO3 heterointerface superconductors remains elusive.
Here, we carry out an experimental study on nonmagnetic a-YAlO3 thin films with a wide energy gap of 7.9 eV grown on the polar KTaO3(111) single-crystal substrates. This energy gap is significantly larger than that of a-LaAlO3 (5.6 eV)30, enabling strong confinement potential to restrict the interfacial conducting electrons to a thinner interfacial layer, thus prompting an intriguing quantum behaviors at their interface31. Electrical transport measurements on the as-grown films reveal two-dimensional superconductivity with a Tc of 1.86 K, and a superconducting layer thickness of 4.5 nm. By tuning the in-plane azimuthal angle φ-dependent magnetic field, both the magnetoresistance and superconducting critical field display pronounced twofold symmetric oscillations deep inside the superconducting state, whereas they vanish in the normal state. These results unambiguously demonstrate that the anisotropy with in-plane rotational symmetry breaking is an intrinsic property of the superconducting phase in a-YAlO3/KTaO3. Through group theory study, we thus classify the inversion symmetry breaking KTaO3 heterointerface superconductors as a mixed-parity unconventional superconductivity with an admixture of s-wave and p-wave pairing components, a candidate platform for realizing Majorana modes32.
Results
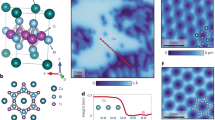
The a-YAlO3/KTaO3 heterostructures are prepared by depositing a-YAlO3 films on (111)-oriented KTaO3 single-crystal substrates using pulsed laser deposition. Atomic force microscopy characterizations show that the surface of KTaO3 substrates and a-YAlO3 films are atomically flat (see Supplementary Fig. 1). X-ray diffraction confirms the absence of epitaxial peaks of YAlO3 (see Supplementary Fig. 2 and Supplementary Fig. 3), thus suggesting that the YAlO3 film is not in a well-defined crystalline phase. The microstructure of the interface is further examined by aberration-corrected scanning transmission electron microscopy (STEM). From the high angle annular dark field (HAADF)-STEM image shown in Fig. 1a, it can be seen that the homogeneous and amorphous phase YAlO3 thin film is grown on the KTaO3(111) substrate (also see Supplementary Fig. 4). Looking at the sample from a larger field of view, the thickness of the a-YAlO3 film is found to be about 60 nm. High-resolution (HR)-STEM imaging shown in Fig. 1a and Supplementary Fig. 4, and energy dispersive X-ray spectroscopy (EDX) elemental mapping shown in Fig. 1b indicate that the abrupt and smooth interface between KTaO3 single-crystal substrate and a-YAlO3 film is resolved structurally and chemically. These results are consistent with previous studies on a-LaAlO3/KTaO3(111)15,16, a-LaAlO3/KTaO3(110)23, a-LaAlO3/KTaO3(001)33, and a-AlOx/KTaO3(111)34.
a HAADF-STEM image of a-YAlO3/KTaO3 viewed along the \([11\bar{2}]\) zone axis. The inset shows the enlarged HR-STEM image of KTaO3 overlapped with atomic configuration. b HR-STEM image and the corresponding EDX elemental mapping of interface. c Distribution of Ta5+ ions along the [111] crystal axis of KTaO3(111) surface. Ta5+ ions are shown with progressively smaller sizes in the three adjacent (111) planes, which are labeled as Ta-I, Ta-II, and Ta-III, respectively. d Hall bar configuration on a-YAlO3/KTaO3(111) heterostructure. Here, φ is defined as the in-plane azimuthal angle between the applied magnetic field B and the \([1\bar{1}0]\)-axis of the lattice, shown in the inset of d.
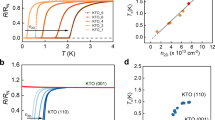
Figure 2a shows the temperature-dependent sheet resistance Rs on two representative as-grown a-YAlO3 thin films (Samples #1 and #2 with growth temperatures of 780 and 650 °C, respectively) with the Hall bar configuration, schematically illustrated in Fig. 1d. A typical metallic behavior is visible in a wide temperature range, indicating that a two-dimensional electron gas is formed at their interface induced by a candidate mechanism of the formation of oxygen vacancies at the surface of KTaO323,35, similar to that in the sister a-LaAlO3/SrTiO336. The transverse Hall resistance Rxy is obtained from Hall measurements at 5 K, and reveals that the charge carriers in the a-YAlO3/KTaO3 are electrons. The estimated carrier density is about 1.45 × 1014 and 6.62 × 1013 cm−2 for Samples #1 and #2, respectively. The electron mobility for Samples #1 and #2 is thus 193.6 and 159.7 cm2V−1s−1. These results are highly universal and reproducible (see Supplementary Fig. 5, Supplementary Note 1, and Supplementary Table 1) and reasonably consistent with previous electrical transport studies on the KTaO3 heterointerfaces15,23. Remarkably, as the temperature is further decreased, the resistance Rs undergoes a narrow and sharp transition with a transition width of less than 0.5 K to a zero-resistance state, signaling the appearance of superconductivity at the heterointerface of a-YAlO3/KTaO3. The critical temperature is determined to be Tc = 1.86 and 0.92 K for Samples #1 and #2, respectively, as defined by where the resistance is at the midpoint of the normal electrical resistance at 5 K, i.e. Rs(Tc) = 0.5 × Rs(5 K).
a Electrical resistance (Rs) as a function of temperature at zero magnetic field for two representative a-YAlO3/KTaO3 heterostructures (Samples #1 and #2). Low temperature dependence of Rs is illustrated in the inset of a. Magnetoresistance for fields b parallel and c perpendicular to the plane surface of Sample #1. d Temperature dependence of the upper critical field μ0Hc2 (μ0H\({}_{c2}^{\parallel }\) for the in-plane field along the \([11\bar{2}]\)-axis shown in Fig. 1d and μ0H\({}_{c2}^{\perp }\) for the out-of-plane field).
To further characterize the superconducting behaviors in a-YAlO3/KTaO3, we measure the magnetoresistance Rs(μ0H) (here, μ0 is the vacuum permeability) at various temperatures between 0.5 and 5 K with fields parallel (μ0H∥) and perpendicular (μ0H⊥) to the plane surface of Sample #1, as shown in Fig. 2b, c, respectively. The fundamental superconducting behavior is clearly perceived. Indeed, the magnetoresistance Rs(μ0H) varies differently with μ0H∥ and μ0H⊥, and both the upper critical fields μ0H\({}_{c2}^{\parallel }\) and μ0H\({}_{c2}^{\perp }\) parallelly shift to a lower value with the increase of the temperature, where μ0Hc2 are evaluated at the midpoints of the normal state resistance at 5 K. These results provide an indication of a two-dimensional superconducting feature in a-YAlO3/KTaO3. The temperature-dependent upper critical fields μ0Hc2 are summarized in Fig. 2d and are well fitted by the phenomenological two-dimensional Ginzburg-Landau (G-L) model37: μ0H\({}_{c2}^{\perp }(T)=\frac{{{{\Phi }}}_{0}}{2\pi {\xi }_{{{{{{{{\rm{GL}}}}}}}}}^{2}}(1-\frac{T}{{T}_{c}})\) and μ0H\({}_{c2}^{\parallel }(T)=\frac{{{{\Phi }}}_{0}\sqrt{12}}{2\pi {\xi }_{{{{{{{{\rm{GL}}}}}}}}}{d}_{{{{{{{{\rm{SC}}}}}}}}}}\sqrt{1-\frac{T}{{T}_{c}}}\), where Φ0, ξGL, and dSC denote a flux quantum, the in-plane superconducting coherence length at T = 0 K, and the effective thickness of superconductivity, respectively. Using the extrapolated μ0H\({}_{c2}^{\perp }(0)\) = 0.98 T and μ0H\({}_{c2}^{\parallel }(0)\) = 13.81 T, we find ξGL = 18.4 nm and dSC = 4.5 nm, where ξGL is significantly larger than dSC, suggesting a two-dimensional nature of superconductivity. Additionally, the in-plane μ0H\({}_{c2}^{\parallel }(0)\) is substantially larger than the Pauli-paramagnetic pair-breaking field BP ≈ 3.46 T based on the BCS theory in the weak-coupling limit38,39. High values of μ0H\({}_{c2}^{\parallel }(0)\) excessing BP could be realized in the presence of strong spin-orbit coupling owing to the elastic scattering, which results in the suppression of spin paramagnetism effects. The violation of this paramagnetic limit is a common phenomenon in heterointerface superconductors15,40, especially when the superconducting layer thickness is in the range dSC < 20 nm. However, the underlying mechanism for realizing μ0H\({}_{c2}^{\parallel }(0)\) value in excess of BP remains an open question15. Furthermore, the thickness of the superconducting layer in a-YAlO3/KTaO3(111) is approximately estimated as thin as dSC = 4.5 nm based on the framework of the phenomenological two-dimensional G-L model37. This result could be intuitively expected, since the strong confinement potential induced by YAlO3 significantly restricts the superconducting electrons to a thinner superconducting layer31. On the other hand, the out-of-plane polar angle θ-dependent upper critical field H\({}_{c2}^{\theta }\) at 1.5 K quantitatively verifies the behavior expected from a two-dimensional structure in a-YAlO3/KTaO3, as shown in Supplementary Fig. 6. The θ-dependent μ0H\({}_{c2}^{\theta }\) are quantitatively fitted by the two-dimensional Tinkham formula and the three-dimensional anisotropic G-L model, given by \(\frac{{{{{{{{{\rm{H}}}}}}}}}_{c2}^{\theta }|\cos \theta|}{{{{{{{{{\rm{H}}}}}}}}}_{c2}^{\perp }}+{(\frac{{{{{{{{{\rm{H}}}}}}}}}_{c2}^{\theta }\sin \theta }{{{{{{{{{\rm{H}}}}}}}}}_{c2}^{\parallel }})}^{2}=1\) and \({(\frac{{{{{{{{{\rm{H}}}}}}}}}_{c2}^{\theta }\cos \theta }{{{{{{{{{\rm{H}}}}}}}}}_{c2}^{\perp }})}^{2}+{(\frac{{{{{{{{{\rm{H}}}}}}}}}_{c2}^{\theta }\sin \theta }{{{{{{{{{\rm{H}}}}}}}}}_{c2}^{\parallel }})}^{2}=1\), respectively41,42. A cusp-like peak is clearly observed at θ = 90° (see Supplementary Fig. 6), which is well described by the two-dimensional Tinkham model, as frequently observed in heterointerface superconductivity42,43 and layered transition metal dichalcogenides44,45.
Since the superconductivity in a-YAlO3/KTaO3 is two-dimensional, the Berezinskii-Kosterlitz-Thouless (BKT) transition describes superconducting phase coherence46,47. Here, the BKT transition temperature defines the vortex unbinding transition, and can be determined using current-voltage (I-V) measurements as a function of temperature T, as shown in Fig. 3a. Below Tc, we find a critical current Ic, whose value decreases with increase in temperature. The maximal value of Ic is ~ 330 μA at 0.5 K, which is substantially larger than that previously observed in the KTaO3 heterointerfaces15,23. Such a high critical current value probably originates from the high charge carrier concentration (about 1.45 × 1014 cm−2, Sample #1 in Fig. 2a) confined in a thinner superconducting layer of a-YAlO3/KTaO3, promising for large-scale applications in superconductor-based devices. In Fig. 3b, we also plot the characteristics I-V on a log-log scale, and observe that the slope of the I-V curve smoothly evolves from the normal ohmic state, V ∝ I, to a steeper power law resulting from the current exciting free-moving vortices, V ∝ Iα(T), with α(TBKT) = 3. In Fig. 3c, a value TBKT = 1.7 K is interpolated, which is consistent with Tc as defined in Fig. 2a. In addition, close to TBKT, an R\({}_{{{{{{{{\rm{s}}}}}}}}}={R}_{0}\exp [-b{(T/{T}_{{{{{{{{\rm{BKT}}}}}}}}}-1)}^{-1/2}]\) dependence, where R0 and b are material parameters, is expected48. As shown in Fig. 3d, the measured Rs(T) is also consistent with this behavior and yields TBKT = 1.85 K, in good agreement with the analysis of the α exponent shown in Fig. 3c.
a Temperature-dependent I-V measurements (Sample #1). b Corresponding logarithmic scale representation of a. The long red dashed line denotes the V ~ I3 dependence. c Temperature dependence of the power-law exponent α, as deduced from the fits shown in b. d Rs(T) dependence of the same sample, plotted on a \({[{{{\rm{d}}}}{{{\rm{ln}}}}({{{\rm{R}}}}_{{{\rm{s}}}})/{{{\rm{d}}}}T]}^{-2/3}\) scale.
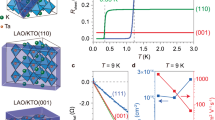
Next, we turn to discuss the in-plane anisotropy of superconductivity in a-YAlO3/KTaO3 using an in-plane azimuthal angle φ-dependent magnetoresistance, where φ is defined as the azimuthal angle between the magnetic field and the \([1\bar{1}0]\)-axis of the lattice, as indicated in Fig. 1d. Care has been taken to rule out the inevitable misalignment effects of an accidental out-of-plane component of the field, when the vector magnet is utilized. In the normal state (T = 1.8 K in Fig. 4a) of Sample #4 (Supplementary Fig. 7), the magnetoresistance Rs is found to be essentially independent of φ, displaying an isotropic behavior. Whereas in the superconducting state (T = 1.5 K in Fig. 4a), we observe a pronounced twofold symmetric oscillations of the Rs (see Fig. 4b), which is consistent across multiple samples including the heterointerfaces of a-YAlO3/KTaO3(111) and sister a-LaAlO3/KTaO3(111) (see Supplementary Fig. 8 − Supplementary Fig. 10 and Supplementary Note 2). In this case, the anisotropic Rs attains the maximum value when the magnetic field is directed along the special \([1\bar{2}1]\)-axis (φ = − 30° or 150°) that is in the direction of one of the principal axes of KTaO3(111) shown in Fig. 1c, and becomes minimum when the position with respect to that of maximum is shifted by 90° (φ = 60° or 240°). This finding implies that an extrinsic error from the experimental setup is unlikely to the source of the observed twofold anisotropy of magnetoresistance in the superconducting state at the heterointerface of a-YAlO3/KTaO3. In particular, the significantly large anisotropic ratio of Rs(φ = 60°)/Rs(φ = 150°) = 0.03 at 1.5 K corresponds to a putative misalignment angle estimated up to 88.03° (\(\cos\) 88.03° = 0.03) between the field and the basal plane49, which is impossible for such a large angle misalignment in the vector magnet, we could exclude the possible contribution from an accidental misalignment of the field with the film plane. Since the magnetoresistance minima approach zero in Rs(φ) curve measured at 1.5 K (see Fig. 4a), and considering the fact that the existence of conspicuous twofold symmetry in magnetoresistance manifests deep inside the superconducting region, which vanishes in the normal state (see Fig. 4a and Supplementary Fig. 11), we could further rule out the possibilities of extrinsic contributions, such as the magnetic field induced Lorentz force effect50 and the Fermi surface inherent to the KTaO3 with respect to the underlying threefold lattice symmetry26 (Fig. 1c and Supplementary Fig. 3), and thus demonstrate that this anisotropy with rotational symmetry breaking is an intrinsic property of the superconducting phase in a-YAlO3/KTaO3.
a In-plane angular-dependent magnetoresistance Rs at various temperatures for an applied field of 1 T. b Polar plots of the data in a. c In-plane angular-dependent μ0H\({}_{c2}^{\varphi }\) at various temperatures. d Polar plots of the data in c. The solid lines in c and d are the theoretical fits of the H\({}_{c2}^{\varphi }\) using the gap function of ∣Δgap∣2 with an admixture of s-wave and p-wave pairings, \({{{\Delta }}}_{{{{{{{{\rm{gap}}}}}}}}}({{{{{{{\bf{k}}}}}}}})=i[{{{\Delta }}}_{s}{\hat{\sigma }}_{0}+{{{\Delta }}}_{p}\sin ({k}_{x}){\hat{\sigma }}_{3}]{\hat{\sigma }}_{2}\). Here, Δs and Δp are the pairing amplitudes of s-wave and p-wave, respectively, \(\hat{\sigma }\) is the vector of Pauli matrices, and k is the momentum.
To further reveal the twofold symmetric superconductivity in a-YAlO3/KTaO3 in terms of the superconducting gap structure, we extract the upper critical field μ0Hc2 from the φ-dependent magnetoresistance Rs in the superconducting region determined by the criterion of 90% sheet resistance dropped from normal state, as shown in Fig. 4c. Here, it should be pointed out that although the values of Hc2 are changed by different criteria, the symmetry of Hc2 itself remains qualitatively (see Supplementary Fig. 12). In addition, it should be noted that the data shown here have been taken by averaging the raw data with positive and negative magnetic fields to avoid the possible asymmetric problem. Remarkably, the in-plane φ-dependent μ0H\({}_{c2}^{\varphi }\) also displays twofold symmetric oscillations (see Fig. 4d), providing additional strong evidence for the twofold rotational symmetry of the superconductivity in a-YAlO3/KTaO3. Furthermore, the oscillation of μ0H\({}_{c2}^{\varphi }\) has a π phase shift compared with that of the Rs (see Fig. 4b) such that for the φ value where superconductivity is hardest to suppress, μ0H\({}_{c2}^{\varphi }\) is the largest and Rs is the lowest (Fig. 4b, d), as expected from our intuitions50,51,52. Since μ0H\({}_{c2}^{\varphi }\) achieves its maximum for the field applied perpendicular to the main crystallographic axis, and minimum for the direction along the main crystallographic axis (see Figs. 1d and 4d), the superconducting gap leads to a maximum (or minimum) direction perpendicular (or parallel) to the main crystallographic axis, manifesting a rotational symmetry breaking state of superconducting a-YAlO3/KTaO3 with the direction of the minimum gap spontaneously pinned to the main crystallographic axis.
Discussion
Having experimentally established the intrinsic twofold anisotropy of the superconducting state of a-YAlO3/KTaO3, we now proceed to elaborate about its origin using the underlying symmetries of the crystal structure without requiring the details of the pairing mechanisms based on the group theoretical formulation of the Ginzburg-Landau theory53(also see Supplementary Note 2 and Supplementary Note 3 in details). This allows us to deduce fundamental information about the superconducting ground state in the a-YAlO3/KTaO3 heterointerface superconductors. From the viewpoint of group symmetry, if a superconductor possesses an inversion symmetry, the Pauli principle requires a totally antisymmetric Cooper pair wavefunction, which imposes the condition that the superconducting states should be either spin-singlet or spin-triplet, whereas mixed-parity states are forbidden53. In the a-YAlO3/KTaO3 the lack of inversion symmetry, however, tends to mix spin-singlet and spin-triplet driven by strong spin-orbit coupling54. Indeed, the conducting electrons with strong spin-orbit coupling originating from the heavy Ta 5d orbitals has been elucidated at the KTaO3 heterointerfaces26,33,55,56,57,58,59,60 (also see Supplementary Fig. 13). Due to the absence of a mirror plane parallel to the interface of a-YAlO3/KTaO3, the point group of a-YAlO3/KTaO3 is C3v, which does not contain the symmetry element of an inversion. This situation is analogue to non-centrosymmetric superconductors54,61. Upon inspecting the character table of C3v point group tabulated in Supplementary Table 2, we notice that the mixed-parity superconducting state only belongs to the A1+E-representation with the possible basis function of s+p. Notably, the two-dimensional irreducible representation of E could spontaneously break the threefold rotational symmetry of the crystal (see Fig. 1c and Supplementary Fig. 3), leading to a subsidiary uniaxial anisotropy or nematic superconductivity62,63, such as a uniaxial px-wave or py-wave pairing. Since the upper critical field is proportional to the square of the superconducting gap amplitude based on the Ginzburg-Landau theory and the Pippard definition of the coherence length49, μ0H\({}_{c2}^{\varphi }\propto|{{{\Delta }}}_{{{{{{{{\rm{gap}}}}}}}}}(\varphi ){|}^{2}\), only the s+px-wave pairing with the gap function of \({{{\Delta }}}_{{{{{{{{\rm{gap}}}}}}}}}({{{{{{{\bf{k}}}}}}}})=i[{{{\Delta }}}_{s}{\hat{\sigma }}_{0}+{{{\Delta }}}_{p}\sin ({k}_{x}){\hat{\sigma }}_{3}]{\hat{\sigma }}_{2}\) (here, Δs and Δp are the pairing amplitudes of s-wave and p-wave, respectively, \(\hat{\sigma }\) is the vector of Pauli matrices, and k is the momentum)61,64, could give rise to an overall twofold anisotropic gap and well reproduce the exact topology of the anisotropic H\({}_{c2}^{\varphi }\) shown in Fig. 4d. Therefore, the mix of s-wave and p-wave pairings driven by strong spin-orbit coupling is suggested to the source of the experimentally observed twofold anisotropic superconductivity at the KTaO3 heterointerfaces, which has long been a topic of interest sought in condensed matter physics. Further experiments, including probes of the superconducting gap by tunneling spectroscopy and/or Josephson junction experiments, will also be helpful for clarifying the underlying mixed-parity pairing nature of the twofold symmetric superconductivity that we observe.
In summary, we have experimentally observed spontaneous rotational symmetry breaking from threefold to twofold in the superconducting state of KTaO3(111) heterointerfaces with respect to an application of in-plane magnetic field. This in-plane anisotropic superconductivity is theoretically attributed to the intrinsic nature of mixed-parity unconventional superconductivity with an admixture of s-wave and p-wave pairing components, bringing with it fresh new insights into the study of emergent fascinating and non-trivial superconducting properties at the heterointerfaces with inversion symmetry breaking.
Methods
Thin film growth and structural characterizations
a-YAlO3 thin films are grown on KTaO3(111) single-crystal substrates (5 × 5 × 0.5 mm3) by pulsed laser deposition in an ultrahigh vacuum chamber (base pressure of 10−9 Torr). Prior to growth, the KTaO3 substrates are annealed at 600 °C for 30 mins in ultrahigh-vacuum to obtain a smooth surface (Supplementary Fig. 1). During deposition, a single crystal YAlO3 target (Kurt J. Lesker Company) is used to grow the a-YAlO3 films with a KrF excimer laser (Coherent 102, wavelength: λ = 248 nm). A pulse energy density of 1.5 J/cm2 and a repetition rate of 2 Hz are used. The a-YAlO3 films are deposited at temperatures ranging from 600 to 900 °C in a vacuum chamber to promote growth of the superconducting phase. All the samples are cooled to room temperature at a constant rate of 20 °C/min in vacuum after deposition. The quality of a-YAlO3 films under ambient conditions is examined by atomic force microscopy (AFM, Asylum Research MFP-3D Classic) and by four-circle X-ray diffraction (XRD, Bruker D8 Discover, Cu Kα radiation, λ = 1.5406 Å) operated in HR mode using a three-bounce symmetric Ge (022) crystal monochromator.
STEM measurements
Cross-sectional specimens for electron microscopy are prepared with Focused Ion Beam (FIB) (Helios-G4-CX, Thermo Fisher Scientific) using lift-out method. The HR-STEM images are performed on a double aberration corrected field-emission STEM (Themis Z, Thermo Fisher Scientific) operated at 300 kV. For HAADF-STEM imaging, the semi-convergent angle of the probe forming lens is set to 21.4 mrad. The geometric aberrations within the probe forming lens aperture have been effectively tuned to zero using probe corrector (SCORR, CEOS GmbH). The semi-collection angle of the HAADF detector is 76–200 mrad. Furthermore, the chemical composition of the interface is qualitatively analyzed using EDX in STEM spectrum imaging mode. The EDX are collected using 4 silicon drift detector (SDD) system (Super X detector, Thermo Fisher Scientific). The beam current for STEM-EDX analysis is about 200 pA.
Electrical transport measurements
The electrical transport measurements are performed using a commercial cryostat with temperature ranging from 1.5 to 300 K (Oxford Instruments TeslatronPT cryostat system), physical properties measurement system with temperature ranging from 0.5 to 300 K (PPMS, Quantum Design), and 10 mK dilution refrigerator with vector magnet (Oxford Instruments Triton 200). The Hall bar structure (Fig. 1d) is fabricated by ion-beam etching to systemically measure the electrical transport properties. The vector magnet is utilized to reveal the in-plane anisotropy of magnetoresistance in the superconducting state shown in Fig. 4a, and the samples are mounted on a mechanical rotator in a 4He cryostat to clarify the anisotropy of Hc2 shown in Fig. 4c. The misalignment of the field with the film plane is estimated to be less than 2° and 7° for vector magnet and mechanical rotator, respectively, as our experimental errors.
Data availability
The relevant data supporting our key findings are available within the article and the Supplementary Information file. All raw data generated during our current study are available from the corresponding authors upon reasonable request.
References
Saito, Y., Nojima, T. & Iwasa, Y. Highly crystalline 2D superconductors. Nat. Rev. Mater. 2, 16094 (2017).
Mannhart, J. & Schlom, D. G. Oxide interfaces: an opportunity for electronics. Science 327, 1607 (2010).
Zubko, P. et al. Interface physics in complex oxide heterostructures. Annu. Rev. Condens. Matter Phys. 2, 141 (2011).
Hwang, H. Y. et al. Emergent phenomena at oxide interfaces. Nat. Mater. 11, 103 (2012).
Reyren, N. et al. Superconducting interfaces between insulating oxides. Science 317, 1196 (2007).
Li, L. et al. Coexistence of magnetic order and two-dimensional superconductivity at LaAlO3/SrTiO3 interfaces. Nat. Phys. 7, 762 (2011).
Bert, J. A. et al. Direct imaging of the coexistence of ferromagnetism and superconductivity at the LaAlO3/SrTiO3 interface. Nat. Phys. 7, 767 (2011).
Dikin, D. A. et al. Coexistence of superconductivity and ferromagnetism in two dimensions. Phys. Rev. Lett. 107, 056802 (2011).
Caviglia, A. D. et al. Electric field control of the LaAlO3/SrTiO3 interface ground state. Nature 456, 624 (2008).
Biscaras, J. et al. Two-dimensional superconducting phase in LaTiO3/SrTiO3 heterostructures induced by high-mobility carrier doping. Phys. Rev. Lett. 108, 247004 (2012).
Biscaras, J. et al. Multiple quantum criticality in a two-dimensional superconductor. Nat. Mater. 12, 542 (2013).
Zegrodnik, M. & Wójcik, P. Superconducting dome in LaAlO3/SrTiO3 interfaces as a direct consequence of the extended s-wave symmetry of the gap. Phys. Rev. B 102, 085420 (2020).
Wójcik, P., Nowak, M. P. & Zegrodnik, M. Impact of spin-orbit interaction on the phase diagram and anisotropy of the in-plane critical magnetic field at the superconducting LaAlO3/SrTiO3 interface. Phys. Rev. B 104, 174503 (2021).
Michaeli, K., Potter, A. C. & Lee, P. A. Superconducting and ferromagnetic phases in SrTiO3/LaAlO3 oxide interface structures: Possibility of finite momentum pairing. Phys. Rev. Lett. 108, 117003 (2012).
Liu, C. et al. Two-dimensional superconductivity and anisotropic transport at KTaO3 (111) interfaces. Science 371, 716 (2021).
Chen, Z. et al. Electric field control of superconductivity at the LaAlO3/KTaO3(111) interface. Science 372, 721 (2021).
Thompson, J. R., Boatner, L. A. & Thomson, J. O. Very low-temperature search for superconductivity in semiconducting KTaO3. J. Low. Temp. Phys. 47, 467 (1982).
Ueno, K. et al. Discovery of superconductivity in KTaO3 by electrostatic carrier doping. Nat. Nanotechnol. 6, 408 (2011).
Han, Y. L. et al. Two-dimensional superconductivity at (110) LaAlO3/SrTiO3 interfaces. Appl. Phys. Lett. 105, 192603 (2014).
Wang, Z. et al. Anisotropic two-dimensional electron gas at SrTiO3(110). Proc. Natl Acad. Sci. 111, 3933 (2014).
Monteiro, A. M. R. V. L. et al. Two-dimensional superconductivity at the (111) LaAlO3/SrTiO3 interface. Phys. Rev. B 96, 020504 (2017).
Pai, Y.-Y. et al. One-dimensional nature of superconductivity at the LaAlO3/SrTiO3 interface. Phys. Rev. Lett. 120, 147001 (2018).
Chen, Z. et al. Two-dimensional superconductivity at the LaAlO3/KTaO3 (110) heterointerface. Phys. Rev. Lett. 126, 026802 (2021).
Liu, C. et al. Tunable superconductivity and its origin at KTaO3 interfaces. Nat. Commun. 14, 951 (2023).
Hu, K. et al. Effects of electron correlation, electron-phonon coupling, and spin-orbit coupling on the isovalent Pd-substituted superconductor SrPt3. Phys. Rev. B 93, 214510 (2016).
Bruno, F. Y. et al. Band structure and spin-orbital texture of the (111)-KTaO3 2D electron gas. Adv. Electron. Mater. 5, 1800860 (2019).
Venditti, G. et al. Anisotropic Rashba coupling to polar modes in KTaO3. J. Phys. Mater. 6, 014007 (2023).
Kozii, V. & Fu, L. Odd-parity superconductivity in the vicinity of inversion symmetry breaking in spin-orbit-coupled systems. Phys. Rev. Lett. 115, 207002 (2015).
Arribi, P. V., Paramekanti, A. & Norman, M. R. Striped electron fluid on (111) KTaO3. Phys. Rev. B 103, 035115 (2021).
Biswas, A., Yang, C.-H., Ramesh, R. & Jeong, Y. H. Atomically flat single terminated oxide substrate surfaces. Prog. Surf. Sci. 92, 117 (2017).
Chen, Z. et al. Carrier density and disorder tuned superconductor-metal transition in a two-dimensional electron system. Nat. Commun. 9, 4008 (2018).
Potter, A. C. & Lee, P. A. Engineering a p+ip superconductor: Comparison of topological insulator and Rashba spin-orbit-coupled materials. Phys. Rev. B 83, 184520 (2011).
Zhang, H. et al. Highly mobile two-dimensional electron gases with a strong gating effect at the amorphous LaAlO3/KTaO3 interface. ACS Appl. Mater. Interfaces 9, 36456 (2017).
Mallik, S. et al. Superfluid stiffness of a KTaO3-based two-dimensional electron gas. Nat. Commun. 13, 4625 (2022).
Ning, Z. et al. Evidence for ferromagnetism in KTaO3 heterointerface superconductors. arXiv:2302.01549 (2023).
Liu, Z. Q. et al. Origin of the two-dimensional electron gas at LaAlO3/SrTiO3 interfaces: The role of oxygen vacancies and electronic reconstruction. Phys. Rev. X 3, 021010 (2013).
Tinkham, M. Introduction to superconductivity. (McGraw-Hill, 1996).
Chandrasekhar, B. S. A note on the maximum critical field of high-field superconductors. Appl. Phys. Lett. 1, 7 (1962).
Clogston, A. M. Upper limit for the critical field in hard superconductors. Phys. Rev. Lett. 9, 266 (1962).
Kim, M. et al. Intrinsic spin-orbit coupling in superconducting δ-doped SrTiO3 heterostructures. Phys. Rev. B 86, 085121 (2012).
Tinkham, M. Effect of fluxoid quantization on transitions of superconducting films. Phys. Rev. 129, 2413 (1963).
Wang, L. et al. Two-dimensional superconductivity at the titanium sesquioxide heterointerface. ACS Nano 16, 16150 (2022).
Zhang, G. et al. Quantum metallic state in the titanium sesquioxide heterointerface superconductor. arXiv:2211.04035 (2022).
Lu, J. M. et al. Evidence for two-dimensional Ising superconductivity in gated MoS2. Science 350, 1353 (2015).
Jiang, D. et al. Strong in-plane magnetic field-induced reemergent superconductivity in the van der Waals heterointerface of NbSe2 and CrCl3. ACS Appl. Mater. Interfaces 12, 49252 (2020).
Kosterlitz, J. M. & Thouless, D. J. Long range order and metastability in two dimensional solids and superfluids. J. Phys. Chem. 5, L124 (1972).
Beasley, M. R., Mooij, J. E. & Orlando, T. P. Possibility of vortex-antivortex pair dissociation in two-dimensional superconductors. Phys. Rev. Lett. 42, 1165 (1979).
Halperin, B. I. & Nelson, D. R. Resistive transition in superconducting films. J. Low. Temp. Phys. 36, 599 (1979).
Xiang, Y. et al. Twofold symmetry of c-axis resistivity in topological kagome superconductor CsV3Sb5 with in-plane rotating magnetic field. Nat. Commun. 12, 6727 (2021).
Xue, H. et al. Fourfold symmetric superconductivity in spinel oxide LiTi2O4(001) thin films. ACS Nano 16, 19464 (2022).
Hamill, A. et al. Two-fold symmetric superconductivity in few-layer NbSe2. Nat. Phys. 17, 949 (2021).
Li, J. et al. Nematic superconducting state in iron pnictide superconductors. Nat. Commun. 8, 1880 (2017).
Sigrist, M. & Ueda, K. Phenomenological theory of unconventional superconductivity. Rev. Mod. Phys. 63, 239 (1991).
Bauer, E. & Sigrist, M. Non-centrosymmetric superconductors: Introduction and overview. (Springer, 2012).
Wadehra, N. et al. Planar Hall effect and anisotropic magnetoresistance in polar-polar interface of LaVO3-KTaO3 with strong spin-orbit coupling. Nat. Commun. 11, 874 (2020).
Rubi, K. et al. Electronic subbands in the a-LaAlO3/KTaO3 interface revealed by quantum oscillations in high magnetic fields. Phys. Rev. Res. 3, 033234 (2021).
Vicente-Arche, L. M. et al. Spin-charge interconversion in KTaO3 2D electron gases. Adv. Mater. 33, 2102102 (2021).
Trier, F. et al. Oxide spin-orbitronics: spin-charge interconversion and topological spin textures. Nat. Rev. Mater. 7, 258 (2022).
Gupta, A. et al. Unique signatures of Rashba effect in angle resolved magnetoresistance. Adv. Quantum Technol. 5, 2100105 (2022).
Gupta, A. et al. KTaO3-The new kid on the spintronics block. Adv. Mater. 34, 2106481 (2022).
Yip, S. Noncentrosymmetric superconductors. Annu. Rev. Condens. Matter Phys. 5, 15 (2014).
Pan, Y. et al. Rotational symmetry breaking in the topological superconductor SrxBi2Se3 probed by upper-critical field experiments. Sci. Rep. 6, 28632 (2016).
Yonezawa, S. Nematic superconductivity in doped Bi2Se3 topological superconductors. Condens. Matter 4, 2 (2019).
Annett, J. F. Symmetry of the order parameter for high-temperature superconductivity. Adv. Phys. 39, 83 (1990).
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant Nos. 61871134, 11927807, 12004251, 12174430, and 92065203), the Strategic Priority Research Program B of Chinese Academy of Sciences (Grant No. XDB33000000), the Beijing Nova Program (Grant No. Z211100002121144), and Shanghai Science and Technology Committee (Grant Nos. 23ZR1404600, 20DZ1100604, 20PJ1410900, 20ZR1436100, and 21YF1429200). The authors thank the Synergetic Extreme Condition User Facility (SECUF) at Institute of Physics, Chinese Academy of Sciences.
Author information
Authors and Affiliations
Contributions
G.Z., L.W., J.W., and G.L. contributed equally to this work. W.L. conceived the project and designed the experiments. G.Z. grew the samples. G.Z., J.W., G.L., G.Y., Y.S., L.W., Z.N., J.S., and J.L. performed the electrical transport measurements. H.X. and Z.A. fabricated the Hall bar structure on the thin films. Y.W., J.X., and Y.C. assisted the electrical transport experiments. G.H. and C.Z. performed scanning transmission electron microscopy measurements. W.L. wrote the paper. All authors discussed the results and gave approval to the final version of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, G., Wang, L., Wang, J. et al. Spontaneous rotational symmetry breaking in KTaO3 heterointerface superconductors. Nat Commun 14, 3046 (2023). https://doi.org/10.1038/s41467-023-38759-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-023-38759-0
This article is cited by
-
Light-induced giant enhancement of nonreciprocal transport at KTaO3-based interfaces
Nature Communications (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.