Abstract
Solid-state control of the thermal conductivity of materials is of exceptional interest for novel devices such as thermal diodes and switches. Here, we demonstrate the ability to continuously tune the thermal conductivity of nanoscale films of La0.5Sr0.5CoO3-δ (LSCO) by a factor of over 5, via a room-temperature electrolyte-gate-induced non-volatile topotactic phase transformation from perovskite (with δ ≈ 0.1) to an oxygen-vacancy-ordered brownmillerite phase (with δ = 0.5), accompanied by a metal-insulator transition. Combining time-domain thermoreflectance and electronic transport measurements, model analyses based on molecular dynamics and Boltzmann transport equation, and structural characterization by X-ray diffraction, we uncover and deconvolve the effects of these transitions on heat carriers, including electrons and lattice vibrations. The wide-range continuous tunability of LSCO thermal conductivity enabled by low-voltage (below 4 V) room-temperature electrolyte gating opens the door to non-volatile dynamic control of thermal transport in perovskite-based functional materials, for thermal regulation and management in device applications.
Similar content being viewed by others
Introduction
Perovskite oxides with nominal general formula ABO3 are well known for their immensely tunable structures and compositions, and thus physical and chemical properties, making them attractive for applications in superconductivity1, catalysis2, various memory devices3, solid oxide fuel cells4, etc. A and B site cations can be readily substituted to tailor the crystal structure, electronic structure, and doping, while oxygen stoichiometry (e.g., oxygen deficiency δ) adds additional control, particularly via oxygen vacancies (VOs). Recently, active control of the oxygen stoichiometry in perovskites has come into the spotlight, enabling reversible voltage control of electronic, magnetic, and optical properties5,6,7,8,9, with much technological potential. Electrochemical operating mechanisms5, often present in electrolyte-gated perovskite-based devices employing ionic liquid or gel electrolytes, provide one powerful approach to this, where perovskite cobaltites have emerged as prototypical targets. In strontium cobaltite, SrCoO3−δ, for example, a reversible non-volatile topotactic phase transformation between perovskite (P) SrCoO3−δ (with randomly distributed VO) and oxygen-vacancy-ordered brownmillerite (BM) SrCoO2.5 has been achieved through electrolyte gating10,11,12. Due to the highly contrasting electronic and magnetic ground states of these two phases, voltage-driven cycling drives metal-insulator and ferromagnetic-antiferromagnetic transitions, as well as large changes in optical properties, drawing increasing attention10,11,12,13. Recent work by some of us established that such phenomena are in fact possible throughout the entire La1−xSrxCoO3−δ phase diagram, providing control over the threshold voltage for the P to BM transformation (via x), and circumventing issues with the air stability of P-SrCoO3 (La0.5Sr0.5CoO3, for example, is much more air-stable)14. In general, the electronic and magnetic properties of La1−xSrxCoO3−δ have been extensively explored and manipulated via electrolyte gating, via both electrostatic and electrochemical mechanisms6,14,15,16.
While the above focuses on structural, electronic, magnetic, and optical properties, electrolyte gating is also attractive for voltage-based control of thermal properties, and associated applications. The latter include thermal diodes, thermal switches, and energy conversion and storage17,18, wherein the thermal conductivity of materials is dynamically tuned to achieve desired performance. For example, Cho et al. demonstrated reversible voltage-based tuning of the thermal conductivity of the battery cathode material LixCoO2, from 3.7 to 5.4 W m−1 K−1, via electrochemical modulation19. More recently, Lu et al. voltage tuned the thermal conductivity of SrCoO3-δ by a factor of ∼2.5 by transforming (oxidizing) as-deposited BM-SrCoO2.5 to P-SrCoO3-δ, and by a further factor of ∼4 by transforming (reducing) BM-SrCoO2.5 to a hydrogenated H-SrCoO2.5 phase, both via non-volatile electrolyte gating10. Notably, the factor of 4 tuning ratio of thermal conductivity via a bi-state (BM phase → H-containing phase) single-step tuning process appears to be a maximum among literature experimental studies10,19,20,21,22,23,24,25,26,27,28. While groundbreaking, it should be noted, however, that this work was not able to achieve continuous control of δ between P-SrCoO3-δ and BM-SrCoO2.5 by room-temperature (RT) electrolyte gating, that reversibility and speed remain open questions (particularly when H is involved), and that electronic contributions to the thermal conductivity tuning were found to be negligible, limiting the magnitude of the thermal conductivity tuning ratio10.
In order to explore the limits of voltage-based tuning of thermal conductivity via electrolyte gating between P and BM phases, in this work we focus on La0.5Sr0.5CoO3−δ (LSCO) as a model system. Critically, this system enables electrolyte gating from an as-deposited P phase with pristine metallic electrical conductivity, to an insulating BM phase, maximally modulating the electrical resistivity, with excellent air stability in both phases14. Such an approach has not been reported with SrCoO3-δ. We combine time-domain thermoreflectance (TDTR) measurements with high-resolution X-ray diffraction (XRD) and electronic transport measurements to explore the thermal conductivity tuning of LSCO through the topotactic P → BM transformation as a function of gate voltage (Vg). The Vg-driven cubic P to orthorhombic BM transformation and associated metal-insulator transition are found to enable continuous, RT tuning of the thermal conductivity of LSCO films by a remarkable factor of over 5, a record value for such an approach. Combining temperature (T)-dependent thermal measurements with model analyses based on molecular dynamics (MD) simulations and the Boltzmann transport equation (BTE), and comparing to accompanying electrical transport measurements, we further establish the scattering mechanisms of heat carriers that enable this tuning of thermal conductivity. The relative impacts of the Sr substitution, the Vg-driven metal-insulator transition (i.e., the electronic contribution to the thermal conductivity), δ variation, crystal structure modification, and lattice symmetry change, are all discussed in detail.
Results
Structural characterization of the P → BM phase transformation
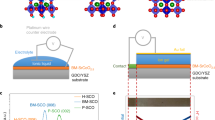
In this work, ~45-nm-thick films of P-LSCO epitaxially deposited on LaAlO3(001) (LAO) substrates were driven to the VO-ordered BM structure (BM-LSCO, δ ~ 0.5) by removing oxide ions (O2−) using an all-solid-state side-gated electrochemically operating electrolyte-gate device, shown schematically in Fig. 1a. Application of positive Vg accumulates cations in the ion-gel electrolyte at the interface with the P-LSCO, producing a large electric field and removing O2− from the LSCO film (equivalently, introducing VOs)14, in a non-volatile fashion. It is known from prior work that this mechanism initially reduces P-LSCO (i.e., increases δ), then leads to the formation of BM-LSCO in a matrix of P-LSCO (i.e., a P-BM mixed phase), and then finally to pure BM-LSCO, as a function of Vg14. The P and BM structures are shown schematically in Fig. 1b, where the perovskite phase (left) is fully oxygenated (with CoO6 octahedra), while the BM phase (right) consists of perovskite layers separated by comparatively oxygen-deficient CoO4 tetrahedra10,11,12,14,29. The VOs in BM are ordered not only in alternate planes along the c-axis, but also in lines in the a-b-plane. The P → BM transformation thus quadruples the c-axis lattice parameter of the original P-LSCO and lowers the lattice symmetry from cubic to orthorhombic10,11,12,14,29.
a Schematic of the La0.5Sr0.5CoO3-δ-film-based side-gated electrolyte-gate devices used in this study, with an overlying ion gel as the electrolyte. I and V are the current and voltage for measurement of four-wire channel resistance, while Vg is the gate voltage. b Crystal structure of P-LSCO (left) and BM-LSCO (right). When Vg is applied, the LSCO film is transformed from P → BM and vice-versa depending on the Vg polarity: Vg > 0 drives to BM, and Vg < 0 drives to P. c X-ray diffraction from LSCO devices on LAO(001) substrates after gating to various Vg. The y-axis represents the XRD intensity in arbitrary units, plotted on a logarithmic scale and offset for better visualization. d T-dependence of the resistivity (from a four-wire measurement) for selected LSCO films after gating to various Vg.
Figure 1c shows high-resolution wide-angle specular XRD scans of representative LSCO film devices after ion-gel gating to various Vg from 0 to 3.5 V. Ion-gel gating was performed by sweeping Vg at 0.5 mV s−1 to the target voltage. Two-wire transport measurements were made during the sweep, while four-wire T-dependent transport and TDTR measurements were made ex situ, after bias removal, enabled by the non-volatility of the gate effect10,11,12,14,29. Purely to facilitate TDTR measurements (which require the deposition of an overlying metallic transducer film), each scan here is from a different ion-gel-gated sample. The ungated (black) and +3.5 V (purple) scans were performed on larger-channel-area devices (4 × 3.5 mm2), specifically for better XRD signal-to-noise ratio (SNR), while the other (intermediate-voltage) scans (1.0 V, 2.0 V, and 3.0 V) were performed on 1 × 1 mm2 channel devices, as used for four-wire transport measurements. The ungated data (black) reveal the expected phase-pure epitaxial P-LSCO on the LAO(001) substrate (in addition to a Pt(111) peak from the device electrodes), consistent with previous reports on LSCO deposited via high-pressure-oxygen sputtering6,14,15,16,30. Additional characterization of P-LSCO films can be found in Supplementary Section 1 and Supplementary Fig. 1, establishing high epitaxial quality and full strain to the substrate.
Moving to the gated-LSCO film XRD patterns in Fig. 1c, we find a clear downshift of the P(002) peaks with increasing Vg, indicating expansion of the P-LSCO c-axis lattice constant due to VO formation in the P phase14,15 (more information on c-axis lattice parameters vs. Vg can be found in Supplementary Table 1). At 2 V and beyond, a (001)-oriented BM structure is then detected via the emergence of additional peaks around 34 and 58°, due to the BM(006) and BM(0010) reflections. This signifies the quadrupling of the unit cell in the VO-ordered BM phase. Initially, these BM-LSCO peaks occur along with P(002) peaks, indicating a mixed phase region, as observed previously and interpreted in terms of phase coexistence across a first-order P → BM transformation14. At 3 V, however, the P(002) peak continues to downshift, indicating further lattice expansion, additional VO formation, and near-complete transformation to BM (the P(002) reflection then becomes the BM(008)). Concomitantly, the BM(006) and (0010) peaks intensify, while the P(002) peak diminishes. By 3 V, the intensity ratio of the BM(008) to BM(006) reflections is in fact ~70, relatively close to the value of ~40 previously observed for fully transformed BM-LSCO after ion-gel gating14. Interestingly, little difference is then observed between films gated to 3 and 3.5 V. We interpret this as resistance to further removal of O2− beyond the BM-LSCO stoichiometry (i.e., δ ~ 0.5) at voltages above 3 V. Regarding the structural perfection of the gated BM-LSCO, more detailed analysis (peak fitting) of the 3.5 V sample (purple) on the larger-channel-area-device revealed additional disorder in the VO sublattice compared to as-deposited BM films (e.g., SrCoO2.5) reported in literature11,12,31,32,33,34 (see Supplementary Section 1). It should also be noted that the P(002) peak intensity, although weak, still remains after 3 V. This relatively low-intensity peak arises from the portion of the P-LSCO film buried beneath the Pt contacts, however, which is ungated. Overall, we thus conclude from Fig. 1c that a reduced P phase exists up to ∼1 V, beyond which P + BM phase coexistence persists to ∼3 V, followed by near phase-pure BM. These findings are in good general agreement with prior LSCO gating studies14. More detailed information on these gated LSCO films, including thicknesses, applied Vg, and estimated phases can be found in Supplementary Section 1. As a final comment on these data, we note that, consistent with prior work on gated LSCO14,15, we find no significant evidence of the hydrogenated phase seen in gating studies of SrCoO3-δ. The transformation in this work is thus simply between P and BM phases; it is therefore bi-state not tri-state switching.
Electronic transport properties of ion-gel-gated LSCO films
Due to the very different electronic characteristics of the LSCO P and BM phases, major changes in electronic transport accompany the Vg-induced P → P + BM → BM transformation deduced above. Figure 1d shows electrical resistivity (ρ) vs. temperature (T) data for an ungated LSCO film, as well as films gated to 1–4 V. The ungated LSCO film is a metallic ferromagnet with a residual resistivity ρ0 ≈ 70 μΩ cm, a residual-resistivity-ratio of 2.95, and TC ≈ 220 K. This is as expected for relatively thick films of La1−xSrxCoO3−δ with x = 0.5, where metallic conduction and long-range ferromagnetism are observed for x > 0.1735,36,37. After gating to 1 V, the metallic conduction in the LSCO film is maintained, albeit with slightly higher ρ, reflecting the additional VO density introduced into the P lattice. As electron donors, VO compensate holes (the dominant charge carriers in LSCO), thus increasing ρ. The relatively small change in ρ for LSCO at 1 V compared to ungated LSCO is consistent with Fig. 1c in that the P phase is retained, but with a higher δ. After applying 2 V, however, the RT ρ increases nearly 100-fold, reflecting not only a substantial increase in VO concentration (larger δ), but also entry into the P + BM phase coexistence region. The unusual form of ρ vs. T for the 2-V-gated sample (note the flattening at low T) is also consistent with this; lateral inhomogeneity would be expected in this situation and indeed we detected in-plane anisotropy in the orthogonal electrical resistances in four-wire van der Pauw measurements at low T. For the samples gated to 3 and 4 V, where XRD reveals near-phase-pure BM (Fig. 1c), the LSCO films then exhibit completely insulating behavior in Fig. 1d, with ρ(RT) of ~0.5 and ∼2 Ω cm, respectively. This represents a factor of ∼104 between the RT ρ of ungated P-LSCO and BM-LSCO, comparable to literature values for electrolyte-gated SrCoO3−δ and La0.5Sr0.5CoO3−δ12,14.
In addition to these ex situ measurements of T-dependent four-wire resistivity (Fig. 1d), in-situ measurements of two-terminal resistance (i.e., source-drain resistance) were also made while sweeping to the target Vg for each sample (see Supplementary Fig. 2). These two-terminal measurements show reassuring overall agreement with the ex-situ trends in resistivity depicted in Fig. 1d, i.e., minor increases in resistance before ~2 V, a sharp increase between ~2–3 V, then a region with relatively weak Vg dependence, indicating completion of the P → P + BM → BM transformation. These data (Supplementary Fig. 2) also highlight the high reproducibility of the gating process, underscoring the robustness of our approach.
Tuning of LSCO thermal conductivity with gate voltage
The thermal conductivities of LSCO thin films gated to various Vg (from 0 to 4 V) were measured with the TDTR approach, which is an ultrafast-laser-based pump-probe technique38,39. All TDTR measurements were made ex-situ, after biasing and ion-gel removal, taking advantage of the non-volatile nature of the electrolyte gating in this case10,11,12,14,29. Figure 2a illustrates the sample configuration for TDTR measurements, which consists of a thin layer of Pt deposited on top of the LSCO films, serving as the heat source and thermometer. Pt was chosen as the transducer for this study, instead of the typical Al, specifically to avoid Al-gettering-induced VO formation in the underlying LSCO40. By varying the modulation frequency in the TDTR approach, the measurement sensitivity to the LSCO thermal conductivity and the thermal interfaces can be tailored. This enables us to also extract the interfacial thermal conductance between the Pt transducer film and the LSCO film (G1), and between the LSCO film and the LAO substrate (G2), by combining data reduction of routine TDTR measurements with dual-frequency TDTR analyses (see Supplementary Section 3 for details).
a Sample configuration for TDTR measurements. b Representative TDTR ratio signals of the ungated LSCO film measured at three modulation frequencies. The solid lines are the best fits to the through-plane thermal measurement data based on a heat diffusion model. The data reduction gives a through-plane thermal conductivity of 4.6 ± 2.0 W m−1 K−1 for this ungated LSCO film.
As part of the input parameter set used in the analysis of TDTR data to determine the thermal conductivity of LSCO films, the thickness (dPt) and thermal conductivity (ΛPt) of the Pt transducer were obtained, respectively, from grazing incidence X-ray reflectometry and four-point probe measurements (incorporated with the Wiedemann-Franz law, WFL) of a standard Si/SiO2(300 nm)/Pt(~70 nm) reference sample at RT. For TDTR data reduction as a function of T, ΛPt is set based on literature data41, as is the T-dependent volumetric heat capacity of the transducer (CPt)42. In addition to the Pt transducer, some dimensional parameters and thermal properties of the LSCO film (dLSCO, CLSCO) and LAO substrate (ΛLAO, CLAO) are also needed. The T-dependent ΛLAO data were obtained from TDTR measurements of a bare LAO substrate. CLSCO and CLAO were calculated as a function of T based on the Debye model using the literature reported Debye temperature43,44, and are in good agreement with literature data43,45,46,47,48 (see details in Supplementary Section 6 and Supplementary Fig. 7). For TDTR measurements at low T (T < 273 K) where the material’s thermal properties (i.e., specific heat and thermal conductivity) exhibit stronger T dependence, we also performed T-dependent corrections, taking into account the impact of steady-state heating and the pump per-pulse heating (details are presented in Methods and Supplementary Section 6).
Figure 2b shows representative TDTR ratio data of the in-phase and out-of-phase thermoreflectance signals (−Vin/Vout) measured on the ungated LSCO film at RT. Three modulation frequencies (1.5, 9.0, and 18.8 MHz) were used to enable tailoring of the measurement sensitivity. The solid lines in Fig. 2b are best fits to the TDTR data based on a heat diffusion model for a multi-layer structure38,49. At RT, the fitted through-plane thermal conductivity of the ungated LSCO sample is 4.6 ± 2.0 W m−1 K−1. The interfacial thermal conductances of the Pt/LSCO (G1) and LSCO/LAO (G2) interfaces are determined as 400 and 800 MW m−2 K−1, respectively. More details about the TDTR thermal measurements and the extraction of G1 and G2 are provided in Methods, and Supplementary Section 3.
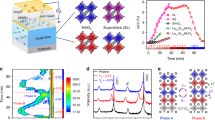
The RT electrical resistivity and thermal conductivity of LSCO thin films are summarized as functions of Vg in Fig. 3a. As Vg increases from 0 to 4 V, the change in ρ reaches almost five orders of magnitude, a clear reflection of the metal-insulator transition shown in Fig. 1d. Coincident with this, the central experimental result of this work is that the through-plane thermal conductivity of LSCO decreases from 4.6 ± 2.0 to 0.85 ± 0.32 W m−1 K−1 as Vg varies from 0 to 4 V, i.e., a factor of more than 5 reduction via ion-gel gating. We consider this record-high tuning factor to be for the through-plane thermal conductivity, acknowledging the possibility of thermal transport anisotropy in the BM-LSCO film. It is reasonable, however, to convert the in-plane electrical resistivity to a through-plane thermal conductivity for the purposes of comparison, as we discussed in Supplementary Section 7. We emphasize that the thermal conductivity can be continuously tuned over this range, in a non-volatile fashion, at room temperature. It should be noted that the thermal conductivity of our as-deposited P-LSCO films (with x = 0.5 and δ ≈ 0.1, see Methods and the discussion below regarding the determination of δ) is 4.6 ± 2.0 W m−1 K−1, which is less than half the equivalent values for several unsubstituted ABO3 perovskites (e.g., 11 W m−1 K−1 for SrTiO350, 13 W m−1 K−1 for BaSnO351, and 13 W m−1 K−1 for LaAlO352). Also, prior experimental studies reported a bulk thermal conductivity of 6 W m−1 K−1 for single-crystal La0.7Sr0.3CoO352,53. The significantly smaller thermal conductivities of La0.7Sr0.3CoO3 and La0.5Sr0.5CoO3 are partially attributed to enhanced phonon-defect scattering resulting from the mass mismatch and local strains induced by Sr substitution for La51,52,53. Below, we analyze the change of thermal conductivity versus Vg in detail, including discussing the contributions to the thermal conductivity from various critical factors.
a The thermal conductivity (left axis) and electrical resistivity (right axis) of LSCO films, b the interfacial thermal conductance between Pt and LSCO, and c oxygen non-stoichiometry due to vacancies, as functions of Vg. In panel a, Λtot represents the measured total thermal conductivity of the LSCO films. The measurement uncertainty of LSCO thermal conductivity decreases versus Vg from ~40% to ~10%. Λel represents the electronic thermal conductivity estimated from electrical conductivity based on the Wiedemann-Franz law. The black dash-dotted lines represent the upper and lower limits of Λel based on different Lorenz numbers (L). The dashed lines serve as guides to the eye. In panel b, the measurement uncertainty shown in the figure also decreases versus Vg, from ~50% to ~30%. In panel c, δ = 0.5 (blue circles) is assumed for the complete transition to brownmillerite (Vg ≥ 3 V), as our method used to estimate δ (red squares) is not valid above δ ≈ 0.25 (see Methods). The red-blue graded dashed line serves as a guide to the eye. d MD simulation results, obtained from both Green-Kubo MD (GKMD) and nonequilibrium MD (NEMD), for the lattice thermal conductivity of LSCO with different δ. The uncertainty of calculation results is within 10%. In all panels, the vertical pink and blue dashed lines represent, respectively, the starting and ending points of the P → P + BM → BM transformations. e Comparison of thermal conductivity tuning factor through bi-state tuning process in this work and previous experimental studies10,19,20,21,22,23,24,25,26,27,28, including PbZr0.3Ti0.7O3 (PZTO, 5 cycles)20,21, PbZrO3 (PZO, 10+ cycles)22, PbTiO3 (PTO)23, BiFeO3 (BFO)24, bio-polymers (B-P, 10+ cycles)25, azobenzene polymers (A-P, 6 cycles)26, liquid crystal networks (LCN)27, LixCoO2 (LCO, 2 cycles)19, WO3 (WO, 3 cycles)28, and SrCoO3-δ (SCO, 1 cycle, and H-SCO)10. Here, one cycle is defined as the transformation from state/phase A to state/phase B, and then return to state/phase A. Cycle numbers are provided when available from the literature. Note: During the review period of this work, several latest papers appeared reporting the tuning of materials’ thermal conductivities that were not included in Fig. 3e. These latest studies report a tuning ratio of ~4x for the thermal conductivity of SCO70, ~1.27x for the thermal conductivity of ferroelectric Pb(Mg1/3Nb2/3)O3–PbTiO371, and ~1.05x for the thermal conductivity of PZT72 at near room temperature.
It is important to note, however, that the Vg-driven P → BM and metal-insulator transitions also impact thermal transport across the Pt/LSCO interfaces. Figure 3b summarizes the results on G1 extracted from TDTR, where a smaller G1 is observed when LSCO is gated to higher Vg. For BM-LSCO, with insulating behavior, heat can be transferred across the Pt/BM-LSCO interface via two channels: electron-phonon interactions in Pt in series with the phonon–phonon interactions (between Pt and BM-LSCO phonons). The average measured G1 (170 MW m−2 K−1) of our BM-LSCO is comparable to the values of interfacial thermal conductance between Pt and oxides reported in literature54,55,56,57 (Supplementary Fig. 4). However, for Vg < 3 V, the P phase in the LSCO films provides an additional channel for interfacial heat transfer, via electron-electron interactions (between Pt and P-LSCO) across the interface58,59, thus leading to larger G1. This increase in G1 reduces the measurement sensitivity to G1 (Supplementary Fig. 3). As a result, we used a nominal value of G1 (400 MW m−2 K−1, black dashed line in Fig. 3b) for LSCO films at Vg < 2 V, when measurement sensitivity is insufficient to determine G1 (i.e., the choice of G1 value does not change the fitting results of the LSCO thermal conductivity). Besides, G2 of the LSCO/LAO epitaxial interface is measured to be 800 WM m−2 K−1 using the dual-frequency TDTR approach with enhanced measurement sensitivity to G260 (see Supplementary Section 3 for more details). This value of G2 is consistent with literature data for strongly bonded interfaces61.
Effects of the P → BM transformation and metal-insulator transition on the thermal conductivity of LSCO
As already noted, the Vg-driven P → BM phase transformation in electrolyte-gated LSCO involves several factors, including a large change in δ, lowered crystal symmetry, VO ordering, and an accompanying metal-insulator transition. The P → BM (cubic to orthorhombic) crystal structure change (Fig. 1b, c), induced by the Vg-driven increase in δ, impacts phonon transport, thus modifying thermal conductivity via the phonon contribution. To better quantify the impact of VO on the thermal conductivity in Fig. 3a, it is useful to correlate Vg with VO concentration. To this end, we estimated δ using an established empirical approach (see Methods), based on electrical transport data14,16,52. The resulting values are plotted in Fig. 3c. The expected increasing trend in δ is observed for Vg from 0 to 2 V. For films gated above 2 V, however, our approach is no longer applicable (see Methods), and we simply assign the nominal δ = 0.5 implied by our XRD observation of near-phase-pure BM-LSCO at 3, 3.5, and 4 V (blue circles in Fig. 3c).
To gain further insight into the thermal conductivity change in Fig. 3a, we decompose it into electronic and lattice contributions, i.e., Λtot = Λel + Λlat (with Λel being the electronic thermal conductivity and Λlat the lattice thermal conductivity). Λel can be estimated from the electrical conductivity (σ = 1/ρ) via the WFL, i.e., Λel = LσT, with L being the Lorenz number. Since the value of L varies non-trivially depending on the nature of the material system, we used the lower and upper limits on L commonly accepted in the literature (1.5 and 2.44 × 10−8 V2 K−2), to estimate Λel62,63,64,65. The results are plotted as the shaded envelope between black dash-dotted lines in Fig. 3a, exhibiting the expected generally decreasing trend with Vg due to the metal-insulator transition. For the as-deposited P-LSCO film with δ ≈ 0.1 (Fig. 3c), the lower and upper limits of Λel are estimated as 2.2 and 3.5 W m−1 K−1, resulting in the upper and lower limits of Λlat = Λtot − Λel of 2.4 and 1.1 W m−1 K−1, respectively. The upper limit of Λlat decreases from 2.4 to 0.85 W m−1 K−1, a 65% reduction, as Vg increases from 0 to 4 V, at which point the P → BM transformation is complete. Importantly, we thus find that electrons contribute comparably with phonons for P-LSCO, which is reasonable for “dirty”, i.e., higher resistivity, metals66. This is notably different from the P-SrCoO3-δ reported by Lu et al.10, where the electronic contribution to thermal conductivity was deduced to be negligible. We attribute this difference to the likely larger δ and disorder level in the P phase in ref. 10, where the P-SrCoO3-δ was achieved from as-deposited BM films via gating, in contrast to our as-deposited high-epitaxial-quality P-LSCO. Supporting this, Lu et al. reported ρ(RT) ≈ 5 × 10−2 Ω cm in their P-SrCoO310, compared to ρ(RT) ≈ 2 × 10−4 Ω cm in our as-deposited P-LSCO, i.e., our P conductivity is ∼250 times higher.
To further understand the trend of Λlat versus Vg (and therefore also δ), we performed Green-Kubo MD (GKMD) and nonequilibrium MD (NEMD) simulations of thermal conductivity (see Supplementary Section 5 for calculation details), with results shown in Fig. 3d. The GKMD and NEMD results agree reasonably well. The MD simulations predict a ~62% Λlat reduction (from 3.9 to 1.5 W m−1 K−1) as δ increases from 0.1 to 0.5, assuming random spatial distributions of VOs. Considering that the VOs in the BM phase of our LSCO films are actually ordered52, we also calculated the thermal conductivity of orthorhombic BM-LSCO, with ordered VOs, using MD simulations; this yields a larger Λlat = 1.9 W m−1 K−1 at δ = 0.5 due to the decrease of phonon-defect scattering. There is thus a ~ 50% lattice thermal conductivity reduction from δ = 0.1 in the disordered P phase to δ = 0.5 in the ordered BM phase. Importantly, these 62% and 50% reductions in Λlat agree reasonably with the upper limit of 65% obtained from our Λlat = Λtot − Λel extraction. Note that the absolute values of Λlat from the experiment and MD simulations are not directly compared because the classical interatomic potential used in our MD simulations provides only qualitative insights. Based on the above discussion, we conclude that the decrease in thermal conductivity with increasing Vg originates from comparable reductions in both the electronic and lattice contributions. This plays an important role in our record-high (>5-fold) tuning of thermal conductivity achieved here via bi-state gating. Figure 3e summarizes the tuning factor of material thermal conductivities in our work, and in prior experimental studies, via a bi-state tuning process10,19,20,21,22,23,24,25,26,27. Evidently, the tuning factor of LSCO thermal conductivity in our work is the largest among experimental reports.
Considering the reversible nature of the Vg-induced P ↔ BM phase transformation in LSCO, we also reverted some gated BM-LSCO films to the P phase by applying reverse gate voltages of up to –4.5 V at RT. While this typically generates an approximately 104 decrease in RT ρ due to the BM → P insulator-metal transition, the resulting RT ρ values of recovered P-LSCO films are typically double that of the initial as-deposited P films, corresponding to approximately half the initial electronic thermal conductivity. The thermal measurement of one such film generated a recovered P-LSCO thermal conductivity of 3.5 ± 1.1 W m−1 K−1 at RT. This ~20% reduction in the Λtot of recovered P-LSCO compared to the as-deposited P-LSCO film no doubt arises from additional structural disorder induced during the cyclic gating (see Supplementary Section 8 for more discussion). Nevertheless, such data confirm the overall reversibility of the approach presented here. Further improvement of reversibility could be achieved through better device design and optimized gating conditions.
Temperature-dependent thermal conductivities of LSCO
To further clarify the mechanisms of the scattering processes of the relevant heat carriers in LSCO, we also performed T-dependent thermal measurements on P-LSCO (ungated) and BM-LSCO (Vg = 3 V) from ~90 to ~500 K. Generally, as T increases, the thermal conductivity of a dielectric crystal should first increase (due to the increase of the specific heat)67 and then decrease with a 1/T trend (due to the increase of Umklapp scattering)68. However, neither of our LSCO samples exhibit such typical features. Instead, both P-LSCO and BM-LSCO show a monotonically increasing trend with T in our measurement range (Fig. 4a). We interpret this observation in terms of the two relevant types of heat carriers (electrons and phonons), with differing T dependencies. In P-LSCO, clearly from the above, both electrons and lattice vibrations contribute to thermal transport. The Λel estimated from the WFL with the lower and upper limits of L (using our measured ρ(T)) is presented as the envelope shaded with blue dashed lines in Fig. 4b. It can be seen that Λel increases with T, dominating the increase in Λtot. It is worth noting that a dip is observed in Λel at ~235 K, however. This is because the Curie temperature of our P-LSCO films is ~230 K14,37, at which the transition from ferromagnetic to paramagnetic behavior induces a change in the ρ(T) behavior, as can be seen in Fig. 1d upon close inspection.
a T-dependent thermal conductivities of P-LSCO (ungated, black squares) and BM-LSCO (Vg = 3 V, blue circles). The measurement uncertainty for P-LSCO is around 40% while for BM-LSCO it is around 10%. b T-dependent Λel and Λlat of P-LSCO. Boltzmann transport equation (BTE) calculations were performed to predict Λlat for a 45-nm La0.5Sr0.5CoO3-δ (δ = 0.1) film (green dashed-dotted line), while Λel (blue dashed line) was calculated from the temperature dependence of the resistivity (Fig. 1d) using the WFL with the common lower and upper limits of L. Red solid lines represent the sum of Λel and Λlat.
The T-dependent Λlat of P-LSCO was also calculated using the BTE to take into account the size effect in the thin film, and is shown as the green dash-dotted line in Fig. 4b52. Λlat exhibits a peak at around 200 K. Generally, the peak temperature of thermal conductivity of insulating single-crystal perovskite oxides in unsubstituted ABO3 perovskites appears around or below 100 K (including LaAlO3, the substrate used in this work, see Supplemental section 6)43,45,46,47,48. The difference in peak temperature between our P-LSCO and other such ABO3 perovskites arises because of the presence of a significant VO concentration, the disorder on the A-site (La/Sr), and the sample boundaries, inducing strong T-independent extrinsic phonon scattering, leading to a higher peak temperature in Λlat compared to pristine ABO3 crystals. Finally, we summed Λel and Λlat (Λel + Λlat, shaded area with red solid lines in Fig. 4b) to compare with Λtot obtained from measurements, obtaining a reasonably good agreement.
In contrast to P-LSCO, BM-LSCO is strongly insulating, with lattice vibrations therefore being the dominant heat carriers, and thus Λtot ≈ Λlat. However, Λlat of BM-LSCO still does not show a peak in the probed temperature range, in contrast to typical behavior of pristine insulating crystals. The reason for this is that BM-LSCO contains an even larger density of VOs, a lattice structure with a lower symmetry due to those VOs, and additional disorder associated with the A-site cations (La/Sr), resulting in strong extrinsic phonon scattering, even at low T. Therefore, the thermal transport in BM-LSCO is more glass-like, rather than crystal-like. Supplementary Fig. 8 also shows the T-dependent thermal conductivity of one BM-LSCO sample gated to 4 V, which exhibits a similar trend to that of the BM-LSCO sample at 3 V shown in Fig. 4a, further supporting these results and conclusions.
Discussion
In summary, we have demonstrated that by applying single-step solid-state electrolyte gating at RT we can achieve a record-high (>5-fold) tuning of the thermal conductivity of ion-gel-gated LSCO films in a non-volatile, continuous manner. This large tunability in the thermal conductivity of epitaxial LSCO films results from the structural modifications and metal-insulator transition induced by the P → BM phase transformation. As Vg increases, more oxygen vacancies are created and the lattice symmetry is lowered, leading to a sizable reduction in the LSCO lattice thermal conductivity. Accompanying these structural modifications, the metal-insulator transition across the P → BM transformation further extends the extent of the tuning of thermal conductivity by controlling the electronic contributions to the thermal conductivity. In addition, T-dependent thermal conductivity measurements provided further physical insights into the scattering mechanisms of the relevant heat carriers. For metallic P-LSCO, the observed increasing trend of Λtot vs. T is partially attributed to the substantial electronic contributions to thermal transport, which are absent for BM-LSCO. For insulating BM-LSCO, the increase in thermal conductivity with T instead represents more of the trend typical of amorphous oxides due to the extensive structural defects (e.g., higher VO concentrations and A-site disorder). This success in actively tailoring the thermal conductivity of thin-film LSCO by over a factor of five, via electrolyte gating, opens the possibility of voltage-driven tunable thermal materials for applications in thermal management and energy conversion, which require dynamic control of heat propagation.
Methods
LSCO film growth, device fabrication, and electrolyte gating
Thin films of LSCO were deposited on commercial (MTI corp.) 5 × 5 mm2 and 10 × 10 mm2 LaAlO3(001) substrates using high-pressure-oxygen sputtering, from 2” polycrystalline sputtering targets of the same nominal stoichiometry. Substrates were first annealed at 900 °C in flowing O2 (99.998%, ~1 Torr) for 15 min, before being cooled to 600 °C for deposition. LSCO was then deposited via DC sputtering at 600 °C in flowing O2 (1.5 Torr) at a power of 60–70 W. This produced epitaxial films at a deposition rate of ~20 Å/min. After deposition, films were cooled to RT in 600 Torr of O2 at ~15 °C/min. These procedures essentially employ optimized parameters reported in prior studies6,14,15,16,30,37. The thicknesses of films in this work varied from 45 to 58 nm, estimated from established growth rates and cross-checked from wide-angle XRD Laue fringe spacings.
Sputtered LSCO films were then used to fabricate electrolyte-gate transistor devices6,14,15. As-deposited LSCO films were first Ar-ion milled selectively using steel masks to form LSCO channels of 1 × 1 mm2. Subsequent Mg(5 nm)/Pt(50 nm) gate and contact electrodes were then sputter-deposited through a separate mask and annealed in O2 (450 °C, 5 min). To complete side-gated transistors, a single piece of ion gel was then cut and laminated atop the LSCO channel, contact electrodes (partially), and gate electrodes (substantially). A schematic of the final device is shown in Fig. 1a. The ion gels were fabricated by spin coating (to ∼50 μm thickness) a solution of ionic liquid and polymer onto ~1 inch2 glass wafers. The ionic liquid solution consisted of: 1-ethyl-3-methylimidazolium bis(trifluoro-methylsulfonyl)imide (EMI-TFSI) ionic liquid, poly(vinylidene fluoride-cohexafluoropropylene) polymer, and acetone, in a weight ratio of 1:4:8, respectively. Gating was performed at RT, in vacuum (<1 × 10−5 Torr), sweeping Vg at 0.5 mV s−1 to the specified target values; Vg was applied between the side gate pads and two diagonal electrodes shorted to the film channel (Fig. 1a). During Vg sweeps, two-wire resistance measurements were made in situ between two diagonal electrodes (the two contacts that were not shorted to the gate counter-electrode), representing a source and drain. Such measurements were made by applying a voltage (VSD) of ±0.2 V and measuring a current (ISD) (see Supplementary Fig. 2). Vg and VSD were applied with separate Keithley 2400 (K2400) source-measure units, while the gate current (Ig) and ISD were measured with the corresponding K2400 units. After reaching the desired Vg, gating was terminated by disconnecting the voltage supply to the gates, removing the ion gel, and cleaning the film surface with acetone to remove any residual ion gel.
X-ray diffraction
LSCO film devices of two dimensions (1 × 1 mm2 films on 5 × 5 mm2 substrates, and 4 × 3.5 mm2 films on 10 × 10 mm2 substrates) were characterized both before and after gating via high-resolution specular wide-angle XRD (using a Rigaku Smartlab XE, with Cu Kα radiation). Reciprocal space mapping was performed with the same instrument and settings. Synchrotron XRD measurements (shown only in Supplementary Fig. 1a) were performed on a representative 4 × 3.5 mm2 LSCO film deposited on a 10 × 10 mm2 LAO(001) substrate at the 12-ID-D beamline of the Advanced Photon Source at Argonne National Lab. The synchrotron XRD set-up was equipped with a six-circle Huber goniometer and a Pilatus II 100 K area detector. The spot size and X-ray beam energy were ~500 μm and 22 keV (λ ~ 0.56 Å), respectively. The measurements were carried out at a temperature of 150 K with a liquid-N2 gas flow cryocooler.
Electronic transport
Four-wire electronic transport measurements were taken in the van der Pauw geometry before and after electrolyte gating of LSCO films (ex situ), to determine the LSCO channel resistivity. Temperature-dependent data were acquired in a Quantum Design Physical Property Measurement System (PPMS). Electronic transport measurements were taken using either quasi-AC with the PPMS internal bridge (for metallic samples), or DC with a Keithley 2400 current source and a Keithley 2002 multimeter (for insulating samples).
Determination of VO concentrations, δ
The oxygen deficiency, δ, of P-phase LSCO films was estimated using a previously established and validated method14, in which the measured film resistivity is compared to La1−xSrxCoO3 (x ≤ 0.30) single crystal resistivity data (where δ is close enough to zero to be considered negligible) to estimate the film δ. First, the known low-temperature single crystal resistivity is plotted vs. x, then the measured film resistivity is used to interpolate an effective x value, xeff, from this master curve. Using xeff = x−2δ (i.e., assuming each VO dopes 2 electrons), with x = 0.5 in our case, the film δ can then be estimated. This estimation can be made only in the P phase, and only up to δ = 0.25. We do apply this method in the mixed phase region, where the current is expected to be shunted by P regions, but it cannot, therefore, be applied in the BM phase. As noted in connection with Fig. 3c, at Vg = 3, 3.5 and 4 V we simply assume δ ≈ 0.5 based on the BM structure evident from XRD.
TDTR measurements
The thermal conductivities of LSCO films were measured with TDTR49. Prior to TDTR thermal measurements, a ~70 nm Pt layer was sputter-deposited onto the LSCO films (after gating to the desired Vg), to act as a transducer layer for TDTR measurements. At the laser wavelength of 783 nm, the extinction coefficient is ~7.4 for Pt69; therefore, the thickness of 70 nm is sufficient for the Pt transducer to be considered optically opaque. A Si/SiO2 substrate was also coated with Pt in the same deposition, providing a reference to cross-check the electrical and thermal properties of the Pt. In TDTR, a mode-locked Ti:sapphire laser produces a train of optical pulses (~100 fs in duration) at a repetition rate of 80 MHz and a central wavelength of ~780 nm. The laser is divided into a pump beam and a probe beam with two orthogonal polarizations by a polarizing beam splitter. The pump beam is modulated by an electro-optical modulator, which heats the sample. The probe beam is modulated by a mechanical chopper and detects the temperature response of the sample upon pump heating. An objective lens is used to focus the pump and probe beams onto the sample surface. A mechanical delay stage then varies the optical path of the pump beam, which produces a time delay of up to 4 ns between pump heating and probe sensing. The probe beam reflected from the sample is collected with a fast-response Si detector and then amplified by an RF lock-in amplifier for the data reduction.
We used a 5× objective lens with a 1/e2 beam spot size of ≈12 μm for all samples. For temperature-dependent TDTR measurements over the range of ~90 to ~500 K, the sample was mounted on a heating/cooling stage. Specifically, measurements at low temperatures (from ~90 K to RT) were done under vacuum, while measurements at elevated temperatures (from RT to ~500 K) were carried out in air. A MK2000 series temperature controller was used to provide temperature control. The set temperature of the controller was defined as the setting temperature. The laser power was optimized as a compromise between the signal-to-noise ratio and steady-state heating (ΔTs) for each set temperature. For measurements at low temperatures, due to the significant decrease in heat capacity, the temperature rise induced by the pump per-pulse can also be large (ΔTp). Therefore, we performed a temperature correction for low-temperature measurements, taking into account both ΔTs and ΔTp. The detailed procedures for this temperature correction are provided in Supplementary Section 6.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
All data needed to evaluate the conclusions in this paper are present in the article and the Supplementary Information. All raw data generated in this study and used for figures in both the main article and the Supplementary Information have been deposited in the DRUM database with free access [https://doi.org/10.13020/kjhp-az69].
Code availability
The code used to perform MD simulations is an open-source package (LAMMPS). All other in-house codes related to this work are available from the authors upon reasonable request.
References
Bednorz, J. G. & Müller, K. A. Perovskite-type oxides—the new approach to high-Tc superconductivity. Rev. Mod. Phys. 60, 585 (1988).
Kumar, A., Kumar, A. & Krishnan, V. Perovskite oxide based materials for energy and environment-oriented photocatalysis. ACS Catal. 10, 10253–10315 (2020).
Auciello, O., Scott, J. F. & Ramesh, R. The physics of ferroelectric memories. Phys. Today 51, 22–27 (1998).
Ishihara, T. Perovskite Oxide for Solid Oxide Fuel Cells. (Springer Science & Business Media, 2009).
Leighton, C. Electrolyte-based ionic control of functional oxides. Nat. Mater. 18, 13 (2019).
Walter, J., Wang, H., Luo, B., Frisbie, C. D. & Leighton, C. Electrostatic versus electrochemical doping and control of ferromagnetism in ion-gel-gated ultrathin La0.5Sr0.5CoO3−δ. ACS Nano 10, 7799–7810 (2016).
Navarro-Senent, C., Quintana, A., Menéndez, E., Pellicer, E. & Sort, J. Electrolyte-gated magnetoelectric actuation: phenomenology, materials, mechanisms, and prospective applications. APL Mater. 7, 030701 (2019).
Herrera Diez, L., Kruk, R., Leistner, K. & Sort, J. Magnetoelectric materials, phenomena, and devices. APL Mater. 9, 050401 (2021).
Bisri, S. Z., Shimizu, S., Nakano, M. & Iwasa, Y. Endeavor of iontronics: from fundamentals to applications of ion‐controlled electronics. Adv. Mater. 29, 1607054 (2017).
Lu, Q. et al. Bi-directional tuning of thermal transport in SrCoOx with electrochemically induced phase transitions. Nat. Mater. 19, 655–662 (2020).
Lu, Q. & Yildiz, B. Voltage-controlled topotactic phase transition in thin-film SrCoOx monitored by in situ x-ray diffraction. Nano Lett. 16, 1186–1193 (2016).
Lu, N. et al. Electric-field control of tri-state phase transformation with a selective dual-ion switch. Nature 546, 124–128 (2017).
Ning, S. et al. Voltage control of magnetism above room temperature in epitaxial SrCo1– xFexO3−δ. ACS Nano 14, 8949–8957 (2020).
Chaturvedi, V. et al. Doping-and strain-dependent electrolyte-gate-induced perovskite to brownmillerite transformation in epitaxial La1–xSrxCoO3−δ films. ACS Appl. Mater. Interfaces 13, 51205–51217 (2021).
Walter, J. et al. Ion-gel-gating-induced oxygen vacancy formation in epitaxial La0.5Sr0.5CoO3−δ films from in operando x-ray and neutron scattering. Phys. Rev. Mater. 1, 071403 (2017).
Walter, J. et al. Giant electrostatic modification of magnetism via electrolyte-gate-induced cluster percolation in La1−xSrxCoO3−δ. Phys. Rev. Mater. 2, 111406 (2018).
Wehmeyer, G., Yabuki, T., Monachon, C., Wu, J. & Dames, C. Thermal diodes, regulators, and switches: Physical mechanisms and potential applications. Appl. Phys. Rev. 4, 041304 (2017).
Roberts, N. A. & Walker, D. A review of thermal rectification observations and models in solid materials. Int. J. Therm. Sci. 50, 648–662 (2011).
Cho, J. et al. Electrochemically tunable thermal conductivity of lithium cobalt oxide. Nat. Commun. 5, 1–6 (2014).
Foley, B. M. et al. Voltage-controlled bistable thermal conductivity in suspended ferroelectric thin-film membranes. ACS Appl. Mater. Interfaces 10, 25493–25501 (2018).
Ihlefeld, J. F. et al. Room-temperature voltage tunable phonon thermal conductivity via reconfigurable interfaces in ferroelectric thin films. Nano Lett. 15, 1791–1795 (2015).
Aryana, K. et al. Observation of solid-state bidirectional thermal conductivity switching in antiferroelectric lead zirconate (PbZrO3). Nat. Commun. 13, 1–9 (2022).
Langenberg, E. et al. Ferroelectric domain walls in PbTiO3 are effective regulators of heat flow at room temperature. Nano Lett. 19, 7901–7907 (2019).
Ning, S. et al. Dependence of the thermal conductivity of BiFeO3 thin films on polarization and structure. Phys. Rev. Appl. 8, 054049 (2017).
Tomko, J. A. et al. Tunable thermal transport and reversible thermal conductivity switching in topologically networked bio-inspired materials. Nat. Nanotechnol. 13, 959–964 (2018).
Shin, J. et al. Light-triggered thermal conductivity switching in azobenzene polymers. Proc. Natl Acad. Sci. USA 116, 5973–5978 (2019).
Shin, J. et al. Thermally functional liquid crystal networks by magnetic field driven molecular orientation. ACS Macro Lett. 5, 955–960 (2016).
Ning, S. et al. Anomalous defect dependence of thermal conductivity in epitaxial WO3 thin films. Adv. Mater. 31, 1903738 (2019).
Jeen, H. et al. Topotactic phase transformation of the brownmillerite SrCoO2.5 to the perovskite SrCoO3–δ. J. Adv. Mater. 25, 3651–3656 (2013).
Yu, B. et al. Soft x-ray absorption spectroscopy and magnetic circular dichroism as operando probes of complex oxide electrolyte gate transistors. Appl. Phys. Lett. 116, 201905 (2020).
Katase, T., Suzuki, Y. & Ohta, H. Reversibly switchable electromagnetic device with leakage‐free electrolyte. Adv. Electron. Mater. 2, 1600044 (2016).
Hu, S., Wang, Y., Cazorla, C. & Seidel, J. Strain-enhanced oxygen dynamics and redox reversibility in topotactic SrCoO3-δ (0 < δ ≤ 0.5). Chem. Mater. 29, 708–717 (2017).
Cui, B. et al. Electric-field control of oxygen vacancies and magnetic phase transition in a cobaltite/manganite bilayer. Phys. Rev. Appl. 8, 044007 (2017).
Jeen, H. et al. Reversible redox reactions in an epitaxially stabilized SrCoOx oxygen sponge. Nat. Mater. 12, 1057–1063 (2013).
Senarıs-Rodrıguez, M. & Goodenough, J. Magnetic and transport properties of the system La1-xSrxCoO3-δ (0<x ≤ 0.50). J. Solid State Chem. 118, 323–336 (1995).
Wu, J. & Leighton, C. Glassy ferromagnetism and magnetic phase separation in La1−xSrxCoO3. Phys. Rev. B 67, 174408 (2003).
Walter, J., Bose, S., Cabero, M., Varela, M. & Leighton, C. Giant anisotropic magnetoresistance in oxygen-vacancy-ordered epitaxial La0.5Sr0.5CoO3−δ films. Phys. Rev. Mater. 4, 091401 (2020).
Zhu, J., Wu, X., Lattery, D. M., Zheng, W. & Wang, X. The ultrafast laser pump-probe technique for thermal characterization of materials with micro/nanostructures. Nanosc. Microsc. Therm. 21, 177–198 (2017).
Lattery, D. M., Zhu, J., Huang, D. & Wang, X. in Nanoscale Energy Transport 9-1-9-30 (IOP Publishing, 2020).
Homonnay, N. et al. Interface reactions in LSMO–metal hybrid structures. ACS Appl. Mater. Interfaces 7, 22196–22202 (2015).
Powell, R., Tye, R. & Woodman Margaret, J. Thermal conductivities and electrical resistivities of the platinum metals. Platin. Met. Rev. 6, 138–143 (1962).
Yokokawa, H. & Takahashi, Y. Laser-flash calorimetry II. Heat capacity of platinum from 80 to 1000 K and its revised thermodynamic functions. J. Chem. Thermodyn. 11, 411–420 (1979).
Schnelle, W., Fischer, R. & Gmelin, E. Specific heat capacity and thermal conductivity of NdGaO3 and LaAlO3 single crystals at low temperatures. J. Phys. D 34, 846 (2001).
He, C. et al. Heat capacity study of magnetoelectronic phase separation in La1−xSrxCoO3 single crystals. Phys. Rev. B 80, 214411 (2009).
Boudali, A., Amrani, B., Abada, A. & Amara, K. First-principles study of structural, elastic, electronic, and thermal properties of LaAlO3 perovskite. Comput. Mater. Sci. 45, 1068–1072 (2009).
Michael, P. C., Trefny, J. U. & Yarar, B. Thermal transport properties of single crystal lanthanum aluminate. J. Appl. Phys. 72, 107–109 (1992).
Morelli, D. T. Thermal conductivity of high temperature superconductor substrate materials: lanthanum aluminate and neodymium aluminate. J. Mater. Res. 7, 2492–2494 (1992).
Langenberg, E. et al. Analysis of the temperature dependence of the thermal conductivity of insulating single crystal oxides. APL Mater. 4, 104815 (2016).
Cahill, D. G. Analysis of heat flow in layered structures for time-domain thermoreflectance. Rev. Sci. Instrum. 75, 5119–5122 (2004).
Oh, D.-W. et al. Thermal conductivity as a metric for the crystalline quality of SrTiO3 epitaxial layers. Appl. Phys. Lett. 98, 221904 (2011).
Chen, L. et al. Roles of point defects in thermal transport in perovskite barium stannate. J. Phys. Chem. C. 122, 11482–11490 (2018).
Wu, X. et al. Glass-like through-plane thermal conductivity induced by oxygen vacancies in nanoscale epitaxial La0.5Sr0.5CoO3−δ. Adv. Funct. Mater. 27, 1704233 (2017).
Berggold, K. et al. Thermal conductivity, thermopower, and figure of merit of La1−xSrxCoO3. Phys. Rev. B 72, 155116 (2005).
Kimling, J., Philippi-Kobs, A., Jacobsohn, J., Oepen, H. P. & Cahill, D. G. Thermal conductance of interfaces with amorphous SiO2 measured by time-resolved magneto-optic Kerr-effect thermometry. Phys. Rev. B 95, 184305 (2017).
Liu, J., Choi, G.-M. & Cahill, D. G. Measurement of the anisotropic thermal conductivity of molybdenum disulfide by the time-resolved magneto-optic Kerr effect. J. Appl. Phys. 116, 233107 (2014).
Chien, H.-C., Yao, D.-J. & Hsu, C.-T. Measurement and evaluation of the interfacial thermal resistance between a metal and a dielectric. Appl. Phys. Lett. 93, 231910 (2008).
Hopkins, P. E., Norris, P. M. & Stevens, R. J. Influence of inelastic scattering at metal-dielectric interfaces. J. Heat. Transf. 130, 022401 (2008).
Li, M., Wang, Y., Zhou, J., Ren, J. & Li, B. Thermal boundary conductance across metal-nonmetal interfaces: effects of electron-phonon coupling both in metal and at interface. Eur. Phys. J. B 88, 1–7 (2015).
Shi, B. et al. Interfacial thermal conductance at metal–nonmetal interface via electron–phonon coupling. Mod. Phys. Lett. B 32, 1830004 (2018).
Jiang, P., Huang, B. & Koh, Y. K. Accurate measurements of cross-plane thermal conductivity of thin films by dual-frequency time-domain thermoreflectance (TDTR). Rev. Sci. Instrum. 87, 075101 (2016).
Wilson, R., Apgar, B. A., Hsieh, W.-P., Martin, L. W. & Cahill, D. G. Thermal conductance of strongly bonded metal-oxide interfaces. Phys. Rev. B 91, 115414 (2015).
Thesberg, M., Kosina, H. & Neophytou, N. On the Lorenz number of multiband materials. Phys. Rev. B 95, 125206 (2017).
Wang, X., Askarpour, V., Maassen, J. & Lundstrom, M. On the calculation of Lorenz numbers for complex thermoelectric materials. J. Appl. Phys. 123, 055104 (2018).
Zhou, A., Zhu, T. & Zhao, X. Thermoelectric properties of perovskite oxides La1−xSrxCoO3 prepared by polymerlized complex method. J. Mater. Sci. 43, 1520–1524 (2008).
Kim, H.-S., Gibbs, Z. M., Tang, Y., Wang, H. & Snyder, G. J. Characterization of Lorenz number with Seebeck coefficient measurement. APL Mater. 3, 041506 (2015).
Klemens, P. & Williams, R. Thermal conductivity of metals and alloys. Int. Met. Rev. 31, 197–215 (1986).
Tritt, T. M. Thermal Conductivity: Theory, Properties, and Applications. (Springer Science & Business Media, 2005).
Wang, X., Ho, V., Segalman, R. A. & Cahill, D. G. Thermal conductivity of high-modulus polymer fibers. Macromolecules 46, 4937–4943 (2013).
Werner, W. S., Glantschnig, K. & Ambrosch-Draxl, C. Optical constants and inelastic electron-scattering data for 17 elemental metals. J. Phys. Chem. Ref. Data 38, 1013–1092 (2009).
Yang, Q. et al. Solid‐state electrochemical thermal transistors. Adv. Funct. Mater. 2214939 (2023).
Negi, A. et al. Ferroelectric domain wall engineering enabled thermal modulation in PMN‐PT single crystals. Adv. Mater. 2211286 (2023).
Wooten, B. L. et al. Electric field–dependent phonon spectrum and heat conduction in ferroelectrics. Sci. Adv. 9, eadd7194 (2023).
Acknowledgements
This work was primarily supported by the National Science Foundation (NSF) through the UMN MRSEC under DMR-2011401 (Y.Z., W.M.P., C.Z., V.C., K.H., C.L., and X.W.). Parts of this work were carried out at the Characterization Facility, UMN, which receives partial support from the NSF through the MRSEC program. Portions of this work were also conducted in the Minnesota Nano Center, which is supported by the NSF through the National Nanotechnology Coordinated Infrastructure under ECCS-2025124 (Y.Z., W.M.P., C.Z., V.C., K.H., C.L., and X.W.). This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science user facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357 (Hua Z.). The MD and BTE calculations were supported by NSF under CBET-2212830 (R.X., Hao Z., and T.F.). The computation used resources of the National Energy Research Scientific Computing Center, supported by the Office of Science of the DOE under Contract DE-AC02-05CH11231 (R.X., Hao Z., and T.F.), the Center for High Performance Computing at the University of Utah, and the Extreme Science and Engineering Discovery Environment.
Author information
Authors and Affiliations
Contributions
C.L. and X.W. originated and supervised the research. Y.Z. and C.Z. carried out the TDTR measurements and analyses under the guidance of X.W. W.M.P., V.C., and K.H. prepared the LSCO samples under the guidance of C.L. W.M.P., V.C., and Hua Z. performed the XRD characterization. W.M.P. fabricated the devices and performed the electrolyte gating and electrical transport measurements and analyses, under the guidance of C.L. R.X., Hao Z., and T.F. did the MD simulations and BTE calculations. Y.Z., W.M.P., R.X., T.F., C.L., and X.W. contributed to the writing of the manuscript. All authors discussed the data and provided input on the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, Y., Postiglione, W.M., Xie, R. et al. Wide-range continuous tuning of the thermal conductivity of La0.5Sr0.5CoO3-δ films via room-temperature ion-gel gating. Nat Commun 14, 2626 (2023). https://doi.org/10.1038/s41467-023-38312-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-023-38312-z
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.