Abstract
Despite recent advances in exfoliated vdW ferromagnets, the widespread application of 2D magnetism requires a Curie temperature (Tc) above room temperature as well as a stable and controllable magnetic anisotropy. Here we demonstrate a large-scale iron-based vdW material Fe4GeTe2 with the Tc reaching ~530 K. We confirmed the high-temperature ferromagnetism by multiple characterizations. Theoretical calculations suggested that the interface-induced right shift of the localized states for unpaired Fe d electrons is the reason for the enhanced Tc, which was confirmed by ultraviolet photoelectron spectroscopy. Moreover, by precisely tailoring Fe concentration we achieved arbitrary control of magnetic anisotropy between out-of-plane and in-plane without inducing any phase disorders. Our finding sheds light on the high potential of Fe4GeTe2 in spintronics, which may open opportunities for room-temperature application of all-vdW spintronic devices.
Similar content being viewed by others
Introduction
Replacing bulk materials with two-dimensional (2D) materials is regarded as a promising way to continue scaling electronic devices as Moore’s law is claimed to meet a dead end and the device scaling approaches quantum limit1. With the van der Waals (vdW) layered structures, 2D materials present a unique opportunity potentially outperforming conventional bulk materials due to their reduced dimensions which massively suppress interfacial bonds, and eliminate gap states. As an emerging member of the vdW family, 2D ferromagnetic materials that use the electron spins as another degree of freedom could pave the way for high-performance, energy-efficient, and non-volatile vdW spintronic devices beyond Moore’s law2,3. To meet device operating standards in industry or aerospace, such a device would need to withstand operating temperatures exceeding 125 °C (~400 K)4. Current Curie temperatures (Tc) of 2D ferromagnetic materials are far below this, and there is an urgent need for new materials with high-temperature ferromagnetic order above 400 K amenable large-scale production.
For 2D magnets, magnetic anisotropy plays an important role in sustaining the long-range ferromagnetic order at a finite temperature5,6. Strong magnetic anisotropy is also a key requirement for satisfying different functionalities in spintronic devices. For instance, materials with perpendicular magnetic anisotropy (PMA) demonstrate a lower switching current and better scalability than materials with in-plane magnetic anisotropy (IMA) for the configuration of magnetic random-access memory. In contrast, an IMA pinned layer may be needed to combine with a PMA-free layer for higher sensitivity in magnetic sensors7. For conventional magnets, the magnetic anisotropy can be controlled by engineering the interface. However, it is quite challenging to manipulate the magnetic anisotropy of 2D ferromagnetic materials, especially at room temperature. Finding a 2D ferromagnetic material with controllable anisotropy is urgent for developing 2D vdW spintronic devices in the future.
Recently, the emergence of Fe-rich vdW ferromagnets FenGeTe2 received intense research interest due to their large magnetization near room temperature (for 3 ≤ n ≤ 5, Tc = 220–310 K)8,9,10,11,12,13,14,15. In the family of FenGeTe2, Fe4GeTe2 has been highlighted as a very promising candidate material for spintronics applications because of its relatively high Tc (270 K) and flexible magnetic anisotropy10,16,17,18. In traditional vdW ferromagnetic materials (for instance, CrI3 or Cr2Ge2Te6), the magnetic atoms are encapsulated by nonmagnetic atoms and form a 2D magnetic system19,20. The pair-exchange interaction between the neighboring magnetic atoms in this 2D plane is weak, resulting in a low Tc. In Fe4GeTe2, however, the Fe-Fe dumbbells form a corrugated honeycomb lattice, and this 3D arrangement of magnetic atoms enhances the spin interaction as well as the Tc in Fe4GeTe2. Moreover, the magnetic anisotropy of Fe4GeTe2 is temperature-dependent17,18, and exhibits an anisotropy transition from IMA to PMA as the temperature decreases because of the competition between the magnetocrystalline anisotropy and the shape anisotropy21. However, realistic applications require a substantial increase in its Tc and arbitrary control of its magnetic anisotropy. Fortunately, pioneering works have shown that the magnetism of vdW materials can be engineered by external stimuli, such as gating22,23,24,25, pressure and strain26,27,28, laser29, and proximity effect30,31. These methods may offer an avenue for simultaneously harnessing the Tc and anisotropy in Fe4GeTe2 to satisfy industry standards for future 2D vdW spintronic applications.
In this work, we successfully synthesized wafer-scale vdW Fe4GeTe2 with controlled thickness by molecular beam epitaxy (MBE). We found that the Tc of the Fe4GeTe2 thin film can be precisely tailored by tuning the thickness and Fe concentration and the value was enhanced to over 500 K, which is high enough to meet the demands of most spintronic devices for high working temperature and is compatible with multiple modern patterning processes. Theoretical analysis revealed that the high-temperature ferromagnetism arises from interfacial orbital coupling, which moves the localized states of the Fe4GeTe2 toward the Fermi level, leading to an increase of the exchange interaction as well as Tc. Meanwhile, we also obtained a stable and controllable magnetic anisotropy in our Fe4GeTe2 through modulating Fe concentration. As it increases, the Fe4GeTe2 demonstrates an anisotropy transition from PMA to IMA without introducing any phase disorders, exhibiting its great potential as a universal base material for magnetic memory or magnetic sensor devices. Our result provides a way for realizing high-Tc and tunable magnetic anisotropy in vdW material.
Results
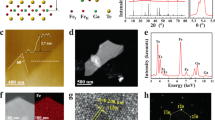
The Fe4GeTe2 has a rhombohedral crystal structure with an R-3m space group, as shown in Fig. 1a. Similar to Fe3GeTe2 (Fig. S1a), Fe4GeTe2 has the structural units of Fe-Fe dumbbells, which are alternatingly off from the horizontal line and form a corrugated honeycomb lattice hosting one Ge atom at the center. In each Fe4GeTe2 monolayer (ML), the covalently-bonded Fe4Ge heterometallic slab is sandwiched between two Te layers. The thickness of an ML is ~9.7 Å and adjacent MLs are separated by a vdW gap. Previous works on the exfoliated bulk Fe4GeTe2 have indicated that the Tc of Fe4GeTe2 can be high because of the relatively strong spin-exchange interaction between the neighboring magnetic atoms15,18. In this work, the 16 nm Fe4GeTe2 also demonstrates a near room temperature Tc, which can be proved by the in-plane M-T curve in Fig. 1b. Here we extract its saturation magnetization (Ms) of 2.13 μB/Fe, which is higher than 1.6 μB/Fe in Fe3GeTe2 single crystal8. To elucidate its crystal structure, X-ray diffraction (XRD) measurement was performed and a typical spectrum is shown in Fig. 1c. The peaks are well ascribed to the {003} family planes of Fe4GeTe2, featuring a perfect single crystal17. The vdW stacking structure is further demonstrated by the high-resolution transmission electron microscopy (HRTEM) image in Fig. 1d. The staggered Te monolayer distinguishes the structure of Fe4GeTe2 from that of Fe3GeTe2, which also leads to a different structural characteristic in the XRD spectrum (as shown in Fig. S1b). Chemical analysis using energy-dispersive X-ray spectroscopy (EDX) confirms the stoichiometry of Fe4GeTe2 in Fig. S2, and EDX mapping (the right side of Fig. 1d) shows that all the elements of Fe, Ge, and Te are uniformly distributed in the film. Together, these results prove that a high-quality single-crystalline Fe4GeTe2 vdW film was synthesized by MBE in our work.
a Schematics of the crystal structure of Fe4GeTe2 stacked in ABC configuration (left), and its rhombohedral structure unit (right). b Temperature dependence of the magnetization for 16 nm Fe4GeTe2. c XRD scan of the Fe4GeTe2 film, showing Al2O3 {001} and Fe4GeTe2 {003} family peaks. d A typical HRTEM image of Fe4GeTe2 films, the color squares show the high-pass filtered images of the vdW structure. Up Inset: The EDX result verifies the 4:1:2 Fe:Ge:Te stoichiometric composition with the uniform element distribution map (right). e Room-temperature magnetic hysteresis loops of 4 nm Fe4GeTe2, the magnetism can survive at an extremely high temperature, the Tc is estimated to be 530 K from the power-law fitting of the in-plane Mr–T curve in (f). g Detailed magnetic field-dependent magnetization of 4 nm Fe4GeTe2 at various temperatures for H//ab. Inset: zoom-in hysteresis loop at 300 K. h Temperature-dependent Mr for Fe4GeTe2 with the thickness of 4, 8, 10, 12, and 16 nm. i Tc for Fe4GeTe2 thin films with different thicknesses, a negative correlation can be observed between the thickness and the Tc of the films. The error bars describe the deviation during the power-law fitting. j Effective magnetic anisotropy energy Keff and Curie temperature Tc for our samples and previous vdW ferromagnets18,34,35,36,37,38.
Traditionally vdW ferromagnets suffer a sharp decrease in Tc when the thickness decreases to the atomic level. It is because that the exchange interactions alone are not able to sustain the magnetic order at finite temperature due to the thermal fluctuations in two dimensions23. However, the Tc shows a distinguishing thickness-dependent feature in our samples. Here, a 4 nm Fe4GeTe2 was prepared, and the ferromagnetism was demonstrated by multiple magnetic characterizations, including vibrating sample magnetometer (VSM), magneto-optical Kerr effect (MOKE), ferromagnetic resonance (FMR), and magnetotransport measurements (Fig. S3). Figure 1e shows the M-H loops taken along the ab and c axis and a robust IMA can be observed even at 300 K. The Tc of the sample can be deduced precisely from the in-plane remanent magnetization (Mr), as shown in Fig. 1f, which shows a power-law dependence on the temperature as \({{{{{{\rm{M}}}}}}}_{{{{{{\rm{r}}}}}}}({{{{{\rm{T}}}}}})\propto {({{{{{{\rm{T}}}}}}}_{{{{{{\rm{c}}}}}}}-{{{{{\rm{T}}}}}})}^{{{{{{\rm{\beta }}}}}}}\). Here the Tc = 530 K, which is much higher than that of previous iron-based vdW ferromagnets14,15,18,32, and the value of β is estimated to be 0.34, which follows the case of the quasi-2D Heisenberg model in easy axis6,33. To further illustrate the magnetic properties, high-temperature M-H loops are displayed in Fig. 1g under an in-plane magnetic field. The inset shows the zoom-in hysteresis at 300 K, with clearly resolvable coercivity verifying the high-temperature magnetism of the sample. A hysteresis loop can still be seen even at 500 K, indicating the presence of high-temperature magnetism in the few-layer Fe4GeTe2.
To precisely depict the thickness dependence of Tc, Mr–T curves for samples of different thicknesses are plotted in Fig. 1h. All Mr–T curves can be fitted with the Heisenberg model, and the relation between the Tc and thickness is summarized in Fig. 1i for more clarity. For 4 nm Fe4GeTe2, magnetic order survives up to ~530 K, while the Tc decreases to ~270 K as the thickness reaches 16 nm. This trend illustrates the interface modulation on magnetism in Fe4GeTe2, the bottom few layers are expected to be affected most by the interface, thereby presenting the highest Tc. As an attempt to confirm the interface-enhanced Tc, we prepared a mechanical exfoliated Fe4GeTe2 flake, which was cleaved from a 10 nm epitaxial Fe4GeTe2 film, and measured its magnetic properties by MOKE (Fig. S4). After exfoliation from the substrate, the Fe4GeTe2 flake cannot sustain room-temperature magnetism. This serves as a strong indication that the Tc enhancement comes from the interfacial modulation between the Fe4GeTe2 film and the sapphire substrate. Figure 1j shows a comparison of the magnetic properties between our samples and previous vdW ferromagnets18,34,35,36,37,38. Our Fe4GeTe2 presents the highest Tc among all the materials while keeping its relatively high magnetic anisotropy.
In the following, density functional theory (DFT) calculations were performed to unveil the mechanism beyond the Tc enhancement. First, electronic structure and the internal exchange interactions of Fe4GeTe2 were determined by ab inito calculation (details in the Supplementary Materials Figs. S5 and S6). As shown in Fig. 2a, Fe4GeTe2 has two different Fe sites, namely as α-Fe and β-Fe. The α-Fe is more localized and has a larger spin than the itinerant β-Fe. Our calculation reveals that the spin at the α-Fe is 3/2 while that of the β-Fe is 1 in both the monolayer and bulk form. Therefore, the average magnetic moment per Fe near 0 K is 2.5 μB, which is consistent with our experimental result. The calculated primitive cell structure of single-layer Fe4GeTe2 contains a dumbbell shape of four Fe atoms, as shown in Fig. 2a. There are three nearest-neighbor exchange interactions called J1, J2, and J2β, at a spatial distance of ~2.5 Å. The other distant exchange interactions are more than 4 Å and are less important. The naming rule of the exchange interactions is illustrated in Fig. 2b (also in the Supplementary Materials Fig. S6). Although the itinerant magnetism in Fe4GeTe2 should be described by the Stoner model39, the local magnetic moments of Fe are large enough that such itinerant ferromagnetism can be equivalently transformed into the classic Heisenberg model with Ruderman–Kittle–Kasuya–Yosida (RKKY) exchange40. The exchange interactions follow the RKKY rule41:
where r is the distance between the two spin sites and kF is the Fermi momentum of the itinerant electrons. Kondo model treats localized electrons as magnetic impurities embedded in the itinerant conducting electrons and J describes the exchange interaction of a localized spin coupled to delocalized electrons. The RKKY model further describes the interaction between two localized spins via the conduction electrons. Figure 2c shows J(r) relations from the nearest exchanges to far above 8 Å.
a Atomic structure of the unit cell of Fe4GeTe2. Two kinds of Fe with different symmetric positions and spins are marked as α-Fe and β-Fe. The most important three exchange interactions are marked as J1, J2, and J2β. b Top view of the spin-lattice of Fe4GeTe2 and marked exchange interactions, only Fe atoms are shown. c J-r dispersion of bulk and interface-modulated Fe4GeTe2 obeying the RKKY rule. d Average magnetization per Fe versus temperature for the ML, bulk, and interface-modulated Fe4GeTe2. The SIA is marked in black. e Atomic structure of 2-layers Fe4GeTe2 onto the sapphire substrate. f PDOS of the Fe4GeTe2 and the substrate. g PDOS of the d orbitals of the α-Fe in bulk, ML with 2% strain and interface-modulated Fe4GeTe2.
To further simulate Tc, Metropolis Monte-Carlo (MMC) method was adopted to calculate the temperature-dependent magnetic moments per Fe. The Hamiltonian can be written as:
where siα is the spin operator on site i, and α, β can be x, y, z. [ Jij]αβ describes the Heisenberg exchange interactions between the spins on site i and j, which is a 3 by 3 matrix. Considering the centrosymmetric structure of Fe4GeTe2, we neglect the non-isotropic exchanges like in Fe3GeTe2 or chromium-based compound23,31, the Heisenberg exchange then degenerates into a scalar. The coefficient of A is the single-ion perpendicular magnetocrystalline anisotropy energy (SIA), which stems from spin-orbit coupling. With the SIA, a ferromagnetic order can be established in 2D at finite temperatures via breaking the continuous rotational symmetry of the Hamiltonian and rendering a gap in the ground state magnon mode. Considering the transition of SIA, the MMC calculation in Fig. 2d predicts the Tc of intrinsic Fe4GeTe2 monolayer is ~200 K while the value of bulk form is ~270 K. Notably, the calculated bulk Tc (cyan line) is consistent with the bulk value of previous exfoliated sample17,18 as well as our experimental result in Fig. 1h. For the monolayer, however, the calculated value (purple line) is close to the exfoliated sample but far below the Tc measured in our Fe4GeTe2. This result indicates the accuracy of our calculation and confirms again the interfacial modulation in our Fe4GeTe2/Al2O3 heterostructure.
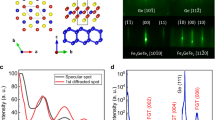
Here we establish a model to simulate the heterostructure and quantify the interface contribution to the Tc enhancement. Considering the ~20% lattice difference between the sapphire substrate (α-Al2O3) and Fe4GeTe2, the elastic energy is too large compared to the adsorption energy for a 1:1 lattice-matched interface of Fe4GeTe2 and α-Al2O3 (Fig. S7). We infer that Fe4GeTe2 rotates 30 degrees and adsorbs onto the substrate with a tensile strain of ~2% during the epitaxy. This lattice match scheme can be described as \({{{{{{\rm{Fe}}}}}}}_{4}{{{{{{\rm{GeTe}}}}}}}_{2}{:{{{{{\rm{Al}}}}}}}_{2}{{{{{{\rm{O}}}}}}}_{3}=2:\sqrt{3}\), which was verified by the RHEED patterns, as shown in Fig. S8. Figure 2e shows the side view of the interface, and the partial density of states (PDOS) of both Fe4GeTe2 and Al2O3 are demonstrated in Fig. 2f. Here the EF lies near the valence edge of Al2O3, and the bandgap of Al2O3 is calculated to be closed to 6 eV. The spin-down bands of the metal inside the gap are mostly unoccupied while that of spin-up are occupied.
According to the mean-field theory, Tc is proportional to the overall exchange interaction as well as S(S + 1), where S is the average onsite spin on Fe and the value is determined by the density difference between up and down states. Notably, in our samples, the spin does not change at the interface because the EF lies between the spin up and spin down d bands and is quite far from either of them (Figs. S5b and S7d). Therefore, the enhancement of the exchange interactions is the main reason for the dramatic Tc increase in Fig. 2d. The Tc of the interfacial Fe4GeTe2 is predicted to be nearly 500 K, much higher than its ML and bulk forms without interfacial contact, which is consistent with our experimental observation. Notably, the change of the exchange interactions stems from J rather than the Fe-Fe distances r as it cannot be changed a lot (Fig. 2c and Fig. S7b). According to the Anderson model, J is related to the distance between the Fermi level (EF) and the localized states that contribute to the formation of magnetic moments (Ed), as well as the Hubbard U which denotes the onsite Coulomb repulsion42,43:
This is under the condition that Ed < EF < Ed + U, where the magnetic moment arises from single occupation of the localized level rather than zero or two. The J2 has a local minimum when the EF is in the mid of Ed and Ed + U. In Fe4GeTe2, the Ed is the energy level of the unpaired d electrons in Fe (Supplementary Materials, Section 2).
As Fig. S9 shows, by contacting with the sapphire substrate, the d electrons shift rightwards, while the deeper level s and p electrons remain almost unchanged, indicating that there is no EF shifting by the interfacial engineering. Here we calculate the PDOS of α-Fe d electrons to inspect the interface-induced Ed shift in Fe4GeTe2. As shown in Fig. S9d and Fig. 2g (the red curve), compared with the bulk or monolayer forms, the integration with the sapphire induces a right shift of unpaired Fe d electrons, which will move the Ed towards the EF, and is the key factor leading to the enhancement of J. To verify our theoretical prediction, we used ultraviolet photoelectron spectroscopy (UPS) to probe the Ed shift induced by the interface in our Fe4GeTe2 thin film, as shown in Fig. S10. As the thickness decreases, we have observed states accumulated towards the EF, which comes from the right shift of the Fe d localized states. The experimental results are consistent with our theoretical calculation in Fig. 2g. According to the Anderson model, the right shift of Ed results in the enhancement of J as well as the Tc, which is the direct consequence of sapphire-induced interfacial orbital coupling. Considering the slight extension on the Fe4GeTe2 lattice with thickness decrease (Fig. S8), we also simulate the d orbital PDOS for α-Fe in ML Fe4GeTe2 with 2% tensile strain (blue line in Fig. 2g). The strain is expected to extend the distance between Ed and EF, which contradicts our UPS results and heterostructure calculation. Therefore, strain is excluded from the factors causing the Tc enhancement in Fig. 1h.
Besides high-temperature magnetism, robust and controllable magnetic anisotropy is also essential for the widespread vdW spintronic applications. Recent works have indicated that as the temperature increases, a magnetic anisotropy reorientation from out-of-plane to in-plane direction appears in Fe4GeTe217,18. Here we attempted to control the magnetic anisotropy with precise manipulation of the stoichiometry in Fe4GeTe2. Three thin films with the same thickness (10 nm) but different Fe concentrations were prepared (named Fe4-xGeTe2, Fe4GeTe2, and Fe4+xGeTe2). All the samples present the same crystalline phase, proving the high quality, as shown in the XRD results in Fig. 3a. Careful examination finds that the (009) peaks of the samples demonstrate a small shift, which indicates that the Fe concentration increase can lead to a slight enlargement of the c lattice constant in Fe4GeTe2 because more Fe atoms are introduced into the crystal unit15. In addition, the enhanced Fe network consists of more spin-pair interactions, which will increase J as well as the Tc of Fe4GeTe2, as shown in Fig. 3b. This stoichiometry-dependent Tc can be proved by multiple magnetic characterizations (Figs. S11–S14), and has been widely recognized in the previous research12,13,14,15,17,18,44.
a XRD scan of the samples with different Fe doping concentrations, which all belong to vdW Fe4GeTe2 structure without any phase disorders. Inset: the (009) peaks of the samples, reflecting a slight shift of the XRD curves under different Fe concentrations. b The c-lattice constants and Tc of all the samples, both parameters have a positive correlation with the Fe concentration. The error bars describe the deviation in calculated Tc between Arrott plots and mean-field fitting (Fig. S11). c Effective magnetic anisotropies Keff as a function of temperature for the samples, an easy axis rotation can be observed in Fe4GeTe2. d Temperature dependence of the longitudinal resistance for 7 nm Fe4GeTe2 thin film. Inset: the schematic image of the Hall bar device. e Normalized Remnant anomalous Hall resistance Rxy as a function of temperature, the resistance values are extracted from the anomalous Hall curves of Fe4-xGeTe2 (f) and Fe4GeTe2 (g). With the temperature increase, an anisotropy transition from PMA to IMA can be well observed In Fe4GeTe2.
Interestingly, we found that the magnetic anisotropy along either out-of-plane or in-plane can be precisely controlled by tailoring the Fe concentration. To quantitively illustrate the magnetism evolution in all three samples, Fig. 3c depicts the effective anisotropy energy (Keff) values extracted from the M-H loops of the samples (Figs. S11, S12). Here the sign of Keff demonstrates the magnetic anisotropy along in-plane (negative sign) or out-of-plane (positive sign). Different from Fe4-xGeTe2 or Fe4+xGeTe2 which always present a definite direction of magnetic anisotropy at all temperatures, Fe4GeTe2 presents a temperature-dependent anisotropy from PMA to IMA, which is consistent with the previous report18. The value of Keff is determined by two competing energies, the easy-axis magnetocrystalline anisotropy (Km) and the easy-plane shape anisotropy (Ksh), they usually follow a relation as\({K}_{eff}={K}_{m}+{K}_{sh}={K}_{m}-({\mu }_{0}/2){M}_{S}^{2}\). Due to the temperature dependence of magnetization, the magnetic anisotropy in Fe4GeTe2 is expected to demonstrate a temperature-driven transition. Notably, when the Fe concentration increases from Fe4-xGeTe2 to Fe4+xGeTe2, the magnetic anisotropy turns from PMA to IMA, which may originate from the Km variation during the stoichiometry change. Similar to the Fe3GeTe2 in the previous reports9,37, our Fe4-xGeTe2 demonstrates a strong PMA with a large Km over 1 J/cm2 at 20 K (Fig. S11). However, this value decreases to 0.88 J/cm2 in Fe4GeTe2 and rapidly drops to 0.23 J/cm2 for Fe4+xGeTe2. While in Fe4+xGeTe2, a robust and stable IMA can be obtained at all temperatures. Thus, we propose that the degradation of the Km comes from the incline of magnetocrystalline anisotropy during the Fe concentration increase, which may change the crystalline structure and promote the magnetocrystalline anisotropy tilt along the in-plane direction.
The spin reorientation could also be revealed by the magnetotransport measurements and the inset of Fig. 3d depicts the schematic image of the Hall bar device in the measurements. Figure 3d shows a resistance versus temperature (R–T) curve for the 7 nm Fe4GeTe2, which exhibits a typical metallic behavior. Figure 3e compares the normalized remnant anomalous Hall resistance Rxy(0)/Rxy(Hs) versus the temperatures for Fe4-xGeTe2 and Fe4GeTe2, where the Rxy(0) and the Rxy(Hs) are defined as the anomalous Hall resistance at zero and out-of-plane saturated magnetic field, and the values were extracted from the Hall curves in Figs. 3f and 3g. At all temperature ranges, the Fe4-xGeTe2 always demonstrates a robust value of ~1, indicating the relatively high remanent magnetization due to the strong PMA. For Fe4GeTe2, despite the value of Rxy(0)/Rxy(Hs) close to 1 at low temperatures, it decreases substantially from 100 K and finally vanishes when the temperature reaches 250 K. The decrease in the remanent magnetization results from the spin reorientation in the Fe4GeTe2, which gives rise to the IMA while suppressing the PMA term in the magnetism. Figures 3f and 3g show the detailed anomalous Hall curves for 7 nm Fe4-xGeTe2 and Fe4GeTe2 films, respectively. A series of square Hall curves can be observed in Fe4-xGeTe2 with a clear coercivity, even at high temperatures. By contrast, for Fe4GeTe2, the coercivity disappears when the temperature increases because of the temperature-driven spin reorientation. The evolution from PMA to IMA in Fe4GeTe2 can be further proved by the Hall curves for H//ab (Fig. S15), which show a clear transition from PMA to IMA, consistent with the above results.
In summary, wafer-scale vdW Fe4GeTe2 was successfully grown by molecular beam epitaxy and exhibited a strong magnetism with a Tc over 500 K. A series of thickness-dependent measurements revealed that the enhanced Tc is induced by the interface between Fe4GeTe2 and the substrate. Theoretical analysis proved that the right shift of the unpaired Fe d localized states is the key factor for the increase in Tc. In addition, the magnetic anisotropy of the Fe4GeTe2 can be flexibly controlled from out-of-plane to in-plane via tuning Fe composition. In low Fe concentration, the perpendicular magnetocrystalline anisotropy dominates the effective magnetic anisotropy while its contribution is overwhelmed by the in-plane shape anisotropy in high Fe concentration. Our work highlights the great potential of van der Waals Fe4GeTe2 as a platform for further research and implementation of 2D vdW spintronic devices.
Methods
Single crystal growth
High-quality Fe4GeTe2 thin films were grown on a commercial sapphire substrate in the MBE system. Before the growth, the substrate was annealed at 600 °C for an hour to remove the impurity layer and then cooled down to 300 °C. Elemental Fe, Ge, and Te solid sources were evaporated from standard Knudsen cells. The Fe concentration can be manipulated easily by controlling the flux rate of the Fe source for growing Fe4-xGeTe2, Fe4GeTe2, and Fe4+xGeTe2 samples. The deposition was in situ monitored by reflection high-energy electron diffraction (RHEED). After growth, 2 nm Ge was deposited on the films as the protection layer.
X-ray diffraction (XRD)
After the growth, the sample was characterized by the PANalytical X’Pert PRO MRD diffractometer with Cu Kα radiation. The generator voltage and current of the setup were set to be 45 kV and 40 mA, respectively. The scanning range was 10°–90° with a step size of 0.03° and a time of 20 s/step.
Superconducting quantum interference device (SQUID)
The Quantum Design MPMS3 SQUID was employed to measure the low-temperature magnetization behavior of our samples (0–300 K) following standard procedures. During the measurements, the magnetic field sweeps were made in no-overshoot, persistent mode, and the temperature sweeps were made at a rate of 3 K per minute. For Mr–T curves (Fig. 1b), the films were firstly field-cooled from 300 K to 20 K with an in-plane field of 2 T, then the field was set to zero and the remanent magnetization was measured as the temperature increased. Each estimated magnetic moment was determined from an average of two scans.
High-resolution transmission electron microscopy (HRTEM)
A JEOL-ARM 200 F Cold FEG transmission electron microscope (TEM) was used to investigate the samples’ structure. The operating voltage of the setup is 200 kV with a point resolution of 0.12 nm. A Carl Zeiss NVision 40 SEM/EDS workstation was used to analyze the chemical composition by plotting the energy-dispersive X-ray spectroscopy (EDX) mapping, which collected the Fe K, Ge K, Te L, O K, and Al K edges.
Vibrating sample magnetometer (VSM)
A commercial Microsense VSM was used to characterize the high-temperature (above 300 K) magnetic features of our samples. Due to the in-plane magnetic anisotropy above room temperature for our Fe4GeTe2, only in-plane M-H loops were measured by VSM in Fig. 1g, where the hysteresis was obtained for every 50 K and the magnetic field was scanned between −2 T and 2 T with a step of 500 Oe. The background magnetic contribution of the sapphire substrate and the sample holder was subtracted from the raw data. To test the remanent magnetization of the samples (Fig. 1h), the magnetic field was first raised to 2 T along the easy axis to make the samples saturated, then decreased to 0 T. After that, the temperature was increased to 300 K from 700 K at a rate of 5 K/min under zero field. During the heating process, the magnetic moment of the samples is continuously measured by VSM.
Transport measurement
Hall bar devices with dimensions of 200 μm × 30 μm were fabricated using standard photolithography for the transport measurements. The in-plane and out-of-plane Hall resistances were measured in the standard four-probe configuration using a Quantum Design Physical Property Measurement System (PPMS-7T). During all the transport measurements, the applied DC current is 50 μA.
Theoretical calculation
Atomic structure, electronic structure calculations as well as magnetic configurations of ferromagnetic order and anti-ferromagnetic order, are implemented by the density functional theory (DFT) code Cambridge Serial Total Energy Package (CASTEP)45. Ultrasoft pseudopotential is used with a plane-wave cutoff energy of 340 eV. The Tkatchenko-Scheffler (TS) scheme46 of the van der Waals correction is taken into account in the bulk form and the heterostructure. Self-consistent dipole correction is applied in the heterostructure calculation to overcome the periodical error induced by the charge transfer. All structures are relaxed and the residual force is less than 0.01 eV/Å. The exchange-correlation functional is the semi-local generalized gradient approximation (GGA) form of Perdew-Burke-Erzerhof (PBE)47. We applied a Hubbard U = 3.5 eV correction only to the 3d orbitals of the α-Fe. With the exchange interactions and the single-ion anisotropy (SIA) obtained from the previous steps, we conduct the Metropolis Monte Carlo (MMC) calculation based on the Hamiltonian in Eq. (2). The size of the spin-lattice is set 24 × 24 × 8 for bulk and 40 × 40 × 1 for monolayer to capture the paramagnetism above Tc and to isolate the mirror images. Each temperature is simulated with 105 loops to converge to the thermal equilibrium state.
Data availability
The data that support the findings of this study are provided in the paper and Supplementary Materials file. Additional data related to this study are available from the corresponding author upon reasonable request.
References
Habermeier, H. U. Scaling problems and quantum limits in integrated circuit miniaturization. AIP Conf. Proc. 122, 192–197 (1984).
Song, T. et al. Giant tunneling magnetoresistance in spin-filter van der Waals heterostructures. Science 360, 1214–1218 (2018).
Jiang, S., Li, L., Wang, Z., Shan, J. & Mak, K. F. Spin tunnel field-effect transistors based on two-dimensional van der Waals heterostructures. Nat. Electron. 2, 159–163 (2019).
Pertijs, M. A. P., Makinwa, K. A. A. & Huijsing, J. H. A single-trim CMOS bandgap reference with a 3σ inaccuracy of ±0.15% from −40 °C to 125 °C. IEEE J. Solid-State Circuits 40, 2805–2815 (2005).
Mermin, N. D. & Wagner, H. Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic Heisenberg models. Phys. Rev. Lett. 17, 1133–1136 (1966).
Gibertini, M., Koperski, M., Morpurgo, A. F. & Novoselov, K. S. Magnetic 2D materials and heterostructures. Nat. Nanotechnol. 14, 408–419 (2019).
Wisniowski, P., Wrona, J., Stobiecki, T., Cardoso, S. & Freitas, P. P. Magnetic tunnel junctions based on out-of-plane anisotropy free and in-plane pinned layer structures for magnetic field sensors. IEEE Trans. Magn. 48, 3840–3842 (2012).
Chen, B. et al. Magnetic properties of layered itinerant electron ferromagnet Fe3GeTe2. J. Phys. Soc. Japan 82, 124711 (2013).
Fei, Z. et al. Two-dimensional itinerant ferromagnetism in atomically thin Fe3GeTe2. Nat. Mater. 17, 778–782 (2018).
Kim, D., Lee, C., Jang, B. G., Kim, K. & Shim, J. H. Drastic change of magnetic anisotropy in Fe3GeTe2 and Fe4GeTe2 monolayers under electric field studied by density functional theory. Sci. Rep. 11, 17567 (2021).
Li, Z. et al. Magnetic critical behavior of the van der Waals Fe5GeTe2 crystal with near room temperature ferromagnetism. Sci. Rep. 10, 15345 (2020).
Liu, S. et al. Wafer-scale two-dimensional ferromagnetic Fe3GeTe2 thin films grown by molecular beam epitaxy. npj 2D Mater. Appl. 1, 30 (2017).
May, A. F., Bridges, C. A. & McGuire, M. A. Physical properties and thermal stability of Fe5-xGeTe2 single crystals. Phys. Rev. Mater. 3, 104401 (2019).
May, A. F. et al. Ferromagnetism near room temperature in the cleavable van der Waals Crystal Fe5GeTe2. ACS Nano 13, 4436–4442 (2019).
Zhang, H. et al. Itinerant ferromagnetism in van der Waals Fe5-xGeTe2 crystals above room temperature. Phys. Rev. B 102, 064417 (2020).
Liu, Q. et al. Layer-dependent magnetic phase diagram in FenGeTe2 (3 ≤ n ≤ 7) ultrathin films. Commun. Phys. 5, 140 (2022).
Mondal, S., Khan, N., Mishra, S. M., Satpati, B. & Mandal, P. Critical behavior in the van der Waals itinerant ferromagnet Fe4GeTe2. Phys. Rev. B 104, 094405 (2021).
Seo, J. et al. Nearly room temperature ferromagnetism in a magnetic metal-rich van der Waals metal. Sci. Adv. 6, eaay8912 (2020).
Gong, C. et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 546, 265–269 (2017).
Huang, B. et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 546, 270–273 (2017).
Goel, S., Anh, L. D., Ohya, S. & Tanaka, M. Temperature dependence of magnetic anisotropy in heavily Fe-doped ferromagnetic semiconductor (Ga,Fe)Sb. J. Appl. Phys. 127, 023904 (2020).
Verzhbitskiy, I. A. et al. Controlling the magnetic anisotropy in Cr2Ge2Te6 by electrostatic gating. Nat. Electron. 3, 460–465 (2020).
Deng, Y. et al. Gate-tunable room-temperature ferromagnetism in two-dimensional Fe3GeTe2. Nature 563, 94–99 (2018).
Wang, Z. et al. Electric-field control of magnetism in a few-layered van der Waals ferromagnetic semiconductor. Nat. Nanotechnol. 13, 554–559 (2018).
Zhang, X.-X. et al. Gate-tunable spin waves in antiferromagnetic atomic bilayers. Nat. Mater. 19, 838–842 (2020).
Li, T. et al. Pressure-controlled interlayer magnetism in atomically thin CrI3. Nat. Mater. 18, 1303–1308 (2019).
Song, T. et al. Switching 2D magnetic states via pressure tuning of layer stacking. Nat. Mater. 18, 1298–1302 (2019).
Webster, L. & Yan, J.-A. Strain-tunable magnetic anisotropy in monolayer CrCl3, CrBr3, and CrI3. Phys. Rev. B 98, 144411 (2018).
Liu, B. et al. Light-tunable ferromagnetism in atomically thin Fe3GeTe2 driven by femtosecond laser pulse. Phys. Rev. Lett. 125, 267205 (2020).
Wang, H. et al. Above room-temperature ferromagnetism in wafer-scale two-dimensional van der Waals Fe3GeTe2 tailored by a topological insulator. ACS Nano 14, 10045–10053 (2020).
Dong, X.-J., You, J.-Y., Zhang, Z., Gu, B. & Su, G. Great enhancement of Curie temperature and magnetic anisotropy in two-dimensional van der Waals magnetic semiconductor heterostructures. Phys. Rev. B 102, 144443 (2020).
Stahl, J., Shlaen, E. & Johrendt, D. The van der Waals ferromagnets Fe5–δGeTe2 and Fe5–δ–xNixGeTe2—crystal structure, stacking faults, and magnetic properties. Z. Anorg. Allg. Chem. 644, 1923–1929 (2018).
Irkhin, V. Y., Katanin, A. A. & Katsnelson, M. I. Self-consistent spin-wave theory of layered Heisenberg magnets. Phys. Rev. B 60, 1082–1099 (1999).
Niu, W. et al. Probing the atomic-scale ferromagnetism in van der Waals magnet CrSiTe3. Appl. Phys. Lett. 119, 172402 (2021).
Zeisner, J. et al. Magnetic anisotropy and spin-polarized two-dimensional electron gas in the van der Waals ferromagnet Cr2Ge2Te6. Phys. Rev. B 99, 165109 (2019).
Richter, N. et al. Temperature-dependent magnetic anisotropy in the layered magnetic semiconductors CrI3 and CrBr3. Phys. Rev. Mater. 2, 024004 (2018).
Kim, D. et al. Antiferromagnetic coupling of van der Waals ferromagnetic Fe3GeTe2. Nanotechnology 30, 245701 (2019).
Ribeiro, M. et al. Large-scale epitaxy of two-dimensional van der Waals room-temperature ferromagnet Fe5GeTe2. npj 2D Mater. Appl. 6, 10 (2022).
Stoner, E. C. Collective electron ferromagnetism. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 165, 372–414 (1938).
Prange, R. E. & Korenman, V. Local-band theory of itinerant ferromagnetism. IV Equivalent Heisenberg model. Phys. Rev. B 19, 4691–4697 (1979).
Ruderman, M. A. & Kittel, C. Indirect exchange coupling of nuclear magnetic moments by conduction electrons. Phys. Rev. 96, 99–102 (1954).
Anderson, P. W. Local moments and localized states. Science 201, 307–316 (1978).
Anderson, P. W. Localized magnetic states in metals. Phys. Rev. 124, 41–53 (1961).
May, A. F., Du, M.-H., Cooper, V. R. & McGuire, M. A. Tuning magnetic order in the van der Waals metal Fe5GeTe2 by cobalt substitution. Phys. Rev. Mater. 4, 074008 (2020).
Clark, S. J. et al. First principles methods using CASTEP. Z. Kristallogr. Cryst. Mater. 220, 567–570 (2005).
Tkatchenko, A. & Scheffler, M. Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data. Phys. Rev. Lett. 102, 073005 (2009).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Acknowledgements
W.Z., T.N., and H.L. acknowledge the financial support from the National Natural Science Foundation of China (Grant No. 62274009, 61774013, and 12204027), the National Key R&D Program of China (Grant No. 2018YFB0407602), the International Collaboration Project (Grant No. B16001), and the National Key Technology Program of China (Grant No. 2017ZX01032101). This work was also supported by FEDER-FSE Lorraine et Massif des Vosges 2014–2020, a European Union Program (to T.H.). H.T. Wang thanks the support from the Academic Excellence Foundation of BUAA for PhD Students.
Author information
Authors and Affiliations
Contributions
H.L., W.Z., J.R., S.M., and T.N. conceived the project; H.W., P.W., and J.L. synthesized the thin films; H.W. and Z.G. carried out the magnetization measurements with the help of A.M.F. and T.H.; H.W. and Z.G. performed electric measurements with the help of H.D. and S.P.-W.; S.M. and J.G. carried out structural identification using TEM; Y.F.-R. and L.M. performed XPS and UPS measurements; H.W., H.L., Z.S., P.L., and T.N. analyzed experimental data; H.L. carried out theoretical calculations and modeling. H.W., H.L., and T.N. wrote the paper and all authors commented on it.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Prabhat Mandal and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, H., Lu, H., Guo, Z. et al. Interfacial engineering of ferromagnetism in wafer-scale van der Waals Fe4GeTe2 far above room temperature. Nat Commun 14, 2483 (2023). https://doi.org/10.1038/s41467-023-37917-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-023-37917-8
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.