Abstract
Understanding diffusive processes in networks is a significant challenge in complexity science. Networks possess a diffusive potential that depends on their topological configuration, but diffusion also relies on the process and initial conditions. This article presents Diffusion Capacity, a concept that measures a node’s potential to diffuse information based on a distance distribution that considers both geodesic and weighted shortest paths and dynamical features of the diffusion process. Diffusion Capacity thoroughly describes the role of individual nodes during a diffusion process and can identify structural modifications that may improve diffusion mechanisms. The article defines Diffusion Capacity for interconnected networks and introduces Relative Gain, which compares the performance of a node in a single structure versus an interconnected one. The method applies to a global climate network constructed from surface air temperature data, revealing a significant change in diffusion capacity around the year 2000, suggesting a loss of the planet’s diffusion capacity that could contribute to the emergence of more frequent climatic events.
Similar content being viewed by others
Introduction
Natural and artificial diffusive processes from the most varied contexts are omnipresent in our everyday lives1,2,3,4,5,6. Advancing our understanding of diffusive processes is a fundamental challenge with critical practical applications across a wide range of spatial scales. For instance, diffusion magnetic resonance is an imaging technique that allows studying the brain’s structural and functional connectivity7,8. A diffusion-like process describes the action of infectious agents that attack our immune system spreading as fast as they can9. On a large scale, the billions of individuals commuting daily between different geographical regions constitute the highly complex global human mobility system10,11,12. Similarly, gossip spreads through vast complex social networks3,4,13,14,15,16,17. All these phenomena have motivated researchers to understand the mechanisms that enhance or suppress diffusion, and to quantify their impacts2,18,19,20,21.
Structural and dynamical properties of diffusion processes have been successfully modeled by networks, structures that are able to encompass this complex combination2,18,19,20,21,22,23,24,25,26,27,28. The analysis of diffusive processes usually assumes that interaction networks represent their average behavior18; some models consider random navigation29,30,31,32,33,34, and others consider the topological shortest paths35. Shortest paths are essential for diffusion processes since they are the ones through which nodes are firstly reached when a process starts diffusing in a structure in which connections are of the same nature. However, geodesical paths are not the only ones that need to be considered, as the characteristics of the connections interfere in a way that could either improve or worsen the transmission of information. Topological features can be considered as connection weights to define the weighted shortest paths. Then, the inclusion of both, geodesical and weighted shortest paths could lead a more precise evaluation of the outcome of the diffusion process34,36,37,38.
The influence of specific topological features, such as community structures or degree heterogeneity of nodes on diffusion processes, has been described in several works39,40,41. However, one interesting point that still needs to be addressed in the literature is the study of the way individual nodes change their performance as diffusing agents during the evolution of the diffusive process. This performance depends not only on the node’s structural connectivity but also on the dynamic process on top of the structure and initial conditions. Considering that nodes change the way they diffuse as the process evolves, we propose a new measure called Diffusion Capacity that is able to track the evolution of the node’s performance. Diffusion-Capacity quantifies the evolving diffusive ability of nodes through the use of a weighted distance distribution that allows the inclusion of dynamical features of the process. We introduce in this work a method that brings many possibilities for strategic interventions to design more efficient diffusive structures.
The concept of Diffusion Capacity is also extended to interconnected networks, structures that represent a system composed by several networks interacting simultaneously. These systems are a good representation of natural systems since they are the result of the complex interaction of many subsystems. Considering this we propose a measure called Relative Gain (\({{{{{{{\mathcal{G}}}}}}}}\)) that compares the diffusive performance of an element acting in an isolated network and its performance when it is part of an interconnected structure. Among the examples presented in this work we consider heat diffusion, Kuramoto oscillators, disease spreading and a climate network. This variety of applications reflects the versatility of the measures here proposed and their efficacy in revealing useful diffusive features.
Results
Single networks
Climate networks
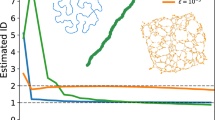
As a real world example of heat diffusion we use the gridded reanalysis dataset of Surface Air Temperature (SAT)42 to analyze the way the diffusion-capacity measure captures the heat flow through the Earth surface. For this example diffusion capacity is computed for each geographical point (2.5 latitude × 2.5 longitude) of a gridded Earth network in which the weights of the connections are the temperature differences between points. Trimestral means of node diffusion-capacity values are depicted in Fig. 1. Some interesting global features can be observed from the diffusion-capacity spatial patterns. In general, superficial air over oceans show lower diffusion-capacity values than superficial air over land, increasing gradually in coastal waters. Considering only land areas, higher diffusion-capacity values are observed in places of higher altitudes as well as in winters of colder places (see extratropical places in South Hemisphere in Fig. 1B, C, and extratropical places in North Hemisphere in Fig. 1A, D). Another interesting fact is that diffusion-capacity variation among seasons is much lower between tropics than in extratropical regions.
Figure 2 depicts the average global temperature and global diffusion-capacity values from 1951 to 2020. It is possible to see that while temperatures rise constantly, diffusion-capacity drastically changes its tendency around 2000. It is worth mentioning, that extreme weather events has increased significantly in the last 20 years almost duplicating the number of natural disasters43,44,45,46.
Disease spreading
The SIR model47,48,49,50 is a simple mathematical model for the spread of epidemic diseases, in which, nodes can be susceptible, infected, or recovered from an infectious agent. Recovered nodes are immune to the disease, while a susceptible node can become infected if it is in contact with an infected node. We study here, the evolution of the SIR model in a small network (Fig. 3A) when one central node is initially infected, and also when a peripheral node initiates the epidemic process. In this experiment, we consider the probability of a susceptible node to become infected is pinf = 0.1 and different recovery rates prec values.
Small network highlighting a central (red) and a peripheral (green) node (A). Network diffusion-capacity evolution of a SIR model when the central node (B) and a peripheral node (C) is initially infected, for three different infection probabilities. D, E depict the evolution of the number of infections respectively. All figures show mean values of 100 realization considering a constant pinf = 0.1 and prec = 0.05, 0.10 and 0.20.
In general, when the process begins with the infection of a central node, the number of new infections grows more and faster, reaching earlier immunity, than when the process is initiated in a peripheral node. In this case, the number of new infected nodes grows less and slower, having its maximum later. The evolution of the dynamic also depends on the probability of recovery (prec) of infected nodes, that induces different outcomes.
In Fig. 3 it is depicted a SIR model when the probability of infection is greater than the probability of recovery (pinf > prec), when the probabilities are equal (pinf = prec), and finally when the probability of infection is lower than the probability of recovery (pinf < prec). The lower the probability of recovery, the faster the disease spreads. Figure 3B, C show the evolution of the diffusion capacity when the central, and peripheral nodes are initially infected for different recovery probability values. For pinf > prec values of diffusion capacity present the highest peak, lower for the process initiated in the peripheral node. The lowest values correspond to the case of prec > pinf.
Figure 3D, E compare the different infection processes explained above. These figures show that the initial diffusion capacity is higher when the process is initiated in the central node. As the process evolves, the diffusion capacity increases until a maximum that appears earlier than the maximum number of cases, showing itself as an early indicator of the peak of the epidemic process. As in this case, weights are the same in all links, peripheral nodes posses a lower diffusion capacity than central nodes, then they are more affected by changes in the dynamical process. As central nodes already are strong diffusive agents, the impact of changes is less significant. This information can be useful to plan strategies to reduce the impact of these kind of spreading diseases.
Interconnected networks
Kuramoto oscillators
To understand the meaning of the relative gain in a different dynamic, we consider the well-known Kuramoto’s model51,52,53,54 in the multiplex system of Fig. 4A. Coupled by a constant Dx, for each vertex \(i\in \overrightarrow{G}\) there is an oscillator with phase θi that varies following the differential equation for any node i belonging to a generic layer L:
where, ωi is the fundamental frequency of the oscillator i, c a constant, and A the adjacency matrix of the multilayered system. Figure 5A, B shows the corresponding relative gains \({{{{{{{{\mathcal{G}}}}}}}}}_{L}\) of each isolated layer for three different coupling constants.
Nodes in blue/red represent those that decrease/increase their diffusion capacity in the fully coupled multilayer structure, compared to their diffusion capacity in isolation (A). Diffusion Capacity Λ of G1, G2 and, for different interlayer strengths (logarithmic scale) the multilayer diffusion capacity \({{{{{{{\mathcal{M}}}}}}}}({G}_{1})\) and \({{{{{{{\mathcal{M}}}}}}}}({G}_{2})\) (B). Evolution of the Multilayer diffusion Capacity for small interlayer strength values (C).
It is possible to see that, for Dx = 0.01 the relative gains of both layers are less than one, and this means that the shortest path between two nodes that belong to the same layer, is in the layer. When Dx = 100 the relative gains of both layers are higher than one showing that shortest paths between pairs of nodes in one layer use connections in the other. For Dx = 3, the relative gain presents an interesting behavior being less than 1 in some periods as for Dx = 0.01 regime, and greater than 1 in other periods as in Dx = 100. Additional information regarding DC is presented in the last three sections of the Supplementary Information. Degree correlations between layers are analyzed in Section G, and a multilayer brain network to study different hearing pathologies is presented in Section H.
Discussion
In this study, we present the concept of Diffusion Capacity, a quantity that offers insights into a node’s ability to diffuse information. By leveraging a probability distribution that encodes information about geodesic and weighted paths, we define Diffusion Capacity and propose a method for computing it. Our approach allows for the inclusion of dynamical characteristics of the diffusion process, providing local and global temporal information about the system’s performance.
We extend the concept of Diffusion Capacity to interconnected networks, enabling us to quantify changes in the node’s diffusive performance when it is connected to other structures. We introduce a new quantity, called Relative Gain, which measures the change in Diffusion Capacity of a node due to the inclusion of new networks into the system. This approach allows to project superdiffusive structures, as well as enhance or suppress diffusion by modifying the network’s topology.
As a real data application, we study the temporal evolution of Diffusion Capacity in a global climate network constructed using SAT data. Our findings reveal a significant change in tendency around the year 2000, despite the continuous rising of global temperatures. This result suggests a loss of the planet’s Diffusion Capacity, which may be a contributing factor to the emergence of more frequent and extreme climatic events. Further research is necessary to investigate this finding and its implications for the planet’s climate.
In conclusion, our work introduces an approach to quantify the Diffusion Capacity of nodes in a network and identify potential interventions for improving the system’s efficiency. We believe that our approach has broad applications in various fields, including transportation, social networks, and epidemiology, among others.
Methods
Paths in single networks
By definition, the geodesic distance between nodes i and j, Dg(i, j) is the minimum number of links separating them. The weighted distance between nodes i and j, Dw(i, j), is the minimum sum of the inverse of the weights connecting both nodes. Then, considering Fig. 6, the geodesical path between nodes 1 and 2 is 1 → 2, then Dg = 1. The weighted path between nodes 1 and 2 is 1 → 3 → 2, as the corresponding weights are 1 (Dw = 1) for link 1 → 3 and 2 (Dw = 1/2) for link 3 → 2, then Dw = 1 + 1/2 = 3/2.
Dg(i, j) and Dw(i, j) allow the proposition of a weighted node distance distribution (wNDD) based on the quantity Δi,j = Dw(i, j)/Dg(i, j), the ratio of the weighted and geodesical distances between nodes i and j55,56,57.
If Δi,j < 1 the weighted distance connecting i to j is smaller than the geodesical distance (Dg > Dw), and 1 − Δi,j quantifies this difference. If Δi,j > 1, the weighted distance connecting i to j is larger than the geodesical distance Dg(i, j) < Dw(i, j), and this difference can be quantified by 1 − 1/Δi,j.
Considering a network G=(V,E), where V is the set of nodes and E is the set of edges, for each i ∈ V and d = 1, 2…∣V∣ − 1, ∞, let Γi(d) = {y ∈ V∣Dg(i, j) = d}. The fraction of disconnected nodes from i is defined as pi(∞) = ∣Γi(∞)∣/(∣V∣ − 1), and the fraction of nodes at geodesic distance d from i for d ≠ ∞, pi(d) = ∣Γi(d)∣/(∣V∣ − 1) as the vector:
in which, \({{{{{{{{\bf{p}}}}}}}}}_{i}^{+}(d)\) is the fraction of nodes at geodesic distance d from i, for which their weighted shortest path is smaller than \(d,\,{{{{{{{{\bf{p}}}}}}}}}_{i}^{-}(d)\) indicates the fraction of nodes at geodesic distance d from i, for which their weighted shortest path is larger than d, and \({{{{{{{{\bf{p}}}}}}}}}_{i}^{0}(d)\) is the fraction of nodes for which there is no difference between the paths. Considering this, if all weights are one, \({{{{{{{{\bf{p}}}}}}}}}_{i}^{+}(d)\,=\,0\) and \({{{{{{{{\bf{p}}}}}}}}}_{i}^{-}(d)\,=\,0\). In the extreme case that weights tend to infinity \, and \({{{{{{{{\bf{p}}}}}}}}}_{i}^{0}(d)\to 0\), being the topological configuration, irrelevant. On the other hand, if weights tend to zero, \({{{{{{{{\bf{p}}}}}}}}}_{i}^{-}(d)\to|{\Gamma }_{i}(d)|/(|V|-1),{{{{{{{{\bf{p}}}}}}}}}_{i}^{+}(d)=0\) and \({{{{{{{{\bf{p}}}}}}}}}_{i}^{0}(d)\,\to\, 0\), approximating to the situation of considering only the geodesic distances. The weighted node distance distribution wNDD is then defined for each node, as:
\({{\mathbb{P}}}_{i}\,=\,(1,\,0,\,0,\ldots,\,0)\) is the form of the distance distribution (wNDD) of a node in a fully connected network with weights tending to infinite. When larger weights accelerate the diffusion process, \({{\mathbb{P}}}_{i}\) corresponds to the distance distribution of a node in the most diffusive structure, and for that, we consider them as our reference structure Gref and distribution \({{\mathbb{P}}}_{ref}\).
Diffusion Capacity in single networks
Then, let G = (V, E, W) be a weighted network composed by a set of vertices V, edges E and weights W. We define the diffusion capacity of node i, Λi(G), as the inverse of the distance between \({{\mathbb{P}}}_{i}(G)\) and \({{\mathbb{P}}}_{i}({G}_{ref})\), where Gref is the graph reference of the same size than G. We measure the distance between these distributions using the cumulative Jensen-Shannon divergence (CDD), described in Section A of the Supplementary Information (SI). Therefore, the Diffusion Capacity (DC) of node i ∈ G, Λi(G), is
and the diffusion capacity of the network G, ΛD(G), is the average over all nodes
To study diffusion processes in networks we propose the embedding of dynamical features in the topological weights. Then, weights considered in this analysis are the result of the combination of topological and dynamical characteristics of the structure and process, respectively. Figure 7 depicts a simple example of a heat diffusion process on a regular network58. In this case, the weights considered in the analysis are the combination of the thermal conductivity of the links wi,j (topological weights), and the temperature difference between the nodes involved (xj − xi) (dynamical feature), Wi,j = wi,j(xj − xi) as explained in Section B of the SI. Nodes interact by exchanging heat with a rate proportional to their temperature difference and to the thermal conductivity. In thermal equilibrium, as there is no energy flow, the diffusion capacity (DC) of nodes, represented by the node’s sizes, depends exclusively on the topological structure. However, when energy flows, the DC of the nodes varies until reaching equilibrium. The system’s DC, defined as the average of the node’s DC, increases to a maximum value and returns to the state in which no flow is present. In Fig. 7A the thermal conductivity is the same in all connections, then, because of their global topological configuration, central nodes have higher DC values. In Fig. 7B the thermal conductivity of some connections is increased, then, the size of the nodes also increase in different proportions depending of their topological location. To better analyze this process, we simulate the evolution of the heat exchange and compute, at each time step, the DC value of the whole structure as depicted in Fig. 7C. First, we increase the temperature of node 1 and compute DC in structure A, as shown by the green and blue lines. By comparing these processes, it is possible to see that, under the same initial conditions, the system in B reaches higher DC values and reaches thermal equilibrium in a shorter time than the system in A. However, after increasing the temperature of node 2 and computing DC in structures A and B, as shown by the red and black lines, respectively, contrary to what it is expected because of the presence of some connections with higher thermal conductivity in structure B, the process in structure A reaches thermal equilibrium earlier.
A and the topological diffusion capacity when some peripheral links possess a higher weight (B). Two different heat diffusion processes are initiated in nodes 1 or 2 in both structures by assigning a temperature 25 degrees higher than the temperature of the other nodes. The time evolution of the diffusion capacity values of the system is shown in (C). The minimum value (DCmin) corresponds to the DC value when (xj − xi) → 0.
Two important DC values exist for every system. By assuming (xj − xi) = 1 as an arbitrary value, we have information about the relative DC values between nodes to represent their structural latent diffusive potential. This value corresponds to the topological diffusion capacity (DCt). Figure 7 shows two regular grids, in which DCt values are represented by the size of the nodes when all connections have the same weight (A) and when some links possess a higher thermal conductivity (thicker lines) in (B). The color scale in Fig. 7B represents the percentage increase in DCt considering only the topological change.
The second important network DC value is the asymptotic minimum depicted in Fig. 7C, where all DC curves converge in different moments, independently of the weights of the connections, the dynamical process involved and the initial conditions. This minimum DC value (DCmin) is unique for each specific adjacency matrix, and corresponds to the case in which (xj − xi) → 0, and only geodesic distances count.
Section C of the SI presents an experiment of DC applied to Kuramoto oscillators, and the computational complexity of DC is discussed in Section D.
Paths in interconnected networks
When considering interconnected networks, represented as multilayer structures, we have to consider paths using more than one layer. Using the concepts of single and doubly connected nodes proposed in the Lace Expansion method59, we define that two nodes i and j, of the same layer, are doubly connected (i ⇔ j) if it exists, between them, at least a shortest path going through two different layers. Then, two nodes are single connected (i ↔ j) if they are not doubly connected. For example, vertices 1 and 3 of Fig. 8 are doubly connected because the shortest path connecting them contains links in more than one layer (1–5–6–3). Vertices 5 and 6, on the other hand, are not doubly connected because the shortest path connecting them corresponds to the same layer. Then, the wNDD of a multilayer system have to consider the intralayer links.
For a weighted multilayer network composed by a set of M weighted networks, \(\overrightarrow{G}\,=\,({G}_{1},\,{G}_{2},\ldots,{G}_{M},\,{\mathbb{E}})\) with GL = (VL, EL, WL), L = 1, 2, …, M, and layers connected by weighted interlayer links \({\mathbb{E}}=\,\{{w}_{x,y}|x\,\in\, {V}_{\alpha },y\,\in\, {V}_{\beta },\alpha \,\ne\, \beta \}\), we define for nodes i, j ∈ VL:
-
1.
Dw(i, j), as the shortest distance over all paths connecting i and j in the multilayered system, being \({{\mathbb{P}}}_{i}\) its corresponding probability distribution;
-
2.
\({D}_{w}^{\beta }(i,j)\), the shortest distance over all paths connecting i and j such that at least one node in the path belongs to a different layer, Gβ with β ≠ L, being \({{\mathbb{P}}}_{i}^{\beta }\) its corresponding probability distribution.
For every \(i\in {V}_{L},{{\mathbb{P}}}_{i}\) captures the impact of the shortest paths reduction due to the multilayer structure, and \({{\mathbb{P}}}_{i}^{\beta }\) captures the impact of the paths that are forced to have, at least, one link connected to layer Gβ. In the SI section E we present, in detail, the construction of the probability distributions for the network depicted in Fig. 8.
Diffusion capacity in interconnected networks
To define DC we use \({{\mathbb{P}}}_{ref}\) that, in this case, corresponds to the most diffusive multilayer structure. In these structures, if there are no interlayer connections, diffusion occurs independently in each layer. However, when the interlayer strength is low, the diffusion time may become excessively long, as these weak interlayer connections slow down the dynamics of both layers. On the other hand, a strong interaction between layers enhances diffusion.
Let \(\overrightarrow{G}\,=\,({G}_{1},\,{G}_{2},\ldots,{G}_{M},\,{\mathbb{E}})\) a multilayer weighted network, we define, for each node i ∈ VL and for all L = 1, 2, …, M:
-
1.
The Node Diffusion Capacity (\({{{{{{{{\mathcal{M}}}}}}}}}_{i}\)):
$${{{{{{{{\mathcal{M}}}}}}}}}_{i}(\overrightarrow{G})\,=\,{\left[\frac{1}{2}CDD({{\mathbb{P}}}_{i},\,{{\mathbb{P}}}_{ref})\,+\,\frac{1}{2M-2}\mathop{\sum }\limits_{\beta=1,\,\beta \,\ne\, L}^{M}CDD({{\mathbb{P}}}_{i}^{\beta },\,{{\mathbb{P}}}_{ref})\right]}^{-1}$$(5) -
2.
The Layer Diffusion Capacity is defined as the average of \({{{{{{{{\mathcal{M}}}}}}}}}_{i}\) over all the nodes in a layer,
$${{{{{{{\mathcal{M}}}}}}}}({G}_{L})\,=\,\frac{1}{|{V}_{L}|}\mathop{\sum}\limits_{i\,\in\, {V}_{L}}{{{{{{{{\mathcal{M}}}}}}}}}_{i}$$(6)
In the first term of Eq. 5, \({{\mathbb{P}}}_{i}\) is the distribution of the multilayer dynamical paths between node i and the other nodes of layer GL (see methods). \(CDD({{\mathbb{P}}}_{i},{{\mathbb{P}}}_{ref})\) compares the diffusive potential of a node through a distance to a reference distribution. In the second term, \({{\mathbb{P}}}_{i}^{\beta }\) represents the distribution of the multilayer paths between node i and the other nodes of layer GL, for which paths are imposed to go through layer β (see methods). The average of \(CDD({{\mathbb{P}}}_{i}^{\beta },\,{{\mathbb{P}}}_{ref})\) captures the effect caused by the presence of all β ≠ L, on node i. In this way, the multilayer DC of node \(i,\,{{{{{{{{\mathcal{M}}}}}}}}}_{i}(\overrightarrow{G})\) is represented by the structural and dynamical dissimilarity between the multilayer connectivity of node i in G, and the multilayer connectivity of node i in Gref.
Relative gain
Figure 4 shows a multiplex system containing nine nodes in each layer, coupled through a constant interlayer weight between layers G1 and G2 (Fig. 4A). Multiplex networks are multilayer structures with the restriction of having the same set of nodes in all layers, and intralayer connections exclusively through the same nodes. Figure 4B depicts the DC values of isolated layers (Λ(G1) and Λ(G2), and for the multiplex system, (\({{{{{{{\mathcal{M}}}}}}}}(G1)\) and \({{{{{{{\mathcal{M}}}}}}}}(G2)\)), for different interlayer weights. In this system, as the coupling increases, the diffusion capacities of the multilayer system also increase up to a point where \({{{{{{{\mathcal{M}}}}}}}}(G1) \, > \,\Lambda (G1)\) and \({{{{{{{\mathcal{M}}}}}}}}(G2) \, > \,\Lambda (G2)\). Figure 4C shows that for small values of the coupling constant, the increase in diffusion capacity is nearly linear. DC values can be found in Table 1. This result is consistent with previous findings in60 in which it is shown that the time for a multiplex network to reach equilibrium, scales with the inverse of the smallest positive eigenvalue of the Laplacian matrix (λ2). In the Section F of the SI we show the relationship between DC and λ2 values.
By comparing the single and multilayer node diffusion capacities Λi and \({{{{{{{{\mathcal{M}}}}}}}}}_{i}\), it is possible to know if it is advantageous or not for a node, in terms of diffusion, to be coupled with another network and, by comparing the diffusion capacities Λ(GL) and \({{{{{{{\mathcal{M}}}}}}}}({G}_{L})\), it is possible to know if it is advantageous or not for a layer, in terms of diffusion, to be part of a multilayer system. Node nine in layer G1 of the structure depicted in Fig. 4A for example, reduces its diffusion-capacity when it is part of the multilayered system.
To explore this relationship between single and multilayer diffusion capacities, we define the relative gain \({{{{{{{\mathcal{G}}}}}}}}\) as the ratio between the multilayer diffusion capacity and the diffusion capacity of the isolated layer. For a node i in a layer GL:
and
In this way, \({{{{{{{{\mathcal{G}}}}}}}}}_{L}\) quantifies the improvement of the DC of layer L when it is connected to the other layer in comparison to DC of itself in isolation.
Relative gain is also an important concept for the study of superdiffusion60,61, phenomenon in which diffusion processes reach a steady state faster on a multilayer structures than in any of their constitutive layers in isolation. In Fig. 9 are represented two multiplex networks composed by two layers with nine nodes and different connectivity configurations. Systems are built in a way that all red nodes satisfy \({{{{{{{{\mathcal{M}}}}}}}}}_{i} \, > \,{\Lambda }_{i}\) meaning that they are more diffusive in the interconnected system than in the isolated layer, and blue nodes satisfy \({{{{{{{{\mathcal{M}}}}}}}}}_{i} \, < \,{\Lambda }_{i}\) meaning that they are more diffusive in it isolated layer than when it is connected to another structure. To study the emergence of superdiffusion on these structures we use 1000 different random initial conditions and we observe the number of times superdiffusion is developed. Results reveal that superdiffusion is found in 99.8% of cases for S1 and in 75.6% of the cases in S2, showing the strong influence of the network topology and its dependence on initial conditions. It is interesting to note that, considering the approach based on spectral properties of Laplacian matrices60, both structures are considered superdiffusive. This experiment highlight the advantage of the possibility of quantifying DC as it allows the design of structures with specific diffusive requirements and also to investigate the initial conditions in which the structure becomes superdiffusive.
Nodes in blue/red represent those that decrease/increase their diffusion capacity in the fully coupled multilayer structure, compared to their diffusion capacity in isolation (A). Diffusion Capacity Λ of G1, G2 and, for different interlayer strengths (logarithmic scale) the multilayer diffusion capacity \({{{{{{{\mathcal{M}}}}}}}}({G}_{1})\) and \({{{{{{{\mathcal{M}}}}}}}}({G}_{2})\) (B). Evolution of the Multilayer diffusion Capacity for small interlayer strength values (C).
Code availability
The source code for computing the Diffusion Capacity and instructions on how to use it are freely available at: tischieber/Diffusion-Capacity-of-Single-and-Interconnected-Networks (github.com)62.
References
De Domenico, M et al. The physics of spreading processes in multilayer networks. Nat. Phys. 12, 901–906 (2016).
Akbarpour, M. & Jackson, M. O. Diffusion in networks and the virtue of burstiness. Proc. Natl. Acad. Sci. 115, E6996–E7004 (2018).
Bovet, A. & Makse, H. A. Influence of fake news in twitter during the 2016 us presidential election. Nat. Commun. 10, 7 (2019).
Pierri, F., Piccardi, C. & Ceri, S. Topology comparison of twitter diffusion networks effectively reveals misleading information. Sci. Rep. 10, 1372 (2020).
Valgañón, P. Contagion–diffusion processes with recurrent mobility patterns of distinguishable agents. Chaos Interdisciplinary J. Nonlinear Sci. 32, 043,102 (2022).
Villegas, P et al. Laplacian renormalization group for heterogeneous networks. Nat. Phys. https://doi.org/10.1038/s41567-022-01866-8 (2023).
Hagmann, P. Mapping human whole-brain structural networks with diffusion mri. PLOS ONE 2, 1–9 (2007).
Qi, S. Structural brain network: What is the effect of life optimization of whole brain tractography? Front. Comput. Neurosci. 10, 12 (2016).
Chen, L et al. Inflammatory responses and inflammation-associated diseases in organs. Oncotarget 9, 7204–7218 (2018).
Morita, S. Six susceptible-infected-susceptible models on scale-free networks. Sci. Rep. 6, 22,506 (2016).
Scarpino, S. V. & Petri, G. On the predictability of infectious disease outbreaks. Nat. Commun. 10, 898 (2019).
Kraemer, M. U. G. Utilizing general human movement models to predict the spread of emerging infectious diseases in resource poor settings. Sci. Rep. 9, 5151 (2019).
Kempe, D, Kleinberg, J, Tardos, E. Maximizing the spread of influence through a social network. In: Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, KDD ’03, pp 137–146. https://doi.org/10.1145/956750.956769 (2003).
Lappas, T et al. Finding effectors in social networks. In: Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, KDD ’10, pp 1059–1068. https://doi.org/10.1145/1835804.1835937 (2010).
Qi, J. Discrete time information diffusion in online social networks: micro and macro perspectives. Sci. Rep. 8, 11,872 (2018).
Shao, C. The spread of low-credibility content by social bots. Nat. Commun. 9, 4787 (2018).
Zhou, B. Realistic modelling of information spread using peer-to-peer diffusion patterns. Nat. Hum. Behav. 4, 1198–1207 (2020).
Myers, S.A., Zhu, C, Leskovec, J. Information diffusion and external influence in networks. In: Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, KDD ’12, pp 33–41. https://doi.org/10.1145/956750.956769 (2012).
de Arruda, G. F. Impact of the distribution of recovery rates on disease spreading in complex networks. Phys. Rev. Res. 2, 013,046 (2020).
Darbon, A. Disease persistence on temporal contact networks accounting for heterogeneous infectious periods. R. Soc. Open Sci. 6, 181,404 (2021).
Iacopini, I. Multilayer modeling of adoption dynamics in energy demand management. Chaos Interdisciplinary J. Nonlinear Sci. 30, 013,153 (2020).
Pastor-Satorras, R. & Vespignani, A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 86, 3200–3203 (2001).
Aral, S., Muchnik, L. & Sundararajan, A. Distinguishing influence-based contagion from homophily-driven diffusion in dynamic networks. Proc. Natl Acad. Sci. 106, 21,544–21,549 (2009).
Centola, D. The spread of behavior in an online social network experiment. Science 329, 1194–1197 (2010).
Banerjee, A. The diffusion of microfinance. Science 341, 1236,498 (2013).
Gleeson, J. P. & Durrett, R. Temporal profiles of avalanches on networks. Nat. Commun. 8, 2041–1723 (2017).
Bertagnolli, G., Gallotti, R. & De Domenico, M. Quantifying efficient information exchange in real network flows. Commun. Phys. 4, 125 (2021).
Bertagnolli, G. & De Domenico, M. Functional rich clubs emerging from the diffusion geometry of complex networks. Phys. Rev. Res. 4, 033,185 (2022).
Beekman, J. A. Gaussian-markov processes and a boundary value problem. Trans. Am. Math Soc. 126, 29–42 (1967).
Havlin, S. & Ben-Avraham, D. Diffusion in disordered media. Adv. Phys. 36, 695–798 (1987).
Bouchaud, J. P. & Georges, A. Anomalous diffusion in disordered media: Statistical mechanisms, models and physical applications. Phys. Rep. 195, 127–293 (1990).
De Domenico, M. Diffusion geometry unravels the emergence of functional clusters in collective phenomena. Phys. Rev. Lett. 118, 168,301 (2017).
Giuggioli, L. Exact spatiotemporal dynamics of confined lattice random walks in arbitrary dimensions: A century after smoluchowski and pólya. Phys. Rev. X 10, 021,045 (2020).
Bertagnolli, G. & De Domenico, M. Diffusion geometry of multiplex and interdependent systems. Physical Review E 103, 042,301 (2021).
Fornito, A, Zalesky, A, Bullmore, E.T. Chapter 7—Paths, Diffusion, and Navigation, Academic Press, pp 207–255. (2016) https://doi.org/10.1016/B978-0-12-407908-3.00007-8 (2016).
Hens, C. Spatiotemporal signal propagation in complex networks. Nat. Phys. 15, 403–412 (2019).
Costa, A. Ecological networks: Pursuing the shortest path, however narrow and crooked. Sci. Rep. 9, 17,826 (2019).
Boguñá, M. Network geometry. Nat. Rev. Phys. 3, 114–135 (2021).
Motter, A. E., Zhou, C. & Kurths, J. Network synchronization, diffusion, and the paradox of heterogeneity. Phys. Rev. E 71, 016,116 (2005).
Gómez-Gardeñes, J. & Latora, V. Entropy rate of diffusion processes on complex networks. Phys. Rev. E 78, 065,102 (2008).
Payne, S. Diffusion profile embedding as a basis for graph vertex similarity. Netw. Sci. 9, 328–353 (2021).
Kalnay, E. The ncep/ncar 40-year reanalysis project. Bull. Am. Meteorolog. Soc. 77, 437–472 (1996).
Gatti, L. V. Amazonia as a carbon source linked to deforestation and climate change. Nature 595, 388–393 (2021).
Tebaldi, C. Extreme sea levels at different global warming levels. Nat. Clim. Change 11, 746–751 (2021).
Vicedo-Cabrera, A. M. The burden of heat-related mortality attributable to recent human-induced climate change. Nat. Clim. Change 11, 492–500 (2021).
Boulton, C. A., Lenton, T. M. & Boers, N. Pronounced loss of amazon rainforest resilience since the early 2000s. Nat. Clim. Change 12, 271–278 (2022).
Kermack, W. O. & McKendrick, A. G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. A 115, 700–721 (1927).
Harko, T., Lobo, F. S. N. & Mak, M. K. epidemic model and of the sir model with equal death and birth rates. Appl. Math. Comput. 236, 184–194 (2014).
te Vrugt, M., Bickmann, J. & Wittkowski, R. Effects of social distancing and isolation on epidemic spreading modeled via dynamical density functional theory. Nat. Commun. 11, 5576 (2020).
Taghvaei, A. Fractional sir epidemiological models. Sci. Rep. 10, 20,882 (2020).
Ji, P. Low-dimensional behavior of kuramoto model with inertia in complex networks. Sci. Rep. 4, 4783 (2014).
Kroma-Wiley, K. A., Mucha, P. J. & Bassett, D. S. Synchronization of coupled kuramoto oscillators under resource constraints. Phys. Rev. E 104, 014,211 (2021).
Menara, T. Functional control of oscillator networks. Nat. Commun. 13, 4721 (2022).
Arola-Fernández, L. Emergence of explosive synchronization bombs in networks of oscillators. Commun. Phys. 5, 264 (2022).
Schieber, T. A. Quantification of network structural dissimilarities. Nat. Commun. 8, 13,928 (2017).
Carpi, L. C. Structural evolution of the tropical pacific climate network. Eur. Phys. J. B 85, 389 (2012).
Carpi, L. C. Assessing diversity in multiplex networks. Sci. Rep. 9, 4511 (2019).
Thanou, D. Learning heat diffusion graphs. IEEE Trans. Signal Inform. Proces. Over Netw. 3, 484–499 (2017).
Hara, T. & Slade, G. Mean-field critical behaviour for percolation in high dimensions. Commun. Math Phys. 128, 333–391 (1990).
Gómez, S. Diffusion dynamics on multiplex networks. Phys.Rev. Lett. 6, 7366 (2013).
Cencetti, G. & Battiston, F. Diffusive behavior of multiplex networks. N. J. Phys. 21, 035,006 (2019).
Schieber, T.A. et al. Diffusion capacity of single and interconnected networks v:1.0.0. https://doi.org/10.5281/zenodo.7689225 (2023).
Acknowledgements
Research partially supported by Brazilian agencies FAPEMIG, CAPES, and CNPq. P.M.P. acknowledges support from the “Paul and Heidi Brown Preeminent Professorship in ISE, University of Florida”, and RSF 14-41-00039, Humboldt Research Award (Germany) and LATNA, Higher School of Economics, RF. C.M. acknowledges partial support from Spanish MINECO (PID2021-123994NB-C21) and ICREA ACADEMIA. A.D.-G. knowledges support from the Spanish grants PGC2018-094754-B-C22 and PID2021-128005NB-C22, funded by MCIN/AEI/ 10.13039/ 501100011033 and “ERDF A way of making Europe”; and from Generalitat de Catalunya (2021SGR00856). M.G.R acknowledges partial support from FUNDEP.
Author information
Authors and Affiliations
Contributions
T.A.S, L.C.C, C.M, P.M.P, A.D.-G and M.G.R develop the methods. T.A.S, L.C.C and M.G.R implemented the code and conducted the experiments. T.A.S, L.C.C, C.M, P.M.P, A.D.-G and M.G.R analyzed the data, results and wrote the paper. All authors read and approved the final version of the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Giulia Cencetti, Chengcheng Shao and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schieber, T.A., Carpi, L.C., Pardalos, P.M. et al. Diffusion capacity of single and interconnected networks. Nat Commun 14, 2217 (2023). https://doi.org/10.1038/s41467-023-37323-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-023-37323-0
This article is cited by
-
Statistical behavioral characteristics of network communication delay in IPv4/IPv6 Internet
Telecommunication Systems (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.