Abstract
Integrated electro-optic (EO) modulators are fundamental photonics components with utility in domains ranging from digital communications to quantum information processing. At telecommunication wavelengths, thin-film lithium niobate modulators exhibit state-of-the-art performance in voltage-length product (VπL), optical loss, and EO bandwidth. However, applications in optical imaging, optogenetics, and quantum science generally require devices operating in the visible-to-near-infrared (VNIR) wavelength range. Here, we realize VNIR amplitude and phase modulators featuring VπL’s of sub-1 V ⋅ cm, low optical loss, and high bandwidth EO response. Our Mach-Zehnder modulators exhibit a VπL as low as 0.55 V ⋅ cm at 738 nm, on-chip optical loss of ~0.7 dB/cm, and EO bandwidths in excess of 35 GHz. Furthermore, we highlight the opportunities these high-performance modulators offer by demonstrating integrated EO frequency combs operating at VNIR wavelengths, with over 50 lines and tunable spacing, and frequency shifting of pulsed light beyond its intrinsic bandwidth (up to 7x Fourier limit) by an EO shearing method.
Similar content being viewed by others
Introduction
Integrated photonics at visible and near-infrared (VNIR) wavelengths is important for applications ranging from sensing1,2,3 and spectroscopy4 to communications5 and quantum information processing6,7. For example, visible integrated photonic platforms can be combined with any of the large variety of atomic or atomic-like systems with transitions in the VNIR such as alkali and alkaline-earth metal atoms8,9,10, rare-earth ions11, diamond color centers12,13 and quantum dots14,15,16. Concerning quantum applications, VNIR photonics enables photon routing17,18, spectral shifting for interfacing disparate quantum emitters11,19, or realizing higher-dimensional encoded quantum states20,21, all in a scalable and compact approach.
A variety of visible integrated photonic platforms have been demonstrated, including silicon nitride2,22,23,24,25, aluminum ntiride26,27, diamond28,29, and lithium niobate (LN)30,31,32. LN is particularly compelling due to its large electro-optic (EO) coefficient, low optical loss, and wide transparency window, making it the workhorse material for the modern day telecommunications industry. Recent work has shown the promise of thin-film lithium niobate (TFLN) at telecommunications wavelengths33. Beyond the inherent miniaturization and integratability achievable with TFLN, the strong optical confinement and increased tailorability have enabled performance not achievable with bulk LN, including CMOS compatible drive voltages and high bandwidth operation34,35,36. As a result of LN’s large transparency window, EO TFLN devices in the visible regime have been demonstrated30,31,32. However, half-wave voltages (Vπ) and large bandwidths beyond that realized in visible bulk devices has yet to be demonstrated in VNIR TFLN. In particular, the combination of high-bandwidth and low drive-voltage optical modulation would enable on-chip routing and spectral control: a critical requirement for quantum applications.
In this work, we realize VNIR TFLN amplitude and phase modulators (Fig. 1a) operating with VπL of sub-1 V ⋅ cm (Fig. 1b), extinction ratios beyond 20 dB, and 3 dB EO bandwidths in excess of 35 GHz. We perform two demonstrations to highlight applications of these devices. We demonstrate an integrated and tunable EO frequency comb source in the VNIR, showing over 50 lines in a single comb at 638, 738, and 838 nm, and displaying flat-top spectra with less than 10 dB power variation. Furthermore, we use our devices to demonstrate spectral shearing of optical pulses over 7 times their intrinsic spectral bandwidth. Together these demonstrations highlight the widespread utility of TFLN modulators operating in the VNIR spectrum.
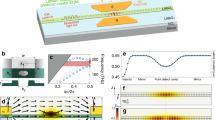
a In the time domain, VNIR amplitude modulators with ultra-low drive voltages ( < 1 V) can modulate continuous-wave optical inputs at CMOS voltages. Similarly, sub-volt phase modulators enable VNIR frequency comb generation and frequency shifting over multiple pulse bandwidths. b Normalized optical transmission of a 10 mm long amplitude (Mach-Zehnder) modulator as a function of the applied voltage. At λ = 738 nm, the Vπ is 0.55 V at 1 MHz. c Cross section illustrations of modulator waveguide and electrode regions. d Optical micrograph of a 5 mm long VNIR TFLN amplitude modulator. The micrograph additionally shows the unbalanced amplitude modulator waveguides, along with the Y-splitters, probe contact region of the electrodes, and the electrode gap taper along the probe contact region to the interaction region.
Results
Design and fabrication
Figure 1c illustrates the design of our TFLN VNIR modulators. We fabricate devices on 300 nm thick X-cut TFLN on 2 μm of thermally grown silicon dioxide on Si (NanoLN). For complete device fabrication details, see methods. Outside of the electrode region, the waveguides are designed to be single mode (support transverse-electric, TE00, and transverse-magnetic, TM00) at 740 nm. We choose this constraint to minimize excitation of higher-order modes, which can lead to a reduction in EO performance in the electrode region. Using finite-difference eigenmode simulations (Lumerical), the required waveguide top width for single mode operation is determined to be approximately 300 nm. A disadvantage of this width is that it reduces mode confinement. This leads to higher optical loss due to mode overlap with sidewalls and cladding, and absorption loss from electrodes. For this reason, we adiabatically increase the waveguide width to 600 nm in the electrode region. Finally, our amplitude modulators feature Y-splitters with excess losses of approximately 0.2 dB/splitter30. An optical micrograph of a fabricated 5 mm long amplitude modulator is provided in Fig. 1d.
For the electrodes, we employ a push-pull configuration with co-planar waveguide (CPW) travelling-wave electrodes. Finite element method (COMSOL) simulations are used to design electrodes with impedance close to 50 Ω and a simulated microwave phase index of nRF = 2.22 at 50 GHz. Due to the relatively large optical group index at VNIR wavelengths compared to telecommunication wavelengths (nvis ≈ 2.38, ntel ≈ 2.25), perfect velocity matching requires a reduction in bottom oxide (BOX) thickness and/or gold thickness, which comes at the expense of increased optical and RF loss. To avoid this, our devices have an index mismatch between the microwave phase and optical group index of the TE00 mode of Δn~0.17. For an impedance matched, 1 cm long lossless modulator, this index mismatch corresponds to a theoretical bandwidth of ~80 GHz.
Visible-to-near-infrared Mach Zehnder modulators
We fabricate 1 cm long Mach-Zehnder modulators (MZMs) with varying gap sizes and experimentally evaluate their performance across both wavelength and electrode gap parameter spaces. The experimental setup is shown in the inset of Fig. 2a (see methods for measurement details).
a Experimental setup illustration and measured low-frequency (1 MHz) Vπ for a 1 cm MZM with an electrode gap of 3 μm. Data shown corresponds to Vπ at λ = 532, 638, 738, 838, and 938 nm. Simulated Vπ is shown by the solid line. b Simulated and measured Vπ (1 MHz) at λ = 738 nm for varied electrode gap. Inset shows a measured extinction ratio of ~21 dB for a 1 cm long, 3 μm gap modulator. c Frequency dependence of Vπ for a 1 cm long MZM. A 3 dB EO bandwidth of ~ 35 GHz is extracted from the response. The bandwidth is measured with respect to a low frequency reference, here taken to be 3 GHz. The grey dashed-lines denote the 3 dB bandwidth w.r.t 3 GHz. d Comparison of modulator figure of merit BW/Vπ between this work, state-of-the-art commercial LN modulators, previous VNIR thin-film LN modulators, and other VNIR modulator platforms. This work exhibits significantly higher BW/Vπ values than all previously reported works, including previously demonstrated TFLN VNIR modulators30 --32,37. The dashed lines correspond to constant values of BW/Vπ. Note that for fair comparison, we compare the reported Vπ at < 1 GHz for all devices. The TFLN data points with cross annotations denote devices for which the reported BW was limited by the equipment used. Detailed comparison of referenced works can be found in supplementary tables 1 and 2. RF Radiofrequency, F.P.C. Fiber polarization controller, TFLN Thin-film lithium niobate, OSC Oscilloscope, OSA Optical Spectrum Analyzer, FP Fabry-Perot.
As shown in Fig. 2a, the Vπ of our 1 cm long, 3 μm gap devices is as low as 0.42 V at 532 nm, and increases only slightly to 0.45, 0.55, and 0.85 V at 638, 738, and 838 nm, respectively. The increase in VπL for longer wavelengths follows from the smaller phase accumulation for the same modulator length. Our VπL is a factor of 2-3 smaller, depending on wavelength considered, than the best previously reported values for VNIR TFLN modulators, without compromising bandwidth or device insertion loss30,31,32. We note that our improvement stems predominantly from the reduction in electrode gap, i.e., enhancement in optical-microwave field overlap.
We perform the same measurements at 738 nm, but with MZMs of varied gap sizes, seeing an increasing VπL for larger gap sizes (Fig. 2b). For comparison, we also theoretically calculate VπL as a function of gap. The simulated response shows excellent agreement with our measured results. Notably, we measure VπL < 1 V ⋅ cm for gap sizes as large as 5 μm. For comparison, recent work on VNIR devices with smaller gaps (2 μm) have reported larger low frequency VπL31.
We extract the on-chip modulator loss by fabricating and measuring 3 μm gap modulators of varying electrode length. From this we obtain an on-chip loss of ~ 0.7 ± 0.2 dB/cm (see supplementary fig. 1 for details). This value is over an order of magnitude smaller than that reported in other recent demonstrations for VNIR LN modulators32,37. Including the lensed fiber-to-chip coupling loss ( ~ 7 dB/facet), the total device insertion loss comes to ~ 15 dB. We note that because the total device insertion loss is dominated by coupling loss (mismatch between the lensed fiber and rib waveguide mode), it can be reduced by nearly an order of magnitude using techniques such as tapered fiber coupling38. In addition, we observe an extinction ratio of over 25 dB for 5 μm gap devices, and ~ 21 dB for 3 μm gap devices (Fig. 2b, inset), comparable with state-of-the-art.
To evaluate the high frequency response of the devices, the 3 dB EO bandwidth of our MZM is extracted via first measuring the optical frequency spectrum of the transmitted light on a Fabry-Perot (FP) cavity or optical spectrum analyzer (OSA) and fitting the sideband powers to a Bessel function for varied frequency applied sinusoidal voltage. Figure 2c shows the high frequency response for a 3 μm gap, 1 cm long MZM operating at 738 nm. The extracted 3 dB bandwidth is approximately 35 GHz (w.r.t. to 3 GHz), and is limited by RF loss of the CPW (1.35 dB cm−1 GHz−1/2). A non-DC reference is chosen due to both the rapid roll-off originating from the CPW impedence mismatch, and the commonly observed instability in LN modulators at low frequencies due to photorefractive effects. We use the measured electrical transmission coefficients of the CPW to also theoretically predict the modulator 3 dB bandwidth, which we find to be ~36 GHz, in excellent agreement with our measured result. We emphasize that since the device bandwidth is limited by CPW RF loss, it can be improved upon by implementing capacitively loaded traveling wave electrodes to reduce current crowding and its associated increase of RF loss39.
To fully contextualize the performance of our device, we compare our results with other previously demonstrated VNIR modulators in terms of bandwidth and low-frequency Vπ (BW/Vπ ratio), including both integrated and non-integrated VNIR modulators (Fig. 2d). We emphasize the improvement in performance between this work and state-of-the-art commercial bulk VNIR LN modulators. While prior works have demonstrated the superior performance of TFLN over bulk LN in the telecommunication band40, to date, the same has not been shown in TFLN VNIR modulators. Here, we show that VNIR TFLN modulators can exhibit voltage-bandwidth performance exceeding 30 GHz V−1, a performance metric not achievable in bulk devices, or other current integrated VNIR photonic platforms. Finally, we note that while other visible modulator platforms have recently been demonstrated41,42, they are presently limited to operating frequencies in the 1–100 kHz range.
Visible-to-near-infrared electro-optic frequency comb
To demonstrate the utility of these EO devices for sensing applications, we fabricate TFLN phase modulators (PM) operating at VNIR wavelengths. Because of the low required driving voltages and broadband optical operation, we use these devices to generate EO frequency combs operating at high-frequency and with variable comb spacing. Our combs feature over 50 sidebands when driven at 30 GHz by a ~ 3 W microwave source ( ~ 8Vπ), and they operate over a broad wavelength range. Results for a 3 μm device operating at 638, 738, and 838 nm are shown in Fig. 3a–c. The insets depicts the comb spacing between two lines at higher magnification. Due to the limited resolution of the OSA at these wavelengths, the comb visibility is not fully resolved. We further note that for shorter wavelengths, the comb envelope displays greater asymmetry. This phenomenon originates from the fact that the waveguides begin to support higher order modes at these wavelengths, each of which propagate at different group velocities and possess varying velocity mismatch with respect to the RF field. We support this assessment by calculating the theoretical comb spectrum after including additional modes which shows good qualitative agreement with our measured results (see supplementary figure 2). Finally, in Fig. 3d, the 1st sideband is shown as a function of applied RF drive frequency, thereby illustrating the tunable nature of the VNIR EO combs.
Tunable frequency combs operating at a, λ = 638, b 738 nm, and c 838 nm with 30 GHz spacing and more than 50 lines. Insets show magnified view of the comb lines. The asymmetry shown in the 638 nm and 738 nm combs is attributable to the waveguide supporting higher order modes at shorter wavelengths (see supplementary fig. 2). d Normalized 1st modulated sideband as a function of applied RF frequency showing comb tunability up to 40 GHz. The pump wavelength is 738 nm. Spectra are under-sampled due to the limited resolution of the spectrometer. Gaussian fits are provided to guide the eye.
This is an important component that can be utilized for a variety of applications including sensing43, astrophysical spectroscopy4, and frequency-bin encoding of quantum information20.
Visible spectral shearing
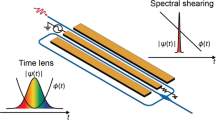
Our low Vπ modulators enable high-bandwidth frequency control of input light. Namely, by applying a quasi-linear phase ramp ϕ(t) = − Kt to the modulator, input light can be shifted in frequency by K. This frequency shift is referred to as spectral shearing44,45. This is useful for quantum applications where frequency shifting can be used to bridge the inhomogenous distribution of quantum emitters or for performing frequency bin operations on non-classical states46. The former is particularly useful at visible wavelengths where a variety of quantum emitters have their optical transitions.
The shift achievable via frequency shearing is dependent on the total phase applicable to the device. This is proportional to \(\frac{V}{{V}_{\pi }}{f}_{{{{{{{{\rm{RF}}}}}}}}}\), where V is the applied voltage, and fRF is the frequency of the applied RF tone. Thus a low Vπ phase modulator is required to achieve a large total shift. Although previous demonstrations of shearing have demonstrated large frequency shifts up to 640 GHz47, these demonstrations relied on ultra-short pulses to utilize a high frequency RF drive45,47,48, and thus shifting beyond the bandwidth of the pulse has not been demonstrated.
We use a 100 MHz RF tone with an amplitude of ~ 20Vπ applied to our device and lock 1 ns duration square-shaped optical pulses (λ = 737 nm) to the rising or falling linear regime of the RF tone to apply a quasi-linear phase profile to the pulse (Fig. 4a, b). Our TFLN device is a 1 cm long, 3 μm gap phase modulator with a Vπ ~ 1 V at 100 MHz. We observe a spectral shift of ± 6.6 GHz when locking the pulse to the rising or falling edge, respectively (Fig. 4c). Approximately 85% of input power is shifted into the desired lobe, with our estimate limited by the finite extinction of the input optical pulses ( ~ 20 dB), which can be improved via gating the detected signal.
a Principle of spectral shearing, where the rising (falling) edge of a sinusoidal tone is used to provide a linear phase across an optical pulse in order to blue (red) shift its frequency. b Diagram of the experimental setup. An arbitrary waveform generator (AWG) is used to generate both 1 ns square electrical pulses and the 100 MHz sinusoidal drive for the phase modulator. The square electrical pulses generate square optical pulses via a commercial amplitude EO modulator, which are then routed to the low Vπ TFLN phase modulator. The RF drive from the AWG is amplified before reaching the device. c Frequency spectrum of the pulses after applying a sinusoidal tone and synchronizing the pulse with the falling (redshift) or rising (blueshift) edge of the RF tone, showing a shift of ± 6.6 GHz (over 7 times the pulse bandwidth) relative to the original spectrum with no RF tone applied. EOM Electro-optic modulator, AWG Analog waveform generator, F.P.C. Fiber polarization controller, TFLN Thin-film lithium niobate, FP Fabry-Perot, OSC Oscilloscope.
Given the pulse’s bandwidth of ~ 0.9 GHz, the observed shift is over 7 times larger than the pulse bandwidth, almost an order of magnitude larger than previous studies have achieved47. We emphasize that the wavelength and pulse duration used in this work is comparable to the wavelength and lifetime of photons emitted from a variety of different visible solid-state quantum emitters and the achieved shift similar to their corresponding inhomogenous distribution, thus providing a route for deterministically bridging this frequency gap49.
Discussion
We have demonstrated VNIR TFLN phase and amplitude modulators featuring sub-1 V half-wave voltage, extinction ratios above 20 dB, on-chip insertion loss as low as 0.7 dB, and electro-optic bandwidths exceeding 35 GHz. With this performance we have demonstrated an integrated VNIR EO frequency comb with over 50 lines, and measured spectral shifting with shifts beyond the intrinsic bandwidth of the pulse. Together, these results show the suitability of these devices for both spatial and spectral control of input light. The performance and scalability of our integrated platform ensures its suitability for a wide variety of applications. Through combining this visible platform with other demonstrated TFLN technologies such as periodically poled lithium niobate (PPLN)50 or laser integration51,52, applications such as visible on-chip spectroscopy, photon pair generation and manipulation, and efficient visible light communication can be realized.
Methods
Device fabrication
The optical waveguide layer is realized using Ar+-based reactive-ion etching (RIE) with a lithographically defined (Elionix ELS-F125) hydrogen silsesquioxane hard-mask30. After etching (180 nm) and cleaning, the device is cladded with silicon dioxide (~1 μm) via plasma-enhanced chemical vapor deposition. To reduce optical loss and mitigate photorefractive effects, devices are subsequently annealed36,53. Next, the electrode layer is defined with an electron beam lithography step, RIE (C3F8, Ar+), electron beam evaporation ( ~ 10/800 nm, Ti/Au), and lift-off.
Measurement details
Measurement of half-wave voltage
Devices are characterized in the 634–638 nm and 720–940 nm ranges using New Focus Velocity and M2 SolsTis tunable lasers. The laser source polarization is set using a fiber polarization controller (Thorlabs, FPC560), and the output is launched into the device coupling waveguide using a single-mode lensed fiber (OZ Optics TSMJ-3A-650-4/125-0.25-20-2-10-1). The transmitted light is then collected using a second lensed fiber at the output waveguide and sent to a high sensitivity avalanche photodetector (APD410A), home-built fabry-perot cavity (FP), or optical spectrum analyzer (OSA, AQ6730) depending on the measurement being performed. Coplanar ground-signal-ground (GSG) electrodes are contacted using 50 Ω GSG probes (GGB Industries, 40A-GSG-100-F). The DC performance is evaluated using a 1 MHz triangle waveform, and the normalized transmission is recorded as a function of applied voltage.
Measurement of high frequency half wave voltage
In order to measure the half-wave voltage (Vπ) of the MZMs at high frequencies, a sinusoidal RF tone is applied at varying frequencies and the resulting optical spectrum is measured. The optical frequency spectrum of an MZM given an input CW optical carrier frequency of ω0, an applied RF tone at frequency ωm and amplitude V0, and internal phase between the arms of ϕ is given by:
where k is an integer of the harmonic of the drive frequency54.
The frequency spectrum is measured using a home-built Fabry-Perot cavity (linewidth = 200 MHz) for lower frequencies ( < 15 GHz) and an optical spectrum analyzer (OSA, AQ6730) or Czerny-Turner spectrometer (Princeton Instruments, SpectraPro HRS) for higher frequencies. For the FP cavity, the intensity of the carrier is measured as a function of applied voltage and fit to (1). For measurements with the OSA, a wider spectrum featuring multiple sidebands is measured at various powers and the relative intensities of the even sidebands of each spectrum is fit to equation (1).
Frequency shearing measurement
To implement spectral shearing, the RF tone applied to the device and optical pulse are generated using the same arbitrary waveform generator (AWG, Tektronix 700001b), while also ensuring minimal jitter between the two. Optical pulses are defined using a commercial amplitude electro-optic modulator (EOSpace, AZ-AV5-40-PFA-PFA-737) with a continuous-wave laser. The spectrum of the pulse is measured using a FP cavity. We numerically find the non-linearity of the sine tone in this quasi-linear region to have a negligible effect on the resulting spectrum for the given drive frequency and pulse duration.
Data availability
All data that supports the conclusions of this study are included in the article and the Supplementary Information file. The data presented in this study is available from the corresponding authors upon request.
References
Hainberger, R. et al. Cmos-compatible silicon nitride waveguide photonic building blocks and their application for optical coherence tomography and other sensing applications (2020).
Sacher, W. D. et al. Visible-light silicon nitride waveguide devices and implantable neurophotonic probes on thinned 200 mm silicon wafers. Opt. Express 27, 37400 (2019).
Goykhman, I., Desiatov, B. & Levy, U. Ultrathin silicon nitride microring resonator for biophotonic applications at 970 nm wavelength. Appl. Phys. Lett. 97, 081108 (2010).
McCracken, R. A., Charsley, J. M. & Reid, D. T. A decade of astrocombs: Recent advances in frequency combs for astronomy. Opt. Express 25, 15058–15078 (2017).
Strinati, E. C. et al. 6g: The next frontier: From holographic messaging to artificial intelligence using subterahertz and visible light communication. IEEE Vehicular Technol. Mag. 14, 42–50 (2019).
Awschalom, D. et al. Development of quantum interconnects (quics) for next-generation information technologies. PRX Quantum 2, 017002 (2021).
Moody, G. et al. Roadmap on integrated quantum photonics. arXiv preprint arXiv:2102.03323 (2021).
Levine, H. et al. High-fidelity control and entanglement of rydberg-atom qubits. Phys. Rev. Lett. 121, 123603 (2018).
Madjarov, I. S. et al. High-fidelity entanglement and detection of alkaline-earth Rydberg atoms. Nat. Phys. 16, 857–861 (2020).
Bruzewicz, C. D., Chiaverini, J., McConnell, R. & Sage, J. M. Trapped-ion quantum computing: Progress and challenges. Appl. Phys. Rev. 6, 021314 (2019).
Sinclair, N. et al. Spectral multiplexing for scalable quantum photonics using an atomic frequency comb quantum memory and feed-forward control. Phys. Rev. Lett. 113, 053603 (2014).
Bradac, C., Gao, W., Forneris, J., Trusheim, M. E. & Aharonovich, I. Quantum nanophotonics with group iv defects in diamond. Nat. Commun. 10, 5625 (2019).
Ruf, M., Wan, N. H., Choi, H., Englund, D. & Hanson, R. Quantum networks based on color centers in diamond. J. Appl. Phys. 130, 070901 (2021).
Uppu, R. et al. Scalable integrated single-photon source. Sci. Adv. 6, eabc8268 (2020).
Zhai, L. et al. Low-noise gaas quantum dots for quantum photonics. Nat. Commun. 11, 4745 (2020).
Liu, J. et al. A solid-state source of strongly entangled photon pairs with high brightness and indistinguishability. Nat. Nanotechnol. 14, 586–593 (2019).
Saha, U. et al. Routing single photons from a trapped ion using a photonic integrated circuit. arXiv preprint arXiv:2203.08048 (2022).
Monroe, C. et al. Large-scale modular quantum-computer architecture with atomic memory and photonic interconnects. Phys. Rev. A 89, 022317 (2014).
Levonian, D. et al. Optical entanglement of distinguishable quantum emitters. Phys. Rev. Lett. 128, 213602 (2022).
Reimer, C. et al. Generation of multiphoton entangled quantum states by means of integrated frequency combs. Science 351, 1176–1180 (2016).
Kues, M. et al. Quantum optical microcombs. Nat. Photonics 13, 170–179 (2019).
Dong, M. et al. High-speed programmable photonic circuits in a cryogenically compatible, visible-near-infrared 200 mm cmos architecture. Nat. Photonics 16, 59–65 (2022).
Muñoz, P. et al. Silicon nitride photonic integration platforms for visible, near-infrared and mid-infrared applications. Sensors 17, 2088 (2017).
Khan, M., Babinec, T., McCutcheon, M. W., Deotare, P. & Lončar, M. Fabrication and characterization of high-quality-factor silicon nitride nanobeam cavities. Opt. Lett. 36, 421 (2011).
Romero-García, S., Merget, F., Zhong, F., Finkelstein, H. & Witzens, J. Silicon nitride cmos-compatible platform for integrated photonics applications at visible wavelengths. Opt. Express 21, 14036 (2013).
Lu, T.-J. et al. Aluminum nitride integrated photonics platform for the ultraviolet to visible spectrum. Opt. Express 26, 11147 (2018).
He, J. et al. Nonlinear nanophotonic devices in the ultraviolet to visible wavelength range. Nanophotonics 9, 3781–3804 (2020).
Burek, M. J. et al. High quality-factor optical nanocavities in bulk single-crystal diamond. Nat. Commun. 5, 5718 (2014).
Nguyen, C. T. et al. An integrated nanophotonic quantum register based on silicon-vacancy spins in diamond. Phys. Rev. B 100, 165428 (2019).
Desiatov, B., Shams-Ansari, A., Zhang, M., Wang, C. & Lončar, M. Ultra-low-loss integrated visible photonics using thin-film lithium niobate. Optica 6, 380–384 (2019).
Celik, O. T. et al. High-bandwidth cmos-voltage-level electro-optic modulation of 780 nm light in thin-film lithium niobate. Opt. Express 30, 23177 (2022).
Li, C. et al. High modulation efficiency and large bandwidth thin-film lithium niobate modulator for visible light. Opt. Express 30, 36394–36402 (2022).
Zhu, D. et al. Integrated photonics on thin-film lithium niobate. Adv. Opt. Photonics 13, 242–352 (2021).
Wang, C. et al. Ultrahigh-efficiency wavelength conversion in nanophotonic periodically poled lithium niobate waveguides. Optica 5, 1438–1441 (2018).
Zhang, M., Wang, C., Cheng, R., Shams-Ansari, A. & Lončar, M. Monolithic ultra-high-q lithium niobate microring resonator. Optica 4, 1536–1537 (2017).
Shams-Ansari, A. et al. Reduced material loss in thin-film lithium niobate waveguides. Apl. Photonics 7, 081301 (2022).
Sund, P. I. et al. High-speed thin-film lithium niobate quantum processor driven by a solid-state quantum emitter. arXiv preprint arXiv:2211.05703 (2022).
Renaud, D., Assumpcao, D., Shams-Ansari, A., Barton, D. & Loncar, M. Low-loss fiber-to-chip visible couplers in thin-film lithium niobate. CLEO Conference 2022, Poster Session (2022).
Kharel, P., Reimer, C., Luke, K., He, L. & Zhang, M. Breaking voltage–bandwidth limits in integrated lithium niobate modulators using micro-structured electrodes. Optica 8, 357–363 (2021).
Wang, C. et al. Integrated lithium niobate electro-optic modulators operating at cmos-compatible voltages. Nature 562, 101–104 (2018).
Kamada, S. et al. Superiorly low half-wave voltage electro-optic polymer modulator for visible photonics. Opt. Express 30, 19771–19780 (2022).
Liang, G. et al. Robust, efficient, micrometre-scale phase modulators at visible wavelengths. Nat. Photonics 15, 908–913 (2021).
Shams-Ansari, A. et al. Thin-film lithium-niobate electro-optic platform for spectrally tailored dual-comb spectroscopy. Commun. Phys. 5, 1–8 (2022).
Johnson, L. M. & Cox, C. H. Serrodyne optical frequency translation with high sideband suppression. J. Lightwave Technol. 6, 109–112 (1988).
Wright, L. J., Karpiński, M., Söller, C. & Smith, B. J. Spectral shearing of quantum light pulses by electro-optic phase modulation. Phys. Rev. Lett. 118, 023601 (2017).
Lukens, J. M. & Lougovski, P. Frequency-encoded photonic qubits for scalable quantum information processing. Optica 4, 8 (2017).
Zhu, D. et al. Spectral control of nonclassical light pulses using an integrated thin-film lithium niobate modulator. Light.: Sci. Appl. 11, 1–9 (2022).
Puigibert, M. G. et al. Heralded single photons based on spectral multiplexing and feed-forward control. Phys. Rev. Lett. 119, 083601 (2017).
Evans, R. E., Sipahigil, A., Sukachev, D. D., Zibrov, A. S. & Lukin, M. D. Narrow-linewidth homogeneous optical emitters in diamond nanostructures via silicon ion implantation. Phys. Rev. Appl. 5, 044010 (2016).
Xin, C. et al. Spectrally separable photon-pair generation in dispersion engineered thin-film lithium niobate. Opt. Lett. 47, 2830–2833 (2022).
Shams-Ansari, A. et al. Electrically pumped laser transmitter integrated on thin-film lithium niobate. Optica 9, 408–411 (2022).
de Beeck, C. O. et al. Iii/v-on-lithium niobate amplifiers and lasers. Optica 8, 1288–1289 (2021).
Xu, Y. et al. Mitigating photorefractive effect in thin-film lithium niobate microring resonators. Opt. Express 29, 5497–5504 (2021).
Shi, Y., Yan, L. & Willner, A. E. High-speed electrooptic modulator characterization using optical spectrum analysis. J. Lightwave Technol. 21, 2358 (2003).
Acknowledgements
This work was supported in part by AFOSR FA9550-20-1-0105 (M.L.), FA9550-19-1-0376 (M.L.), ARO MURI W911NF1810432 (M.L.), NSF EEC-1941583 (M.L.), OMA-2137723 (M.L.), and OMA-2138068 (M.L.), DOE DE-SC0020376 (M.L.), MIT Lincoln Lab 7000514813 (M.L.), AWS Center for Quantum Networking’s research alliance with the Harvard Quantum Initiative (M.L.), Ford Foundation Fellowship, (D.R.), NSF GRFP No. DGE1745303 (D.R., D.A.), NSERC PGSD scholarship (G.J.), Harvard Quantum Initiative (HQI) postdoctoral fellowship (D.Z.), A*STAR Central Research Fund (D.Z.), AQT Intelligent Quantum Networks and Technologies (N.S.), and NSF Center for Integrated Quantum Materials No. DMR-1231319 (D.R., N.S.). We acknowledge fruitful discussions with Lingyan He, Prashanta Kharel, Ben Dixon, and Alex Zhang. Device fabrication was performed at the Center for Nanoscale Systems (CNS), a member of the National Nanotechnology Coordinated Infrastructure Network (NNCI), which is supported by the National Science Foundation under NSF Grant No. 1541959.
Author information
Authors and Affiliations
Contributions
G.J. and D.R. designed devices. D.R. fabricated devices. D.A., D.R., and G.J. designed and performed the measurements. A.S. assisted with electronics measurements. D.A., D.R., and D.Z. analyzed the data. Y.H. provided a theory on frequency combs. D.R., D.A., and A.S. wrote the manuscript with extensive input from the other authors. M.L. and N.S. supervised the project. These authors contributed equally: D.R. and D.A.
Corresponding authors
Ethics declarations
Competing interests
M.L. is involved in developing lithium niobate technologies at HyperLight Corporation. The remaining authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Renaud, D., Assumpcao, D.R., Joe, G. et al. Sub-1 Volt and high-bandwidth visible to near-infrared electro-optic modulators. Nat Commun 14, 1496 (2023). https://doi.org/10.1038/s41467-023-36870-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-023-36870-w
This article is cited by
-
Cavity-enhanced narrowband spectral filters using rare-earth ions doped in thin-film lithium niobate
npj Nanophotonics (2024)
-
Active optical phased array integrated within a micro-cantilever
Communications Engineering (2024)
-
On-demand photonic Ising machine with simplified Hamiltonian calculation by phase encoding and intensity detection
Communications Physics (2024)
-
Differential phase-diversity electrooptic modulator for cancellation of fiber dispersion and laser noise
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.