Abstract
The electronic correlations (e.g. unconventional superconductivity (SC), chiral charge order and nematic order) and giant anomalous Hall effect (AHE) in topological kagome metals AV3Sb5 (A = K, Rb, and Cs) have attracted great interest. Electrical control of those correlated electronic states and AHE allows us to resolve their own nature and origin and to discover new quantum phenomena. Here, we show that electrically controlled proton intercalation has significant impacts on striking quantum phenomena in CsV3Sb5 nanodevices mainly through inducing disorders in thinner nanoflakes and carrier density modulation in thicker ones. Specifically, in disordered thin nanoflakes (below 25 nm), we achieve a quantum phase transition from a superconductor to a “failed insulator” with a large saturated sheet resistance for T → 0 K. Meanwhile, the carrier density modulation in thicker nanoflakes shifts the Fermi level across the charge density wave (CDW) gap and gives rise to an extrinsic-intrinsic transition of AHE. With the first-principles calculations, the extrinsic skew scattering of holes in the nearly flat bands with finite Berry curvature by multiple impurities would account for the giant AHE. Our work uncovers a distinct disorder-driven bosonic superconductor-insulator transition (SIT), outlines a global picture of the giant AHE and reveals its correlation with the unconventional CDW in the AV3Sb5 family.
Similar content being viewed by others
Introduction
The layered kagome metals AV3Sb5 (A = K, Rb and Cs) that possess topological electron bands and geometrical frustration of vanadium lattices are of great interests1,2,3. This is in no small part due to the many quantum phenomena that they support including unconventional SC4,5,6,7,8,9,10,11, novel nematic order12, chiral charge density order13,14,15,16,17,18,19,20,21,22, giant anomalous Hall effect23,24,25 as well as the interplay between two-gap SC and CDW in CsV3Sb526. The unique coexistence of electronic correlations and band topology in AV3Sb5 allows for investigating intriguing transitions of these correlated states, such as the superconductor-insulator transition (SIT), a protocol quantum phase transition (QPT) that is usually tuned by disorders, magnetic fields and electric gating27,28. Moreover, the origin of giant AHE in AV3Sb5 and its correlation with chiral CDW remain elusive29,30, in spite of several recently proposed mechanisms including the extrinsic skew scattering of Dirac quasiparticles with frustrated magnetic sublattice23, the orbital currents of novel chiral charge order13 or the chiral flux phase in the CDW phase31. Thus the ability to tune the carrier density and the corresponding Fermi surfaces would play a vital role in understanding and manipulating these novel quantum states and further realizing exotic QPTs.
In this work, we find that electrically controlled proton intercalation32,33 exhibits crucial impacts on the superconducting state, CDW state and the associated AHE in CsV3Sb5 nanoflakes via disorders and carrier density modulation. In thinner nanoflakes (below 25 nm) with large gate voltages (e.g. with an amplitude above 15 V), the enhanced disorders from intercalated protons suppressed both CDW and superconducting phase coherence and gave rise to a SIT associated with the localized Cooper pairs, featuring a saturated sheet resistance reaching up to 106 Ω for T → 0, dubbed a “failed insulator”. While in thicker CsV3Sb5 nanoflakes with much lower gate voltages (within 7 V), the superconducting transition instead retained with nearly unchanged sheet resistance in normal state at 5 K, indicating very limited impact of disorder. However, the Hall measurements demonstrate a large modulation of carrier density (with the modulation up to 1022 cm−3) and the relevant Fermi surface topology changes from a hole pocket to an electron pocket. Consequently, we find that the giant anomalous Hall conductivity (AHC) with a maximal amplitude exceeding 104 Ω−1 cm−1 mainly pinned down to a narrow hole-carrier-density window around \(p=\left(2.5\pm 1.2\right)\times {10}^{22}\,{{{{{{\rm{cm}}}}}}}^{-3}\) at low temperatures. Meanwhile, the AHE exhibits a clear extrinsic-intrinsic transition as the Fermi level shifts across the CDW gap near the saddle point. The observed giant AHE can be ascribed to the extrinsic skew scattering of the holes in the flat bands with nonzero Berry curvature by V vacancies and magnetic field tilted paramagnetic (PM) impurities.
Results
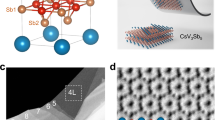
The layered material CsV3Sb5 has a hexagonal crystal structure with space group P6/mmm (No. 191). As shown in the upper panel of Fig. 1a, the V3Sb layers are sandwiched by antimonene layers and Cs layers. X-ray diffraction (XRD) (see Supplementary Fig. 1), reveals a sharp (001) diffraction peak, indicating a single crystal possessing (001) preferred orientation, in line with previous work4. The striking feature of CsV3Sb5 is that the V atoms form a 2D kagome network. This frustrated magnetic sublattice of V was expected to induce novel correlation effects, such as spin-liquid states34,35. The lower panel of Fig. 1a illustrates a schematic of the gating device. A CsV3Sb5 nanoflake is mounted on the solid proton conductor with an underlying Pt electrode to form a solid proton field effect transistor (SP-FET). Next we demonstrate how the proton intercalation significantly affects the SC state, CDW state and the giant AHE in CsV3Sb5 nanoflakes with distinct thicknesses.
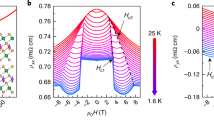
a Schematic of proton gating on CsV3Sb5 nanoflakes (upper) and Hall-bar device (lower). b Temperature dependence of sheet resistance at various gate voltages in device #5. c Sheet resistance as a function of charge density ne near SIT. The critical resistance Rc ~ 316 Ω is obtained with carrier density \({{{{{{\rm{n}}}}}}}_{{{{{{\rm{c}}}}}}} \sim 7.91\times {10}^{17}{{{{{{\rm{m}}}}}}}^{-2}\). d Sheet resistance as the function of 1/T under the same voltages. It exhibits a “failed insulator” with a large saturated resistance for T → 0 K on the insulating side. e Multiple sets of Rs (T, B) curves can collapse onto a single function, akin to a 2D SIT. f shows the derivatives of the resistance curves Rxx (T) under different voltages. As the voltage changes from 0 V to −6.5 V, the CDW transition temperature Tcdw gradually decreases from 85 K to 73 K at Vg = −6.5 V. CDW is largely suppressed when the gate voltage exceeds −7.0 V.
Protonic gate on thinner CsV3Sb5 nanoflakes
We first investigate the impacts of proton intercalation on the correlated electron states including SC and CDW in thinner CsV3Sb5 flakes below 25 nm. Figure 1b shows the temperature-dependent sheet resistance of device #5 with thickness of 21 nm at various gate voltages. A clear SC phase appears with the offset transition temperature \({{{{{{\rm{T}}}}}}}_{{{{{{\rm{c}}}}}}}^{{{{{{\rm{offset}}}}}}}\) around 3 K in the absence of a protonic gate. Besides, a resistance anomaly as a characteristic of CDW near 80 K can be identified on Rs − T curve (around 90 K in bulk, also in Supplementary Fig. 2). Applying a protonic gate, SC is clearly suppressed and disappeared when \({{{{{{\rm{V}}}}}}}_{{{{{{\rm{g}}}}}}}\le -2\,{{{{{\rm{V}}}}}}\) and Rs fattens at around \({{{{{{\rm{V}}}}}}}_{{{{{{\rm{g}}}}}}}=-11\,{{{{{\rm{V}}}}}}\). At \({{{{{{\rm{V}}}}}}}_{{{{{{\rm{g}}}}}}} < -11\,{{{{{\rm{V}}}}}}\), temperature-dependent Rs gradually exhibits an upturn at low temperature region and it eventually reaches up to above 106 Ω at \({{{{{{\rm{V}}}}}}}_{{{{{{\rm{g}}}}}}}=-25\,{{{{{\rm{V}}}}}}\), indicating a quantum phase transition from a superconductor to an insulator. We plot the sheet resistance as a function of carrier density near SIT at temperatures between 2 K and 50 K and obtain a critical resistance Rc ≈ 316 Ω with a critical carrier density \({{{{{{\rm{n}}}}}}}_{{{{{{\rm{c}}}}}}}\approx 7.91\,\times {10}^{17}\,{{{{{{\rm{m}}}}}}}^{-2}\), as shown in Fig. 1c. Converting this critical resistance Rc to the sheet resistance per layer, \({{{{{{\rm{R}}}}}}}_{{{{{{\rm{c}}}}}}/{{{{{\rm{layer}}}}}}}\) = (ρc/l) with l being the thickness of a single layer, we get \({{{{{{\rm{R}}}}}}}_{{{{{{\rm{c}}}}}}/{{{{{\rm{layer}}}}}}}=7268\) \(\Omega\), very close to the quantum resistance of Cooper pair \({{{{{{\rm{R}}}}}}}_{{{{{{\rm{Q}}}}}}} \sim 6450\) \(\Omega\). In spite of the big Rs reaching up to 106 Ω on insulating side, however, a saturated resistance trend appeared for T → 0 K, as shown in Fig. 1d. Note that this insulating state with a saturated resistance for T → 0 K is not a typical insulator but a “failed insulator”, probably due to the incoherent tunneling between localized Cooper pairs36,37. This type of superconductor to “failed insulator” transition has also been observed in another sample #8 in Supplementary Fig. 5 and mainly results from the enhanced effective disorders due to the intercalated protons in the thinner nanoflakes with higher gate voltages38.
SIT can be usually characterized by two distinct scenarios (bosonic and fermionic) according to the nature of insulating phase, while the finite-size scaling analysis could yield its critical exponents and further reveal the universality class of QPT39,40,41,42. To get the critical exponents of SIT, we plot more than twenty sets of \({R}_{s}\left(T,B\right)\) curves and find that they can collapse onto a single function, as predicted for a 2D SIT. The appearance of flatten resistance near Rc suggests the bosonic nature of SIT, in which the coherent Copper pairs in the SC phase are localized by disorders with loss of macroscopic phase coherence in the insulating phase27,28. The finite size scaling dependence of Rs on T and a tuning parameter has the form \({{{{{\rm{\rho }}}}}}\left({{{{{\rm{T}}}}}},{{{{{{\rm{n}}}}}}}_{{{{{{\rm{s}}}}}}}\right)={{{{{\rm{\rho }}}}}}[\frac{{{{{{\rm{T}}}}}}}{{{{{{{\rm{T}}}}}}}_{0}({{{{{{\rm{n}}}}}}}_{{{{{{\rm{s}}}}}}})}]\) with \({{{{{{\rm{T}}}}}}}_{0}\propto {\left|{{{{{{\rm{n}}}}}}}_{{{{{{\rm{s}}}}}}}-{{{{{{\rm{n}}}}}}}_{{{{{{\rm{c}}}}}}}\right|}^{{{{{{\rm{\nu }}}}}}{{{{{\rm{z}}}}}}}\) where ns is the charge density, nc is the critical carrier density with the value of \({{{{{{\rm{n}}}}}}}_{c}\approx 7.91\times {10}^{17}{m}^{-2}\) (or \(1.3\times {10}^{18}{{{{{{\rm{m}}}}}}}^{-2}\) in device #8) and T0 is the scaling parameter which approaches to zero at ns = nc. ν is the correlation-length exponent and z is the temporal critical exponent42. By extracting the exponent product νz and plotting lnT0 versus \({{{{{\rm{ln}}}}}}{{{{{\rm{|}}}}}}{{{{{{\rm{n}}}}}}}_{{{{{{\rm{s}}}}}}}-{{{{{{\rm{n}}}}}}}_{{{{{{\rm{c}}}}}}}{{{{{\rm{|}}}}}}\) curve, we can obtain νz = 1.85 (or 1.68 in device #8) with an uncertainty of ±0.14 (see Supplementary Fig. 3). This estimated exponent product is close to that of magnetic-field tuned SIT in the hybrid system of SC indium islands deposed on 2D indium oxide thin film43, which was also attributed to localization of persisting Cooper pairs. Note that the critical exponent here is distinct from those of 2D conventional models for SIT28 such as classical percolation model (vz = 4/3), quantum percolation model (vz = 7/3), which probably results from the complexity of SC gap and multiple impurities44. Thus, CsV3Sb5 provides us with a unique example system to explore rich QPTs involving intrinsic superconductors with topological energy bands and frustrated kagome lattice.
Figure 1d shows the derivatives of the RT curves at various Vg. Interestingly, CDW transition temperature \({{{{{{\rm{T}}}}}}}_{{{{{{\rm{CDW}}}}}}}=85\,{{{{{\rm{K}}}}}}\) at \({{{{{{\rm{V}}}}}}}_{{{{{{\rm{g}}}}}}}=0\,{{{{{\rm{V}}}}}}\) gradually decreases to 73 K at \({{{{{{\rm{V}}}}}}}_{{{{{{\rm{g}}}}}}}=-6.5\,{{{{{\rm{V}}}}}}\) where SC has been suppressed. More importantly, at \({{{{{{\rm{V}}}}}}}_{{{{{{\rm{g}}}}}}}\le -7\,{{{{{\rm{V}}}}}}\), we found this resistance anomaly totally disappeared on RT curve, indicating the disappearance of the CDW. The non-synchronous disappearance of SC and CDW reveals that SC is more sensitive to disorders. The suppression of CDW is also consistent with recent works for CsV3Sb5 under high pressures, possibly due to band reconstructions or Fermi level shift4,5,6,7,8. It is clear that the protonic gate significantly modifies the CDW and SC phases, facilitating the further investigation of the intertwinement among these novel electronic correlations in AV3Sb5.
Protonic gate on thicker CsV3Sb5 nanoflakes
For a given gate voltage, the thick samples would diminish the impact of disorder of intercalated protons, leaving a large tune of the carrier density. Let us concentrate on the significance of the carrier density modulation on the AHE in CDW phase. We choose thicker CsV3Sb5 nanoflakes with much lower gate voltages within 7 V and find that the proton intercalation mainly changes the carrier density in those thicker ones, leading to only a slight modulation of SC transition temperature (Supplementary Fig. 6), which is consistent with recent reports45,46,47. Figure 2a shows the Hall traces of device #4 (around 80 nm) at various temperatures and selected gate voltages. At low magnetic fields, the Hall resistance Ryx at \({{{{{{\rm{V}}}}}}}_{{{{{{\rm{g}}}}}}}=6.4\,{{{{{\rm{V}}}}}}\) exhibited a nonlinear behavior at 5 K. This antisymmetric “S”-shape Ryx was attributed to field induced AHE in KV3Sb523 and CsV3Sb524. At high fields, Ryx exhibits an approximately linear field dependence associated with the ordinary Hall effect induced by the Lorentz force. Note that AV3Sb5 is a multi-band kagome metal with its transport properties mainly determined by the hole pocket near the M points48. Thus we can use a simple band model to fit this linear Hall resistivity at high field region and extract the approximate hole carrier density at the M-points. When \({6.4{{{{{\rm{V}}}}}}\ge {{{{{\rm{V}}}}}}}_{{{{{{\rm{g}}}}}}}\ge -2.7\,{{{{{\rm{V}}}}}}\), the Hall traces in device #4 exhibit two distinct features. For each gating voltage, the temperature-dependent Hall effects demonstrate a sign reversal at the critical temperature T*, probably due to the temperature-induced band renormalization48. In addition, the Hall slope decreases gradually as the voltage is swept towards −2.7 V, indicating a gradual increase of the hole carrier density. At \({{{{{{\rm{V}}}}}}}_{{{{{{\rm{g}}}}}}}=-4.6\,{{{{{\rm{V}}}}}}\), however, the Fermi surface topology suddenly changes from a hole pocket to an electron pocket with a negative Hall slope. This doping-induced sign reversal of Hall resistance has also been observed in other samples (Supplementary Fig. 9). In contrast to the hole pockets, the Hall traces in the electron pockets exhibit no sign reversal as the temperature is increased, as shown in the bottom right panel of Fig. 2a at \({{{{{{\rm{V}}}}}}}_{{{{{{\rm{g}}}}}}}=-6.1\,{{{{{\rm{V}}}}}}\), indicating a dramatic suppression of T* in the electron pocket. We further plot the gate-dependent carrier density at 5 K in device #4 in Fig. 2b. At \({{{{{{\rm{V}}}}}}}_{{{{{{\rm{g}}}}}}}=-4.6\,{{{{{\rm{V}}}}}}\), the Fermi level is shifted across the electro-hole crossover point. We note that the discontinuity of the carrier density under gate voltage probably stems from the complex evolution of density of states (DOS) during the proton intercalation (See theoretical calculations below). Figure 2c shows the carrier-density (obtained at 5 K) dependent T* for bulk crystals and four nanodevices. In hole pockets, a higher hole density may lead to a smaller T*. However, T* approaches 0 K for the electron pockets, due to the sudden change of the Fermi surface topology.
a Temperature-dependent Hall effect in device #4 under different gating voltages. b Gate-dependent carrier density in device #4 at 5 K. Sweeping the gate voltage from 6.4 V to −6.1 V, the band structure evolves from a hole band to an electron band in the low temperature region. c Carrier density dependent T* in different samples.
We now discuss the gate-dependent AHE in CsV3Sb5. The total Hall resistivity ρyx consists of two components49: \({{{{{{\rm{\rho }}}}}}}_{{{{{{\rm{yx}}}}}}}={{{{{{{\rm{\rho }}}}}}}_{{{{{{\rm{yx}}}}}}}^{{{{{{\rm{N}}}}}}}+{{{{{\rm{\rho }}}}}}}_{{{{{{\rm{yx}}}}}}}^{{{{{{\rm{A}}}}}}}\), with \({{{{{{\rm{\rho }}}}}}}_{{{{{{\rm{yx}}}}}}}^{{{{{{\rm{N}}}}}}}\) the normal Hall resistivity and \({{{{{{\rm{\rho }}}}}}}_{{{{{{\rm{yx}}}}}}}^{{{{{{\rm{A}}}}}}}\) the anomalous Hall resistivity. In order to extract the AHE component, the Hall resistivity was linearly fitted at high field to subtract \({{{{{{\rm{\rho }}}}}}}_{{{{{{\rm{yx}}}}}}}^{{{{{{\rm{N}}}}}}}\). Figure 3a shows the gate-dependent anomalous Hall resistivity \({{{{{{\rm{\rho }}}}}}}_{{{{{{\rm{yx}}}}}}}^{{{{{{\rm{A}}}}}}}\) of device #4 at 5 K under various gate voltages. The maximum \({{{{{{\rm{\rho }}}}}}}_{{{{{{\rm{yx}}}}}}}^{{{{{{\rm{A}}}}}}}\) occurs at Vg = 4.5 V with an amplitude of 0.041 μΩ∙cm that is approximately eight-fold larger than the minimum \({{{{{{\rm{\rho }}}}}}}_{{{{{{\rm{yx}}}}}}}^{{{{{{\rm{A}}}}}}}\) (0.0048 μΩ∙cm) measured at −4.6 V. Interestingly, the AHE also exhibits a sign reversal at Vg = −4.6 V which is probably due to the sign change of the Berry curvature in different energy bands, as shown in Fig. 3a. To get the AHC \({{\sigma }}_{{{{{{\rm{xy}}}}}}}^{{{{{{\rm{A}}}}}}}\), we first convert the Hall resistivity into the Hall conductivity \({{\sigma }}_{{{{{{\rm{xy}}}}}}}={{{{{{\rm{\rho }}}}}}}_{{{{{{\rm{yx}}}}}}}/\left({{{{{{{\rm{\rho }}}}}}}_{{{{{{\rm{yx}}}}}}}}^{2}+{{{{{{\rm{\rho }}}}}}}_{{{{{{\rm{xx}}}}}}}^{2}\right)\), followed by linearly fitting the conductivity at high field and subtracting the normal Hall conductivity \({{\sigma }}_{{{{{{\rm{xy}}}}}}}^{{{{{{\rm{N}}}}}}}\). Figure 3b displays the non-monotonic variation of both the AHC and the anomalous Hall angle (AHA) \({{{{{\rm{\theta }}}}}}=\left|{{\sigma }}_{{{{{{\rm{xy}}}}}}}^{{{{{{\rm{A}}}}}}}/{{\sigma }}_{{{{{{\rm{xx}}}}}}}\right|\). The maximal AHC reaches \(1.24\times {10}^{4}{\Omega }^{-1}{{{{{{\rm{cm}}}}}}}^{-1}\) with an AHA of 2.2% at 4.5 V. Moreover, the AHC (AHA) can be modulated by more than ten times in device #4, revealing the high tunability of the AHE in CsV3Sb5. Figure 3c shows two carrier density regions that exhibit large AHE for different devices. The first region is mainly pinned down in the hole pocket around \({{{{{\rm{p}}}}}}=(2.5\pm 1.2)\times {10}^{22}{{{{{{\rm{cm}}}}}}}^{-3}\) with the maximum AHC exceeding 104 Ω−1 cm−1. Remarkably, another large AHE appears in the electron pocket between n = (3 ± 0.6) × 1022 cm−3 with the AHC around 5 × 103 Ω−1 cm−1. Shifting away from these two regions, however, the AHC either keeps a finite value or approaches zero for devices #1 and #2 (Supplementary Fig. 9).
a Gate-dependent anomalous Hall effect at 5 K after subtraction of the linear Hall background in the high field regions (ordinary Hall part). b Gate-dependent AHC and anomalous Hall angles (AHA). c Carrier density dependent AHC in different devices #1, #2, #3 and #4. The maximum AHC occurred with a hole carrier density of ~2 × 1022 cm−3.
The scaling law between AHC and σxx may assist in identifying the underlying mechanism of the AHE49,50. Figure 4a displays the scaling relations \({{\sigma }}_{{{{{{\rm{xy}}}}}}}^{{{{{{\rm{A}}}}}}}\) vs σxx at various gate voltages and temperatures. In the high conductivity region (σxx exceeds \(5\times {10}^{5}\,{\Omega }^{-1}{{{{{{\rm{cm}}}}}}}^{-1}\)), the maximal AHC obtained in device #4 (4.5 V) and device #7 (at 3.8 V) can be well captured by a linear scaling relation \({{\sigma }}_{{{{{{\rm{xy}}}}}}}^{{{{{{\rm{A}}}}}}}\propto 0.14\,{{\sigma }}_{{{{{{\rm{xx}}}}}}}\), revealing that the skew-scattering mechanism may dominate the AHE49,50,51,52,53. The possible side jump contribution is also discussed in Supplementary section 9. However, at Vg = −4.6 V, a finite AHC around \({10}^{3}\,{\Omega }^{-1}\,{{{{{{\rm{cm}}}}}}}^{-1}\) is approximately independent of the longitudinal conductivity σxx, implying that the intrinsic AHE from the Berry curvature becomes dominant. For other gating voltages, AHEs are likely linked to the mixing region. The gate-induced crossover between the extrinsic (at Vg = 4.5 V) and intrinsic regimes (at Vg = −4.6 V) reveals a strong dependence of AHE on the Fermi energy of CsV3Sb5.
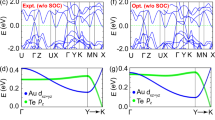
a The scaling relation of AHC against the longitudinal conductivity in devices #4 and #7 (with thickness around 50 nm). Near the high conductivity region (above 5 × 105 Ω−1 cm−1), the giant AHE is dominated by the skew scattering (#4 at 4.5 V and #7 at 3.8 V). At −4.6 V (#4, electron band), the AHE is dominated by the intrinsic Berry curvature. b Band structures of the paramagnetic phase with different doping levels in CsV3Sb5. Ne refers the charge number in each primitive cell. c Illustration of the evolution of Fermi energy under different gate voltages. Red dashed arrow shows the probable Fermi level in bulk crystal (slightly above VHS1). Cs vacancies in CsV3Sb5 nanoflakes will significantly lower the Fermi level (black arrow). Applying a negative (positive) voltage will shift the Fermi level downward (upward). The giant AHE occurs when the Fermi level approaches the upper sub-band with relatively large DOS.
To gain more insights into AHE, we performed the first-principles calculations of the band structure, the DOS and the intrinsic AHC (Supplementary Fig. 12). The calculated AHC due to the field induced magnetization of the spin of V atoms over a broad energy region, exhibits a maximum (~\({1500\Omega }^{-1}{{{{{{\rm{cm}}}}}}}^{-1}\)) in the hole band, one order smaller than the maximum experimental value. This suggests that the intrinsic contribution from the Berry curvature of single-particle energy bands should not dominate the giant AHE in experiments. Note that, because of the tiny observed magnetic moments of V atoms45, the realistic intrinsic AHC from field-induced magnetization should be much smaller than the observed intrinsic AHC. It has been known that the extrinsic skew scattering of AHE essentially originates from the asymmetric scattering of carriers by nonmagnetic/magnetic impurities. Usually, there are three distinct scenarios to produce the extrinsic skew scattering and the resultant AHE49. By careful examination of each scenario, we could exclude the Kondo scattering and resonant skew scattering (Supplementary section 9). We found that the scenario associated with finite Berry curvature of energy bands and scattering by nonmagnetic/magnetic impurities primarily accounts for extrinsic AHE in AV3Sb549,54.
Discussion
We further investigate the impact of charge doping on the band structure and AHE. Since the charge doping in CsV3Sb5 is orbitally selective, the hole (electron) doping can significantly shift the van Hove singularity (VHS1) upward (downward) with respect to the Fermi level within the rigid-band approximation, as shown in Fig. 4b. In our pristine CsV3Sb5 single crystal, the Fermi level lies slightly above VHS1 near the M point (Supplementary section 2), with some nearly flat bands consist of \({{{{{{\rm{d}}}}}}}_{{{{{{\rm{xz}}}}}},{{{{{\rm{yz}}}}}}}\) and \({{{{{{\rm{d}}}}}}}_{{{{{{\rm{xy}}}}}},{{{{{{\rm{x}}}}}}}^{2}-{{{{{{\rm{y}}}}}}}^{2}}\) orbitals of V atoms (Supplementary Fig. 13)55,56,57,58. When T < Tcdw, a CDW gap opens near VHS1, splits the bands at VHS1 into two sub-bands and suppresses the DOS near the Fermi level, as shown in Fig. 4c. Accordingly, the Fermi level in bulk CsV3Sb5 lies in the CDW gap11,55 near the M point (red dashed arrow), exhibiting a large AHE. In exfoliated CsV3Sb5 nanoflakes, the Fermi level approaches the lower sub-band due to the increasing Cs vacancies and the AHC at Vg = 0 V reduces to about one third of the maximal value, i.e., 4500 \(\Omega\)−1 cm−1. Applying a negative voltage will accordingly lower the Fermi level (details in Supplementary section 14) and generate a relatively large AHE region (with AHC around 5000 \(\Omega\)−1 cm−1) in the electron pockets. At Vg > 0 V, however, the Fermi level will be shifted upward and back to the upper sub-band again (dashed red arrow), the giant AHE reappears at 4.5 V in device #4. This giant AHE primarily comes from the skew scatterings of holes in the nearly flat bands at VHS1 with nonzero Berry curvature by the V vacancies and/or PM impurities. The large discrepancy of AHE in the electron and hole pockets is consistent with asymmetric distribution of DOS in the CDW bands near the M points11. Note that the intrinsic AHC at Vg = −4.6 V near the electron-hole crossover point is mainly ascribed to the large suppression of the DOS at the middle of the CDW gap. After evaluating the possible AHE from the electron near the Γ point and the Dirac bands, we find this intrinsic AHE mainly originates from the recent chiral charge order forming from the electronic states near the saddle point59,60,61.
In summary, we revealed two major impacts of proton intercalation on CsV3Sb5, inducing disorders in thinner nanoflakes and carrier density modulation in thicker ones. In thin nanoflakes below 25 nm with \(\left|{{{{{{\rm{V}}}}}}}_{{{{{{\rm{g}}}}}}}\right|\ge 15\,{{{{{\rm{V}}}}}}\), we first observed a distinct superconductor-to-“failed insulator” transition associated with localized Cooper pairs. In thicker nanoflakes, a moderate gate voltage can lead to a large modification of the carrier density and induce a clear extrinsic-intrinsic transition of AHE. The giant AHE in AV3Sb5 can be attributed to the intense extrinsic skew scattering of holes in the nearly flat bands with finite intrinsic AHE in the CDW phase at the saddle points by multiple impurities. This significant and electrically controlled SIT and AHE in CsV3Sb5 should inspire more investigations of the relevant intriguing physics and promising energy-saving nanoelectronic devices.
Methods
Single crystal growth
Single crystals of CsV3Sb5 were synthesized via Sb flux method. The elemental Cs, V and Sb were mixed at a molar ratio of 1:3:20, and loaded in into a MgO crucible. This process was performed in a glove box in Ar ambience. Then the crucible was sealed in a vacuumed quartz tube. The ampule was slowly heated to 1000 ˚C and kept for 20 h. After cooling at a rate of 2 °C/min, the extra flux was removed by fast centrifuging at 640 °C. (Also in Supplementary Section 1).
Device fabrication and transport measurements
Solid protonic electrolyte was prepared by the sol-gel processes by mixing tetraethyl orthosilicate (from Alfa Aesar), ethanol, deionized water, phosphoric acid (from Alfa Aesar, 85% wt%) with a typical molar ratio 1:18:6:0.03. The mixed solution was then stirred for 2 h and annealed for another 2 h at 50 °C in a sealed bottle to form polymerized Si–O–Si chains. Finally, the substrate with bottom gate electrodes was spin-coated with the prepared protonic solution and baked at 150 °C for 25 mins. Transport measurements were performed in a commercial Physical Property Measurement System (PPMS) with magnetic field up to 9 T and a commercial magnetic property measurement system (MPMS) with magnetic field of 7 T.
Data availability
The data used in Figs. 1–4 of the main text are provided in the Source Data. Additional data related to this study are available from the corresponding authors upon reasonable request. Source data are provided with this paper.
References
Ortiz, B. R. et al. New kagome prototype materials: discovery of KV3Sb5, RbV3Sb5, and CsV3Sb5. Phys. Rev. Mater. 3, 094407 (2019).
Ortiz, B. R. et al. CsV3Sb5: A Z2 topological kagome metal with a superconducting ground state. Phys. Rev. Lett. 125, 247002 (2020).
Ortiz, B. R. et al. Superconductivity in the Z2 kagome metal KV3Sb5. Phys. Rev. Mater. 5, 034801 (2021).
Zhang, Z. Y. et al. Pressure-induced reemergence of superconductivity in topological kagome metal CsV3Sb5. Phys. Rev. B 103, 224513 (2021).
Du, F. et al. Pressure-induced double superconducting domes and charge instability in the kagome metal KV3Sb5. Phys. Rev. B 103, L220504 (2021).
Zhao, C. C. et al. Nodal superconductivity and superconducting domes in the topological Kagome metal CsV3Sb5. arXiv http://arxiv.org/abs/2102.08356 (2021).
Chen, K. Y. et al. Double superconducting dome and triple enhancement of Tc in the kagome superconductor CsV3Sb5 under high pressure. Phys. Rev. Lett. 126, 247001 (2021).
Yu, F. H. et al. Unusual competition of superconductivity and charge-density-wave state in a compressed topological kagome metal. Nat. Commun. 12, 3645 (2021).
Yin, Q. et al. Superconductivity and normal-state properties of kagome metal RbV3Sb5 single crystals. Chin. Phys. Lett. 38, 037403 (2021).
Wu, X. et al. Nature of unconventional pairing in the kagome superconductors AV3Sb5 (A = K,Rb,Cs). Phys. Rev. Lett. 127, 177001 (2021).
Liang, Z. et al. Three-dimensional charge density wave and surface-dependent vortex-core states ina kagome superconductor CsV3Sb5. Phys. Rev. X 11, 031026 (2021).
Nie, L. et al. Charge-density-wave-driven electronic nematicity in a kagome superconductor. Nature 604, 59–64 (2022).
Jiang, Y.-X. et al. Unconventional chiral charge order in kagome superconductor KV3Sb5. Nat. Mater. 20, 1353 (2021).
Li, H. et al. Observation of unconventional charge density wave without acoustic phonon anomaly in kagome superconductors AV3Sb5 (A = Rb, Cs). Phys. Rev. X 11, 031050 (2021).
Zhou, X. et al. Origin of charge density wave in the kagome metal CsV3Sb5 as revealed by optical spectroscopy. Phys. Rev. B 104, L041101 (2021).
Shumiya, N. et al. Intrinsic nature of chiral charge order in the kagome superconductor RbV3Sb5. Phys. Rev. B 104, 035131 (2021).
Tan, H., Liu, Y., Wang, Z. & Yan, B. Charge density waves and electronic properties of superconducting kagome metals. Phys. Rev. Lett. 127, 046401 (2021).
Park, T., Ye, M. & Balents, L. Electronic instabilities of kagome metals: Saddle points and Landau theory. Phys. Rev. B 104, 035142 (2021).
Lin, Y.-P. & Nandkishore, R. M. Complex charge density waves at Van Hove singularity on hexagonal lattices: Haldane-model phase diagram and potential realization in the kagome metals AV3Sb5 (A = K,Rb,Cs). Phys. Rev. B 104, 045122 (2021).
Chen, H. et al. Roton pair density wave in a strong-coupling kagome superconductor. Nature 599, 222 (2021).
Zhao, H. et al. Cascade of correlated electron states in the kagome superconductor CsV3Sb5. Nature 599, 216 (2021).
Denner, M. M., Thomale, R. & Neupert, T. Analysis of charge order in the kagome metal AV3Sb5 (A = K,Rb,Cs). Phys. Rev. Lett. 127, 217601 (2021).
Yang, S.-Y. et al. Giant, unconventional anomalous Hall effect in the metallic frustrated magnet candidate KV3Sb5. Sci. Adv. 6, eabb6003 (2020).
Yu, T. F. H. et al. Concurrence of anomalous Hall effect and charge density wave in a superconducting topological kagome metal. Phys. Rev. B 104, L041103 (2021).
Wang, Z. et al. Electronic nature of chiral charge order in the kagome superconductor CsV3Sb5. Phys. Rev. B 104, 075148 (2021).
Xu, H.-S. et al. Multiband superconductivity with sign-preserving order parameter in kagome superconductor CsV3Sb5. Phys. Rev. Lett. 127, 187004 (2021).
Goldman, A. M. & Markovic, N. Superconductor-insulator transitions in the two-dimensional limit. Phys. Today 51, 39 (1998).
Gantmakher, V. F. & Dolgopolov, V. T. Superconductor-insulator quantum phase transition. Phys. Usp. 53, 1 (2010).
Nguyen, T. & Li, M. Electronic properties of correlated kagomé metals AV3Sb5 (A = K,Rb,Cs): A perspective. J. Appl. Phys. 131, 060901 (2022).
Jiang, K. et al. Kagome superconductors AV3Sb5 (A = K,Rb,Cs). Natl. Sci. Rev. nwac199 (2022).
Feng, X., Jiang, K., Wang, Z. & Hu, J. Chiral flux phase in the Kagome superconductor AV3Sb5 (A = K,Rb,Cs). Sci. Bull. 66, 1384 (2021).
Zheng, G. et al. Gate-tuned interlayer coupling in van der Waals ferromagnet Fe3GeTe2 nanoflakes. Phys. Rev. Lett. 125, 047202 (2020).
Zheng, G. et al. Tailoring Dzyaloshinskii-Moriya interaction in a transition metal dichalcogenide by dual-intercalation. Nat. Commun. 12, 3639 (2021).
Han, T.-H. et al. Fractionalized excitations in the spin-liquid state of a kagome-lattice antiferromagnet. Nature 492, 406 (2012).
Zhou, Y., Kanoda, K. & Ng, T.-K. Quantum spin liquid states. Rev. Mod. Phys. 89, 025003 (2017).
Li, Y. et al. Tuning from failed superconductor to failed insulator with magnetic field. Sci. Adv. 5, eaav7686 (2019).
Zhang, X., Palevski, A. & Kapitulnik, A. Anomalous metals: From “failed superconductor” to “failed insulator”. Proc. Natl Acad. Sci. USA 119, e2202496119 (2022).
Chen, Z. et al. Electric field control of superconductivity at the LaAlO3/KTaO3 (111) interface. Science 372, 721 (2021).
Fisher, M. P. A. Quantum phase transitions in disordered two-dimensional superconductors. Phys. Rev. Lett. 65, 923 (1990).
Fisher, M. P. A., Grinstein, G. & Girvin, S. Presence of quantum diffusion in two dimensions: Universal resistance at the superconductor-insulator transition. Phys. Rev. Lett. 64, 587 (1990).
Cha, M.-C., Fisher, M. P. A., Girvin, S., Wallin, M. & Young, A. P. Universal conductivity of two-dimensional films at the superconductor-insulator transition. Phys. Rev. B 44, 6883 (1991).
Liu, Y. et al. Observation of in-plane quantum Griffiths singularity in two-dimensional crystalline superconductors. Phys. Rev. Lett. 127, 137001 (2021).
Hen, B., Zhang, X., Shelukhin, V., Kapitulnik, A. & Palevski, A. Superconductor-insulator transition in two-dimensional indium-indium-oxide composite. Proc. Natl Acad. Sci. USA 118, e2015970118 (2021).
Kenney, E. M., Ortiz, B. R., Wang, C., Wilson, S. D. & Graf, M. J. Absence of local moments in the kagome metal KV3Sb5 as determined by muon spin spectroscopy. J. Phys.: Condens. Matter 33, 235801 (2021).
Song, B. Q. et al. Competing superconductivity and charge-density wave in Kagome metal CsV3Sb5: evidence from their evolutions with sample thickness. arXiv http://arxiv.org/abs/2105.09248 (2021).
Wang, T. et al. Enhancement of the superconductivity and quantum metallic state in the thin film of superconducting Kagome metal KV3Sb5. arXiv http://arxiv.org/abs/2105.07732 (2021).
Song, Y. et al. Competition of superconductivity and charge density wave in selective oxidized CsV3Sb5 thin flakes. Phys. Rev. Lett. 127, 237001 (2021).
Liu, Z. et al. Charge-density-wave-induced bands renormalization and energy gaps in a Kagome superconductor RbV3Sb5. Phys. Rev. X 11, 041010 (2021).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539 (2010).
Hou, D. et al. Multivariable scaling for the anomalous Hall effect. Phys. Rev. Lett. 114, 217203 (2015).
Majumdar, A. K. & Berger, L. Hall effect and magnetoresistance in pure Iron, Lead, Fe-Co, and Fe-Cr dilute alloys. Phys. Rev. B 7, 4203 (1973).
Shiomi, Y., Onose, Y. & Tokura, Y. Extrinsic anomalous Hall effect in charge and heat transport in pure iron, Fe0.997Si0.003, and Fe0.97Co0.03. Phys. Rev. B 79, 100404 (2009).
Ishizuka H. & Nagaosa, N. Theory of giant skew scattering by spin cluster. arXiv http://arxiv.org/abs/1906.06501(2019).
Yang, S. A., Pan, H., Yao, Y. & Niu, Q. Scattering universality classes of side jump in the anomalous Hall effect. Phys. Rev. B 83, 125122 (2011).
LaBollita, H. & Botana, A. S. Tuning the Van Hove singularities in AV3Sb5 (A = K,Rb,Cs) via pressure and doping. Phys. Rev. B 104, 205129 (2021).
Hu, Y. et al. Rich nature of Van Hove singularities in kagome superconductor CsV3Sb5. Nat. Commun. 13, 2220 (2022).
Luo, H. et al. Electronic nature of charge density wave and electron-phonon coupling in kagome superconductor KV3Sb5. Nat. Commun. 13, 273 (2022).
Nakayama, K. et al. Multiple energy scales and anisotropic energy gap in the charge-density-wave phase of the kagome superconductor CsV3Sb5. Phys. Rev. B 104, L161112 (2021).
Mielke, C. III et al. Time-reversal symmetry-breaking charge order in a kagome superconductor. Nature 602, 245 (2022).
Yu, L. et al. Evidence of a hidden flux phase in the topological kagome metal CsV3Sb5. arXiv http://arxiv.org/abs/2107.10714 (2021).
Li, H. et al. No observation of chiral flux current in the topological kagome metal CsV3Sb5. Phys. Rev. B 105, 045102 (2022).
Acknowledgements
The authors thank Y. M. Dai, H. LaBollita, Y. M. Li, H. W. Liu, K. Nakayama, Q. Niu, T. Sato, J. M. Tranquada, C. Xiao, Z. Y. Wang, H. Yang, J. J. Ying and L. Yu for insightful discussions. This research was supported by the Australian Research Council Centre of Excellence in Future Low-Energy Electronics Technologies (Project No. CE170100039), National Key R&D Program of the MOST of China (Grant No. 2022YFA1602603), the National Natural Science Foundation of China (Grants No. 12274413, U19A2093, U2032164, 12174394), the HFIPS Director’s Fund (Grant No. YZJJQY202304) and the CASHIPS Director’s Fund (Grant No. E26MMG71131). This work was also partially supported by Youth Innovation Promotion Association of CAS (Grant No. 2021117) and the High Magnetic Field Laboratory of Anhui Province.
Author information
Authors and Affiliations
Contributions
L.W. and M.T. conceived the project. G.Z. and C.T. fabricated the devices and performed the transport measurements, assisted by S.A., M.A. and L.F., Z.C., X.Z. and W.N. synthesized the single crystals. M.,W. and J.Z. provided theoretical support. G.Z., C.T., J.Z., J.P., M.S.F., M.T. and L.W. analyzed the data and wrote the manuscript with assistance from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zheng, G., Tan, C., Chen, Z. et al. Electrically controlled superconductor-to-failed insulator transition and giant anomalous Hall effect in kagome metal CsV3Sb5 nanoflakes. Nat Commun 14, 678 (2023). https://doi.org/10.1038/s41467-023-36208-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-023-36208-6
This article is cited by
-
Quantum states and intertwining phases in kagome materials
Nature Reviews Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.