Abstract
Understanding the timing and trajectory of atmospheric oxygenation remains fundamental to deciphering its causes and consequences. Given its origin in oxygen-free photochemistry, mass-independent sulfur isotope fractionation (S-MIF) is widely accepted as a geochemical fingerprint of an anoxic atmosphere. Nevertheless, S-MIF recycling through oxidative sulfide weathering—commonly termed the crustal memory effect (CME)—potentially decouples the multiple sulfur isotope (MSI) record from coeval atmospheric chemistry. Herein, however, after accounting for unrecognised temporal and spatial biases within the Archaean–early-Palaeoproterozoic MSI record, we demonstrate that the global expression of the CME is barely resolvable; thereby validating S-MIF as a tracer of contemporaneous atmospheric chemistry during Earth’s incipient oxygenation. Next, utilising statistical approaches, supported by new MSI data, we show that the reconciliation of adjacent, yet seemingly discrepant, South African MSI records requires that the rare instances of post-2.3-billion-year-old S-MIF are stratigraphically restricted. Accepting others’ primary photochemical interpretation, our approach demands that these implied atmospheric dynamics were ephemeral, operating on sub-hundred-thousand-year timescales. Importantly, these apparent atmospheric relapses were fundamentally different from older putative oxygenation episodes, implicating an intermediate, and potentially uniquely feedback-sensitive, Earth system state in the wake of the Great Oxidation Event.
Similar content being viewed by others
Introduction
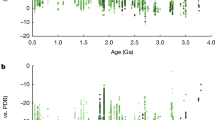
Atmospheric oxygenation represents perhaps the most profound chemical change experienced by the Earth system, revolutionising biogeochemical cycles1,2,3,4 while priming the planet for the rise of complex life5,6,7,8,9. Although a wealth of geological observations and geochemical data have been combined to articulate the story of Earth’s oxygenation1,5,10,11 (Fig. 1a, b), the recognition of mass-independent sulfur isotope fractionation (S-MIF) within the geological multiple sulfur isotope (MSI) record remains the most widely accepted means to directly trace the oxygen content of Earth’s early atmosphere12,13.
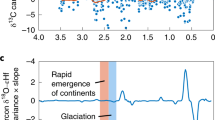
a A schematic representation of competing ideas surrounding the oxygenation of Earth’s atmosphere1 contextualised within a framework of biological innovations. b The secular evolution of ∆33S values compiled herein (Supplementary Data File 1). The grey box locates the interval over which atmospheric oxygen is thought to have first accumulated, while the horizontal bars illustrate more traditional redox indicators, whose red and blue colouration discriminates between those disclosing oxic and anoxic conditions, respectively4,5. Triangular and circular points represent spot and bulk ∆33S analyses respectively. Stratigraphic distributions of ∆33S data from the South African Kaapvaal (c core EBA-2; d core KEA-4) and Western Australian Pilbara (e cores T1–T3) cratons, whose discrepant interpretations have led to the emergence of conflicting models of atmospheric oxygenation. Each of the chronologically constrained lithostratigraphic columns follow those presented with the ∆33S data22,25,30,32,33, with the superimposed vertical grey bars illustrating the ±0.3‰ threshold for identifying S-MIF by ∆33S alone25. The lowermost horizontal blue band in c, d corresponds to the apparently sustained presence of mass-independent sulfur isotope fractionation (S-MIF) within the Rooihoogte Formation (Ro(oi)) seen throughout the Carletonville area22,25,30,37. The subsequent blue horizontal bars in panel c mark isolated instances of S-MIF within the Timeball Hill Formation (TBH) that have been interpreted to represent returns to an anoxic atmospheric state (Supplementary Information). Contrastingly, the persistence of low-magnitude non-zero ∆33S values throughout cores T2–T3 has been ascribed to the crustal memory effect, with atmospheric oxygenation occurring much earlier (blue horizontal bar, e, Supplementary Information). Lithostratigraphic abbreviations: Reit. Reitfontain Member, WR Woongarra Rhyolite, BF Boolgeeda Iron Formation, MB1, 2 the diamictites within the Meteorite Bore Member, KF Koolbye Formation, Kaz. Fm. Kazput Formation, BQ Beasley River Quartzite, CB Cheela Springs Basalt.
Manifest as non-zero ∆3X-values (“Methods”; Eqs. 1 and 2)12,14,15, the generation and geological preservation of S-MIF is linked to low atmospheric oxygen concentrations in several ways: Starting with its production, anoxic SO2 photochemistry remains the only experimentally demonstrated means of creating S-MIF that remotely resembles the geological record13 (Fig. 1b). Here, in the absence of photon-shielding O2/O3, photolysis and/or photo(de)excitation reactions are understood to yield reduced (i.e., S0 or S8) and oxidised (i.e., H2SO4) sulfur phases that carry positive and negative ∆33S values, respectively12,13,16,17,18. Importantly, one-dimensional photochemical models indicate that atmospheric oxygen concentrations must remain below 0.001% of modern levels to retain the photochemical exit channels necessary to communicate S-MIF to the Earth’s exogenic sulfur cycle19. Further, in terms of preservation, oxygen-deficient environments are less likely to homogenise these photochemical derivatives, thereby increasing their preservation potential and, thus, their overall likelihood of passing into the sedimentary record20. Understandably, it follows that the geological presence of S-MIF is now almost unanimously accepted as a robust geochemical fingerprint of a long-lived oxygen-free atmospheric state, persisting for more than half of Earth’s 4.5-billion-year (Ga) history.
Despite the clear and direct links between oxygen and S-MIF, constraining the exact timing and nature of atmospheric oxygenation has proven difficult. Although it is generally agreed that oxygen began to accumulate within the atmosphere between 2.5–2.3 Ga, different readings of the S-MIF record have been used to portray dramatically different oxygenation trajectories—with some workers arguing for a unidirectional geologically rapid rise in O221,22,23, while others envisage an oscillatory trajectory whereby pO2 repeatedly crossed the threshold necessary to resume S-MIF genesis24,25,26 (Fig. 1a–d). While inadequate age constraints and ambiguous stratigraphic correlations22,23,24,26,27,28,29,30 currently prevent discrimination between these models (Supplementary Information), both interpretations are reliant on the assumption that sedimentary S-MIF chronicles contemporaneous atmospheric conditions. Again, this premise is not universally accepted and some contend that the operation of a so-called crustal memory effect (CME) decouples the MSI record from coeval atmospheric chemistry16,31,32,33. Specifically, it is argued that the late-Neoarchaean–Palaeoproterozoic MSI record is dominated by S-MIF inherited from an adulterated seawater sulfate reservoir supplied by the oxidative weathering of older crustal pyrite, rather than being a syndepositional atmospheric signal (Fig. 1e). Hence, before we can begin to reconcile the conflicting narratives of atmospheric oxygenation, the feasibility and potential magnitude of a CME must first be addressed.
Results and discussion
The crustal memory effect
Noting a post-2.45 Ga shift toward muted positive ∆33S values, Farquhar and Wing were the first to suggest that weathering-induced crustal recycling of S-MIF may hinder our ability to precisely reconstruct atmospheric oxygenation from the MSI record16. Subsequently, predicated on a crustal 33S excess16,18,31,34,35 manifest as a cumulative database mean ∆33S value of ~1.5‰31, Reinhard et al. presented a series of box-model simulations designed to quantify the CME31. Their proof-of-concept approach demonstrated that once mass-independent weathering fluxes permeated an entirely mass-dependant marine sulfur cycle, the weathering-derived non-zero ∆33S values exceeded those imparted by mass-dependent processes (e.g., >|0.3‰|)36 for upwards of 10–100 million years31. Importantly, such longevity has the potential to induce a temporal lag between the cessation of atmospheric S-MIF production and its loss from the rock record, thereby masking the operation of atmospheric chemistry during this transformative interval of Earth history31.
While alarming, the paucity of demonstrably contemporaneous MSI datasets has prevented empirical scrutiny of these computational predictions, leaving the significance of the CME untested. Even now, despite a recent explosion of data21,22,25,30,32,37, opinions surrounding the CME remain divided21,22,25,26,30,32,33. For instance, while emerging data from the Western Australian Turee Creek Basin support the notion of a long-lived CME32,33, purportedly time equivalent (Supplementary Information) observations from the Carletonville area of the South African Transvaal Basin do not (Fig. 1c–e)22,25,37—thereby questioning the operation of a CME as a global phenomenon. Furthermore, these spatial differences imply unrecognised biases within the MSI, with the important corollary that an unweighted cumulative mean may ineffectively approximate the isotopic composition of the weatherable sulfur pool, thus confounding previous estimates of the persistence and magnitude of the CME31,32.
To explore the source of this data–model mismatch, we start by compiling a comprehensive MSI database (“Methods”; Supplementary Data 1), which we then examine in its raw form and, in a reduced state wherein we compensate for potential sample density biases via averaging replicate and intra-sample analyses, termed the Spot Sample Averaged(SSA) database (“Methods”; Supplementary Information). Here, while a cursory evaluation of this new compilation confirms the plateau used by Reinhard et al.31 to infer the capture of a representative global mean ∆33S value, augmentation with the data published over the ensuing decade reveals a subtle downward trajectory, resulting in a pre-2.3 Ga mean ∆33S value of 0.74 ± 1.97‰ (1σ) for the entire database, increasing to 1.12 ± 2.06‰ (1σ) if the SSA database is considered (Fig. 2a).
a A cumulative plot depicting the evolving mean ∆33S value of the pre-2.3 Ga data in the compiled multiple sulfur isotope (MSI) database, with solid and dashed lines representing those derived from the full database and its spot sample averaged (SSA) counterpart, respectively (“Methods”). Line colour distinguishes the craton(s) being analysed, with green signalling the full database, blue illustrating the combined Kaapvaal–Pilbara datasets, and orange showing the remainder. For reference, the respective mean ∆33S values of the Time Adjusted (TA) and Craton Adjusted (CA) synthetic datasets are plotted as a blue-coloured circle and triangle. A vertical dashed line separates the data considered by Reinhard et al.31 (i.e., ≤2012) from those published subsequently, while the horizontal dashed line denotes the 0.3‰ ∆33S-threshold for identifying mass-independent sulfur isotope fractionation (S-MIF)25. b The cumulative percentage of the Kaapvaal–Pilbara-derived data (blue) relative to those sourced from elsewhere (orange). The horizontal dashed line denotes 50% of the dataset, while the x-axis scaling follows (a). c A time-binned distribution of ∆33S data within the unfiltered database. Mesoprot. abbreviates Mesoproterozoic.
A more detailed interrogation of the new MSI database reveals lithological, spatial, and temporal biases (Fig. 2; Supplementary Information). Though the lithological bias (e.g., carbonates vs. siliciclastics) was not found to significantly influence our analyses (“Methods”; Supplementary Information; Supplementary Figs. 4 and 5), the impacts of the temporal and spatial biases were substantial. For example, even after compensating for sample replication via the SSA database, more than 70% of the pre-2.3 Ga data were found to originate from either the Kaapvaal or Pilbara cratons, with roughly two-thirds derived from Neoarchaean- (35.5%) and Palaeoproterozoic-aged (33.3%) successions (Fig. 2b, c). To estimate how these biases impact the database mean, we subjected the SSA database to bias-specific bootstrap sampling routines, arriving at two synthetic datasets, which we term the Temporally Adjusted (TA) and Craton Adjusted (CA) datasets (“Methods”). Compared to the mean ∆33S value obtained from the unweighted SSA database (1.12‰), the mean ∆33S values obtained from the TA and CA datasets were found to be lower, averaging 0.62 and 0.36‰, respectively (Fig. 2a). Consequently, this simple exercise confirms our data-based inferences, demonstrating that the magnitude of the positive ∆33S skew apparent within the rock record is, at least partially, a function of bias.
To determine how these biases propagate into our understanding of the size and longevity of the CME, we then incorporated the TA and CA datasets into an updated geochemical model22 (“Methods”). Augmenting the model with a bootstrap sampling subroutine, the ∆33S of the seawater sulfate pool was computed utilising the size and isotopic composition of the major marine sulfate fluxes and sinks (“Methods”; Supplementary Information). Here, using the TA dataset, the estimated maximum ∆33S value of the seawater sulfate reservoir (SWSR) was found to be 0.35 ± 0.2‰ (1σ), which was further reduced to 0.21 ± 0.17‰ (1σ) when utilising the CA dataset (Fig. 3a–b). These bias-corrected estimates of the CME are much smaller than those reported by Reinhard et al.31 (centred on 1.5‰ and up to 2.5‰) and, indeed, those derived from our updated unadjusted database (0.65 ± 0.6‰; Fig. 3c; “Methods”), thus reaffirming the importance of our bias-correction routine. That said, while small, the fact that the globally integrated CME remains slightly positive despite our bias corrections is a pertinent observation. Inspection of the MSI record shows that the final appreciably negative ∆33S value occurs at least 60 million years before its positive ∆33S counterpart (Fig. 1b; Supplementary Information). This asymmetry implicates a muted positive CME persisting beneath an atmosphere capable of S-MIF genesis. Indeed, support for the early onset of a subdued CME is found within a temporal synthesis of molybdenum abundance and isotope data that has similarly been interpreted to signal the onset of oxidative pyrite weathering before pO2 rose sufficiently to curtail S-MIF-yielding photochemistry38. These observations, therefore, begin to reconcile conflicting interpretations derived from various atmospheric and marine-based geochemical proxies30,38, yielding a complementary picture of Earth’s oxygenation.
Here, the presented simulations are derived from exploration of a the Temporally Adjusted (TA), b the Craton Adjusted (CA) and c the unadjusted spot sample averaged (SSA) datasets. Colours are common throughout, with blue depicting the ∆33S value carried by the weathered sulfur flux and orange showing the ∆33S composition of the seawater sulfate reservoir (SWSR). Colour-coded lines depict the LOESS smoothed mean of the bootstrap outputs, while their envelopes indicate their 1σ uncertainty. The horizontal grey band depicts the existing CME estimate derived using the most feasible boundary conditions31, while the dashed lines bracket the 0.3‰ ∆33S-based S-MIF discriminatory threshold.
Reminiscent of Reinhard and colleagues’ predictions31, weathering-derived ∆33S values have long residence times within the SWSR, failing to return to zero within the timespan of our model. Nevertheless, our approach significantly reduces the magnitude of the CME-derived ∆33S values, arriving at a conservative maximum of approximately 0.5‰, with <0.3‰ being more likely (Fig. 3). This estimate is more consistent with ∆33S values from Palaeoproterozoic-aged sulfate minerals (|0.1–0.2|‰) that should, in principle, record the coeval SWSR composition39. Ergo, beyond validating the MSI record as an archive of Earth’s incipient oxygenation, our results can be considered as a conservative discriminatory threshold (i.e., 0.5‰), separating weathering-induced non-zero ∆33S values from those derived from syndepositional oxygen-free photochemistry. Returning to the MSI record, the small magnitude of the modelled CME, coupled with the fact that less than 5% of ∆33S values within the entire pre-2.3 Ga database exceed 5‰ (Supplementary Information; Supplementary Fig. 3), strongly supports the interpretation that large magnitude ∆33S values must originate from oxygen-free photochemistry. Examples of sustained large values are last seen within the Rooihoogte Formation, Transvaal Basin (≤8.76‰), therefore signalling the presence of an oxygen-impoverished atmosphere well after 2.45 Ga22,25,30(Supplementary Information).
Spatial heterogeneities in the expression of the CME
Independent support for a diminished CME is found within the MSI systematics of contemporary riverine sulfates derived from Archaean-aged terrains40. For instance, the circum-zero ∆33S values (−0.01 ± 0.10‰) found within rivers draining the S-MIF-bearing Superior Craton empirically demonstrate our prediction that catchment-level integration modulates the magnitude of ∆33S values communicated to the SWSR via weathering. Nevertheless, measurements of sulfates from other riverine systems41 and, indeed, a South African groundwater sample40 do, in fact, feature moderate ∆33S values, demonstrating at least some capacity for the communication of 33S anomalies to weathered sulfur fluxes. Accordingly, given the clearly uneven distribution of large ∆33S values (Fig. 2; Supplementary Table 3, Supplementary Information), a hinterland featuring large ∆33S values draining into a (semi-)isolated, sulfate-impoverished, basin could hypothetically combine to promote a more pronounced and spatially heterogeneous CME.
Recalling that the Pilbara Craton features some of the most pronounced ∆33S values seen within the MSI record (Fig. 4; Supplementary Table 3), not to mention the pronounced dichotomy seen between the Australian and South African MSI records (Fig. 1)25,30,32, we modified our bootstrap sampling subroutine to test whether the apparent persistence of S-MIF within the foreland Turee Creek Basin26,32 could reflect regional amplification of the CME (“Methods”). Here, drawing from a TA dataset comprising data derived solely from the Pilbara Craton, the resultant weathering flux was found to carry a much larger ∆33S value (0.68 ± 0.5‰, 1σ; Fig. 4a) when compared to our estimates of a globally felt CME. Furthermore, the good 1σ agreement between our model output and the ∆33S data obtained from the two youngest cores (T2 & T3) retrieved during the Turee Creek Drilling Project32 supports previous calls for a weathering-derived component within the Turee Creek MSI record (Fig. 4a, b)32,33. Taking this further, the apparent lithological control seen in the δ34S and ∆33S systematics of the Kazput Formation32,33 implies a higher order depositional control (T3, Fig. 1e). Here, muted ∆33S values reminiscent of those we estimate for the globally integrated CME are captured within the more distal fine-grained facies, while the near-shore carbonates seem to record more pronounced ∆33S values akin to those we compute for our Pilbara-derived weathering flux (Figs. 1e, 4). These observations demand that the CME should not be considered in a vacuum and, in reality, the expression of any CME is likely dependent on the interplay between the catchment-specific sulfate weathering flux and sulfate derived from a globally mixed SWSR. This premise is further supported by the fact that barites from the Kazput Formation are distinctly different from SWSR estimates derived from globally-distributed sedimentary sulfates of similar age39 and, instead, mirror cooccurring sedimentary sulfide ∆33S values33(Fig. 1e). The persistence of S-MIF within Western Australia beyond its demise in South Africa, therefore, need not question the available radiometric age constraints on the Meteorite Bore Member that are used to link the Turee Creek and Transvaal MSI records26,32,42,43,44 (Fig. 1e; Supplementary Information).
a Here, the blue line indicates the simulated ∆33S evolution of the Pilbara-specific weathering flux, with its associated envelope capturing the 1σ uncertainty. Superimposed on these, the available Pilbara-derived ∆33S data are plotted in blue, while those from the Turee Creek Group are distinguished as red open symbols32. The vertical dashed line marks the Great Oxidation Event(GOE) sensu Luo et al.22, while the horizontal dashed line represents the globally expressed CME modelled using the CA dataset (Fig. 3b). The 2500–2000 Ma expansion (insert) follows (a). b Core-specific density distributions of the ∆33S data from the Boolgeeda Iron Formation and Turee Creek Group32, younging from left to right (i.e., cores T1→T3). The horizontal blue line and envelope follow (a).
Contrasting with the monotonous and muted ∆33S values observed within the Turee Creek Group, several discrete instances of elevated ∆33S values of up to 2.9‰ are observed to perturb a near-zero baseline within the Timeball Hill Formation, South Africa25. While the Kaapvaal Craton is also known to harbour elevated ∆33S values, application of an analogous craton-specific CME simulation returns a broadly similar weathering flux (0.84 ± 0.6‰), whose theoretical maximum (c.1.5‰) is barely half of the most extreme ∆33S value reported from the Timeball Hill (Figs. 1 c, 5; Supplementary Table 3; Supplementary Fig. 7). Consequently, the pronounced, yet highly variable, nature of these post-2.3 Ga 33S-enrichements strongly argue against derivation from a regionally amplified CME and, instead, require an alternate explanation.
Constraining the duration of post-2.3 Ga S-MIF occurrences
The CME as previously defined31,32, and adopted herein, does not account for the physical delivery of erosion-derived sulfides. While such detritus has been widely publicised as a potential source of atmospherically estranged sulfur with ∆33S values of effectively any magnitude29,45,46, it is hard to envisage a scenario where detrital signals can repeatedly dominate the MSI record without detection—a stance strengthened given the apparent predominance of authigenic pyrites throughout the Carletonville area22,25,30,37. Consequently, while we await a detailed and dedicated grain-scale isotopic appraisal designed to unequivocally dismiss a detrital explanation of the elevated Timeball Hill ∆33S values, it seems rationalisations reliant on recycling can be dismissed. Indeed, Poulton and colleagues25 argued that the elevated Timeball Hill ∆33S values recorded primary atmospheric dynamics (Fig. 1c). Enigmatically, however, as testified by a more recent quadruple sulfur isotope appraisal reporting only sub-0.3‰ ∆33S values within a proximal (<5 km) and indisputably equivalent core (KEA-4), these supposed atmospheric oscillations are not universally resolved30 (Fig. 1c, d). Consequently, providing the inferred atmospheric significance of the elevated ∆33S values seen within the Timeball Hill Formation holds true, then the recognised kilometre-scale dichotomy apparent within the Carletonville area requires that the non-zero ∆33S values must persist over sufficiently stratigraphically restricted intervals to escape detection via conventional sampling campaigns.
To constrain the duration of the Timeball-Hill-housed S-MIF-bearing intervals and, therefore, elucidate their mechanistic driver(s), we started with a simplified Bayesian approach (“Methods”; Supplementary Fig. 9). Here, after converting from the relative abundance of S-MIF in each core, we found the most likely average stratigraphic thickness of each S-MIF re-emergence was 1.42 m, equating to some 0.3–3 million years when combined with average compacted sedimentation rates (“Methods”). Significantly, however, while this Bayesian-derived estimate best explains the available data, Izon and colleagues’ inability to detect any S-MIF within their higher-resolution search of the Timeball Hill Formation30 (Supplementary Table 5) remains salient, emphasising the inherently conservative nature of this estimate (“Methods”). Accordingly, we designed a series of simulations to constrain the likelihood of avoiding S-MIF within a 60-sample sampling campaign akin to that reported by Izon et al.30 (Fig. 5a, Supplementary Fig. 9; “Methods”; Supplementary Table 5). Strikingly, however, from our 1000 bootstrap replicates, only twice (i.e., 0.2% of the replicates) were we able to avoid detecting S-MIF after prescription of the Bayesian-derived 1.42-metre-thick S-MIF window. Rather, given these boundary conditions, on average, we detected S-MIF 6 ± 2 (1σ) times per replicate, equating to 7–13% of the population size (Fig. 5a; Supplementary Table 6). Extending our statistical approach to increasingly narrower S-MIF windows reveals that their thickness must recede to well below a metre before the likelihood of avoiding S-MIF becomes statistically feasible, implying, in turn, that any re-emergence of S-MIF was likely short lived (Fig. 5a; Supplementary Table 6).
a Colour-coded frequency distributions resulting from 1000 replicate 60-sample bootstrap sampling routines, targeting synthetic cores with variably thick mass-independent sulfur isotope fractionation (S-MIF)-bearing windows (y-axis) positioned using the pre-existing EBA-2 ∆33S dataset25, as exemplified using the sample from 1224.0 m core depth (insert; Supplementary Fig. 10). The median and 25th and 75th quartiles are shown as vertical white lines. b Pre-existing ∆33S data from core EBA-225 (blue circles), augmented with our new quadruple sulfur isotope(QSI) measurements (red triangles), are superimposed on the 0.3‰ ∆33S-based S-MIF identification threshold (vertical grey band). The green shading in (b) locates the intervals shown in (c), providing an expanded view of four stratigraphic intervals where ∆33S values exceeding 0.3‰ were reported25. Given the bounding mass-dependant samples, the annotated vertical orange lines denote the maximum thickness of S-MIF-bearing intervals, which, in reality, are likely much smaller; their constraint, however, awaits detailed high-resolution chemical and petrographic conformation. The colour coding follows (b).
To empirically test the statistically inferred brevity of these S-MIF-bearing intervals, we analysed the MSI systematics of additional samples from core EBA-2, focusing on those bracketing the most pronounced ∆33S value reported from the Timeball Hill Formation (+2.9‰; “Methods”; Fig. 5; Supplementary Data 2)25. Here, as predicted, several samples within approximately 30 cm of the S-MIF-bearing sample found at 1275.5 m core-depth were found to possess mass-dependent MSI systematics, demonstrating that S-MIF was restricted to, at most, 40 centimetres of core (Fig. 5b, c). The presence of several other stratigraphically isolated S-MIF-bearing samples within a metre of those possessing mass-dependant MSI systematics25 (Fig. 5b, c) supports our inferences and justifies their extension to the wider Timeball Hill Formation. Combining these analytical observations with the preceding statistical analyses reduces the temporal duration of the post-2.33 Ga instances of S-MIF by an order of magnitude, thus signalling the return of S-MIF for perhaps tens-of-thousands of years.
Implications for the operation of the atmosphere after 2.33 Ga
Having established that any occurrences of S-MIF in the Timeball Hill Formation must have been short lived, we can now begin to assess the implications for the operation of the atmosphere after 2.3 Ga. First, acknowledging that c.40% of the pre-2.3 Ga ∆33S record falls within 0.3‰ of zero (Supplementary Fig. 8), it could be argued that the elevated ∆33S values seen within the Timeball Hill Formation signal deposition beneath an oxygen-free backdrop. Here, rather than a repeated return to an S-MIF yielding anoxic atmospheric state, this stance requires that the Timeball-Hill-housed S-MIF recurrences record some unknown localised preservation bias, leading to only sporadic expression of elevated ∆33S values. Such an interpretation, however, beyond contradicting the available ∆36S/∆33S data, is also inconsistent with the wider ∆33S database. For instance, if we exclude the data from the crustally influenced Turee Creek Group, the overwhelming majority (>90%) of the 2.3–2.1 Ga ∆33S record comprises values between –0.3 and 0.3‰ (Supplementary Fig. 8). Thus, rather than mirroring the older MSI record derived from an almost unanimously accepted anoxic background state, the Timeball-Hill-derived ∆33S distribution is much more reminiscent of the post-GOE record. Within this framework, the loss of S-MIF within the Rooihoogte Formation appears to mark a fundamental transition within the Earth system, with the global predominance of S-MIF seen prior to the Timeball Hill Formation (Supplementary Fig. 8) signalling a dominantly anoxic background state that yields to a more oxidising equivalent at around 2.3 Ga22,30.
Accepting the premise that the post-2.3 Ga atmosphere was predominantly oxygenated enough to inhibit S-MIF production/preservation, we are left with describing a mechanism for the short-lived re-emergences of S-MIF in the Timeball Hill Formation. Given that stratospheric volcanic eruptions are known to communicate ∆33S values as large as |2.0|‰ to contemporary ice-core records47,49,49, such events could hypothetically act as a geologically instantaneous source of S-MIF in more ancient settings. Indeed, the sulfate-impoverished oceans of the Palaeoproterozoic22,45,50,51, in principle, would offer little buffering capacity against such a point-source injection of S-MIF. That said, while S-MIF genesis and preservation against a modern oxygenated backdrop is a good starting point, its application to the Timeball Hill Formation and, indeed, the wider sedimentary record is problematic. Aside from the distinct differences between the ice-core (−4.3)49 and rock-housed ∆36S/∆33S records (–0.9)14, their mode of preservation is also fundamentally different. In essence, the survival of ice-core-housed ∆33S anomalies is not only a function of evading dilution with mass-dependently fractionated sulfur, but it specifically requires time-resolved differential rainout. Here, rather than spatially separating two isotopically distinct sulfur phases (i.e., S8 and SO42-), the ice-core housed S-MIF bearing sulfates are separated in time over the course of several years by the relatively rapid and pristine accumulation of the snow/ice pack47,48,49. In the absence of this time separation, mass-balance requires that 33S anomalies would be eradicated when the two pools were re-mixed47. Given the marine setting of the Timeball Hill Formation, it is realistic to assume that any volcanogenic sulfates would be homogenised, and therefore any 33S anomaly would be erased by mixing within the SWSR and the subsequent diagenetic realm. Theoretically, these issues could be circumnavigated by the model proposed by Gallagher et al., who envisage the volcanic injection of subduction-derived recycled sedimentary sulfur carrying positive ∆33S values52. While we concede that such a model offers an intriguing, not to mention potentially substantial, point-source of S-MIF, recalling the logic presented previously for the CME, we dispute its relevance in this case. Rather, we anticipate that, similar to the mixing that occurs under surficial weathering, homogenisation within the subduction system would minimise the ∆33S value of the re-entrained sulfur pool to values smaller than those seen in the Timeball Hill Formation (Supplementary Information, Supplementary Table 4.1–4.3).
All told, we are unable to explain the transient post-2.3 Ga instances of S-MIF without invoking high-order atmospheric dynamics with episodic relapses toward an anoxic atmospheric state. While we stress that the pre-Rooihoogte-aged oxidation episodes await definitive demonstration (Supplementary Information), it is clear that the S-MIF variability seen within the Timeball Hill Formation implicates atmospheric dynamics operating on fundamentally different timescales than their alleged precursors24,25,26. Such a system not only requires a background state susceptible to transient atmospheric perturbations, but also one that is conducive to S-MIF preservation. Preservation of significantly positive S-MIF signatures is thought to require a small SWSR53, which implies slow rates of oxidative weathering of continental sulfides and, by extension, relatively low pO2. It follows, therefore, that the periodic reappearance of S-MIF in the Timeball Hill Formation may signal a protracted, intermediate, and extremely sensitive atmospheric state that was uniquely susceptible to perturbation as oxygen contents vacillated around the threshold for S-MIF genesis and preservation. Speculatively, such a state could have been established and maintained through the interplay of biological feedbacks54,55 encountered as organisms gradually evolved the biochemical machinery to thrive in increasingly more oxidising regimes5. Superimposed on this intermediary atmospheric state, large injections of reducing gasses, perhaps sourced via the emplacement of large igneous provinces or, more likely, through climate-paced methane fluxes, could have episodically outpaced the biological O2 flux to ephemerally reinstate S-MIF production56. Interestingly, support for these claims can be found in recent photochemical modelling efforts that demonstrate the feasibility of 10–100 thousand-year returns to oxygen-free S-MIF yielding atmospheres, providing the predominant boundary conditions remain near to those necessary for S-MIF genesis56. The prediction of a highly dynamic and intermediate atmospheric state represents a paradigm shift, departing from the conventional view that atmospheric oxygenation occurred as a step function between bistable endmember compositions57,58. As such, there is now a pressing need for more detailed high-resolution MSI studies to better constrain the nature and duration of this transitionary period, and thereby refine the framework of Earth’s most significant redox revolution.
Methods
Isotopic nomenclature
Following convention, sulfur isotope data are expressed in delta (δ) notation, reflecting permille (‰) deviations of the less abundant isotope, X (33,34,36S), normalised to 32S, relative to the same ratio in the international reference standard, Vienna Canyon Diablo Troilite, (VCDT):
Most processes fractionate S-isotopes mass-dependently, whereby δ3XS ≈ λ3X × δ34S, with respective λ3X values of 0.515 and 1.91 for δ33S and δ36S. Departure from mass-dependent behaviour, termed mass-independent fractionation (MIF), however, is expressed in capital-delta (Δ) notation, where:
Database description
The sulfur isotope data used herein (n = 10,765 with at least ∆33S values) were compiled from 84 studies, forming a new and comprehensive database complete with metadata (Supplementary Information; Table 1; Supplementary Data 1). Given that many studies fail to report δ33S and δ36S values, to assess the effects of non-linear mixing in ∆–∆ space14,36 we calculated the missing δ-values via algebraic rearrangement of Eqs. 1 and 2. Overall, however, our presented solutions were found to be broadly equivalent irrespective of whether the mean ∆33S values were used directly or whether the ∆33S values were calculated retrospectively. To remove complications arising from the myriad of published sample lithological descriptions, our assessment of lithological bias uses a simplified parameter (simp.lith), allowing the compiled data to be allotted to one of ten generalised lithotypes (i.e., high energy siliciclastic, low energy siliciclastic, carbonates, sulfates, chemical, microbial, altered/late addition, glacial/diamictite/detrital, igneous/volcanic sed., and none provided). The individual lithologies assigned to each of our generalised lithotypes are listed in Supplementary Table 6. Finally, to ensure that inclusion of replicate sample analyses did not impact our analyses and resultant conclusions, we compared the full database to a Spot Sample Averaged database (SSA) where all stratigraphic replicates and intra-sample measurements (e.g., SIMS, KrF spot fluorination, in-situ laser, SHRIMP, CO2 spot laser fluorination, LA MC-ICP-MS) were averaged. All database interrogation, statistical analysis and figure generation was performed in R via the Tidyverse family of packages59, as well as the patchwork60, ggridges61 and MetBrewer62 packages.
Besides forming the backbone of our statistical analyses, the compiled database has been used to create an interactive HTML interface that allows the construction of user-defined time vs. Δ33S plots (Supplementary Information). The HTML interface was generated using R and the Plotly package63.
Modelling the crustal memory effect
The base geochemical model was run in MATLAB. The model follows ref. 22., however, we alter the oxidative pyrite weathering constant to emulate empirically demonstrated half-order kinetics64 (Eq. 3; Table 2). The sulfur isotope model was constructed using the flux outputs of the base geochemical model, including oxygen concentrations (Ox) and Eqs. 4–10 (Table 2). Here, the isotopic imbalance between the various sulfur reservoirs was achieved via the direct sequestration of a given proportion of S8 (FS8py) within the sedimentary pyrite pool, communicating a positive ∆33S value to the continental reservoir and its negative counterpart to the seawater sulfate reservoir.
The ∆33S value of the weathered sulfur flux at each time step (tstep) was calculated directly from the database using a bootstrap sampling subroutine. Here, two different versions of the database were analysed, with each optimised to minimise biases: First, we generated a Temporally Adjusted (TA) synthetic dataset whose overall ∆33S distribution reflected that of the precursor SSA database, yet featured a consistent sample density within each 50-million-year time-bin. Next, we derived a second Craton Adjusted (CA) synthetic dataset, using the same parameters as before, however, now we stipulated that once featured within a given time-bin each craton was equally represented. For the model run using the unadjusted database, the raw form of the SSA database was utilised using the same model parameters as above. Naturally, to protect the integrity of our findings, samples that were initially described as altered and/or late addition were excluded from our analyses.
The ∆33S value of the weathered sulfur flux at each time step (tstep), was calculated directly from the TA and CA synthetic datasets using a MATLAB-based bootstrap sampling subroutine. Here, each calculation was restricted to older samples (i.e., t > tstep) whose likelihood of selection was reduced as t and tstep diverged, via an age weighting equation (Eq. 10) modelled after Ref. 65. Importantly, an oxygen scalar (Ox; Eq. 3) designed to curb sulfide weathering at low pO2 was also employed, allowing sulfide weathering to become more pronounced as atmospheric oxygen rose. Using these weighting protocols to quasi-regulate the age and sulfur phase of selection, the bootstrap sampling subroutine then selected n samples and calculated their mean. Repeating this process m times then allowed us to assess the variability of the output. For instance, considering Fig. 3, the lighter coloured envelopes depict the standard deviation (±1σ) of the bootstrap means, while the central line gives the mean of the replicate bootstrap outputs (i.e., the grand mean). After exploring the sensitivity of the model to these parameters, respective n and m values of 10 and 20 were selected for the final model (Supplementary Information; Supplementary Fig. 6).
Given its targeting of the same sulfide pool as oxidative weathering, photochemically catalysed pyrite oxidation, as recently described by Hao et al.66, would not significantly change our isotopic estimates of the post-2.3 Ga CME and, therefore, is not considered in the model. This process, we concede, could provide an underappreciated source of sulfate to the oceans that has the potential to drive the ∆33S composition of the SWSR closer to 0‰ prior to the intensification of oxidative sulfide weathering.
Statistical analyses of post-Rooihoogte-aged S-MIF
To better characterise the prevalence of S-MIF after 2.33 Ga within the Transvaal Basin, and thus ascertain its regional–global significance, we employed a simple Bayesian approach coupled with a data-parameterised25,30 bootstrap-driven synthetic sampling experiment (Fig. 5; Supplementary Figs. 9 and 10). Here, to avoid potential sampling density biases introduced by the presence of variably sized and distributed diabase intrusions, we focused our attention on the intrusion-free lower Timeball Hill Formation prior to the Gatsrand Member (Fig. 2; Supplementary Fig. 10). In each of the explored cores, the expression of the lower Timeball Hill Formation is roughly equivalent, spanning 168.5, 151.6, and 158.3 m in cores EBA-1, EBA-2, and KEA-4, respectively22,25,30,37. Comparison between these different expressions of the lower Timeball Hill Formation is presented in Supplementary Table 5.
Using the parameters outlined in Supplementary Table 5, we started with a simplistic Bayesian approach to estimate the likelihood that a given stratigraphic interval is S-MIF bearing. In essence, we can liken the mass-dependency preserved within the lower Timeball Hill MSI record to a biased coin flip, where S-MIF-bearing samples (i.e., ∆33S ≥ 0.3) are assigned heads and their mass-dependant counterparts (i.e., ∆33S \(\le\) 0.3) assigned tails. Here, our hypothetical coin is biased, meaning that the odds of returning heads or tails is unfairly weighted (i.e., ≠50:50). Consequently, informed by the outcomes of a given number of coin flips, we are effectively determining the bias (θ) of this hypothetical coin. In this context, each coin flip equates to an analytical ∆33S measurement and θ to the likelihood of randomly selecting a S-MIF-bearing sample from a core.
Bayesian analysis requires the definition of a prior distribution and a likelihood distribution. Accordingly, applying Poulton and colleagues’ data25 to Eqs. 11 and 12, a prior was generated using a beta distribution:
This prior describes the probability of a particular θ, given the parameters a and b, or p(θ|a,b), which represents the respective number of ‘heads’ (S-MIF) and ‘tails’ (S-MDF) in cores EBA-1 and EBA-2. Here, the mean θ of the resultant distribution was 0.203 and its mode was 0.190 (Supplementary Fig. 9a), empirically consistent with the 20.3% (=13/64) S-MIF detection frequency reported by Poulton et al.25
Next, a Bernoulli likelihood distribution was generated using the data presented by Izon et al.30 (Eq. 13):
with N representing the number of samples in the lower Timeball Hill Formation, and z being the number of S-MIF-bearing samples (60 and 0, respectively; Supplementary Fig. 9b). This distribution describes the likelihood of reproducing the data (D) at a given θ, or p(D|θ). Returning to our numismatic analogy, Eq. 13 gives the likelihood of returning ‘tails’ 60 times given a specific weighting of a coin. Naturally, given Izon and colleagues’ 0% S-MIF detection frequency in the lower Timeball Hill Formation within core KEA-430, the mode of the resultant Bernoulli likelihood distribution was 0.
Finally, by combining the previously described prior (i.e., p(θ|a,b)) and likelihood (i.e., p(D|θ)) distributions a posterior distribution was constructed using Bayes theorem (Eqs. 14 and 15; Supplementary Fig. 9c):
This final distribution describes the updated probability of θ given the new data parameters z and N, or, p(θ|z,N). The resultant mean of the posterior distribution was 0.105 and its mode was 0.100. Given the combined probabilities in the posterior distribution, the most likely θ, or probability of randomly selecting an S-MIF-bearing sample (i.e., the coin returning ‘heads’) is 10.0–10.5%. This likelihood can then be translated into the proportion of a given core possessing mass-independent versus mass-dependant S-isotope systematics. Returning to the proximal (<5 km) Carletonville cores, given that the lower Timeball Hill Formation is roughly of equivalent thickness, we assume that the relative occurrence of S-MIF and the stratigraphic interval over which it’s expressed would be broadly analogous within each core. Maintaining these assumptions, we predict that 10.25% of the lower Timeball Hill Formation within core EBA-2 (151.6 m), equating to 15.54 m, should be S-MIF-bearing, which, if accommodated by the 11 S-MIF-bearing samples found in EBA-225, results in an average S-MIF-bearing interval of 1.42 m.
Pursuing this tactic further, we devised a bootstrap sampling method that would allow us to estimate the likelihood of failing to find S-MIF within a 60-sample sample set taken at random from synthetic cores constructed using different stratigraphic distributions of S-MIF. Designed to emulate the typical sample thickness used by Izon et al.30 and, indeed, that typically administered by core repositories, we constructed a 150-m-long synthetic core comprising 3000 5-cm-thick samples. Then, by centring a hypothetical S-MIF window of a given thickness (0.02–10.0 m) on the S-MIF-bearing samples (i.e., ∆33S > 0.3‰) reported by Poulton et al.25, we prescribed the mass-dependency of the surrounding samples (Supplementary Fig. 10). Selecting 60 samples from the resultant synthetic core, and repeating the operation 1000 times, then yielded a frequency distribution illustrating how often S-MIF would be expected to be detected within a hypothetical 60-sample analytical campaign. Repeated analysis with variably thick S-MIF windows (0.02–10.0 m), demonstrated that non-detection of S-MIF within a 60-sample population only became likely as the size of the S-MIF window diminished (Fig. 5a; Supplementary Table 6). Recalling our Bayesian analysis, the likelihood of randomly selecting 0 or 11 S-MIF-bearing samples is roughly equivalent given a 1.42-m-thick S-MIF window. That said, it is important to stress that the likelihood of achieving either is very low, falling outside of 2σ of the mean (Fig. 5a). It follows, therefore, that while our Bayesian approach yields a S-MIF window that most adequately explains the current data, it is unlikely to accurately describe the true distribution of S-MIF. Indeed, it is only when the thickness of the prescribed S-MIF window drops to well below a metre do the chances of avoiding S-MIF within a 60-sample analytical campaign become probable (Fig. 5a; Supplementary Table 6).
Sulfur isotope analysis
Augmenting previously published EBA-2 data22, herein we report an additional 32 quadruple sulfur isotope (QSI) measurements. First, to ensure consistency, we targeted two previously reported samples from the Rooihoogte Formation22 before measuring a new sample suite spanning the Timeball Hill Formation (Supplementary Data 2). While previous work over-looked acid volatile sulfur (AVS)22, herein we follow the sequential two-step approach detailed in Izon et al.30 that liberates AVS upon reaction with ethanoic 6 M HCl followed by the release of chromium reducible sulfur (CRS; principally pyrite) via reduction using acidified 2 M CrCl2. In both AVS- and CRS-yielding refluxes, the resultant H2S was swept into zinc acetate traps where it was captured as zinc sulfide before being converted to silver sulfide (Ag2S) with silver nitrate. Given the relative paucity of QSI data within core EBA-2, we universally converted the Ag2S to sulfur hexafluoride (SF6) via overnight reaction with excess of fluorine gas (F2) at 300 °C. The resultant SF6 was then purified cryogenically at liquid-nitrogen-temperatures before final isolation by preparative gas chromatography within the Geobiology laboratory at MIT. The QSI isotope composition of the pure SF6 was measured by dual-inlet gas-source isotope ratio mass spectrometry using a Thermo-Finnigan MAT 253 equipped with four collectors arranged to measure the intensity of SF5+ ion beams at mass/charge ratios (m/z) of 127, 128, 129 and 131 (32SF5+, 33SF5+, 34SF5+, and 36SF5+). Over the course of this study, several fluorinations of the IAEA-distributed reference materials S1, -S2 and -S3 were performed, returning 1σ δ34S, Δ33S and Δ36S uncertainties of better than 0.4, 0.022 and 0.16, respectively (Supplementary Data File Table SX2). Here, the resultant VCDT-normalised values are inseparable from their certified values and, indeed, those reported initially by Ono et al.67 (Table SX2). Importantly, the reproducibility of these pure Ag2S standards approximates those calculated from repeated sample processing (i.e., extraction–fluorination; Supplementary Data 2).
Code availability
The code used in this study can be found online in a GitHub repository https://github.com/buveges/Sulfur-MSI-Database along with an updating version of the MSI database. The MATLAB model was originally created by S.O. for Luo et al.22, and subsequently modified and augmented by S.O. and B.T.U. for this study. The R code was written by B.T.U.
References
Lyons, T. W., Reinhard, C. T. & Planavsky, N. J. The rise of oxygen in Earth’s early ocean and atmosphere. Nature 506, 307–315 (2014).
Stüeken, E. E., Kipp, M. A., Koehler, M. C. & Buick, R. The evolution of Earth’s biogeochemical nitrogen cycle. Earth Sci. Rev. 160, 220–239 (2016).
Reinhard, C. T. et al. Evolution of the global phosphorus cycle. Nature 541, 386–389 (2017).
Holland, H. Volcanic gases, black smokers, and the Great Oxidation Event. Geochim. Cosmochim. Acta 66, 3811–3826 (2002).
Fischer, W. W., Hemp, J. & Valentine, J. S. How did life survive Earth’s great oxygenation? Curr. Opin. Chem. Biol. 31, 166–178 (2016).
Gold, D. A., Caron, A., Fournier, G. P. & Summons, R. E. Paleoproterozoic sterol biosynthesis and the rise of oxygen. Nature 543, 420–423 (2017).
Schopf, J. W. Geological evidence of oxygenic photosynthesis and the biotic response to the 2400-2200 Ma “Great Oxidation Event”. Biochem 79, 165–177 (2014).
Hodgskiss, M. S. W., Crockford, P. W., Peng, Y., Wing, B. A. & Horner, T. J. A productivity collapse to end Earth’s Great Oxidation. Proc. Natl Acad. Sci. USA 116, 17207–17212 (2019).
Sánchez-Baracaldo, P., Bianchini, G., Wilson, J. D. & Knoll, A. H. Cyanobacteria and biogeochemical cycles through Earth history. Trends Microbiol. 1–15. https://doi.org/10.1016/j.tim.2021.05.008 (2021)
Sessions, A. L., Doughty, D. M., Welander, P. V., Summons, R. E. & Newman, D. K. The continuing puzzle of the great oxidation event. Curr. Biol. 19, R567–R574 (2009).
Reinhard, C. T. & Planavsky, N. J. The history of ocean oxygenation. Ann. Rev. Mar. Sci. 14, 331–353 (2022).
Farquhar, J., Bao, H. & Thiemens, M. Atmospheric influence of Earth’s earliest sulfur cycle. Science 289, 756–758 (2000).
Ono, S. Photochemistry of sulfur dioxide and the origin of mass-independent isotope fractionation in Earth’s atmosphere. Annu. Rev. Earth Planet. Sci. 45, 301–329 (2017).
Ono, S., Wing, B., Johnston, D., Farquhar, J. & Rumble, D. Mass-dependent fractionation of quadruple stable sulfur isotope system as a new tracer of sulfur biogeochemical cycles. Geochim. Cosmochim. Acta 70, 2238–2252 (2006).
Hulston, J. R. & Thode, H. G. Variations in the S33, S34, and S36 contents of meteorites and their relation to chemical and nuclear effects. J. Geophys. Res. 70, 3475–3484 (1965).
Farquhar, J. & Wing, B. A. Multiple sulfur isotopes and the evolution of the atmosphere. Earth Planet. Sci. Lett. 213, 1–13 (2003).
Chen, M., Huang, Z., Campbell, I. H., Sambridge, M. & Ávila, J. N. Simultaneous fractionation of sulfur dioxide explains mass independent fractionation of sulfur isotopes in Archean sedimentary pyrites. Chem. Geol. 587, 120640 (2022).
Ono, S. et al. New insights into Archean sulfur cycle from mass-independent sulfur isotope records from the Hamersley Basin, Australia. Earth Planet. Sci. Lett. 213, 15–30 (2003).
Pavlov, A. A. & Kasting, J. F. Mass-independent fractionation of sulfur isotopes in Archean sediments: strong evidence for an anoxic Archean atmosphere. Astrobiology 2, 27–41 (2002).
Ono, S., Beukes, N. J., Rumble, D. & Fogel, M. L. Early evolution of atmospheric oxygen from multiple-sulfur and carbon isotope records of the 2.9 Ga Mozaan Group of the Pongola Supergroup, Southern Africa. S. Afr. J. Geol. 109, 97–108 (2006).
Guo, Q. et al. Reconstructing Earth’s surface oxidation across the Archean-Proterozoic transition. Geology 37, 399–402 (2009).
Luo, G. et al. Rapid oxygenation of Earth’s atmosphere 2.33 billion years ago. Sci. Adv. 2, e1600134 (2016).
Warke, M. R. et al. The Great Oxidation Event preceded a Paleoproterozoic “snowball Earth”. Proc. Natl Acad. Sci. 117, 13314–13320 (2020).
Gumsley, A. P. et al. Timing and tempo of the Great Oxidation Event. Proc. Natl Acad. Sci. USA 114, 1811–1816 (2017).
Poulton, S. W. et al. A 200-million-year delay in permanent atmospheric oxygenation. Nature 592, 232–236 (2021).
Bekker, A., Krapež, B. & Karhu, J. A. Correlation of the stratigraphic cover of the Pilbara and Kaapvaal cratons recording the lead up to Paleoproterozoic Icehouse and the GOE. Earth Sci. Rev. 211, 103389 (2020).
Coetzee, L. L. Genetic Stratigraphy of the Paleoproterozoic Pretoria Group in the Western Transvaal. Dissertation (Rand Afrikaans University, 2001).
Warke, M. R. & Schröder, S. Synsedimentary fault control on the deposition of the Duitschland Formation (South Africa): Implications for depositional settings, Paleoproterozoic stratigraphic correlations, and the GOE. Precambrian Res. 310, 348–364 (2018).
Johnson, J. E. et al. Manganese-oxidizing photosynthesis before the rise of cyanobacteria. Proc. Natl Acad. Sci. USA 110, 11238–11243 (2013).
Izon, G. et al. Bulk and grain-scale minor sulfur isotope data reveal complexities in the dynamics of Earth’s oxygenation. Proc. Natl. Acad. Sci. USA 119, e2025606119 (2022).
Reinhard, C. T., Planavsky, N. J. & Lyons, T. W. Long-term sedimentary recycling of rare sulphur isotope anomalies. Nature 497, 100–103 (2013).
Philippot, P. et al. Globally asynchronous sulphur isotope signals require re-definition of the Great Oxidation Event. Nat. Commun. 9, 2245 (2018).
Killingsworth, B. A. et al. Constraining the rise of oxygen with oxygen isotopes. Nat. Commun. 10, 1–10 (2019).
Farquhar, J. et al. Pathways for Neoarchean pyrite formation constrained by mass-independent sulfur isotopes. Proc. Natl Acad. Sci. USA 110, 17638–17643 (2013).
Jamieson, J. W., Wing, B. A., Hannington, M. D. & Farquhar, J. Evaluating isotopic equilibrium among sulfide mineral pairs in Archean ore deposits: case study from the Kidd Creek VMS deposit, Ontario, Canada. Econ. Geol. 101, 1055–1061 (2006).
Johnston, D. T. et al. Multiple sulfur isotope fractionations in biological systems: a case study with sulfate reducers and sulfur disproportionators. Am. J. Sci. 305, 645–660 (2005).
Bekker, A. et al. Dating the rise of atmospheric oxygen. Nature 427, 117–120 (2004).
Johnson, A. C. et al. Reconciling evidence of oxidative weathering and atmospheric anoxia on Archean Earth. Sci. Adv. 7, 1–10 (2021).
Crockford, P. W. et al. Claypool continued: extending the isotopic record of sedimentary sulfate. Chem. Geol. 513, 200–225 (2019).
Torres, M. A., Paris, G., Adkins, J. F. & Fischer, W. W. Riverine evidence for isotopic mass balance in the Earth’s early sulfur cycle. Nat. Geosci. 11, 661–664 (2018).
Asael, D., Planavsky, N. J., Bellerfroid, E., Hofmann, A. & Reinhard, C. T. Sulfur non mass dependent anomalies in modern river water of Archean catchment. in Goldschmidt2017 Abstract (Goldschmidt2017, 2017).
Caquineau, T., Paquette, J.-L. & Philippot, P. U-Pb detrital zircon geochronology of the Turee Creek Group, Hamersley Basin, Western Australia: timing and correlation of the Paleoproterozoic glaciations. Precambrian Res. 307, 34–50 (2018).
Philippot, P. et al. Comment on ‘Correlation of the stratigraphic cover of the Pilbara and Kaapvaal cratons recording the lead up to Paleoproterozoic Icehouse and the GOE’ by Andrey Bekker, Bryan Krapež, and Juha A. Karhu, 2020, Earth Science Reviews. Earth Sci. Rev. 218, 103594 (2021).
Bekker, A., Krapež, B., Karhu, J. A. & Chamberlain, K. Reply to comment on “Bekker, A., Krapež, B., Karhu, J.A., 2020. Correlation of the stratigraphic cover of the Pilbara and Kaapvaal cratons recording the lead up to Paleoproterozoic Icehouse and the GOE. Earth-Science Reviews, 211, 103,389” by Pascal Phili. Earth Sci. Rev. 218, 103607 (2021).
Williford, K. H., Van Kranendonk, M. J., Ushikubo, T., Kozdon, R. & Valley, J. W. Constraining atmospheric oxygen and seawater sulfate concentrations during Paleoproterozoic glaciation: In situ sulfur three-isotope microanalysis of pyrite from the Turee Creek Group, Western Australia. Geochim. Cosmochim. Acta 75, 5686–5705 (2011).
Guy, B. M. et al. A multiple sulfur and organic carbon isotope record from non-conglomeratic sedimentary rocks of the Mesoarchean Witwatersrand Supergroup, South Africa. Precambrian Res. 216–219, 208–231 (2012).
Baroni, M., Thiemens, M. H., Delmas, R. J. & Savarino, J. Mass-independent sulfur isotopic compositions in stratospheric volcanic eruptions. Science 315, 84–87 (2007).
Burke, A. et al. Stratospheric eruptions from tropical and extra-tropical volcanoes constrained using high-resolution sulfur isotopes in ice cores. Earth Planet. Sci. Lett. 521, 113–119 (2019).
Savarino, J. UV induced mass-independent sulfur isotope fractionation in stratospheric volcanic sulfate. Geophys. Res. Lett. 30, 2131 (2003).
Canfield, D. E. & Farquhar, J. Animal evolution, bioturbation, and the sulfate concentration of the oceans. Proc. Natl Acad. Sci. USA 106, 8123–8127 (2009).
Planavsky, N. J., Bekker, A., Hofmann, A., Owens, J. D. & Lyons, T. W. Sulfur record of rising and falling marine oxygen and sulfate levels during the Lomagundi event. Proc. Natl Acad. Sci. USA 109, 18300–18305 (2012).
Gallagher, M., Whitehouse, M. J. & Kamber, B. S. The Neoarchaean surficial sulphur cycle: An alternative hypothesis based on analogies with 20th-century atmospheric lead. Geobiology 15, 385–400 (2017).
Halevy, I., Johnston, D. T. & Schrag, D. P. Explaining the structure of the archean mass-independent sulfur isotope record. Science 329, 204–207 (2010).
Liu, C. & Zhang, J. Methane might be made by all living organisms. Nature 603, 396–397 (2022).
Shang, H., Rothman, D. H. & Fournier, G. P. Oxidative metabolisms catalyzed Earth’s oxygenation. Nat. Commun. 13, 1328 (2022).
Wogan, N. F., Catling, D. C., Zahnle, K. J. & Claire, M. W. Rapid timescale for an oxic transition during the Great Oxidation Event and the instability of low atmospheric O2. Proc. Natl Acad. Sci. USA 119, 2–9 (2022).
Goldblatt, C., Lenton, T. M. & Watson, A. J. Bistability of atmospheric oxygen and the Great Oxidation. Nature 443, 683–686 (2006).
Alcott, L. J., Mills, B. J. W. & Poulton, S. W. Stepwise Earth oxygenation is an inherent property of global biogeochemical cycling. Science 366, 1333–1337 (2019).
Wickham, H. et al. Welcome to the Tidyverse. J. Open Source Softw. 4, 1686 (2019).
Pedersen, T. L. patchwork: The Composer of Plots R package https://cran.r-project.org/ (CRAN, 2020).
Wilke, C. O. ggridges: Ridgeline Plots in ggplot2 R package https://cran.r-project.org/ (CRAN, 2021).
Mills, B. R. MetBrewer: Color Palettes Inspired by Works at the Metropolitan Museum of Art R package https://cran.r-project.org/ (CRAN, 2022).
Sievert, C. Interactive Web-Based Data Visualization with R, plotly, and shiny (Chapman and Hall/CRC, 2020).
Johnson, A. C. et al. Experimental determination of pyrite and molybdenite oxidation kinetics at nanomolar oxygen concentrations. Geochim. Cosmochim. Acta 249, 160–172 (2019).
Peters, S. E. & Husson, J. M. Sediment cycling on continental and oceanic crust. Geology 45, 323–326 (2017).
Hao, J. et al. Anoxic photochemical weathering of pyrite on Archean continents. Sci. Adv. 8, 1–8 (2022).
Ono, S., Keller, N. S., Rouxel, O. & Alt, J. C. Sulfur-33 constraints on the origin of secondary pyrite in altered oceanic basement. Geochim. Cosmochim. Acta 87, 323–340 (2012).
Acknowledgements
We dedicate this paper to our co-author Prof. Nicolas J. Beukes who sadly passed away after the acceptance of this contribution. As a colleague, mentor, and friend “Prof. Nic” worked tirelessly to bring South African geology to the world. Beyond his many contributions, Nic’s work has, and continues to, revolutionise our understanding of Earth’s evolution. This study was supported by the Simons Collaboration on the Origins of Life (#290361FY18 to R.E.S. & #874698 to B.T.U. and R.E.S.) and the National Science Foundation (#EAR-1338810 to R.E.S. and S.O.). G.I. acknowledges receipt of a MISTI Global Seed Award. N.J.B. acknowledges financial support from DSI-NRF CIMERA in South Africa. We recognise formative discussions with various members of the Summons Lab.
Author information
Authors and Affiliations
Contributions
B.T.U. and G.I. designed the study. B.T.U. compiled the chemical data, constructed the database and performed its statistical interrogation. B.T.U. implemented and augmented the geochemical model with guidance from S.O. N.J.B. and S.O. collected the samples from which G.I. conducted the isotopic analyses. B.T.U. and G.I. synthesised the data–model interpretations, writing the manuscript with input from all authors. R.E.S., S.O., G.I., N.J.B., and B.T.U. acquired the funding to support various aspects of this study.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Bryan Killingsworth, Guillaume Paris and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Uveges, B.T., Izon, G., Ono, S. et al. Reconciling discrepant minor sulfur isotope records of the Great Oxidation Event. Nat Commun 14, 279 (2023). https://doi.org/10.1038/s41467-023-35820-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-023-35820-w
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.