Abstract
Being the first intrinsic antiferromagnetic (AFM) topological insulator (TI), MnBi2Te4 is argued to be a topological axion state in its even-layer form due to the antiparallel magnetization between the top and bottom layers. Here we combine both transport and scanning microwave impedance microscopy (sMIM) to investigate such axion state in atomically thin MnBi2Te4 with even-layer thickness at zero magnetic field. While transport measurements show a zero Hall plateau signaturing the axion state, sMIM uncovers an unexpected edge state raising questions regarding the nature of the “axion state”. Based on our model calculation, we propose that the edge state of even-layer MnBi2Te4 at zero field is derived from gapped helical edge states of the quantum spin Hall effect with time-reversal-symmetry breaking, when a crossover from a three-dimensional TI MnBi2Te4 to a two-dimensional TI occurs. Our finding thus signifies the richness of topological phases in MnB2Te4 that has yet to be fully explored.
Similar content being viewed by others
Introduction
Combining magnetism with topological order greatly expands the family of topological materials and gives rise to new topological phases such as the Chern insulator, the axion insulator and magnetic Weyl semimetal. While the Chern insulator and the magnetic Weyl semimetal phases have been unambiguously observed in experiments1,2,3,4,5,6,7, the definite material realization of the axion insulator remains elusive. In the original theoretical framework, such axion state could be realized if the topological surface states of a three-dimensional (3D) topological insulator (TI) are gapped out by ferromagnetic (FM) order on the surface with magnetizations pointing inward or outward8. This hedgehog configuration is, however, extremely challenging to be realized in real materials. There was a proposal that one could circumvent this problem by adopting a FM-TI-FM thin film heterostructure with antiparallel magnetizations on the top and bottom surfaces9. Experimental efforts along this route followed and reported the transport evidence of axion insulator state by observing a zero Hall plateau (ZHP)10,11,12. However, such ZHP is not unique to axion state but has been observed in many other magnetically doped TI systems13,14,15, and thus may not be used as an experimental proof of the existence of the axion state15. New theoretical schemes other than ZHP are therefore proposed to distinguish an axion insulator from other trivial cases in experiments16,17,18.
MnBi2Te4 emerges as the first intrinsic antiferromagnetic (AFM) TI19,20,21,22,23,24,25. As shown in Fig. 1a, it is a tetradymite compound consisting of stacked Te-Bi-Te-Mn-Te-Bi-Te septuple layers (SLs) in the vertical direction. The spins of Mn have a FM intralayer exchange coupling and an AFM interlayer coupling forming an A-type AFM with an out-of-plane easy axis. For MnBi2Te4 with even-layer thickness, the magnetizations of the top and bottom layers are antiparallel, which is ideal for the realization of the axion state based on a theoretical prediction23. Although this prediction gains support from a transport experiment reporting ZHP in a 6-SL MnBi2Te4 at zero magnetic field26, it is far from conclusive to determine the axion state based on ZHP. Other factors, such as multi-domain states inside a TI could also generate a zero Hall conductance. It was also pointed out in theory that, to realize an axion state, the thickness of sample should be thick enough to eliminate the finite-size effect but reasonably thin to get rid of side surface conduction23. It is thus critical to employ spatially resolved imaging techniques to compliment the transport study. Such microscopic characterization is essential to rule out multi-domain states or side surface conduction for the determination of the axion state.
In this article, we combine both transport and scanning microwave impedance microscopy (sMIM) to study the electronic states of the even-layer MnBi2Te4 with an emphasis on its characteristics at zero magnetic field. Both transport and sMIM reveal a magnetic field driven topological phase transition with the high field phase to be the previously known Chern insulator phase. The insulating phase at zero field, while featuring a ZHP in transport measurements, exhibits a persistent edge state under sMIM that is unexpected for an axion insulator. Based on our model calculations, we show that the even-layer MnBi2Te4 at zero field is not an axion state, but hosts gapped helical edge states from the time-reversal-symmetry (TRS) breaking quantum spin Hall (QSH) phase.
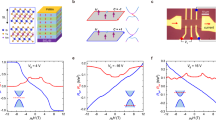
Results
We mechanically exfoliate MnBi2Te4 thin flakes whose thickness is determined by optical reflectance (see Supplementary Note 1). We have fabricated and measured two 6-SL MnBi2Te4 devices in this study (see Supplementary Note 7 for another 6-SL device). Given recent controversy regarding the even-odd layer thickness determination in MnBi2Te4 thin flakes which is critical for data interpretation27, we check the even-odd layer property of the sample using scanning superconducting quantum interference device (sSQUID) by directly measuring the static magnetic flux generated by net magnetization of the sample (see Supplementary Note 2). Being an ultra-sensitive probe of magnetization, sSQUID provides an independent way to confirm the correctness of our even-odd layer thickness assignment. Figure 1b shows the experimental setup of sMIM used for probing local conductivity28. A 3 GHz microwave is delivered to an atomic force microscope tip with its reflected signal collected and demodulated into two output channels, i.e., sMIM-Im and sMIM-Re. The sMIM-Im signal increases monotonically with the local conductivity, and is thus adopted here for nanoscale conductivity imaging. Also shown in Fig. 1b is an optical image of our 6-SL MnBi2Te4 device with transport electrodes attached. Note that the transport and sMIM measurements were not conducted simultaneously. Figure 1c shows the magnetic field dependent longitudinal resistance \({R}_{{xx}}\) and Hall resistance \({R}_{{yx}}\) taken at +33 V gate voltage. \({R}_{{yx}}\) remains zero from −4 T to 4 T, forming a ZHP. As the field goes up, \({R}_{{yx}}\) rapidly increases and approaches to a quantized Hall plateau above 6 T, accompanied by a vanishing \({R}_{{xx}}\) (see Supplementary Note 3 for more gate voltage and field dependent measurements). We conclude from these transport measurements that a Chern insulator phase is realized above 6 T, while the phase with ZHP at low fields will be described as ZHP phase hereafter.
Figure 1d displays a sMIM image taken at 9 T and +40 V gate voltage demonstrating the capability of sMIM to visualize topological edge states of the Chern insulator phase. When the bulk is gated to charge neutral at this gate voltage, the sMIM signal in the sample interior is even lower than the SiO2 substrate indicating a highly insulating bulk. A bright line runs along the sample’s geometric edge signaling a highly conductive edge. These observations are consistent with the characteristic features of the Chern insulator phase where a conductive edge encloses an insulating bulk29,30.
The gate voltage dependent sMIM imaging results are presented in Fig. 2. For a topological edge mode like a chiral edge state in the Chern insulator phase, its energy dispersion goes across the bulk gap. Therefore, while the bulk conductivity can vary with gating due to the Fermi level shift, the edge should remain highly conductive irrespective of gating. That is what we observed at 9 T in Fig. 2a. The bulk interior becomes progressively insulating as the gate voltage increases from 0 V to +40 V corresponding to the Fermi level shift from the bulk valence band to the middle of the band gap. Meanwhile, a conductive edge persists into the band gap giving rise to strong bulk edge signal contrast. Figure 2b shows the same gate voltage dependent sMIM imaging at zero magnetic field. To our surprise, as the bulk is tuned from a metallic to an insulating state after the Fermi level moves into the bulk gap, a conductive edge is resolved, resembling what happens at 9 T. We show additional transport and sMIM data to demonstrate the uniformity of such ZHP phase and its in-gap edge state in our device in supplementary (see Supplementary Note 4). This observation raises serious concerns whether the nature of the ZHP phase is an axion state. We leave it to the final discussion.
We then probe the magnetic field driven quantum phase transition (QPT) from ZHP phase to the Chern insulator phase when the magnetic order of MnBi2Te4 changes from AFM to FM. Figure 3a shows a series of field dependent sMIM images taken at +40 V to track this transition. Three regimes can be clearly distinguished: 1) For low field regime of \(0{{{{{\rm{T}}}}}}\le {{{{{\rm{\mu }}}}}}{{{{{\rm{H}}}}}}\le 4{{{{{\rm{T}}}}}}\) corresponding to the ZHP phase, strong bulk edge imaging contrast persists demonstrating the existence of an edge state; 2) In intermediate field regime of \(4{{{{{\rm{T}}}}}}\le {{{{{\rm{\mu }}}}}}{{{{{\rm{H}}}}}}\le 5{{{{{\rm{T}}}}}}\), the conductivity of the sample interior quickly increases to the point that bulk edge imaging contrast is barely visible (4.5 T case), i.e., there is an insulator to metal transition of the bulk. Crossing the point, the bulk edge imaging contrast reappears indicating a metal to insulator transition (MIT) of the bulk; 3) In high field regime of \(6{{{{{\rm{T}}}}}}\le {{{{{\rm{\mu }}}}}}{{{{{\rm{H}}}}}}\le 9{{{{{\rm{T}}}}}}\), one again observes a conductive edge enclosing an insulating bulk as the device enters the Chern insulator phase. The fact that a metallic bulk state exists in the middle of the transition suggests that this field-driven QPT is essentially a topological phase transition, along which the bulk band gap has to close and reopen to connect two topologically distinct insulating phases. It also manifests the close correlation between magnetic order and non-trivial band topology in MnBi2Te4, i.e., the AFM (FM) magnetic order directly results in the ZHP (Chern insulator) phase.
Additional evidence of bulk MIT transition comes from the global transport measurement adopting a special experimental set-up following the spirit of the Corbino measurement (see Supplementary Note 5). In the Hall bar device, this method chooses a pair of opposite electrodes as the source and drain while grounding all the other electrodes. A 100 nA current is injected from the source electrode and the current collected at the drain electrode is denoted as the bulk current \({I}_{{bulk}}\). Due to the existence of conductive edge state, most of the injected current will flow through the edge to the ground. Current that can be measured at the drain must go across the sample interior, thus reflecting the bulk resistance state. The magnetic field dependent \({I}_{{bulk}}\) is presented in Fig. 3b. As expected, a small amount of the injected current (<1%) is detected as \({I}_{{bulk}}\) at both low and high field regimes indicating an insulating bulk state. \({I}_{{bulk}}\) undergoes a rapid increase by an order of magnitude in the intermediate field regime signaling the bulk MIT transition. The bulk sMIM signal is extracted from Fig. 3a and laid over \({I}_{{bulk}}\left(\mu H\right)\) in Fig. 3b after a proper scaling. Note that \({I}_{{bulk}}\) is plotted in logarithmic scale in Fig. 3b to be directly compared to sMIM signal because the latter is proportional to the logarithmic scale of the conductivity28. sMIM and transport measurement show qualitatively the same field dependence, i.e., they all show a metallic bulk state between two insulating ones as a result of bulk MIT transition. However, a large quantitative discrepancy exists between sMIM and \({I}_{{bulk}}\) at both low and high field regimes corresponding to ZHP and Chern insulator phase, respectively. This is attributed to the non-ideal scheme of the bulk transport set-up to probe the bulk resistance state for which a true Corbino geometry is required31. For example, there might be tiny current leakage along the edge channel between the drain electrode and other grounded electrodes resulting in an inaccurate measurement of \({I}_{{bulk}}\). It is noted that similar field dependence of the bulk transport state was reported in another work27.
The width of the edge state seen in sMIM images in both ZHP and Chern insulator phases is around 2 μm, which is far above the sMIM spatial resolution (<100 nm). Such a large width cannot be taken as a real physical dimension of topological edge state (see Fig. 4d–f). Interestingly, several sMIM imaging works on similar TI all show edge state width in μm range29,32,33. Theoretically, the width of a topological edge state is inversely proportional to the exchange energy gap \(\triangle\), i.e., \(w \sim \hslash {v}_{F}/\triangle\)34. In addition, disorders can cause the spatial broadening of a topological edge state via strong bulk edge scattering30,35,36. Therefore, we attribute the observed wide edge state in our experiment to the strong disorders in the system that enhance bulk edge scattering as well as suppress the averaged exchange energy gap37.
a–c Evolution of band structures of 6-SL MnBi2Te4 by sweeping the magnetic field \(B\). The red (blue) line indicates the helical (chiral) edge mode. The system employs a periodic boundary condition in the \(x\) direction and an open boundary conditions in the \(y\) direction. d–f Spatial distributions of the typical wave functions along \(y\) direction at \({{{{{\rm{E}}}}}}=0.006\)eV for different \(B\). The model parameters are \({M}_{z}=0.04\)eV, \({A}_{2}=2\)eV∙Å, \({B}_{2}=24\)eV∙Å2, \({m}_{0}=0.116\) eV, \({A}_{1}=3.1964\) eV∙Å, and \({B}_{1}=9.4048\) eV∙Å2.
Discussion
Regarding the physical origin of the edge state observed at zero field, the following mechanisms can be firstly ruled out: (1) Trivial edge states due to edge contaminations or bulk disorders. These trivial edge states are usually localized and not involved in charge transport. Nonlocal transport measurement is conducted to identify edge conduction at zero field (see Supplementary Note 6)38. The large nonlocal signal in ZHP phase indicates the current carrying character of the edge state that cannot be attributed to bulk disordering effect. The fact that this edge state has been observed in another 6-SL MnBi2Te4 device (see Supplementary Note 7) also rules out an accidental trivial edge state; (2) Chiral edge state of the quantum anomalous Hall (QAH) phase at zero field. This cannot be the case because a topological phase transition happens in this device which links topologically distinct phases at two ends; (3) The axion insulator. We estimate the edge conductivity at zero field to be 1 μs/□ (see Supplementary Note 5). Such edge conductivity value is close to the edge conductivity in QSH insulator WTe233 and Chern insulator of magnetically doped TI29, but two orders of magnitude larger than that in the reported axion insulator phase29.
Having ruled out the aforementioned mechanisms, we now discuss the physical origin of the edge state. We perform a model calculation to show that 6-SL MnBi2Te4 at zero field hosts gapped helical edge states as a result of a TRS breaking QSH state. The intrinsic magnetic TI MnBi2Te4 can be described by a 3D \(4\times 4\) effective Hamiltonian23:
in the basis of (\(\left|{{{{{{\rm{P}}}}}}1}_{z}^{+},\uparrow \right\rangle,\left|{{{{{{\rm{P}}}}}}2}_{z}^{-},\uparrow \right\rangle,\left|{{{{{{\rm{P}}}}}}1}_{z}^{-},\downarrow \right\rangle,\,\left|{{{{{{\rm{P}}}}}}2}_{z}^{+},\downarrow \right\rangle\)), where \({k}_{\pm }={k}_{x}\pm i{k}_{y}\), the mass term \({M}_{k}={m}_{0}-{B}_{1}({k}_{x}^{2}+{k}_{y}^{2})-{B}_{2}{k}_{z}^{2}\) and the spatial-dependent exchange field \({H}_{M}={{{{{{\rm{M}}}}}}}_{z}{{{{{{\rm{\sigma }}}}}}}_{z} \, {f}_{o,e}\) with \({{{{{{\rm{\sigma }}}}}}}_{z}\) the Pauli matrix acting on spin space and \({k}_{x,y,z}\) wave vectors in x, y, and z directions. \({A}_{{{{{\mathrm{1,2}}}}}},{B}_{{{{{\mathrm{1,2}}}}}},\) \({m}_{0}\) and \({{{{{{\rm{M}}}}}}}_{z}\) are model parameters. For an AFM phase at zero field, \({f}_{o,e}=\pm \!1\) for even (odd) layers, respectively. The system preserves a combined symmetry \({{{{{\rm{S}}}}}}=\Theta {{{{{{\rm{T}}}}}}}_{1/2}\), where \(\Theta\) is TRS and \({{{{{{\rm{T}}}}}}}_{1/2}\) is half translation symmetry. \({{{{{\rm{S}}}}}}\) could lead to a \({{{{{{\rm{Z}}}}}}}_{2}\) topological classification39. On the other hand, \({f}_{o,e}=1\) for an FM phase, and it can generally lead to QAH phase for MnBi2Te4 multilayers. Following the literature40, we investigate the crossover behavior from a 3D to two-dimensional (2D) with reducing the layer thickness in z direction and find that, 6-SL MnBi2Te4 hosts gapped helical edge states. Figure 4a–c show the band structure of 6-SL MnBi2Te4 with different magnetic field \({{{{{\rm{B}}}}}}\), where the magnetic switching is simulated by \({f}_{e}={{\tanh }}\left(\frac{B-{B}_{c}}{{B}_{0}}\right)\) with \({B}_{c}=\)4.7 T and \({B}_{0}=\)0.28 T. Figure 4d–f are the corresponding spatial distribution of wave functions. At zero magnetic field, the system is a \({{{{{\rm{C}}}}}}=0\) phase hosting a pair of gapped helical edge states. In contrast to the gapless helical edge state of QSH phase protected by TRS, a tiny edge gap (~1.3 meV) exists here due to the TRS breaking by its AFM order (inset of Fig. 4a). Then, the bulk band gap is closed during the magnetic reversal at \({{{{{\rm{B}}}}}}=4.5{{{{{\rm{T}}}}}}\), and the system finally turns into a \({{{{{\rm{C}}}}}}=1\) Chern insulator phase with chiral edge states at \({{{{{\rm{B}}}}}}=9{{{{{\rm{T}}}}}}\). It is noted that, for odd-layer MnBi2Te4, our model calculation predicts a QAH state (see Supplementary Note 8).
For MnBi2Te4 in a 3D limit, due to the aforementioned \({{{{{\rm{S}}}}}}\) symmetry, the system is an AFM TI with a gapped surface state on the top and bottom surface, and a gapless one at side surfaces22,23,24,25. For exfoliated MnBi2Te4 thin flakes, a crossover from a 3D TI to a 2D TI occurs, and the system is now evolved into a TRS breaking QSH phase with a pair of gapped helical edge state. The concept of TRS broken QSH state was first introduced in the literature41, which argued it to preserve spin Chern number and is therefore topologically indistinct from the QSH with TRS. Different from QSH protected by TRS, a small energy gap exists in the edge state spectrum and a low-dissipation spin transport is anticipated. This TRS breaking QSH has also been proposed in MnBi2Te4 family in the 2D limit42. Inspired by our experiment, a recent first-principle calculation suggests 6SL-MnBi2Te4 to be such TRS breaking QSH state43. More importantly, it concludes that such gapped helical edge state will become gapless due to disorders and generate dissipative edge transport. Our experiment indeed observes a dissipative edge conduction at zero field (\({R}_{{xx}} \sim 36k\Omega\)) and the effect of disorders on the edge state width is also prominent.
Our experiment uncovers a significant edge conduction that doesn’t comply with the original axion state proposal which requires an insulating edge (gapped side surface)8,9,23. Instead, it suggests the coexistence of gapped top/bottom surfaces with massive Dirac fermions and gapless side surfaces with massless Dirac fermions in even-layer MnBi2Te4, which turns out to be an intriguing setting to observe a half-quantized surface Hall effect from a single gapped Dirac cone44,45,46,47. Such half-quantized surface Hall effect was used to interpret ZHP in axion state, and now becomes a feasible experimental object to identify an axion state16,17. To search for this half-quantized surface Hall effect in even-layer MnBi2Te4, the experimental challenges are twofold. First, a dissipationless side surface conduction is required to ensure a coherent transport with quantization. Second, a complete decoupling between the top and bottom surfaces upon current flowing is also required, which can only be achieved in thicker sample (>100 SL) whose bulk, yet tends to be more conductive17. The disorder level of MnBi2Te4 should be further reduced to ensure both an intrinsic insulating bulk and a coherent side surface conduction.
In summary, we study the even-layer MnBi2Te4 at zero field combining transport and sMIM measurements. The observation of edge state challenges the existence of the axion state in 6-SL MnBi2Te4. Instead, we argue that the 6-SL MnBi2Te4 is a TRS breaking QSH phase hosting a pair of gapped helical edge states. The robustness of such helical edge states under modest magnetic fields could find applications in spintronics. Our work also indicates the richness of topological phases in MnBi2Te4 family awaiting for continuous explorations.
Methods
Crystal growth
The MnBi2Te4 single crystal were grown by direct reaction of a 1:1 mixture of Bi2Te3 and MnTe in a sealed silica ampoule under a dynamic vacuum. The mixture was first heated to 973 K then slowly cooled down to 864 K. The crystallization occurred during the prolonged annealing at this temperature.
Device fabrication
Most of the device’s fabrication processes were carried out in argon-filled glove box with the O2 and H2O levels below 0.1 ppm. Before device fabrication, marker array was first prepared on 285 nm-thick SiO2/Si substrates for precise alignment between selected area and patterns. Before exfoliation, the 285 nm-thick SiO2/Si substrates were pre-cleaned in air plasma for 5 min at 125 Pa. The thin MnBi2Te4 flakes were exfoliated by using the Scotch tape method onto the 285 nm-thick SiO2/Si substrates. Before spin coating PMMA, the surrounding thick flakes were scratched by a sharp needle. By using electron-beam lithography, metal electrodes (Cr/Au, 5/50 nm) were deposited in a thermal evaporator connected to the glove box. When transferred between glove box, electron-beam lithography and the cryostat, the devices were covered by a layer of PMMA to mitigate air contamination and sample degradation.
Transport measurement
Electrical measurements of magneto transport properties were performed in a commercial cryostat Attodry 2100 with a base temperature 1.7 K and magnetic field up to 9 T. The AC current of 100 nA was generated by the AC voltage of 1 V applied on a 10 MΩ resistor. The longitudinal and Hall voltages drops were detected simultaneously by using lock-in amplifiers with AC current. The bottom-gate voltage with SiO2 dielectric were applied by a Keithley 2400 multimeter.
sMIM measurement
The sMIM in this work is based on a commercial LT ScanWave system from PrimeNano Inc. All the sMIM measurements were performed at 1.7 K. The technique utilizes a cantilever-based AFM combined with a 3 GHz microwave signal delivered through a customized shielded cantilever probes also commercially available from PrimeNano Inc.
Data availability
All raw and derived data used to support the findings of this work are available from the authors on reasonable request.
References
Chang, C. Z. et al. Experimental observation of the quantum anomalous hall effect in a magnetic topological insulator. Science 340, 167–170 (2013).
Checkelsky, J. G. et al. Trajectory of the anomalous Hall effect towards the quantized state in a ferromagnetic topological insulator. Nat. Phys. 10, 731–736 (2014).
Kou, X. F. et al. Scale-invariant quantum anomalous hall effect in magnetic topological insulators beyond the two-dimensional limit. Phys. Rev. Lett. 113, 137201 (2014).
Chang, C. Z. et al. High-precision realization of robust quantum anomalous Hall state in a hard ferromagnetic topological insulator. Nat. Mater. 14, 473–477 (2015).
Belopolski, I. et al. Discovery of topological Weyl fermion lines and drumhead surface states in a room temperature magnet. Science 365, 1278–1281 (2019).
Liu, D. F. et al. Magnetic Weyl semimetal phase in a Kagome crystal. Science 365, 1282–1285 (2019).
Morali, N. et al. Fermi-arc diversity on surface terminations of the magnetic Weyl semimetal Co3Sn2S2. Science 365, 1286–1291 (2019).
Qi, X. L., Hughes, T. L. & Zhang, S. C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
Wang, J., Lian, B., Qi, X. L. & Zhang, S. C. Quantized topological magnetoelectric effect of the zero-plateau quantum anomalous Hall state. Phys. Rev. B 92, 081107 (2015).
Mogi, M. et al. A magnetic heterostructure of topological insulators as a candidate for an axion insulator. Nat. Mater. 16, 516–521 (2017).
Mogi, M. et al. Tailoring tricolor structure of magnetic topological insulator for robust axion insulator. Sci. Adv. 3, eaao1669 (2017).
Xiao, D. et al. Realization of the axion insulator state in quantum anomalous hall sandwich heterostructures. Phys. Rev. Lett. 120, 056801 (2018).
Feng, Y. et al. Observation of the zero hall plateau in a quantum anomalous hall insulator. Phys. Rev. Lett. 115, 126801 (2015).
Kou, X. F. et al. Metal-to-insulator switching in quantum anomalous Hall states. Nat. Commun. 6, 8474 (2015).
Fijalkowski, K. M. et al. Any axion insulator must be a bulk three-dimensional topological insulator. Phys. Rev. B 103, 235111 (2021).
Gu, M. et al. Spectral signatures of the surface anomalous Hall effect in magnetic axion insulators. Nat. Commun. 12, 3524 (2021).
Chen, R. et al. Using nonlocal surface transport to identify the axion insulator. Phys. Rev. B 103, L241409 (2021).
Li, H. L., Jiang, H., Chen, C. Z. & Xie, X. C. Critical behavior and universal signature of an axion insulator state. Phys. Rev. Lett. 126, 156601 (2021).
Otrokov, M. M. et al. Highly-ordered wide bandgap materials for quantized anomalous Hall and magnetoelectric effects. 2D Materials 4, 025082 (2017).
Otrokov, M. M. et al. Prediction and observation of an antiferromagnetic topological insulator. Nature 576, 416–422 (2019).
Gong, Y. et al. Experimental realization of an intrinsic magnetic topological insulator. Chin. Phys. Lett. 36, 076801 (2019).
Li, J. H. et al. Intrinsic magnetic topological insulators in van der Waals layered MnBi2Te4-family materials. Sci. Adv. 5, eaaw5685 (2019).
Zhang, D. Q. et al. Topological axion states in the magnetic insulator MnBi2Te4 with the quantized magnetoelectric effect. Phys. Rev. Lett. 122, 206401 (2019).
Otrokov, M. M. et al. Unique thickness-dependent properties of the van der waals interlayer antiferromagnet MnBi2Te4 films. Phys. Rev. Lett. 122, 107202 (2019).
Li, J. H. et al. Magnetically controllable topological quantum phase transitions in the antiferromagnetic topological insulator MnBi2Te4. Phys. Rev. B 100, 121103 (2019).
Liu, C. et al. Robust axion insulator and Chern insulator phases in a two-dimensional antiferromagnetic topological insulator. Nat. Mater. 19, 522–527 (2020).
Ovchinnikov, D. et al. Intertwined topological and magnetic orders in atomically thin chern insulator MnBi2Te4. Nano Lett. 21, 2544–2550 (2021).
Chu, Z., Zheng, L. & Lai, K. Microwave microscopy and its applications. Annu. Rev. Mater. Res. 50, 105–130 (2020).
Allen, M. et al. Visualization of an axion insulating state at the transition between 2 chiral quantum anomalous Hall states. Proc. Natl Acad. Sci. USA 116, 14511–14515 (2019).
Lin, W. et al. Influence of the dissipative topological edge state on quantized transport in MnBi2Te4. Phys. Rev. B 105, 165411 (2022).
Rodenbach, L. K. et al. Bulk dissipation in the quantum anomalous Hall effect. APL Mater. 9, 081116 (2021).
Ma, E. Y. et al. Unexpected edge conduction in mercury telluride quantum wells under broken time-reversal symmetry. Nat. Commun. 6, 7252 (2015).
Shi, Y. M. et al. Imaging quantum spin Hall edges in monolayer WTe2. Sci. Adv. 5, eaat8799 (2019).
Zhang, F., Kane, C. L. & Mele, E. J. Surface states of topological insulators. Phys. Rev. B 86, 081303 (2012).
Jiang, H., Wang, L., Sun, Q. F. & Xie, X. C. Numerical study of the topological Anderson insulator in HgTe/CdTe quantum wells. Phys. Rev. B 80, 165316 (2009).
Li, Y.-H. & Cheng, R. Spin fluctuations in quantized transport of magnetic topological insulators. Phys. Rev. Lett. 126, 026601 (2021).
Li, H., Chen, C.-Z., Jiang, H. & Xie, X. C. Coexistence of quantum hall and quantum anomalous hall phases in disordered MnBi2Te4. Phys. Rev. Lett. 127, 236402 (2021).
Yaoxin, Li et al. Nonlocal transport in axion insulator state of MnBi2Te4. arXiv https://doi.org/10.48550/arXiv.2105.10390 (2021).
Mong, R. S. K., Essin, A. M. & Moore, J. E. Antiferromagnetic topological insulators. Phys. Rev. B 81, 245209 (2010).
Liu, C. X. et al. Oscillatory crossover from two-dimensional to three-dimensional topological insulators. Phys. Rev. B 81, 041307 (2010).
Yang, Y. et al. Time-reversal-symmetry-broken quantum spin hall effect. Phys. Rev. Lett. 107, 066602 (2011).
Sun, H. Y. et al. Rational design principles of the quantum anomalous hall effect in superlatticelike magnetic topological insulators. Phys. Rev. Lett. 123, 096401 (2019).
Zhaochen L., Dongheng Q., Yadong J. & Wang, J. Dissipative edge transport in disordered axion insulator films. arXiv https://doi.org/10.48550/arXiv.2109.06178 (2021).
Ming G., Haiwen L., Hua J., Chui-Zhen C. & Xie, X. C. Half-quantized helical hinge currents in axion insulators. arXiv https://doi.org/10.48550/arXiv.2203.12982 (2022).
Zou, J.-Y., Fu, B., Wang, H.-W., Hu, Z.-A. & Shen, S.-Q. Half-quantized Hall effect and power law decay of edge-current distribution. Phys. Rev. B 105, L201106 (2022).
Humian, Z. et al. Transport theory of half-quantized hall conductance in a semi-magnetic topological insulator. arXiv https://doi.org/10.1103/PhysRevLett.129.096601 (2022).
Mogi, M. et al. Experimental signature of the parity anomaly in a semi-magnetic topological insulator. Nat. Phys. 18, 390–394 (2022).
Acknowledgements
The work at Fudan University is supported by National Natural Science Foundation of China (Grant Nos. 12074080, 12274088, 11904053, and 11827805), National Postdoctoral Program for Innovative Talents (Grant No. BX20180079), Shanghai Science and Technology Committee Rising-Star Program (19QA1401000), Major Project (Grant No. 2019SHZDZX01) and Ministry of Science and Technology of China (Grant Nos. 2016YFA0301002 and 2017YFA0303000). The work at Tsinghua University is supported by National Natural Science Foundation of China (Grant Nos. 21975140, 51991343), the Basic Science Center Project of National Natural Science Foundation of China (Grand No. 51788104) and the National Key R&D Program of China (Grand No. 2018YFA0307100). The work at Soochow University is funded by the National Natural Science Foundation of China (Grant No. 11974256), the Priority Academic Program Development (PAPD) of Jiangsu Higher Education Institutions and the Natural Science Foundation of Jiangsu Province (Grant No. BK20190813).
Author information
Authors and Affiliations
Contributions
J.S. and X.D.Z. supervised the research. H.L. and Y.W. grew the MnBi2Te4 crystals. Y.C.W. and Z.C.L. fabricated the devices. W.L. and Y.F. performed the sMIM and transport measurements. J.J.Z. performed the sSQUID measurement. H.Y.Z., C.L., Y.H.W., J.S.Z., and Y.Y.W. assisted in the data analysis. C.Z.C. performed an effective model calculation. X.D.Z. and J.S. prepared the manuscript with comments from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Yukako Fujishiro, and the other, anonymous, reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lin, W., Feng, Y., Wang, Y. et al. Direct visualization of edge state in even-layer MnBi2Te4 at zero magnetic field. Nat Commun 13, 7714 (2022). https://doi.org/10.1038/s41467-022-35482-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-35482-0
This article is cited by
-
High spin axion insulator
Nature Communications (2024)
-
Fabrication-induced even-odd discrepancy of magnetotransport in few-layer MnBi2Te4
Nature Communications (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.