Abstract
Sample return missions have provided the basis for understanding the thermochemical evolution of the Moon. Mare basalt sources are likely to have originated from partial melting of lunar magma ocean cumulates after solidification from an initially molten state. Some of the Apollo mare basalts show evidence for the presence in their source of a late-stage radiogenic heat-producing incompatible element-rich layer, known for its enrichment in potassium, rare-earth elements, and phosphorus (KREEP). Here we show the most depleted lunar meteorite, Asuka-881757, and associated mare basalts, represent ancient (~3.9 Ga) partial melts of KREEP-free Fe-rich mantle. Petrological modeling demonstrates that these basalts were generated at lower temperatures and shallower depths than typical Apollo mare basalts. Calculated mantle potential temperatures of these rocks suggest a relatively cooler mantle source and lower surface heat flow than those associated with later-erupted mare basalts, suggesting a fundamental shift in melting regime in the Moon from ~3.9 to ~3.3 Ga.
Similar content being viewed by others
Introduction
There is a broad consensus that most of the Apollo returned mare basalts contain variable quantities of material derived from a KREEP (potassium, rare earth element and phosphorus) component mixed into their mantle source(s), possibly due to mantle overturn after extensive lunar magma ocean (LMO) crystallization1, widely known as ‘urKREEP’2. The ‘KREEPy-ness’ of these basalts are supported by high abundances of other incompatible trace elements (ITE). A complementary argument posits that some lunar basalts are of KREEP-free origin with ITE enrichment produced purely through simple magmatic processes such as low-degree melting of depleted lunar mantle followed by extensive fractional crystallization; a mechanism distinct from urKREEP addition3,4,5,6. KREEP-free mantle sources are considered to have low initial 87Sr/86Sr (≤0.700) and high 143Nd/144Nd or positive εNd, in contrast to KREEP-rich materials which have high initial 87Sr/86Sr (>0.701) and low 143Nd/144Nd or negative εNd.
While ambiguities related to the exact origin of KREEP components exist for some mare basalts, the search for extremely depleted mare basaltic samples remains critical for characterizing the earliest (before mantle overturn) LMO cumulates, which are predicted to be relatively devoid of the ITE and heat-producing elements. Study of these samples would enable elucidation of the early thermal and chemical state of the lunar interior. Previously identified KREEP-free lunar basalts (NWA 0323; LAP basalts4; Chang’E 5 basalts6) are typically low in TiO2 (0.45–5.70 wt.%) and are Fe-rich (Mg# [molar Mg/(Mg+Fe) × 100] 32–49; Fig. 1), with characteristically low initial 87Sr/86Sr (0.699–0.700) and positive εNd (+0.8 to +7.0) indicating mantle source depletion (Fig. 2).
TiO2 plotted against bulk Mg# (molar Mg/(Mg+Fe) × 100), showing YAMM basalts are the low-Ti and most Fe-rich variety. Compositions of Apollo basalts are taken from the ApolloBasalt DB(v2) database72.
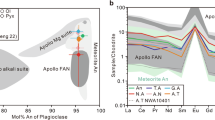
a Plot of age (Ga, billion years) against εNd composition showing the depleted nature of YAMM meteorites in comparison to other lunar meteorites and Apollo mare basalts. εNd(t) = ((143Nd/144Nd)sample(t)/(143Nd/144Nd)CHUR−1) × 10,000, where (143Nd/144Nd)sample(t) and (143Nd/144Nd)CHUR are the Nd isotopic compositions of sample and Chondritic Uniform Reservoir (CHUR) at time (t) of crystallization of the rock, respectively. b Calculated present day values of 147Sm/144Nd plotted against the present day 87Rb/86Sr for the source regions of YAMM and other lunar mare basalts (cf. ref. 4) using a model where the Moon differentiates at 4558 Ma with an initial 87Sr/86Sr of LUNI = 0.69903 (ref. 73). The 147Sm/144Nd of basalt source regions are calculated assuming a two-stage model where the Moon follows a chondritic path until differentiation occurs at 4.42 Ga, at which time mare basalt source regions were formed. Data Sources: YAMM meteorites (A-881757, ref. 7; Y-793169, ref. 8; MIL 05035, ref. 9), Kalahari 009 (ref. 74), Chang’E 5 basalts6 and other Apollo mare basalts and meteorites (ref. 4 and references therein).
In this work, we investigate the petrogenesis of the ‘YAMM’ (Y-793169, A-881757, MIL 05035, MET 01210) lunar meteorites, with special emphasis on Asuka-881757 (A-881757) to understand ancient lunar volcanism. These basaltic meteorites are likely launch-paired as suggested by their similar mineral assemblage, pyroxene crystallization trends, REE abundances, crystallization ages (~3.8–3.9 Ga7,8,9), and low U/Pb, Rb/Sr, and high Sm/Nd10. The YAMM meteorites span crystallization ages broadly coinciding with the putative late heavy bombardment (LHB)11 that pre-dates Apollo (~3.8–3.1 Ga) and Chang’E 5 (~2.0 Ga) mare basalts. The YAMM meteorites are Fe-rich (Mg# 32–41; Fig. 1) with low bulk REE and other ITE (e.g., 0.48 ppm Th). The low Rb/Sr (87Sr/86Sri = 0.69908–0.69910), high Sm/Nd (εNd = +7.2 to +7.4), and unusually low U-Pb (μ = 9–20) of their sources suggest a KREEP-free source distinct from the Procellarum KREEP Terrane12 (PKT) basalts (Fig. 2).
Results and discussion
Petrology and geochemistry of YAMM basalts
Asuka-881757 is a coarse-grained (up to 8 mm), holocrystalline, unbrecciated mare basalt with pyroxene and plagioclase as primary constituents (Supplementary Figs. 1 and 2), consistent with other YAMM basalts. Coarse-grained basalts with gabbroic textures are rare amongst the returned samples10,13. Sample A-881757 pyroxenes are Fe-rich and cover a wide spectrum of compositions (Supplementary Text 1, Supplementary Fig. 3 and Supplementary Data 1), consistent with other YAMM and Luna 24 ferrobasalts14 (Supplementary Text 2). The compositional zoning in maskelynitized plagioclase grains range from An96 to An87 with rims close to late-stage crystallizing phases reaching An75 (Supplementary Fig. 4), following a typical fractionation trend shown by other low-Ti lunar basalts. Unlike most Apollo, Luna, and Chang’E basalts, forsteritic olivine is absent in A-881757.
Asuka-881757 is a very low-Ti, low-Al, and low-K basaltic rock (Supplementary Data 2)15,16. It consists of low Ti/Sm (0.96), low Th/Sm (0.16) and low Th/Hf (0.24). Further, the CI-normalized (cn) LREE-depleted values ([La/Sm]cn = 0.68, [La/Lu]cn = 0.67 and [La/Yb]cn = 1.05) and a relatively flat HREE ratio ([Tb/Yb]cn = 1.04) are consistent with other YAMM basalts (Fig. 3 and Supplementary Data 2). A similar LREE depleted pattern is also observed for the low-Ti Luna 24 ferrobasalts ([La/Sm]cn = 0.43)17, and Kalahari 009 ([La/Sm]cn = 0.91)18. These patterns are distinct from the KREEP basalts (high Th/Sm = 0.45; [La/Sm]cn = 1.46 and [La/Yb]cn = 2.13)2 or Apollo basaltic rocks with KREEP components (La/Sm]cn = 1.32–1.50)19 (Fig. 3). Unlike most Apollo mare basalts, A-881757 and other YAMM members, Kalahari 009 and Luna 24 ferrobasalts do not possess a negative Eu-anomaly (Fig. 3).
Chondrite-normalized rare earth element plots for YAMM (magenta), Kalahari 009 (blue), Luna 24 ferrobasalts (FB; dashed line), NWA 032 (orange), LAP basalts (olive green), along with Apollo 12 and Apollo 15 olivine basalts, Apollo 12 ilmenite basalts, Apollo 11 and Apollo 17 high-Ti basalts and KREEP basalts. YAMM basalts along with Luna 24 ferrobasalts and Kalahari 009 show depleted REE pattern while there is a lack of prominent Eu anomaly in YAMM and Luna 24 ferrobasalts, which are distinct from Apollo mare and KREEP basalts. Data Sources: A-881757 (this study); Y-793169 (ref. 16); MIL 05035 (ref. 20); MET 01210 (ref. 75); Luna 24 ferrobasalts14; Kalahari 009 (ref. 18); Apollo and KREEP basalts19. Abbreviations are A-11 HTB: Apollo 11 high-Ti basalts; A-17 HTB: Apollo 17 high-Ti basalts; A-12 IB: Apollo 12 ilmenite basalts; A-12 OB: Apollo 12 olivine basalts; A-15 OB: Apollo 15 olivine basalts; L-24 FB: Luna 24 ferrobasalts.
The most LREE-depleted YAMM meteorites suggest limited fractionation from a primitive partial melt20. Notably, the relative REE abundances of MIL 05035 ([La/Sm]cn = 0.55–0.63 and [La/Lu]cn = 0.41–0.48)20,21 is the lowest in the YAMM meteorites, suggesting MIL 05035 represents the most primitive melt while partial melting links the clan members (Supplementary Figs. 5 and 6). Using exchange coefficient, \({{{{{{\boldsymbol{K}}}}}}}_{{{{{{\boldsymbol{D}}}}}}{{{{{\boldsymbol{,}}}}}}{{{{{\boldsymbol{Fe}}}}}}{{{{{\boldsymbol{-}}}}}}{{{{{\boldsymbol{Mg}}}}}}}^{{{{{{\boldsymbol{Pyx}}}}}}{{{{{\boldsymbol{-}}}}}}{{{{{\boldsymbol{melt}}}}}}}\) = 0.2822,23, the melt in equilibrium with the most magnesian pyroxene (Mg# 54 in A-881757 and MIL 05035, and Mg# 61 in Y-793169) would have Mg# 25 and 30, respectively. The bulk compositions of A-881757 and MIL 05035 are however more Mg-rich (Mg# 34–38 in A-881757, Mg# 37–40 in MIL 05035). The difference between the measured and calculated compositions of Mg-rich pyroxenes in these samples indicates partial pyroxene accumulation in the whole-rock, consistent with samples approaching a parental melt composition (Supplementary Text 3 and Supplementary Fig. 7).
Strontium-neodymium isotope systematics indicate a distinct depleted mantle source produced the YAMM meteorites (87Rb/86Sr = 0.019; 147Sm/144Nd = 0.24–0.31), which are the most depleted among mare basalts (Fig. 2b and Supplementary Fig. 8). Along with the lack of Eu anomalies, Sr-Nd isotope systematics indicate that the YAMM and other KREEP-free basalts (Luna 24 ferrobasalts, Kalahari 009) have sources formed prior to large-scale plagioclase separation. Sample analysis and experiments reveal that a stratified relatively Fe-rich upper mantle is viable from the low-pressure origin of Luna 24 ferrobasalts24. Collectively, these results demonstrate that the YAMM meteorites along with Kalahari 009 and Luna 24 ferrobasalts originated from a distinct depleted, Fe-rich and plagioclase-saturated lunar mantle that is free of urKREEP.
A critical aspect of the KREEP-free basalts is to determine the degree of melting at the YAMM basalts’ source region in the backdrop of LMO scenario3,5,25,26. Using trace-element modeling (Methods, Supplementary Text 3 and 5), the YAMM basalts are consistent with forming from ~3–6% partial melting of the LMO cumulates at ~75–80 percent solid (PCS) containing ~1% trapped interstitial residual liquid (TIRL) (Supplementary Fig. 9 and Supplementary Data 3). The other KREEP-free lunar basalts, e.g., Kalahari 009 and Luna 24 ferrobasalts underwent 7–9% and 3–6% partial melting, respectively, of their mantle sources (Supplementary Figs. 9 and 14). Similarly, the Apollo mare basalts also underwent ~1–9% partial melting of their respective mantle source5,25,27 (Supplementary Fig. 10).
Contextually, the younger (~2.9 Ga) LAP and NWA 032 basalts are also KREEP-free and, therefore, merit discussion. Despite being unrelated to early formed KREEP reservoirs3,4, LAP and NWA 032 basalts have elevated ITE (~40–50 × CI of LREE and ~30–45 × CI of HREE) abundances, prominent Eu anomaly and LREE-enriched ([La/Sm]cn = ~1.10–1.17) signatures (Fig. 3), quite similar to that of the Apollo basalts19. Because NWA 032 and the LAP basalts have low initial 87Sr/86Sr (0.699–0.700) and positive εNd (+3.0 to +9.7), even a limited (<0.5%) urKREEP contribution would significantly shift their Sr-Nd isotopic composition3,4 towards high 87Rb/86Sr (>0.19) and low 147Sm/144Nd (<0.173) ratios (Supplementary Fig. 8). It was postulated that the LAP basalts were either extensively fractionated28,29,30 or formed by low-degree of partial melting (0.7–1.5%) from an Fe-rich cumulate mantle4 without urKREEP signatures31. The elevated ITE abundances relative to their low Mg# and previously suggested Apollo 12 like parent composition28,29,30 indicate LAP and NWA 032 basalts to be fractionation products. However, the chemical modeling suggests that the REE composition of LAP and NWA 032 basalts can be reproduced by a small degree of partial melting4,31. While the petrogenesis of these rocks remains controversial, we calculated their estimated formation pressure-temperature (P-T) using whole-rock compositions, considering that these basalts represent melt composition based on the latest petrological experiments31 (Supplementary Text 6).
Calculation of formation P-T
We use pMELTS32,33 model calculations and traditional thermobarometric approaches34,35 to estimate the formation P-T of A-881757 (YAMM), KREEP-free samples, and Apollo basalt parental melts (Methods). The formation of A-881757 and YAMM basalts initiated at 0.3–0.8 GPa P and 1100–1190 °C T. By comparison, the calculated P-T of the oldest mare basalt Kalahari 009 is 0.7–1.0 GPa, and 1195–1235 °C (Fig. 4a and Supplementary Fig. 12). Collectively, formation of the KREEP-free mare basalts in the lunar mantle range between 0.3–1.0 GPa (~60–200 km) and 1100–1235 °C (Fig. 4a and Supplementary Data 4). The estimated P-T conditions are significantly lower when compared to that obtained for the melt compositions of the Apollo mare basalts (1310–1410 °C at 0.9–1.3 GPa; Supplementary Data 4, Supplementary Text 4 and 7). Our calculated P-T values for the Apollo samples are similar to experimentally derived results31,36 (Supplementary Text 7). The experimentally derived P-T conditions of the Apollo picritic glasses are even higher (1430–1560 °C at 1.3–2.5 GPa; refs. 31, 36 and references therein) than the lunar basalts. Among the returned lunar samples, only Luna 24 ferrobasalts show a similar P-T range (0.4–0.5 GPa and 1180 °C)24. The lower estimated temperatures can be attributed to the lower Mg# (48–32) than the Apollo mare basalts, although the bulk composition of the KREEP-free rocks suggest that they were in equilibrium with their lunar mantle sources. To understand this disparity in the formation conditions between the KREEP-free basalts and the Apollo mare basalts, we further calculate mantle potential temperature (Tp) to examine likely thermal conditions.
a The KREEP-free basalts (red field) show lower formation P-T (see Methods and Supplementary Data 4) than Apollo mare basalts and pyroclastic glasses (orange field). Mantle potential temperatures (Tp) in °C, are shown as dashed lines. The estimates of P-T for pyroclastic glasses are multiple saturation point data and are adopted from refs. 31, 36 and references therein. The P-T for the KREEP-free and Apollo mare basalts are obtained from pMELTS and thermobarometry (Methods, Supplementary Text 6 and 7). Solidus curve is drawn based on refs. 37, 48. b Surface heat flow is calculated assuming variable depth (0–65 km) of magma stalling. For a constant assumed depth, KREEP-free basalts show lower estimated heat flow (shown as dashed lines in mW/m2) than Apollo mare basalts (Methods and Supplementary Data 4). Lunar pressure-depth relationship is from ref. 48.
Mantle potential temperature and surface heat flux
Our result indicates that the KREEP-free basalts were sourced from a cooler lunar mantle than the mantle source of Apollo mare basalts. Estimates of average Tp, considering ~1–9% partial melting (Supplementary Text 4 and Supplementary Fig. 10), correcting for the average P-T using lunar mantle adiabatic gradient, and correcting for the effect of latent heat of fusion on T (Methods), ranges from 1110–1250 °C for the KREEP-free basalts (Supplementary Data 4). The highest Tp of 1210–1250 °C is yielded by the oldest (~4.36 Ga) Kalahari 009, followed by 1110–1200 °C by YAMM basalts (~3.9 Ga), and 1160–1170 °C by Luna 24 ferrobasalts. The youngest NWA 032 and LAP basalts yield 1150–1190 °C Tp. These values are, however, lower than that of our calculations (1295–1385 °C for Apollo basalts) and the results obtained for picrites (1350–1450 °C) from previous studies36,37. Even when the error (up to ±50 °C; Supplementary Data 4) is considered in the calculated Tp, there remains a significant difference in Tp (100–200 °C) between the generally older KREEP-free and younger PKT samples. Such differences can be explained in terms of the distinct evolution of the KREEP-free basalts in comparison to the later mare basalts, highlighting the regional differences between PKT and non-PKT regions.
Lower Tp and shallower depth of formation of the KREEP-free basalts in comparison to the Apollo basalts imply lower surface heat flow (56–63 mW/m2) possibly due to KREEP-free magmatism compared to that at the PKT region (64–67 mW/m2), assuming magma stalling at 40 km depth for both cases (Fig. 4b, Supplementary Data 4 and Supplementary Fig. 13). In all likelihood, the PKT mare basalts were stalled at greater depths beneath the surface31,36 while the YAMM basalts were emplaced at shallower depths, which influences surface heat flow. The high heat flow at the PKT region was plausibly controlled by mantle overturn induced KREEP accumulation at source, or by some other process. The low Tp obtained for the non-PKT samples even at 3.9 Ga can explain the likely causes of the lower mare basalt fill at the South Pole Aitken basin and Feldspathic Highland Terrain than the PKT region, where Tp was elevated even up to 3.3 Ga.
Calculated high Tp and elevated surface heat flow values obtained from Apollo mare basalts indicate they reflect a localized thermal anomaly possibly near the PKT region. Colder Tp and lower heat flows of KREEP-free regions, having low-Th (YAMM, Kalahari 009 and Luna 24 ferrobasalts), obtained from samples of varying ages and localities may likely provide higher fidelity information on the global thermal regime. Our results also support the long-standing idea that the lunar mantle was thermally heterogeneous at various scales36,38,39. The lower degree of melting and relatively Fe-rich source of KREEP-free rocks in comparison to the PKT mare basalts may indicate that a shallower Fe-rich mantle is more ubiquitous for the KREEP-free basalts than the deeper mantle source of PKT-region basalts. These results are also supported by recent remote sensing observations of pyroxene-rich mantle40,41 at shallow depth (~100 km)40. Indeed, the high proportion of pyroxene in the KREEP-free basalt mantle source(s) suggests mantle with pyroxene > olivine (Supplementary Fig. 11, Supplementary Text 5 and 8).
A possible melting mechanism for KREEP-free basalts
The melting regimes in most terrestrial bodies, including Earth, Mars, Venus, and Mercury suggest the dominance of partial melting either by decompression of adiabatically rising melts, from thermally anomalous, hot and buoyant portions of the mantle, or by lowering the solidus with addition of H2O-dominated volatiles (flux) into the mantle. In contrast, it has been widely accepted that lunar mantle melting was aided by heating from radioactive elements in KREEP materials to generate mare basalts. Our calculation shows that the primary radioactive elements (K, Th, and U) can produce heat in the order of ~109 J/g/y for the terrestrial planets, corresponding to 1 °C increase of temperature over ~107 years for 1 g of peridotite. Considering an end-member case of extreme (100%) enrichment of the urKREEP layer in the Moon’s mantle, 1 °C temperature rise in 1 g peridotite can take place over a period of ~105 years. In the previously studied lunar returned samples and meteorites, the maximum KREEP-enrichment observed is <40% in a few lunar samples and meteorites5,42 (e.g., 14310, 15382, 15386, SaU 169). If we assume this maximum case as the enrichment of urKREEP layer in the Moon’s mantle, then the increase of temperature by 1 °C could have taken place between 107 and 105 years.
To melt the Moon’s mantle, however, the supplied heat by radioactive source must also cross the latent heat of fusion of minerals and rocks, which is few hundred times more than the specific heat required to bring the minerals and rocks up to their melting temperatures. Further, dissipation of heat or thermal decay would hinder the melting process. This makes the production of sufficient melt even more difficult. Furthermore, being incompatible, the heat-producing elements would largely concentrate in the melt and escape, leaving the residual mantle too depleted to melt further and produce the volcanism observed at the lunar surface43.
An estimated total mare basaltic fill volume on the Moon is ~8.6 × 106 km3 (ref. 44). Here, we calculate the energy stored in the 10 km KREEP-rich layer and evaluate whether the energy budget was enough to generate the mare basalts on the lunar surface as a first order approximation. Assuming the density as 3270–3460 kg/m3 and the latent heat of crystallization as 4 × 105 J/kg of basalts, our first order estimate indicates that the total energy required to produce ~2.9 × 1010 kg mare basalts is ~1.2 × 1025 J (or 3.3 × 109 TWh). In contrast, the total energy obtained from the radiogenic heat, for an assumed 10 km thick global urKREEP layer with a density close to ilmenite bearing cumulates (~3719 kg/m3), is only 5.49 × 107 TWh, which is not a sufficient (<2%) total energy budget. The radioactive materials are concentrated within the PKT region, while the calculated volume of mare volcanism is probably more substantial as some of the older volcanic signatures are buried as cryptomare. Radioactive heating might have played an important role in generating the PKT KREEP basalts but the generally limited KREEP component seen in most Apollo mare basalts suggest that the energy generated by radioactive materials alone cannot be a major driving force for lunar magmatism. This contrasts with the earlier studies39, which postulated radioactive and internal heating as the driving mechanisms for melting in the PKT terrain assuming a completely molten (KREEP) layer between the lunar crust and mantle, globally. This model of mare basalt generation is strictly valid for KREEP-rich samples (residing in the PKT region) with unusually high amounts of KREEP addition, which have been questioned on the basis of the variable depth of mare basalt generation and the viability of heating mechanisms, e.g., adiabatic decompression versus conductive heating, to form a small amount of melt generated at variable depths in the mantle source regions36,45. Alternatively, impact-induced decompression might have also engendered melting of the lunar mantle, given the coincidence of YAMM basalts’ crystallization ages with the LHB.
A perhaps more likely scenario is that the latent heat of lunar formation together with the interior heat sources were sufficient to engender low degree partial melting of pre-existing mafic LMO cumulates, at least until the youngest Chang’E 5 basalt volcanism (~2.0 Ga)46. Our result shows that the formation mechanism of KREEP-free basalt volcanism cannot solely due to heating by radioactive elements. Nevertheless, the oldest KREEP-free basalts, those originated from the shallowest depths, most probably underwent low-pressure decompression type melting pyroxene-rich mantle in contrast to the traditional idea that they were the byproducts of lunar mantle overturn.
Methods
Scanning electron microscope analysis
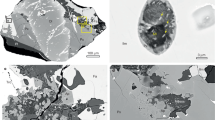
The studied samples were provided by the National Institute for Polar Research, Japan (NIPR). Analysis was performed on two polished thick sections of A-881757 (88a, 88b). Detailed imaging of the sections was carried out on a JEOL JSM-7100F field emission scanning electron microscope (FE-SEM) equipped with an energy dispersive spectrometer (Oxford AZtec Energy) at the NIPR. The sections were coated with carbon. Acceleration voltage was 15 kV. Back-scattered electron (BSE) and X-ray mapping were taken (Supplementary Figs. 1 and 2). The X-ray images obtained for different elements were merged together using AZtec energy software, for the combined elemental X-ray image.
Electron probe microanalysis
Major and minor-element compositions of minerals were determined using JEOL JXA-8200 electron probe micro-analyzers (EPMA) at the NIPR. Olivine, chromite, ilmenite, troilite, and Fe-metals were analyzed with a beam current of 30 nA by a focused beam, plagioclase (maskelynite) with a current of 10 nA by a focused beam, and phosphates with a beam current of 5 nA by a broad beam (~5 µm in diameter), all at 15 kV. Data were reduced using a ZAF correction procedure. The typical counting time for all elements in minerals was 30 s except for Na. The Si, Mg, Fe Mn, Ca, Na, P, and Al were analyzed using PET, PETH, LIF, LIFH, and LDE spectrometer crystals. The standards used for elements are natural and synthetic materials. The results are given in Supplementary Data 1.
Inductively coupled plasma mass spectrometry
Given the coarseness of constituent primary mineral phases in A-881757 and the limited masses typically available for study, a single reported analysis may not be truly representative of the average bulk composition of the sample. The measurement of a representative bulk chemical composition for A-881757 required a substantial amount of the sample (0.71 g) to be homogenized and analyzed for a texturally and mineralogically representative sample with no sampling bias.
Analytical procedures were undertaken at the Scripps Isotope Geochemistry Laboratory (SIGL) and Physical Research Laboratory (PRL). For major and trace element abundances, A ~50 mg aliquot of homogenized sample powder was digested in Teflon-distilled concentrated HF (4 mL) and HNO3 (1 mL) for >72 h on a hotplate at 150 °C, along with total procedural blanks and terrestrial basalt and andesite standards (BHVO-2, AGV-2). Samples were sequentially dried and taken up in concentrated HNO3 to destroy fluorides, followed by doping with indium to monitor instrumental drift during analysis, and then diluted to a factor of 50,000 for major-element determination and 5000 for trace-element determination. Major-element abundances were obtained using a ThermoScientific iCAP Qc quadropole inductively coupled plasma mass spectrometer (ICP-MS) in low resolution mode. For major-elements, Si was derived by difference, with reproducibility of other elements measured on the BHVO-2 reference material being better than 3%, except Na2O (7.1%). The results are provided in Supplementary Data 2.
Mantle melting model
We applied both batch and fractional melting to calculate the REE concentrations in the parental melts to ascertain the petrological history of the samples, assuming that each mineral phase melts in proportion to its modal abundance in the source. In most cases, the bulk rock composition was taken as a parental melt composition for the reasons discussed in Supplementary Text 3. Assuming the parental melt compositions represent compositions of the primary melt and no major process had occurred to significantly change the REE composition between source partial melting and parental melts, we calculated the degree of partial melting that likely occurred to generate each rock. The chemical modeling, similar to Snyder et al.25 and Hallis et al.5, was applied assuming an initial LMO source REE composition of 3× chondrite REE composition, using the rationale of Hughes et al.47. With the advancement of LMO crystallization, equilibrium crystallization gave way to fractional crystallization at about 50–70 PCS25,26,48,49,50,51,52,53. Plagioclase appeared on the liquidus just after ~75 PCS in the modeling, similar to experimental and thermodynamic modeling results52,53. Given YAMM, Kalahari 009 and Luna 24 ferrobasalts were low-Ti varieties with low REE abundance and had slight negative to positive Eu anomaly, the best fit was obtained by assuming a modal mineralogy close to 75–80 PCS LMO crystallization with addition of 1–2 % TIRL (Supplementary Fig. 9 and Supplementary Data 3). While for NWA 032 and LAP basalts, our estimated model mineralogy was obtained at 86 PCS with addition of 1–2 % TIRL (Supplementary Figs. 9 and 14, Supplementary Data 3). All deduced source modal mineralogy shows a dominance of clinopyroxene (pigeonite) over early formed olivine and orthopyroxene with small amount of plagioclase suggesting that KREEP-free basalts were sourced from a pyroxene-rich mantle. The individual source mineralogy of the studied samples and their feasibility is discussed in Supplementary Text 3 and 5. The REE partition coefficients for olivine54, orthopyroxene55, augite55, pigeonite56 and plagioclase57, are shown in Supplementary Table 1.
Batch and fractional melting are two end member process and in nature partial melting can be a combination of the two. Batch melting is calculated using the following equation:
while fractional melting is calculated using equation:
where CL is the weight concentration of a trace element in the melt, C0 is the weight concentration of a trace element in the original cumulate source, F is the weight fraction of melt produced and D0 is the bulk distribution coefficient of the original solid material. The bulk distribution coefficient is calculated by multiplying each mineral partition coefficient with the fraction of that mineral in the source.
Estimation of pressure (P) and temperature (T)
We applied two methods to estimate the pressure and temperature condition of the studied rocks. First, we used pMELTS model calculations. The pMELTS mode32 of program alphaMELTS, which is based on equilibrium phase diagram calculations and uses an internally consistent thermodynamic data set33,58, was used to calculate formation T and P of A-881757, other YAMM and non-KREEP basalts. Since A-881757 and other YAMM meteorites are not extensive fractionation products and rather represent parental melt composition from their mantle source, an equilibrium batch crystallization is more suitable than the fractionation process. Therefore, the equilibrium phase diagram calculation method may infer actual P–T conditions. Previous studies have shown that these phase diagram calculations are capable of providing models and comparing that with petrographic observations in the terrestrial32,58, martian59,60,61 and lunar30,62,63,64 mantle and melt. The phase diagram calculations further allow the modes and composition of the mineral and melt phases to be tracked through P–T space, which along with the aid of petrographic observations can yield the P–T conditions of crystallization. A range of pressure (12.0–0.001 kbar), temperature (1500–1000 °C), and fO2 (IW −1.0) conditions were set for the crystallization calculations in this method.
Second, we used thermobarometry techniques. With no signs of extensive fractional crystallization, the composition of the most Mg-rich minerals (high Mg#) were considered to be in equilibrium with the parental melt and were chosen for the thermobarometric calculations. The primary and the first crystallization phase in A-881757 and other YAMM meteorites is clinopyroxene. We used clinopyroxene-liquid34, clinopyroxene-only35,37 thermobarometry and olivine-liquid65 thermometry to estimate the formation pressure and temperature of the YAMM basalts and other studied rocks. The list of thermobarometers along with the standard error of estimate (SEE) associated with each are compiled in Putrika34. In the case of a sample with olivine on their liquidus, we also performed olivine-liquid thermometry using the Beattie’s65 thermometer, which uses a liquid (whole rock) composition. This model is preferred over others because of its insensitivity to the fO2 and the lowest SEE of ±44 °C. For calculations, we used the range of pressures estimated from phase diagram mode pMELTS, as well as clinopyroxene thermobarometers.
For YAMM meteorites which lack olivine, we applied clinopyroxene-liquid and clinopyroxene-only thermobarometry. We utilized equation 30 (for P) and 34 (for T) from Putirka34 for clinopyroxene-liquid thermobarometry. The SEE for the pressure and temperature are ±3.6 kbar and ±45 °C, respectively. The obtained results for the clinopyroxene-liquid thermobarometry are affected by volatile (Na) loss due to the open furnace nature of earlier experiments leading to systematically high P–T estimates66. Clinopyroxene-only thermobarometers, however, obviate this problem. We used equations 32a (for P) and 32d (for T) from Putrika34, and Eq. 1 (for P) and 2 (for T) from ref. 35 for clinopyroxene-only thermobarometry. The given SEE for the equations 32a and 32d is ±3.1 kbar and ±58 °C, respectively. Wang et al.35 provided a new clinopyroxene-only thermobarometer, which is applicable to most basaltic-andesitic compositions and is insensitive to the fugacity conditions (Fig. 8 of Wang et al.35) with ±36.6 °C and ±1.66 kbar SEE. Further we compare the range of pressure and temperature obtained from both the methods in Supplementary Text 4 and Supplementary Data 4.
Estimation of mantle potential temperature
The estimated pressure and temperature of formation of the YAMM basalts allow us to place further constraints on the mantle potential temperature for the Moon and its plausible evolution following the approach of Filberto and Dasgupta67,68. The calculation was performed first by evaluating the percentage of melt fraction needed to produce the primary magma composition from trace element modeling (Supplementary Text 3). Further, to calculate the mantle potential temperature, Tp, of the lunar mantle, we also corrected the average pressure and temperature of the bulk Moon composition to zero pressure using a lunar mantle adiabatic gradient of 0.17 K/km36. We corrected the effect of latent heat of fusion on the temperature using the expression:
where F is the melt fraction; Hfus (6 × 105 J K−1kg−1; ref. 69) is the heat of fusion; and Cp (1000 J K−1kg−1; ref. 69) is the heat capacity at a constant pressure. Finally, we use the formula:
where \({T}_{{avg\_eq}}\) is the average equilibrium (formation) temperature; \(\triangle {T}_{{fus}}\) is the latent heat of fusion; and \(\triangle {T}_{{{{{\mathrm{lg}}}}}}\) is the lunar temperature gradient correction for adiabatic cooling.
Estimation of surface heat flow
The thermal boundary layer structure of a terrestrial body mainly comprises of two parts; in the upper part (crust and upper mantle), heat is transported by conduction while convection dominates in the lower part (lower mantle), also called the convective boundary layer. In a steady state scenario and in the absence of heat-producing elements, heat flow is supposed to be constant in the conductive crust, suggesting a relatively constant temperature gradient for constant thermal conductivity. The calculated steady state heat flux at the base of the lithosphere may directly represent the surface heat flux (assuming no contribution of heat sources in crust and lithospheric mantle). Therefore, in the absence of heat-producing elements, the heat flow is calculated using the relationship between the depth and the mantle potential temperature70. We use here the steady state equation:
where Q is the heat flow at the surface; \({k}_{{crust}}\) is the thermal conductivity of lunar crust; Tp is the mantle potential temperature; Ts is the surface temperature; and d is the depth of the conductive (crust) - convective (mantle) boundary layer that is the thickness of crust. Considering the persisting uncertainty in the lunar thermal boundary layer structure and its rheological properties, we took a simplistic case where we calculated the heat flow assuming a constant thermal conductivity of crust, \({k}_{{crust}}\) ~2.0 W m−1 K−1 (ref. 71) and variable thickness of conductive boundary layer (0–60 km), consistent with the GRAIL observations. The variable crustal thickness allows us to compare the thermal condition during the placement of the non-KREEP basalts and Apollo mare basalts, independent to their age and location (Fig. 4b and Supplementary Fig. 13). Heat flow values are reported for varying depth in Supplementary Data 4.
Data availability
The data generated in this study are provided in the Supplementary files.
References
Neal, C. R. & Taylor, L. A. Petrogenesis of mare basalts: A record of lunar volcanism. Geochim. Cosmochim. Acta 56, 2177–2211 (1992).
Warren, P. H. & Wasson, J. T. The origin of KREEP. Rev. Geophys. 17, 73–88 (1979).
Borg, L. E. et al. Mechanisms for incompatible-element enrichment on the Moon deduced from the lunar basaltic meteorite Northwest Africa 032. Geochim. Cosmochim. Acta 73, 3963–3980 (2009).
Elardo, S. M. et al. The origin of young mare basalts inferred from lunar meteorites Northwest Africa 4734, 032, and LaPaz Icefield 02205. Meteorit. Planet. Sci. 49, 261–291 (2014).
Hallis, L. J., Anand, M. & Strekopytov, S. Trace-element modelling of mare basalt parental melts: Implications for a heterogeneous lunar mantle. Geochim. Cosmochim. Acta 134, 289–316 (2014).
Tian, H. C. et al. Non-KREEP origin for Chang’e-5 basalts in the Procellarum KREEP Terrane. Nature 600, 59–63 (2021).
Misawa, K., Tatsumoto, M., Dalrymple, G. B. & Yanai, K. An extremely low UPb source in the Moon: U- Th-Pb, Sm-Nd, Rb-Sr, and 40Ar-39Ar isotopic systematics and age of lunar meteorite Asuka 881757. Geochim. Cosmochim. Acta 57, 4687–4702 (1993).
Torigoye-Kita, N., Misawa, K., Dalrymple, G. B. & Tatsumoto, M. Further evidence for a low U/Pb source in the moon: U-Th-Pb, Sm-Nd, and Ar-Ar isotopic systematics of lunar meteorite Yamato-793169. Geochim. Cosmochim. Acta 59, 2621–2632 (1995).
Nyquist, L. E., Shih, C. Y. & Reese, Y. D. Sm-Nd and Rb-Sr Ages for MIL 05035: Implications for Surface and Mantle Sources. in 38th Annual Lunar and Planetary Science Conference 1702 (2007).
Arai, T. et al. Antarctic lunar meteorites Yamato-793169, Asuka-881757, MIL 05035, and MET 01210 (YAMM): Launch pairing and possible cryptomare origin. Geochim. Cosmochim. Acta 74, 2231–2248 (2010).
Bottke, W. F. & Norman, M. D. The late heavy bombardment. Annu. Rev. Earth Planet. Sci. 45, 619–647 (2017).
Jolliff, B. L., Gillis, J. J., Haskin, L. A., Korotev, R. L. & Wieczorek, M. A. Major lunar crustal terranes: Surface expressions and crust-mantle origins. J. Geophys. Res. Planets 105, 4197–4216 (2000).
Rhodes, J. M., Blanchard, D. P., Dungan, M. A., Brannon, J. C. & Rodgers, K. V. Chemistry of Apollo 12 mare basalts: Magma types and fractionation processes. Proc. 8th Lunar Sci. Conf. 2, 1305–1338 (1977).
Vaniman, D. T. & Papike, J. J. Ferrobasalts from Mare Crisium: Luna 24. Geophys. Res. Lett. 4, 497–500 (1977).
Yanai, K. Gabbroic meteorite Asuka-31-Preliminary examination of a new type of lunar meteorite in the Japanese collection of Antarctic meteorites. Proc. Lunar Planet. Sci. 21, 317–324 (1991).
Warren, P. H. & Kallemeyn, G. W. Geochemical Investigation of two lunar meteorites: Y-793197 and Asuka-881757. Antarct. Meteor. Res. 6, 35 (1993).
Ma, M. S. et al. Chemistry and petrology of Luna 24 lithic fragments and <250 μm soils: constraints on the origin of VLT mare basalts. in Mare Crisium: The View From Luna 24 (eds. Merrill, R. B. & Papike, J. J.) p. 569–592 (1978).
Sokol, A. K. et al. Geochemistry, petrology and ages of the lunar meteorites Kalahari 008 and 009: New constraints on early lunar evolution. Geochim. Cosmochim. Acta 72, 4845–4873 (2008).
Warren, P. H. & Taylor, G. J. The Moon. Treatise on Geochemistry: Second Edition vol. 2, pp. 213-250 (Elsevier, 2013).
Liu, Y., Floss, C., Day, J. M. D., Hill, E. & Taylor, L. A. Petrogenesis of lunar mare basalt meteorite Miller Range 05035. Meteorit. Planet. Sci. 44, 261–284 (2009).
Joy, K. H. et al. The petrology and geochemistry of Miller Range 05035: A new lunar gabbroic meteorite. Geochim. Cosmochim. Acta 72, 3822–3844 (2008).
Grove, T. L. & Bence, A. E. Experimental study of pyroxene-liquid interaction in quartz-normative basalt 15597. Lunar Planet. Sci. Conf. Proc. 2, 1549–1579 (1977).
Longhi, J. Experimental petrology and petrogenesis of mare volcanics. Geochim. Cosmochim. Acta 56, 2235–2251 (1992).
Grove, T. L. & Vaniman, D. T. Experimental petrology of very low Ti (VLT) basalts. In Mare Crisium: The view from Luna 24 (eds. Merrill, R. B. & Papike, J. J.) 445–471 (Pergamon Press, 1978).
Snyder, G. A., Taylor, L. A. & Neal, C. R. A chemical model for generating the sources of mare basalts: Combined equilibrium and fractional crystallization of the lunar magmasphere. Geochim. Cosmochim. Acta 56, 3809–3823 (1992).
Elardo, S. M., Draper, D. S. & Shearer, C. K. Lunar Magma Ocean crystallization revisited: Bulk composition, early cumulate mineralogy, and the source regions of the highlands Mg-suite. Geochim. Cosmochim. Acta 75, 3024–3045 (2011).
Snyder, G. A., Neal, C. R., Taylor, L. A. & Halliday, A. N. Anatexis of lunar cumulate mantle in time and space: Clues from trace-element, strontium, and neodymium isotopic chemistry of parental Apollo 12 basalts. Geochim. Cosmochim. Acta 61, 2731–2747 (1997).
Zeigler, R. A., Korotev, R. L., Jolliff, B. L. & Haskin, L. A. Petrography and geochemistry of the LaPaz Icefield basaltic lunar meteorite and source crater pairing with Northwest Africa 032. Meteorit. Planet. Sci. 40, 1073–1101 (2005).
Righter, K., Collins, S. J. & Brandon, A. D. Mineralogy and petrology of the LaPaz Icefield lunar mare basaltic meteorites. Meteorit. Planet. Sci. 40, 1703–1722 (2005).
Day, J. M. D. et al. Comparative petrology, geochemistry, and petrogenesis of evolved, low-Ti lunar mare basalt meteorites from the LaPaz Icefield, Antarctica. Geochim. Cosmochim. Acta 70, 1581–1600 (2006).
Elardo, S. M., Shearer, C. K., Vander Kaaden, K. E., McCubbin, F. M. & Bell, A. S. Petrogenesis of primitive and evolved basalts in a cooling Moon: Experimental constraints from the youngest known lunar magmas. Earth Planet. Sci. Lett. 422, 126–137 (2015).
Smith, P. M. & Asimow, P. D. Adiabat_1ph: A new public front-end to the MELTS, pMELTS, and pHMELTS models. Geochem. Geophys. Geosyst. 6, Q02004 (2005).
Ghiorso, M. S., Hirschmann, M. M., Reiners, P. W. & Kress, V. C. The pMELTS: A revision of MELTS for improved calculation of phase relations and major element partitioning related to partial melting of the mantle to 3 GPa. Geochem. Geophys. Geosyst. 3, 1030 (2002).
Putirka, K. D. Thermometers and Barometers for Volcanic Systems. Rev. Mineral. Geochem. 69, 61–120 (2008).
Wang, X. et al. A new clinopyroxene thermobarometer for mafic to intermediate magmatic systems. Eur. J. Mineral. 33, 621–637 (2021).
Elkins-Tanton, L. T., Hager, B. H. & Grove, T. L. Magmatic effects of the lunar late heavy bombardment. Earth Planet. Sci. Lett. 222, 17–27 (2004).
Putirka, K. Rates and styles of planetary cooling on Earth, Moon, Mars, and Vesta, using new models for oxygen fugacity, ferric-ferrous ratios, olivine-liquid Fe-Mg exchange, and mantle potential temperature. Am. Mineral. 101, 819–840 (2016).
Solomon, S. C. & Head, J. W. Lunar mascon basin: lava filling, tectonics, and evolution of the lithosphere. Rev. Geophys. 18, 107–141 (1980).
Wieczorek, M. A. & Phillips, R. J. The “Procellarum KREEP Terrane”: Implications for mare volcanism and lunar evolution. J. Geophys. Res. Planets 105, 20417–20430 (2000).
Melosh, H. J. et al. South Pole–Aitken basin ejecta reveal the Moon’s upper mantle. Geology 45, 1063–1066 (2017).
Moriarty, D. P., Dygert, N., Valencia, S. N., Watkins, R. N. & Petro, N. E. The search for lunar mantle rocks exposed on the surface of the Moon. Nat. Commun. 12, 1–11 (2021).
Lin, Y. et al. Very high-K KREEP-rich clasts in the impact melt breccia of the lunar meteorite SaU 169: New constraints on the last residue of the Lunar Magma Ocean. Geochim. Cosmochim. Acta 85, 19–40 (2012).
Turcotte, D. L. & Ahern, J. L. Magma production and migration within the moon. Lunar Planet. Sci. Conf. Proc. 1, 307–318 (1978).
Needham, D. H. & Kring, D. A. Lunar volcanism produced a transient atmosphere around the ancient Moon. Earth Planet. Sci. Lett. 478, 175–178 (2017).
Elkins-Tanton, L. T., Van Orman, J. A., Hager, B. H. & Grove, T. L. Re-examination of the lunar magma ocean cumulate overturn hypothesis: melting or mixing is required. Earth Planet. Sci. Lett. 196, 239–249 (2002).
Qian, Y. et al. Young lunar mare basalts in the Chang’e-5 sample return region, northern Oceanus Procellarum. Earth Planet. Sci. Lett. 555, 116702 (2021).
Hughes, S. S., Delano, J. W. & Schmitt, R. A. Petrogenetic modeling of 74220 high-Ti orange volcanic glasses and the Apollo 11 and 17 high-Ti mare basalts. Lunar Planet. Sci. Conf. Proc. 19, 175–188 (1989).
Elkins-Tanton, L. T., Burgess, S. & Yin, Q.-Z. The lunar magma ocean: reconciling the solidification process with lunar petrology and geochronology. Earth Planet. Sci. Lett. 304, 326–336 (2011).
Longhi, J. A new view of lunar ferroan anorthosites: postmagma ocean petrogenesis. J. Geophys. Res. Planets 108, 5083 (2003).
Shearer, C. K. et al. Thermal and magmatic evolution of the Moon. Rev. Mineral. Geochem. 60, 365–518 (2006).
Charlier, B., Grove, T. L., Namur, O. & Holtz, F. Crystallization of the lunar magma ocean and the primordial mantle-crust differentiation of the Moon. Geochim. Cosmochim. Acta 234, 50–69 (2018).
Rapp, J. F. & Draper, D. S. Fractional crystallization of the lunar magma ocean: updating the dominant paradigm. Meteorit. Planet. Sci. 53, 1432–1455 (2018).
Johnson, T. E., Morrissey, L. J., Nemchin, A. A., Gardiner, N. J. & Snape, J. F. The phases of the Moon: modelling crystallisation of the lunar magma ocean through equilibrium thermodynamics. Earth Planet. Sci. Lett. 556, 116721 (2021).
McKay, G. A. Crystal/liquid partitioning of REE in basaltic systems: extreme fractionation of REE in olivine. Geochim. Cosmochim. Acta 50, 69–79 (1986).
Yao, L., Sun, C. & Liang, Y. A parameterized model for REE distribution between low-Ca pyroxene and basaltic melts with applications to REE partitioning in low-Ca pyroxene along a mantle adiabat and during pyroxenite-derived melt and peridotite interaction. Contrib. Mineral. Petrol. 164, 261–280 (2012).
McKay, G., Le, L. & Wagstaff, J. Constraints on the origin of the mare basalt europium anomaly: REE partition coefficients for pigeonite. Lunar Planet. Sci. Conf. 22, 883 (1991).
Phinney, W. C. & Morrison, D. A. Partition coefficients for calcic plagioclase: Implications for Archean anorthosites. Geochim. Cosmochim. Acta 54, 1639–1654 (1990).
Asimow, P. D. & Longhi, J. The significance of multiple saturation points in the context of polybaric near-fractional melting. J. Petrol. 45, 2349–2367 (2004).
Liu, Y., Balta, J. B., Goodrich, C. A., McSween, H. Y. & Taylor, L. A. New constraints on the formation of shergottite Elephant Moraine 79001 lithology A. Geochim. Cosmochim. Acta 108, 1–20 (2013).
Basu Sarbadhikari, A., Babu, E. V. S. S. K., Vijaya Kumar, T. & Chennaoui Aoudjehane, H. Martian meteorite Tissint records unique petrogenesis among the depleted shergottites. Meteorit. Planet. Sci. 51, 1588–1610 (2016).
Basu Sarbadhikari, A., Babu, E. V. S. S. K. & Vijaya Kumar, T. Chemical layering in the upper mantle of Mars: Evidence from olivine-hosted melt inclusions in Tissint. Meteorit. Planet. Sci. 52, 251–267 (2017).
Fagan, T. J., Kashima, D., Wakabayashi, Y. & Suginohara, A. Case study of magmatic differentiation trends on the Moon based on lunar meteorite Northwest Africa 773 and comparison with Apollo 15 quartz monzodiorite. Geochim. Cosmochim. Acta 133, 97–127 (2014).
Arai, T. & Maruyama, S. Formation of anorthosite on the Moon through magma ocean fractional crystallization. Geosci. Front. 8, 299–308 (2017).
Elardo, S. M. & Astudillo Manoslava, D. F. Ancient igneous differentiation trends in the Moon’s crust can be produced by secondary magmatism from a common source. In 52nd Lunar and Planetary Science Conference, LPI Contribution No. 2548 (2021).
Beattie, P. Olivine-melt and orthopyroxene-melt equilibria. Contrib. Mineral. Petrol. 115, 103–111 (1993).
Tormey, D. R., Grove, T. L. & Bryan, W. B. Experimental petrology of normal MORB near the Kane Fracture Zone: 22°−25°N, mid-Atlantic ridge. Contrib. Mineral. Petrol. 96, 121–139 (1987).
Filiberto, J. & Dasgupta, R. Fe2+-Mg partitioning between olivine and basaltic melts: applications to genesis of olivine-phyric shergottites and conditions of melting in the Martian interior. Earth Planet. Sci. Lett. 304, 527–537 (2011).
Filiberto, J. & Dasgupta, R. Constraints on the depth and thermal vigor of melting in the Martian mantle. J. Geophys. Res. Planets 175, 238 (2015).
Laneuville, M., Wieczorek, M. A., Breuer, D. & Tosi, N. Asymmetric thermal evolution of the Moon. J. Geophys. Res. Planets 118, 1435–1452 (2013).
Jaupart, C. & Mareschal, J. C. Heat Flow and Thermal Structure of the Lithosphere. In Treatise on Geophysics (ed. Schubert, G.) 217–253 (Elsevier, 2015).
Maurice, M., Tosi, N., Schwinger, S., Breuer, D. & Kleine, T. A long-lived magma ocean on a young Moon. Sci. Adv. 6, eaba8949 (2020).
Cone, K. A. ApolloBasalt DB_V2, Version 1.0. Interdisciplinary Earth Data Alliance (IEDA). https://doi.org/10.26022/IEDA/111982 (2021)
Nyquist, L. E. Lunar Rb-Sr chronology. Phys. Chem. Earth 10, 103–142 (1977).
Shih, C. Y., Nyquist, L. E., Reese, Y. D. & Bischoff, A. Sm-Nd and Rb-Sr isotopic studies of meteorite kalahari 009: an Old VLT mare basalt. In 39th Annual Lunar and Planetary Science Conference 2165 (2008).
Day, J. M. D., Floss, C., Taylor, L. A., Anand, M. & Patchen, A. D. Evolved mare basalt magmatism, high Mg/Fe feldspathic crust, chondritic impactors, and the petrogenesis of Antarctic lunar breccia meteorites Meteorite Hills 01210 and Pecora Escarpment 02007. Geochim. Cosmochim. Acta 70, 5957–5989 (2006).
Acknowledgements
Y.S. and A.B.S. acknowledge the support by the Indian Space Research Organization, Department of Space, Government of India. This work is a part of the PhD work of Y.S. Director PRL, Head of Planetary Science Division, PRL, and Director IIT Gandhinagar are gratefully acknowledged for constant encouragement during the work. J.M.D.D. acknowledges the NASA Solar System Workings program for supporting his participation in this work (80NSSC22K0098). A.Y. acknowledges the support from JSPS KAKENHI (JP19H01959) and NIPR Project Research (KP307). A.T. acknowledges the support from JSPS KAKENHI (JP19J00954).
Author information
Authors and Affiliations
Contributions
Y.S. and A.B.S. conceived the research and developed the central ideas. A.B.S. and J.M.D.D. helped in refining the ideas. Y.S. and A.B.S. performed melting-crystallization model calculations, thermobarometric calculations, mantle potential temperature, and heat flow calculations. J.M.D.D., Y.S., and A.B.S. performed bulk analyses. A.Y. and A.T. performed in-situ analyses. Y.S. and A.B.S., analyzed the results, interpreted the data and wrote the manuscript with inputs from J.M.D.D., A.Y. and A.T.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Ananya Mallik and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Srivastava, Y., Basu Sarbadhikari, A., Day, J.M.D. et al. A changing thermal regime revealed from shallow to deep basalt source melting in the Moon. Nat Commun 13, 7594 (2022). https://doi.org/10.1038/s41467-022-35260-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-35260-y
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.