Abstract
Light harvesting, separation of charge carriers, and surface reactions are three fundamental steps that are essential for an efficient photocatalyst. Here we show that these steps in the TiO2 can be boosted simultaneously by disorder engineering. A solid-state reduction reaction between sodium and TiO2 forms a core-shell c-TiO2@a-TiO2-x(OH)y heterostructure, comprised of HO-Ti-[O]-Ti surface frustrated Lewis pairs (SFLPs) embedded in an amorphous shell surrounding a crystalline core, which enables a new genre of chemical reactivity. Specifically, these SFLPs heterolytically dissociate dihydrogen at room temperature to form charge-balancing protonated hydroxyl groups and hydrides at unsaturated titanium surface sites, which display high reactivity towards CO2 reduction. This crystalline-amorphous heterostructure also boosts light absorption, charge carrier separation and transfer to SFLPs, while prolonged carrier lifetimes and photothermal heat generation further enhance reactivity. The collective results of this study motivate a general approach for catalytically generating sustainable chemicals and fuels through engineered disorder in heterogeneous CO2 photocatalysts.
Similar content being viewed by others
Introduction
Amorphous solids may behave as metals1,2, semiconductors3,4, insulators5,6, or superconductors7,8 and can exhibit electrical, optical, thermal, and mechanical properties distinct from those of their crystalline analogues. Disorder, for example, can introduce both deep and shallow defect states and extended tail states into the band structure of solids, leading to profound changes in the optical and electrical properties of solid-state devices, including those of solar cells9,10. The broadly tunable band structure of amorphous metal oxides, together with other merits such as transparency and good stability, has even led them to supersede their crystalline counterparts as promising electron injection layer materials for organic light-emitting diodes11,12. In the context of electron mobility, extensive disorder can also impede electron and phonon transport, lowering electrical and thermal conductivity relative to the corresponding ordered phase, thereby making them promising materials for use in thermoelectric power generation and solid-state refrigeration devices13,14,15. These examples demonstrate how engineering the physical properties of solids using disorder enables advances in materials science and technology16,17. Little is known, however, about the influence of disorder on surface chemistry and catalysis18,19, which is the focus of the research described herein.
As a key example, disordered (black) titania is renowned for its enhanced photocatalytic properties relative to its crystalline (white) counterpart20,21,22,23. Despite great efforts to understand the origin of its reactivity (focusing, for example, on its electronic bandgap24,25, photon absorption26,27, and charge-carrier separation kinetics28,29, pivotal aspects of its surface chemistry remain essentially unknown to this day, due largely to the challenges of defining the surface structure and understanding the physicochemical properties of the amorphous state.
In this article, by means of in situ diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS), solid-state magic angle spinning proton nuclear magnetic resonance (1H-MAS-NMR), electron paramagnetic resonance (EPR), and density functional theory (DFT) modeling of the amorphous state, we present a molecular-level description of surface frustrated Lewis pairs (SFLPs), active for the photocatalytic reduction of CO2 to CO, in a titania heterostructure material comprised of a crystalline core surrounded by an amorphous shell denoted c-TiO2@a-TiO2-x(OH)y.
At the crux of this new kind of SFLP30, embedded in a disordered a-TiO2-x(OH)y surface, is the quasi-dative bonding that exists between the Lewis base surface hydroxyl group (OH) and the Lewis acid mixed valence Ti(III,IV) induced by the presence of an oxygen vacancy ([O]) denoted HO-Ti(III)-[O]-Ti(IV), (Fig. 1). Such SFLPs engender high reactivity towards heterolytic H2 dissociation to produce a protonated/hydridic SFLP represented as HOH-Ti-[O]-Ti-H. The capture of CO2, via interaction of the electrophilic carbon of CO2 with the hydride and nucleophilic oxygen of the hydroxide of the SFLP HOH-Ti-[O]-Ti-H site, creates a formic acid (HCOOH) intermediate, which fragments to CO and H2O.
a Depiction of the central role played by the physicochemical properties in the catalytic hydrogenation of CO2-to-CO by SFLPs. b–d Reactive chemistry of an SFLP in c-TiO2@a-TiO2-x(OH)y, highlighting the heterolysis of H2 to form a protonated hydroxyl and a hydridic titanium SFLP. Structures are shown of (b) an unmodified crystalline surface, (c) formation of an SFLP site, (d) a ground-state SFLP site following activation by hydrogen, and (e) the enhanced activity excited-state SFLP generated by photoexcitation of the ground-state SFLP.
The SFLPs, confined to the surface of the amorphous shell covering the c-TiO2@a-TiO2-x(OH)y heterostructure, serve multiple functions: they improve the harvesting of visible and near-infrared photons, facilitate the generation and separation of photoexcited charge carriers, prolong charge-carrier lifetimes, and promote local heat generation. Collectively, these effects boost the chemical reactivity of the SFLPs, resulting in a record CO2-to-CO conversion rate of 5.3 mmol gcat−1 h−1 (350 times superior to that of crystalline c-TiO2) and a turnover frequency of 592 h−1, under solar light irradiation of 4.0 W cm−2. Thus, the results of this study motivate a general approach to sustainable fuels through engineered disorder in metal oxide-based CO2 photocatalysts.
Results and discussion
Na/c-TiO2-H2O synthesis of oxygen-vacancy- and hydroxyl-laden c-TiO2@a-TiO2-x(OH)y
The core@shell c-TiO2@a-TiO2-x(OH)y was prepared by ball-milling c-TiO2 (crystalline, 2.2 g) with Na/NaCl mixture (8.8 g) at solid state in Ar atmosphere under ambient pressure. A matrix of excess NaCl was added to facilitate the thorough mixing of the two reactants. Through the mechanochemical-driven redox reaction, mixed oxides with low-valent titanium (Ti(III)) atoms and oxygen vacancies ([O]) were obtained. During this process, we managed to confine the mechanochemistry to a nanometer-thick c-TiO2 surface layer by controlling the ball-milling time.
To understand the charge and stoichiometric balance of the sample preparation, electron paramagnetic resonance (EPR) analysis was employed (Fig. 2a–c). The room-temperature first-derivative spectrum of the reacted mixture showed two major peaks at g = 2.003 and g = 1.977, which are typical for an unpaired free electron (such as in [O] or Na(0)) and Ti(III), respectively31,32,33 (Fig. 2a)). Spectra acquired at 110 K provided better resolution and intensity for these signals, allowing anatase and rutile Ti(III) to be distinguished by g values of (1.990, 1.990, 1.962) and (1.975, 1.975, 1.951), respectively (Fig. 2b). Although the [O] signal in TiO2 typically demonstrates a symmetric Lorentzian line shape, while the Na(0) shows a Dysonian line34, it is difficult to distinguish the two in the spectra of the reacted mixture due to the complexity of overlapping peaks (Supplementary Fig. 1). Removing the residuals in the synthesis mixture by thorough washing (by deionized water) helped to resolve this dilemma, resulting in the desired product c-TiO2@a-TiO2-x(OH)y, the EPR spectra of which showed prominently increased Ti(III) and [O] signals (Fig. 2c). These results evidence that the low-valent Ti(III) and oxygen vacancies were generated mainly during sample washing. Based on this information, the following reaction sequence with balanced equations is proposed to explain the synthesis:
Upon the contact of Na and c-TiO2, Na(0) clusters inserted into the TiO2 lattice inducing new coordination of Ti(IV)-ONa-Ti(IV). Subsequently, an electron was transferred from Na(0) to Ti(IV) forming a Ti(III) ion, the Ti(III)-ONa-Ti(IV), followed by reacting with water to generate a Ti(III)-[O]-Ti(IV)-OH. The last step is also believed to be the origin of surface disorder in c-TiO2@a-TiO2-x(OH)y (Fig. 2d). Powder X-ray diffraction (PXRD) confirmed the reaction model, showing evidence of a crystalline intermediate Na2TiO3 being formed by ball-milling c-TiO2 with metallic Na(0), with a decrease in crystallinity for the TiO2, Fig. 2e. Then, this intermediate was transformed by Na de-intercalation during the washing process and did not remain in the resulting c-TiO2@a-TiO2-x(OH)y according to the PXRD and extended X-Ray absorption fine structure (EXAFS) results (Supplementary Fig. 2).
Ti(III)-[O]-Ti(IV)-OH-related atomic/electronic structure
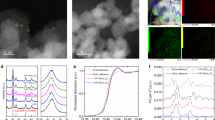
The thickness of the surface a-TiO2-x(OH)y in the c-TiO2@a-TiO2-x(OH)y was approximated to be 2 to 6 nm, as indicated by the formation of an amorphous shell/crystalline core heterostructure in the high-resolution transmission electron microscopy (HRTEM) image (Fig. 3a and Supplementary Figs. 3 and 4). HRTEM video and Raman analysis proved that both the c-TiO2 and the c-TiO2@a-TiO2-x(OH)y surfaces are stable under measurement conditions, and thus excluded the possibility of the electron beam induced surface amorphization for the c-TiO2@a-TiO2-x(OH)y (Supplementary Movie 1 and Supplementary Fig. 5). Ti L-edge electron energy loss spectroscopy (EELS) scans taken at several points on a c-TiO2@a-TiO2-x(OH)y nanoparticle supported this model. Conventional Ti(IV) L2,L3-edge features of tg-e2g splitting emerged in the core region, which were similar to those of c-TiO2, but no such splitting features were observed on the nanoparticle surface, and the L-edge energies shifted to low values by ~2.2 eV (Fig. 3b, c and Supplementary Fig. 6). Given the fact that the tg-e2g splitting stems from the energy difference between Ti 3d-orbitals with different geometric orientations, it is sensitive to the valence of Ti and the presence of point defects in titania35. Therefore, the above result suggests a low-valent Ti(III)- and [O]-rich amorphous a-TiO2-x(OH)y shell with Ti-O6 octahedra distorted and reconstructed to lower symmetry (e.g., distorted Ti-O5 pyramids).
a HR-TEM micrograph of c-TiO2@a-TiO2-x(OH)y (anatase phase). The amorphous/crystalline interfaces are marked with dotted lines. b, c High-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) image of c-TiO2@a-TiO2-x(OH)y (b) and corresponding Ti-L edge EELS spectra at different positions (c). d Comparison of geometrical and electronic structures between bridging and terminal hydroxyl. e, f 1H MAS-NMR (e) and ATR-FTIR (f) spectra of c-TiO2@a-TiO2-x(OH)y and c-TiO2.
Furthermore, the X-ray photoelectron spectroscopy (XPS) spectra of c-TiO2@a-TiO2-x(OH)y showed consistent results. Compared with the c-TiO2, the Ti 2p spectra of c-TiO2@a-TiO2-x(OH)y exhibited a slight peak shift from 459.5 eV to 459.3 eV with an emerging shoulder peak at 456.9 eV, signifying the presence of Ti(III) (Supplementary Fig. 7a). The temperature-dependent EPR spectra of c-TiO2@a-TiO2-x(OH)y showed that the intensity ratio of Ti(III) to [O] decreased from 15.28 at 207 K to 1.716 at room temperature (Fig. 2c), indicating their vicinity enabled an electron shuttle. These results supported our model of mixed-valence [O]-laden Ti(III)-[O]-Ti(IV)-OH with the presence of surface hydroxyl groups, confirmed by a peak at 533.4 eV in the O1s XPS spectra of c-TiO2@a-TiO2-x(OH)y (Supplementary Fig. 7b).
Theoretically, to obtain the above Ti(III)-[O]-Ti(IV)-OH via the TiO2-x+0.5y + 0.5yH2O → TiO2-x(OH)y reaction, the H2O should dissociate on the surface O(-II) and Ti(IV) sites to make charge-balancing Lewis base hydroxide OH(-I) on the Ti(III,IV) sites and protons on the O(-II) as Bronsted acid OH, namely the SFLP. Alternatively, the H2O can bind at the oxygen vacancy through its oxygen and dissociate to hydroxide and a proton where the latter binds to a lattice oxygen—this reaction pathway generates only Bronsted acid sites on the oxide lattice contrasting with the SFLP model.
To confirm the function of the c-TiO2@a-TiO2-x(OH)y surface as a SFLP [Ti(III)-[O]-Ti(IV)-OH] instead of a conventional Bronsted acid [Ti(IV)-OH-Ti(IV)], we now focus on distinguishing the two models. Theoretically, the terminal hydroxyl Ti(IV)-OH in the SFLP possesses a higher degree of freedom compared to that of the bridging hydroxyl (Fig. 3d). Thus, their charge density and molecular vibrations should be distinct, which can be monitored through solid-state 1H magic-angle spinning nuclear magnetic resonance (1H MAS NMR) and attenuated total reflection Fourier transform infrared (ATR-FTIR) spectroscopy, respectively. The 1H MAS NMR spectrum of c-TiO2 showed peaks at 5.8, 1.6, and −1.65 ppm. The peak around 5.8 ppm is typically ascribed to absorbed water, and the peak at 2.2 ppm on neat titanium dioxide is assigned to hydroxyl group36. Both water and hydroxyl group are naturally existing species when a metal oxide sample is exposed to air. The peak at −1.65 ppm appeared to be a background signal as similar signal emerged on the 1H MAS NMR spectra of c-TiO2@a-TiO2-x(OH)y as well. Interestingly, the water and hydroxyl peaks of c-TiO2@a-TiO2-x(OH)y shifted to 5.2 ppm and 1.7 ppm, respectively, and two additional peaks (2.2 and 0.6 ppm) emerged around the hydroxyl peak. Since the chemical shift of 1H-NMR reflects the shielding effect, compared to c-TiO2, the lower chemical shift of water on c-TiO2@a-TiO2-x(OH)y indicated the possible electron donation from oxygen vacancies and/or Ti(III) in a-TiO2-x(OH)y, while the higher chemical shift of hydroxyl (1.7 and 2.2 ppm)37 suggested the proton of less electron density, which agreed well the Lewis base -OH in the SFLP model. The peak at 0.6 ppm can be assigned to several species38, including terminal hydroxyl group and proton bonded to oxygen vacancy, which are closely related to the amorphous a-TiO2-x(OH)y shell (Fig. 3e). Furthermore, ATR-FTIR spectra of c-TiO2@a-TiO2-x(OH)y demonstrated a 1340 cm−1 peak, which is likely the bending mode of terminal OH39 induced by the symmetry-breaking of a bridging OH (Fig. 2d and Supplementary Fig. 8). Additionally, new peaks in the 3610~3680 cm−1 region, belonging to the stretching mode of terminal OH39,40, appeared on the ATR-FTIR spectra of c-TiO2@a-TiO2-x(OH)y, while that of c-TiO2 only showed the bridging OH feature located in the 3690~3750 cm−1 region (Supplementary Fig. 8). Despite the OH stretching peaks being low in intensity compared to the OH bending peaks, it was quite clear that the terminal OH species increased with the introduction of disorder TiO2-x(OH)y on the c-TiO2 surface. Both theoretic and experimental results confirm the SFLP feature of c-TiO2@a-TiO2-x(OH)y, where mixed-valence Ti(III, IV), [O], and terminal OH are in close proximity, forming the Ti(III)-[O]-Ti(IV)-OH.
SFLPs-related electronic properties, light absorption, and charge carrier separation
The reduction extent of titania during sample preparation determined the degree of non-stoichiometry (x) and surface disorder as well as the population of Ti(III), oxygen vacancies, and OH sites, which further corresponds to their optical spectra and band gaps41. The optical reflectance spectrum (UV-Vis-NIR) of c-TiO2 demonstrated UV light absorption with a band edge at ~380 nm, while that for c-TiO2@a-TiO2-x(OH)y (0.0015 < x < 0.0031) demonstrated strong broadband light absorption (Fig. 4a). Increasing the x value from 0.0002 < x < 0.0004 to 0.0015 < x < 0.0031 in c-TiO2@a-TiO2-x(OH)y samples (1→4) showed the evolution of Vis-NIR absorption, and red shifting of the absorption edges (Fig. 4a), corresponding to bandgaps of 3.49, 3.46, 3.43 and 3.38 eV (Supplementary Fig. 9), respectively; all of these bandgap energies were smaller than the value of 3.57 eV for pristine c-TiO2, indicating the increased sunlight harvest of c-TiO2@a-TiO2-x(OH)y compared with c-TiO2. The detailed band-edge positions of c-TiO2@a-TiO2-x(OH)y was provided by ultraviolet photoelectron spectroscopy (UPS). Valence band (EVB) positions of c-TiO2 and a-TiO2-x(OH)y (0.0015 < x < 0.0031) were found at −7.7 and −7.59 eV (vs. vacuum), and the corresponding conduction band (ECB) positions were found at −4.13 and −4.21 eV (vs. vacuum), respectively (Supplementary Fig. 10).
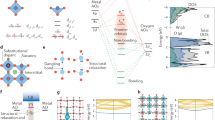
a UV–Vis-NIR diffuse reflectance spectra (DRS) of c-TiO2@a-TiO2-x(OH)y as a function of reduction degree. The x was quantified in each sample. b, c The total density of states (black line, right axis) and the corresponding values of the inverse participation ratio (IPR) (blue dots, left axis) for a-TiO2-x(OH)y (b) and crystalline TiO2-x (c) surfaces. d Schematic of charge carrier separation and transfer pathways in c-TiO2@a-TiO2-x(OH)y. The colors of arrows indicate the wavelength of incident light. e Time-resolved photoluminescence spectroscopy decay curves of c-TiO2 and c-TiO2@a-TiO2-x(OH)y.
Density of states (DOS) and the delocalization degree of electrons were then simulated computationally in both the amorphous and crystalline components to provide mechanistic insights. Specifically, inverse participation ratio (IPR) analysis was conducted to investigate charge mobility and the localization of energy states on amorphous TiO2-x(OH)y and crystalline TiO2-x surfaces. In Fig. 4b, c, the IPR and DOS of amorphous TiO2-x(OH)y and crystalline TiO2-x are depicted, where a large IPR value represents highly localized states and a small IPR value represents delocalized states. The IPR results showed that the Ti 3d in the bottom of the CB (conduction band) and O 2p states at the top of the VB (valence band) for amorphous TiO2-x(OH)y are strongly localized as compared to crystalline TiO2-x. Specifically, the OH and [O] vacancy resulted in shallow band states near the VB edge and the [O] vacancy resulted in shallow band states near the CB edge, respectively (Supplementary Fig. 11). These results indicate the high-concentration self-trapped polarons and excitons of a-TiO2-x(OH)y compared to crystalline TiO2-x, which facilitate charge carrier separation by trapping photo-generated holes and electrons by SLFPs OH and Ti(III), respectively.
Based on CB and VB positions obtained from the UPS experiment, DOS and charge localization analyses via DFT, a schematic illustration for electron-hole transfer, separation, and recombination, is proposed in Fig. 4d. The UV light can excite both the core c-TiO2 and the shell a-TiO2-x(OH)y because the photon energy of the UV light (λ < 347 nm or E > 3.57 eV) is larger than the bandgap energy of c-TiO2 (Eg = 3.57 eV) or a-TiO2-x(OH)y (Eg = 3.38 eV). The calculated penetration depth (Dp) of UV light for TiO2 further supported the above results (Supplementary Figs. 12 and 13). c-TiO2 and a-TiO2-x(OH)y demonstrate similar UV-absorbing capacities, thus showing a similar penetration depth in UV region. Given the Dp is larger than the 3─6 nm thickness of the shell, the UV light will be partially absorbed by surface a-TiO2-x(OH)y and then reach the core c-TiO2 in the c-TiO2@a-TiO2-x(OH)y. Therefore, both the core c-TiO2 and shell a-TiO2-x(OH)y will be excited by the UV light to yield photo electrons and holes. Simultaneously, the visible light penetration depth of black titania is within several micrometers, so the visible light cannot be fully absorbed by a 3–6 nm surface a-TiO2-x(OH)y layer but will be absorbed by the sub-surface catalyst particles with a stacking thickness of several micrometers. Accordingly, the visible and IR light can excite electrons on the defect- and OH-related energy levels of the a-TiO2-x(OH)y. Because the CB of a-TiO2-x(OH)y is lower than that of c-TiO2, the photogenerated electrons on the c-TiO2 preferentially transfer across the crystalline-amorphous interface to reach the a-TiO2-x(OH)y and get trapped by an unsaturated Ti(III) and/or oxygen-vacancy sites. Therefore, the crystalline core-amorphous shell structure facilitates the charge carrier spatial separation, which enhances the excited-state Lewis basicity and acidity of the Ti(III)-[O]-Ti(IV)-OH, namely the ES SFLP, by the trapped electrons and holes. This ES SFLP not only enhances chemical reactivity compared to its GS counterpart but also possibly prolongs the lifetime of the photogenerated electrons and holes during the H2 and CO2 reaction.
Inspired by above calculation, time-resolved photoluminescence (PL) spectroscopy was performed at room temperature to testify the diffusion and recombination processes of photogenerated electron-hole pairs in c-TiO2@a-TiO2-x(OH)y. All PL decay curves exhibited extremely fast relaxation (Fig. 4e) and were fitted by a bi-exponential model. The pristine TiO2 gave an average exciton-decay time of 10.4 ns, while a longer exciton-decay time of 23.6 ns was observed for the c-TiO2@a-TiO2-x(OH)y (Supplementary Table 1). This supports the proposed model (depicted in Fig. 4d) of charge transfer between the c-TiO2 core and the a-TiO2-x(OH)y shell, prolonging the lifetime of charge carriers for subsequent photoreaction.
Activation of CO2 and H2 by SFLPs on c-TiO2@a-TiO2-x(OH)y
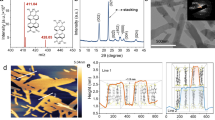
Previous studies evidenced a key feature of the frustrated Lewis pair as triggering H2 activation42 under ambient temperatures. The obtained products are a proton and a hydride, of which the latter shows high chemical reactivity for CO2 reduction. Therefore, to check the chemical function of the SFLP in the c-TiO2@a-TiO2-x(OH)y, its reaction with H2 was monitored through the NMR. Solid state 1H MAS NMR of c-TiO2@a-TiO2-x(OH)y showed a major peak at ca. 5.2 ppm which was typically ascribed to Ti-OH2 species43, and peaks between −1.6─2.2 ppm with negligible intensities compared to that at 5.2 ppm. After exposure to H2 at room temperature, a protonated Ti-OH2 peak at 3.8 ppm, and two intense hydridic Ti-H peaks44,45 at 0.14 ppm & −0.2 ppm emerged, signifying the heterolytic dissociation of H2 on SFLPs (Fig. 5a). In contrast, there was no significant change in the NMR spectra of c-TiO2 before and after introducing H2 (Fig. 5b).
a, b Ex situ solid-state 1H MAS-NMR spectra of c-TiO2@a-TiO2-x(OH)y (a) and c-TiO2 (b) before (purple) and after (orange) exposure to H2 at atmospheric pressure and room temperature. c–e H2 adsorption resulting in the formation of two surface OH (c) or a Ti-H and an OH on amorphous titania surfaces (d), or absorbed H atoms on crystalline TiO2-x (e). The Ti, O and H atoms are represented in gray, red, and blue, respectively. f, g In situ DRIFTS spectra of CO2 reduction over c-TiO2@ a-TiO2-x(OH)y (f) and c-TiO2 (g) at various temperatures while flowing 2 sccm H2, 2 sccm CO2, and 16 sccm He.
Theoretical calculations on the amorphous structure were then conducted to provide mechanistic understanding of the origin of the facile H2 heterolysis over the SFLP site of c-TiO2@a-TiO2-x(OH)y. The interaction of H2 with amorphous TiO2 (a-TiO2) was screened on three Ti sites (Ti-4c, Ti-5c, and Ti-6c) and ten O sites (a to i) via geometry optimization (Supplementary Fig. 14). In all cases (except sites ‘i’ and ‘Ti-4c’), H2 adsorption on surface was exothermic but only resulted in the formation of surface OH, as shown in Fig. 5c. Surprisingly, the introduction of O vacancies on amorphous surfaces resulted in facile exothermic H2 heterolysis, with δEads = −0.06 Ry and the generation of a surface OH and a Ti-H, Fig. 5d. Bader charge analysis showed that the hydrogen in the OH bore a charge of +0.99e while −0.6e in the hydride (Supplementary Table 2), bonding to weakly non-coordinative Lewis basic O (−1.7e) and Lewis acidic Ti (+2.1e), respectively. In contrast, the H2 could not dissociate to form OH when it interacted with the crystalline c-TiO2-x surface having vacancies at O-2c (Fig. 5e) and O-3c sites (Supplementary Fig. 15).
Subsequently, in situ DRIFTS was applied to monitor the CO2 reduction over the SFLP-laden c-TiO2@a-TiO2-x(OH)y at molecular level. In the presence of both H2 and CO2, three major C-related peaks emerged at 1307 cm−1, 1370 cm−1, and 1677 cm−1 (Fig. 5f), which could be assigned as carboxylate species (1307 cm−1)46,47 and formate (1370 cm−1 and 1677 cm−1)48,49. Such a formate species agreed well with the reaction model of CO2 addition to the protonated and hydridic SFLPs by its nucleophilic O(-II) and electrophilic C(IV), respectively (Fig. 1). Consistently, the peak intensities of formate species decreased at high temperature (200 → 300 °C) as they were converted to CO, with the increased intensity at 1643 cm−1 corresponding to the H2O product induced scissor modes. By contrast, carbonates (1345 cm−1, 1625 cm−1, and 1574 cm−1) and bicarbonates (1248 cm−1, 1407 cm−1, and 1672 cm−1)48,50,51 were generated on the surface of c-TiO2 (Fig. 5g). The distinct surface chemistry between c-TiO2 and amorphous TiO2-x(OH)y in RWGS reaction was also confirmed by the apparent activation energy (Ea). Arrhenius plots of temperature-dependent CO rates suggest an Ea of 75.40 kJ mol−1 for c-TiO2@a-TiO2-x(OH)y, which decreased by ~17% compared with 90.27 kJ mol−1 of c-TiO2 (Supplementary Fig. 16).
Photocatalytic performance
With the favorable band structure and surface reactivity, the SFLPs-laden c-TiO2@a-TiO2-x(OH)y (0.0015 < x < 0.0031) demonstrated CO2 photocatalytic activity of 5.3 mmol gcat−1 h−1 under solar light irradiation (4.0 W cm−2), which was 350 times that of the pristine c-TiO2 (Fig. 6a). The turnover frequency (TOF) of c-TiO2@a-TiO2-x(OH)y was as high as 592 h−1, superb among known catalysts tested under comparable photocatalytic conditions52 (Supplementary Table 3). The apparent quantum yield (AQY) of the full Xe lamp spectrum can achieve 0.09% (Supplementary Note). This is likely a lower limit as neither the photocatalyst nor photoreactor architectures have been engineered and optimized for high photon capture efficiency, the key to high energy efficiency of the integrated system.
a Non-stoichiometry dependent CO production rates of the c-TiO2@a-TiO2-x(OH)y under full-spectrum Xe light, 4.0 W cm−2. b Stability of c-TiO2@a-TiO2-x(OH)y under full-spectrum Xe light (4.0 W cm−2) in 8 h. c CO production rates of c-TiO2@a-TiO2-x(OH)y, pristine c-TiO2 and 2% Na/c-TiO2 under visible light (2.8 W cm−2).
Notably, the c-TiO2@a-TiO2-x(OH)y (0.0015 < x < 0.0031) demonstrated no apparent activity decrease in eight consecutive runs in the batch reactor (Fig. 6b) or a 48-h on-stream reaction under 300 °C in a flow reactor (Supplementary Fig. 17). The structural stability of spent c-TiO2@a-TiO2-x(OH)y was supported by PXRD and XPS, which showed no significant changes compared to that before reaction (Supplementary Figs. 18 and 19).
Furthermore, using an isotopically labeled 13CO2-H2 feedstock gave 13CO as the only product for c-TiO2@a-TiO2-x(OH)y, confirming the carbon source from the CO2 feedstock (Supplementary Fig. 20).
ICP-OES analysis of c-TiO2@a-TiO2-x(OH)y suggested a 2 wt% residual Na, while our control sample prepared by loading 2 wt% Na (NaOH) on c-TiO2 demonstrated 0.19 mmol gcat−1 h−1 activity, a negligible increase compared with the pristine sample, excluding the possibility that Na-dominated activity enhancement of the c-TiO2@a-TiO2-x(OH)y sample (Supplementary Fig. 21). These results support the SFLP-laden c-TiO2@a-TiO2-x(OH)y (0.0015 < x < 0.0031) as a promising CO2 photocatalyst.
Interestingly, the aforementioned synergy effect between the c-TiO2 core and the a-TiO2-x(OH)y shell, as shown in Fig. 4d, could also be reflected in the activity by varying the non-stoichiometry of the c-TiO2@a-TiO2-x(OH)y catalyst. To amplify, the CO production rate of c-TiO2@a-TiO2-x(OH)y samples first increased from 0.17 mmol gcat−1 h−1 (0.0002 < x < 0.0004) to 5.3 mmol gcat−1 h−1 (0.0015 < x < 0.0031), then decreased to 4.7 mmol gcat−1 h−1 by further increasing the non-stoichiometry to 0.0021 < x < 0.0039, demonstrating a volcano activity-non-stoichiometry relationship (Fig. 6a, Supplementary Fig. 22). HRTEM images evidenced the optimal sample (0.0015 < x < 0.0031) with an amorphous shell of 3–6 nm in thickness, while the samples of 0.0002 < x < 0.0004 and 0.0021 < x < 0.0039 showed negligible and ~10 nm shell thickness, respectively (Supplementary Fig. 23). Given the efficiency of a photocatalytic reaction is determined by the efficiencies of light absorption, charge separation and finally the surface reaction, above results suggested the synergy effect resulting from a tradeoff between 1) the high charge-carrier separation efficiency and high photo-available surface area related to the core (c-TiO2) and 2) the high surface reactivity induced by the SFLP shell (a-TiO2-x(OH)y) (Supplementary Fig. 13).
In addition, wavelength-dependent activity tests further shed light on the contribution of the core-shell synergy effect in the c-TiO2@a-TiO2-x(OH)y (0.0015 < x < 0.0031). After deactivating the core c-TiO2 by filtering the UV part (λ < 420 nm) of the Xe lamp, the c-TiO2@a-TiO2-x(OH)y sample exhibited visible light-driven activity of 3.0 mmol CO gcat−1 h−1 (Fig. 6c). By comparing the UV-corresponded activity [(5.3–3.0) mmol gcat−1 h−1] with that of the pure c-TiO2 (0 mmol gcat−1 h−1), the contribution of the synergy effect is 43% of the full-spectrum activity (2.3 vs. 5.3 mmol gcat−1 h−1), which is the upper limit. While the lower limit is estimated by comparing the UV activity (2.3 mmol gcat−1 h−1) with that of the TiO2@a-TiO2-x(OH)y sample bearing the highest x value (0.0021 < x < 0.0039; 1.9 mmol gcat−1 h−1), which is 8% [(2.3–1.9) vs. 5.3 mmol gcat−1 h−1]. In the Vis-IR region devoid of the synergy effect, wavelength-dependent CO production rate agreed well with the light-absorbing capability as reflected by DRS spectra (Supplementary Fig. 24). The photothermal contribution to the activity was identified by changing the CO2/H2 gas ratio in the reactor from 1:1 to 5:1 without varying the light intensity (Supplementary Fig. 25). The CO production rate doubled to 11.2 mmol gcat−1 h−1 due to the better insulating effect of CO2 relative to H2. ASPEN Plus was also employed to calculate the local temperature of c-TiO2@a-TiO2-x(OH)y using a CO2/H2 ratio of 5:1. The predicted temperature reached as high as 200 °C (Supplementary Table 4).
Intentionally engineered SFLPs in the amorphous shell of c-TiO2@a-TiO2-x(OH)y boost the harvesting potential of solar photons and the effectiveness of the photothermal effect, while the heterostructure benefits the generation, separation, and lifetime of electron-hole pairs on the photo reactivity of HOTi-[O]-Ti SFLPs towards H2 heterolysis and CO2 reduction. The paradigm of integrating disorder engineering with surface frustrated Lewis pairs in a core-shell crystalline-amorphous c-TiO2@a-TiO2-x(OH)y heterostructure provides a new paradigm for designing and implementing photocatalysts for synthesizing sustainable fuels from carbon dioxide feedstock.
Methods
Material synthesis
All chemicals used were of analytical grade and used without any further purification. Commercial P25(c-TiO2) (99%) was purchased from Alfa Aesar.
The Na/NaCl mixture, composed of small Na particles dispersed within NaCl, is expected to be an effective agent for the reduction of metal oxides. The weight ratio between Na and NaCl is about 1:10 and the milling speed is 150–200 rpm. Following a typical experiment for synthesizing c-TiO2@a-TiO2-x(OH)y, P25 was milled with Na/NaCl powder in a weight ratio of 1:4 under argon atmosphere at room temperature using a Retsch PM400 planetary ball mill, at a milling rate of 180 rpm. All above procedures were conducted in a glovebox filled with Ar. The samples (4-c-TiO2@a-TiO2-x(OH)y) were milled for 4 h before being collected and washed several times with deionized water to remove the residual Na/NaCl. Finally, the samples were vacuum-dried at room temperature to isolate the final, dark-blue a-TiO2-x(OH)y@c-TiO2 powder. All characterized and tested c-TiO2@a-TiO2-x(OH)y samples were washed 3 times with Na content of about 2 wt% Na if not mentioned or emphasized the wash times. Other samples with different oxygen-vacancy concentrations (1- c-TiO2@a-TiO2-x(OH)y, 2- c-TiO2@a-TiO2-x(OH)y and 3-c-TiO2@a-TiO2-x(OH)y) were prepared by milling P25 with Na/NaCl powder in a weight ratio of 1:1 at a milling rate of 150 rpm for 4 h, milling with Na/NaCl powder in a weight ratio of 1:1 at a milling rate of 180 rpm for 4 h, and milling with Na/NaCl powder in a weight ratio of 1:2 at a milling rate of 180 rpm for 4 h, respectively.
Materials characterization
EPR measurements were conducted on a Bruker EMXmicro-6/1 EPR spectrometer. The powdered samples were packed into a Wilmad EPR quartz tube and closed with a cap. At least two co-added scans were performed for each sample (receiver gain: 30 dB) using a 1000.0 G sweep width of 60.0 s (or a 1500.0 G sweep width of 90.0 s), and a microwave power of ~5.0 mW (attenuation: 16 dB). The DPPH was used as a standard to calibrate the central field every time before the sample measurements. Low-temperature experiments were enabled by liquid nitrogen. PXRD was performed on a Bruker D2-Phaser X-ray diffractometer, using Cu Kα radiation at 30 kV. XPS was performed in an ultrahigh vacuum chamber with base pressure of 10−9 torr. This system used a Thermo Scientific K-Alpha XPS spectrometer with an Al Kα X-ray source (1,486.7 eV) operating at 12 kV and 6 A. The spectra were obtained using an analyzer pass energy of 50 eV with a resolution of 0.1 eV. HR-TEM images were acquired on an aberration-corrected FEI Titan 380–300 microscope operated at a 300 kV accelerating voltage. HR-TEM images were also evaluated by calculating their 2D Fourier transform, yielding information regarding their crystal lattices. ICP-OES was carried out on a Thermo Scientific iCAP 7000 Series ICP Spectrometer. The surface areas of samples were measured on an Autosorb-1 system (Quantachrome, USA) from N2 adsorption isotherms obtained via the BET method. UV-visible diffuse reflectance spectra were obtained for dry-pressed disk samples using a Cary 500 Scan Spectrophotometer (Varian, USA) over a range of 200 to 800 nm. BaSO4 was used as a reflectance standard in the UV-visible diffuse reflectance experiment. The photoluminescence (PL) spectra were measured on an Andor Shamrock SR-750 fluorescence spectrometer with a Xe-lamp as an excitation source (Andor Technology Ltd, Belfast, UK). A CCD detector combined with a monochromator was used for signal collection. The 1H solid state MAS NMR spectra were obtained at a spinning rate of 20 kHz. The NMR Spectra were calibrated to reference adamantane with optimized parameters: pulse width (pwX90) = 3.45 microseconds, fine power (aX90) = 2700, course power (tpwr) = 59, and synthesizer offset (tof) = 1192.9. Number of scans = 64, delay time = 6 s. Samples for 1H solid state MAS NMR were treated by H2 and then transferred to a glovebox with an Ar atmosphere for sample loading. The overall local temperature of the sample in a high-intensity batch reactor (CO2/H2 ratio = 5:1, 40 suns illumination) was estimated by allowing the system to approach equilibrium and comparing the final composition with ASPEN Plus V9 output, using the Peng-Robinson property package with the Gibbs reactor.
Measurements of the gas-phase photocatalytic reduction CO2
For gas-phase photocatalytic testing in a batch reactor, the samples were prepared by drop-casting samples, dispersed in DI water, onto binder-free borosilicate glass microfiber filters with an area of 1 cm2 and then drying them under ambient conditions prior to reactor testing. Gas-phase photocatalytic experiments were conducted in a custom-fabricated 11.8 mL stainless steel batch reactor with a fused silica view port sealed with a Viton O-ring. The reactor was evacuated using an Alcatel dry pump before being purged with H2 (99.9995%) at a flow rate of 15 sccm. The pressure inside the reactor was monitored during the reaction using an Omega PX309 pressure transducer. After H2 purging, the reactor was infiltrated with H2 and CO2 gas, to achieve the desired pressure ratio, before being sealed. The reactor was irradiated using a 300 W Xe lamp at 4.0 W cm−2 light intensity for a duration of 1 h per run. For the tests using a CO2/H2 gas ratio of 1:1, the reactor was infiltrated with 15 psi CO2 and 15 psi H2. For the tests using a CO2/H2 gas ratio of 5:1, CO2 was infiltrated until pressures of 25 psi CO2 and 5 psi H2 were reached. Visible light with an intensity of 2.8 W cm−2 was obtained using a 420 nm optical cut-off filter to remove UV light from the Xe source. Product gases were analyzed using flame ionization and thermal conductivity detectors installed in an SRI-8610 gas chromatograph equipped with 30 Mole Sieve 13a and 60 Haysep D column. Isotope product gases were measured using an Agilent 7890 A gas chromatographic mass spectrometer with a 60 m GS-Carbon PLOT column fed to the mass spectrometer. The hydrogenation experiments in a flow system were conducted in a tubular quartz reactor with an inner diameter of 2 mm, in which ∼20 mg of catalyst sample was packed and irradiated using an unfiltered 300 W Xe lamp. The diameter of the light spot was ~2 cm, with an area of about 3.14 cm2, which could fully cover the sample. An OMEGA temperature controller was attached to a heating cartridge inserted into the copper block, along with a thermocouple inserted into the quartz tube (in contact with the catalyst bed) for control of the catalyst temperature.
In situ DRIFTS measurement
The in situ DRIFTS experiments were performed on a Thermo Scientific Nicolet iS50 FTIR Spectrometer with a mercury cadmium telluride detector cooled with liquid nitrogen. The spectrometer was equipped with a Harrik Praying Mantis diffuse reflection accessory and a Harrick high-temperature reaction chamber. The temperature was controlled with a Harrick ATC-024-3 Temperature Controller. Fresh reduced oxide sample was loaded onto a sampling accessory with a diamond-coated zinc selenide window and then sealed in the reactor. The reactor was heated to 300 °C and kept for 2 h in He (20 sccm) to remove the moisture and surface contaminants on the sample. After cooling the reactor down to 25 °C in He, the IR spectrum was collected to provide the baseline for subsequent differential spectra. The spectra were collected at 25 °C in H2 (5 sccm) and He (15 sccm) within 0 to 20 min. The H2 was then turned off while He (15 sccm) was kept purging at 25 °C for 30 min to remove residual H2 within the reactor. Afterward, the spectra were collected under flowing H2 (2 sccm), CO2 (2 sccm), and He (16 sccm) at various temperatures (25 °C, 100 °C, 150 °C, 200 °C, 250 °C, and 300 °C). Each temperature was held for 20 min.
Computational details
The amorphous TiO2 (a-TiO2) model was prepared via the melting and quenching method as demonstrated elsewhere53. The properties of the prepared a-TiO2 model were in agreement with experimental and theoretical data available. The structural analysis of these models suggests that local structural features of bulk crystalline TiO2 (c-TiO2) are retained in the a-TiO2 model.
In order to obtain the a-TiO2 surface in the present study, a vacuum of about 20 Å was added in the z-direction of 2 × 2 × 4 bulk supercell (96-atom model)54. The a-TiO2-x model was created by removing the surface O atoms coordinated to Ti having coordination numbers of four, five, and six, denoted by Ti-4c, Ti-5c, and Ti-6c, respectively (Fig. 4a), creating, in total, 10 a-TiO2-x model surfaces. For c-TiO2, we investigated the most thermodynamically stable (101) surface of anatase with two models of crystalline TiO2-x (c-TiO2-x) surface created by removing a two-fold coordinated O atom (denoted as O2c) and a three-fold coordinated O atom (denoted as O3c) (Supplementary Fig. 26). The anatase (101) surface is represented by a periodic supercell slab of 144 atoms and a vacuum region greater than 12 Å.
The plane wave pseudopotential approach, together with the Perdew-Burke-Ernzerhof55 exchange-correlation functional and Vanderbilt ultrasoft pseudopotentials56, was utilized throughout. The kinetic energy cutoffs of 544 and 5440 eV were used for the smooth part of the electronic wavefunctions and augmented electron density, respectively. The Quantum-ESPRESSO software package57, was used to perform the calculations. All calculations were spin polarized. The structures were relaxed by using a conjugate gradient minimization algorithm until the magnitude of residual Hellman-Feynman force on each atom was less than 10−2 Ry/Bohr. In all electronic density of states (DOS) plots, a conventional Gaussian smearing of 0.007 Ry was utilized.
Appreciable underestimation of band gap and delocalization of d and f electrons are well-known limitations of DFT. Therefore, DFT with Hubbard energy correction (DFT + U) formalism was used in this study with U = 4.2 eV applied to Ti 3d electrons for analyzing electronic properties of crystalline and amorphous TiO2. The value of U for Ti was chosen not solely on the basis of band gap but also depending on the property of interest58, which in the current study is the catalytic behavior of TiO2 that in-turn depends upon the position of band gap states and their effect on the electronic structure. This value of U for Ti is consistent with theoretical investigations by ref. 59, who calculated it by fitting the peak positions for surface oxygen vacancies to experimental X-ray photoelectron spectroscopy data.
In order to understand the charge mobility (i.e., localization of energy states in a-TiO2-x and c-TiO2-x), we further conducted Inverse Participation Ratio (IPR) analysis. IPR is capable of determining the charge localization of the tail states and the mobility band gap of materials60. The IPR of an orbital ψn(\(\vec{{r}_{i}}\)), I(ψn), is accordingly defined by
where N is the number of volume elements in the cell and i is the index of the volume element. Ideally, a localized orbital means I(ψ) = N, whereas a delocalized orbital means I(ψ) = 1. The IPR can identify a level as belonging to the delocalized band, to the partially localized band tail, or to the highly localized band gap.
Data availability
The data that support the plots within this paper and other finding of this study are available from the corresponding author upon reasonable request.
References
Finney, J. L. Modelling the structures of amorphous metals and alloys. Nature 266, 309–314 (1977).
Pei, Y. et al. Synthesis and catalysis of chemically reduced metal–metalloid amorphous alloys. Chem. Soc. Rev. 41, 8140–8162 (2012).
Kamiya, T. & Hosono, H. Material characteristics and applications of transparent amorphous oxide semiconductors. NPG Asia Mater. 2, 15–22 (2010).
Jeon, S. et al. Gated three-terminal device architecture to eliminate persistent photoconductivity in oxide semiconductor photosensor arrays. Nat. Mater. 11, 301–305 (2012).
Mitchell, N. P., Nash, L. M., Hexner, D., Turner, A. M. & Irvine, W. T. M. Amorphous topological insulators constructed from random point sets. Nat. Phys. 14, 380–385 (2018).
Wesenberg, D., Liu, T., Balzar, D., Wu, M. & Zink, B. L. Long-distance spin transport in a disordered magnetic insulator. Nat. Phys. 13, 987–993 (2017).
Sacépé, B. et al. Localization of preformed Cooper pairs in disordered superconductors. Nat. Phys. 7, 239–244 (2011).
Dubouchet, T. et al. Collective energy gap of preformed Cooper pairs in disordered superconductors. Nat. Phys. 15, 233–236 (2019).
Ball, J. M. & Petrozza, A. Defects in perovskite-halides and their effects in solar cells. Nat. energy 1, 16149 (2016).
Taylor, F. H., Buckeridge, J. & Catlow, C. R. A. Defects and oxide ion migration in the solid oxide fuel cell cathode material LaFeO3. Chem. Mater. 28, 8210–8220 (2016).
Yu, X., Marks, T. J. & Facchetti, A. Metal oxides for optoelectronic applications. Nat. Mater. 15, 383–396 (2016).
Hosono, H., Kim, J., Toda, Y., Kamiya, T. & Watanabe, S. Transparent amorphous oxide semiconductors for organic electronics: application to inverted OLEDs. Proc. Natl Acad. Sci. USA 114, 233–238 (2017).
Cahill, D. G. & Pohl, R. O. Thermal conductivity of amorphous solids above the plateau. Phys. Rev. B 35, 4067–4073 (1987).
Beekman, M., Morelli, D. T. & Nolas, G. S. Better thermoelectrics through glass-like crystals. Nat. Mater. 14, 1182–1185 (2015).
Moya, X., Kar-Narayan, S. & Mathur, N. D. Caloric materials near ferroic phase transitions. Nat. Mater. 13, 439–450 (2014).
Simonov, A. & Goodwin, A. L. Designing disorder into crystalline materials. Nat. Rev. Chem. 4, 657–673 (2020).
Catlow, R. Defects and disorder in crystalline and amorphous solids, vol. 418. Springer Science & Business Media, 2012.
Jia, J. et al. Heterogeneous catalytic hydrogenation of CO2 by metal oxides: defect engineering—perfecting imperfection. Chem. Soc. Rev. 46, 4631–4644 (2017).
Goldsmith, B. R., Peters, B., Johnson, J. K., Gates, B. C. & Scott, S. L. Beyond ordered materials: understanding catalytic sites on amorphous solids. ACS Catal. 7, 7543–7557 (2017).
Chen, X., Liu, L. & Huang, F. Black titanium dioxide (TiO2) nanomaterials. Chem. Soc. Rev. 44, 1861–1885 (2015).
Liu, X. et al. Progress in black titania: a new material for advanced photocatalysis. Adv. Energy Mater. 6, 1600452 (2016).
Dhakshinamoorthy, A., Navalon, S., Corma, A. & Garcia, H. Photocatalytic CO2 reduction by TiO2 and related titanium containing solids. Energy Environ. Sci. 5, 9217–9233 (2012).
Xu, H. et al. Recent advances in TiO2-based photocatalysis. J. Mater. Chem. A 2, 12642–12661 (2014).
Tao, J., Luttrell, T. & Batzill, M. A two-dimensional phase of TiO2 with a reduced bandgap. Nat. Chem. 3, 296–300 (2011).
Scanlon, D. O. et al. Band alignment of rutile and anatase TiO2. Nat. Mater. 12, 798–801 (2013).
Chen, X., Liu, L., Yu, P. Y. & Mao, S. S. Increasing solar absorption for photocatalysis with black hydrogenated titanium dioxide nanocrystals. Science 331, 746–750 (2011).
Li, L. et al. Sub-10 nm rutile titanium dioxide nanoparticles for efficient visible-light-driven photocatalytic hydrogen production. Nat. Commun. 6, 5881 (2015).
Sachs, M. et al. Effect of oxygen deficiency on the excited state kinetics of WO3 and implications for photocatalysis. Chem. Sci. 10, 5667–5677 (2019).
Zhao, Y. et al. Ultrafine NiO nanosheets stabilized by TiO2 from monolayer NiTi-LDH precursors: An active water oxidation electrocatalyst. J. Am. Chem. Soc. 138, 6517–6524 (2016).
Stephan, D. W. The broadening reach of frustrated Lewis pair chemistry. Science 354, aaf7229 (2016).
Chiesa, M., Paganini, M. C., Livraghi, S. & Giamello, E. Charge trapping in TiO2 polymorphs as seen by Electron Paramagnetic Resonance spectroscopy. Phys. Chem. Chem. Phys. 15, 9435–9447 (2013).
Hurum, D. C., Agrios, A. G., Gray, K. A., Rajh, T. & Thurnauer, M. C. Explaining the enhanced photocatalytic activity of degussa P25 mixed-phase TiO2 using EPR. J. Phys. Chem. B 107, 4545–4549 (2003).
Zhao, Y. et al. Tuning oxygen vacancies in ultrathin TiO2 nanosheets to boost photocatalytic nitrogen fixation up to 700 nm. Adv. Mater. 31, 1806482 (2019).
Damay, P., David, T. & Sienko, M. J. Conduction electron spin resonance in metallic calcium. J. Chem. Phys. 61, 4369–4371 (1974).
Guo, Y. et al. Hydrogen-location-sensitive modulation of the redox reactivity for oxygen-deficient TiO2. J. Am. Chem. Soc. 141, 8407–8411 (2019).
Nosaka, A. Y., Fujiwara, T., Yagi, H., Akutsu, H. & Nosaka, Y. Characteristics of water adsorbed on TiO2 photocatalytic systems with increasing temperature as studied by solid-state 1H NMR spectroscopy. J. Phys. Chem. B 108, 9121–9125 (2004).
Li, G. et al. Ionothermal synthesis of black Ti3+-doped single-crystal TiO2 as an active photocatalyst for pollutant degradation and H2 generation. J. Mater. Chem. A 3, 3748–3756 (2015).
Crocker, M. et al. 1H NMR spectroscopy of titania. Chemical shift assignments for hydroxy groups in crystalline and amorphous forms of TiO2. J. Chem. Soc., Faraday Trans. 92, 2791–2798 (1996).
Jackson, P. & Parfitt, G. D. Infra-red study of the surface properties of rutile. Water and surface hydroxyl species. Trans. Faraday Soc. 67, 2469–2483 (1971).
Liu, C. et al. Structure–activity relationship of surface hydroxyl groups during NO2 adsorption and transformation on TiO2 nanoparticles. Environ. Sci. Nano 4, 2388–2394 (2017).
Davies, D. W. et al. Descriptors for electron and hole charge carriers in metal oxides. J. Phys. Chem. Lett. 11, 438–444 (2020).
Stephan, D. W. Frustrated lewis pairs: from concept to catalysis. Acc. Chem. Res. 48, 306–316 (2015).
Nosaka, A. Y., Fujiwara, T., Yagi, H., Akutsu, H. & Nosaka, Y. Photocatalytic reaction sites at the TiO2 surface as studied by solid-state 1H NMR spectroscopy. Langmuir 19, 1935–1937 (2003).
Yang, Y. et al. An unusual strong visible-light absorption band in red anatase TiO2 photocatalyst induced by atomic hydrogen-occupied oxygen vacancies. Adv. Mater. 30, 1704479 (2018).
Chen, X. et al. Properties of disorder-engineered black titanium dioxide nanoparticles through hydrogenation. Sci. Rep. 3, 1510 (2013).
Ramis, G., Busca, G. & Lorenzelli, V. Low-temperature CO2 adsorption on metal oxides: spectroscopic characterization of some weakly adsorbed species. Mater. Chem. Phys. 29, 425–435 (1991).
Nelson, N. C., Nguyen, M.-T., Glezakou, V.-A., Rousseau, R. & Szanyi, J. Carboxyl intermediate formation via an in situ-generated metastable active site during water-gas shift catalysis. Nat. Catal. 2, 916–924 (2019).
Liao, L. F., Lien, C. F., Shieh, D. L., Chen, M. T. & Lin, J. L. FTIR study of adsorption and photoassisted oxygen isotopic exchange of carbon monoxide, carbon dioxide, carbonate, and formate on TiO2. J. Phys. Chem. B 106, 11240–11245 (2002).
Chuang, C. C., Wu, W. C., Huang, M. C., Huang, I. C. & Lin, J. L. FTIR study of adsorption and reactions of methyl formate on powdered TiO2. J. Catal. 185, 423–434 (1999).
Mino, L., Spoto, G. & Ferrari, A. M. CO2 capture by TiO2 anatase surfaces: A combined DFT and FTIR study. J. Phys. Chem. C. 118, 25016–25026 (2014).
Baltrusaitis, J., Schuttlefield, J., Zeitler, E. & Grassian, V. H. Carbon dioxide adsorption on oxide nanoparticle surfaces. Chem. Eng. J. 170, 471–481 (2011).
Wang, Z.-J., Song, H., Liu, H. & Ye, J. Coupling of solar energy and thermal energy for carbon dioxide reduction: status and prospects. Angew. Chem. Int. Ed. 59, 8016–8035 (2020).
Kaur, K. & Singh, C. V. Amorphous TiO2 as a photocatalyst for hydrogen production: A DFT study of structural and electronic properties. Energy Procedia 29, 291–299 (2012).
Staykov, A., Kamachi, T., Ishihara, T. & Yoshizawa, K. Theoretical study of the direct synthesis of H2O2 on Pd and Pd/Au surfaces. J. Phys. Chem. C. 112, 19501–19505 (2008).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 41, 7892–7895 (1990).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys.: Condens. Matter 21, 395502 (2009).
Deskins, N. A. & Dupuis, M. Electron transport via polaron hopping in bulk TiO2: A density functional theory characterization. Phys. Rev. B 75, 195212 (2007).
Morgan, B. J. & Watson, G. W. A DFT+U description of oxygen vacancies at the TiO2 rutile (110) surface. Surf. Sci. 601, 5034–5041 (2007).
Justo, J. F., de Brito Mota, F. & Fazzio, A. First-principles investigation of a-SiNx:H. Phys. Rev. B 65, 073202 (2002).
Acknowledgements
G.A.O. acknowledges the financial support of the Ontario Ministry of Research and Innovation (MRI), the Ministry of Economic Development, Employment and Infrastructure (MEDI), the Ministry of the Environment and Climate Change’s (MOECC) Best in Science (BIS) Award, Ontario Center of Excellence Solutions 2030 Challenge Fund, Ministry of Research Innovation and Science (MRIS) Low Carbon Innovation Fund (LCIF), Imperial Oil, the University of Toronto’s Connaught Innovation Fund (CIF), Connaught Global Challenge (CGC) Fund, and the Natural Sciences and Engineering Research Council of Canada (NSERC). L.H. and X.H.Z. acknowledges the support from the National Natural Science Foundation of China (51920105005, 51821002, 21902113), 111 Project, and the Collaborative Innovation Center of Suzhou Nano Science & Technology. K.K.G. acknowledges Calcul Québec (www.calculquebec.ca) and Compute Canada (www.computecanada.ca) supercomputing facility; infrastructural support from Canada Foundation for Innovation, and the financial support from the Natural Sciences and Engineering Research Council of Canada (NSERC) Discovery grant program, (RGPIN-2020-05924) and the Canada Research Chairs Program. C.M. acknowledges financial support from the UofT Faculty of Arts & Science Postdoctoral Fellowship. P.N.D. acknowledges financial support from the NSERC PDF program. This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract no. DE-AC02-06CH11357. A. Tountas’ help on ASPEN estimation is acknowledged by all authors.
Author information
Authors and Affiliations
Contributions
Z.L. and C.M. contributed equally to this work. G.A.O., X.Z., and Z.L. conceived and designed the experiments. Z.L. and Q.P. carried out the synthesis of the materials and catalytic testing. K.K.G. conducted and analyzed the DFT calculations. Z.L., C.M., M.X., J.W., F.M.A., and D.M.M. performed materials characterizations. Z.L., C.M., L.W., T.H., R.S., Q.G., and P.N.D. contributed to data analysis. G.A.O., X.Z., and K.K.G. supervised the project. G.A.O., X.Z., K.K.G., L.H., C.M., and Z.L. wrote the paper. P.N.D. edited the paper. All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, Z., Mao, C., Pei, Q. et al. Engineered disorder in CO2 photocatalysis. Nat Commun 13, 7205 (2022). https://doi.org/10.1038/s41467-022-34798-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-34798-1
This article is cited by
-
A contact-electro-catalysis process for producing reactive oxygen species by ball milling of triboelectric materials
Nature Communications (2024)
-
A Review on Engineering Transition Metal Compound Catalysts to Accelerate the Redox Kinetics of Sulfur Cathodes for Lithium–Sulfur Batteries
Nano-Micro Letters (2024)
-
Progress in design and preparation of multi-atom catalysts for photocatalytic CO2 reduction
Science China Materials (2024)
-
Photocatalytic CO2 reduction
Nature Reviews Methods Primers (2023)
-
Sub-nanomaterials for Photo/Electro-catalytic CO2 Reduction: Achievements, Challenges, and Opportunities
Chemical Research in Chinese Universities (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.