Introduction

The physics of open quantum systems (OQS), which is related with universality features and generic exotic quantum phenomena, has become one of the most intriguing topics in modern physics. An OQS may be defined as a system which is found to be in interaction with an external system, the environment. In the case of nuclear physics, the light nuclei far from the valley of beta stability are characterized by extremely low binding energies and extended nuclear matter distributions, leading in some cases to the formation of an exotic halo structure1. Such nuclei are hence excellent examples of a many-body OQS. Couplings to the continuum states play a significant role in the structure and reactions of these systems, a manifestation of which is the large breakup probability in nuclear collisions. The continuum hence provides a large environment, which strongly interacts with the subsystems, like, the elastic scattering channel related to the ground state2. Moreover, the influence of the continuum on the fusion reaction, especially at energies around the Coulomb barrier, is the frontier of fusion studies3. In this respect, studies of the breakup mechanism of a halo nuclear system open up a path for extended exploration of the dynamics of a nuclear OQS4,5.

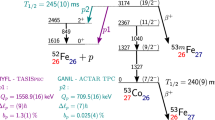
Complementary information of the breakup dynamics comes from correlations in relative motions between the breakup fragments6,7,8,9. For neutron-halo systems, owing to the difficulties of effective detection of neutrons, a few attempts have been made to measure the alphas and neutrons in coincidence for the 6He+209Bi system10. The results established that 2n−transfer, rather than breakup, was the dominant direct process. For a proton halo nucleus, however, the Coulomb barrier between the core and the valence proton prevents it from reaching the state of an OQS5. Moreover, the dynamic Coulomb polarization effect11,12 may produce a hindrance of both the proton transfer and breakup processes13. Compared to their neutron counterparts, these distinctive properties result in the rather elusive character of proton halo systems. The proton dripline nucleus 8B has a very small proton separation energy of merely 138 keV, and it is one of the few observed cases where the ground state presents a proton halo, which could be indicated by the measurements of proton elastic scattering14 and longitudinal momentum distributions of 7Be at high energies15,16,17,18. Hence, 8B provides an excellent candidate to investigate the breakup dynamics of proton halo nuclei. The breakup process of 8B is schematically depicted in Fig. 1.

Fig. 1: Illustration of 8B breaking up into 7Be and proton.
figure 1

In the initial state, the nucleons in 8B occupy bound single particle orbits in the potential well. Although located in the potential well, the halo proton is extremely weakly-bound in an extended distribution around the centrum 7Be core. It hence can be regarded as a semi-open quantum system. During the collision, 8B is excited to the unbound states above the breakup threshold (either resonant or non-resonant), forming an open quantum system.

Full size image

Exclusive breakup measurements, namely breakup fragments measured in coincidence, have been achieved at high beam energies (40−80 MeV per nucleon) to investigate the Coulomb dissociation of 8B19,20,21. Multiple reaction models22,23,24,25,26,27 were developed as well to study the breakup process at high energies. However, it becomes more challenging for incident energies close to the Coulomb barrier, since it is not easy to carry out a coincidence measurement between the breakup fragments as was done at higher energies, due to the much reduced kinematic focusing. Despite the substantial efforts devoted28,29,30,31, the low beam intensity and insufficient detection efficiency have prevented so far coincident measurements of the 8B system. To date, a few inclusive breakup measurements (only one of the breakup fragments is recorded), namely, 8B+58Ni28, 64Zn31, and 208Pb30, have been reported at energies around the Coulomb barrier. The inclusive angular distributions of the 7Be core are consistent with continuum discretized coupled channel (CDCC) calculations30,31,32,33, indicating the predominance of the elastic breakup (EBU), i.e., all of the outgoing particles are emitted in their ground states. Experiments are desired to verify this conclusion. Moreover, the elastic scattering measurements of 8B+12C34, 27Al35, 58Ni36, 64Zn31, and 208Pb29 demonstrate modest coupling effects to the continuum. By contrast, for fusion reactions, contradictory conclusions were obtained from the measurements of 8B+28Si37, 40Ar38, and 58Ni39: striking enhancement was reported for 8B+58Ni, which was not observed in 8B+28Si and 40Ar. The breakup mechanism is essential to understand this inconsistency, since, if the breakup occurs on the incoming trajectory, it might cause a loss of flux for fusion and suppress the cross section. Due to the lack of coincident measurements, however, the detailed breakup mechanism of a proton-halo nuclear system remains an open question.

In this work, we present the results of the complete kinematics measurement of 8B+120Sn at two energies around the Coulomb barrier to elucidate the breakup mechanism of 8B. We choose 120Sn as the target, since the maximum available 8B beam energy could match with its Coulomb barrier height, which enables us to investigate the Coulomb polarization effect and the Coulomb-nuclear interference as well. Using a detector array with large solid-angle coverage, we derived the correlation between the breakup fragments, 7Be and p. The breakup intermediate states are reconstructed accordingly and a comprehensive breakup picture is derived successfully. The results show that the prompt breakup mechanism dominates, occurring predominantly on the outgoing trajectory.

Results and discussion

The experiment was performed at the low-energy radioactive-ion beam facility CNS Radioactive Ion Beam separator (CRIB)40,41 of the Center for Nuclear Study (CNS), the University of Tokyo. The secondary 8B radioactive beam with a typical intensity of 1 × 104 particles per second and a purity of ~20%, impinged onto a 2.7 mg cm−2-thick, self-supporting 120Sn secondary target (97% isotopically enriched). By inserting an aluminum degrader after the primary target, we obtained 8B beams with two distinct energies of 38.7 ± 0.5 and 46.1 ± 0.6 MeV in the middle of the 120Sn target. Two parallel plate avalanche counters (PPACs)42 were installed in front of the target to reconstruct the trajectory of each incident beam ion event by event. A highly efficient silicon detector array43 was employed to detect the reaction products. A summary on the experiment is given in the “Methods” section (see below).

Angular distributions

The angular distributions of elastic scattering relative to Rutherford scattering at 38.7 and 46.1 MeV are shown, respectively, in Fig. 2a, b by squares, where only the statistical uncertainties are considered. The scattering data were normalized to a Monte Carlo simulation44, which assumes a pure Rutherford scattering at all angles and considers the geometry of the detector array and the beam position determined by the PPACs. To interpret the scattering data, CDCC calculations were performed using the codes THOx45 and FRESCO46. In Fig. 2, the elastic scattering data are compared with the CDCC results (solid curves). Overall, the agreement is very satisfactory. We include also the “one-channel” calculations (dashed curves) in which the couplings to the continuum are switched off. One can see that, although it is not as significant as in the neutron halo systems47,48, the influence of the continuum states on the elastic scattering cannot be neglected, showing a suppression of the Coulomb-nuclear interference peak. The total reaction cross section derived from the elastic scattering data are 874.1 and 1264.0 mb for 38.7 and 46.1 MeV, respectively.

Fig. 2: Angular distributions of elastic scattering and breakup reactions.
figure 2

Squares, diamonds and stars denote the experimental data of elastic scattering, inclusive and exclusive breakup at a 38.7 and b 46.1 MeV, respectively. The elastic scattering and breakup data are respectively related to the left and right axes. The error bars indicate the statistical uncertainties. CDCC results for elastic scattering and elastic breakup (EBU) are shown by the blue and magenta solid curves, respectively. As a comparison, the one-channel calculations for the elastic scattering are represented by the dashed curves. The dotted lines correspond to the non-elastic breakup (NEB) contributions, which are derived from the IAV model calculations. The dash-dotted lines stand for the sum of EBU and NEB.

Full size image

The angular distributions of inclusive and exclusive 7Be produced from 8B+120Sn reactions are shown in Fig. 2 as well by diamonds and stars, respectively. One can see that the inclusive and exclusive results are almost identical to each other within the uncertainties, providing a clear experimental evidence that breakup, rather than the proton transfer, dominates the 7Be production mechanism in the reaction of the proton halo 8B system. This is opposed to the situation for the neutron halo nucleus 6He, for which the neutron transfer dominates according to the coincident measurement of ref. 10. In semiclassical terms, Coulomb polarization favors neutrons in the halo residing in the region between the core and the target, which then enhances the transfer probabilities. It is similar to the so-called Oppenheimer-Phillips process49, a manifestation of which is that the cross section of (d, p) is enhanced as compared to (d, n) cross section owing to the strong electric polarizability of the weakly bound deuteron. For the case of the proton halo nucleus 8B, the Coulomb polarization would result in the valence proton being displaced behind the core leading to a decoupling between the core and the valence proton50. In this sense, the breakup cross section of a proton halo nucleus is expected to be large.

Two types of non-elastic breakup (NEB) processes might be included in the exclusive data: the core (7Be) and the target excitations. Due to the energy straggling of the 8B beam and the limitation of statistics, these excited states cannot be resolved from the ground state experimentally. The 7Be system has one bound excited state (Ex = 0.43 MeV, Jπ = 1/2−) below the breakup threshold. As shown in Fig. 2 by the solid curves, even though not included the 7Be excitation, CDCC calculations describe both the elastic scattering and exclusive breakup data fairly well, indicating that the contribution of the core excitation may not be significant. As a comparison, for the neutron halo nuclear system 11Be+197Au47, the elastic scattering data could only be described when the core-excited admixtures are taken into account. On the other hand, extended CDCC calculations based on the formalism of ref. 51 were performed to estimate the contribution of 120Sn target excitation to the first excited state (Ex = 1.17 MeV, Jπ = 2+) on the breakup cross sections. The results indicate that this contribution is very small: 2.4 and 2.7 mb for 38.7 and 46.1 MeV, respectively. This clearly corroborates the dominance of the elastic breakup mechanism on the measured coincidence data.

Furthermore, calculations based on the Ichimura–Austern–Vincent (IAV)31,52 model were performed to evaluate the contributions to the inclusive 7Be yield from the NEB processes, which include non-capture breakup accompanied by target excitation, proton absorption by the target (incomplete fusion) and proton transfer leading to bound states of 121Sb. The NEB calculations results as well as the sum of EBU and NEB are displayed in Fig. 2 by the dotted and dash-dotted curves, respectively. One can see that the inclusive breakup data agree well with the sum of EBU and NEB. The calculated cross-sections of EBU and NEB are, respectively, σEBU = 351.5 (420.5) mb and σNEB = 78.3 (91.4) mb for 38.7 (46.1) MeV. It demonstrates clearly that NEB contribution, although not negligible (~18% of the total 7Be yield), is just minor.

Correlations between the breakup fragments

Correlations between the breakup fragments provide key information to pin down the underlying breakup dynamics. In particular, the relative energy Erel between the breakup fragments is a critical quantity to infer the projectile excitation and location of breakup6,8,53. Erel is defined as:

$${E}_{{{{{{{{\rm{rel}}}}}}}}}=\frac{{m}_{1}{E}_{2}+{m}_{2}{E}_{1}-2\sqrt{{m}_{1}{E}_{1}{m}_{2}{E}_{2}}\cos {\theta }_{12}}{{m}_{1}+{m}_{2}},$$
(1)

where, m1, m2 and E1, E2 are the deduced masses and energies of the breakup fragments and θ12 their opening angles. The reconstructed Erel distributions (without efficiency correction) of 7Be+p at 38.7 and 46.1 MeV are presented with the circles in Fig. 3a and b, respectively, where the solid curves denote the Erel distributions reconstructed with the simulation described in the “Methods” section. In the simulation, the detector geometry, pixelation54 and energy resolution were incorporated explicitly. Overall, the simulations agree well with the experimental data at both energies, although some deviations are apparent at 46.1 MeV. This might be due to the choice of the 7Be and proton+120Sn potentials, which are derived from global parameterizations. The effect of these potentials will be more important at 46.1 MeV because it is more above the Coulomb barrier. A peak at around 0.6 MeV is observed in Fig. 3. This peak is very close to the first resonance of 8B (Ex = 0.77 MeV, Jπ = 1+, Γ = 35.6 keV), the position of which in Erel is indicated by the vertical line. Owing to the narrow width, this 1+ resonance might be the only state that can be observed as a distinctive peak in the Erel distribution. To highlight its relative contribution, we show in the insets of Fig. 3 the calculated Erel distributions for the calculation with the orbital angular momentum up to l = 3 (solid lines) and for the p-wave 1+ state (dashed curves). The simulated Erel distributions via the p-wave 1+ state are shown in Fig. 3 by the dashed curves. By integrating the peak region, the contributions from the 1+ resonance are determined as (4.4 ± 2.0)% and (3.8 ± 2.5)% at 38.7 and 46.1 MeV, respectively. The lifetime of this resonance is about 10−20 s. According to the result of 8Li8, such a timescale is sufficiently long that breakup via this state mainly occurs on the outgoing trajectory, receding from the target. The small fraction of the 1+ resonance compared to non-resonant contributions suggests nevertheless that the prompt component dominates the breakup mechanism.

Fig. 3: Measured Erel distributions for breakup fragments 7Be and proton.
figure 3

The experimental data (circles) at a 38.7 and b 46.1 MeV are compared with the simulated distributions of Erel (solid curves). The error bars show the associated statistical uncertainties. The dashed curves denote simulation results of p-wave 1+ state. The raw theoretical Erel distributions from CDCC are shown in the insets, where the solid and dashed curves represent the calculations with the orbital angular momentum up to l = 3 (total) and the contributions from the p-wave (l = 1) 1+ state. The vertical line indicates the expected location of the peak from the first 1+ resonance of 8B.

Full size image

Additional information on the timescale of breakup can be obtained from the distribution of θ12 and the orientation of the relative momentum of the breakup fragments (β) in their center-of-mass frame53,54,55. The angle β is determined from

$$\sin \beta=\frac{{v}_{1}{v}_{2}\sin {\theta }_{12}}{{({v}_{2}^{2}{u}_{1}^{2}+{v}_{1}^{2}{u}_{2}^{2}+2{u}_{1}{u}_{2}{v}_{1}{v}_{2}\cos {\theta }_{12})}^{1/2}},$$
(2)

where vi and ui are the particle velocities in the laboratory and composite rest frames, respectively. The definitions of θ12 and β, as well as the corresponding velocities are depicted in the inset of Fig. 4a. The angles θ12 and β are highly correlated when breakup occurs asymptotically with a well-defined excitation energy. The measured θ12-β distributions are shown in Fig. 4a, d. The dashed lines overlaid on the data correspond to the expected correlation between θ12 and β53 for asymptotic breakup from the 1+ resonant state of 8B. The events following the dashed lines are identified with breakup products which are weakly affected by the presence of the target Coulomb field and therefore they presumably break up far from the target. Conversely, for events arising from breakup near the target, the θ12-β correlation will be distorted due to the Coulomb postacceleration53. As shown in Fig. 4a, d, a majority of the events deviate from the asymptotic limit, further confirming that the near-target component is the dominant breakup mode in the present reaction.

Fig. 4: Angular correlations of breakup fragments 7Be and proton.
figure 4

Comparison of experimental data (circles, with error bars indicating the associated statistical uncertainties) with simulations (squares) for correlations of β and θ12 at a 38.7 and d 46.1 MeV. The dashed curves show the expected β-θ12 correlation assuming asymptotic breakup from the 1+ resonance of 8B. The projections of β and θ12 at the corresponding energies are shown in b, c, and e, f, respectively, where the solid curves represent the simulations based on the CDCC calculations. The inset in a illustrates the definitions of β and θ12. The error bars show the associated statistical uncertainties.

Full size image

The simulations based on the CDCC calculations reasonably reproduce the experimental θ12-β distributions as shown in Fig. 4a, d. The projections of β and θ12 at 38.7 MeV are shown in Fig. 4b, c, and the results at 46.1 MeV are presented in Fig. 4e, f, where the solid curves represent the simulations. For θ12, the bulk of the events appears at low angles, which peaks around 30°, and the simulation qualitatively reproduces the experimental data. It has been shown that the θ12 distribution gives information on the location of breakup53: When the projectile breaks up on the incoming trajectory, the initial velocity of the breakup fragments is towards the target nucleus, which is against the repulsive Coulomb field and results in a large θ12. By contrast, in the case of breakup along the outgoing trajectory, the initial velocities of the fragments are in the same direction as the Coulomb interaction from the target nucleus, leading to a small θ12. Therefore, the strongly forward-peaked θ12 distributions suggest that most of the breakup, while prompt, occurs along the outgoing trajectory, and hence with potentially insignificant influence on the complete fusion cross section of 8B.

The β distribution is reconstructed assuming the breakup occurs far from the target. If breakup occurs close to the target, the reconstructed β will be distorted by the post-breakup fragment-target interactions. Therefore, owing to the dominance of the near-target breakup, the distribution of β will not reflect the initial orientation of 8B*. Although the postacceleration effect is taken into account by the CDCC calculations, the simulation is found to underestimate the experimental data around 90∘. This discrepancy might indicate some inadequacy of the 7Be+120Sn interaction parameters and/or the simplified 8B structure model adopted in the CDCC calculation, which would deserve further investigation.

Before closing this section, we would like to add a brief comment about the halo property of the 8B nucleus as reflected in the longitudinal momentum distribution of the 7Be fragment. Indeed, it has been found that the narrow longitudinal momentum distribution of the 7Be fragment from breakup reactions is regarded as prominent evidence of a halo structure of 8B. Therefore, we extracted the corresponding results from the present coincident data. Gaussian-like structures are observed at both energies, and the full widths at half maximum (FWHM) are determined as 88 ± 22 and 106 ± 14 MeV/c for 38.7 and 46.1 MeV, respectively. These results are comparable with those derived with high-energy 8B beams, like, 93 ± 7 MeV/c at 38 MeV/nucleon17, 85 ± 4 MeV/c at 41 MeV/nucleon16, 81 ± 6 MeV/c at 1471 MeV/nucleon15, and 92 ± 7 MeV/c at 36 MeV/nucleon18. It is worth noting that the present result extracted from low energies includes the influence from couplings, Coulomb post-acceleration and beam energy straggling. These effects, however, are still difficult to be precisely estimated.

The breakup dynamics of a proton halo nucleus is a longstanding question. Using a highly efficient detector array, the correlation between the breakup fragments of 8B colliding with a 120Sn target was obtained at energies close to the Coulomb barrier. The results show that the yield of 7Be is almost exhausted by the elastic breakup, which occurs mainly via the short-lived continuum states, on the outgoing trajectory. Compared with the neutron halo system, the present results demonstrate distinctive OQS dynamics of a proton-halo nucleus, which is mainly due to the Coulombian effect of the halo proton. This breakup picture indicates that, although it provides a large environment, the continuum has minor influence on elastic scattering and complete fusion. To further elucidate the breakup behavior of a proton halo nuclear system, a detailed and quantitative analysis on the orientation effect is desired. This work demonstrates the applicability of the complete kinematics measurement combining the fully quantum analysis framework. This technique will be applied to further understanding the dynamics of nuclear OQS via the breakup reaction.

Methods

Experiment and data analysis

The 8B radioactive beam was produced via the 3He(6Li,8B) reaction in inverse kinematics by using a 11.2 MeV/nucleon 6Li primary beam accelerated by the RIKEN AVF cyclotron. A cryogenic 3He gas target56 was used as the primary target. 7Be and 3He were the main contaminants in the secondary beam.

The experimental setup is presented in Fig. 5. Two position-sensitive PPACs were installed in front of the 120Sn target. The distances from the upstream PPAC (PPACa) to the downstream PPAC (PPACb) and to the 120Sn target are 248 and 544 mm, respectively. The trajectory of each incident beam ion was reconstructed event by event according to the time difference between the signals arriving at the ends of the delay lines of the PPAC cathodes. The reaction products were detected by a highly efficient silicon-detector array, which comprises ten independent telescopes, arranged in a spherical shape with a radius around 70 mm. Each telescope consists of three stages of silicon detectors: the first layer is one 40/60 μm double-sided silicon strip detector (DSSD) with an effective area of 50 × 50 mm2, followed by two layers of quadrant silicon detectors with thicknesses of 1000/1500 μm. Thanks to such a compact structure, the array covered about 40% of the total solid angle with an angular coverage of 24∘−158∘. A collimator with a diameter of 20 mm was installed at the entrance of the silicon detector array (116 mm to the target) to confine the beam spot profile. The data acquisition (DAQ) system trigger condition employed was the AND of the anode signal of the upstream PPAC and the OR of the silicon detectors. This trigger condition was used for both the inclusive and exclusive measurements. Trigger rates of about 1 kHz were typically recorded during the experiment. Besides the DAQ for physical runs, another independent DAQ (CRIB-DAQ) was used for the beam tuning and PPAC on-line monitoring. For this CRIB-DAQ, the down-scaled PPACa anode signal was used as the trigger, and the “pileup" circuit was introduced to reject the sequential signals from PPACa within 500 ns. With the data recorded by the CRIB-DAQ, the efficiency of the PPACs were around 95% during the beam time.

Fig. 5: Schematic view of the experimental setup.
figure 5

The upstream and downstream parallel plate avalanche counters (PPACs) are denoted as the PPACa and PPACb, respectively. Ten silicon detector telescopes surround the 120Sn target, arranged in a spherical shape with a radius around 70 mm. To demonstrate clearly, only the first layers of the silicon detector array are displayed.

Full size image

The detectors were calibrated in energy by means of the scattered beam particles of 8B and 7Be, as well as the standard α sources containing the following radioisotopes: 148Gd, 237Np, 241Am, and 244Cm. After the energy calibration, all of the DSSD pixels can be aligned in energy. A typical ΔE − Er (residual energy) spectrum recorded by one strip of the forward-angle telescope is shown in Fig. 6a, where the loci of scattering events of the 8B and 7Be beams, as well as protons are clearly visible. The 7Be fragment resulting from 8B reactions was unambiguously separated from 7Be beam impurities using time-of-flight (TOF) techniques, as illustrated in Fig. 6b, since the 7Be from 8B breakup has the same TOF as the 8B beam. The TOF was obtained from the time difference between the occurrence of an E signal in a telescope and the radio-frequency timing pulse from the cyclotron. To identify the coincident 7Be-p events, besides setting the energy gates in the ΔE − Er spectrum to select the 7Be and p particles, we also set a timing gate, that is, for each selected breakup fragment 7Be, we search for the coincident p within a timing window of 20 ns. The events hitting the inter-strip gap were removed by setting an energy gate that both sides of the DSSD have registered the same energy in each event within 150 keV. The fraction of these inter-strip events is estimated to be less than 5%. This efficiency loss has been considered in the Monte Carlo simulation.

Fig. 6: Particle identification.
figure 6

a Typical ΔE − Er spectrum at 46.1 MeV, taken by one strip of the forward-angle telescope, covering the polar angular range of 30.4∘–50.9∘. b ΔE-TOF spectrum of two radio-frequency cycles illustrating the separation between the 7Be from 8B reactions (7Bereac.) and elastically scattered 7Be in the secondary beam (7Bebeam), as surrounded by the dashed and solid circles, respectively.

Full size image

CDCC framework

Standard CDCC calculations are employed to describe the elastic scattering and exclusive data in the present work, assuming a two-body model (p+7Be) for the 8B projectile. Bound and unbound (continuum) wave functions of this system are generated with the THOx code45 using the pseudo-state method, which consists in diagonalizing the projectile two-body Hamiltonian in a basis of square-integrable functions. In particular, we use the analytical Transformed Harmonic Oscillator (THO) basis57,58, which is obtained by application of a local scaled transformation to the conventional harmonic oscillator basis. The calculated wave functions are then used to calculate the coupling potentials which, in turn, are used to solve the set of coupled differential equations with the coupled-channels code FRESCO46. The p+7Be interaction contains central (Vc(r)) and spin-orbit (VLS(r) and VLI(r)) terms:

$$V(r)={V}_{{{{{{{{\rm{c}}}}}}}}}(r)+{V}_{{{{{{{{\rm{LS}}}}}}}}}(r){{{{{{{\bf{l}}}}}}}}\cdot {{{{{{{\bf{s}}}}}}}}+{V}_{{{{{{{{\rm{LI}}}}}}}}}(r){{{{{{{\bf{l}}}}}}}}\cdot {{{{{{{\bf{I}}}}}}}},$$
(3)

where l is the p-7Be relative orbital angular momentum, and s and I are the proton and 7Be spins, respectively. The radial dependence of each of these terms and their associated parameters can be found in ref.  31, where this model was successfully employed to analyze the 8B+64Zn reaction. The model reproduces the position of the well-known low-lying 1+ and 3+ resonances at Ex = 0.77 and 2.32 MeV, respectively, and the tentative 0+ resonance reported in ref.  59 at 1.90 MeV. It also predicts a 2+ resonance at 2.48 MeV, which might correspond to the 2+ resonance at 2.55 MeV proposed in the R-matrix analysis of ref.  59.

For the angular momentum part, the adopted coupling scheme is given by \(\left|(ls)j,\, I; \, JM \right \rangle\), J and M the total 8B spin and its z-axis projection. Using this basis, and with the adopted model Hamiltonian, the 8B states include some configuration mixing. For example, the 8B ground state is a mixture of p1/2 and p3/2 configurations with weights 0.059 and 0.941, respectively, which are in reasonable agreement with ab-initio variational Monte Carlo spectroscopic factors 0.062(1) and 0.871(4)60.

The calculation of the coupling potentials require also effective interactions (optical potentials) between the projectile subsystems and the target. For 7Be+120Sn, since there are no experimental elastic scattering data of 7Be+120Sn, we relied on a global 7Li potential of Cook61, whereas the proton-120Sn potential was taken from the global parametrization of Koning and Delaroche62.

Detection efficiency

For the exclusive breakup measurement, it is essential to determine the efficiency of detecting the breakup fragments in coincidence. To find this efficiency realistically, a novel simulation approach is established, based on the detailed outputs of CDCC. First, five-fold differential cross sections, \(d\sigma /d{\Omega }_{{}^{7}{{{{{{{\rm{Be}}}}}}}}}d{E}_{{}^{7}{{{{{{{\rm{Be}}}}}}}}}d{\Omega }_{p}\), are produced from the CDCC breakup amplitudes63. The Markov chain Monte Carlo (MCMC) method64, which is widely used in machine learning, is then employed to sample and obtain the \({E}_{{}^{7}{{{{{{{\rm{Be}}}}}}}}}\), \({\theta }_{{}^{7}{{{{{{{\rm{Be}}}}}}}}},{\theta }_{p}\) and ϕp in the laboratory frame from the five-fold parameter space, assuming \({\phi }_{{}^{7}{{{{{{{\rm{Be}}}}}}}}}\) has a flat distribution. The only unknown parameter, the proton energy Ep, can be determined based on the kinematics of the breakup reaction. Finally, the coincident detection efficiency is deduced from a Monte Carlo simulation with the complete kinematics information of each fragment and the detector array geometry.