Abstract
Muons are puzzling physicists since their discovery when they were first thought to be the meson predicted by Yukawa to mediate the strong force. The recent result at Fermilab on the muon g-2 anomaly puts the muonic sector once more under the spotlight and calls for further measurements with this particle. Here, we present the results of the measurement of the 2S1/2, F = 0 → 2P1/2, F = 1 transition in Muonium. The measured value of 580.6(6.8) MHz is in agreement with the theoretical calculations. A value of the Lamb shift of 1045.5(6.8) MHz is extracted, compatible with previous experiments. We also determine the 2S hyperfine splitting in Muonium to be 559.6(7.2) MHz. The measured transition being isolated from the other hyperfine levels holds the promise to provide an improved determination of the Muonium Lamb shift at a level where bound state QED recoil corrections not accessible in hydrogen could be tested. This result would be sensitive to new physics in the muonic sector, e.g., to new bosons which might provide an explanation of the g-2 muon anomaly and allow to test Lorentz and CPT violation. We also present the observation of Muonium in the n = 3 excited state opening up the possibility of additional precise microwave measurements.
Similar content being viewed by others
Introduction
The discovery of muons has an intriguing history. They were first detected in cosmic radiation by Anderson and Neddermayer in 19361. Interestingly, the first hints of muons were already seen in 1933 by Kunze2 in his Wilson chamber, but he was not confident enough about his results to claim the discovery of a novel particle.
The muon was first thought to be the pion predicted by Yukawa3, the heavy quantum (meson) responsible of mediating the nuclear (strong) force in analogy to the light quantum (photon) for the electromagnetic interaction. The pion, based on the range of the nuclear force, should have had a mass of 100–200 times the mass of the electron and should be both positively and negatively charged. The muon (207 times the electron mass) seemed to have just the expected value. However, in 1946 an experiment of Conversi et al.4 showed that their interaction with nuclei was too weak to be attributed to pions. They observed that the negative mesotron would decay instead of being absorbed by carbon after having formed a pionic atom as predicted by Tomonaga-Araki5. This was the first indication of the formation of muonic atoms as it was realized a few years later. Moreover, the lifetime of the muon was of the order of 10−6 s which is 1012 times longer than expected by strong interaction processes. Finally in 1947, Powell et al.6 detected the pion using photographic emulsions at high altitudes and verified that it decays into a muon and a neutral particle that was identified to be a neutrino. This led Isidor Rabi to come up with his famous quote: “Who ordered that?”.
The fascinating history of the muon continues to this day. The recent results at Fermilab7 confirming the results at Brookhaven National Laboratory8 that the measured muon anomalous magnetic moment (g-2 muon) deviates from the standard model prediction9 by 4.2 standard deviations calls for further scrutiny. Muonium (M), the bound state of the positive muon (μ+) and an electron is an ideal system to study the muon properties and hunt for possible new effects. Due to its lack of sub-structure, it is free from finite nuclear size effects and is therefore an excellent candidate to probe bound-state QED10, and search for physics beyond the Standard Model11,12,13.
Precise measurements of the ground-state hyperfine structure (HFS)14 and the 1S − 2S transition15 in Muonium were performed, with improvements proposed by MuSEUM (HFS,16) and Mu-MASS (1S − 2S,17) ongoing. All the measurements so far of the M Lamb shift (LS) are limited by statistics18,19,20. Only recently, the formation of an intense metastable M(2S) beam was demonstrated by the Mu-MASS collaboration at the low-energy muon beamline (LEM) at PSI21, opening up the possibility for precision measurements of the Muonium Lamb shift.
A first measurement at the LEM beamline resulted in a LS value of 1047.2(2.5) MHz22, representing an order of magnitude improvement upon the previous measurements. With the muCool beamline23 and (if approved) the high intensity muon beam (HiMB) upgrade at PSI24, the μ+ beam quality and flux will further improve, making it feasible to reach statistical uncertainties of the order of a few tens of kHz within a few days of beamtime.
The prospect of not being limited by statistics calls for a systematically more robust method to extract the Lamb shift. Following the example of the most precise measurements of the hydrogen Lamb shift25,26,27, extracting the LS from the isolated transition 2S1/2, F = 0 → 2P1/2, F = 1 is preferred over the other two allowed transitions (see Fig. 1). Due to the reduced influence of other nearby transitions, the systematic uncertainties related to line-pulling would become negligible.
The theoretical 2S and 2P hyperfine splittings are included. F is the quantum number describing the coupling of orbital angular momentum J and nuclear spin I, whereas mF is its magnetic quantum number. The Lamb shift is defined as the difference between the centroid values of the 2S1/2 and 2P1/2 levels.
We report here the measurement of the isolated transition between certain hyperfine components of the Muonium the Lamb shift. Combining this result with our previous measurement22, we determine the 2S hyperfine splitting in Muonium. Additionally, we present the observation of Muonium in the n = 3 excited state.
Results
The experimental data and the fits are shown in Fig. 2 and Table 1, respectively. Since for the analysis, the TL OFF data point (Sc = 20.4(4) × 10−4) was set far off-resonance at 2000 MHz, it is not displayed in the figure. When the data are fit without any 3S contribution and hence B3S fixed to 0, the reduced χ2 is 6.7 (5 degrees of freedom) and one obtains a −24.8(7.4) MHz offset compared to the theoretical value. By freeing the 3S population parameter, the fit improves to a reduced χ2 of 2.0 (4 degrees of freedom, P value of 0.09). The frequency offset is found to be 2.3(6.8) MHz. Both fits of the data are shown in Fig. 2, where the gray line corresponds to the fit without and the black line with a B3S contribution. The colored lineshapes represent the underlying transitions with resonances around 583 MHz (blue), 1140 MHz (orange), 1326 MHz (green), and a combined 3S − 3P1/2 line-shape (yellow).
The fitted black line is with, the gray line without the 3S contribution. The error bars correspond to the counting statistical error. The colored areas represent the underlying contributions from 2S − 2P1/2 transitions, namely 583 MHz (blue), 1140 MHz (orange), 1326 MHz (green), and the combined 3S − 3P1/2 (yellow). The data point with TL OFF is not displayed in the figure, but is included in the fit; it lies at 20.4(4) × 10−4.
The main systematic uncertainties are similar to the ones we calculated in ref. 22 and total in 0.19 MHz. The results are summarized in Table 2. The main difference is that the beam contamination in form of 3S states is taken into account in the fitting error already. Furthermore, due to their dependence on the resonance frequency, the systematic error stemming from the Doppler shift is approximately halved and the one coming from the uncertainty in the MW field intensity is doubled.
From this measurement, we extract the 2S1/2, F = 0 → 2P1/2, F = 1 resonance frequency to be 580.6(6.8) MHz. Using the calculated values of the 2S and 2P hyperfine splittings (557.9 MHz and 186.1 MHz, see also Table 3), we determine the M LS to be 1045.5(6.8) MHz. Our result agrees well with the theoretical value of 1047.498 (1) MHz28 and is limited by statistical uncertainty. A summary of all available measured values of the M LS is shown in Fig. 3. Using our results of the 2S1/2, F = 1 → 2P1/2, F = 1 resonance frequency22, we extract the 2S hyperfine splitting in Muonium to be 559.6(7.2) MHz.
The detected B3S/B2S ratio is 0.20(4). In the 60 ns from the foil to the entrance of the detection setup for an average M atom, 32% of the 3S states relax back to the ground state. An additional uncertainty in the estimated 3S/2S ratio arises from the assumption that the detection efficiency of Lyα and Lyβ is similar. Those efficiencies depend on a number of factors, which make an accurate determination of its wavelength-dependency challenging. From refs. 29,30,31,32, one can evaluate a systematic uncertainty of \(0.29\pm 0.07{({{{{{{{\rm{stat}}}}}}}})}_{-0.09}^{+0.05}({{{{{{{\rm{syst}}}}}}}})\). This agrees with the estimations done by C. Fry33 of 0.36 and is slightly lower than the estimate of 0.44(4) from a combination of hydrogen population measurements34,35.
To conclude, we measured the 2S1/2, F = 0 → 2P1/2, F = 1 transition in Muonium. This is the same transition as the one used for the most precise determination of the hydrogen Lamb shift27. Since this transition is even more isolated from the others compared to hydrogen, it is the best candidate for future precision LS measurements. By combining the data set with the scan of the 1140 MHz resonance and leaving the 2S HFS splitting as a free parameter, we extract the 2S hyperfine splitting in Muonium. This measurement, combined with the experimental toolbox developed in this work, is the very first step towards a future high-precision measurement of the Muonium 2S HFS, which can be done in a beam as demonstrated in hydrogen36. Such a measurement becomes interesting at a challenging precision goal of 63 Hz, corresponding to 1/8th of the uncertainty in the ground state HFS stemming from the muon mass. Furthermore, we detected M(3S). This observation opens up the possibility for microwave spectroscopy experiments with Muonium such as the n = 3 Lamb shift or the two-photon transition 3S − 3D5/2. Both these transitions were measured in hydrogen to a high precision37,38. A measurement of the 3S − 3D5/2 transition would be a unique test of Lorentz- and CPT symmetry in the muonic sector39.
In our measurement, the comparably large population of 3S states distorts the line-shape and introduces line-pulling, which might seem to defeat the purpose of choosing the isolated n = 2 transition. This is also supported by the marginal p value obtained in the analysis. However, the n = 3 population can be electrically quenched with a weak electrical field, leaving a large fraction of the n = 2 population unharmed as shown by measurements from ref. 40. Extending the beamline to depopulate the 3S due to its lifetime is another option, but the strong beam straggling at the foil and resulting diffuse beam would reduce the 2S flux significantly. This problem could be overcome by exchanging the carbon foil with only a few layers of graphene (around 1-nm thickness)41 or moving to a gaseous target. Additionally, with a state-of-the-art apparatus such as muCool to compress and cool the beam, or the HiMB project to increase the μ+ flux at PSI, the measurements would not be statistically limited anymore. This would allow to probe QED effects such as the Barker–Glover and the nucleus self-energy, which are not accessible in hydrogen yet28.
Methods
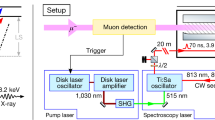
Muonium beam formation
The LEM beamline at PSI provides low (1–30 keV) energy muons with a rate of up to 20 kHz using a solid neon moderator42. In our experiment, we set the energy of the μ+ to 7.5 keV in order to maximize the number of M(2S) available for the measurement21. The beam transport is optimized with several lenses along the beamline, eventually focusing the muons onto a carbon foil at the entrance of the setup shown in Fig. 4.
The signal signature consists of a coincidence signal between Tag, Lyα and Stop-MCP. The colored lineshapes above the transmission lines (TLs) correspond to the observable transitions (1326 MHz (green), 1140 MHz (orange), 583 MHz (blue), and the combined 3S1/2 − 3P1/2 (yellow) contribution). The time scale is given for the most-probable Muonium atom with an energy of 5.7 keV.
In contrast to the LS measurements with protons, the flux of muons is around ten orders of magnitude smaller, which makes it essential to have an efficient background suppression without sacrificing efficiency. Therefore, the incoming muons are tagged on an event-by-event basis to be able to discriminate their times-of-flight (TOFs).
When impinging onto the 10-nm thin carbon foil, a μ+ releases secondary electrons. These electrons are detected by a microchannel plate (Tag MCP) to give the start signal of the TOF measurement. Upon leaving the foil, the tagged μ+ has a probability of picking up an electron and form M, primarily in the ground state. From measurements with hydrogen34,35, 5–10% is expected to be formed in n = 2 and 2% in n = 3. This expectation was confirmed with a measurement of 11(4)%21 for M in the metastable state. The M(2S) lifetime is limited by the decay time of the muon itself (τM(2S) = 2.2 μs). M(3S) is unstable (τM(3S) = 158 ns) and will relax back to the ground state via the intermediate 2P state (τM(2P) = 1.6 ns).
Microwave system
The formed beam passes first through a transmission line (TL) which depopulates unwanted hyperfine states (HFS TL). As established by the most precise hydrogen Lamb shift measurements, this reduces the background and at the same time narrows and simplifies the overall line-shape to be fitted. By setting the HFS TL at a frequency of 1140 MHz and with an average power of roughly 29 W, according to our simulation, we depopulate the F = 1, mF = ±1 states by 88% and the F = 1, mF = 0 state by 16%. The transition of interest 2S1/2, F = 0 → 2P1/2, F = 1 at 583 MHz remains almost unaffected, where its initial state F = 0, mF = 0 is only depopulated by 4%. With a second TL (Scanner TL) we scan the line-shape of this transition. Seven frequency points are measured in the range of 200–800 MHz with an average power of 22.3 W. An additional data point is taken with the Scanner TL turned off. The output powers of both TLs are continuously monitored with 50-Ohm terminated power meters to ensure the stability of the measurement. We then apply a small correction originating from the measured frequency-dependent power loss from the center of the TL to the power meter. The specific frequency points, as well as the corrected average power \(\varnothing\)P for each frequency, are summarized in Table 4.
Detection system
Due to the short lifetime of the 2P states, the atoms excited by the microwave relax to the ground state before reaching the detection setup. The remaining excited states are quenched by applying an electrical field of about 250 V cm−1 between the two grids mounted in front of the coated Lyα-MCPs (see Fig. 4) and relax back to the ground state with the emission of UV photons (2P Lyα: 121.5 nm, 3P Lyβ: 102.5 nm). These photons interact with the coating and release single electrons, which are in turn detected by the Lyα-MCPs. The beam then continues onto the Stop-MCP, giving the stop time for the TOF measurement. An event is recorded only if a coincidence signal between the Tag- and Stop-MCP is seen above threshold (double coincidence). The time window for a valid event is set to 10 μs and multiple hits in the detectors are recorded.
Analysis
The signature for the detection of M(2S) atoms is defined as the double coincidence and additionally the Lyα-MCP signal in the time region of interest (triple coincidence, see also Fig. 4).
In Fig. 5, the measured TOFs between Tag- and Stop-MCP (x axis) are correlated with the TOFs between Tag- and Lyα-MCP (y axis). The energy distribution of the M atoms after the carbon foil is well-known from previous measurements at the LEM beamline and reproduced by simulation43. The most-probable energy of the μ+ after the foil is 5.7(2) keV. The expected TOF of an M atom from the Tag- to the Stop-MCP ranges from 90 ns to 135 ns, with a most-probable TOF of 117 ns. Applying this time cut, we extract the detected amount of M and μ+, which serves as normalization factor \({S}_{{{{{{{{\rm{Norm}}}}}}}}}={N}_{M}+{N}_{{\mu }^{+}}\), accounting for variations in the beam intensity. The TOF between the tagging and the emission of a Lyα photon is calculated to be in the range of 30 ns to 75 ns. Applying both of these cuts, we identify our signal region, portrayed in Fig. 5. The amount of signal events are extracted for each frequency point (SLyα(f)). The normalized signals per frequency point are then calculated as S(f) = SLyα(f)/SNorm. The summary of the statistics gathered and the rates achieved is shown in Table 4.
In region A of Fig. 5, events with longer TOFs than expected are summarized. Those events might be caused by either convoy electrons created at the foil44 or by ionization products of a μ+ interacting with the residual gas. The region A is leaking into the signal region, contributing to the measured background. The region B contains the events where the TOFs between the Lyα- and Stop-MCP are almost zero. These MCPs are close to each other, which leads to the risk of one detector picking up a noise signal when the other one is firing or vice versa. This noise signal can have a large amplitude with an intense after-ringing, which is mistaken as an additional signal that contributes to the events in region C.
The average power inside the TLs is frequency-dependent as seen in Table 4. To be able to fit a line-shape, all frequency points are corrected to the same global power of 22.5 W, obtaining the corrected signal Sc. The applied correction is given by:
where SBKG is the background level. The correction factors C(f) are extracted by simulating the scaling ratio between the excitation probabilities at the effectively measured power and the global power for each frequency.
Fitting procedure
Because of the linear polarization of the field in the TLs, we can approximate our system to two levels and use the relevant optical Bloch equations45 in the simulation. Single-atom trajectories through both TLs reaching the Stop-MCP are simulated. While being in one of the TLs, the optical Bloch equations are numerically solved by an adaptive stepsize Runge–Kutta algorithm46. To reproduce the non-uniform field inside the TLs, for each TL a field map is generated in SIMION, following the procedure of Lundeen and Pipkin26. The numbers of excited and ground-state atoms detected in the Stop-MCP are counted and from that the average excitation probability calculated. As input parameter to the simulation we assign to each atom an initial state with its specific resonance frequency from Table 3, and the power for both TLs operating at random phases of the fields. The momentum and initial position of the specific particle from the LEM is simulated with the musrSIM package47 beforehand, from which the simulation randomly draws an atom.
The individual line-shape P(i), where i stands for the assigned resonance frequency in MHz, is constructed by simulating the excitation probability for each initial state with large statistics over a frequency range between 200 MHz and 2000 MHz in steps of 1 MHz. Combining all relevant transitions, a global line-shape Pn for a n state is obtained:
where the constant factors are coming from spin statistics.
The fitting function is constructed with the simulated lineshapes:
where Bn is scaling the line-shape Pn for a specific n state and foffset is introduced to allow for a global frequency offset compared to the simulated resonance frequencies.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon request.
Code availability
The simulation and the data analysis are developed using custom codes based on publicly available frameworks: geant4 (https://geant4.web.cern.ch/) and ROOT. The codes are available from the corresponding author upon request.
References
Neddermeyer, S. H. & Anderson, C. D. Note on the nature of cosmic-ray particles. Phys. Rev. 51, 884–886 (1937).
Kunze, P. Untersuchung der ultrastrahlung in der wilsonkammer. Zeitschrift für Physik 83, 1–18 (1933).
Yukawa, H. On the interaction of elementary particles. i. Proc. Physico-Mathematical Soc. Japn. 3rd Series 17, 48–57 (1935).
Conversi, M., Pancini, E. & Piccioni, O. On the disintegration of negative mesons. Phys. Rev. 71, 209–210 (1947).
Tomonaga, S. & Araki, G. Effect of the nuclear coulomb field on the capture of slow mesons. Phys. Rev. 58, 90–91 (1940).
Lattes, C. M. G., Occhialini, G. P. S. & Powell, C. F. Observations on the tracks of slow mesons in photographic emulsions. 1. Nature 160, 453–456 (1947).
Abi, B. et al. Measurement of the positive muon anomalous magnetic moment to 0.46 ppm. Phys. Rev. Lett. 126, 141801 (2021).
Bennett, G. W. et al. Final report of the Muon E821 anomalous magnetic moment measurement at BNL. Phys. Rev. D 73, 072003 (2006).
Aoyama, T. et al. The anomalous magnetic moment of the muon in the standard model. Phys. Rep. 887, 1–166 (2020).
Karshenboim, S. G. Precision physics of simple atoms: Qed tests, nuclear structure and fundamental constants. Phys. Rep. 422, 1–63 (2005).
Karshenboim, S. G., McKeen, D. & Pospelov, M. Constraints on muon-specific dark forces. Phys. Rev. D 90, 073004 (2014). [Addendum: Phys. Rev. D 90, 079905 (2014)].
Gomes, A. H., Kostelecký, V. A. & Vargas, A. J. Laboratory tests of Lorentz and cpt symmetry with muons. Phys. Rev. D 90, 076009 (2014).
Frugiuele, C., Pérez-Ríos, J. & Peset, C. Current and future perspectives of positronium and muonium spectroscopy as dark sectors probe. Phys. Rev. D 100, 015010 (2019).
Liu, W. et al. High precision measurements of the ground state hyperfine structure interval of muonium and of the muon magnetic moment. Phys. Rev. Lett. 82, 711–714 (1999).
Meyer, V. et al. Measurement of the 1s − 2s energy interval in muonium. Phys. Rev. Lett. 84, 1136–1139 (2000).
Nishimura, S. et al. Rabi-oscillation spectroscopy of the hyperfine structure of muonium atoms. Phys. Rev. A 104, L020801 (2021).
Crivelli, P. The mu-mass (muonium laser spectroscopy) experiment. Hyperfine Interactions 239, 1–9 (2018).
Oram, C. J. et al. Measurement of the lamb shift in muonium. Phys. Rev. Lett. 52, 910–913 (1984).
Woodle, K. A. et al. Measurement of the lamb shift in the n = 2 state of muonium. Phys. Rev. A 41, 93–105 (1990).
Kettell, S. H. Measurement of the 2S1/2 - 2P3/2 Fine Structure Interval in Muonium. Ph.D. thesis, Yale University (1990).
Janka, G. et al. Intense beam of metastable Muonium. Eur. Phys. J. C 80, 804 (2020).
Ohayon, B. et al. Precision measurement of the lamb shift in Muonium. Phys. Rev. Lett. 128, 011802 (2022).
Antognini, A. & Taqqu, D. muCool: muon cooling for high-brightness μ+ beams. SciPost Phys. Proc. 5, 030 (2021).
Aiba, M. et al. Science case for the new high-intensity muon beams himb at psi. Preprint at https://arxiv.org/abs/2111.05788 (2021).
Newton, G., Andrews, D. A., Unsworth, P. J. & Blin-Stoyle, R. J. A precision determination of the lamb shift in hydrogen. Philos.Transact. Royal Soc. London. Ser. A, Math. Phys. Sci. 290, 373–404 (1979).
Lundeen, S. R. & Pipkin, F. M. Separated oscillatory field measurement of the lamb shift in h, n = 2. Metrologia 22, 9–54 (1986).
Bezginov, N. et al. A measurement of the atomic hydrogen lamb shift and the proton charge radius. Science 365, 1007–1012 (2019).
Janka, G., Ohayon, B. & Crivelli, P. Muonium Lamb shift: theory update and experimental prospects. EPJ Web Conf. 262, 01001 (2022).
Siegmund, O. H. W., Everman, E., Vallerga, J. V., Sokolowski, J. & Lampton, M. Ultraviolet quantum detection efficiency of potassium bromide as an opaque photocathode applied to microchannel plates. Appl. Opt. 26, 3607–3614 (1987).
Tremsin, A. & Siegmund, O. The dependence of quantum efficiency of alkali halide photocathodes on the radiation incidence angle. In Proceedings of SPIE - The International Society for Optical Engineering (SPIE, 1999).
Siegmund, O., Vallerga, J. & Tremsin, A. Characterization of microchannel plate quantum efficiency. In UV, X-Ray, and Gamma-Ray Space Instrumentation for Astronomy XIV (ed. Siegmund, O. H. W.) Vol. 5898, 113–123. International Society for Optics and Photonics (SPIE, 2005).
Tremsin, A. & Siegmund, O. The stability of quantum efficiency and visible light rejection of alkali halide photocathodes. In Proceedings of SPIE - The International Society for Optical Engineering (SPIE, 2000).
Fry, C. A. Measurement of the Lamb Shift in Muonium. Ph.D. thesis, University of British Columbia (1985).
Gabrielse, G. Measurement of the n = 2 density operator for hydrogen atoms produced by passing protons through thin carbon targets. Phys. Rev. A 23, 775–784 (1981).
Tielert, R., Bukow, H. H., Heckmann, P. H., Woodruff, R. & Buttlar, H. V. Ionenstrahlspektroskopie mit Wasserstoffionen als Primärteilchen. Zeitschrift fur Physik 264, 129–138 (1973).
Rothery, N. E. & Hessels, E. A. Measurement of the 2s atomic hydrogen hyperfine interval. Phys. Rev. A 61, 044501 (2000).
Van Baak, D. A., Clark, B. O., Lundeen, S. R. & Pipkin, F. M. The \({3}^{2}{s}_{\frac{1}{2}}-{3}^{2}{d}_{\frac{5}{2}}\) interval in atomic hydrogen. iii. separated-oscillatory-field measurement. Phys. Rev. A 22, 591–608 (1980).
Fabjan, C. W. & Pipkin, F. M. Resonance-narrowed-lamb-shift measurement in hydrogen, n = 3. Phys. Rev. A 6, 556–570 (1972).
Kostelecký, V. A. & Vargas, A. J. Lorentz and cpt tests with hydrogen, antihydrogen, and related systems. Phys. Rev. D 92, 056002 (2015).
Bezginov, N. Measurement of the 2S1/2, f = 0 2P1/2, f = 1 Transition in Atomic Hydrogen. Ph.D. thesis, York U., Canada (2020).
Allegrini, F. et al. Charge state of 1 to 50 keV ions after passing through graphene and ultrathin carbon foils. Optical Eng. 53, 1–7 (2014).
Prokscha, T. et al. The new μe4 beam at psi: a hybrid-type large acceptance channel for the generation of a high intensity surface-muon beam. Nucl. Instr. Methods Phys. Res. Sec. A: Accelerators Spectrometers Detectors Associated Equipment 595, 317 – 331 (2008).
Khaw, K. et al. Geant4 simulation of the PSI LEM beam line: energy loss and muonium formation in thin foils and the impact of unmoderated muons on the μSR spectrometer. J. Instrument. 10, P10025–P10025 (2015).
Focke, P., Meckbach, W., Nemirovsky, I. & Bernardi, G. Beam-foil convoy electron double differential distributions for 60 − 300 keV protons incident on carbon foils. Nucl. Instrument. Methods Phys. Res. Sec. B: Beam Interactions Mater. Atoms 17, 314–320 (1986).
Haas, M. et al. Two-photon excitation dynamics in bound two-body coulomb systems including ac stark shift and ionization. Phys. Rev. A 73, 052501 (2006).
Press, W. H. & Teukolsky, S. A. Adaptive stepsize runge kutta integration. Comput. Phys. 6, 188–191 (1992).
Sedlak, K. et al. Musrsim and musrsimana—simulation tools for μsr instruments. 12th International Conference on Muon Spin Rotation, Relaxation and Resonance (μSR2011). Phys. Procedia 30, 61–64 (2012).
Eides, M. I. Hyperfine splitting in muonium: accuracy of the theoretical prediction. Phys. Lett. B 795, 113–116 (2019).
Karshenboim, S. & Ivanov, V. Hyperfine structure of the ground and first excited states in light hydrogen-like atoms and high-precision tests of QED. Eur. Phys. J. D 19, 13–23 (2002).
Horbatsch, M. & Hessels, E. A. Tabulation of the bound-state energies of atomic hydrogen. Phys. Rev. A 93, 022513 (2016).
Acknowledgements
This work is based on experiments performed at the Swiss Muon Source SμS, Paul Scherrer Institute, Villigen, Switzerland. This work is supported by the ERC consolidator grant 818053-Mu-MASS (P.C.) and the Swiss National Science Foundation under grant 197346 (PC). B.O. acknowledges support from the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No. 101019414, as well as ETH Zurich through a Career Seed Grant SEED-09 20-1.
Author information
Authors and Affiliations
Contributions
G.J., B.O., I.C., Z.B., L.S.B., E.D., A.G., X.N., Z.S. A.S., T.P., and P.C. have contributed to this publication, being variously involved in the design and construction of the detectors, writing software, calibrating sub-systems, operating the detectors, acquiring data, and analyzing the processed data.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Sohtaro Kanda, Krzysztof Pachucki and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Janka, G., Ohayon, B., Cortinovis, I. et al. Measurement of the transition frequency from 2S1/2, F = 0 to 2P1/2, F = 1 states in Muonium. Nat Commun 13, 7273 (2022). https://doi.org/10.1038/s41467-022-34672-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-34672-0
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.