Abstract
Reconfigurable field effect transistors are an emerging class of electronic devices, which exploit a structure with multiple independent gates to selectively adjust the charge carrier transport. Here, we propose a new device variant, where not only p-type and n-type operation modes, but also an ambipolar mode can be selected solely by adjusting a single program voltage. It is demonstrated how the unique device reconfigurability of the new variant can be exploited for analog circuit design. The non-linearity of the ambipolar mode can be used for frequency doubling without the generation of additional harmonics. Further, phase shifter and follower circuits are enabled by the n- and p-type modes, respectively. All three functions can be combined to create a 3-to-1 reconfigurable analog signal modulation circuit on a single device enabling wireless communication schemes. Both, the concept as well as the application have been experimentally demonstrated on industrial-scale fully-depleted SOI platform. The special transport physics in those structures has been analyzed by TCAD simulations as well as temperature dependent measurements.
Similar content being viewed by others
Introduction
Advances in complementary metal-oxide-semiconductor (CMOS) industry are driven by the continuous shrinking of transistor features sizes, which is traditionally associated with increased operation frequencies, lower power consumption and decreased cost per unit. This trend, however, is impeded since the transition from bulk transistors to more complex technologies like FinFETs and silicon-on-insulator (SOI) devices results in approaching physical limitations and the need for cost-intensive processing technology. However, while the single thread performance and power dissipation are stagnating, the density of transistors on a chip is further growing exponentially. This is reasoned in a second electronic mega-trend, which is functional diversification1. Microprocessors are not anymore designed for the sole purpose of performing arithmetic and logic functions. For instance, embedded non-volatile memory functionality is intensively researched as an option to enable microprocessors to overcome the van Neumann bottleneck, by manipulating the data directly where it is stored2,3. Another example is the integration of analog functionalities into the digital system, like mmWave/radar processing needed for automotive application4. A further increase in functional density is expected from the co-integration of emerging devices, whose functionality goes beyond that of classical MOSFETs such as resonant tunnel diodes5 and single-electron transistors6.
A particularly promising group of devices providing such an added functionality are reconfigurable field effect transistors (RFETs). While the polarities in classical CMOS are defined mainly by impurity doping of the channel and contact regions7, RFETs employ electrostatic doping to control the carrier injection through Schottky barriers (SB) at source and drain8,9,10,11. As a result, the user can electrically select the device functionality to be p-type or n-type. This feature can be exploited for a variety of applications, from general digital circuit design12,13,14 over hardware security primitives11,15,16 to neuronal networks17,18. However, research in the field has been mainly focused on digital applications, neglecting the potential of device-level reconfiguration for analog signal processing. Here, particularly the non-linear characteristics of Schottky barrier FETs are of interest for frequency multiplication, an important property needed in communication systems19.
In this article, we propose a ew reconfigurable device variant that can be used for three-to-one analog signal processing. The devices are built on a modified industrial FDSOI platform proving full CMOS compatibility and scalability. The unique property of applied dynamic back-bias (BB) offered by the FDSOI technology is used for programming the device characteristics. In particular, p-type, n-type, and ambipolar device modes are used to demonstrate a signal follower, phase shifter, and frequency multiplier operation, respectively. Dynamic switching between the three modes solely by adjusting the voltage of a single independent electrode is demonstrated experimentally.
Results
Back-bias reconfigurable field effect transistor
Reconfigurable transistor operation is based on the ambipolar transport in nanoscale Schottky junctions, where the current is dominated by tunneling injection of either electrons or holes through the Schottky barrier. The current ION can be approximated by the Wenzel-Kramers-Brillouin (WKB) approximation20:
where λ is the geometric screening length, m* is the effective mass, and ΦSBH the natural Schottky barrier height for electrons or holes, respectively. If the product m* ⋅ ΦSBH is equally large for holes and electrons, a symmetric ambipolar operation between p-type branch and n-type branch can be achieved. Thus, reconfigurable FETs require metal/semiconductor contacts that align close to the mid-gap Fermi level (EF) of the channel material. For silicon devices this is the case with contacts made from NiSi2. This material also provides an epitaxial relation to silicon with low-lattice mismatch21.
In order to be applicable for complementary logic, the ambipolar operation must be controlled to yield p- or n-operation modes. Thereto, the injection of undesired carriers, i.e., the undesired branch of the ambipolar transfer characteristics, is suppressed by structures with multiple independent gates. Recent attempts include implementations with two9, three22, or even more frontgates23. Also buried gates24 or a mixture of front and backgates11,25 have been used. Independent of the actual layout, all of these device concepts have in common that they aim on a deliberate spacial separation of the control gates, which steer the device, and the polarity gates, which select the active carrier type. Most often, either electrons or holes are completely filtered, leading to a clear separation between the p- and n-type mode and very low OFF-currents IOFF (see also Supplementary Table 1). However, the large multi-gate structures come at the cost of a high-area overhead, which hinders an effective co-integration with CMOS. Also, the properties of the underlying ambipolar operation mode are only accessible if several gates are tied together.
Both facts are distinctively different in the back-bias RFET variant conceived in this work. Instead of well separated independent gates, both, control gate as well as polarity gate, couple to the whole channel region. This is achieved by a thin planar channel, having a front and backgate both covering the whole channel. Naturally, this design consumes less space to be brought onto a chip. We will show that in addition to the p- and n-type modes the ambipolar characteristics, to be used for analog applications, are well preserved due to the altered band alignment.
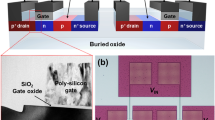
The concept has been demonstrated for FDSOI channels as shown by the schematic representation in Fig. 1a. A thin intrinsic Si channel on a 20 nm thick buried oxide (BOX) is used. A stack consisting of polysilicon/TiN (gate electrode), HfO2 (high-k dielectric), and SiO2 (interface layer) forms the frontgate (FG). At the source and drain contacts Ni is intruded by a rapid thermal annealing process to form metallic NiSix/semiconductor junctions directly within the channel. The n-doped well under the BOX is contacted separately to form a second gate on the back-side of the device. Devices have been fabricated with various gate dimensions ranging from 70 nm to 2 μm in length and 160 nm to 2 μm in width, making them compatible with the i/o devices of the 22 nm FDSOI CMOS. All transistors have been fully integrated next to working MOSFETs on 300 mm wafers with complete back-end-of-line (see also Supplementary Fig. 1).
a Schematic image of a single device with materials and contacts, comprising source (S), drain (D), front-gate (FG), and a back-bias (BB) contact. b Three distinct operation modes accessible by changing the applied back-bias (VBB). c Distribution of minimal subthreshold swing SS in ambipolar mode for VDS = 0.1 V measured at devices with varying width as compared to Fig. 1b. Boxplot shows median with 25% and 75% quartile. Outliers are indicated. d Full families of transfer characteristics for n-type (blue) and p-type (red). VDS is varied from 0.1 to 1.5 V in steps of 0.1 V. e Family of output characteristics in n-type operation. f Family of output characteristics in p-type operation. w is the channel width in all plots.
Key transfer characteristics of an exemplary device with 100 nm gate length and 250 nm width are shown in Fig. 1b. The device was tailored for an operation voltage VDD of 1.5 V, i.e., both front-gate voltage VFG and drain-source VDS are ranging between 0 and 1.5 V. It can be seen that the ambipolar transfer curve of the underlying Schottky barrier FET is well preserved if a back-bias of zero volt is applied. The minimal voltage point VMIN is centered at 0.70 V and relatively equal on-currents of 1.62E-7 A and 1.9E-7 A are achieved for the p- and n-branch, respectively. A high symmetry around VMIN is imperative for the frequency doubling application explained later. Thus, in Fig. 1c the variability of minimal swing for both branches in the ambipolar mode at VDS = +0.1 V are compared for different device sizes. Especially for medium and high channel width, which are the relevant ones for analog designs, hole and electron conductance show a very homogeneous distribution of slopes, which indicates a good p/n-symmetry. More narrow devices tend to show an increased swing and higher variability. Here, a further fine-tuning of the silicidation process is needed. Thus, we focused our analysis in this paper on the medium size and wide devices.
By application of a back-bias, the ambipolar transfer curve can be shifted seamlessly together with the voltage point VMIN. Figure 1b shows how for a sufficiently large positive back-bias voltage VBB the falling branch is shifted out of range of the front-gate voltage so that only the rising branch of the curve remains and the transistor shows the behavior of an n-type FET. Correspondingly, for sufficiently large negative VBB, only the falling branch of the curve remains, i.e., the transistor behaves like a p-type FET. Therefore, the transistor can be operated effectively in three distinctively different operation modes: ambipolar (green), n-type (blue) and p-type (red). Note that the transition between them is transition-free, as indicated by the dashed intermediate characteristics. For the p-type (n-type) operation, an applied back-bias VBB = –4.0 V (VBB = +4.6 V) was chosen such that VMIN of the corresponding saturation curve is aligned to VDD or GND, respectively. Simultaneously, the p- and n-type curve cross at VDD/2 = 0.75 V, which is desirable for digital operation. Note that it would also be possible to choose the VBB values in favor of an even better alignment of the on-currents, instead. The full set of ID–VFG characteristics of p- and n-type for various VDS are given in Fig. 1d. In order to keep the terminal at which the carriers are injected on the same side, the source contact is biased to 0 V for n-configuration and 1.5 V for p-configuration. In full ON-state, currents of 18 (10) μA/μm and an ON/OFF ratio of 890 (350) for p-type (n-type) mode are achieved. The ON/OFF ratio is limited by a flattening of the subthreshold characteristics close to the OFF-state for high absolute ∣VDS∣. The flattening originates from the on-setting injection of the opposite carrier type in the ambipolar curve. Minimal subthreshold swings of 300 mV/dec (308 mV/dec) in p- (n-) configuration are achieved for VDS = 0.6 V. Threshold voltages for a current criterion of 100 nA/μm are 0.42 V and 0.33 V for p- and n-configuration, respectively. Note that higher ON/OFF ratios can be achieved by choosing higher values of ∣VBB∣ so that the current minimum is further shifted out of the front voltage range and coincidentally resulting in higher ON-currents.
In Fig. 1e, f, the recorded output characteristics are presented for n- and p-characteristics for a VDS voltage range between 0 and 1.5 V in steps of 0.1 V. The FET-typical saturation of currents sets on for high absolute values of ∣VDS∣. For low ∣VDS∣, the curves follow a sublinear shape, which is a signpost behavior of FETs with Schottky barrier contacts20. The behavior is caused by the drain-sided Schottky barrier that limits the current additionally to the source-sided Schottky barrier as long as potential at the drain is not sufficiently pulled below the Fermi level of the source side by ∣VDS∣. At a first glance, the performance of the presented device has some natural limitations because of the concept of using a Schottky barrier contact. However, please note that this technology is not planned to completely replace classic CMOS devices, but rather provide an add-on functionality, where beneficial. Still, there are several pathways to explore in order to yield increased performance. Naturally, performance metrics can be improved with further scaling of channel length and gate oxide thickness26. Further, low-bandgap channel materials such as Ge or SiGe, which is already established for p-type transistors in CMOS, can be employed to lower VTH and increase the drive currents and gain values. Also note that the analyzed devices have a quite equal width/length ratio, while for analog applications typically ultra-wide multi-finger devices are used. Finally, it is also possible to transfer the device variant to channel materials featuring a smaller screening length like semi-metallic graphene27 layered 2D materials, such as black-phosphorus and WSe2, as channel materials10,11 once the CMOS co-integration barrier of those materials has been lowered28.
Transport analysis
In order to yield more insights into the transport physics of the new device variant, we performed temperature-dependent measurements (Fig. 2a, b) and extracted the barrier properties of our transistors. A TCAD process simulation of our device has been set up and fitted to the experimental data (Fig. 2c). Effective barrier values have been calculated from the simulated band diagrams in the on- and off-states (Fig. 2d, e) using a simple tunneling distance model and are compared to the barrier values extracted from the experiment (Fig. 2f).
a, b p-type and n-type transfer characteristics in the temperature range from 25 to 125 °C, respectively. c Fitting of the measured transfer characteristics by TCAD simulations using a process simulation approach. d, e Band diagrams for a ∣VDS∣ of 1.5 V for p-type (red, VBB = –4.0 V) and n-type (blue, VBB = 4.6 V) program, respectively. Solid lines represent ON-states, dashed lines represent OFF-states. Potential along the channel is given relative to the overall channel length L. f Extracted effective barrier values from both TCAD simulations and temperature-dependent measurements in the on- and off-states, respectively. A fixed tunneling distance deff of 2.8 nm was used to yield simulation results. Both methods agree qualitatively good. Lines are guides to the eye.
As it can be seen in Fig. 2a, b, the device exhibits a stable temperature behavior in the range from 25 to 125 °C. Other than classical MOSFETs having an inversion channel, both ON-current and OFF-current increase with temperature. This is reasoned in the increased injection of charge carriers over the Schottky barrier in the ON-state, which overshadows the effect of increased phonon scattering typically observed in MOSFETs. From the temperature data an effective barrier height ϕB,eff can be derived, which equals a thermal activation energy of the system20. If all external voltages converge towards zero, ϕB,eff is expected to approach the natural Schottky barrier height ΦSBH for the respective carrier type. The resulting barrier values extracted from an Arrhenius plot of \(\ln ({I}_{{{{{{\mathrm{D}}}}}}}/{T}^{2})\) versus 1/T as a function of VBB and VDS are shown in Fig. 2f. Note that we worked under the assumption that the thermal velocity as well as the density of states of the devices are rather independent of temperature in the elaborated temperature range29. We focused the analysis towards four distinct states, the ON- and OFF-states for p- and n-type mode, respectively. Unsurprisingly, for both modes the effective barrier is larger in the subthreshold region than in the respective saturation region. At ∣VGS∣ = 1.5 V, a small VDS-dependent barrier is present. Interestingly, the barrier does not vanish even at ∣VDS∣ = 1.5 V, indicating that higher ON-currents could be achieved by a more optimized device design, e.g., a better coupling of the front-gate or a channel material with a smaller bandgap30. The increase of ϕB,eff towards lower VDS shows the build-up of a the drain-sided Schottky barrier, which limits the ejection of the current31. This matches nicely with the observed typical Schottky-type sublinear shape of the output characteristics visible for low VDS in Fig. 1e, f. In the OFF-state, the energy barrier is mostly independent from VDS. Interestingly, ϕB,eff for p- and n-mode only sum up to 0.5 eV, which is roughly half of the bandgap Eg. This is different to other RFET concepts and reasoned in the competing blocking potential between front-gate voltage and back-gate voltage. If VBB would also be reduced towards 0 V also the barrier property would be expected to converge towards ΦSBH again. The trend of the measured barrier values (circles and squares) agrees well with the predicted effective barrier height, assuming an effective tunneling distance deff of 2.8 nm, as extracted from the band diagrams yielded by the TCAD simulations (stars). Details on the approach are given in Supplementary Fig. 3 in the supplementary information.
Frequency multiplication
Non-linear circuit elements can be used to generate an analog output signal, whose frequency is a multiple (harmonic) of its input frequency19. This functionality is of great interest in a variety of analog applications such as frequency mixers32,33, amplifiers and modulators34. A key challenge is to provide such frequency multiplication in a way that most of the energy is confined in the target frequency as often additional unwanted harmonics are generated5. Such harmonic generation leads to low conversion efficiencies. While it is possible to compensate for those effects with additional circuitry, this would largely increase area and power overheads. One approach to avoid higher order generation is the exploitation of symmetric device characteristics5. Given a perfect parabolic relation between the output and input of the device:
with A and B being constant parameters, and a sinusoidal input wave VIN of frequency f having the form
an output voltage with the following form can be derived
From there it follows that perfect parabolic transfer characteristics lead to a perfect doubling of the frequencies without the generation of higher order harmonics35. Consequently, devices providing a symmetric parabolic output have been studied intensively, including Schottky FETs36, resonant tunnel diodes5, graphene FETs32,37, carbon nanotube (CNT) FETs35, and ferroelectric (FE) FETs33,38. Especially semi-metallic graphene devices have been proposed as promising material for frequency doubling, due to their high-current throughput and large achievable gains34,39,40. However, they need very high gate voltages, are limited with respect to the on/off ratio due to the missing bandgap, and CMOS co-integration is still not solved28. Moreover, frequency doubling has been demonstrated in principle, but a sophisticated solution to adaptively tune the operation point VMIN is missing. In most cases, the carrier wave and the input signal are superimposed at the gate33,39. Therefore, VMIN has to be adjusted by carefully tuning the fabrication process, instead. For example, the usually unwanted gate-induced-drain-leakage (GIDL) is engineered to achieve parabolic transfer characteristics in FE-FETs38. As opposed to all those technologies, the bias point VMIN in BB-RFETs is not fixed by the technology. Instead, the ambipolar transfer curve can be seamlessly shifted by the applied back-bias. Thus, the working point of frequency doubling can be adapted to the DC-offset of the input signal (see also Supplementary Fig. 2). It is conceivable that an adaptive use of the back-bias as proposed for digital designs, can be established to largely improve conversion efficiencies41.
In this study, we usually aimed for centering VMIN around VDD/2. Figure 3a shows that the near perfect parabolic shape of the transfer characteristics is achieved when a back-bias VBB = –0.6 V is applied. Fitting the curve with an ideal parabola yields an R-Square value of 0.989. By superimposing a sinusoidal input signal with frequency f0 at the frontgate, which is biased to VMIN, the drain current will output a signal whose fundamental frequency is 2 ⋅ f0. Owing to the non-linearity, both positive and negative input half cycles will result in positive drain current half cycles, so that each half cycle of the input signal will lead to a full cycle at the output. The behavior follows out of equation (4) and is depicted schematically by the insets in Fig. 3a. The frequency doubling is experimentally proven using a setup employing a single BB-RFET as shown in Fig. 3b. Here, a device with 2 μm width and 90 nm gate length is used for demonstration. One S/D terminal of the transistor has been grounded while the other S/D terminal is connected via a 3.3 kΩ resistor to the supply voltage. Meanwhile, the output is measured behind a dc-decoupling capacitor of 100 nF.
a Ambipolar transfer characteristics of the used BB-RFET when steered by VBB = –0.6 V at the backgate and a drain-source voltage of VDS = 1.5 V(green). Drawn-in sine curves schematically symbolize the input and output signals at the operation point. b Circuit diagram of the single transistor setup used for frequency manipulation. The output VOUT is capacitively coupled to the Vdd node tapped between a 3.3 kΩ load resistor RDD at the supply potential and the BB-RFET. The sinusoidal input VIN is applied at the frontgate, while the back-bias voltage VBB determines the manipulation mode of the circuit. c Measured input (black, left ordinate) and output (orange, right ordinate) signal of the setup over time. Here, VDD of 1.75 V and VBB of –0.4 V are applied. d Frequency spectra of the input and output signals plotted in c calculated by fast-Fourier transform (FFT).
In Fig. 3c, the frequency doubling is clearly visible. For a sinusoidal input (left axis) with 0.75 V for both amplitude and dc-offset and a frequency of 100 kHz, the output (right axis) results in a cosine with 200 kHz. Spectral analysis via fast-fourier-transform (FFT) confirms that the majority of the output signal power is confined to 200 kHz. Higher order harmonics are nicely suppressed having a peak power of 2% or less as compared to the target harmonic. Frequency multiplication was also tested for other input frequencies in the range from 10 to 100 kHz. For frequencies exceeding 1 MHz the analysis is limited by setup parasitics and the resolution of the used measurement hardware (see also Supplementary Fig. 5).
Reversible phase shifter
The same setup as shown in Fig. 3b can also be used as a digital phase modulator42. Here, instead of the ambipolar mode, the p- and n-modes of the device are utilized. If the RFET is put into the n-type program at VBB = 6 V (see Fig. 4a), a rudimentary NMOS-inverter-like behavior is achieved. In case of a sine as input signal at the gate, the result is an inversion of the sine or in other words a 180° phase shift. We will therefore call this operation mode shifter in the following. The operation is experimentally verified for an input frequency of 100 kHz in Fig. 4b. Data for higher frequencies can be found in Supplementary Fig. 6 in the supplementary information. In general, an ideal sine-shaped output signal can be achieved when the gm of the transfer curve is almost constant over the input signal voltage range. For this analysis we have therefore limited the input signal amplitude to 0.4 V around a dc-offset of 0.75 V. Nevertheless, it should also be noted that a further shifting of the transfer curve towards lower voltages by means of the back-bias will move a more linear segment of the transfer curve into the voltage range of the frontgate.
a Individual transfer characteristics showing the underlying p-type (red) and n-type (blue) behavior for varied back-bias voltages VBB. b When the BB-RFET operates in n-configuration, the output signal VOUT (orange) is delayed by 205.1°. c When the BB-RFET is steered to p-configuration, the circuit is in the follower mode so that the output signal is equal to the input signal in frequency and phase except for some delay of 21.5°. This is a 183.6° phase shift compared to the mode in b.
When the transistor operation is changed to p-type behavior, the output voltage is not inverted anymore and the same setup turns into an input phase follower circuit. To access the p-operation, the back-bias voltage has to be changed to –5 V. Figure 4c shows the resulting output voltage behind the capacitor for a frequency of 100 kHz and an input signal amplitude of 0.4 V with a dc-offset of 0.75 V. The phase has changed by 183.6° compared to Fig. 4b and now almost follows the input signal, except for a delay of 21.5° due to the capacitive load.
Naturally, the applied back-bias voltage allows to reversibly switch between the phase shifter and follower operation modes. It should be noted that both modes only transport the fundamental wave to the output. This is because the non-linear behavior around the bias point VMIN is outside of the operation range of the input signal. This indicates that also the frequency doubling mode can be turned on and off at run-time, which we will prove in the following.
Three-in-one signal modulation
Ultimately, we demonstrate in Fig. 5 that the single transistor setup can be also reversibly and rapidly switched between follower, phase shifter and frequency doubler operation modes at run-time. For this sake the back-bias voltage is steered consecutively to –1.0 V, –5 V, –6 V, and –1.0 V so that a seamless transition between all three operation modes as shown in Fig. 5a is achieved. The measurement was carried out using the setup and transistor from Fig. 3b, using VDD of 1.5 V and an input frequency of 100 kHz. Figure 5b–g display zoomed in images at the crucial operation points. At the beginning and end of the measurement, the device is set to the ambipolar mode and the output frequency is doubled to 200 kHz (Fig. 5b). After switching to a negative VBB, an instantaneous transition to the follower mode is shown in 5c. It can be seen that an additional dc-offset is present until charging the capacitive load after switching. Figure 5d presents the steady-state operation in the follower mode for which the output phase almost equals the input phase. In Fig. 5e the mirroring of the output signal in the moment of switching between follower and phase shifter mode is shown. The phase shifter mode is then depicted at steady back-bias in Fig. 5f. Finally, a reconfiguration back to the frequency doubler mode is achieved, proving the reversibility of the configuration (Fig. 5g). Thus, a dynamic reconfigurable 3-to-1 signal modulation is possible with our back-bias RFET base structure.
A single device can be dynamically reconfigured between follower (red shade), phase shifter (blue shade) and frequency doubler (green shade) by the applied voltage at the back-gate VBB. a Large-scale overview of the applied and measured voltages for the complete reconfiguration sequence measured at 100 kHz. b–g 100 μs long sections of the signals for the individual operation modes or moments of switching. The back-bias voltage is plotted in the upper plots and the input (left axis) and output voltage (right axis) in the lower plots. Arrows indicate the chronological order of the plots. Please note that the DC component in the output waveforms is due to the transitory effect of the measurement.
Discussion
The proposed setup can be used to emulate a variety of modulation schemes as needed for wireless communication systems. Two basic concepts that can be derived from our data are binary phase shift keying (BPSK) or binary frequency shift keying (BFSK). Details on both schemes are given in Supplementary Fig. 7 in the supplementary information. Here, digital data (1s or 0s) applied at the back-gate are used to modify either phase or frequency of a carrier signal applied at the front-gate VIN. This way the data bit stream is used to shift the bias point VMIN of the ID–VG curve. In case of the BPSK the back-bias is switched in the whole voltage range between VBB,p and VBB,n. In case of BFSK only half of the voltage range is required. Beyond those simple schemes, it can be conceived that the back-bias RFET concept can also be applied for more sophisticated frequency processing applications, like frequency mixing32. The main benefit for our technology is that a frequency doubling can be achieved with a suppression of additional harmonics and without the need for inductive elements, which are hard to integrate in a CMOS platform. Owing to this, a lot of area can be saved using the BB-RFET technology. For example a compact low-power frequency doubler in the very same base technology needs 33,128 μm2 of area43, while our core as proposed in Fig. 3b requires only 2.1 μm2. This massive gain comes at the trade-off of a substantial lower operation frequency. Also, no amplifiers or stabilizing circuits are considered. Application scenarios have to be found, where the benefits of the new technology out-weight the challenges. One specific area could be hardware security11 for analog systems, where the back-bias is operated as a key to set the functionality at the front side, nicely hiding the actual functionality in the design. We believe that our work will stimulate the design and application of reconfigurable field effect transistors, both due to the newly available platform based on a 22 nm FDSOI process, as well as the added functionality of our 3-to-1 analog signal modulation circuits.
In summary, we have demonstrated a back-bias reconfigurable transistor (BB-RFET) variant that can be switched between p-type, n-type and ambipolar modes solely by the chosen applied back-bias voltage. The physical mechanisms behind the different operation modes have been analyzed in detail by electrical measurements and simulations. The potential of the reconfigurability for analog circuit designs has been explored. In the ambipolar mode, the device exhibits nearly perfect parabolic transfer characteristics, which can be applied for frequency doubling without the generation of additional harmonics. Furthermore, p- and n-type modes enable a reversible switching between a signal follower and a 180° phase shifting mode. The modes can be combined to yield a 3-to-1 reconfigurable frequency modulation circuit on a single device enabling wireless communication schemes, such as BPSK and BFSK. Both, the device as well as the application have been experimentally demonstrated on an industrial-scale fully depleted SOI platform. By the unique device design of the BB-RFET, having front and back-gate coupling to the whole channel, the individual device size has been reduced compared to prior-art RFETs and enables a co-integration into scaled CMOS processes.
Methods
Device fabrication
The presented back-bias reconfigurable field effect transistors have been processed based on GlobalFoundries 22FDX™ platform7. The devices are built on thin virtually doping-free SOI substrates with 20 nm buried oxide thickness. The integration flow shares most modules with 22 nm n-FETs, such as shallow-trench isolation (STI), gate-first high-k metal gate (HKMG) front-gate integration, and spacer deposition. In order to allow for high gate voltages, an extended SiO2 gate oxide interface has been used. Modified source and drain terminals are applied to allow for a sufficient silicide intrusion into the channel in order to create silicide-to-semiconductor junctions. A post-STI hybrid etch process is used to form back-gate contacts7. Finally, the back-end-of-line (BEOL) connections are processed. The entire process requires no changes to the 22FDX™ design rules and no additional masks with critical dimensions.
Electrical characterization
In all, 300 mm wafers have been characterized on an Accretec UF3000-e fully automatic probe station. The chuck temperature has been adjusted from 25 to 125 °C. Device characteristics have been collected using a Keithley 4200A Semiconductor Characterization System with four 4210-SMU source measurement units. The sinusoidal waveforms have been supplied by an arbitrary waveform generator (Agilent 81160A). Analog output waveforms of VOUT were collected using an Agilent DSO5054A digital oscilloscope, having an amplitude resolution limit of 2 mV and with activated low-pass-filter limiting the measurements to 25 MHz. The tool exhibited a small DC-offset of 2 mV, which was corrected in Figs. 3 and 4. To improve the readability of the graphs, noise has been reduced by a running average filter, which also slightly reduced the signal amplitudes. For reference, the original data can be found in Supplementary Fig. 8 in the supplementary information.
Device modeling
Drift-diffusion transport simulations were carried out in Synopsis TCAD. The device structure was setup using process simulations resembling the FDSOI process integration flow. Barrier tunneling was modeled using the WKB approximation for finite-element-method-based simulations. A silicide workfunction of 4.54 eV and a TiN top-gate electrode having a workfunction of 4.65 eV have been used. On-currents have been fitted by the tunneling masses of 0.60 ⋅ m0 for electrons and holes 0.27 ⋅ m0, respectively. Band diagrams have been extracted using SVisual.
Data availability
The data that support the plots within this paper and other findings of this study are under restricted access for company policy reason and are available from the corresponding author upon reasonable request.
Code availability
The computer code used in this study is available from the corresponding author upon reasonable request.
References
Salahuddin, S., Ni, K. & Datta, S. The era of hyper-scaling in electronics. Nat. Electron. 1, 442–450 (2018).
Ielmini, D. & Wong, H.-S. P. In-memory computing with resistive switching devices. Nat. Electron. 1, 333–343 (2018).
Aziz, A. et al. Computing with ferroelectric fets: devices, models, systems, and applications. In: 2018 Design, Automation & Test in Europe Conference & Exhibition (DATE). 1289–1298 (IEEE, 2018).
Ong, S. et al. A 22 nm FDSOI technology optimized for RF/mmwave applications. In: 2018 IEEE Radio Frequency Integrated Circuits Symposium (RFIC). 72–75 (IEEE, 2018).
Tolmunen, T. J. & Frerking, M. A. Theoretical performance of novel multipliers at millimeter and submillimeter wavelengths. Int. J. Infrar. Millim. Waves 12, 1111–1133 (1991).
Postma, H. W. C., Teepen, T., Yao, Z., Grifoni, M. & Dekker, C. Carbon nanotube single-electron transistors at room temperature. Science 293, 76–79 (2001).
Carter, R. et al. 22 nm FDSOI technology for emerging mobile, internet-of-things, and RF applications. In: 2016 IEEE International Electron Devices Meeting (IEDM). 2–2 (IEEE, 2016).
Mikolajick, T. et al. 20 years of reconfigurable field-effect transistors: from concepts to future applications. Solid State Electron. 186, 108036 (2021).
Heinzig, A., Slesazeck, S., Kreupl, F., Mikolajick, T. & Weber, W. M. Reconfigurable silicon nanowire transistors. Nano Lett. 12, 119–124 (2012).
Resta, G. V. et al. Polarity control in wse 2 double-gate transistors. Sci. Rep. 6, 1–6 (2016).
Wu, P., Reis, D., Hu, X. S. & Appenzeller, J. Two-dimensional transistors with reconfigurable polarities for secure circuits. Nat. Electron. 4, 45–53 (2021).
Gaillardon, P.-E., Amaru, L., Zhang, J. & De Micheli, G. Advanced system on a chip design based on controllable-polarity fets. In: 2014 Design, Automation & Test in Europe Conference & Exhibition (DATE). 1–6 (IEEE, 2014).
Rai, S. et al. Designing efficient circuits based on runtime-reconfigurable field-effect transistors. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 27, 560–572 (2018).
Rai, S. et al. Emerging reconfigurable nanotechnologies: can they support future electronics? In: 2018 IEEE/ACM International Conference on Computer-Aided Design (ICCAD). 1–8 (IEEE, 2018).
Bi, Y. et al. Emerging technology-based design of primitives for hardware security. ACM J. Emerg. Technol. Comput. Syst. (JETC) 13, 1–19 (2016).
Rai, S. et al. Security promises and vulnerabilities in emerging reconfigurable nanotechnology-based circuits. IEEE Trans Emerg Topic Comput 10, 763–778 (2020).
Pan, C. et al. Reconfigurable logic and neuromorphic circuits based on electrically tunable two-dimensional homojunctions. Nat. Electron. 3, 383–390 (2020).
Bae, J.-H. et al. Reconfigurable field-effect transistor as a synaptic device for xnor binary neural network. IEEE Electron. Device Lett. 40, 624–627 (2019).
Camargo, E. Design of FET Frequency Multipliers and Harmonic Oscillators (book) (Artech House, Inc, 1998).
Sze, S. M., Li, Y. & Ng, K. K. Physics of Semiconductor Devices (John wiley & sons, 2021).
Weber, W. M. et al. Silicon-nanowire transistors with intruded nickel-silicide contacts. Nano Lett. 6, 2660–2666 (2006).
De Marchi, M. et al. Polarity control in double-gate, gate-all-around vertically stacked silicon nanowire fets. In: 2012 International Electron Devices Meeting. 8–4 (IEEE, 2012).
Simon, M. et al. A wired-and transistor: Polarity controllable FET with multiple inputs. In: 2018 76th Device Research Conference (DRC). 1–2 (IEEE, 2018).
Müller, M. et al. Gate-controlled wse 2 transistors using a buried triple-gate structure. Nanoscale Res. Lett. 11, 1–6 (2016).
Krauss, T., Wessely, F. & Schwalke, U. Fabrication and simulation of electrically reconfigurable dual metal-gate planar field-effect transistors for dopant-free cmos. In: 2017 12th International Conference on Design & Technology of Integrated Systems In Nanoscale Era (DTIS). 1–6 (IEEE, 2017).
Sessi, V. et al. S2–2 back-bias reconfigurable field effect transistor: a flexible add-on functionality for 22 nm FDSOI. In: 2021 Silicon Nanoelectronics Workshop (SNW). 1–2 (IEEE, 2021).
Nakaharai, S. et al. Electrostatically-reversible polarity of dual-gated graphene transistors with he ion irradiated channel: toward reconfigurable cmos applications. In: 2012 International Electron Devices Meeting. 4–2 (IEEE, 2012).
Zhu, K. et al. The development of integrated circuits based on two-dimensional materials. Nat. Electron. 4, 775–785 (2021).
Gulyamov, G., Sharibaev, N. Y. & Erkaboev, U. I. The temperature dependence of the density of states in semiconductors. World J. Condens. Matter Phys. 3, 216–220 (2013).
Baldauf, T., Heinzig, A., Mikolajick, T. & Weber, W. M. Scaling aspects of nanowire schottky junction based reconfigurable field effect transistors. In: 2019 Joint International EUROSOI Workshop and International Conference on Ultimate Integration on Silicon (EUROSOI-ULIS). 1–4 (IEEE, 2019).
Beister, J. et al. Temperature dependent switching behaviour of nickel silicided undoped silicon nanowire devices. Phys. Status Solidi (c.) 11, 1611–1617 (2014).
Wang, H., Hsu, A., Wu, J., Kong, J. & Palacios, T. Graphene-based ambipolar RF mixers. IEEE Electron Device Lett. 31, 906–908 (2010).
Mulaosmanovic, H. et al. Frequency mixing with HFO2-based ferroelectric transistors. ACS Appl. Mater. Interfaces 12, 44919–44925 (2020).
Yang, X., Liu, G., Balandin, A. A. & Mohanram, K. Triple-mode single-transistor graphene amplifier and its applications. ACS Nano 4, 5532–5538 (2010).
Wang, Z. et al. Large signal operation of small band-gap carbon nanotube-based ambipolar transistor: a high-performance frequency doubler. Nano Lett. 10, 3648–3655 (2010).
Raisanen, A. V. Frequency multipliers for millimeter and submillimeter wavelengths. Proc. IEEE 80, 1842–1852 (1992).
Wang, Z. et al. A high-performance top-gate graphene field-effect transistor based frequency doubler. Appl. Phys. Lett. 96, 173104 (2010).
Mulaosmanovic, H., Breyer, E. T., Mikolajick, T. & Slesazeck, S. Reconfigurable frequency multiplication with a ferroelectric transistor. Nat. Electron. 3, 391–397 (2020).
Lee, S., Lee, K., Liu, C.-H., Kulkarni, G. S. & Zhong, Z. Flexible and transparent all-graphene circuits for quaternary digital modulations. Nat. Commun. 3, 1–7 (2012).
Wang, H., Nezich, D., Kong, J. & Palacios, T. Graphene frequency multipliers. IEEE Electron Device Lett. 30, 547–549 (2009).
Höppner, S. et al. Adaptive body bias aware implementation for ultra-low-voltage designs in 22fdx technology. IEEE Trans. Circuits Syst. II: Express Briefs 67, 2159–2163 (2019).
Harada, N., Yagi, K., Sato, S. & Yokoyama, N. A polarity-controllable graphene inverter. Appl. Phys. Lett. 96, 012102 (2010).
Cui, M., Carta, C. & Ellinger, F. Design of an ultra compact low power 60 ghz frequency doubler in 22 nm FD-SOI. In: 2020 IEEE International Symposium on Radio-Frequency Integration Technology (RFIT). 40–42 (IEEE, 2020).
Acknowledgements
The authors gratefully acknowledge the contributions of the GlobalFoundries development and operations teams. This work is funded by the Federal Ministry for Economics and Energy (BMWi) and by the Free State of Saxony in the framework of Important Project of Common European Interest (IPCEI). Further support comes from the German Federal Ministry of Education und Research (BMBF) in the framework of VE-CirroStrato.
Author information
Authors and Affiliations
Contributions
M.S., S.S., T.M., and J.T. conceived the device design and planned the experiments. V.S., M.D., and M.W. performed device integration. H.M. and M.S. conceived and designed the analog measurement setup. M.S. and J.T. performed the measurements, analyzed the data, and prepared the Figures. N.B. performed TCAD simulations. M.S. and J.T. wrote the manuscript. All authors contributed to discussion of the data and to the manuscript revision. All authors have given approval to the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Simon, M., Mulaosmanovic, H., Sessi, V. et al. Three-to-one analog signal modulation with a single back-bias-controlled reconfigurable transistor. Nat Commun 13, 7042 (2022). https://doi.org/10.1038/s41467-022-34533-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-34533-w
This article is cited by
-
Reconfigurable frequency multipliers based on graphene field-effect transistors
Discover Nano (2023)
-
Reconfigurable signal modulation in a ferroelectric tunnel field-effect transistor
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.