Abstract
A remarkable prediction of quantum field theory is that there are quantum electromagnetic fluctuations (virtual photons) everywhere, which leads to the intriguing Casimir effect. While the Casimir force between two objects has been studied extensively for several decades, the Casimir force between three objects has not been measured yet. Here, we report the experimental demonstration of an object under the Casimir force exerted by two other objects simultaneously. Our Casimir system consists of a micrometer-thick cantilever placed in between two microspheres, forming a unique sphere-plate-sphere geometry. We also propose and demonstrate a three-terminal switchable architecture exploiting opto-mechanical Casimir interactions that can lay the foundations of a Casimir transistor. Beyond the paradigm of Casimir forces between two objects in different geometries, our Casimir transistor represents an important development for controlling three-body virtual photon interactions and will have potential applications in sensing and information processing.
Similar content being viewed by others
Introduction
The interaction between three objects give rise to many fascinating phenomena such as chaos of astronomical objects1, Efimov bound states of ultracold atoms2, and frustrated states of quantum spin systems3. It is intriguing to consider the potential of three-body interactions arising solely from quantum electromagnetic fluctuations (virtual photons)4,5,6. As quantum electromagnetic fluctuations exist everywhere in the universe and in human-made devices, the Casimir effect is ubiquitous. However, the Casimir effect is often neglected or treated as a detrimental effect in micro-electromechanical systems and nano-electromechanical systems7. It will be beneficial to develop useful applications of the Casimir effect. One application of the Casimir effect is to provide a new approach to couple mechanical resonators8. Different from optomechanical coupling with real photons in cavity optomechanics9,10,11,12, optomechanical coupling with virtual photons will not suffer from cavity loss and thus will not require a high-quality cavity. Compared to electrostatic coupling, the Casimir effect does not require charge and will work for both conductors and insulators. Compared to the optical force, the Casimir force works for both transparent and opaque materials. Meanwhile, the use of the Casimir force does not prevent the use of the electrostatic force and the optical force. They may be combined to achieve more advanced functions. In addition, the Casimir effect is energy efficient as it does not require a voltage source or a light source to maintain, which will be particularly important for devices operating in the quantum regime at low temperatures.
Recently, the Casimir effect was used to increase the quality factor of a mechanical resonator13 and couple two separate mechanical resonators14,15. In addition, the Casimir effect has been utilized to realize nonlinear oscillation16, quantum trapping and self-assembling17,18. While the paradigm of Casimir effect between two objects has been extensively explored19,20,21,22,23,24,25,26, the Casimir force between three macroscopic objects has not been detected yet. The Casimir effect between three objects will be important in studying gravity at short distances as a metal film is often used to separate two test masses to shield electrostatic interactions27,28,29. Precision measurement of the Casimir effect has been used to search for a new force beyond the standard model30. Beyond its fundamental interest, a Casimir system with three objects can open the route to realize crucial technological building blocks such as a transistor-like three-terminal device with quantum vacuum fluctuations.
In this article, we report the experimental demonstration of an object under the Casimir force exerted by two other objects simultaneously. We also propose and demonstrate a three-terminal Casimir system that can switch and amplify quantum-vacuum-mediated energy transfer, in analogy to a field effect transistor. Our unique sphere-plate-sphere Casimir system consists of three closely-spaced optomechanical oscillators, as shown in Fig. 1a. A micrometer-thick cantilever is placed in between two microspheres which are attached to two other cantilevers. Their motions are monitored by three independent fiber-optic interferometers. There are random quantum vacuum fluctuations between them and hence each cantilever experiences a separation-dependent Casimir force. We first measure the Casimir force in this sphere-plate-sphere system. We then apply parametric modulation on cantilever 2 to couple their motion by the Casimir effect. In this way, energy can flow from cantilever 1 to cantilever 2 and to cantilever 3. The center cantilever serves as a gate for controlling the energy transfer through the Casimir effect. By adding gain to the center cantilever with active feedback, we also realize amplification of the quantum-fluctuation-mediated energy transfer. Our Casimir transistor will have promising application in sensing31,32 and information processing33,34.
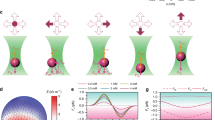
a Three modified cantilevers with resonant frequencies ω1, ω2 and ω3 experience Casimir force between each two nearby surfaces. The vibration amplitudes of three cantilevers are denoted as A1, A2 and A3. Additional parametric modulations are applied on the center cantilever to couple them by the Casimir effect. We can switch on and off the Casimir coupling between cantilever 1 and cantilever 3 by controlling the parametric modulations. In addition, we can amplify the energy transfer through Casimir effect by adding an extra gain to cantilever 2. b Measured Casimir force gradient on cantilever 2 (center) as a function of its position when the other two surfaces are fixed such that d1 + d2 = 760 nm. The blue circles are experimental measurements and the red solid line are the theoretical prediction. c The measured Casimir force on cantilever 2 is shown as a function of d2. d Measured Casimir force gradient experienced by cantilever 2 as a function of d1 when d2 is fixed at 310 nm. The red diamonds are the total force gradient \(-\frac{1}{R}\frac{dF}{dx}\) measured from cantilever 2. The blue circles are the force gradient contributed from cantilever 1. The red solid curve is the theoretical prediction of the interaction between cantilever 1 and 2. The gray dashed line is the theoretical prediction of the interaction between cantilever 2 and 3 and hence it is independent of d1 under additivity approximation. e Measured Casimir force gradient on cantilever 2 as a function of d2 when d1 is fixed at 276 nm.
Results
Casimir force in the sphere-plate-sphere configuration
We first measure the Casimir force in our sphere-plate-sphere system (Fig. 1). Assuming three surfaces are all made of ideal conductive metal and they are sufficiently thick, the Casimir force on the center one is23:
where d1 and d2 are the separations between cantilever 1 and cantilever 2, and the separation between cantilever 2 and cantilever 3 as shown in the inset of Fig. 1b. R1 and R2 are the radii of the sphere on cantilever 1 and cantilever 3, respectively. The Casimir force strongly depends on the separations and is highly nonlinear. Such a large nonlinearity is crucial for achieving parametric coupling as described in the next section. The Casimir interaction between real materials can be calculated by the Lifshitz theory15,35. Our custom Matlab codes to calculate the Casimir interaction in a sphere-plate-sphere system are provided in the Supplementary Software. We use the dynamic force measurement scheme to measure the Casimir force. More details about the calculation of Casimir interaction in our system can be found in Methods and Supplementary Note 1. The detailed force measurement schemes and results are presented in Supplementary Note 2 and Supplementary Figs. 2–5.
The measured Casimir force gradient on cantilever 2 in our three-body system is shown in Fig. 1b. We fix the position of cantilever 1 and 3 such that d1 + d2 = 760 nm. Meanwhile, we change the position of the cantilever 2 (center). As the center cantilever moves from left side to the right side, the gradient meets the lowest value when d1 = d2 if R1 = R2. At this specific separation, the net Casimir force on cantilever 2 is zero. The calculation based on Lifshitz’s formula and proximity force approximation is shown in the solid red curve. The measurement is in good agreement with the calculation. We also show the measured Casimir force gradient on cantilever 2 when separation d1 is changed by moving cantilever 1 in Fig. 1d, and similarly when separation d2 is changed by moving cantilever 3 in Fig. 1e. While there have been many studies of Casimir interaction between two objects, our work reports the measurement of the Casimir force between three separate objects. It opens up the possibility for studying Casimir interaction between more complicated configurations, and can study the nonadditivity nature36,37,38,39 of the Casimir interaction by reducing the thickness of the center plate (see Supplementary Fig. 1).
Casimir vibration coupling
We now use the Casimir effect to efficiently couple the motions of three cantilevers for realizing a more advanced Casimir-based device. The natural frequencies and damping rates of three cantilevers are ω1 = 2π × 5661 Hz, ω2 = 2π × 6172 Hz, ω3 = 2π × 4892 Hz, γ1 = 2π × 3.22 Hz, γ2 = 2π × 6.06 Hz, and γ3 = 2π × 3.58 Hz when they are far apart. These frequencies shift under Casimir interaction. The direct Casimir coupling strength between three cantilevers is smaller than the frequency differences between them. To solve this issue, we use parametric coupling15,40 by modulating the separation between each two cantilevers at a slow rate ωmod1,2 and a modulation amplitude δd1,2. This is achieved by changing the position of the cantilever 2 as \({\delta }_{{{{{{{{\rm{d1}}}}}}}}}\cos ({\omega }_{{{{{{{{\rm{mod1}}}}}}}}}t)+{\delta }_{{{{{{{{\rm{d2}}}}}}}}}\cos ({\omega }_{{{{{{{{\rm{mod2}}}}}}}}}t)\). Such parametric modulation effectively couples three cantilevers when ωmod1 = ∣ω1 − ω2∣ and ωmod2 = ∣ω3 − ω2∣, as shown in Fig. 2a. Different from direct coupling that requires identical resonant frequencies, parametric coupling provides more freedom to couple different resonators. Under the parametric coupling scheme, the simplified Hamiltonian of the three-cantilever system in the interaction picture is (see Methods and Supplementary Note 4 for detailed derivations)15:
where γ1,2,3 denote the damping rates of the three cantilevers. \({g}_{12}=\frac{{{{\Lambda }}}_{1}}{2\sqrt{{m}_{1}{m}_{2}{\omega }_{1}{\omega }_{2}}}\) and \({g}_{23}=\frac{{{{\Lambda }}}_{2}}{2\sqrt{{m}_{2}{m}_{3}{\omega }_{2}{\omega }_{3}}}\) are the coupling strengths between cantilever 1 and cantilever 2, and between cantilever 2 and cantilever 3, respectively. Here we have \({{{\Lambda }}}_{1}=\frac{{d}^{2}{F}_{C}}{d{x}^{2}}{|}_{{d}_{10}}{\delta }_{{{{{{{{\rm{d1}}}}}}}}}\) and \({{{\Lambda }}}_{2}=\frac{{d}^{2}{F}_{C}}{d{x}^{2}}{|}_{{d}_{20}}{\delta }_{{{{{{{{\rm{d2}}}}}}}}}\). Here d10,20 is the equilibrium separation when there is no modulation applied. δ2 = ω1 + ωmod1 − ω2 and δ3 = ω1 + ωmod1 − ωmod2 − ω3 are the detuning of the system which depend on the modulation frequencies. The eigenvalues of this Hamiltonian near resonant coupling conditions are shown in Fig. 2b. We can observe a clear two-fold anti-crossing when the detunings δ3 = δ2 = 0.
a Parametric modulation of the Casimir interaction is applied in our system. When ωmod1 = ω2 − ω1, cantilever 1 and cantilever 2 are coupled. Similarly, cantilever 2 and cantilever 3 are coupled when ωmod2 = ω2 − ω3. Here \({\omega }_{{{{{{{{\rm{mod}}}}}}}}1,2}\) is the modulation frequency. b Three eigenvalues of the Hamiltonian in Eq. (2) as a function of δ3 when δ2 = 0 and ∣g12∣ = ∣g23∣ = 2π × 20 Hz. Here δ2 = ω1 + ωmod1 − ω2 and δ3 = ω1 + ωmod1 − ωmod2 − ω3 are the detuning of the system. g12 and g23 are the coupling strengths between cantilever 1 and cantilever 2, and between cantilever 2 and cantilever 3, respectively. c Measured power spectrum density (PSD) of cantilever 3 as a function of the modulation frequency ωmod2. e PSD of cantilever 2 as a function of ωmod2. The modulation amplitudes are δd1 = 10.4 nm and δd2 = 14.1 nm. The modulation frequency ωmod1 is fixed at 440 Hz. d, f The simulated PSD for two cantilevers. The separations are d10 = 88 nm and d20 = 90 nm.
Our experimental results of the level repulsion behavior due to the Casimir coupling between three cantilevers are show in Fig. 2c, e. We study this behavior experimentally by scanning the power spectrum densities (PSD) of cantilever 3 (Fig. 2c) and cantilever 2 (Fig. 2e) as a function of the modulation frequency ωmod2 when ωmod1 = ∣ω1 − ω2∣. Figure 2e shows three branches which correspond to the hybrid modes of three cantilevers after being projected to cantilever 2. Since ωmod1 is fixed at the resonant value that can couple cantilever 1 and cantilever 2, we notice a clear anti-crossing behavior (a horizontal dark line around 6080 Hz) independent of ωmod2. The two horizontal branches describe the coupled motion of cantilevers 1 and 2. When we vary ωmod2, we also observe an inclined branch with a frequency ω3 + ωmod2 which corresponds to the motion of cantilever 3. When this inclined branch intersects with the other two branches at ωmod2 = ∣ω3 − ω2∣, a more complicated level repulsion is observed. One mode disappears in the PSD of cantilever 2 as this mode only involves the motion of cantilever 1 and 3. More detailed discussions about the eigenvalues and PSD of the system is included in Supplementary Note 4. Numerical simulation results are shown in Fig. 2d, f, which agree well with experimental results. Thus we have strongly coupled the motions of three objects with quantum vacuum fluctuations.
Casimir switch
Our three-terminal Casimir system enables switching (Fig. 3a) and amplifying quantum-fluctuation-mediated energy transfer in analogy to a field effect transistor (Fig. 3b). The quantum-fluctuation-mediated energy transfer between cantilever 1 and 3 can be easily switched on and off by controlling the modulation on cantilever 2 (Fig. 3c). When ωmod1 and ωmod2 are on resonance, vibration energy from cantilever 1 can be transferred to cantilever 3 efficiently (Fig. 3e). However, when the modulation is off, the excitation on cantilever 1 can not be transferred to cantilever 3 efficiently (Fig. 3d). In Fig. 3f, the measured amplitude ratio A3/A1 is shown as a function of modulation frequency ωmod2 for both switch on and off cases. We notice that the amplitude ratio can achieve up to 0.44 when the modulation is on resonance, and close to zero when the modulation if off resonance. Thus we can switch on and off the quantum-fluctuation-mediated energy transfer with high contrast. The separations in Figs. 3 and 4 are larger than those separations in Fig. 2 and give smaller coupling strengths: g12 = 2π × 3.5 Hz and g23 = 2π × 3.9 Hz. These coupling strengths are comparable to the damping rates of the cantilevers so there is no mode splitting in this case.
a A symbolic switch. b A symbolic field effect transistor. c The quantum-fluctuation-mediated energy transfer between cantilever 1 and 3 can be switched on and off by the modulation on cantilever 2. The position of cantilever 2 is modulated with modulation amplitudes δd1,2 and modulation frequencies ωmod1,2. d Measured displacement of two cantilevers (x1 and x3) when modulation is off. e Measured displacement of two cantilevers when modulation is on. Energy from cantilever 1 is transferred efficiently to cantilever 3. Here ωmod1,2 = 2π × 465 Hz, ωmod2 = 2π × 1230 Hz, δd1 = 6.0 nm, and δd2 = 8.5 nm. The separations are d10 = 100 nm and d20 = 105 nm. f The transduction ratio A3/A1 is shown as a function of the modulation frequency ωmod2 when ωmod1 is on resonant. A1 and A3 are the vibrational amplitudes. The blue circles and the red diamonds correspond to the switch on and off case, respectively. The magenta solid line is the simulation. g The transduction ratio A3/A1 as a function of modulation amplitude δd1 when ωmod2 = 2π × 1231 Hz (on resonant, blue circles) and ωmod2 = 2π × 1150 Hz (off resonant, red diamonds). ωmod1 is on resonant for both cases. The magenta solid curve is the simulation and the green solid curve is the calculation based on Eq. (3).
a An extra gain G is applied on cantilever 2 by feedback control together with parametric modulation. b The signal on cantilever 1 (x1) is transmitted to cantilever 3 (x3) with amplification. c The transduction ratio A3/A1 is shown as a function of modulation frequency ωmod2 when the gain is on (red diamonds) and off (blue circles). ωmod1 is on resonant for both cases. G is the gain coefficient on cantilever 2. Under the extra gain, the damping rate of cantilever 2 becomes γ2 = γ20 − G, where γ20 is the natural damping rate. The cyan and magenta solid curve are the simulations. d The vibrational amplitude A3 is shown as a function of amplitude A1 for three different gain coefficients G. The parametric modulation is applied resonantly at the same time. The green, magenta and blue solid line are the simulated results for three different gain coefficients. e The ratio A3/A1 is shown as a function of modulation amplitude δd1 for cases with gain, no gain, and off-resonant modulation. δd2 = 1.42δd1. f The transduction ratio A3/A1 (blue circles) is shown as a function of the extra feedback gain G applied on cantilever 2. The red solid curve is the simulation.
Under the steady state when the cantilever 1 is driven at ω1 with a small amplitude and the parametric modulation on cantilever 2 is on resonant, the transduction ratio A3/A1 in this three-cantilever Casimir system is (see Methods):
where \({{{\Lambda }}}_{1}=\frac{{d}^{2}{F}_{C}}{d{x}^{2}}{|}_{{d}_{10}}{\delta }_{{{{{{{{\rm{d1}}}}}}}}}\) and \({{{\Lambda }}}_{2}=\frac{{d}^{2}{F}_{C}}{d{x}^{2}}{|}_{{d}_{20}}{\delta }_{{{{{{{{\rm{d2}}}}}}}}}\). For Fig. 3, the cantilever 1 is driven at 5649 Hz, which is its resonant frequency in this situation. In Fig. 3g, the measured transduction ratio A3/A1 is shown as a function of modulation amplitude δd1 when δd2 = 1.42δd1. The transduction ratio is close to zero when the parametric modulation is off-resonant. As expected, the ratio A3/A1 increases when δd1 increases under resonant coupling. Our experimental results agree well with Eq. (3) and numerical simulation results (Fig. 3g).
Casimir amplification
To realize a Casimir transistor with high efficiency, we introduce an extra gain to the system (Fig. 4a) to amplify the quantum-fluctuation-mediated energy transfer. The extra gain is applied to cantilever 2 by feedback control such that the damping rate of cantilever 2 becomes γ2 = γ20 − G, where γ20 is the natural damping rate of cantilever 2 and G is the gain coefficient (More details can be found in Supplementary Note 3 and Supplementary Fig. 6). γ2 becomes negative when G > γ20. Based on Eq. (3), the transduction ratio A3/A1 increases when γ2 decreases. Under such condition, energy from cantilever 1 is first transferred to cantilever 2 and get amplified and then transferred to cantilever 3. For example, we apply a fixed gain to cantilever 2 such that G = 2π × 8.73 Hz to realize the amplification of energy transfer, as shown in Fig. 4b. Other parameters are the same as those in Fig. 3e.
Figure 4c shows amplification of quantum-fluctuation-mediated energy transfer with our Casimir transistor. When a gain is applied to cantilever 2, energy transfer from cantilever 1 to cantilever 3 shows a similar resonant behavior as the no-gain case, but has an improvement by a factor of 8 on the transduction ratio . The additional gain improves the quantum-fluctuation-mediated energy transfer efficiency significantly. As expected, the transduction ratio A3/A1 increases when the parametric modulation amplitude (Fig. 4e) or the gain coefficient (Fig. 4d, f) increases until the system becomes unstable when the modulation amplitude or the gain is too large. Thus we have demonstrated amplification in a three-terminal Casimir system. The amplification function will be crucial for future applications of Casimir-based devices. For example, Casimir parametric amplification has been theoretically proposed for zeptometer metrology31 and ultrasensitive magnetic gradiometry32.
Discussion
We have measured the Casimir interaction between three objects, and demonstrated efficient coupling of three optomechanical resonators with virtual photons. Compared to the conventional optomechanical coupling with real photons in a high-Q cavity9,10, optomechanical coupling with virtual photons8,41 does not need a high-Q cavity. Inspired by a field effect transistor, we also demonstrate switching and amplifying quantum-fluctuation-mediated energy transfer in our three-terminal Casimir system. As proposed by former theoretical studies, Casimir-based amplification and switching will have applications in sensing31,32 and information processing33,34. The realization of Casimir coupling between three resonators is an important step toward realizing a scalable Casimir array. The three resonators can also be modified to realize a circulator in the future, which can have non-reciprocity between any two of the three resonators42. By reducing the thickness of the center cantilever, the system can be used to study non-pairwise additive effects38,39. The Casimir effect between three objects is also important in studying gravity at short distances27,28,29.
Methods
Casimir force calculation
At a finite temperature, the Casimir interaction comes from both quantum and thermal fluctuations. At temperature T and separation x, the Casimir energy per unit area between two surfaces is given by35:
where \({\xi }_{l}=\frac{2\pi {k}_{B}Tl}{\hslash }\) is the Matsubara frequency and \({k}_{\perp }=\sqrt{{k}_{x}^{2}+{k}_{y}^{2}}\) is the wave vector parallel to the surface. rTE(iξl, k⊥) and rTM(iξl, k⊥) are reflection coefficients of the transverse-electric and transverse-magnetic modes. The separation between two surfaces is far smaller than the dimensions of the cantilever and the sphere. Therefore, we can apply the proximity-force approximation and the Casimir force between a sphere with radius R and a plate is FC(x, T) = − 2πRE(x, T). The calculation in ref. 15 has shown that the contribution from thermal fluctuations at room temperature is less than 4% when the separation is less than 800 nm. Thus, the Casimir interaction in our system is dominated by quantum vacuum fluctuations. In our system, the thickness of the center cantilever is 1 μm and the typical separation in our measurement is from 50 to 800 nm. Under such condition, the contribution from the nonadditivity is negligible compared to the sum of the pair potential and hence we take the additivity approximation36. Under the thermal equilibrium, the force on the center cantilever can be simplified as F2,C = − FC(d1, T) + FC(d2, T). Under the additivity approximation, the force gradient between cantilever 1 and cantilever 2 is calculated by subtracting the force gradient between cantilever 2 and cantilever 3 from the total gradient experienced by cantilever 2, as shown in Fig. 1d.
Experimental setup and force measurement
In the experiment, we use three modified AFM cantilevers to build the three-terminal Casimir system. The left and right cantilever has a dimension of 450 × 50 × 2 μm3. The center cantilever has a dimension of 500 × 100 × 1 μm3. Two 70-μm-diameter polystyrene spheres are attached to the free end of the left and right cantilevers to create the sphere-plate-sphere geometry. Additional 100-nm-thick gold layers are coated on both the sphere and cantilever surfaces.
During the measurement, we use phase-lock loop to track the resonant frequency in the presence of the Casimir interaction. Then we can get the force gradient as \(\frac{dF}{dx}=-2k\frac{\delta \omega }{\omega }\), where k is the spring constant of the cantilever, δω is the frequency shift in the presence of the interaction and ω is the natural resonant frequency. The separation between each two surfaces is calibrated by the electrostatic force. The frequency shift due to the electrostatic force and the Casimir force is \({{\Delta }}\omega=-\frac{\omega }{2k}\frac{\pi {\epsilon }_{0}R}{{x}^{2}}[{({V}_{{{{{{{{\rm{ext}}}}}}}}}-{V}_{{{{{{{{\rm{c}}}}}}}}})}^{2}+{V}_{{{{{{{{\rm{rms}}}}}}}}}^{2}]-\frac{\omega }{2k}\frac{d{F}_{C}}{dx}\), where Vext is the external voltage applied on the surface, Vc is the patch potential, Vrms is the rms voltage fluctuations. \(\frac{d{F}_{C}}{dx}\) is the force gradient of the Casimir interaction at separation x. By measuring the frequency shift of the cantilever for different external voltage Vext, we can calculate the real separation between two surfaces. Our measurements show that the contribution from the rms voltage fluctuations is negligible compared to the Casimir force. After canceling the contribution from electrostatic force, we can get the Casimir force gradient. The Casimir force gradient can be integrated over separation to obtain the Casimir force.
Casimir force coupling and energy transfer
Under a slow modulation on cantilever 2, the separation between each two cantilevers is time-dependent such that:
Here d10,20 is the equilibrium separation when there is no modulation applied, δd1,d2 is the modulation amplitude, and ωmod1,2 are two modulation frequencies. x1(t), x2(t) and x3(t) describe vibrations of three cantilevers near their equilibrium positions. The motions of the cantilevers follow equations:
Here we generalize the displacements x1,2,3(t) to complex values z1,2,3(t) such that x1,2,3(t) = Re[z1,2,3(t)]. We separate the fast-rotating term and the slow-varying term for z1,2,3(t) such that:
where B1,2,3(t) is the slow-varying amplitudes and we can neglect their second derivative terms \({\ddot{B}}_{1,2,3}(t)\) in the equations of motion. Under the limit of the small damping rate of three cantilevers such that γ1,2,3 ≪ ω1,2,3 and the rotating wave approximation, the equation of motion can written as:
where \({{{\Lambda }}}_{1,2}=\frac{{d}^{2}{F}_{C}}{d{x}^{2}}{|}_{{d}_{10,20}}{\delta }_{{{{{{{{\rm{d1,2}}}}}}}}}\). We have applied the transformation such that \({B}_{1}^{\prime}(t)={B}_{1}(t)\), \({B}_{2}^{\prime}(t)={B}_{2}(t){e}^{i{\delta }_{2}t}\), and \({B}_{3}^{\prime}(t)={B}_{3}(t){e}^{i{\delta }_{3}t}\), where δ2 = ω1 + ωmod1 − ω2 and δ3 = ω1 + ωmod1 − ωmod2 − ω3 are the system detunings. Under the steady condition, \({\dot{B}}_{1}\), \({\dot{B}}_{2}\), and \({\dot{B}}_{3}\) all equal to zero. The vibration amplitude of three cantilevers A1,2,3 is the absolute value of the slow-varying component so we have A1,2,3(t) = ∣B1,2,3(t)∣. In this way, the ratio of A3/A1 is:
The vibrations of the three cantilevers can be quantized as phonons. By introducing normalized amplitudes \({c}_{1}=\sqrt{\frac{{m}_{1}{\omega }_{1}}{\hslash }}{B}_{1}^{\prime}\), \({c}_{2}=\sqrt{\frac{{m}_{2}{\omega }_{2}}{\hslash }}{B}_{2}^{\prime}\), and \({c}_{3}=\sqrt{\frac{{m}_{3}{\omega }_{3}}{\hslash }}{B}_{3}^{\prime}\), we obtain the equation of motion for the phonon modes as:
where \({g}_{12}=\frac{{{{\Lambda }}}_{1}}{2\sqrt{{m}_{1}{m}_{2}{\omega }_{1}{\omega }_{2}}}=\frac{{d}^{2}{F}_{C}}{d{x}^{2}}{|}_{{d}_{10}}{\delta }_{{{{{{{{\rm{d1}}}}}}}}}\frac{1}{2\sqrt{{m}_{1}{m}_{2}{\omega }_{1}{\omega }_{2}}}\), and \({g}_{23}=\frac{{{{\Lambda }}}_{2}}{2\sqrt{{m}_{2}{m}_{3}{\omega }_{2}{\omega }_{3}}}=\frac{{d}^{2}{F}_{C}}{d{x}^{2}}{|}_{{d}_{20}}{\delta }_{{{{{{{{\rm{d2}}}}}}}}}\frac{1}{2\sqrt{{m}_{2}{m}_{3}{\omega }_{2}{\omega }_{3}}}\). Here we consider a special case that g12 = g23, γ1 = γ3, and δ2,3 = 0. The eigenvalues of the Hamiltonian are:
When the coupling strength is large compared to the damping difference such that \(|{g}_{12}|\, > \, \frac{|{\gamma }_{1}-{\gamma }_{2}|}{2\sqrt{2}}\), we have \({{\rm{Im}}}({\lambda }_{2})=-\frac{{\gamma }_{1}+{\gamma }_{2}}{4}\) and hence the steady state requires that:
When the coupling strength is small compared to damping difference such that \(|{g}_{12}| < \frac{|{\gamma }_{1}-{\gamma }_{2}|}{2\sqrt{2}}\), we have \({{\rm{Im}}}({\lambda }_{2})=-\frac{{\gamma }_{1}+{\gamma }_{2}}{4}+\frac{\sqrt{{({\gamma }_{1}-{\gamma }_{2})}^{2}-8{g}_{12}^{2}}}{4}\). The steady state requires that:
Data availability
All other data that support the plots within this paper and other findings of this study are available from the corresponding authors upon request. Source data are provided with this paper.
Code availability
The custom codes that support the findings of this study are provided with this paper.
References
Musielak, Z. E. & Quarles, B. The three-body problem. Rep. Prog. Phys. 77, 065901 (2014).
Kraemer, T. et al. Evidence for efimov quantum states in an ultracold gas of caesium atoms. Nature 440, 315–318 (2006).
Lacroix, C., Mendels, P. & Mila, F. Introduction to Frustrated Magnetism: Materials, Experiments, Theory, Vol. 164 (Springer Science & Business Media, 2011).
Casimir, H. B. G. On the attraction between two perfectly conducting plates. Proceedings 51, 793–795 (1948).
Woods, L. M. et al. Materials perspective on Casimir and van der Waals interactions. Rev. Mod. Phys. 88, 045003 (2016).
Gong, T., Corrado, M. R., Mahbub, A. R., Shelden, C. & Munday, J. N. Recent progress in engineering the Casimir effect—applications to nanophotonics, nanomechanics, and chemistry. Nanophotonics 10, 523–536 (2021).
Zhao, Y. P., Wang, L. S. & Yu, T. X. Mechanics of adhesion in MEMS—a review. J. Adhes. Sci. Technol. 17, 519–546 (2003).
Di Stefano, O. et al. Interaction of mechanical oscillators mediated by the exchange of virtual photon pairs. Phys. Rev. Lett. 122, 030402 (2019).
Xu, H., Mason, D., Jiang, L. & Harris, J. Topological energy transfer in an optomechanical system with exceptional points. Nature 537, 80–83 (2016).
Yang, C., Wei, X., Sheng, J. & Wu, H. Phonon heat transport in cavity-mediated optomechanical nanoresonators. Nat. Commun. 11, 4656 (2020).
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014).
Barzanjeh, S. et al. Optomechanics for quantum technologies. Nat. Phys. 18, 15–24 (2022).
Pate, J. M., Goryachev, M., Chiao, R. Y., Sharping, J. E. & Tobar, M. E. Casimir spring and dilution in macroscopic cavity optomechanics. Nat. Phys. 16, 1117–1122 (2020).
Fong, K. Y. et al. Phonon heat transfer across a vacuum through quantum fluctuations. Nature 576, 243–247 (2019).
Xu, Z., Gao, X., Bang, J., Jacob, Z. & Li, T. Non-reciprocal energy transfer through the Casimir effect. Nat. Nanotechnol. 17, 148–152 (2022).
Chan, H. B., Aksyuk, V. A., Kleiman, R. N., Bishop, D. J. & Capasso, F. Nonlinear micromechanical Casimir oscillator. Phys. Rev. Lett. 87, 211801 (2001).
Zhao, R. et al. Stable Casimir equilibria and quantum trapping. Science 364, 984–987 (2019).
Munkhbat, B., Canales, A., Küçüköz, B., Baranov, D. G. & Shegai, T. O. Tunable self-assembled Casimir microcavities and polaritons. Nature 597, 214–219 (2021).
Sparnaay, M. Measurements of attractive forces between flat plates. Physica 24, 751 – 764 (1958).
Bressi, G., Carugno, G., Onofrio, R. & Ruoso, G. Measurement of the Casimir force between parallel metallic surfaces. Phys. Rev. Lett. 88, 041804 (2002).
Lamoreaux, S. K. Demonstration of the Casimir force in the 0.6 to 6 μm range. Phys. Rev. Lett. 78, 5 (1997).
Mohideen, U. & Roy, A. Precision measurement of the Casimir force from 0.1 to 0.9 μm. Phys. Rev. Lett. 81, 4549–4552 (1998).
Chan, H. B., Aksyuk, V. A., Kleiman, R. N., Bishop, D. J. & Capasso, F. Quantum mechanical actuation of microelectromechanical systems by the Casimir force. Science 291, 1941–1944 (2001).
Munday, J. N., Capasso, F. & Parsegian, V. A. Measured long-range repulsive Casimir-Lifshitz forces. Nature 457, 170–173 (2009).
Garrett, J. L., Somers, D. A. T. & Munday, J. N. Measurement of the Casimir force between two spheres. Phys. Rev. Lett. 120, 040401 (2018).
Tang, L. et al. Measurement of non-monotonic Casimir forces between silicon nanostructures. Nat. Photonics 11, 97–101 (2017).
Geraci, A. A., Papp, S. B. & Kitching, J. Short-range force detection using optically cooled levitated microspheres. Phys. Rev. Lett. 105, 101101 (2010).
Blakemore, C. P. et al. Search for non-Newtonian interactions at micrometer scale with a levitated test mass. Phys. Rev. D 104, L061101 (2021).
Westphal, T., Hepach, H., Pfaff, J. & Aspelmeyer, M. Measurement of gravitational coupling between millimetre-sized masses. Nature 591, 225–228 (2021).
Chen, Y.-J. et al. Stronger limits on hypothetical Yukawa interactions in the 30–8000 nm range. Phys. Rev. Lett. 116, 221102 (2016).
Javor, J. et al. Zeptometer metrology using the Casimir effect. J. Low. Temp. Phys. 208, 147–159 (2022).
Javor, J., Yao, Z., Imboden, M., Campbell, D. K. & Bishop, D. J. Analysis of a Casimir-driven parametric amplifier with resilience to Casimir pull-in for MEMS single-point magnetic gradiometry. Microsyst. Nanoeng. 7, 73 (2021).
Benenti, G., D’Arrigo, A., Siccardi, S. & Strini, G. Dynamical Casimir effect in quantum-information processing. Phys. Rev. A 90, 052313 (2014).
Liu, X.-F., Li, Y. & Jing, H. Casimir switch: steering optical transparency with vacuum forces. Sci. Rep. 6, 27102 (2016).
Lifshitz, E. M. The theory of molecular attractive forces between solids. Sov. Phys. JETP 2, 73–83 (1956).
Messina, R. & Antezza, M. Three-body radiative heat transfer and Casimir-Lifshitz force out of thermal equilibrium for arbitrary bodies. Phys. Rev. A 89, 052104 (2014).
Milton, K. A. et al. Three-body effects in Casimir-Polder repulsion. Phys. Rev. A 91, 042510 (2015).
Intravaia, F. et al. Strong Casimir force reduction through metallic surface nanostructuring. Nat. Commun. 4, 2515 (2013).
Chan, H. B. et al. Measurement of the Casimir force between a gold sphere and a silicon surface with nanoscale trench arrays. Phys. Rev. Lett. 101, 030401 (2008).
Huang, P. et al. Demonstration of motion transduction based on parametrically coupled mechanical resonators. Phys. Rev. Lett. 110, 227202 (2013).
Macrì, V. et al. Nonperturbative dynamical Casimir effect in optomechanical systems: Vacuum casimir-rabi splittings. Phys. Rev. X 8, 011031 (2018).
Del Pino, J., Slim, J. J. & Verhagen, E. Non-Hermitian chiral phononics through optomechanically induced squeezing. Nature 606, 82–87 (2022).
Acknowledgements
We are grateful to supports from the Defense Advanced Research Projects Agency (DARPA) NLM program and ARRIVE program, and the Office of Naval Research under Grant No. N00014-18-1-2371.
Author information
Authors and Affiliations
Contributions
T.L., Z.X. and Z.J. conceived and designed the project. Z.X., P.J., X.G. and K.S. built the setup. Z.X. performed measurements and calculations. Z.X. and T.L. analyzed the results. T.L. and Z.J. supervised the project. All authors contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Mingkang Wang and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xu, Z., Ju, P., Gao, X. et al. Observation and control of Casimir effects in a sphere-plate-sphere system. Nat Commun 13, 6148 (2022). https://doi.org/10.1038/s41467-022-33915-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-33915-4
This article is cited by
-
Dynamical Casimir effect in a hybrid cavity optomechanical system
Quantum Information Processing (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.