Abstract
Understanding the out-of-equilibrium properties of noisy microscale systems and the extent to which they can be modulated externally, is a crucial scientific and technological challenge. It holds the promise to unlock disruptive new technologies ranging from targeted delivery of chemicals within the body to directed assembly of new materials. Here we focus on how active matter can be harnessed to transport passive microscopic systems in a statistically predictable way. Using a minimal active-passive system of weakly Brownian particles and swimming microalgae, we show that spatial confinement leads to a complex non-monotonic steady-state distribution of colloids, with a pronounced peak at the boundary. The particles’ emergent active dynamics is well captured by a space-dependent Poisson process resulting from the space-dependent motion of the algae. Based on our findings, we then realise experimentally the de-mixing of the active-passive suspension, opening the way for manipulating colloidal objects via controlled activity fields.
Similar content being viewed by others
Introduction
Evolution has enabled living systems to achieve an exquisite control of matter at the microscopic level. From the precise positioning of chromosomes along the mitotic spindle1 to the many types of embryonic gastrulation2 cells harness their internal and external motility to reach a predictable order despite the stochasticity intrinsic to the microscopic realm3. Understanding how order emerges in these active systems is a fundamental scientific challenge with the potential to bring disruptive technologies for the macroscopic control of microscopic structures. Here we address this problem within a minimal active-passive experimental model system.
From a physical perspective, living systems fall under the general category of active matter4, characterised by emergent phenomena including flocking5,6,7, active turbulence8,9,10,11 and motility-induced phase separation12,13. As our understanding of single-species active systems progresses, attention has started to veer towards more complex cases where components with different levels of activity interact. Indeed this is often the case for biological active matter. Intracellular activity, for example, can be used for spatial organisation of passive intracellular organelles14,15,16; and clustering induced by motility differentials helps bacterial swarms expand despite antibiotic exposure17. In order to study the emergent properties of these complex systems, an important and phenomenologically rich minimal model is one that mixes active and inert agents. Active impurities have been used to alter the dynamics of grain boundaries in colloidal crystals18,19 and favour the formation of metastable clusters in semi-dilute suspensions20. Sufficiently large concentrations of both active and passive species often reveal a rich spectrum of phases depending on the interactions between constituents21,22,23,24,25,26,27,28,29.
Active baths, where individual passive inclusions are dispersed within an active suspension, are particularly appealing. Their conceptual simplicity makes them a natural starting point to develop a statistical theory of active transport30,31,32,33 with potential applications to micro-cargo delivery, micro-actuation34,35,36 and nutrient transport37,38. In general, passive particles in homogeneous and isotropic active baths display enhanced diffusion due to a continuous energy transfer from the active component via direct collisions and hydrodynamic interactions39,40,41,42,43,44,45,46,47. Designing larger objects with asymmetric shapes can then turn active diffusion into noisy active translation or rotation30,48,49. However the strategies for the predictable patterning and transport of passive cargo are still very limited. This is in contrast with the exquisite level of external control possible on the motility of biological and synthetic active particles themselves50,51,52,53,54,55, such as photokinetic bacteria whose swim speed depends on the local light intensity; property that can be harnessed to pattern surfaces53,54.
Here we show that a steady gradient of activity within active-passive suspensions can be harnessed to control the fate of generic passive particles. Quasy-2D microfluidic channels are filled with a binary suspension of polystyrene colloids and unicellular biflagellate microalgae Chlamydomonas reinhardtii (see Supplementary Movie 1). Confinement induces a spatially inhomogeneous and anisotropic distribution of microswimmers as a result of wall scattering56,57,58,59, which translates into a space-dependent active noise for the colloids. We show that this produces complex non-monotonic colloidal distributions with accumulation at the boundaries and then develop an effective microscopic jump-diffusion model for the colloidal dynamics. The latter shows excellent analytical and numerical agreement with the experimental results. Finally we demonstrate how confinement with aptly designed microfluidic chips can fuel the de-mixing of active-passive suspensions, opening the way for manipulating passive colloidal objects via controlled activity fields.
Results
Colloid concentration is non-homogeneous under confinement
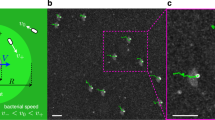
A full description of the experimental procedures (culturing, video microscopy and data analysis) can be found in the Methods section and Supplementary Materials (data and codes also available on Zenodo60). Figure 1a shows a detail of the main section of the first type of microfluidic setup used. These devices, between 14 μm and 20 μm thick, are composed of two reservoir chambers connected by long and straight channels of constant width 2W ranging from 50 to 200 μm. These are filled with a dilute mixture of Chlamydomonas reinhardtii (CR; strain CC-125, radius R ~ 4–5 μm) and weakly Brownian colloids (radius a = 5 ± 0.5 μm) at surface fractions ϕCR ≈ ϕcol ≈ 2–3% (bulk concentrations ~2−3 × 107 particles/mL). The design ensures a steady concentration along the connecting channels for both species (see Supplementary Movie 1). Figure 1a shows the coordinate system employed, which has been symmetrized with respect to the channel axis.
a Dark-field image of cells and beads within a straight microfluidic channel (here width 2W = 200 μm). The two species are highlighted with, respectively, green ellipses and red circles. The schematic illustrates the coordinate system used throughout. b Steady-state colloidal probability distribution functions across the channel (edge to midpoint) for different W values. Boundary accumulation is followed by a depleted adjacent region which gives way to a uniform distribution within the channel. c Example of a typical colloidal trajectory inside a 100 μm-width channel. Colours represent the mean frame-to-frame speed. The dynamics is composed of slow diffusive-like motion (blue sections) interspersed with fast straighter jumps (red sections).
As typical of self-propelled particles, the algae tend to accumulate at the boundaries due to their interactions with the side walls56,57,58. This appears as a significant peak in their time-averaged concentration profile at a position yCR ≈ 15 μm (Supplementary Fig. 1), roughly equivalent to the sum of the cell radius and the flagellar length. Unexpectedly, we find that also the colloids explore the available space in an inhomogeneous way. Their steady-state distribution (Fig. 1b) shows a clear peak at about one particle radius (ycol = 5.9 ± 1.5 μm), followed by a depleted region between 10 μm and 20 μm from the wall, which roughly corresponds to the peak in algal density, before plateauing to a uniform concentration further inside the channels. This effect is also observed within circular chambers (Supplementary Fig. 2) suggesting it is a robust feature of the system. These distributions are in stark contrast with the equilibrium case (i.e., without microswimmers) for which the colloids are expected to be uniformly distributed despite spatial variations in colloidal diffusivity due to hydrodynamics61 (Supplementary Fig. 3).
As a first step to gain insight into the colloids’ experimental distributions, we characterise their dynamics within our active bath. Figure 1c shows a typical colloidal trajectory (561 s) colour-coded for the average frame-to-frame speed v. The dynamics can be understood as a combination of periods of slow diffusive-like displacements (v ~ 5 μm/s;) and fast longer jumps (v ~ 30 μm/s; see Supplementary Section 1). The latter is reminiscent of hydrodynamic entrainment events reported for micron-sized colloids47,62, although for these larger particles the prominent role appears to be played by direct flagellar interactions (see Supplementary Movie 2). Irrespective of their specific origin, jump events dominate the active transport of colloids within the system. Following47,63, we use time-correlation of displacements along individual trajectories and an estimate for the expected magnitude of frame-to-frame diffusive displacements to identify active colloidal jumps and extract their statistical properties as a function of starting position y (we assume translational invariance along the channels’ axis). Figure 2a shows the space-dependent distributions of waiting times between successive jumps, with colours representing the distance from the boundary. Regardless of the position, all the distributions are exponential above ~3 s but deviate from it at shorter times. This deviation from a simple Poisson process is due to the large colloidal size influencing the motility of nearby algae as reported also in the case of bacteria64. Here, this can lead to a rapid succession of interactions with the same cell (see Supplementary Movie 3). Nevertheless, for our purposes, the waiting dynamics can still be approximated with a single effective rate λ(y) (Fig. 2a solid lines; for further details see Supplementary Section 2). Figure 2b shows that these rates increase monotonically with increasing distance from the wall. Notice that this curve does not mirror the algal accumulation at the boundary (Supplementary Fig. 1), a reflection of the fact that proximity to the wall curtails the range of possible swimming directions that algae can have when interacting with the colloid.
a Probability distribution function of waiting times between consecutive jumps (W = 50 μm, semilog plot) Circles: experiments. Solid lines: exponential fits. The distributions are shifted vertically for clarity. Colours code for position across the channel (red: boundary; blue: channel centre). b Characteristic encounter rates λ(y) for the four values of W, as a function of distance from the channel boundaries. For better comparison, the values have been rescaled to the cell concentration of the 100 μm-wide channel (see Supplementary Section 3). Circles: experiments. Solid Lines: exponential fits (see Methods). Error bars from the fit uncertainties. c Probability distribution function P(θ, y) for the direction θ of active jumps vs. distance y from the channel boundary (W = 50 μm). d Semilog plot of active jump distributions, qy(yJ), for different distances y from the boundary (Colours as in C). Circles: experiments. Solid lines: exponential fits. The distributions are shifted vertically for clarity.
Next, we look at the modulation in jump orientation and magnitude. Figure 2c shows the distribution of jump directions P(θ, y), with motion towards or away from the boundary corresponding to negative and positive values of θ respectively. Approaching the wall, the distribution develops a marked peak at θ = 0 indicating a strongly anisotropic active motion preferentially parallel to the boundary. This feature reflects the anisotropy in algal dynamics that results from the interaction with the wall56 and that can be measured up to ~100 μm from the boundary because of the persistence in cells’ trajectories59. The distribution functions of jump magnitudes are similar to those already reported for micron-sized particles47,62, with an exponential decay above ~4 μm (Supplementary Fig. 4a). These can be used to calculate the average jump length 〈l(y)〉 (Supplementary Fig. 4b) which decreases by ~30% from the bulk level within the first 10−15 μm from the boundary (first 5−10 μm accessible to the beads). A decrease is indeed expected due to the obvious limitations to the active movement of the colloids imposed by a nearby boundary.
As we are interested in the passive particles’ dynamics across the channels, it is useful to reduce the full two-dimensional jump distribution functions to their projection qy(yJ) along the y axis. Here yJ is the y-coordinate of the active displacement and the subscript indicates the distance from the nearest wall (see Fig. 1a for the frame of reference). Figure 2d shows that these distributions are generally well approximated by the combination of two exponentials, one each for positive and negative directions (respectively away from and towards the boundary). The exception is for the positive tails of the distributions closest to the wall, which decay slower than expected from the exponential fit. They will not be considered in the following. The distributions qy(yJ) can then be approximated as
where L±(y) are the characteristic lengths of the exponential fits to positive and negative jumps respectively (see Methods for details on how the characteristic lengths were extracted). As shown in Fig. 3-inset (red and blue symbols and solid lines) these are identical in the core of the channel (L+ = L− ≃ 4 μm) and decrease to the same small value close to the wall (~0.5 μm) as a consequence of the increasing polarisation of the active displacements along the boundary (Fig. 2c). However, the length scale for the transition between boundary and core values is shorter for L+(y) than for L−(y) (~12 μm vs. ~25 μm, see Fig. 3-inset). This behaviour, common to all values of W explored (Supplementary Fig. 5), gives rise to a net drift L+(y)−L−(y) > 0 towards the bulk of the system (green symbols and solid line, Fig. 3-inset) which, as discussed below, is responsible for the depleted region observed in the experimental colloidal distributions. The difference between the L’s is likely due to a combination of local anisotropy in the distribution of swimming directions of the algae, and the stopping of colloids’ active displacements by the wall.
Steady-state colloidal probability distribution functions in a 2W = 100 μm channel: experiments (circles); full dynamics (black solid line); constant encounter rate (λ(y) := bulk value) (teal dashed line); no thermal diffusion (D0 = 0) (purple dashed line); homogeneous and isotropic jump size distribution (qy(yJ):=bulk distribution) (orange solid line); analytical model (olive solid line). The analytical model curve has been shifted downward for clarity. Inset: characteristic jump size away from the boundary (L+(y), red circles) and toward the boundary (L−(y), blue circles) together with the first and second moments m1(y) and \(\sqrt{{m}_{2}(y)}\) derived from them (Eq. (5)). Solid lines are fitted heuristic analytical functions used to reconstruct the colloidal distribution (see Methods). Error bars propagated from fit uncertainties.
The focus on the active jumps displayed by the passive particles can only be justified if this part of the dynamics is indeed sufficient to capture the experimental steady-state distributions. This was first tested within a 1D numerical simulation of a weakly Brownian particle (diffusivity D0), moving in y ∈ [0, 2W] and subject to a space-dependent Poisson noise of rate λ(y) and value drawn from qy(yJ) (see Methods Sec. 4.5 for details on the integration scheme). Figure 3 shows that the resulting steady-state distribution (black solid curve) is in excellent agreement with the experimental one (black circles) (2W = 100 μm). Numerical simulations also provide a convenient way to explore which elements of the effective colloidal dynamics play the most prominent role. For example, fixing λ(y) to the bulk value everywhere leads to a very minimal change in the spatial distribution (Fig. 3, teal dashed line), showing that the spatial dependence of the jump frequency close to the wall is not a major factor in the present case. Similarly, removing completely the background diffusion by setting D0 = 0 leaves the distribution unchanged (Fig. 3, purple dashed line) consistent with the fact that, in our experimental system, colloidal transport is dominated by the Poissonian jumps. On the other hand, simulations that remove the spatial dependence of the jump distributions qy(yJ) and use their isotropic bulk value everywhere, show a boundary accumulation of colloids that is narrower and higher than the experimental curve and has no intermediate depletion (Fig. 3, orange solid line). This confirms that space-dependent jump anisotropy plays a key role in determining the experimental colloidal distribution.
Minimal continuum model for the dynamics of the colloids
The numerical validation of the jump-diffusion dynamics motivates a simple analytical model for the evolution of Pt(y), the probability density of finding a colloid at position y at time t:
In this master equation, local changes in Pt(y) are due either to diffusion (first term in the r.h.s) or to the balance between active jumps from the current position or towards it from elsewhere (second and third terms in the r.h.s., respectively). This continuum equation can also be derived more formally from a stochastic description of the dynamics of single colloids, following Denisov and Bystrik65 (see Supplementary Section 4). It is worth noting also that Eq. (2) assumes infinitely fast jumps ("teleportation”). While this might seem like a drastic approximation, it is not expected to impact the resulting spatial distributions as long as the typical jump duration is sufficiently shorter than the average waiting time between jumps. This is indeed the case in the current system (~1.2 s vs. ≳3.5 s respectively; see Fig. 2b and Supplementary Fig. 6).
The non-local term in Eq. (2) means that the model is non-tractable for generic kernels λ(y)qy(y−yJ). In order to make progress, we, therefore, perform a Kramers-Moyal expansion66 and truncate the series at second-order, providing an approximation of the system at the drift-diffusion level. This type of approximation has already been used successfully to capture the essential features of run-and-tumble bacteria67, active Brownian particles68 and active Ornstein-Uhlenbeck particles69. This approximation is expected to hold if the characteristic jump size is small compared to the length scale of the heterogeneities in the dynamics. In our case we have 〈lbulk〉 ≈ 5 μm (Supplementary Figure 4b) while a length scale for the heterogeneity can be estimated for example from the L± curves (≳ 12 μm). As detailed in the Supplementary Materials (Supplementary Section 5) the second-order expansion of Eq. (2) gives a drift-diffusion equation which depends on λ(y) and the first and second moments m1,2(y) of qy(yJ):
Notice that Deff is similar to the asymptotic diffusivity obtained in47 for homogeneous and isotropic entrainment-dominated transport, with a contribution from the jump events given by the product of jump frequency and variance of jump size. Enforcing no-flux at the boundaries one obtains a closed form for the steady-state solution:
where B is the normalisation constant. Without a net asymmetry in the dynamics (i.e., when m1(y) ≡ 0), the solution is that of a state-dependent diffusive process with Itô convention for multiplicative noise integration. In our case, however, the first moment of qy takes significant values in the first ~30 μm from the boundaries (green solid line Fig. 3-Inset) and should not be neglected.
Comparison between Eq. (4) and the experiments is facilitated by having analytical expressions for λ, m1 and m2. Figure 2b shows that λ can be described heuristically by a simple exponential relaxation from the wall to the bulk values (black solid line). As for m1 and m2, the description of qy(yJ) given by Eq. (1) implies that
Given that L±(y) themselves are well approximated by exponentials, this affords analytical approximations also for m1,2(y) (Fig. 2c-Inset). Armed with this description we can now compare the experimental curves with the prediction from the approximate jump-diffusion model. The olive-coloured curve in Fig. 3 shows that the theoretical distributions recapitulate extremely well the experimental ones. On one hand, this provides a justification a posteriori for the modelling approach taken above. On the other it reveals that, at a continuum level, the dynamics of colloids in an active bath can be reduced to two quantities: the first and the second moments of the active displacements. This provides an intuitive way to conceptualise the complex dynamics of colloidal particles within an active suspension.
Induced de-mixing of the passive particles
What we learned so far on the colloids’ emergent active dynamics can be harnessed to induce the de-mixing of our active-passive suspensions, as a first step towards more complex control of microscale cargo transport. The idea is to include a confining boundary which acts as a kind of selective membrane, letting the beads cross but not the algae. This is achieved by considering circular chambers decorated with 190 μm-long side channels whose width d (Fig. 4a) is smaller than the swimmer diameter but larger than the bead diameter (here taken as 2a = 6 μm < d = 7−8 μm < 2R = 8−10 μm). Due to the active dynamics of the colloids, we expect them to be pushed inside the side channels by the algae, therefore depleting the particles in the main chamber and spatially separating the active and passive species. As shown Fig. 4b (see also Supplementary Movie 4) this is exactly what we obtain, with the number of particles in the circular chamber Nc (red solid line) quickly decreasing and the number in the side channels Ns (cyan solid line) increasing. Notice that the total number of particles Nt = Nc + Ns in the system (purple solid line) remains constant over the duration of the experiment. The process follows a first order kinetic with rates kin and kout for transitions towards or out-of the side channels respectively (see Supplementary Section 6). The occupancy numbers follow an exponential relaxation with time-scale 1/(kin + kout) = 77 ± 4 min and stationary values \({N}_{{{{{{{{\rm{c}}}}}}}}}^{{{{{{{{\rm{\infty }}}}}}}}}/{N}_{{{{{{{{\rm{t}}}}}}}}}={k}_{{{{{{{{\rm{out}}}}}}}}}/({k}_{{{{{{{{\rm{in}}}}}}}}}+{k}_{{{{{{{{\rm{out}}}}}}}}})=0.64\pm 0.02\) and \({N}_{{{{{{{{\rm{s}}}}}}}}}^{{{{{{{{\rm{\infty }}}}}}}}}/{N}_{{{{{{{{\rm{t}}}}}}}}}={k}_{{{{{{{{\rm{in}}}}}}}}}/({k}_{{{{{{{{\rm{in}}}}}}}}}+{k}_{{{{{{{{\rm{out}}}}}}}}})=0.36\pm 0.02\), leading to estimates for the two rates of kin = (7.8 ± 0.6) × 10−5 s−1 and kout = (13.9 ± 0.8) × 10−5 s−1. The latter results from the passive dynamics of the colloids within the side channels, which depends on their thermal diffusivity, potential electrostatic interactions with the boundaries, short-range hydrodynamic interactions between the beads70, channel design, etc71. The former, instead, is the consequence of active colloidal displacements. Assuming no colloid/wall attraction within the side channels (as confirmed by our control experiment, see below), it encapsulates the intrinsic out-of-equilibrium nature of the system, a property which is immediately clear from the significant difference in steady-state densities between the side channels (ρs = 0.0295 ± 0.007 beads/μm2) and in the main chamber (ρc = 0.0019 ± 0.0001 beads/μm2) (Fig. 4c). The value of kin can be compared with an estimate derived from the effective colloidal dynamics from Eq. (3) (see Supplementary Section 7). The mean first passage time of a colloid to the entrance of any of the side channels returns a rate of \({k}_{{{{{{{{\rm{in}}}}}}}}}^{V,D}=(7.408\pm 0.1)\times 1{0}^{-5}\)s−1 which agrees very well with the experimental value. This shows that the simplified advection-diffusion model for the passive particles is a good description not just for time-independent properties like the steady-state distribution of Fig. 3, but also for dynamic ones like the rate of active cargo transport to the side channels. It is instructive also to use the model to explore the contributions of the different parts of the dynamics. Hence we see that setting Veff ≡ 0 and Deff ≡ 3.55 μm2 s−1, the effective diffusivity far from the boundaries, one obtains a rate \({k}_{{{{{{{{\rm{in}}}}}}}}}^{D}=(16.2\pm 4.1)\times 1{0}^{-5}\)s−1. The stark difference between \({k}_{{{{{{{{\rm{in}}}}}}}}}^{V,D}\) and \({k}_{{{{{{{{\rm{in}}}}}}}}}^{D}\) suggests that, in our case, it is not sufficient to know the behaviour of the active-passive suspension in the bulk of the chamber. The behaviour close to the boundary, where the inhomogeneities are found, is essential to grasp the dynamics of the de-mixing process. Repeating the same experiment only with colloids shows indeed no appreciable filling of the side channels within the duration of the experiment (~10 h; see Supplementary Movie 5) and the particle density in the main chamber remaining constant (Fig. 4b red dashed line).
a Schematics and details of the microfluidic chamber: 200 μm-radius circular chambers decorated with side channels of width d = 7−8 μm. Both cells (2R = 8−10 μm) and polystyrene beads (2a = 6 μm) are visible in the picture. b, c Time evolution of the number of particles and surface number density within the circular chamber (Nc, ρc red solid line) and the side channels (Ns, ρs cyan solid line) in presence of the microalgae. Within this time the total number of particles in the chamber remains constant (purple solid line). Dashed/dash-dot lines are a fit to the first order kinetics (see Supplementary Section 6). Dotted lines indicate the initial values of Nc and ρc. Dashed red line corresponds to the control experiment without microalgae.
Although the microfluidic chip in Fig. 4 leads to a much higher concentration of colloids in the side channels than in the main chamber, this still involves only ~36% of the colloids. A different design, however, could maximise the fraction of de-mixed colloids instead of their concentration. For example, modifying the current design to have two identical chambers connected by a narrow gap of size d = 7−8 μm should produce a fraction of de-mixed colloids given by \({k}_{{{{{{{{\rm{in}}}}}}}}}/\left({k}_{{{{{{{{\rm{in}}}}}}}}}+{k}_{{{{{{{{\rm{in}}}}}}}}}^{{{{{{{{\rm{th}}}}}}}}}\right)\simeq 95\%\). The design could then be tailored to different needs.
Discussion
In this study we used an active-passive system as a minimal model to investigate the active transport of passive microscopic objects. Leveraging the well-known boundary accumulation of microswimmers, we saw that the emerging interactions between active and passive components are also heterogeneous and anisotropic. In turn, they lead to a complex spatial distribution of colloids and to the possibility of de-mixing the suspension. These properties are well described by a simple advection-diffusion model for the passive species, based only on the first and second moments of their ensuing active displacements. This type of approximation, then, provides a degree of universality in the description of the dynamics of active systems including purely active and active-passive species. From the targeted delivery of chemicals, biomarkers or contrast agents at specific locations in the body to the remediation of water and soils, artificial and biological microscopic self-propelled particles hold a great potential to address critical issues in areas ranging from personalised medical care to environmental sustainability72,73. Development in these areas will depend on our ability to use and control micro/nano-swimmers to perform essential basic functions, such as sensing, collecting and delivering passive cargoes in an autonomous, targeted and selective way74. Within this perspective, we have shown here that heterogeneous activity fields can be employed to control the fate of colloidal objects in a manner similar to biological systems, where the spatial modulation of the activity can control, for example, the positioning of organelles within cells14,15,16. Although this was achieved here through simple confinement, many microswimmers possess -or can be designed to have- the ability to respond to a range of external physico-chemical cues or stimuli51,52,53,54. We expect that similar phenomenologies should also emerge whenever the active particles in a mixed system autonomously generate a space-dependent concentration profile. Our work paves the way to using these to dynamically manipulate the fate of colloidal cargoes by externally altering microswimmers’ dynamics. Advance in this area will require to understand how to predict the active displacements of passive cargoes directly from the dynamics of microswimmers75, a theoretical development that we leave for a future study.
Methods
Microorganism culturing
Cultures of CR strain CC-125 were grown axenically in a Tris-Acetate-Phosphate medium76 at 21 °C under periodic fluorescent illumination (16h light/8h dark cycles, 100 μEm−2 s−1, OSRAM Fluora). Cells were harvested at ~5 × 106cells/ml in the exponentially growing phase, then centrifuged at 10 × g for 10 min and the supernatants replaced by DI-water containing the desired concentration of polystyrene colloids (Polybead® Carboxylate Microspheres, radius a = (5 ± 0.5) μm, Polysciences).
Microfluidics and microscopy
The mixed colloid-swimmer solution was injected into polydimethylsiloxane-based microfluidic channels, previously passivated with a 0.5% w/w Pluronic-127 solution to prevent sticking of the particles to the surfaces of the chips. The microfluidic devices were then sealed with Vaseline to prevent evaporation. The channels of varying widths were observed under bright-field illumination on a Zeiss AxioVert 200M inverted microscope. A long-pass filter (cutoff wavelength 765 nm) was added to the optical path to prevent phototactic responses of the cells. For each channel width stacks of 80,000 images at ×10 magnification were acquired at 10 fps with an IDS UI-3370CP-NIR-GL camera.
Data analysis: trajectories
Particle Trajectories were digitised using a standard Matlab particle tracking algorithm (The code can be downloaded at http://people.umass.edu/kilfoil/downloads.html). After the particle trajectories were reconstructed, the large jumps were isolated using a combination of move size and directional correlation along the trajectory (see detailed protocol in47,63).
Data analysis: fitting of L +(y), L −(y) and λ(y)
The experimental curves L+(y), L−(y) and λ(y) have been fitted by the following analytical functions:
with \({L}_{+}^{w}={L}_{-}^{w}=0.375\) μm fixed. The best fits (dotted lines in Figs. 2 and 3) are given by the parameters in Table 1.
The experimental curves L+(y) and L−(y) were obtained from the experimental jump size distributions qy(yJ) by fitting the logarithm of each side (i.e., positive and negative yJ) with affine functions. Because these distributions deviate from simple exponentials as we get closer to the boundary (Fig. 2d), the fits were restricted to \(|{y}_{{{{{{{{\rm{J}}}}}}}}}| < \lim (y)\) in order to extract the characteristic length scales of the initial decay of the distributions. The resulting fits are shown in Fig. 2d (solid lines). The limits for the fits of the experimental distributions were fixed as in Table 2.
Numerical simulations
One hundred trajectories composed of 10,000 time-steps (with δt = 0.1 s, equal to the acquisition period of the experiments) were simulated for each condition. At each time step an acceptance-rejection scheme is performed to decide whether the particle undergoes a jump: (i) a (uniform) random number is first drawn from the interval [0,1], (ii) if this number sits within the interval [(1−λ(y)δt)/2; (1 + λ(y)δt)/2], the particle undergoes a jump whose size is taken from the experimental distribution qy(yJ) (using inverse transform sampling), (iii) otherwise the particle simply undergoes Brownian motion with diffusivity D0 = 0.0439 μm2 s−1 (the theoretical bulk diffusivity for a 5 μm-radius particle at room temperature). Upon reaching a boundary jump moves undergo a stopping boundary condition, stopping at ±5 μm (the particle’s radius) from the boundary (this is to be as faithful with our experimental observations as possible). For simplicity, diffusive moves that cross the boundary undergo a reflective boundary condition. More accurate boundary implementations for the diffusive motion do not lead to different results as the impact of thermal diffusivity in the channel experiments is negligible.
Data availability
The main data used in this study are available in the Zenodo database with https://doi.org/10.5281/zenodo.6866462.
Code availability
The codes used in this study are available in the Zenodo database with https://doi.org/10.5281/zenodo.6866462.
Change history
03 October 2022
A Correction to this paper has been published: https://doi.org/10.1038/s41467-022-33600-6
References
Civelekoglu-Scholey, G. & Scholey, J. M. Mitotic force generators and chromosome segregation. Cell. Mol. Life Sci 67, 2231 (2010).
Honerkamp-Smith, A. R. et al. The noisy basis of morphogenesis: mechanisms and mechanics of cell sheet folding inferred from developmental variability. PLoS Biol. 16, 1 (2018).
Tsimring, L. S. Noise in biology. Rep. Prog. Phys 77, 026601 (2014).
Ramaswamy, S. The mechanics and statistics of active matter. Annu. Rev. Condens. Matter Phys 1, 323 (2010).
Vicsek, T., Czirk, A., Ben-Jacob, E., Cohen, I. & Shochet, O. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett 75, 1226 (1995).
Bricard, A., Caussin, J.-B., Desreumaux, N., Dauchot, O. & Bartolo, D. Emergence of macroscopic directed motion in populations of motile colloids. Nature 503, 95 (2013).
Giavazzi, F., Malinverno, C., Scita, G. & Cerbino, R. Tracking-free determination of single-cell displacements and division rates in confluent monolayers. Front. Phys 6, 1 (2018).
Dombrowski, C., Cisneros, L., Chatkaew, S., Goldstein, R. E. & Kessler, J. O. Self-concentration and large-scale coherence in bacterial dynamics. Phys. Rev. Lett 93, 098103 (2004).
Wensink, H. et al. Meso-scale turbulence in living fluids. Proc. Natl. Acad. Sci. USA 109, 14308 (2012).
Wu, K. T. et al. Transition from turbulent to coherent flows in confined three-dimensional active fluids. Science 355, 1705.02030 (2017).
Doostmohammadi, A., Shendruk, T. N., Thijssen, K. & Yeomans, J. M. Onset of meso-scale turbulence in active nematics. Nat. Commun 8, 1 (2017).
Cates, M. E. & Tailleur, J. Motility-induced phase separation. Annu. Rev. Condens. Matter Phys 6, 219 (2015).
Grobas, I., Polin, M. & Asally, M. Swarming bacteria undergo localized dynamic phase transition to form stress-induced biofilms. eLife 10, 1 (2021).
Almonacid, M. et al. Active diffusion positions the nucleus in mouse oocytes. Nat. Cell Biol 17, 470 (2015).
Cadot, B., Gache, V. & Gomes, E. R. Moving and positioning the nucleus in skeletal muscle-one step at a time. Nucleus 6, 373 (2015).
Lin, C. et al. Active diffusion and microtubule-based transport oppose myosin forces to position organelles in cells. Nat. Commun 7, 11814 (2016).
Be’er, A. & Ariel, G. A statistical physics view of swarming bacteria. Mov. Ecol 7, 1 (2019).
Van Der Meer, B., Filion, L. & Dijkstra, M. Fabricating large two-dimensional single colloidal crystals by doping with active particles. Soft Matter 12, 3406 (2016).
Ramananarivo, S., Ducrot, E. & Palacci, J. Activity-controlled annealing of colloidal monolayers. Nat. Commun 10, 3380 (2019).
Kümmel, F., Shabestari, P., Lozano, C., Volpe, G. & Bechinger, C. Formation, compression and surface melting of colloidal clusters by active particles. Soft Matter 11, 6187 (2015).
McCandlish, S. R., Baskaran, A. & Hagan, M. F. Spontaneous segregation of self-propelled particles with different motilities. Soft Matter 8, 2527 (2012).
Stenhammar, J., Wittkowski, R., Marenduzzo, D. & Cates, M. E. Activity-induced phase separation and self-assembly in mixtures of active and passive particles. Phys. Rev. Lett 114, 018301 (2015).
Takatori, S. C. & Brady, J. F. A theory for the phase behavior of mixtures of active particles. Soft Matter 11, 7920 (2015).
Wysocki, A., Winkler, R. G. & Gompper, G. Propagating interfaces in mixtures of active and passive Brownian particles. New J. Phys 18, 123030 (2016).
Weber, S. N., Weber, C. A. & Frey, E. Binary mixtures of particles with different diffusivities demix. Phys. Rev. Lett 116, 058301 (2016).
Ma, Z., Lei, Q. L. & Ni, R. Driving dynamic colloidal assembly using eccentric self-propelled colloids. Soft Matter 13, 8940 (2017).
Jahanshahi, S., Lozano, C., TenHagen, B., Bechinger, C. & Löwen, H. Colloidal Brazil nut effect in microswimmer mixtures induced by motility contrast. J. Chem. Phys 150, 1 (2019).
Ilker, E. & Joanny, J.-F. Phase separation and nucleation in mixtures of particles with different temperatures. Phys. Rev. Res. 2, 23200 (2020).
RogelRodriguez, D., Alarcon, F., Martinez, R., Ramírez, J. & Valeriani, C. Phase behaviour and dynamical features of a two-dimensional binary mixture of active/passive spherical particles. Soft Matter 16, 1162 (2020).
Kaiser, A. et al. Transport powered by bacterial turbulence. Phys. Rev. Lett 112, 158101 (2014).
Razin, N., Voituriez, R., Elgeti, J. & Gov, N. S. Generalized Archimedes’ principle in active fluids. Phys. Rev. E 96, 1 (2017).
Pietzonka, P., Fodor, É., Lohrmann, C., Cates, M. E. & Seifert, U. Autonomous engines driven by active matter: energetics and design principles. Phys. Rev. X 9, 41032 (2019).
Knežević, M. & Stark, H. Effective Langevin equations for a polar tracer in an active bath. New J. Phys 22, 113025 (2020).
Palacci, J., Sacanna, S., Vatchinsky, A., Chaikin, P. M. & Pine, D. J. Photoactivated colloidal dockers for cargo transportation. JACS 135, 15978 (2013).
Koumakis, N., Lepore, A., Maggi, C., & Leonardo, R. Di. Targeted delivery of colloids by swimming bacteria. Nat. Commun. 4, 2588 (2013).
Wang, L. & Simmchen, J. Review: interactions of active colloids with passive tracers. Condens. Matter 4, 78 (2019).
Mathijssen, A. J. T. M., Guzmán-Lastra, F., Kaiser, A. & Löwen, H. Nutrient transport driven by microbial active carpets. Phys. Rev. Lett. 121, 248101 (2018).
F. Guzmán-Lastra, H. Löwen, and A. J. Mathijssen. Active carpets drive non-equilibrium diffusion and enhanced molecular fluxes. Nat. Commun. 12, 1906 (2021).
Wu, X. L. & Libchaber, A. Particle diffusion in a quasi-two-dimensional bacterial bath. Phys. Rev. Lett 84, 3017 (2000).
Leptos, K. C., Guasto, J. S., Gollub, J. P., Pesci, A. & Goldstein, R. E. Dynamics of enhanced tracer diffusion in suspensions of swimming eukaryotic microorganisms. Phys. Rev. Lett 103, 198103 (2009).
Valeriani, C., Li, M., Novosel, J., Arlt, J. & Marenduzzo, D. Colloids in a bacterial bath: simulations and experiments. Soft Matter 7, 5228 (2011).
Miño, G. et al. Enhanced diffusion due to active swimmers at a solid surface. Phys. Rev. Lett 106, 048102 (2011).
Kurtuldu, H., Guasto, J. S., Johnson, K. A. & Gollub, J. P. Enhancement of biomixing by swimming algal cells in two-dimensional films. Proc. Natl. Acad. Sci. USA 108, 10391 (2011).
Miño, G., Dunstan, J., Rousselet, A., Clément, E. & Soto, R. Induced diffusion of tracers in a bacterial suspension: theory and experiments. J. Fluid Mech. 729, 423 (2013).
Jepson, A., Martinez, V. A., Schwarz-Linek, J., Morozov, A. & Poon, W. C. Enhanced diffusion of nonswimmers in a three-dimensional bath of motile bacteria. Phys. Rev. E 88, 041002(R) (2013).
Patteson, A., Gopinath, A., Purohit, P. K. & Arratia, P. E. Particle diffusion in active fluids is non-monotonic in size. Soft. Matter 12, 2365 (2016).
Jeanneret, R., Pushkin, D. O., Kantsler, V. & Polin, M. Entrainment dominates the interaction of microalgae with micron-sized objects. Nat. Commun 7, 12518 (2016).
DiLeonardo, R. et al. Bacterial ratchet motors. Proc. Natl. Acad. Sci. USA 107, 9541 (2010).
Sokolov, A., Apodaca, M. M., Grzybowski, B. A. & Aranson, I. S. Swimming bacteria power microscopic gears. Proc. Natl. Acad. Sci. USA 107, 969 (2010).
Palacci, J., Sacanna, S., Steinberg, A. P., Pine, D. J. & Chaikin, P. M. Living crystals of light-activated colloidal surfers. Science 339, 936 (2013).
Kirkegaard, J. B., Bouillant, A., Marron, A. O., Leptos, K. C. & Goldstein, R. E. Aerotaxis in the closest relatives of animals. eLife 5, e18109 (2016).
Arrieta, J., Barreira, A., Chioccioli, M., Polin, M. & Tuval, I. Phototaxis beyond turning: persistent accumulation and response acclimation of the microalga Chlamydomonas reinhardtii. Sci. Rep 7, 3447 (2017).
Frangipane, G. et al. Dynamic density shaping of photokinetic E. Coli. eLife 7, e36608 (2018).
Arlt, J., Martinez, V. A., Dawson, A., Pilizota, T. & Poon, W. C. K. Painting with light-powered bacteria. Nat. Commun. 9, 768 (2018).
Lozano, C., tenHagen, B., Löwen, H. & Bechinger, C. Phototaxis of synthetic microswimmers in optical landscapes. Nat. Commun. 7, 12828 (2016).
Kantsler, V., Dunkel, J., Polin, M. & Goldstein, R. E. Ciliary contact interactions dominate surface scattering of swimming eukaryotes. Proc. Natl. Acad. Sci. USA 110, 1187 (2013).
Contino, M., Lushi, E., Tuval, I., Kantsler, V. & Polin, M. Microalgae scatter off solid surfaces by hydrodynamic and contact forces. Phys. Rev. Lett 115, 258102 (2015).
Ostapenko, T. et al. Curvature-guided motility of microalgae in geometric confinement. Phys. Rev. Lett 120, 068002 (2018).
M. Contino, Characterisation and control of the dynamical properties of swimming microorganisms under confinement, PhD thesis, Warwick, 2017.
S. Williams, R. Jeanneret, I. Tuval, and M. Polin, Supplementary data and codes for "Confinement-induced accumulation accumulation and de-mixing of microscopic active-passive mixtures”, Zenodo https://zenodo.org/record/6866462#.YvMOx3ZBy3A (2022).
Lançon, P., Batrouni, G., Lobry, L. & Ostrowsky, N. Drift without flux: Brownian walker with a space-dependent diffusion coefficient. Europhys. Lett 54, 0005004 (2001).
Mathijssen, A. J., Jeanneret, R. & Polin, M. Universal entrainment mechanism controls contact times with motile cells. Phys. Rev. Fluids 3, 033103 (2018).
Mosby, L. S., Polin, M. & Köster, D. V. A Python based automated tracking routine for myosin II filaments. J. Phys. D: Appl. Phys 53, 304002 (2020).
Lagarde, A. et al. Colloidal transport in bacteria suspensions: from bacteria collision to anomalous and enhanced diffusion. Soft Matter 16, 7503 (2020).
Denisov, S. I. & Bystrik, Y. S. Statistics of bounded processes driven by Poisson white noise. Physica A 515, 38 (2019).
H. Risken & H. Haken, The Fokker-Planck Equation: Methods of Solution and Applications Second Edition (Springer, 1989).
Schnitzer, M. Theory of continuum random walks and application to chemotaxis. Phys. Rev. E 48, 2553 (1993).
M. E. Cates and J. Tailleur. When are active Brownian particles and run-and-tumble particles equivalent? Consequences for motility-induced phase separation. Eur. Phys. Lett. 101, 20010 (2013).
Martin, D. et al. Statistical mechanics of active Ornstein-Uhlenbeck particles. Phys. Rev. E 103, 2008.12972 (2021).
Misiunas, K., Pagliara, S., Lauga, E., Lister, J. R. & Keyser, U. F. Nondecaying hydrodynamic interactions along narrow channels. Phys. Rev. Lett 115, 038301 (2015).
Locatelli, E. et al. Single-file escape of colloidal particles from microfluidic channels. Phys. Rev. Lett. 117, 038001 (2016).
Wang, J. & Gao, W. Nano/microscale motors: biomedical opportunities and challenges. ACS Nano 6, 5745 (2012).
Gao, W. & Wang, J. The environmental impact of micro/nanomachines: a review. ACS Nano 8, 3170 (2014).
Bechinger, C. et al. Active particles in complex and crowded environments. Rev. Mod. Phys. 88, 045006 (2016).
Cammann, J. et al. Emergent probability fluxes in confined microbial navigation. Proc. Natl. Acad. Sci. USA 118, 1 (2021).
E. S. Harris, The Chlamydomonas sourcebook (Elsevier, 2009).
Acknowledgements
R.J. would like to thank Denis Bartolo, Jean-François Rupprecht and Jérémie Palacci for enlightening discussions. This work was supported in part through the Ramón y Cajal Programme (RYC-2018-02534; MP), the Spanish Ministry of Science and Innovation (Grant PID2019-104232GB-I00 funded by MCIN/AEI/ 10.13039/501100011033; M.P. and I.T.), the Margalida Comas Programme (PD/007/2016; R.J.), the Juan de la Cierva Incorporación Programme (IJCI-2017-32952; R.J.), the Junior Research Chair Programme (ANR-10-LABX-0010/ANR-10-IDEX-0001-02 PSL; R.J.).
Author information
Authors and Affiliations
Contributions
R.J., I.T. and M.P. conceived and designed the experiments. R.J. and S.W. performed the experiments. R.J., S.W. and M.P. analysed the data. R.J. developed the analytical model and S.W. performed the numerical simulations. All authors discussed the results and wrote the article.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Giovanni Volpe and the other anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Williams, S., Jeanneret, R., Tuval, I. et al. Confinement-induced accumulation and de-mixing of microscopic active-passive mixtures. Nat Commun 13, 4776 (2022). https://doi.org/10.1038/s41467-022-32520-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-32520-9
This article is cited by
-
Long-range velocity correlations from active dopants
Communications Physics (2024)
-
Non-reciprocity across scales in active mixtures
Nature Communications (2023)
-
Confinement-induced accumulation and de-mixing of microscopic active-passive mixtures
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.