Abstract
Polysulfur species have been proposed to be the unknown near-UV absorber in the atmosphere of Venus. Recent work argues that photolysis of one of the (SO)2 isomers, cis-OSSO, directly yields S2 with a branching ratio of about 10%. If correct, this pathway dominates polysulfur formation by several orders of magnitude, and by addition reactions yields significant quantities of S3, S4, and S8. We report here the results of high-level ab-initio quantum-chemistry computations that demonstrate that S2 is not a product in cis-OSSO photolysis. Instead, we establish a novel mechanism in which S2 is formed in a two-step process. Firstly, the intermediate S2O is produced by the coupling between the S and Cl atmospheric chemistries (in particular, SO reaction with ClS) and in a lesser extension by O-abstraction reactions from cis-OSSO. Secondly, S2O reacts with SO. This modified chemistry yields S2 and subsequent polysulfur abundances comparable to the photolytic cis-OSSO mechanism through a more plausible pathway. Ab initio quantification of the photodissociations at play fills a critical data void in current atmospheric models of Venus.
Similar content being viewed by others
Introduction
Spacecraft missions and Earth-based observations have reported images of the Venusian atmosphere at different wavelengths with the aim of characterizing the cloud morphology and the exotic chemical processes that take place in this planet. At visible wavelengths, the planet is bland and smooth, whereas recordings at near-ultraviolet light (around 365 nm) reveal intriguing “dark” and “light” areas indicating highly active UV absorption in the top clouds1,2,3,4,5,6,7,8.
The identity of the “unknown UV absorber(s)” in Venus represents an important enigma in the current field of research on planetary atmospheres. Even though several particulate and gaseous candidates have been proposed, the nature of the unidentified absorber remains an unsolved problem as no satisfactory match has been found yet in terms of atmospheric abundance and spectral properties. Since sulfur is abundant in the Venusian atmosphere, it is not surprising that many candidates are sulfur-based compounds1,3,4,5,9,10,11,12,13,14,15. It has been proposed that 1(SO)2 isomers (mostly cis- and trans-OSSO) generated from the association reaction of 3SO (Eq. 1),
could be the UV absorber since the calculated absorption spectra match previous estimates of the spectral properties of the unknown UV absorber1,9,16. The short photochemical lifetimes of 1(SO)2 (between 2 and 5 s) derived from photolysis rates16 imply a short existence of these species during daytime, nevertheless, the chemical equilibrium with 3SO will be continuously replenishing 1(SO)2. Since both 3SO association (Eq. 1) and photochemical dissociation to 3SO + 3SO are swift processes, the global 1(SO)2 lifetime is controlled by 3SO concentrations1,16,17,18,19. These can vary greatly, in agreement with observations4,20. Since the lifetimes of the UV dark features range from minutes to hours, to an excess of 12 h20, a long-lived absorber is unlikely since short lived features would then not be possible. Therefore, the UV absorber concentration is likely tied to something other than direct sunlight, which matches the 1(SO)2 behavior dependent on the 3SO levels. Recent literature has brought into question the level of contribution of the two 1OSSO isomers to the UV absorption17,18,19,21, pointing to a too low 3SO concentration at lower altitudes of the Venus middle atmosphere (ca. 60 km). However, there is still significant uncertainty in these 3SO data, and 1OSSO role as the UV absorber has not been fully refuted yet.
Using data from the Venus Express mission and a photochemical model, Pinto et al.19 have recently assessed in detail the role of 3SO dimers as key intermediates in the production of polysulfur (Sn) and polysulfur oxides (SnO). Polysulfur species are presented by the authors as solid candidates accounting for the enigmatic UV absorption on Venus, apart from being of relevance in other processes such as the production of SnO or key to explain the 1SO2 inversion layer observed in the Venusian atmosphere at altitudes above 90 km12,13,21. The model considers the photodissociation of the most predominant isomer of 1(SO)2, cis-OSSO, into 3S2 and 3O2 as a source of diatomic sulfur (Eq. 2):
while subsequent self-propagation polymerizations of 3S2 give access to Sn.
The photoreaction shown in Eq. 2 is proposed based on recent results reported by Wu et al.11 who studied the photoconversions of several 1(SO)2 isomers condensed on a cryogenic N2-matrix from gaseous 3SO. 3S2 in Wu’s experiment initially came from dissociation of the ethylene episulfoxide used as source of 3SO. Yellow light irradiation (579 nm) slightly decreased the peak at 287 nm attributed to 3S2. Further irradiation by 365 nm light depleted the 375 nm band with a simultaneous increase of the 287 nm band. The 375 nm band was assigned to cis-OSSO; however, recently Frandsen et al.9 have suggested that the cis isomer only accounts for the part of the band at wavelengths shorter than 360 nm, while the other part at lower energies is likely to be originated by trans-OSSO based on their simulated spectra for the trans isomer9. Regarding the increase of the 287 nm band, it was ascribed to the production of 3S2 due to the characteristic vibrational structure shown by the absorption band, motivating in this way the proposal of photoreaction (Eq. 2) by Pinto et al.19. Nevertheless, Wu et al. also pointed to other decomposition products (cyclic-OS(=O)S, SO2, C2H4, SO) as contributors to the 287 nm strong absorption and irradiation times lasted up to several tens of minutes11. Furthermore, extrapolation of the observations of photochemical experiments in matrix environments with long irradiation times to atmospheric conditions is not straightforward. Comparable experiments (low-temperature and solid matrixes) focused on HOSO radical photochemistry have given rise to different photodissociation channels after laser irradiation (H + OSO22 or HO + SO23,24). Hence, in spite of the recent advances, a convincing mechanism for the generation of Sn and SnO from 1(SO)2 isomers is still missing.
In this work, we identify the main photochemical routes of 1(SO)2 isomers by accurately simulating the gas-phase conditions of the Venus atmosphere through non-adiabatic molecular dynamics (NAMD)25,26,27,28,29,30,31, a well-established state-of-the-art methodology32,33,34,35,36,37,38,39,40,41,42, especially in combination with multiconfigurational quantum chemistry43,44,45,46,47. For HOSO48,49 and HOSO250,51 radical photochemistry, NAMD has recently demonstrated that the ejection of OH is the main photodissociation channel for both systems in Earth’s atmosphere24,52. Guided by the photochemical outcomes, in the present work we also use multiconfigurational quantum chemistry to improve the conventional kinetics description of other reactions that give access to 3S2 through deoxygenation reactions of 1(SO)2 mediated by 3SO (Eqs. 3 and 4):
and other species X=NO, O, S, H present in Venus’ atmosphere12,17,21,53. We also add high-level quantum chemistry information for the reaction involving Cl (Eq. 5), which is an important source of S2O (see Pinto et al.19):
Results
(SO)2 excited-state dynamics
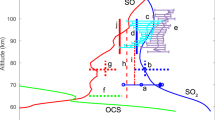
The distribution of the cis- and trans-OSSO photoproducts simulated for the atmosphere of Venus, and that of other relevant isomers, is shown in Fig. 1a, b, including quantum yields and illustrative snapshots of the geometries along the dynamics (see also Supplementary Tables 1 and 4). Note that the yields can be directly implemented as quantum yields for the photoinduced dissociations in the present and future Venus atmospheric modelings. Excitation of cis-OSSO and trans-OSSO in the atmospherically relevant window (310–496 nm), which mainly populates their second excited electronic state (S2), triggers exclusively photodissociations into 3SO + 3SO in less than 140 fs, with quantum yields of ca. 95% and 90%, respectively. These results clearly establish previous proposals by Frandsen et al.9. The decay of the S2 state into the energetically lower S1 state is faster in the cis isomer as compared to the trans species (Supplementary Figs. 8 and 10, respectively), whereas the triplet population is negligible for both isomers. Within our simulation time, 5% of cis-OSSO and 10% of trans-OSSO did not show any photolysis. Instead, the systems showed motions that could lead either to photoisomerizations (e.g., cis ↔ trans or cyclic-OS(=O)S) or to non-reactive decays. S–O bond breakings in the populated low-lying states are hindered by high-energy requirements (Supplementary Fig. 12).
a cis-OSSO and b trans-OSSO non-adiabatic molecular dynamics (NAMD) were computed with the multi-state complete-active-space second-order perturbation theory (MS-CASPT2) method (SHARC2.1/OpenMolcas)25,46, whereas the excited-state dynamics of the other systems (c–f) were run using the time-dependent density functional theory (TD-DFT) method (SHARC2.1/Gaussian 16)25,71. Photodynamics of cis-OSSO and trans-OSSO are clearly dominated by photocleavage to 3SO + 3SO, while 3S production arises also as another relevant light-induced decomposition product in cyclic-OS(=O)S, S=SO2, cis-OSOS, and trans-OSOS. Note that the spin multiplicity of the photoproducts corresponds to their respective ground-state, assumed to be reached at the end of the photodissociation process. The sensitivity of the yields to the number of trajectories is analyzed in Supplementary Table 4. See time evolution of relevant bond distances along the simulations in Supplementary Figs. 6, 7, 9, and 18–23. Red and yellow balls represent oxygen and sulfur atoms, respectively.
Excitation at 225–496 nm of the cyclic-OS(=O)S species (which has been recently detected11 in the laboratory using matrix isolation spectroscopy) populates mostly the S4 and S5 states (Supplementary Fig. 24), producing a mixture of photoproducts (Fig. 1c). The dominant (67%) photodissociation gives rise to 3S + 1SO2, whereas 33% leads to 3SO + 3SO via either cis-/trans-OSOS or the trigonal isomer S=SO2. Surprisingly, 1% of molecules produced 1S2O + 3O, a reaction that has not been documented until now.
As expected, the trigonal S=SO2, the most stable 1(SO)2 isomer in the ground-state9,54,55, photodissociates exclusively into 3S + 1SO2 when irradiated at 225–496 nm (Fig. 1d), confirming the proposal of 1(SO)2 photolysis from Krasnopolsky et al. based on theoretical estimations of energy profiles53,54. On the other hand, excitation (310–496 nm) of cis-OSOS (Fig. 1e) activates the dominant fragmentation into 3SO + 3SO (67%), whereas the photolysis into 3S + 1SO2 is less competitive (27%) although significant. A similar scenario is found for trans-OSOS (Fig. 1f).
Overall, the photodynamics of 1(SO)2 dimers give rise mainly to 3SO, while 3S atoms are produced from 3SO photodissociation (Supplementary Table 13) and are also generated indirectly from the minor isomeric photoproducts of cis-/trans-OSSO (cyclic-OS(=O)S, S=SO2, cis-OSOS, and trans-OSOS) as found herein from the simulations. Considering the photolysis rate of cis-OSSO and trans-OSSO of 0.20 and 0.62 s−1 (ref. 16), respectively, and the yields computed in this work for the non-photoreactive species (Fig. 1), an upper limit of 0.01–0.03 s−1 can be established for the rate of photoproduction of 3S from 1(SO)2. Such 3S atoms could recombine giving rise to 3S2 via reaction (Eq. 6) or oxidized by 3O2 (Eq. 7). Measured 3-body rate constants for reaction (Eq. 6) differ by nearly a factor of 104 (see Supplementary Table 13). Nevertheless, as shown in Supplementary Table 6, when considering high-pressure conditions for (Eq. 6) and the concentrations of 3S and 3O2 at the relevant altitude of ~64 km from Zhang et al.12, the pseudo-first order rate (k) appears lower for 3S recombination (Eq. 6) than that for oxidation (Eq. 7).
3SO deoxygenation reactions
Taking into account the significant photoproduction of 3SO from cis-/trans-OSSO, cyclic-OS(=O)S, and cis-/trans-OSOS (Fig. 1), formed in situ, we characterized the thermal (i.e., ground-state) deoxygenation reactions (Eqs. 3 and 4) that yield 1S2O, 3S2, and 1SO2 (Fig. 2, Supplementary Figs. 25 and 27, and Supplementary Table 6), which open the path toward aerosols (SnO and Sn). Since other species (2NO, 3O, 3S, and 2H) could also produce analogous reactions12,19,53, we accurately determined their reactivity with cis-OSSO (Supplementary Table 6 and Supplementary Figs. 28–35) to update previous estimations for the rate of these reactions. Furthermore, reaction between the abundant 3SO species and 2ClS (Eq. 5), which gives 1S2O, and subsequently 3S2 via (Eq. 4), was also characterized (Supplementary Figs. 39–41). The strong electron correlation character of the involved species forbids the general use of the single-reference DFT- or CC-based methodologies, which are popular in this field, requiring high-level multiconfigurational quantum chemistry (see analyses in the Supplementary Note 7). The obtained results indicate that reaction (Eq. 3) generates 1S2O with an energy barrier of ~9 kcal mol−1, in reasonable agreement with the estimates from reported rate constants (~7.5 kcal mol−1)56. Production of 1S2O by the reaction between cis-OSSO and 2NO, 3O, and 3S must overcome higher energy barrier heights (Supplementary Table 6), while a lower value is found for the reaction with 2H. On the contrary, reaction in Eq. 5 shows no activation energy. Once 1S2O is produced, the subsequent reaction to produce 3S2 shows a low-energy barrier especially for the reaction with 3SO (Eq. 4), as shown by the energy profile in Fig. 2. Analogous reaction energetics should apply for trans-OSSO.
Two approaches of multiconfigurational quantum chemistry (CASPT2) are shown, with a wavefunction based only on the lowest-lying electronic state (1 State) or a wavefunction allowing the interaction between the 3 lowest-lying nearby states (3 States). Benchmark analyses demonstrate the latter to be of higher accuracy, while the former is used as sensitivity test (see section 4.1 in the SI). A two-step process is found via an intermediate adduct 3(SOSSO) involving energy barriers heights of at most ~2 kcal mol−1 for both approaches to access the transition states for the adduct formation (TS1) and S–O bond cleavage from the adduct (TS2). The values of the imaginary frequency that characterize the TSs are also shown. Red and yellow balls represent oxygen and sulfur atoms, respectively.
The complex thermal reactivity between two cis-OSSO molecules was also explored (Supplementary Figs. 45–47), giving rise first to a cyclic species (cyclic-S4O4) by an energy barrier of ~9 kcal mol−1 and next to cis-S3O2 and 1SO2 involving a barrier of ~12 kcal mol−1 (Supplementary Table 6). Further reaction of 1cis-S3O2 with 3SO becomes faster (energy penalty of ~5 kcal mol−1) and ultimately results in 1SnO molecular systems and 1SO2 (Supplementary Fig. 48). Note also that SnO can photolyze to Sn (Supplementary Fig. 42).
Photochemical steady-state model for Venus middle atmosphere
With our 1(SO)2 photoreaction rates and branching ratios and the thermal reactivity properties, an approximate photochemical steady-state model was built to determine the reaction rate profiles and number densities for the key sulfur species for Venus middle atmosphere. Apart from 1SO2, most middle and upper atmosphere sulfur species have photochemical lifetimes shorter than their vertical transport timescales, making a steady-state approximation viable. Using 1SO2 number density and photodissociation rate profiles from Zhang et al.12 we computed steady abundances of 3SO, cis-OSSO, 1S2O, and 3S2 (see Supplementary Note 8). Number densities of 2NO, 3O, 3S, 2H, and 2ClS reported by Zhang et al.12 were also used. We treated 3S2 as a proxy for sulfur aerosols, but we did not include sulfur allotrope condensation reactions.
According to the calculated pseudo-first order rates (k) (Supplementary Table 6), thermal reactivity of cis-OSSO (k < 10−4 s−1) is clearly much slower than its photochemistry (0.19 s−1). This confirms previous assessments made by Frandsen et al.4 based on their calculated photochemical lifetime (0.20 s−1)4,16 and the thermal reactivity of OSSO reported by Yung and DeMore57. In the present work, we expand the amount of thermal reactions and the level of accuracy, which clearly strengthen the argument that OSSO photochemistry dominates over thermochemistry. Regarding the comparison for the thermal reactivity between cis-OSSO and 3SO/2NO/3O/3S/2H (see reaction rates in Supplementary Figs. 54 and 55), 3SO has a rate clearly higher than the others. As can be seen in Supplementary Table 6, for 2NO, 3O, and 3S, the reason is their larger energy barrier heights, while for 2H, it can be associated with the much lower abundance of this species (Supplementary Table 8). For reaction between 2ClS and 3SO (Eq. 5), the reaction rate (Supplementary Figs. 54 and 55) exceeds the rates of the other processes. Meanwhile, the lower concentration obtained for cis-OSSO in comparison to 3SO gives rise also to a lower k (Supplementary Table 6), and associated reaction rate, for the reactivity initiated by two cis-OSSO molecules as compared to that by 3SO or as compared to (Eq. 5).
Figure 3a displays the number density profiles obtained for the key sulfur species and comparative analysis with those previously reported. For the assumption of 10% 3S2 produced during cis-OSSO as in Pinto et al.19, the 3S2 profile closely tracks the cis-OSSO profile (Fig. 3a). If we instead assume zero 3S2 photoproduction and allow for 3S2 production primarily from 3S atom recombination, we obtain an 3S2 number density a factor of 104 lower (or lower) at 65 km, depending on the 3-body rate coefficient used for 3S atom recombination. At greater depth 3S2 abundance rises but to a value dependent on the widely varying published 3-body rate constants (Fig. 3a).
a S2 profiles for several possible model conditions. “S2 Pinto” is derived from photolysis of cis-OSSO as in Pinto et al.19. Turning off this reaction and using a fast 3S + 3S rate coefficient79 yields “S2 Nic”, and using a slower 3S + 3S rate coefficient80 yields “S2 Du”. In both cases 3S2 is dramatically reduced. b With the Pinto et al. S2 formation mechanism turned off, reaction of 3SO with 1S2O becomes the dominant pathway for 3S2. 3S2 and 1S2O profiles are shown for a rate constant of 1 × 10−10 cm3 s−1 (solid lines) and for a rate constant of 1 × 10−14 cm3 s−1 (dashed lines). The higher rate constant is consistent with ab initio calculations presented here and yields substantial 3S2.
With zero 3S2 production from cis-OSSO photolysis, we included reaction (Eq. 4) for several possible values of the rate constant. Ab initio reactivity calculations presented here (Supplementary Table 6) indicate that reaction (Eq. 4) is fast. Evaluating (Eq. 4) over a span of 4 orders of magnitude to consider estimations from similar reactions (Supplementary Table 13) and the updated value in the present work yields a peak 3S2 abundance comparable to that reported by Pinto et al.19 for the highest rate constant, but with a more narrow vertical distribution (Fig. 3b).
Discussion
The photochemistry study of 1(SO)2 isomers, herein performed with state-of-the-art photodynamics simulations reproducing Venus’ atmosphere conditions, points to an overwhelming prevalence of the S–S photodissociations over the S–O ruptures, which must be attributed to the larger S–O bond strength in comparison to that of S–S. Clearly, the S–S cleavage drives the photochemistry of 1(SO)2. The findings (displayed in Fig. 1) show that the major photoproducts are 3SO, 3S, and 1SO2. This seriously questions a significant occurrence of (Eq. 2), as assumed by Pinto et al.19 on the basis of experiments by Wu et al.11 in cold conditions and solid matrixes, since no 3S2 + 3O2 production has been observed in our thorough simulations. As a matter of fact, the release of a single oxygen atom rarely takes place. Therefore, it is reasonable to conclude that the reaction shown in Eq. 2 is not able to explain a significant generation of polysulfur reactions in Venus through irradiation of 1(SO)2 species. The more usual mechanism for 3S2 formation is 3S atom recombination (Eq. 6). 3S atoms are produced from 3SO photodissociation and are also generated indirectly from the minor isomeric photoproducts of cis-/trans-OSSO (cyclic-OS(=O)S), S=SO2, cis-OSOS, and trans-OSOS) as obtained in the present study (Fig. 1). However, polysulfur production by Eq. 6 is limited when formation of allotropes of size 3S2 and larger must proceed through this pathway as 3S atoms are lost rapidly through oxidation by 3O2 (Eq. 7). This 3S atom bottleneck greatly prevents significant production of polysulfur species in the Venusian atmosphere from this source.
Contrary to the situation in Venus’ atmosphere, the production of 3S2 in matrix monitored by Wu et al.11 through the absorption increase at 287 nm seems to be the result of the recombination (Eq. 6), fed by the sulfur atoms largely released by four out of six 1(SO)2 isomers (Fig. 1c–f), whereas the depletion of the 375 nm absorption band is likely the result of the fragmentations exposed in Fig. 1. It must be emphasized that the experimental conditions (cold molecules adsorbed on a solid matrix) are not strictly comparable to our simulations in the gas-phase at standard temperature neither to those of the Venus atmosphere, even more considering the extremely long irradiation times (tens of minutes) used by Wu et al.11 as compared to the ultrafast photodissociations studied in our work.
Instead of an 3S atom pathway, we propose that 3S2 formation in the atmosphere occurs primarily from the precursor 1S2O by Eq. 4, which is generated by Eqs. 3 and 5, and other sources reported in the literature (see Supplementary Figs. 54 and 55). This is motivated by the fact that when switching on our highly accurate energetics and rate for Eq. 4 computed herein and 1S2O generation rates available in the literature (supported in this work for the relevant Eqs. 3 and 5 by quantum chemistry profiles) in our photochemical steady-state model of the Venus middle atmosphere, 3S2 abundance increases 4 orders of magnitude approaching the number density reported by Pinto et al.19 but without the photochemical pathway shown in Eq. 2. A similar peak of 3S2 abundance is found although the vertical distribution is narrower in our case. We can clearly state that the sulfur cycle in the Venus middle atmosphere can maintain a high fraction of elemental sulfur aerosols by converting 3SO or 1(SO)2 to 3S2 via the 1S2O intermediate and the coupling between S and Cl chemistry in Venus. Assessment of deoxygenation pathways analogous to Eqs. 3 and 4 but mediated by 2NO, 3O, 3S, and 2H shows that they are not competitive with 3SO. Therefore, 3SO is a more efficient agent in comparison to 2NO, 3O, 3S, and 2H to convert thermally cis-OSSO (predominant 1(SO)2 isomer in Venus’ atmosphere) first into 1S2O by Eq. 3 and subsequently to 3S2 by Eq. 4. Nevertheless, the most efficient process leading to the intermediate 1S2O involves the reaction between 3SO and 2ClS (Eq. 5). Reactivity of two cis-OSSO molecules can produce SnO, Sn, and 1SO2 via a complex mechanism as shown herein. However, it does not compete with reactions shown in Eqs. 3–5, also since this reaction is limited by the lower concentration of cis-OSSO in the Venusian atmosphere predicted by the present modeling. This reactivity can be expected during the night or in conditions of weak radiation, and it should contribute to the reported day/night variation of the 1SO2/3SO concentration ratio58.
The findings obtained in this study allow for a more complete understanding of the current Venusian atmosphere. Because of the complexity of the sulfur chemistry in the middle atmosphere, which includes many species of the form SxOyClz, and because of the paucity of laboratory rate coefficient data for most of the reactions among these species, high-level ab initio calculations are essential for understanding the chemistry of the Venus atmosphere. Those improvements are needed also to guide the next terrestrial measurements, spacecraft missions (recently announced by the National Aeronautics and Space Administration motivated in part by the studies on the phosphine detection in Venus atmosphere)59,60,61,62,63, and to assist with geoengineering of Earth’s climate and monitor stratospheric volcanic eruptions’ clouds. Furthermore, they are beneficial to better understand the atmosphere of early Earth (pre-oxygenation of Earth’s atmosphere) and shall be used in describing Earth-like exoplanet atmospheres in conjunction with future high-resolution spectroscopy measurements of said exoplanets.
Methods
Thermal and photochemical reaction channels and associated rates
Herein, photolysis of 1(SO)2 has been studied in detail by means of NAMD propagated with the multi-state complete-active-space second-order perturbation theory (MS-CASPT2) method43,44,64 with the OpenMolcas and SHARC programs25,46, including the mixing of singlet and triplet states (see active space orbitals in Supplementary Fig. 1). Multireference configuration interaction (MRCI)47,65,66 profiles validate this level of theory (Supplementary Figs. 2–5). These high-level results have been used to validate NAMD simulations propagated at the faster time-dependent density functional theory (TD-DFT) method67,68,69,70 with the Gaussian and SHARC programs25,71 (Supplementary Figs. 11–17 and Supplementary Table 3). Simulation settings and method validations are fully detailed in the Supplementary Information (SI), Supplementary Notes 1–3 and Supplementary Tables 2 and 372,73,74,75,76,77.
Minima and transition states that describe the thermal reaction profiles have been optimized for the lowest-lying electronic state, with the single-state (SS)-CASPT2 method using state-specific complete-active-space self-consistent field (SS)-CASSCF wave functions as reference. The nature of the stationary points has been verified through the corresponding frequency analyses whereas the transition states have been unambiguously connected with their corresponding reactants and products through intrinsic reaction coordinates determinations. To allow the coupling between nearby electronic states, state-average (SA)-CASSCF wave functions have been computed on top of the mentioned optimized structures and the final energy profiles were corrected with the MS-CASPT2 method using the same protocol as for the SS-CASSCF determinations. The strong electron character and the multiconfigurational nature of some of these ground-state reactions have been evidenced by comparisons with the DFT and coupled-cluster methods used in Gaussian71 and ORCA78. Static excited-state pathways and ground-state reaction channels with problematic transition-state optimizations have been explored through relaxed scans of the reaction coordinate or by means of linear interpolations of internal coordinates between relevant structures. Further information on the specific computational parameters (active spaces, basis sets, number of computed states), the employed optimization algorithms, and data used for computing rates can be found in the SI, Supplementary Notes 4–7, Supplementary Figs. 25–50 and Supplementary Tables 5–12.
Photochemical steady-state calculations: abundances of sulfur species
We use photochemical steady-state calculations to estimate the abundance profiles for several sulfur species of particular importance in the Venus atmosphere. As the photochemical lifetimes of many of the trace sulfur species are shorter than the eddy transport timescale, this approximation is valid to first order, and allows us a rapid assessment of the implications of the new chemical schemes proposed here based on our ab initio results. For non-sulfur species, long-lived sulfur species, and photodissociation rate constants, we use profiles from Pinto et al.19 and Zhang et al.12. Mixing ratio profiles for [3O], [3O2], [2NO], [2H], [1SO2], [3S], and [2ClS] are digitally read-in from Zhang et al.12 or Pinto et al.19. The vertical profiles for the photodissociation rate coefficients for 3SO and 1SO2 were taken from the bibliography as described in Supplementary Note 8. Condensation reactions for sulfur allotropes have not been included here, as appears to be the case for Pinto et al.19. Photochemical steady-state calculations are carried out from 58 to 112 km, following the temperature and total number density profiles given by Zhang et al.12. Steady-state number densities are computed for 3SO, 1(SO)2, which we assume in these calculations to be primarily cis-(SO)2, 1S2O, and 3S2. A reduced set of 19 reactions involving these species is given in Supplementary Table 13. Setting production rate equal to loss rate for each of the 4 species of interest, and using the reactions in Supplementary Table 13, we arrive at the Equations for steady-state number density S1–S4. These Equations are solved in the order presented in the SI, Supplememntary Note 8, and the steady-state values are used as applicable. Loss of 3S2 to S4 formation is accounted for, but we are not attempting to accurately account for sulfur allotrope abundances. For this reason, 3S2 may be taken as a proxy for total sulfur aerosol production. Further details on the photochemical steady-state model and benchmarking analyses can be found in the SI, Supplementary Note 8 and Supplementary Figs. 51–53.
Data availability
All data to evaluate the conclusions in the paper are available in the main text and/or the Supplementary Materials.
References
Pérez-Hoyos, S. et al. Venus upper clouds and the UV absorber from MESSENGER/MASCS observations. J. Geophys. Res. Planets 123, 145–162 (2018).
Peralta, J. et al. Overview of useful spectral regions for Venus: an update to encourage observations complementary to the Akatsuki mission. Icarus 288, 235–239 (2017).
Titov, D. V., Ignatiev, N. I., McGouldrick, K., Wilquet, V. & Wilson, C. F. Clouds and hazes of Venus. Space Sci. Rev. 214, 126 (2018).
Molaverdikhani, K., McGouldrick, K. & Esposito, L. W. The abundance and vertical distribution of the unknown ultraviolet absorber in the Venusian atmosphere from analysis of Venus Monitoring Camera images. Icarus 217, 648–660 (2012).
Pollack, J. B. et al. Distribution and source of the UV absorption in Venus’ atmosphere. J. Geophys. Res. Sp. Phys. 85, 8141–8150 (1980).
Pollack, J. B. et al. Nature of the ultraviolet absorber in the Venus clouds: inferences based on pioneer Venus data. Science 205, 76–79 (1979).
Barker, E. S. Detection of SO2 in the UV spectrum of Venus. Geophys. Res. Lett. 6, 117–120 (1979).
Heyden, F. J., Kiess, C. C. & Kiess, H. K. Spectrum of Venus in the violet and near-ultraviolet. Science 130, 1195 (1959).
Frandsen, B. N., Wennberg, P. O. & Kjaergaard, H. G. Identification of OSSO as a near-UV absorber in the Venusian atmosphere. Geophys. Res. Lett. 43, 11146–11155 (2016).
Mills, F. P., Esposito, L. W. & Yung, Y. L. Atmospheric composition, chemistry, and clouds. in. Geophys. Monogr. Ser. 176, 73–100 (2007).
Wu, Z. et al. The near-UV absorber OSSO and its isomers. Chem. Commun. 54, 4517–4520 (2018).
Zhang, X., Liang, M. C., Mills, F. P., Belyaev, D. A. & Yung, Y. L. Sulfur chemistry in the middle atmosphere of Venus. Icarus 217, 714–739 (2012).
Zhang, X. et al. Photolysis of sulphuric acid as the source of sulphur oxides in the mesosphere of Venus. Nat. Geosci. 3, 834–837 (2010).
Parkinson, C. D. et al. Photochemical control of the distribution of Venusian water. Planet. Space Sci. 113–114, 226–236 (2015).
Toon, O. B., Turco, R. P. & Pollack, J. B. The ultraviolet absorber on Venus: Amorphous sulfur. Icarus 51, 358–373 (1982).
Frandsen, B. N., Farahani, S., Vogt, E., Lane, J. R. & Kjaergaard, H. G. Spectroscopy of OSSO and other sulfur compounds thought to be present in the Venus atmosphere. J. Phys. Chem. A 124, 7047–7059 (2020).
Krasnopolsky, V. A. Disulfur dioxide and its near-UV absorption in the photochemical model of Venus atmosphere. Icarus 299, 294–299 (2018).
Marcq, E. et al. Climatology of SO2 and UV absorber at Venus’ cloud top from SPICAV-UV nadir dataset. Icarus 335, 113368 (2020).
Pinto, J. P. et al. Sulfur monoxide dimer chemistry as a possible source of polysulfur in the upper atmosphere of Venus. Nat. Commun. 12, 175 (2021).
Murray, B. C. et al. Venus: atmospheric motion and structure from mariner 10 pictures. Science 183, 1307–1315 (1974).
Bierson, C. J. & Zhang, X. Chemical cycling in the Venusian atmosphere: a full photochemical model from the surface to 110 km. J. Geophys. Res. Planets 125, e2019JE006159 (2020).
Isoniemi, E., Khriachtchev, L., Lundell, J. & Räsänen, M. HSO2 isomers in rare-gas solids. Phys. Chem. Chem. Phys. 4, 1549–1554 (2002).
Chen, C. et al. Capture of the sulfur monoxide-hydroxyl radical complex. J. Am. Chem. Soc. 142, 2175–2179 (2020).
Carmona-García, J. et al. Photochemistry and non-adiabatic photodynamics of the HOSO radical. J. Am. Chem. Soc. 143, 10836–10841 (2021).
Mai, S., Marquetand, P. & González, L. Nonadiabatic dynamics: the SHARC approach. Wiley Interdiscip. Rev. Comput. Mol. Sci. 8, e1370 (2018).
Mai, S., Marquetand, P. & Gonz, L. A general method to describe intersystem crossing dynamics in trajectory surface hopping. Int. J. Quantum Chem. 115, 1215–1231 (2015).
Richter, M., Marquetand, P., González-Vázquez, J., Sola, I. & González, L. SHARC: ab initio molecular dynamics with surface hopping in the adiabatic representation including arbitrary couplings. J. Chem. Theory Comput. 7, 1253–1258 (2011).
Mai, S. et al. SHARC2.1: surface hopping including arbitrary couplings– program package for non-adiabatic dynamics. sharc-md.org (2019).
Barbatti, M. Nonadiabatic dynamics with trajectory surface hopping method. Wiley Interdiscip. Rev. Comput. Mol. Sci. 1, 620–633 (2011).
Wang, L., Akimov, A. & Prezhdo, O. V. Recent progress in surface hopping: 2011–2015. J. Phys. Chem. Lett. 7, 2100–2112 (2016).
Park, J. W. & Shiozaki, T. On-the-fly CASPT2 surface-hopping dynamics. J. Chem. Theory Comput. 13, 3676–3683 (2017).
Francés‐Monerris, A. et al. Photodissociation mechanisms of major mercury(II) species in the atmospheric chemical cycle of mercury. Angew. Chem. Int. Ed. 59, 7605–7610 (2020).
Saiz-Lopez, A. et al. Photochemistry of oxidized Hg(I) and Hg(II) species suggests missing mercury oxidation in the troposphere. Proc. Natl Acad. Sci. USA 49, 30949–30956 (2020).
Francés-Monerris, A., Lineros-Rosa, M., Miranda, M. A. A., Lhiaubet-Vallet, V. & Monari, A. Photoinduced intersystem crossing in DNA oxidative lesions and epigenetic intermediates. Chem. Commun. 56, 4404–4407 (2020).
Nazari, M. et al. Ultrafast dynamics in polycyclic aromatic hydrocarbons: the key case of conical intersections at higher excited states and their role in the photophysics of phenanthrene monomer. Phys. Chem. Chem. Phys. 21, 16981–16988 (2019).
Grisanti, L., Sapunar, M., Hassanali, A. & Došlić, N. Toward understanding optical properties of amyloids: a reaction path and nonadiabatic dynamics study. J. Am. Chem. Soc. 142, 18042–18049 (2020).
Rauer, C., Nogueira, J. J., Marquetand, P. & González, L. Cyclobutane thymine photodimerization mechanism revealed by nonadiabatic molecular dynamics. J. Am. Chem. Soc. 138, 15911–15916 (2016).
Mai, S. et al. The origin of efficient triplet state population in sulfur-substituted nucleobases. Nat. Commun. 7, 13077 (2016).
Mondal, P., Granucci, G., Rastädter, D., Persico, M. & Burghardt, I. Azobenzene as a photoregulator covalently attached to RNA: a quantum mechanics/molecular mechanics-surface hopping dynamics study. Chem. Sci. 9, 4671–4681 (2018).
Martinez-Fernandez, L., Corral, I., Granucci, G. & Persico, M. Competing ultrafast intersystem crossing and internal conversion: a time resolved picture for the deactivation of 6-thioguanine. Chem. Sci. 5, 1336–1347 (2014).
Zhou, Z. et al. Control of charge carriers trapping and relaxation in hematite by oxygen vacancy charge: ab initio non-adiabatic molecular dynamics. J. Am. Chem. Soc. 139, 6707–6717 (2017).
Abdelgawwad, A. M. A. et al. Light-induced on/off switching of the surfactant character of the o-cobaltabis(dicarbollide) anion with no covalent bond alteration. Angew. Chem. Int. Ed. 60, 25753–25757 (2021).
Roca-Sanjuán, D., Aquilante, F. & Lindh, R. Multiconfiguration second-order perturbation theory approach to strong electron correlation in chemistry and photochemistry. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2, 585–603 (2012).
Finley, J., Malmqvist, P. Å., Roos, B. O. & Serrano-Andrés, L. The multi-state CASPT2 method. Chem. Phys. Lett. 288, 299–306 (1998).
Roos, B. O. et al. In Recent Advances in Multireference Theory (ed. Hirao, K.) 161–195 (World Scientific Publishing, 1999).
Fernández Galván, I. et al. OpenMolcas: from source code to insight. J. Chem. Theory Comput. 15, 5925–5964 (2019).
Werner, H.-J. et al. The Molpro quantum chemistry package. J. Chem. Phys. 152, 144107 (2020).
Ruiz-López, M. F., Martins-Costa, M. T. C., Anglada, J. M. & Francisco, J. S. A new mechanism of acid rain generation from HOSO at the air–water interface. J. Am. Chem. Soc. 141, 16564–16568 (2019).
Trabelsi, T., Anglada, J. M., Ruiz-López, M. F. & Francisco, J. S. Photochemistry of HOSO radical in the gas phase. J. Chem. Phys. 151, 111103 (2019).
Mai, T. V.-T., Duong, M. V., Nguyen, H. T. & Huynh, L. K. Ab initio kinetics of the HOSO2 + 3O2 → SO3 + HO2 reaction. Phys. Chem. Chem. Phys. 20, 6677–6687 (2018).
Nakajima, M. & Endo, Y. Spectroscopic detection of gas-phase HOSO2. Phys. Chem. Chem. Phys. 23, 25063–25069 (2021).
Carmona-García, J. et al. Photochemistry of HOSO2 and SO3 and implications for the production of sulfuric acid. J. Am. Chem. Soc. 143, 18794–18802 (2021).
Krasnopolsky, V. A. A photochemical model for the Venus atmosphere at 47–112 km. Icarus 218, 230–246 (2012).
Marsden, C. J. & Smith, B. J. An ab initio study of many isomers of S2O2. A combined theoretical and experimental analysis of the harmonic force field and molecular structure of cis-planar OSSO. Chem. Phys. 141, 335–353 (1990).
Goodarzi, M., Vahedpour, M. & Nazari, F. Theoretical study on the mechanism of S2 + O2 reaction. Chem. Phys. Lett. 497, 1–6 (2010).
Herron, J. T. & Huie, R. E. Rate constants at 298 k for the reactions SO+SO+M→(SO)2+M and SO+(SO)2→SO2+S2O. Chem. Phys. Lett. 76, 322–324 (1980).
Yung, Y. L. & Demore, W. B. Photochemistry of the stratosphere of Venus: implications for atmospheric evolution. Icarus 51, 199–247 (1982).
Jessup, K. L. et al. Coordinated hubble space telescope and Venus express observations of Venus’ upper cloud deck. Icarus 258, 309–336 (2015).
Greaves, J. S. et al. Phosphine gas in the cloud decks of Venus. Nat. Astron. 5, 655–664 (2021).
Villanueva, G. L. et al. No evidence of phosphine in the atmosphere of Venus from independent analyses. Nat. Astron. 5, 631–635 (2021).
Greaves, J. S. et al. Addendum: phosphine gas in the cloud deck of Venus. Nat. Astron. 5, 726–728 (2021).
Lincowski, A. P. et al. Claimed detection of PH3 in the clouds of Venus is consistent with mesospheric SO2. Astrophys. J. Lett. 908, L44 (2021).
Omran, A. et al. Phosphine generation pathways on rocky planets. Astrobiology 21, 1264–1276 (2021).
Andersson, K., Malmqvist, P. & Roos, B. O. Second‐order perturbation theory with a complete active space self‐consistent field reference function. J. Chem. Phys. 96, 1218–1226 (1992).
Werner, H. J. & Knowles, P. J. An efficient internally contracted multiconfiguration-reference configuration interaction method. J. Chem. Phys. 89, 5803–5814 (1988).
Knowles, P. J. & Werner, H. J. An efficient method for the evaluation of coupling coefficients in configuration interaction calculations. Chem. Phys. Lett. 145, 514–522 (1988).
Stephens, P. J., Devlin, F. J., Chabalowski, C. F. & Frisch, M. J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 98, 11623–11627 (1994).
Becke, A. Density‐functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98, 5648–5652 (1993).
Runge, E. & Gross, E. K. U. Density-functional theory for time-dependent systems. Phys. Rev. Lett. 52, 997–1000 (1984).
Casida, M. E. In Recent Advances in Density Functional Methods (Part I) (ed. Chong, D. P.) 155–192 (World Scientific, 1995).
Frisch, M. J. et al. Gaussian 16, Revision C.01. Wallingford, CT (Gaussian, Inc., 2016).
Granucci, G., Persico, M. & Zoccante, A. Including quantum decoherence in surface hopping. J. Chem. Phys. 133, 134111 (2010).
Ghigo, G., Roos, B. O. & Malmqvist, P. Å. A modified definition of the zeroth-order Hamiltonian in multiconfigurational perturbation theory (CASPT2). Chem. Phys. Lett. 396, 142–149 (2004).
Plasser, F. et al. Strong influence of decoherence corrections and momentum rescaling in surface hopping dynamics of transition metal complexes. J. Chem. Theory Comput. 15, 5031–5045 (2019).
Forsberg, N. & Malmqvist, P. Å. Multiconfiguration perturbation theory with imaginary level shift. Chem. Phys. Lett. 274, 196–204 (1997).
Barbatti, M. et al. NEWTON-X: a package for Newtonian dynamics close to the crossing seam, version 1.2. Mülheim an der Ruhr, Ger. (Max-Planck-Institut für Kohlenforsch, 2011).
Lee, T. J. & Taylor, P. R. A diagnostic for determining the quality of single-reference electron correlation methods. Int. J. Quantum Chem. 36, 199–207 (1989).
Neese, F. Software update: the ORCA program system, version 4.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 8, e1327 (2018).
Nicholas, J. E., Amodio, C. A. & Baker, M. J. Kinetics and mechanism of the decomposition of H2S, CH3SH and (CH3)2S in a radio-frequency pulse discharge. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 75, 1868–1875 (1979).
Du, S., Francisco, J. S., Shepler, B. C. & Peterson, K. A. Determination of the rate constant for sulfur recombination by quasiclassical trajectory calculations. J. Chem. Phys. 128, 204306 (2008).
Acknowledgements
Calculations have been partially conducted at the local QCEXVAL cluster and the Lluis Vives v2 and Tirant v3 superclusters of the Servei d’Informàtica (University of Valencia), and at the local LPCT cluster and the regional ExpLor center (University of Lorraine, France). A.F.-M. thanks Generalitat Valenciana and the European Social Fund for the postdoctoral contract APOSTD/2019/149 and the project GV/2020/226, and the Ministerio de Ciencia e Innovación (MICINN) for the Juan de la Cierva contract IJC2019-039297-I. D.R.-S. is grateful to the MICINN for the project CTQ2017-87054-C2-2-P and the Ramón y Cajal grant RYC2015-19234. The project that gave rise to these results received also the support of a fellowship for J.C.-G. from “la Caixa” Foundation (ID 100010434); the fellowship code is LCF/BQ/DR20/11790027.
Author information
Authors and Affiliations
Contributions
A.F.-M., J.R.L., J.S.F., and D.R.-S. designed the work. Data acquisition and curation was carried out by A.F.-M., J.C.-G., T.T., and J.R.L. All authors contributed to interpret and discuss the data. The manuscript was initially prepared by A.F.-M., J.C.-G., J.R.L., and D.R.-S, and was revised by J.S.F. and A.S.-L.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Benjamin Frandsen and Joseph Lane for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Francés-Monerris, A., Carmona-García, J., Trabelsi, T. et al. Photochemical and thermochemical pathways to S2 and polysulfur formation in the atmosphere of Venus. Nat Commun 13, 4425 (2022). https://doi.org/10.1038/s41467-022-32170-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-32170-x
This article is cited by
-
Laboratory infrared spectra and fragmentation chemistry of sulfur allotropes
Nature Communications (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.