Abstract
Modulation of the energy landscape by external perturbations governs various thermally-activated phenomena, described by the Arrhenius law. Thermal fluctuation of nanoscale magnetic tunnel junctions with spin-transfer torque (STT) shows promise for unconventional computing, whereas its rigorous representation, based on the Néel-Arrhenius law, has been controversial. In particular, the exponents for thermally-activated switching rate therein, have been inaccessible with conventional thermally-stable nanomagnets with decade-long retention time. Here we approach the Néel-Arrhenius law with STT utilising superparamagnetic tunnel junctions that have high sensitivity to external perturbations and determine the exponents through several independent measurements including homodyne-detected ferromagnetic resonance, nanosecond STT switching, and random telegraph noise. Furthermore, we show that the results are comprehensively described by a concept of local bifurcation observed in various physical systems. The findings demonstrate the capability of superparamagnetic tunnel junction as a useful tester for statistical physics as well as sophisticated engineering of probabilistic computing hardware with a rigorous mathematical foundation.
Similar content being viewed by others
Introduction
A dynamical system is classified by the stability of its potential landscape, especially by the local bifurcation of the dynamical equation. Under finite stochasticity, the Arrhenius law, a general principle for thermally-activated events, describes a variety of dynamical phenomena ranging from chemical reactions to physical processes. According to the Arrhenius law, the relaxation time τ in staying at a certain state is given by τ = τ0 expΔ with the thermal stability factor Δ ≡ E0/kBT, where τ0 is the intrinsic time constant of each system, kB the Boltzmann constant, T the absolute temperature, and E0 an intrinsic energy barrier for switching to different states without perturbation. Under the perturbation by normalised external input x, E0 is replaced by an effective energy barrier E = \({E}_{0}{\left(1-x\right)}^{{n}_{x}}\), where the switching exponent \({n}_{x}\) is determined by the effective energy landscape with x. In general, when the dynamical equation dΘ/dt = f(Θ,x) is given, where t is the time and Θ is the state variable (e.g. particle position, spin quantisation direction, amount of unreacted substance, etc.), the types of local bifurcation of f(Θ,x) determines \({n}_{x}\); for example, \({n}_{x}\) = 2 for the pitchfork bifurcation and \({n}_{x}\) = 3/2 for the saddle-node bifurcation1. This suggests that the switching exponent serves as a unique lens for the local structure, especially the stability of the energy landscape under the perturbations in the relevant system.
In magnetic materials, which have served as a model system to study the physics of thermally-activated phenomena, the basis of the Arrhenius law was built by Néel2 and Brown3, known as the Néel–Arrhenius law. For single-domain uniaxial magnets with a magnetic field H applied along the easy axis, E under magnetic field can be simply derived as E = E0(1 – H/HKeff)2 by the Stoner–Wohlfarth model, where HKeff is the effective magnetic anisotropy field4. However, theoretical studies pointed out that the value of exponent nH, 2 in the above equation, should vary when one considers some realistic factors such as misalignment of magnetic field5,6 and higher-order terms of anisotropy7; in other words, the local bifurcation varies with them.
The magnetisation of nanomagnets can also be controlled by spin-transfer torque (STT) under current application through the angular momentum transfer8,9,10,11,12,13. The STT-induced magnetisation switching in thermally-stable magnetic tunnel junctions (MTJ) is a key ingredient for non-volatile magnetoresistive random access memory14,15,16. Moreover, recent studies have demonstrated an unconventional paradigm of computing, e.g. neuromorphic computing with population coding17, and probabilistic computing18, which utilises a combinatorial effect of STT and thermal fluctuation in superparamagnetic tunnel junctions (s-MTJs). By further combining the effect of external magnetic fields, additional tunabilities of the s-MTJs for probabilistic computing have been shown19. In this regard, understanding how the effective energy of s-MTJs is characterised under STT, as well as magnetic field, is of significant interest not only from fundamental but also from technological aspects. The Néel–Arrhenius law under STT has been a long-standing question partly because the STT itself does not modulate the energy landscape due to its non-conservative nature, preventing one from defining its effective potential energy. Despite the difficulty, the expectation value of event time of the magnetisation switching, i.e. the Néel relaxation time τ, under field H and current I is phenomenologically expressed in a form:
where τ0 is ~1 ns in magnetic systems3, and IC0 an intrinsic critical current. Regarding the exponent nI for the factor of current, different values, 1 (refs. 20,21) or 2 (refs. 22,23,24), have been theoretically derived, where the former was obtained by considering a fictitious temperature, whereas the latter was obtained by analysing the stochastic process based on the Fokker–Planck equation. Experimentally, it has been practically inaccessible as far as one examines conventional thermally-stable MTJs and consequently, their decade-long unperturbed retention property has been extrapolated from limited data obtained in a reasonable time while assuming a certain number for nH or nI25,26,27,28,29,30,31,32,33. For applications with superparamagnetic tunnel junctions that actively utilise thermal fluctuation under STT, such uncertainty makes sophisticated engineering impractical as a rigorous description of modulation of the effective energy landscape is indispensable.
Here we experimentally study the Néel–Arrhenius law of a nanomagnet under STT utilising superparamagnetic tunnel junctions that allow direct determination of the event time under fields and currents34,35,36,37,38,39. Through measurements of homodyne-detected ferromagnetic resonance (FMR) under current biases, high-speed STT switching with various pulse widths, and random telegraph noise (RTN) under various fields and currents, values of nH and nI are uniquely determined for given conditions. Furthermore, we show that by considering the local bifurcations under magnetic field and STT, which have not been considered for magnetic systems, the obtained results can be comprehended with the effects of the torques of the field and current without the difficulties to define the effective potential of STT.
Sample preparation and strategy of following experiments
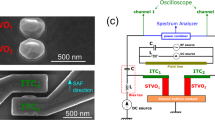
As shown in Fig. 1a, a stack structure, Ta(5)/Pt(5)/[Co(0.3)/Pt(0.4)]7/Co(0.3)/Ru(0.45)/[Co(0.3)/Pt(0.4)]2/Co(0.3)/Ta(0.3)/CoFeB/MgO(1.0)/CoFeB(tCoFeB = 1.88)/Ta(5)/Ru(5) (numbers in parenthesis are nominal thickness in nm), is deposited by dc/rf magnetron sputtering on a sapphire substrate. The stack possesses essentially the same structure as what was utilised in the demonstration of probabilistic computing18. Resistance (R)-area (A) product, RA, of the MgO tunnel barrier is 5.5 Ωμm2. The stack is patterned into MTJ devices, followed by annealing at 300 °C. The MTJ device we will mainly focus on hereafter (device A) has a diameter D of 34 nm (results for device B with tCoFeB = 1.82 nm, RA = 8.1 Ωμm2, and D = 28 nm will be also shown later). In this size range, the magnetisation can be represented by a single vector without significant effects of spatial inhomogeneity for the present stack structure16,27,40. Both CoFeB layers have a perpendicular easy axis. Figure 1b shows the junction resistance R as a function of the perpendicular magnetic field Hz. Gradual variation of mean R with Hz and scattering of data points at the transition region reflects a superparamagnetic nature of the MTJ whose switching time is shorter than the measurement time of R (~ 1 s).
To determine nH and nI in actual MTJs, we take into account the following two effects: electric-field modulation of magnetic anisotropy41,42,43,44 and uncompensated stray field HS from the reference layer. Consequently, Δ, the argument of the exponential in Eq. (1), is rewritten as
with \( {{\it\Delta}}_{0}\equiv {E}_{0}/{k}_{{{{{{\rm{B}}}}}}}T\), \(h({H}_{z},V)\equiv \left({H}_{z}-{H}_{{{{{{\rm{S}}}}}}}\right)/{H}_{K}^{{{{{{\rm{eff}}}}}}}(V)\), and \({v}_{{{{{{\rm{P}}}}}}\left({{{{{\rm{AP}}}}}}\right)}(V)\equiv V\!/\!{V}_{{{{{{\rm{C}}}}}}0,{{{{{\rm{P}}}}}}({{{{{\rm{AP}}}}}})}\). VC0,P(AP) denotes the intrinsic critical voltage for STT switching from parallel, P, to antiparallel, AP, states (AP to P states). Because the electric-field effect on anisotropy is governed by the applied voltage V, we use an expression based on voltage input rather than current input. Equation (2) contains so many unknown variables (E0, HS, HKeff(V), VC0,P(AP), nH and nI) that one cannot directly determine the exponents by only measuring RTN. Thus, in the following, we first separately determine HKeff(V) from a homodyne-detected FMR and the next VC0 from the STT switching probability. After that, we determine HS and the exponents nH and nI from RTN measurement34,35,36,37,38 as a function of V.
Electric-field effect on anisotropy field
Firstly, we determine HKeff(V) from homodyne-detected FMR under dc bias voltage45,46. Figure 2a shows the circuit configuration for the measurement. Homodyne-detected voltage spectra are measured while sweeping Hz at various frequencies and HKeff is determined from the peak position (see Methods and Supplementary Information for details). We perform this measurement at various dc biases and obtain HKeff vs. V, as shown in Fig. 2b. HKeff changes nonlinearly with V. We fit a quadratic equation to the obtained dependence and determine the coefficients for constant, linear, and quadratic terms to be μ0HKeff(0) = 77.0 ± 0.5 mT, μ0dHKeff/dV = −57.8 ± 1.6 mT V−1, and μ0d2HKeff/dV2 = −49.9 ± 7.5 mT V−2 (μ0 is the permeability of vacuum). Note that the constant term represents the magnetic anisotropy field at zero bias whereas the linear and quadratic terms mainly originate from the electric-field modulation of anisotropy and an effect of Joule heating, respectively. The determined coefficients will be used in the analysis of RTN later.
a Electrical circuit for homodyne-detected ferromagnetic resonance (FMR). b DC bias voltage V dependence of effective anisotropy field (μ0HKeff) determined by FMR. Red curves are fitting with a quadratic function to the plots. The error bar shows the standard error of fitting Kittel’s resonant condition to the experimentally obtained resonant frequency versus perpendicular magnetic field Hz.
Intrinsic critical voltage for STT switching
Secondly, we determine VC0 for the STT switching. Because the fluctuation timescale of the studied system is on the order of milliseconds, we need to measure the junction state right after the switching pulse application when they are still non-volatile. To this end, we use a circuit configuration shown in Fig. 3a. This configuration is similar to that we used in our previous work to study the switching error rate47; a voltage waveform composed of initialisation, write, and read pulses [Fig. 3b] is applied to the MTJ by an arbitrary waveform generator, and the transmitted signal at the read pulse is monitored by a high-speed oscilloscope to identify the final state of magnetisation configuration. The typical transmitted signals for P and AP states are shown in Fig. 3c. A clear difference is observed in the amplitude of the transmitted signal for different configurations due to the tunnel magnetoresistance. Write and read pulses are separated by 30 ns, which is much shorter than the shortest relaxation time shown later (~0.3 ms), ensuring a sufficiently low read-error rate (unintentional switching probability before the read pulse) <10−4 (see Methods). The waveform is applied 200 times repeatedly and switching probability is evaluated.
a Circuit configuration to measure spin-transfer-torque (STT) switching probability of low thermal stability factor MTJs. b Schematics of voltage waveform applied to MTJs. c Transmitted voltage monitored at oscilloscope during read sequence with a duration of 85 ns. d Switching probability as a function of pulse voltage amplitude V with different write pulse duration tpulse. e Switching voltage VC as a function of tpulse−1. Lines are linear fits, whose intercept yields intrinsic critical voltages VC0,P(AP).
Figure 3d shows the write pulse voltage dependence of the switching probability with different write pulse durations tpulse. The switching voltage VC, defined as the voltage at 50% probability, is plotted as a function of the inverse of tpulse in Fig. 3e. In the precessional regime (typically tpulse ≲ several nanoseconds) where the switching/non-switching is determined by an amount of transferred angular momenta, VC is known to linearly depend on tpulse−1 and the intercept yields VC020,48. From a linear fitting, VC0,P and VC0,AP are obtained as 313 ± 45 mV and −247 ± 42 mV, respectively.
Random telegraph noise measurement to determine the switching exponents
With the results above, we are now ready to determine the switching exponents, nH and nI, from RTN measurement under various V and Hz. Figures 4a, b show the circuit configurations for the measurement with V ~ 0 and |V| ≥ 25 mV, respectively. For V ~ 0, we apply a small direct current I = 200 nA and monitor R by an oscilloscope connected in parallel to the MTJ and probe the temporal magnetisation configuration. For |V| ≥ 25 mV, we monitor the divided voltage at reference resistor Rr serially connected to the MTJ using an oscilloscope. Note that Rr (= 470 Ω) is set to be much smaller than R to prevent a change in the electric-field effect on the magnetic anisotropy between P and AP states. Figure 4c shows typical results of RTN with various Hz and the definition of the magnetisation switching event time t. Figure 4d shows the distribution of the number of unique t for μ0Hz = −30.5 mT. As expected, the exponential distribution is confirmed, i.e., the number of events ∝ τ−1exp(-t/τ), indicating that the fluctuation is characterised by a Poisson process. From the fitting, expectation values of the event time for P and AP states, i.e., the relaxation time τP and τAP, are obtained as a function of Hz as shown in Fig. 4e. Subsequently, ΔP(AP) can be determined from the relation τ = τ0expΔP(AP).
a, b Circuit configuration to measure random telegraph noise (RTN) with V ~ 0 and V ≥ 25 mV, respectively. c Typical RTN signal monitored at the oscilloscope. d Histogram of event time (duration between two sequential switching events) for P and AP states for μ0Hz = −30.5 mT. e Expected switching time as a function of perpendicular magnetic field Hz.
We measure τP(AP) and ΔP(AP) for various Hz and V. Figure 5a shows the obtained ΔP and ΔAP as a function of Hz for various V. ΔP(AP) increases (decreases) with increasing Hz for each V, as expected from the energy landscape modulation by Hz. Also, the mean Δ gradually decreases with increasing V, which is also consistent with the trend of HKeff shown in Fig. 2b. To derive nH and nI, we then take the natural logarithm of the ratio between ΔP and ΔAP, which can be expressed from Eq. (2) as
ln(ΔP/ΔAP) vs. Hz for each V is plotted in Fig. 5b. At a small perturbation limit, i.e., h, vP, vAP ≪ 1, Eq. (3) is reduced to ln(ΔP/ΔAP) = 2nHh + nI(vAP − vP); thus, the slope and intercept of the linear fit to the data shown in Fig. 5b give nH and nI, respectively. One can see that the results are well fitted by the linear function, validating the employed model.
We analyse Fig. 5 with Eq. (3) and obtain nH and nI as a function of V for device A as shown in Fig. 6a. One can see that both nH and nI show similar values at each V and gradually decreases to about 1.5 with decreasing V. We perform the same procedure for the device B, whose properties are determined as μ0HKeff(0) = 129.0 ± 0.7 mT, μ0dHKeff/dV = −61.7 ± 2.3 mT V−1, μ0d2HKeff/dV2 = −58 ± 13 mT V−2, VC0,P = 672 ± 4 mV and VC0,AP = −541 ± 2 mV. The obtained nH and nI are shown in Fig. 6b. At V = 0, the two devices show the same value for nH within experimental inaccuracy. Also, both nH and nI of device B show similar values with each other as in device A. However, in contrast to device A, they do not show meaningful variations at around 2 with V.
a, b Field- and current-induced switching exponents nH and nI as a function of bias voltage V for a device A and b device B. Error bars show standard error propagated from ferromagnetic resonance measurement and critical current measurement. The green band is a guide to the eye. c, d Bifurcation diagrams of the dθ/dt projected upon (θ,x)(= (θ,H) or (θ,I)) for c K2/K1eff < 0.25 and d K2/K1eff > 0.25, where K1eff, K2, θ, t, H, and I are the first- and second-order effective anisotropy fields, polar angle of magnetisation vector, the time, perpendicular magnetic field, and current. e, f Schematics of energy barrier of the effective magnetic potential corresponding to the yellow region in c and d, respectively.
Discussion
As shown above, we have found that nH and nI show virtually the same value with each other for both devices A and B. Also, they are almost constant at around 2.0 for device B whereas change from 2.0 to 1.5 with V for device A. The main difference between devices A and B is tCoFeB, which manifests in a difference in μ0HKeff(0) [77.0 ± 0.5 mT for device A and 129.0 ± 0.7 mT for device B]. In the following, we will discuss the mechanism that can account for the obtained results in the context of the energy landscape and its bifurcation.
In systems with uniaxial anisotropy where the magnetic field is applied along the easy axis where the macrospin approximation holds, Brown derived nH = 2 in a high barrier region, E0 ≳ kBT, using Kramers’ analysis on the Fokker–Planck equation that is equivalent to the Landau–Lifshitz–Gilbert (LLG) equation with the Langevin term3. Taking into consideration the second-order anisotropy, where the magnetic anisotropy energy density is given by \({{{{{\mathcal{E}}}}}}\) = K1effsin2θ + K2sin4θ, nH was pointed out to vary with K2/K1eff 7, where K1eff, K2 and θ are the first- and second-order effective anisotropy fields and polar angle of magnetisation vector, respectively. In the CoFeB/MgO system, positive voltage, which decreases electron density at the interface, was found to increase K1eff, while keeping μ0HK2 (≡μ0K2/4MS) constant at around 45 mT46,49,50. Accordingly, as shown in the upper axes of Fig. 6a, b, in the present cases, K2/K1eff is calculated to be around 0.22 for device B whereas it increases up to 0.45 for device A. The numerical calculation, assuming material parameters of magnetic recording media (Δ0 ≳ 60), shows that nH decreases from 2.0 to 1.5 in the range of K2/K1eff from 0 to 0.257. In general, a dynamical system with pitchfork bifurcation leads to the switching exponent of nx = 2, while saddle-node bifurcation results in nx = 3/2. Note that the aforementioned magnetic energy density \({{{{{\mathcal{E}}}}}}\) gives the LLG equation dθ/dt = f(θ,Hz) = −αγμ0[(2K1eff/MS)cosθ − (4K2/MS)cos3θ − Hz]sinθ. We show f(θ,Hz) takes two types of local bifurcations: pitchfork bifurcation appears at K2/K1eff < 0.25, while saddle-node bifurcation at K2/K1eff > 0.25 as shown in Fig. 6c, d, respectively [see Supplementary Information in detail]. Thus, the experimentally observed transition of the switching exponents is attributed to the transition of the bifurcation of the potential landscape through the modulation of K2/K1eff. However, the experiment shows the transition of nH at K2/K1eff ≈ 0.45, which is larger than that expected by the macrospin model (K2/K1eff = 0.25). This deviation implies that the local bifurcation of the magnetic potential and the resultant nH in the real MTJ device is more insensitive to higher-order anisotropy field K2 than the macrospin limit, for example, due to the micromagnetic effects.
Regarding nI, some theoretical studies derived 1 by considering a fictitious temperature in LLG equation with the Langevin term20,21, whereas others derived 2 from an analysis of the Fokker–Planck equation22,23,24. Matsumoto et al. pointed out that nI rapidly decreases from 2 to 1.4 with increasing K2/K1eff from 0 to ~0.2551. Experimentally, some assumed 125,27,28,29,30,36,39 whereas others assumed 226,31,32,33, and importantly no studies access the number. The present experimental results support the scenario of Matsumoto et al., but, similarly to nH, the reduction of nI is more moderate than the theoretical prediction. This fact indicates that the mechanism for nH could be also applicable for the case with STT perturbation as well. Another important implication of our results is that, despite the non-conservative nature of STT, the pseudo energy landscape under STT can be investigated through the switching exponents. LLG equation with STT τSTT can be represented as dθ/dt = f(θ,x) = {−αγμ0[(2K1eff/MS)cosθ − (4K2/MS)cos3θ] + τSTT}sinθ. Since nH and nI show virtually the same value for all K2/K1eff conditions, meaning that f(θ,τSTT) takes the same local bifurcation type as that for f(θ,H), our experiment reveals that in MTJ devices with perpendicular easy axis, the magnetic field and the STT effectively similarly modulate the energy landscape.
In summary, this work has experimentally revealed the hitherto-inaccessible representation of thermally-activated switching rate under field and STT, using a relevant material system for applications. The obtained results could allow for sophisticated engineering of non-volatile memory and unconventional computing hardware. Through the switching exponents, we have also accessed the local bifurcation of energy landscape under STT, and have found that, despite the qualitative difference between magnetic field and STT, their effect on the energy landscape is equivalent in the case of perpendicular MTJ. This work has also demonstrated that superparamagnetic tunnel junctions and analysis of their local bifurcation can serve as a versatile tool to investigate unexplored physics relating to thermally-activated phenomena in general with various configurations and external perturbations.
Methods
Sample preparation
Stacks with Ta(5)/Pt(5)/[Co(0.3)/Pt(0.4)]7/Co(0.3)/Ru(0.45)/[Co(0.3)/Pt(0.4)]2/Co(0.3)/Ta(0.3)/CoFeB(1.0)/MgO(1.0)/CoFeB(tCoFeB)/Ta(5)/Ru(5) (numbers in parenthesis are thickness in nm) were deposited by dc/rf magnetron sputtering on a sapphire substrate. The nominal CoFeB thicknesses tCoFeB = 1.88 nm (device A) and 1.82 nm (device B). After the deposition, the stacks were processed into MTJs by a hard-mask process with electron-beam lithography, followed by annealing at 300 °C under a perpendicular magnetic field of 0.4 T for 1 h. The resistance (R)-area (A) product (RA) was determined from the physical size determined from scanning electron microscopy observation and measured resistance for large devices with diameter D > 45 nm. The resistance-area product of device A (device B) is 5.5 Ωμm2 (8.1 Ωμm2), and the tunnel magnetoresistance ratio is 73% (74%). The nominal thickness of the MgO is 1.0 nm for both devices, and the difference of the RA corresponds to the ~7% variation of the actual thickness due to the process variations between the two runs. D of devices A and B are determined from their resistance and RA to be D = 34 and 28 nm, respectively.
Homodyne-detected ferromagnetic resonance (FMR)
With the circuit shown in Fig. 2a, homodyne-detected voltage-Hz spectra were measured at various frequencies. As shown in previous papers, the spectra were well fitted by the Lorentz function and peak position was determined by the fitting45,46. From resonance frequency fr vs. Hz, the effective anisotropy field HKeff was determined while assuming a constant second-order anisotropy field μ0HK2 = 45 mT46,49,50 (μ0 is the permeability of vacuum). The measurement was performed at various dc biases at AP configuration and obtained HKeff vs. V, as shown in Fig. 2b. A quadratic equation was fitted to the obtained dependence and the coefficients for constant, linear and quadratic terms were determined. Note that, in the error of HKeff, we have included the effect of HKeff difference in P and AP configurations due to the different device resistances and resultant Joule heatings in these configurations under the identical bias voltage.
Switching probability measurement
With the circuit shown in Fig. 3a, the switching probability was measured as functions of write pulse voltage amplitude and duration to determine intrinsic critical voltage VC0. A voltage waveform composed of initialisation (0.45 V/300 ns), write (amplitude Vwrite/duration tpulse), and read (Vread = 0.15 V/75 ns) pulses as shown in Fig. 3b, was generated by an arbitrary waveform generator (AWG). Both the interval of initialisation/write and write/read pulses were 30 ns, which is much shorter than the shortest relaxation time measured here (~0.3 ms), ensuring a sufficiently low read-error rate due to unintentional switching probability before the read pulse, exp(−30 ns/0.3 ms) \(\le\) 10−4. Single-shot-transmitted voltage for write pulse was monitored to determine the magnetisation configuration; the transmitted voltage is ~2Z0Vread/(R + Z0), where Z0 is characteristic impedance 50 Ω, and due to the tunnel magnetoresistance, the transmitted voltage changes with magnetisation configuration. The typical transmitted signal for P and AP states is shown in Fig. 3c. Transmitted signals for 5 ns (between 15 and 20 ns in Fig. 3c) were averaged. Its averaged value 〈V〉 and standard error 〈(V-〈V〉)2〉0.5/N 0.5 for P and AP states were 2.44 ± 0.03 mV and 1.40 ± 0.03 mV, respectively (N is averaged points; 20 Gbit/s × 5 ns duration = 100 points), ensuring low read-error rate due to misassignment of the magnetisation configuration47. As shown in Fig. 3d, switching probability as a function of the voltage amplitude V at MTJ with write pulse duration tpulse from 1 to 5 ns was measured. The probability of the switching was determined from 200 times measurement. The switching measurement was conducted under Hz of the stray field HS which was determined from the random telegraph noise measurement. Note that the anomaly of the switching probability at V ~ −900 mV can be attributed to a change of the magnetic easy axis through the electric-field effect on the magnetic anisotropy, which is reported in previous works52. In addition, the slope of the switching probability at Psw ~ 0.5 for P to AP switching increases with decreasing the pulse duration, which is opposite to the thermally-stable MTJs. The decreases of the effective field and the thermal stability factor through the electric-field effect on magnetic anisotropy reasonably explain the behaviour.
Random telegraph noise (RTN)
With the circuit shown in Fig. 4a, the RTN signal of the MTJs for V ~ 0 was measured. Small direct current I = 200 nA was applied and R was monitored by an oscilloscope connected in parallel to the MTJ to probe the temporal magnetisation configuration. The voltage applied to MTJ here was up to 2.5 mV (5 mV) for device A (device B), which is small enough to prevent major voltage/current-induced effects in MTJs focused here. If one utilises the same circuit, the applied voltage for P and AP states varies by a factor of about 1.7 due to the tunnel magnetoresistance effect. Therefore, to prevent variation of effective anisotropy field for P and AP states, the circuit shown in Fig. 4b was utilised for |V| ≥ 25 mV. Direct voltage V to the MTJ was applied and divided voltage at reference resistor Rr connected in serial to the MTJ was monitored using the oscilloscope. For measuring RTN on device A (device B), with setting Rr = 0.47 kΩ (1 kΩ) much smaller than R, variation of applied voltages between P and AP states was prevented.
Attempt frequency
In determining Δ with the random telegraph noise measurement, Néel–Arrhenius raw τP(AP) = τ0expΔP(AP) with attempt frequency τ0 of 1 ns was assumed. This assumption is widely adopted because τ is an exponential function of Δ and the value of τ0 does not affect the estimated Δ, and τ0 ranges between 0.1 and 10 ns. According to Brown’s calculation with Kramer’s method on the Fokker–Planck equation3, the attempt frequency τ0 of the magnetic materials with uniaxial perpendicular magnetic anisotropy is [2αγμ0HKeff(1 − h2)(1 + h)]−1(π/Δ0)0.5 under large barrier approximation Δ0\(\gg\)1, where α, γ, and μ0 are damping constant 0.006, gyromagnetic ratio, and permeability of vacuum, respectively. In our devices, the Brown’s attempt frequency above is derived to be 1.1 and 2.4 ns for device A and device B, respectively. Thus, the switching time τ vs. thermal stability factor Δ of device A should be well described by the Néel–Arrhenius law with τ0 = 1 ns.
Data availability
The data that support the plots within this paper have been deposited in Zenodo at https://zenodo.org/record/676782853.
References
Strogatz, S. H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering (Studies in Nonlinearity) (CRC Press, 2001).
Néel, L. Theorie du trainage magnetique des ferromagnetiques en grains fins avec application aux terres cuites. Ann. Geophys. 5, 99–136 (1949).
Brown, W. F. Thermal fluctuations of a single-domain particle. Phys. Rev. 130, 1677–1686 (1963).
Stoner, E. C. & Wohlfarth, E. P. A mechanism of magnetic hysteresis in heterogeneous alloys. Philos. Trans. R. Soc. A 240, 599–642 (1948).
Victora, R. H. Predicted time dependence of the switching field for magnetic materials. Phys. Rev. Lett. 63, 457–460 (1989).
Tannous, C. & Gieraltowski, J. The Stoner-Wohlfarth model of ferromagnetism. Eur. J. Phys. 29, 475–487 (2008).
Kitakami, O., Shimatsu, T., Okamoto, S., Shimada, Y. & Aoi, H. Sharrock relation for perpendicular recording media with higher-order magnetic anisotropy terms. Jpn. J. Appl. Phys. 43, L115–L117 (2004).
Slonczewski, J. C. Current-driven excitation of magnetic multilayers. J. Magn. Magn. Mater. 159, L1–L7 (1996).
Berger, L. Emission of spin waves by a magnetic multilayer traversed by a current. Phys. Rev. B 54, 9353–9358 (1996).
Tsoi, M. et al. Excitation of a magnetic multilayer by an electric current. Phys. Rev. Lett. 80, 4281–4284 (1998).
Myers, E. B., Ralph, D. C., Katine, J. A., Louie, R. N. & Buhrman, R. A. Current-induced switching of domains in magnetic multilayer devices. Science 285, 867–870 (1999).
Katine, J. A., Albert, F. J., Buhrman, R. A., Myers, E. B. & Ralph, D. C. Current-driven magnetization reversal and spin-wave excitations in Co/Cu/Co pillars. Phys. Rev. Lett. 84, 3149–3152 (2000).
Brataas, A., Kent, A. D. & Ohno, H. Current-induced torques in magnetic materials. Nat. Mater. 11, 372–381 (2012).
Kent, A. D. & Worledge, D. C. A new spin on magnetic memories. Nat. Nanotechnol. 10, 187–191 (2015).
Apalkov, D., Dieny, B. & Slaughter, J. M. Magnetoresistive random access memory. Proc. IEEE 104, 1796–1830 (2016).
Jinnai, B., Watanabe, K., Fukami, S. & Ohno, H. Scaling magnetic tunnel junction down to single-digit nanometers-Challenges and prospects. Appl. Phys. Lett. 116, 160501 (2020).
Mizrahi, A. et al. Neural-like computing with populations of superparamagnetic basis functions. Nat. Commun. 9, 1533 (2018).
Borders, W. A. et al. Integer factorization using stochastic magnetic tunnel junctions. Nature 573, 390–393 (2019).
Lv, Y., Bloom, R. P. & Wang, J. Experimental demonstration of probabilistic spin logic by magnetic tunnel junctions. IEEE Magn. Lett. 10, 4510905 (2019).
Koch, R. H., Katine, J. A. & Sun, J. Z. Time-resolved reversal of spin-transfer switching in a nanomagnet. Phys. Rev. Lett. 92, 088302 (2004).
Li, Z. & Zhang, S. Thermally assisted magnetization reversal in the presence of a spin-transfer torque. Phys. Rev. B 69, 134416 (2004).
Taniguchi, T. & Imamura, H. Thermally assisted spin transfer torque switching in synthetic free layers. Phys. Rev. B 83, 054432 (2011).
Butler, W. H. et al. Switching distributions for perpendicular spin-torque devices within the macrospin approximation. IEEE Trans. Magn. 48, 4684–4700 (2012).
Pinna, D., Mitra, A., Stein, D. L. & Kent, A. D. Thermally assisted spin-transfer torque magnetization reversal in uniaxial nanomagnets. Appl. Phys. Lett. 101, 262401 (2012).
Fuchs, G. D. et al. Adjustable spin torque in magnetic tunnel junctions with two fixed layers. Appl. Phys. Lett. 86, 152509 (2005).
Sato, H. et al. Perpendicular-anisotropy CoFeB-MgO magnetic tunnel junctions with a MgO/CoFeB/Ta/CoFeB/MgO recording structure. Appl. Phys. Lett. 101, 022414 (2012).
Thomas, L. et al. Perpendicular spin transfer torque magnetic random access memories with high spin torque efficiency and thermal stability for embedded applications (invited). J. Appl. Phys. 115, 172615 (2014).
Zhao, H. et al. Low writing energy and sub nanosecond spin torque transfer switching of in-plane magnetic tunnel junction for spin torque transfer random access memory. J. Appl. Phys. 109, 07c720 (2011).
Heindl, R., Rippard, W. H., Russek, S. E., Pufall, M. R. & Kos, A. B. Validity of the thermal activation model for spin-transfer torque switching in magnetic tunnel junctions. J. Appl. Phys. 109, 073910 (2011).
Sukegawa, H. et al. Spin-transfer switching in full-Heusler Co2FeAl-based magnetic tunnel junctions. Appl. Phys. Lett. 100, 182403 (2012).
Nakayama, M. et al. Spin transfer switching in TbCoFe/CoFeB/MgO/CoFeB/TbCoFe magnetic tunnel junctions with perpendicular magnetic anisotropy. J. Appl. Phys. 103, 07A710 (2008).
Van Beek, S. et al. Thermal stability analysis and modelling of advanced perpendicular magnetic tunnel junctions. AIP Adv. 8, 055909 (2018).
Lourembam, J., Chen, B. J., Huang, A. H., Allauddin, S. & Ter Lim, S. A non-collinear double MgO based perpendicular magnetic tunnel junction. Appl. Phys. Lett. 113, 022403 (2018).
Urazhdin, S., Birge, N. O., Pratt, W. P. Jr. & Bass, J. Current-driven magnetic excitations in permalloy-based multilayer nanopillars. Phys. Rev. Lett. 91, 146803 (2003).
Wegrowe, J. E. Magnetization reversal and two-level fluctuations by spin injection in a ferromagnetic metallic layer. Phys. Rev. B 68, 214414 (2003).
Rippard, W., Heindl, R., Pufall, M., Russek, S. & Kos, A. Thermal relaxation rates of magnetic nanoparticles in the presence of magnetic fields and spin-transfer effects. Phys. Rev. B 84, 064439 (2011).
Chiba, D., Ono, T., Matsukura, F. & Ohno, H. Electric field control of thermal stability and magnetization switching in (Ga,Mn) As. Appl. Phys. Lett. 103, 142418 (2013).
Enobio, E. C. I., Bersweiler, M., Sato, H., Fukami, S. & Ohno, H. Evaluation of energy barrier of CoFeB/MgO magnetic tunnel junctions with perpendicular easy axis using retention time measurement. Jpn. J. Appl. Phys. 57, 04FN08 (2018).
Zink, B. R., Lv, Y. & Wang, J. P. Independent control of antiparallel- and parallel-state thermal stability factors in magnetic tunnel junctions for telegraphic signals with two degrees of tunability. IEEE Trans. Electron Devices 66, 5353–5359 (2019).
Sun, J. Z. et al. Spin-torque switching efficiency in CoFeB-MgO based tunnel junctions. Phys. Rev. B 88, 104426 (2013).
Chiba, D. et al. Magnetization vector manipulation by electric fields. Nature 455, 515–518 (2008).
Maruyama, T. et al. Large voltage-induced magnetic anisotropy change in a few atomic layers of iron. Nat. Nanotechnol. 4, 158–161 (2009).
Endo, M., Kanai, S., Ikeda, S., Matsukura, F. & Ohno, H. Electric-field effects on thickness dependent magnetic anisotropy of sputtered MgO/Co40Fe40B20/Ta structures. Appl. Phys. Lett. 96, 212503 (2010).
Kanai, S., Matsukura, F. & Ohno, H. Electric-field-induced magnetization switching in CoFeB/MgO magnetic tunnel junctions. Jpn. J. Appl. Phys. 56, 0802A0803 (2017).
Tulapurkar, A. A. et al. Spin-torque diode effect in magnetic tunnel junctions. Nature 438, 339–342 (2005).
Kanai, S., Gajek, M., Worledge, D. C., Matsukura, F. & Ohno, H. Electric field-induced ferromagnetic resonance in a CoFeB/MgO magnetic tunnel junction under dc bias voltages. Appl. Phys. Lett. 105, 242409 (2014).
Saino, T. et al. Write-error rate of nanoscale magnetic tunnel junctions in the precessional regime. Appl. Phys. Lett. 115, 142406 (2019).
Bedau, D. et al. Spin-transfer pulse switching: From the dynamic to the thermally activated regime. Appl. Phys. Lett. 97, 262502 (2010).
Okada, A. et al. Electric-field effects on magnetic anisotropy and damping constant in Ta/CoFeB/MgO investigated by ferromagnetic resonance. Appl. Phys. Lett. 105, 052415 (2014).
Okada, A., Kanai, S., Fukami, S., Sato, H. & Ohno, H. Electric-field effect on the easy cone angle of the easy-cone state in CoFeB/MgO investigated by ferromagnetic resonance. Appl. Phys. Lett. 112, 172402 (2018).
Matsumoto, R., Arai, H., Yuasa, S. & Imamura, H. Efficiency of spin-transfer-torque switching and thermal-stability factor in a spin-valve nanopillar with first- and second-order uniaxial magnetic anisotropies. Phys. Rev. Appl. 7, 044005 (2017).
Ohshima, N. et al. Current-induced magnetization switching in a nano-scale CoFeB-MgO magnetic tunnel junction under in-plane magnetic field. AIP Adv. 7, 055927 (2017).
Funatsu, T. et al. Dataset: “local bifurcation with spin-transfer torque in superparamagnetic tunnel junctions.” Zenodo. https://zenodo.org/record/6767828 (2022).
Acknowledgements
The authors thank O. Kitakami, M. Stiles, W. A. Borders and Y. Utsumi for fruitful discussion and B. Jinnai, H. Sato, K. Watanabe, J. Igarashi, M. Shinozaki, T. Saino, Z. Wang, T. Hirata, H. Iwanuma, I. Morita, R. Ono, S. Musya and C. Igarashi for technical supports. This work was partly supported by the ImPACT Programme of CSTI (S.F. and H.O.), JST-OPERA JPMJOP1611 (S.F. and H.O.), JST-CREST JPMJCR19K3 (S.F.), JST-PRESTO JPMJPR21B2 (S.K.), JSPS Core-to-Core Programme (S.K., S.F. and H.O.), JSPS Kakenhi 19H05622 (S.K., J.I. and S.F.), Shimadzu Research Foundation (S.K.), and RIEC Cooperative Research Projects (S.K., S.F. and H.O.).
Author information
Authors and Affiliations
Contributions
S.F. and H.O. planned the study. S.K. and T.F. designed the experiment and analysis. T.F. prepared samples, performed measurements and analysed the data under the support of S.K. S.K. formulated the bifurcation of the dynamics of nanomagnet. S.K. and S.F. wrote the manuscript with input from H.O. and J.I. All authors discussed the results.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Jian-Ping Wang and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Funatsu, T., Kanai, S., Ieda, J. et al. Local bifurcation with spin-transfer torque in superparamagnetic tunnel junctions. Nat Commun 13, 4079 (2022). https://doi.org/10.1038/s41467-022-31788-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-31788-1
This article is cited by
-
CMOS plus stochastic nanomagnets enabling heterogeneous computers for probabilistic inference and learning
Nature Communications (2024)
-
Local bifurcation with spin-transfer torque in superparamagnetic tunnel junctions
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.